Molecular Dynamics Simulations Show That Conformational Selection Governs the Binding Preferences of Imatinib for Several Tyrosine Kinases

Abstract

Tyrosine kinases transmit cellular signals through a complex mechanism, involving their phosphorylation and switching between inactive and active conformations. The cancer drug imatinib binds tightly to several homologous kinases, including Abl, but weakly to others, including Src. Imatinib specifically targets the inactive, so-called “DFG-out” conformation of Abl, which differs from the preferred, “DFG-in” conformation of Src in the orientation of a conserved Asp-Phe-Gly (DFG) activation loop. However, recent x-ray structures showed that Src can also adopt the DFG-out conformation and uses it to bind imatinib. The Src/Abl-binding free energy difference can thus be decomposed into two contributions. Contribution i measures the different protein-imatinib interactions when either kinase is in its DFG-out conformation. Contribution ii depends on the ability of imatinib to select or induce this conformation, i.e. on the relative stabilities of the DFG-out and DFG-in conformations of each kinase. Neither contribution has been measured experimentally. We use molecular dynamics simulations to show that contribution i is very small, 0.2 ± 0.6 kcal/mol; imatinib interactions are very similar in the two kinases, including long range electrostatic interactions with the imatinib positive charge. Contribution ii, deduced using the experimental binding free energy difference, is much larger, 4.4 ± 0.9 kcal/mol. Thus, conformational selection, easy in Abl, difficult in Src, underpins imatinib specificity. Contribution ii has a simple interpretation; it closely approximates the stability difference between the DFG-out and DFG-in conformations of apo-Src. Additional calculations show that conformational selection also governs the relative binding of imatinib to the kinases c-Kit and Lck. These results should help clarify the current framework for engineering kinase signaling.

Introduction

Tyrosine kinases regulate essential aspects of cell growth and differentiation (1–5). They modify other proteins by transferring a phosphate from ATP to a tyrosine side chain; this results in a functional change of the target protein and a cellular signal. Their activity must be tightly controlled, so they assume an inactive conformation and only become active when switched on by phosphorylation (or dephosphorylation) or binding of other proteins or small molecules (6). Unregulated kinase activity can lead to excessive cell division and is a cause of many forms of cancer, such as chronic myeloid leukemia, where the kinase Abl is improperly activated (7, 8). Developing kinase inhibitors is thus an important therapeutic goal. Obtaining inhibitors that are specific for a particular kinase or group of kinases is difficult, because of the sequence similarity of kinase active sites (9–13). There are 518 known kinases in the human genome (3), and the average sequence identity between any two is about 30% for the catalytic domain (12). Within the subgroup involving Abl and Src, the 32 human nonreceptor tyrosine kinases, the mutual sequence identities are typically higher, around 40–50%. Expression levels can also influence ligand binding specificity; they depend on many factors but do not appear to vary dramatically when different kinases are compared; for example, Abl and Src expression levels are within about a factor of 20 in several cell types (14).

To achieve inhibitor specificity, one strategy has been to target the kinase inactive conformation, because structural differences between kinases tend to be larger in the inactive state (15, 16). Thus, the inhibitor PP1 binds to the inactive conformation of Hck (17), and the cancer drug imatinib binds to the inactive conformations of Abl, c-Kit, and platelet-derived growth factor receptor (15, 18–20). These inhibitors block the kinases by stabilizing the inactive state. In several cases, including Abl and c-Kit (18, 21), the inactive conformation is observed in the absence of the inhibitor, in an apoprotein crystal structure. Thus, the inhibitor “selects” a conformation that is already populated in its absence. In other cases, such as Src, the DFG-out conformation that is competent for imatinib binding has not been seen in an apocrystal structure and is shown below to have a rather high free energy. Thus, it may be more intuitive to describe the imatinib-Src binding mechanism as an induced fit (22). Both conformational selection and induced fit are of broad interest for drug design and molecular recognition (22–27), as well as allosteric signaling (28, 29), energy transduction (25), and enzyme catalysis (30–32).

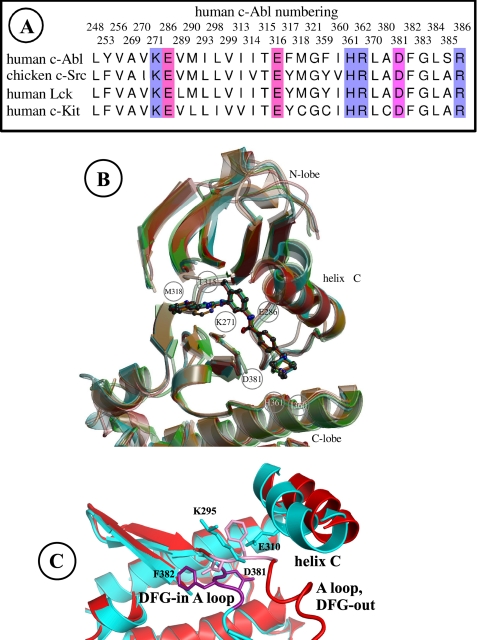
Imatinib binding to the Src kinase is about 2400 times weaker than imatinib-Abl binding (33). This was initially puzzling, because Src and Abl share a high sequence identity, 47% identity for the catalytic domains of human c-Src and c-Abl. In fact, the Abl crystal structure (18) revealed that the inactive conformation of Abl is structurally distinct from the one seen in both Src and Hck (6, 18, 34). A defining feature of all the inactive conformations of these kinases concerns the so-called activation loop, or A-loop, which includes a conserved DFG motif (Asp³⁸¹–Phe³⁸²–Gly³⁸³ in human c-Abl; see Fig. 1). In Abl, this motif adopts a “DFG-out” orientation. In the active state, the DFG motif is in a different “DFG-in” orientation, with its backbone flipped by 180° with respect to DFG-out; the Phe³⁸² side chain then occupies a position that overlaps with the imatinib-binding site (18). In the inactive Src crystal structure (6), the DFG backbone shares the same DFG-in orientation as active Abl and Src, with its Phe side chain overlapping the imatinib site. Thus, the poor Src-imatinib binding has a simple structural explanation.

FIGURE 1.

A, Abl, Src, Lck, and c-Kit sequences; residues less than 5 Å from imatinib and part of the A-loop are included. B, three-dimensional structures, DFG-out inactive conformation; Abl is red; Src is cyan; Lck is green; and c-Kit is orange; residue selection as in A. C, Src three-dimensional structure, comparing the DFG-in (blue and violet) and DFG-out (red and pink) conformations. The A loop, selected backbone portions, and side chains are shown. The viewpoint is perpendicular to B (B viewed from above).

Recently, however, an additional complexity was brought to light for inhibitor binding. Nuclear magnetic resonance experiments on a related kinase, p38, showed that the DFG-in and DFG-out conformations were actually in dynamic equilibrium over fairly short time scales (milliseconds) (35). An x-ray structure revealed that the two inactive conformations could coexist in the same crystal (35). It was then found that both Src and Abl can also interconvert between two inactive conformations: an Abl-like, DFG-out inactive conformation and a Src-like, DFG-in inactive conformation. Indeed, a recent x-ray structure of Abl (36) has a DFG-in inactive conformation, whereas a recent structure of Src (33) has a DFG-out inactive conformation. What is more, the Src structure includes an imatinib ligand, bound in the same manner as in DFG-out Abl. This raises a new question regarding the specificity of imatinib. Is the preference for Abl solely due to the intrinsic preference Abl for the DFG-out, Abl-like inactive conformation or is it partly also due to superior protein-ligand interactions?

Seeliger et al. (33) addressed this question with site-directed mutagenesis experiments. To increase the affinity of Src for imatinib, they swapped residues with the corresponding residues in Abl. They were able to slightly increase drug sensitivity by introducing mutations that are expected to destabilize the DFG-in inactive conformation. Earlier resistance screens had identified Abl mutants with decreased imatinib sensitivity, which may act by destabilizing the DFG-out state, because they involve amino acids that have different positions in the DFG-out and DFG-in states (37, 38). In contrast, Seeliger et al. (33) could not increase Src-imatinib binding by mutating residues that are in direct contact with imatinib. However, imatinib carries a net positive charge when bound to Abl and probably Src (39), so there could be long range stabilizing interactions with more distant Abl residues that are absent in Src but have not yet been identified. For a quantitative answer on the sources of imatinib selectivity, we should decompose the imatinib-kinase binding free energy into the following two components: (i) free energy to bind imatinib to the DFG-out, Abl-like inactive conformation and (ii) the remainder of the binding free energy. This decomposition can be performed in a three-step thought experiment as follows: (a) Abl is first restrained to the DFG-out conformation; (b) imatinib binds; and (c) the restraints are released. The second step, step b, corresponds to free energy contribution i; the other two steps, steps a and c, make up contribution ii. For a kinase like Src, as detailed below, contribution ii can be thought of as the free energy difference between the DFG-in and DFG-out conformations in the absence of imatinib. Indeed, step a essentially pushes Src into a high free energy state (because apo-Src prefers to be DFG-in), whereas the free energy for step c is very small (releasing the restraints has no effect, because holo-Src prefers to be DFG-out). In the general case, the interpretation of contribution ii can be more complicated (see below), but it is always closely related to the relative stability of the DFG-out and DFG-in inactive conformations. We would like to determine the exact contributions i and ii to the total standard imatinib binding free energy difference between Src and Abl, ΔΔG_bind = 4.6 kcal/mol (favoring Abl binding). So far, it has not been possible to directly measure either contribution for any kinase.

We estimate contribution i to ΔΔG_bind using computer simulations. Because the overall ΔΔG_bind is known from experiments, we can then deduce the second “conformational” contribution ii. Specifically, we compare imatinib binding to c-Abl, c-Src, c-Kit, and a fourth kinase, Lck, all in their Abl-like, DFG-out inactive conformations. The DFG-out conformation is the preferred inactive conformation of c-Kit (21), and imatinib is used to inhibit c-Kit in the treatment of gastrointestinal cancer (11, 40). Lck is more similar to Src and prefers the DFG-in inactive conformation. Although imatinib binds to Lck (12, 41), the conformation to which it binds is unknown (42). For Src and Abl, we use a rigorous method, which reversibly deletes imatinib from the binding pocket during a molecular dynamics (MD)² simulation (43, 44). This method was applied recently to the binding of benzamidine and diazamidine to trypsin (45), and of various nonpolar aromatic ligands to lysozyme (46), giving close agreement with experimental binding constants. Agreement was obtained not only for relative binding constants (comparing several ligands) but also for the absolute binding constants of the individual ligands. Other systems that gave close agreement for relative binding constants include peptides binding to the Src domain 2 (47) and nucleotide triphosphates binding to the CK2 kinase (48). Several recent reviews document the reliability of this approach for protein-ligand binding (49–51). To study the present system, we previously developed an accurate molecular mechanics description (a “force field”) for imatinib; we also performed extensive MD simulations to determine its predominant protonation state (positively charged) (39). Here, using long MD simulations of Src and Abl (totaling 0.5 μs of molecular dynamics), we obtain excellent precision for contribution i.

For the other kinases, Lck and c-Kit, we use a more approximate and much less expensive technique, which employs a continuum electrostatic model to estimate the binding free energy differences. Below, we refer to the first rigorous technique as the “MD free energy method.” The second method involves solving the Poisson-Boltzmann equation numerically, and so we refer to it as the “PB free energy method.” A group of similar continuum electrostatic methods are commonly referred to in the literature with the acronym “MM/PBSA” (for Molecular Mechanics/Poisson-Boltzmann-Surface Area) (49–56). Comparisons between the PB method, the more rigorous MD method, and experiment have been performed for several systems, as reviewed recently (49–53). Comparisons for imatinib binding to Abl have been performed and are reported in the supplemental material. Overall, the PB method is expected to be a reasonable proxy for the more rigorous and expensive MD method.

Using these methods, we show that for the Src/Abl pair, but also for Src/Kit, Lck/Abl, and Lck/Kit, the binding free energy difference is dominated by the conformational term ii. Contribution i is smaller. Thus, conformational selection is the main factor governing the relative affinities of imatinib, in agreement with the earlier hypothesis (33, 37) data. What is more, by combining the MD data with experimental data and thermodynamic relations, we show that the imatinib ligand actually reports on the conformational free energy surface of apo-Src. Indeed, the Src/Abl binding free energy difference ΔΔG_bind closely approximates the free energy difference between the DFG-out and DFG-in inactive conformations of Src in the absence of imatinib (a quantity that is very hard to measure or compute directly (57–59)). This makes it difficult to engineer increased binding by chemically modifying the imatinib ligand, although it is not impossible as shown very recently (60).

Before concluding this section, we must consider the relation between conformational selection and induced fit (22, 29, 61) and explain a choice of vocabulary. According to equilibrium statistical mechanics, even the highest energy conformations of an apokinase have a non-zero population, so a ligand always “selects” a pre-existing conformation. Thus, there is no real theoretical distinction between conformational selection and induced fit. In practice, in the biochemical literature, the distinction is often made depending on the high or low free energy of the selected conformation; if the free energy is “high” in the apoprotein, one speaks of induced fit (22, 29, 61). In this study, we prefer to describe the imatinib-binding mechanism in all cases as a conformational selection and to simply distinguish cases where the relevant DFG-out conformation is “easy” to select (it has a “low” free energy in the apokinase) or “hard” to select (it has a high free energy in the apokinase). Thus, induced fit is viewed as a special case of conformational selection. This choice of vocabulary is made for convenience, because the mechanism of binding will always be evident from the context. It does not question in any way the importance of the induced fit concept (particularly for nonequilibrium processes (30–32)).

MATERIALS AND METHODS

MD Free Energy Method, Imatinib Deletion

Human Abl and chicken Src were taken from the Protein Data Bank (entries 2HYY and 2OIQ; DFG-out conformation with bound imatinib; resolution 2.4 and 2.1 Å) (33, 62). In the Src structure, residues 407–421 in the activation loop were disordered. They were modeled from Abl by superimposing the backbones of residues 406 and 422 and mutating 7 Abl residues into the Src amino acid types. The resulting loop conformation proved stable over several hundred ns of dynamics. We used crystal structures of human Lck and Kit with bound imatinib (Protein Data Bank entries 2PL0 and 1T46; resolution of 2.8 and 1.6 Å) (21, 42). In Lck, the imatinib pyridine ring E was positioned in an unusual orientation, sterically clashing with the Met³¹⁹ backbone. This was corrected by rotating the ring back to the orientation observed in all other imatinib complexes. Histidine protonation states were assigned by visual inspection. For imatinib, recent simulations showed that it is positively charged when bound to Abl and protonated on the methylated nitrogen of its piperazine ring (39). Because of the high sequence homology, we infer that it is protonated in all four kinases. The simulations included protein residues and water molecules within a 26-Å radius sphere centered on imatinib. The region beyond 26 Å was treated as a dielectric continuum with a dielectric constant of 80, corresponding to bulk water (63). Electrostatic interactions were computed without any cutoff (64). The CHARMM22 force field was used for the protein (65) and the TIP3P model for water (66). Imatinib was specifically parameterized earlier (39). Newtonian dynamics were used for atoms within 20 Å of the center of the sphere; Langevin dynamics were used for the others, with a 292 K bath. Calculations were done with the CHARMM and NAMD programs (67, 68).

To obtain ΔΔG_i, imatinib was reversibly deleted in both the Abl and Src binding pockets. At the same time, 14 water molecules were reversibly introduced. They were confined within the same space as imatinib through weak, flat-bottomed harmonic restraints, which penalized excursions of more than 2 Å away from the imatinib atoms. The mean restraint energy was 1.4 ± 0.1 kcal/mol for both kinases; its contribution to the free energy difference accurately cancels when the two kinases are compared. The imatinib interactions were scaled to zero (and the water interactions were increased from zero) over 10 MD simulations, lasting 12 ns each. The scaling factor λ had the values 0.01, 0.05, 0.1, 0.2, 0.4, 0.6, 0.8, 0.9, 0.95, and 0.99. The kinases remained in their DFG-out inactive conformations without the need for any restraints. For each kinase, one simulation was done in each direction, λ = 0 → 1 and the reverse. The derivative of the free energy with respect to the scaling factor was estimated as ∂G/∂λ = 〈∂U/∂λ〉_λ; U is the energy function, and the angle brackets represent an average over an MD simulation with the scaling value λ (43, 44, 49). Notice that even when λ = 0.99, imatinib remains confined within its binding pocket by the weak remaining van der Waals interactions with the protein. The effect of this confinement is essentially the same for the Abl and Src complexes. The deletion free energy is obtained by numerical integration of the derivative (49).

Poisson-Boltzmann Free Energy Method

The electrostatic contribution to the binding free energy was obtained by subtracting the electrostatic free energies of the ligand-protein complex and of the separate ligand and protein (69). The electrostatic potential was calculated by numerically solving the PB equation, using a cubic grid and a finite-difference algorithm (PBEQ module in CHARMM) (67, 70). The calculations were done at physiological ionic strength. The solvent dielectric constant was set to 80. For the solute dielectric constant, values of 4 and 6 were compared. PB calculations were performed for multiple structures, sampled every 4 ps along the last 500 ps of an MD simulation. The separate ligand and protein structures were obtained by excluding the unwanted partner from the energy evaluation. Structural reorganization in the unbound state is accounted for through the protein dielectric constant (69, 71). Indeed, the use of a protein dielectric greater than 1 (4 or 6) should reflect the ability of the protein to adjust its structure in response to a perturbation, such as the removal of the ligand.

A second term is included in the model, which attempts to capture contributions from van der Waals interactions and the hydrophobic effect. We compare two empirical treatments, which have both been used for a variety of protein-ligand systems. The first uses a surface area term (54–56, 72–75) shown in Equation 1,

where ΔS is the change in solvent-accessible surface area of the solutes upon binding, and γ is an atomic surface free energy. Previous applications to protein kinase A used a protein dielectric of 2 for the PB term, and γ values of 17–25 cal/mol/Å ² (54, 55), and gave a mean error for over 20 inhibitors of 1.5 kcal/mol. Application to another kinase used γ values of 5–10 cal/mol/Å ² (56). Applications to peptide-protein binding (73) used surface coefficients of up to 50 cal/mol/Ų.

The second treatment is a “Linear Interaction Energy” model (76, 77). The nonpolar contribution includes both a surface area term and a van der Waals energy as shown in Equation 2,

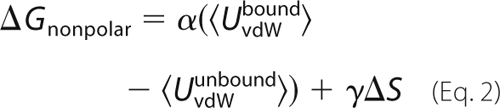Here, U_vdW^bound and U_vdW^unbound are the van der Waals interaction energies between the ligand and its surroundings in the bound and unbound states, respectively; the angle brackets represent averaging over an MD trajectory (done with explicit solvent). The van der Waals coefficient α is usually around 0.18, whereas γ is small, around 8 cal/mol/Å ² (76–78).

RESULTS

Imatinib Binding to Abl, Src, Kit, and Lck

We first consider Abl and Src and compute their imatinib-binding free energy difference when they are in their DFG-out, inactive conformations ΔΔG_i (“contribution i”). We use a rigorous MD free energy method with long simulations. Imatinib is reversibly “deleted” from the binding pocket of each kinase by gradually scaling its interactions to zero (43, 44). Meanwhile, 14 new water molecules are reversibly introduced within the same space. A “reverse” simulation is also performed, where imatinib is created and the waters deleted. Each kinase is modeled in its DFG-out inactive conformation (Fig. 1), which is maintained throughout the 120-ns simulations, without any special restraints. The individual deletion free energies cannot be interpreted as dissociation free energies (43, 44), because they omit several contributions as follows: solvation of the unbound imatinib, mixing entropy lost by the new waters, rotation/translation entropy gained by the uncoupled imatinib, and partial deprotonation of imatinib in solution (39). These contributions cancel either exactly (imatinib solvation, entropy, and deprotonation) or very closely (water mixing) between the two kinase systems. Therefore, the difference between the deletion free energies can be accurately interpreted as the binding free energy difference, ΔΔG_i. Results are summarized in Table 1. The deletion free energies are very large, 151.3 (Abl) and 151.1 kcal/mol (Src), but the four simulations, totaling 480 ns, are long enough to provide a very high precision, around ±0.5 kcal/mol in each case. Overall, we find ΔΔG_i = ΔG_i(Src) − ΔG_i(Abl) = 0.2 ± 0.6 kcal/mol. Thus, interactions of imatinib are very similar in Src and Abl (including the long range electrostatic interactions with its positive charge).

TABLE 1.

Imatinib binding to Abl, Src, Kit, and Lck in their inactive DFG-out conformations

Binding free energies shown in kilocalories/mol. Upper part, rigorous, MD free energy method; lower part, simpler, PB free energy method.

Method	Protein	Electrostatic terma	Nonelectrostatic termb	Total, ΔΔGi	ΔΔGexptc	Difference, ΔΔGiid
MD method	Abl	126.1/125.6e	25.8/25.1e	151.9/150.7f
	Src	119.6/119.5	31.7/31.3	151.3/150.8
	Src/Abl differenceg			0.2 ± 0.6	4.6 [33]	4.4
PB method	Src/Abl differenceg	0.1 [0.2]a	0.4/0.9h	0.5/1.0 (1.5) f	4.6 [33]	4.1/3.6
	Src/Kit difference	0.6 [0.3]a	0.7	1.3 (1.5) f	3.2 [81]	1.9
	Lck/Abl differenceg	−0.2 [−0.1]a	−2.4	− 2.6 (1.5) f	2.1 [33]	4.7
	Lck/Kit difference	0.3 [0.0]a	−2.3	− 2.0 (1.5) f	0.7 [33]	2.7

^a With MD, this is the Coulombic free energy component; with PB, it is the continuum dielectric term, which uses an ionic strength of 0.1 m monovalent salt and a protein dielectric of 4 (in square brackets, PB results with a protein dielectric of 6).

^b With MD, this is the van der Waals free energy component; with PB, it is the nonpolar term, which uses the surface area model with an atomic surface free energy of γ = 50 cal/mol/Ų.

^c Total experimental binding free energy difference is shown.

^d ΔΔG_ii = ΔΔG_bind −ΔΔG_i is the conformational contribution to the binding free energy difference.

^e Results from the forward/reverse simulation (deleting/creating imatinib) are shown.

^f Uncertainty was estimated from earlier PB error analyses (49, 54, 55).

^g A negative value disfavors Abl binding.

^h A second nonpolar model was compared, the “Linear Interaction Energy” model (second value; see under “Materials and Methods”).

To study Kit and Lck, we use a simpler PB free energy method (49, 50, 52–56). Comparisons to experiments are reported in the supplemental material. As another test, the PB method is first applied to Src and Abl and compared with the rigorous method shown above. The kinases are simulated by MD, surrounded by a bath of explicit water molecules. The resulting conformations are used as input for a continuum electrostatic free energy estimation. Results are in Table 1. The Src/Abl difference, ΔΔG_i = 0.8 ± 0.9 kcal/mol, is small and close to the rigorous MD result. The difference between DFG-out Src and Kit is ΔΔG_i = 1.3 kcal/mol. The positive sign indicates a preference for Kit, which is only slightly larger than the result for Src/Abl. Indeed, the sequences and structures of Abl, Src, and Kit are all very similar (Fig. 1). Lck (in its DFG-out conformation) is predicted to bind imatinib a bit more strongly, because of a greater burial of the ligand, with an extra 48 Ų of buried surface, compared with Abl.

As discussed above, the overall binding free energy differences include a second contribution, ΔΔG_ii, a restraint free energy that depends on the stability difference between the DFG-in and DFG-out inactive conformations. ΔΔG_ii is obtained by subtracting ΔΔG_i from the experimental binding free energy, ΔΔG_expt (Table 1). In all cases, Src/Abl, Src/Kit, Lck/Abl, and Lck/Kit, most of the affinity difference arises from ΔΔG_ii. Thus, conformational selection governs the ligand specificity. Below, we show that ΔΔG_ii has a simple relation to the conformational free energies.

Src/Abl-binding Free Energy Difference Measures the Conformational Free Energy Difference in Apo-Src

In this section, we begin by deriving a rather general relation between the binding and conformational free energies. This relation applies when two kinases are compared that prefer, respectively, the DFG-out and DFG-in inactive conformations (like Abl and Src). Next, we use this relation to analyze several kinase pairs, including Src/Abl.

Thermodynamic Analysis, Relation between the Binding and Conformational Free Energies

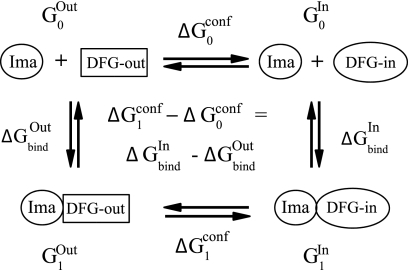
Here, we compare a DFG-out kinase, K, to a DFG-in kinase, K′, and we show that ΔΔG_ii has a simple interpretation, approximating closely the DFG-out/DFG-in conformational free energy difference in apo-K′. We make the following four assumptions: A1, holo-K prefers to be DFG-out; A2, apo-K prefers to be DFG-out; A3, holo-K′ prefers to be DFG-out; and A4 apo-K′ prefers to be DFG-in.

These assumptions are all experimentally verified if K = unphosphorylated, inactive Abl and K′ = inactive Src. We start from the thermodynamic cycle in Fig. 2, linking four states as follows: DFG-out holo-K (Gibbs free energy G₁^Out), DFG-in holo-K (Gibbs free energy G₁^In), and apo-K with either conformation (free energies G₀^Out and G₀^In). Notice that the apo-states include the unbound ligand, as indicated in Fig. 2. The partition functions for the apo- and holo-states are shown in Equations 3 and 4, respectively.

and

where β = 1/kT; k is Boltzmann constant; T is the temperature; p is the pressure, and V₀ and V₁ are the volumes in the bound and unbound states. At this stage, in the DFG-in conformations, we actually include the active conformations of the kinase. The binding free energy, ΔG_bind = −kT ln Z₁/Z₀ + p(V₁ − V₀), can be written as shown in Equation 5.

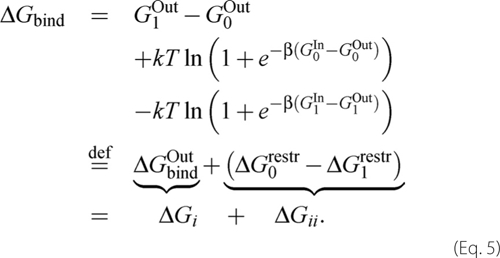The three terms in Equation 5 are as follows: the free energy to bind imatinib when K is restrained to be DFG-out (denoted ΔG_bind^Out), the free energy to impose the restraints initially (ΔG₀^restr), and to remove them after imatinib binds (−ΔG₁^restr). In the Introduction, we referred to the steps imposing and removing the restraints as steps a and c, respectively. The first term, ΔG_bind^Out, corresponds to ΔG_i; the other two terms, a + c, make up ΔG_ii. Notice that the ligand itself does not make any contribution to ΔG₀^restr, whereas it contributes to both ΔG_bind^Out and ΔG₁^restr. The K′/K binding free energy difference can be written as shown in Equations 6 and 7,

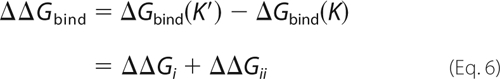with

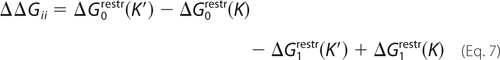FIGURE 2.

Thermodynamic cycle to study imatinib (Ima) binding to the DFG-out (Abl-like) and DFG-in (Src-like) conformations (labeled In and Out) of a given kinase. Horizontal arrows correspond to conformational changes; vertical arrows correspond to ligand binding. States and transitions are labeled with the corresponding free energies.

Using assumptions A1–A4, we will now derive a relation between ΔΔG_ii and ΔG₀^conf(K′). A1 implies that ΔG₁^conf ≥ 0, so that ΔG₁^restr is small, 0 ≤ ΔG₁^restr ≤ 0.4 kcal/mol. Indeed, as shown in Equation 8,

and ln and exp are increasing functions, so the stated inequalities are easily obtained. This result means that releasing the restraints after imatinib binds to K has little effect, because the DFG-in state is weakly populated in holo-K, even without restraints. Similarly, A2 implies ΔG₀^conf ≥ 0 kcal/mol, so that 0 ≤ ΔG₀^restr ≤ 0.4 kcal/mol. A3 implies that ΔG₁^conf(K′) ≥ 0, so that 0 ≤ ΔG₁^restr(K′) ≤0.4 kcal/mol. Finally, A4 implies ΔG₀^conf ≤ 0 kcal/mol; it follows that 0 ≤ ΔG₀^restr(K′) + ΔG₀^conf(K′) ≤ 0.6 kcal/mol. Indeed, it is easy to obtain Equation 9 as follows.

Combining the upper and lower bounds for each term, we obtain the following desired relation: −0.8 kcal/mol ≤ ΔΔG_ii + ΔG₀^conf(K′) ≤ 1.0 kcal/mol, which can be rewritten as Equation A,

Because A1–A4 are experimentally verified for K = Abl and K′ = Src, Equation A can be considered exact for this pair.

In fact, slightly stronger assumptions are very likely verified as well: B1, ΔG₁^conf ≥ 1 kcal/mol; B4, ΔG₀^conf(K′) ≤ −1 kcal/mol. Indeed, the DFG-in conformation appears to have a 100% occupancy in the apo-Src crystal structures, so that ΔG₀^In(Src) must be significantly lower than ΔG₀^Out(Src) (ensuring B4). Continuum electrostatic calculations show that for Abl, ΔG₁^conf ≫ 1 kcal/mol (ensuring B1; see supplemental material). With these stronger assumptions, along with B2 = A2 and B3 = A3, we obtain a more precise relation as shown in Equation B,

Until now, within the DFG-in conformations of K′, we included the active conformations. We will now focus on the inactive conformations; therefore, we divide the DFG-in conformations of K′ into an active and an inactive subset. In active Src, the A-loop shifts out from the catalytic site, whereas the C-helix has a more inward orientation, recruiting several side chains to the active site (6, 18, 57–59). For the homologous Hck kinase, the active and inactive subsets were shown to form two distinct free energy basins (59), with a free energy difference of about δg = 1 kcal/mol, favoring the inactive conformations (with the inactive phosphorylation pattern). We denote ΔG₀^CONF(K′) the free energy difference between the DFG-out conformation and the inactive DFG-in conformation. ΔG₀^CONF(K′) and ΔG₀^conf(K′) differ by a term ϵ = ΔG₀^CONF(K′) − ΔG₀^conf(K′) = kT ln(1 + e^−βδg). Because the active state is disfavored (59), we may safely assume A5, δg ≥ 0, and therefore 0 < ϵ ≤ 0.4 kcal/mol. If we make the stronger assumption B5, δg ≥ 1 kcal/mol (as in Hck), ϵ is just 0.02 kcal/mol. With assumptions A (respectively, B), we obtain Equations A′ and B′,

As above, Equation A′ can be considered experimentally proven for the Src/Abl pair, whereas Equation B′ is highly probable. We recall that ΔG₀^CONF(K′) is the DFG-in/DFG-out free energy difference in apo-K′, considering only the inactive DFG-in conformations.

To conclude this section, we say a few words about the enthalpic and entropic components of free energy contribution ii for Src and Abl. Indeed, ΔG_ii involves the application and removal of conformational restraints, and it is useful to examine how this affects the system entropy. We saw above that ΔG₁^restr is small for both Src and Abl (holo-Src and Abl prefer to be DFG-out, even without restraints); it is easy to show that its enthalpic and entropic components are also small. Therefore, we focus on ΔG₀^restr, which was defined as shown in Equation 10,

Using ΔS₀^restr = −∂ΔG₀^restr/∂T and ΔG₀^restr = ΔH₀^restr − TΔS₀^restr it is easy to obtain Equation 11,

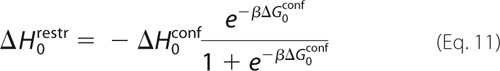For Src, ΔG₀^conf is large and negative (as shown precisely below), so that the fraction on the right of Equation 11 is close to 1, and we have ΔH₀^restr ≈ −ΔH₀^conf. We also have ΔG₀^restr ≈ −ΔG₀^conf from Equation 10, so that TΔS₀^restr ≈ −TΔS₀^conf. Thus, for Src, ΔG_ii is essentially the free energy −ΔG₀^conf to push the kinase from its DFG-in to its DFG-out conformation in the absence of imatinib. The enthalpic and entropic components of ΔG_ii are essentially those of −ΔG₀^conf(Src). Unfortunately, these cannot be deduced from our calculations, partly because the experimental binding enthalpies and entropies are not known. However, there is no reason to assume that ΔG₀^conf(Src) is dominated by one component or the other; most probably, it is a mixture of enthalpic and entropic contributions. For Abl, ΔG_ii and its enthalpic and entropic components are all small.

Application to Specific Pairs of Kinases

We now use the relations above to analyze several specific pairs of kinases. We begin by choosing K = Abl and K′ = Src. We have ΔΔG_bind = 4.6 ± 0.4 kcal/mol (33) and ΔΔG_i = 0.2 ± 0.6 kcal/mol (Table 1), so that ΔΔG_ii = 4.4 ± 0.7 kcal/mol. Equation B′ then gives ΔG₀^CONF(Src) = −4.7 ± 1.2 kcal/mol (favoring DFG-in). The allowed range includes experimental and simulation uncertainty and the finite precision of Equation B′.

The same analysis applies with K′ = Src and K = Kit, because apo- and holo-Kit prefer to be DFG-out. The experimental ΔΔG_bind is 3.2 ± 0.4 kcal/mol, whereas ΔΔG_i = +1.3 ± 1.5 kcal/mol (Table 1; the uncertainty in ΔΔG_i is taken from previous PB error analyses (49, 54, 55)). Thus, ΔΔG_ii ≈ 1.9 ± 1.5 kcal/mol, giving ΔG₀^CONF(Src) = −2.2 ± 2.1 kcal/mol. Agreement with our first estimate (−4.7 ± 1.2 kcal/mol) is only fair but is compatible with the uncertainty estimates. The rough agreement is probably due to the approximate nature of the PB free energy method and the underlying continuum electrostatic model (49, 50, 53). We expect that the first estimate, using the more rigorous, MD free energy method, is the most reliable.

We can also consider K = Abl and K′ = Lck, if we accept assumption A3, imatinib binds to DFG-out Lck. The experimental Lck/Abl binding free energy is 2.1 ± 0.4 kcal/mol (33), whereas ΔΔG_i = −2.4 ± 1.5 kcal/mol (Table 1). Thus, ΔΔG_ii = 4.5 ± 1.6 kcal/mol, giving a large ΔG₀^CONF(Lck) of −4.8 ± 2.1 kcal/mol. With K′ = Lck and K = c-Kit, we obtain ΔG₀^CONF(Lck) = −3.0 ± 2.1, in fair agreement.

It would also be interesting to consider K = inactive, unphosphorylated Abl and K′ = active, phosphorylated Abl. Indeed, this pair obeys the assumptions A1–A4, and ΔΔG_bind is known from experimental inhibition constants, ΔΔG_bind = 3.1 kcal/mol (17). To obtain ΔΔG_i, we should then compare imatinib binding to phosphorylated and unphosphorylated Abl, both restrained to be in the DFG-out conformation. This can be done with the PB method used above for Lck and Kit, and we leave it for future work. Nevertheless, a rough guess can be made here, without any simulations. Indeed, with the phosphorylated and unphosphorylated forms of Abl restrained to be in the same, DFG-out, inactive conformation, the difference ΔΔG_i will arise entirely from the phosphate group that is added to Tyr-393 in phosphorylated Abl. Because Tyr-393 is rather far from the imatinib-binding site (12 Å away), this contribution should be small. Thus, we might simply guess that ΔΔG_i ≈ 0 kcal/mol. We would then deduce ΔΔG_ii ≈ 3.1 kcal/mol and, finally, ΔG₀^conf ≈ −3.4 kcal/mol (from Equation A′). This represents a rough but educated guess for the DFG-in/DFG-out free energy difference for active, phosphorylated Abl; the negative sign means that active, phosphorylated Abl prefers to be DFG-in (as expected). A precise estimate of ΔG₀^conf for active Abl would require additional simulations and is left for future work.

Conclusions

Understanding and manipulating the detailed mechanism of tyrosine kinase signaling is of considerable biological and technological interest; developing inhibitors is one important aspect. With over 500 kinases in the human genome (3), specificity is hard to achieve (11), and new molecules are needed as resistance mutants appear (8, 79). Imatinib, nilotinib, and other “type II” inhibitors act by stabilizing the inactive DFG-out conformation, seen in eight kinases so far (16, 80) and, which probably exists in many others. More recent inhibitors seek to exploit both the allosteric imatinib site made available in the DFG-out state and the catalytic ATP-binding pocket (8). In Src and many other kinases, it is known that the DFG-out conformation is less stable than DFG-in, and this can explain at least part of the Src/Abl specificity of type II inhibitors like imatinib (33). Similarly, resistance screens have identified amino acids in Abl that reduce the effectiveness of imatinib and whose structure differs in the DFG-out and DFG-in states; they were postulated to act by destabilizing the DFG-out state, increasing ΔG_ii (8, 33, 37, 38, 79). However, no direct experimental proof or quantitative measurement of ΔG_ii has been obtained for any kinase. Because imatinib is positively charged when bound to Abl (39), long range electrostatic interactions could also contribute to specificity, through ΔG_i; the same could be true for other protonatable inhibitors, such as nilotinib.

These questions can be addressed very precisely through simulations. With computers and sophisticated methods of today (49, 50, 53, 59, 67), accurate free energies can be obtained. Here, we computed the “interaction” contribution to the Src/Abl binding free energy difference, ΔΔG_i. The conformational contribution, ΔΔG_ii, was then obtained by subtracting out the total, experimental binding free energy difference. For ΔΔG_ii, an alternative approach would have been to directly compute the free energy difference between the DFG-out and DFG-in conformations of both Src and Abl. In principle, this can be done by driving the protein reversibly from one conformation to the other. However, it is very difficult and expensive (36, 57–59), because many residues change positions (Fig. 1C). Therefore, we preferred to use the indirect strategy described above. The results were combined with thermodynamic relations and experimental data. This yielded a precise decomposition of the Src/Abl binding free energy difference into its two contributions; the conformational term is clearly predominant. What is more, we showed that the Src/Abl binding free energy difference (4.6 kcal/mol) approximates rather closely the DFG-out/DFG-in conformational free energy difference in apo-Src. Thus, the ligand actually reports on the free energy surface of the apoprotein (and different ligands should report the same conformational free energy). Using a simpler continuum electrostatics method to compute ΔΔG_i, we showed that conformational selection is also the main source of the preference of imatinib for c-Kit over Src and Lck and for Abl over Lck. (Recall that, as stated in the Introduction, we use “conformational selection” in a broad sense, which includes induced fit as a special case.) The PB free energy method represents an inexpensive, semi-quantitative method to estimate the ΔΔG_i term for type II inhibitors; their overall relative binding affinities can then be obtained through the thermodynamic analysis above, where ΔΔG_ii accounts for their complex, allosteric inhibition mechanism. The supplemental material reports additional validation of the continuum method.

These results should help clarify the current framework for engineering kinase signaling. They establish quantitatively the role of conformational selection for imatinib binding to four kinases. Furthermore, they provide a simple computational route to study individual mutations in a quantitative way. Indeed, as with series of inhibitors, it is straightforward to estimate the change in the binding contribution, ΔΔG_i, for a mutant relative to native Src or Abl, using the PB free energy method. The conformational contribution, ΔΔG_ii, can then be deduced by subtracting out the experimental binding free energy change, and the importance of the two terms can be compared. It would be of interest to use this approach for mutants like F405A, G406A, L407G, or W260A, which have been studied experimentally and are thought to act by destabilizing the DFG-out conformation of Abl (33).

Because the DFG-in/DFG-out conformational free energy difference ΔG₀^CONF in apo-Src determines the preference of imatinib for Abl, it is hard though not impossible (60) to modify the Src/Abl specificity by chemically modifying the ligand; thus, nilotinib should have the same Src/Abl binding free energy difference as imatinib. The slightly smaller Src/Kit binding free energy difference arises from slightly more favorable imatinib-Kit contacts. More generally, type II inhibitors all pay the same specificity penalty, ΔG₀^CONF, for binding to a kinase that prefers the DFG-in conformation. Overall, the present combination of simulations, experiments, and thermodynamic analysis represents a powerful route for understanding and engineering tyrosine kinases and signaling pathways.