Conformer Generation with OMEGA: Algorithm and Validation Using High Quality Structures from the Protein Databank and Cambridge Structural Database

Abstract

Here, we present the algorithm and validation for OMEGA, a systematic, knowledge-based conformer generator. The algorithm consists of three phases: assembly of an initial 3D structure from a library of fragments; exhaustive enumeration of all rotatable torsions using values drawn from a knowledge-based list of angles, thereby generating a large set of conformations; and sampling of this set by geometric and energy criteria. Validation of conformer generators like OMEGA has often been undertaken by comparing computed conformer sets to experimental molecular conformations from crystallography, usually from the Protein Databank (PDB). Such an approach is fraught with difficulty due to the systematic problems with small molecule structures in the PDB. Methods are presented to identify a diverse set of small molecule structures from cocomplexes in the PDB that has maximal reliability. A challenging set of 197 high quality, carefully selected ligand structures from well-solved models was obtained using these methods. This set will provide a sound basis for comparison and validation of conformer generators in the future. Validation results from this set are compared to the results using structures of a set of druglike molecules extracted from the Cambridge Structural Database (CSD). OMEGA is found to perform very well in reproducing the crystallographic conformations from both these data sets using two complementary metrics of success.

Introduction

Conformer generation has been a topic of considerable interest to the modeling community for a number of years, and a large number of methods for conformer generation have been presented.¹⁻⁸ These methods have utilized a wide variety of approaches to the problem, including systematic enumeration, knowledge-based rule sets, random coordinate embedding, and energy-based or energy-biased sampling. All these approaches attempt to generate a set of conformations designated to be different from one another by some measure, usually geometric, and thereby aim to sample some subset of the conformational space available to a molecule. The method used by OMEGA is based on random coordinate embedding and refinement, followed by torsion driving using a set of rules derived from experimental structures and energy profile calculations, and then subsequent sampling of the resulting conformer ensemble by geometric and energetic criteria.

Publications that demonstrate the utility of conformer generators have approached the problem of validation of such tools in a number of different ways. Conformer generation is not an end in itself but a means to obtain input for other applications, most frequently shape comparison tools (or other 3D ligand matching approaches) and docking engines. Indeed conformer generation is often subsumed as a portion of a docking algorithm, which prevents independent evaluation of the conformer generation within such tools. One approach to validation has, therefore, been to generate conformer ensembles for use in a downstream tool (e.g., pharmacophore perception).(9) The quality of the conformer ensembles is then judged by the quality of the output from the downstream tool. While it might be argued that the “real-life” use of conformer generators is well reflected in this approach, judging the quality of a conformer generator based on the performance of a separate tool is fraught with problems. If this tool has been optimized to use conformers from a certain engine, then it would be expected to produce “better” results from this engine over all others. Other approaches to validating conformer generators have emphasized estimation of conformational coverage based on both pharmacophoric and geometric measures.(10) In studies of this kind, coverage of conformational space is held to be an absolute good and the tools under study are assessed based on their ability to cover the greatest amount of conformational space. However, there are large areas of “accessible” conformational space for a flexible molecule that are populated by conformers very different in shape and geometry from any experimentally determined conformer (be it in the solid state, in solution, or in the gas phase). As such, simply maximizing coverage of conformational space may result in generation of a conformer set containing a high proportion of conformers irrelevant to any measurable experimental property of the molecule.

By far, the most common, though not always the most well-executed, method for validation of conformer generators, and the method used in this paper, is the reproduction of experimental crystal structures(11) (often those retrieved from the Protein Databank (PDB)(12)). The implicit argument proffered for this approach is that coverage of conformational space near an experimental conformation of a molecule is more important than coverage in other regions of conformational space. Since experimental structures, while frequently not at a local minimum for a force field,(13) are generally considered to exhibit low levels of strain,(14) the regions of conformational space near an experimental structure can be considered as basins in the molecule’s energy profile. Accordingly, assessing sampling in these regions of the energy hypersurface can be a good guide to the performance of a method in generating low-energy conformations. To perform this sort of validation, a number of protein−ligand cocomplexes are selected and the ligands are extracted. The connection tables of these ligands are used as input for the conformer generator to provide a set of conformers for each ligand, unbiased by any structural information of the original experimental conformation. A metric of quality is then calculated that provides a measure of the three-dimensional similarity between the experimental conformation for the ligand and the conformers in the set. There are, therefore, two critical choices to this method of validation: selection of the appropriate metric of quality to perform the comparison and selection of suitable cocrystal structures to provide the ligands. While many metrics for comparing computed and experimental conformations are available, such as rms error in Cartesian space (rmsd), rms error in torsion space (RMST), and relative displacement error (RDE),(15) choosing the metric of quality presents some subtle problems. Atom-based metrics like rmsd, while very popular, have significant problems in their interpretation and necessarily have a dependence for their significance on the experimental error/precision of the crystal structure (a particularly difficult issue for PDB ligands). In addition, RDE and rmsd have no easily calculable upper bound (unlike RMST), and all these measures have a size dependence that is not easily compensated for. In this paper, two different metrics are used to compare computed and experimental conformations of druglike molecules, one atom based (rmsd) and one shape based (Tanimoto combo). The conformational coverage close to the experimental conformation is also assessed. In this way, it is hoped to provide a more complete picture of the ability of OMEGA (or any other conformer generator) to match experimental conformations. Identifying suitable cocomplex structures from the PDB to provide the experimental conformations of small molecules is a difficult and complex process. Unfortunately, in most publications in this area, insufficient care is taken in the selection of the structures, resulting in unwarranted or questionable conclusions being drawn based on unreliable data. Some of the issues that should be considered in the selection of structures from the PDB include the following:

Are the deposited models of good quality at both the global and local levels? There is little sense in trying to reproduce a deposited structure that is a poor model of the experimental density or a model that is not completely defined by the density.

Do the structures possess an appropriate degree of precision in their atomic coordinates? When using atom-based metrics like rmsd, paying attention to the precision in the atomic coordinates is critical: an rmsd or any measure of conformer reproduction more precise than the inherent inaccuracy/experimental error in the atomic coordinates is meaningless. Do the structures show intra- or intermolecular clashes? Significant atomic clashes, either between the ligand and the protein or between atoms of the ligand, must be artifacts of the process of fitting the ligand to the experimental electron density and not an inherent property of the structure. The binding energy available upon protein−ligand complexation is unlikely to be sufficient to drive atoms into close contact with one another. Are the ligands covering a reasonable amount of structural or chemical space? A set of ligands with a large degree of structural redundancy does not provide as rigorous a test of conformer generators as a structurally nonredundant set does. Also, in order for the results of the validation to be useful in a predictive or prospective manner, they should be readily generalizable to any set of applicable molecules. This can only be done with validation sets that cover chemical space in a reasonable way.

Consideration of these questions has allowed the development of quantitative criteria for structural quality in the PDB. These criteria were applied as successive filters to three previously published large data sets of cocrystal structures, PDBbind,(16) the Sadowski set(13) and the Kirchmair set,(17) to provide a high quality group of cocrystal structures to establish a gold standard for the validation of approaches to conformer sampling. A set of small molecule structures from the Cambridge Structural Database (CSD)(18) was also collected to provide complementary data to that obtained with the ligands from the PDB. These two data sets are applied to the evaluation of the OMEGA conformer generation application using the metrics mentioned above.

Methods

Here, the OMEGA algorithm is introduced in some detail; the metrics for comparison of the generated conformers to the experimental structures are outlined, and the criteria for the identification of suitable protein−ligand cocomplexes and small molecule structures with which to validate the algorithm are discussed.

OMEGA Algorithm

The design goal for OMEGA is to provide a thorough, though not exhaustive, sampling of conformational space for druglike molecules at as high a speed as possible (typically 2−2.5 s per molecule on a workstation running SLED 10 with a 2.4 GHz processor and 4 GB of RAM). The process used by OMEGA for conformer generation can be considered in several parts, two of which are generic and are precalculated and the rest of which are molecule specific and occur at run time. The first two steps are construction of a database of fragments from which the molecule will be assembled and derivation of a torsion library; the remaining steps generate a large ensemble of conformations and sample from this ensemble to deliver the final set of conformers.

1. Fragment Database Preparation

The OMEGA fragment database contains one or more 3D conformations for every entry (flexible rings have multiple conformations, rigid rings and acyclic groups have one conformation). The database is generated by fragmenting a very large collection of commercially available compounds into contiguous ring systems and small linear linkers. One or more 3D conformations for each fragment are generated by the following procedure: A distance bounds matrix is generated based on the connection table of the fragment; the distance bounds are augmented by volume constraints for chirality and planarity; the coordinates of each atom are randomly embedded in a Cartesian space and optimized to fulfill the bounds and constraints; the fragment is further refined against a modified version of the Merck molecular force field (MMFF94),(19) in which the electrostatic and attractive van der Waals’ terms are removed. The procedure is repeated hundreds of times for each fragment, with cycles being sampled more heavily than acyclics, and the lowest energy conformers that are unique in rmsd space are retained.

2. Torsion Sampling Dictionary

A hierarchy of torsions defined by SMARTS patterns is preorganized so that every rotatable bond in a small molecule matches at least one torsion rule. Every torsion definition is associated with a list of angles at which the torsion should be sampled. Very common or structurally unique torsions may be represented by very specific rules, while unusual torsions are only covered by generic torsion rules, often with relatively heavy sampling. Specific rules are employed when the barrier to rotation is high and the minima in the torsion profile are well-known. The torsion angles specified by the torsion library were derived by analysis of a set of experimental crystal structures (mostly from the PDB) and from energy scans of certain torsions against MMFF94.

3. 3D Structure Generation

OMEGA requires a completely connected molecular graph as input. Each graph is fragmented in the same manner as the fragment database and fragment conformations are drawn directly from the fragment database described in step 1. If a molecular fragment is not found in the fragment database, the procedure described in step 1 is carried out on-the-fly to generate coordinates for the missing fragment. The fragments are assembled into the parent molecule by overlapping fragments using geometric and chemical rules, thereby providing one or a small number of initial conformations for the molecule. This set of conformers includes all necessary ring conformer sampling.

4. Torsion Driving

Every rotatable bond in the conformers generated in step 3 is compared to the torsion library from step 2, and the appropriate torsion angles are noted. A torsion buildup procedure is applied to all the torsions in the molecule to generate a large ensemble of conformations that does not contain severe internal clashes or duplicates due to common symmetries.

5. Sampling

The design goal of OMEGA is to produce up to a few hundred low energy, structurally diverse conformers, and as such, the much larger collection of conformers produced by step 4 must be sampled. This process is begun by ordering the conformers using a simple scoring function that eliminates conformers with internal clashes. While many functions are suitable for this process, OMEGA uses a modified form of MMFF94 (vide supra). Next, beginning with the lowest scoring conformer, all higher scoring conformers that are less than a user-defined rmsd (including heavy atom automorphisms) to the lower scoring conformer are eliminated (the default rmsd cutoff is 0.5 Å). This process is continued with each successive conformer in the ordered list until (a) all conformers have a score less than 10 units higher than the lowest energy conformer produced or (b) 200 mutually unique conformers are identified. At no stage in this process is minimization performed because this tends to produce highly compact (folded) conformations not reflective of the conformation(s) found in solution or bound to a protein. This is mostly due to the differences between the gas phase and the solution phase or complexed potential energy surfaces for small molecules. Extensive experimentation in-house has shown that minimization of ensembles of conformers either before or after deduplication improves neither solid-state structure reproduction nor virtual screening performance with tools like ROCS or FRED.

Suitable Metrics for Comparing Conformers

Two metrics for comparison of conformer ensembles to an experimental conformation were chosen, rmsd and the Tanimoto combo, calculated using the Shape Toolkit from OpenEye Scientific Software. The Tanimoto combo (or TC) score represents a combination of shape matching (shape Tanimoto) and functional group matching (color Tanimoto). TC offers a complementary approach to the atom-based rmsd measure for a number of reasons treated at greater length in the Discussion section. An important difference between TC and rmsd is that TC is bounded (by 0 and 2). It should be noted that the processes used to overlay and score conformers using rmsd or TC are very different, and therefore, the conformer giving the minimum rmsd to the experimental structure will almost always be different than the conformer giving the maximum TC to the experimental structure.

Identifying Suitable Small Molecule Structures

Two sources of small molecule structures, the PDB and the CSD, were utilized. To find small molecules from the PDB, first, suitable cocrystal structures were identified from larger sets using global criteria; then, the ligands were extracted and inappropriate ligands were removed using local, ligand-centric criteria. Small molecule structures from the CSD were obtained from a previously published data set,(18) which was subjected to some of the ligand-centric criteria used to identify suitable PDB ligands.

Identifying Suitable Cocomplexes from the PDB

There are two kinds of criteria that must be considered here: global criteria for the structure as a whole and local criteria pertaining to the fit of the ligand to its local density and the properties of the ligand itself. A number of possible criteria of quality for crystal structures were enumerated in a paper by Hartshorn et al. on the selection of a set of structures suitable for validating docking programs for pose prediction.(20) The global criteria identified by Hartshorn et al. were that all structures must have good nominal resolution and have deposited structure factors, while the local criteria were that the ligand must be well fit to its local density and cannot be covalently bound to the protein. This list has been extended in this work, both at the global level and the local level. In addition to the Hartshorn criteria at the global level (good nominal resolution, deposited structure factors in the PDB), the model must have good overall metrics of model quality and reasonable coordinate precision. At the local level, it is demanded that a ligand be well fit (using different criteria to Hartshorn et al., vide infra) and be noncovalent. It is further required that the ligands show no intra- or intermolecular clashes and that they be diverse at the graph level.

Nominal resolution, while very commonly used as a measure of structure quality, is in fact a measure of the quantity of data gathered, not quality of the structure, and as such can only be used as a very rough guide to selecting a good structure.(21) In many studies in this area, the nominal resolution has been used as a surrogate for experimental accuracy, which is inappropriate (see ref (22) and the Discussion). However, since nominal resolution indicates the quantity of data gathered, at a resolution of 2.7 Å or better, the ratio of experimental data points to parameters in the model is greater than 1. As such, structures with a resolution of 2.7 Å or better offer the possibility (but only the possibility) of a well determined model. The quality of a deposited model can be independently checked only if structure factors (electron density maps) are available in the PDB, so all structures must have deposited structure factors. In order to ensure that the models used are globally well fit to the data (and not overfit), we use the difference between the R-factor and the R_free, as introduced by Brunger.(23) In this work, we demand that a structure must have a R_free within 0.05 of the R-factor.(24) In comparing computed and experimental poses for ligands, it is almost uniformly assumed that the experimental pose is infinitely precise and without error, which is untrue for any piece of experimental data. The average positional errors for atoms in a crystal structure can be assessed using the diffraction-component precision index (DPI).(25) We calculate DPI according to the approximation published by Blow(26) (using the Blow rearrangement allows us to calculate an estimate for DPI based solely upon information commonly contained in the header of a PDB file). The comparison of a computed conformer to the experimental conformer by rmsd obviously requires comparison of atom positions between the two conformers. Accordingly, the positional uncertainty in the atoms in the experimental structures should be less than the rmsd for the comparison to be meaningful. In this work, we estimate positional uncertainty in atomic positions as sqrt(2) × DPI, following Goto et al.(27) The maximum for the average positional uncertainty in a structure was set at 0.6 Å, which sets the maximum for the DPI to be 0.42 Å. In this way, any rmsd result from this set greater than 0.6 Å is guaranteed to be a prediction greater than the error in the experimental data, and therefore, such a prediction will be significant. Whatever the magnitude of the rmsd, a correction to it will have to be made to account for positional uncertainty in the ligand atoms (see the Results section). The assumption used in this paper is that the ligand atoms have average positional uncertainty. While the real uncertainty for the ligand atoms may well be different, it is not reliably calculable at the present time; therefore, we use DPI as our best estimate.

When considering whether or not a ligand is suitable for conformer generation studies, the local quality of fit of the ligand to its density, as well as global metrics of quality, should be considered. In this study, three local metrics, the real-space correlation coefficient (RSCC),(28) the real-space R-value (RSR),(29) and the occupancy-weighted B-factor (OWAB) were used to ensure that the ligand has been sensibly fitted to the electron density. The use of the occupancy weighted B-factor as a criterion was based not on the idea that this number necessarily measures thermal mobility in the ligand, as is often assumed. Rather, we used the OWAB to indicate either structures where the ligand is genuinely disordered in the active site, and therefore, the idea of reproducing “the” bioactive conformation is questionable or structures where there is some pathology of the model that led, in the process of fitting the ligand to its density, to very high or very low B-factors. These models are inherently of dubious value and should not be included in the set. The criteria used in this work were that RSCC > 0.9, RSR < 0.2, and 1 < OWAB < 50. These data were obtained by download from the electron density server (EDS).(30)

When applied sequentially, these global and local filters should ensure that a ligand structure arises from a good quality overall model and has been well fit to its local density. The filters were applied to a large set of PDB structures (see Results), and the cocomplexes that survived were then processed to separate the ligand and the protein. These pairs were checked to ensure that they do not show any intermolecular clashes, and those ligands that showed no clashes were designated as well-solved structures, to be used in the final, ligand-based filters. In these final steps, we focus on identifying suitable molecules using simple physicochemical and graph-based properties.

Identifying Suitable Ligands from the PDB

In the last filtering step, we removed ligands that are not representative of the population of molecules for which this validation is intended. As a first step, we removed all well-known cofactors, as these were not as relevant to the goals of this study (validation of OMEGA’s performance on druglike molecules). As mentioned above, OMEGA depends upon MMFF94 for its energy calculations, so molecules that contain elements unknown to MMFF94 (such as boron) must be removed. To ensure that we used a collection of ligands that provides as broad a set of tests for the OMEGA algorithm as possible, we attempted to select a structurally diverse set of ligands. At the simplest level, the molecules can be neither too rigid (so that the conformer sampling problem is trivial) nor too flexible (so that a close reproduction of the experimental conformation is more a matter of good luck than a good algorithm because of the high dimensional nature of the search space) and neither too small nor too large. We, therefore, applied the following criteria: 3 ≤ maximum number of rotatable bonds ≤ 16; 8 ≤ heavy atom count ≤ 50.

Preliminary analysis revealed that molecules designed to bind to thrombin were over-represented in the set of well-solved ligands identified by the criteria used thus far. These ligands tended to share a high degree of substructural similarity, so a method to introduce some level of structural diversity at the graph level was sought. We applied a simple measure of molecular similarity using the LINGOS method;(31) any pair of molecules that had a LINGOS Tanimoto >0.9 was flagged for removal, and the molecule with the better set of local fitting metrics for the pair (RSCC, RSR and OWAB) was retained. The use of graph-based metrics like LINGOS for structural diversity is a surrogate for the more relevant but more difficult to assess diversity in the torsions and flexible rings present in the molecule.

To further reduce the influence of experimental error on this data set, we demand that the ligand does not show any nonbonded intramolecular atomic clashes, as these are a mark of a poorly solved model. As further discussed in the Results section, we turned to the CSD for precise distributions of interatomic distances with which to identify clashing atoms. A final visual check was performed to remove molecules that are structurally analogous but were not identified as such by the LINGOS comparison (those with large common substructures and/or a large fraction of their functional groups in common). This gave us 197 ligands whose conformations we then attempted to reproduce using OMEGA. The attrition rates for the different data sets and an analysis of OMEGA’s ability to reproduce these 197 surviving structures is given in the Results section.

A parallel analysis was performed on high quality small molecule structures from the CSD, as outlined in the following paragraphs.

Identifying Suitable Molecules from the CSD

An important part of the selection criteria for structures from the PDB focused on removing structures that were not reliably and accurately fit to their density, and a large majority of the candidate structures failed these criteria (see the Results section). A further problem with molecules from the PDB is the high level of inherent experimental uncertainty in the atomic positions. Both of these problems can be avoided entirely if small molecule structures from the Cambridge Structural Database (CSD) are used. A high quality set of 492 druglike structures has been extracted from the CSD as part of a previously published study,(18) and these were used as the basis for generating a complementary set of structures to those we obtained from the PDB. No filtering of these structures based on model fit (global or local) was necessary as all atoms are accurately located in these models. Applying the same physicochemical and diversity criteria as were used for the ligands from the PDB gave a set of 480 small molecule structures upon which we could perform the same validation experiments. Comparison of these results to those from the ligands from the PDB can be found in the Results section.

All code was written in Python (version 2.4), and statistical calculations were performed with Rpy version 1.03. Cheminformatics functions (including rmsd and LINGOS calculations) were performed using OpenEye’s OEChem (version 1.6.1), and shape calculations were performed using the OpenEye Shape toolkit (version 1.6). Protein−ligand cocrystal structures were downloaded from the PDB and filtered according to the criteria laid out in the Methods section. RSCC, RSR, and OWAB data for each PDB ligand were obtained from the EDS. Molecules from the CSD were obtained from one of the authors of the original study (personal communication, K. Brameld).

Molecules were converted into isomeric SMILES format using the OEChem toolkit before being used for conformer generation. Conformer databases were generated using OMEGA version 2.3, with an energy window for acceptable conformers of 10 kcal/mol above the ground state using a modified version of the MMFF94 force field, a maximum number of conformations per molecule of 200, and an rmsd cutoff of 0.5 Å (the default settings in OMEGA2.3). Interatomic distance analysis of the CSD was carried out with ConQuest v.1.6.(32)

Results

Molecules from the PDB

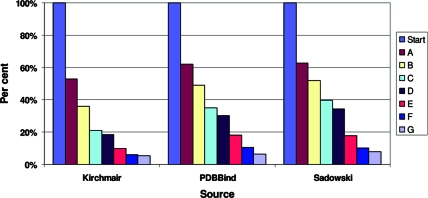
In the Methods section, we presented a set of criteria for selecting suitable protein−ligand cocomplexes from the PDB and then identifying suitable ligands from those complexes. We applied these criteria to three large data sets (two of which have previously been used in conformer validation studies) that together consist of over 4500 cocrystal structures: 778 structures that Kirchmair et al. used in their comparison of Catalyst and OMEGA,(17) the set used by Sadowski and Bostrom in their study on the OMEGA 1.8.1 torsion library(13) (1267 structures) and a subset of the PDBBind database(16) (2516 structures). The percentages of structures remaining after each filter was applied are illustrated in Figure 1. In all three databases, we found very large levels of loss when we applied our filtering criteria (over 90% of the structures in every database were removed). It can easily be seen from Figure 1 that there are three criteria that, when applied in the given order, remove the highest percentages of the structures: nominal resolution greater than 2.7 Å (criterion A), poor fits of the ligand to its density (criterion E), and inappropriate physicochemical properties (criterion F).

Figure 1.

Attrition rates for three data sets of cocrystallized ligands. The filters used are (A) nominal resolution ≤2.7 Å; (B) structure factors must be present; (C) R − R_free must be <0.05; (D) DPI < 0.42 Å; (E) RSCC > 0.9, RSR < 0.2, OWAB < 50, no intermolecular clashes; (F) physicochemical properties; (G) pairwise LINGOS similarity <0.9, no intramolecular clashes.

The problem of identifying atom−atom clashes (filters E and G) based on analysis of interatomic distances in structures from the PDB is nontrivial, due to the inherent uncertainty in those atom positions. Therefore, we chose to perform an analysis of nonbonded contacts for commonly occurring atoms (C, N, O, S, P, F, Cl) using high quality structures (R-factor <0.05, no disorder) of organic molecules from the CSD, where the atoms are located with very high precision. The cutoffs identifying clashes were set at an interatomic distance above which 95% of the distances for that (nonbonded) atom pair in the CSD occurred. These cutoffs are shown in Table 1 in the Supporting Information.

Table 1. Reproduction of the Experimental Conformations for 197 Structures from the PDB^a.

Tanimoto combo (mean/median)	rmsd (Å) (mean/median)	rmsd-U (Å) (mean/median)	max (rmsd,U) (Å) (mean/median)
1.56/1.64	0.67/0.51	0.35/0.20	0.72/0.62

^aResults are shown as mean/median for each column heading; U = the coordinate uncertainty (sqrt(2) × DPI).

The only well fit ligands that can show intermolecular clashes are those that are covalently bound to their target protein, and these are explicitly excluded from this set. Therefore, noncovalent ligands that have clashes, by these criteria, with their cognate protein are incorrectly solved. None of the ligands that passed the previous filters (A to E in Figure 1) showed any intermolecular clashes, indicating that the criteria used in these filters (especially the RSR and RSCC filters) can be useful in identifying misfitted ligands. Similarly, no ligands were removed based on the intramolecular clash filter, further reinforcing the idea that RSCC and RSR can provide useful information on the quality of a ligand’s fit to its density. However, it is noteworthy that several structures from such well-known data sets as the Perola and Charifson set(33) show intramolecular clashes, as these authors selected structures using only global criteria of fit, omitting local measures. As such, these structures should not be used in conformer generation studies, as has been done by some authors,(34) because the deposited coordinates for the ligand are incorrect; atom−atom clashes cannot be enforced by protein binding and simply reflect an error in the solution of the structure.

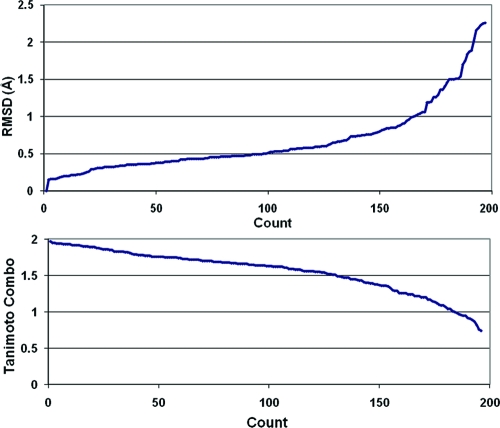
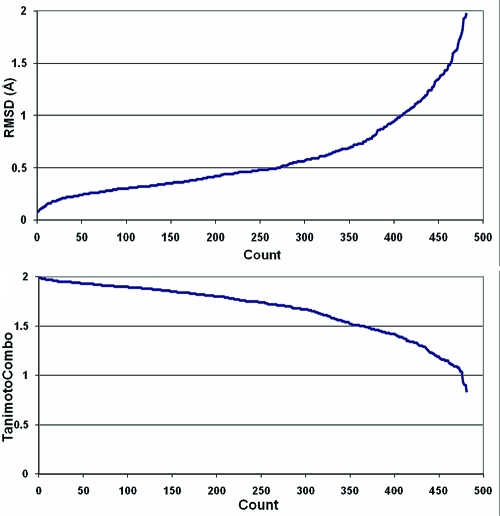
After the filters had been applied, the surviving ligands from each of these three sets were combined and deduplicated and close analogues were removed as discussed in the Methods section. This left 197 high-quality ligand structures on which to perform the validation. The mean pairwise similarity of these molecules using the LINGOS Tanimoto measure is 0.18, so the structures are relatively diverse from one another at a graph level. Conformers were generated for these molecules using OMEGA with the default settings (see the Methods section). The average CPU time per molecule in this set was 2.05 s. In Figure 2, we show the reproduction of the experimental conformation using the lowest rmsd and highest Tanimoto combo metrics. Approximately 83% of the structures are reproduced within a 1 Å rmsd and 66% are reproduced with a Tanimoto combo of 1.5 or better.

Figure 2.

Distribution of rmsd and Tanimoto combo between the closest conformer in a set and the experimental conformation for 197 ligands from the PDB.

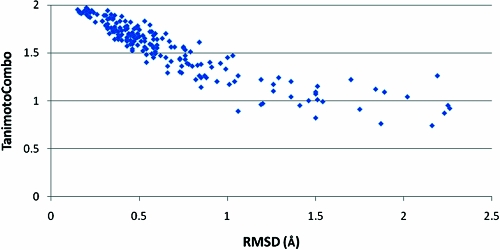
The relationship between best (lowest) rmsd and best (highest) Tanimoto combo for this data set is shown in Figure 3, where the lowest rmsd for any conformer to the experimental conformation in a set is plotted against the highest Tanimoto combo for any conformer to the same experimental conformation. As expected, the cases where the rmsd is low (<0.25 Å) all show very high Tanimoto combos. As rmsd increases, the relationship to Tanimoto combo becomes increasingly less linear, in that there are several examples where constant rmsd gives a widely varying Tanimoto combo and vice versa. Quantitatively, we can assess the correlation between the two measures using either the Spearman rank correlation coefficient or the Kendall tau. For this data, the Spearman coefficient is 0.925 and the Kendall tau is 0.775. As such, the two measures of conformer reproduction are correlated (as would be hoped for two measures attempting to assess the same thing) but are by no means identical.

Figure 3.

Best rmsd v. best 3D shape and chemical similarity (Tanimoto combo) for reproduction of 197 ligands from the PDB.

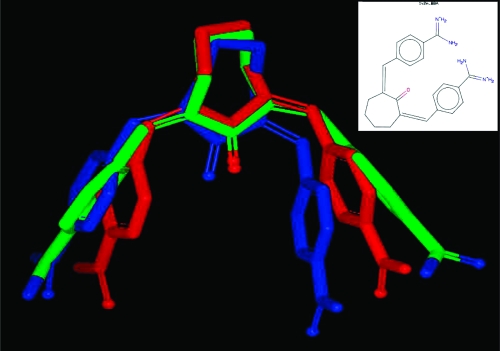
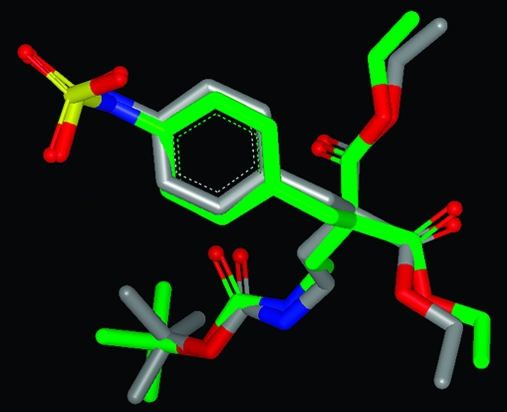
That these two measures are assessing conformer reproduction differently is to be expected, since they are generated in rather different ways and, therefore, provide complementary means to compare conformations. A striking difference in the two overlay methods is illustrated in Figure 4, where two different overlays of conformers of the ligand from the PDB structure 1 V2N are shown. The experimental conformation is in green; the best overlay based on lowest rmsd is in red, and the best overlay based on highest Tanimoto combo is in blue. The best rmsd overlay here is 0.89 Å, while the best Tanimoto combo is only 1.06 (Tanimoto combo’s range is 0−2, see Methods section). The origin of this difference in the assessment of the quality of reproduction when using these two different metrics is most clearly seen by inspecting the alignments of the benzamidine functional groups.

Figure 4.

Comparison of the experimental conformation of the ligand 1 V2N (green) with the best overlay as provided by rmsd (red) and the best overlay as provided by Tanimoto combo (blue).

As can easily be seen in Figure 4, the rmsd overlay in red symmetrically, but poorly, matches both benzamidine functional groups, while the Tanimoto combo overlay matches one benzamidine group very well (the one on the left in Figure 4) while the position of the other benzamidine group is much less well reproduced, giving the surprisingly low Tanimoto combo. This illustrates a consistent difference between the two methods of comparison; rmsd tends to produce overlays that are equally good (or bad) everywhere across the molecule, while Tanimoto combo tends to produce overlays that are very close in some portions but can be much more divergent in others.

While all the structures in this validation set have high coordinate precision, there is still some level of inherent uncertainty in the atomic coordinates. Therefore, when comparing a computed pose to an experimental pose using atom-based metrics like rmsd, this experimental uncertainty, U, in the atom positions must be taken into account. There are two possible approaches to this, both of which are shown in Table 1. The first is to use as the figure of merit the maximum of the rmsd and the coordinate uncertainty, U (max(rmsd,U) in Table 1), since the prediction cannot be more accurate than the error in the experimental data (the coordinate uncertainty). The second is to use the difference between the rmsd and the coordinate uncertainty (rmsd-U in Table 1), which reflects the additional error in the model introduced by conformer generation. This number is set to zero if rmsd < U.

As can be seen from column 3 (rmsd-U) in Table 1, the average amount of “noise” introduced by OMEGA in generating a conformer close to the experimental is small. Also, due to carefully choosing structures that have low levels of uncertainty, the mean and median for the maximum of the rmsd and experimental uncertainty (column 4) are very close to the mean and median for the “raw” rmsd (column 2). Therefore, the level of accuracy in our predictions is only minimally affected by the experimental uncertainty in the structures that make up the data set.

An issue that is most often ignored in studies of this kind is the prospective utility of the performance metrics presented, or how robust are the performance metrics to changes in the composition of the data set and, therefore, how predictive are the results of future performance? This question is addressed here by bootstrapping: we omit a randomly selected 10% of the results (allowing duplicates), recalculate the mean rmsd and repeat 10 000 times, and then find the 5% and 95% quantiles. The 5% quantile is 0.647 Å, and the 95% quantile is 0.688 Å, thereby giving us the 90% confidence interval. Therefore, we can say that for a future experiment on a set of molecules with similar properties to those of this PDB-derived set 90% of the time the mean rmsd will lie in the range 0.647−0.688 Å. This small interval implies that, even though the data set is not as large as we had hoped, the mean found here is a reliable indicator of OMEGA’s average performance on as yet untested collections of ligands. The 90% confidence interval for the mean Tanimoto combo can be calculated in the same fashion and is 1.54 to 1.64. We may also use these confidence intervals as a method of comparing two sets of results to determine if they are significantly different from one another (see Discussion).

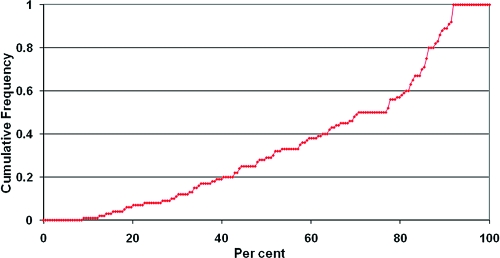
So far, we have dealt with the properties of the single conformer closest by a given metric to the experimental. While this measure has significant utility, in another view of the problem, the proportion of conformers within a certain distance of the experimental structure is important. This method of measuring success is very rarely used(35) but provides a useful complement to focusing solely on the matching of only the best single conformer from a possibly large set, as we have done to this point. A common upper bound for successful reproduction of an experimental structure in docking is an rmsd of 2 Å, this number being thought of as providing a sufficiently close match of the important interaction points on the ligand (hydrogen bond partners, etc.). Accordingly, a “close” reproduction of an experimental pose could be considered to have an rmsd of less than 2 Å. In this work, since we calculate each metric after aligning the conformers to the experimental structure, a smaller cutoff is more relevant, so we have selected an rmsd of 1.25 Å as our definition of “close”. Figure 5 shows the cumulative frequency of cases where conformers are close to the experimental.

Figure 5.

Distribution of percentages of conformers that are close (rmsd < 1.25 Å) to the experimental conformation of 197 structures from the PDB.

It can be seen from the figure that, for around half of the cases (47%), less than 25% of the conformers generated for a given molecule are close to the experimental conformation, while for around 8% of the cases 100% of the conformers generated are close. In total, 19% of the conformers generated for this set are within 1.25 Å rmsd of the protein-bound conformation. Having a reasonable proportion of the conformers in the set close to the protein-bound structure is helpful for downstream protein-based tasks such as docking. However, as is seen in the next section, the same molecule may have multiple solid-state structures and, therefore, have too high a fraction of the conformational ensemble, for that molecule close to only one of them would not be desirable.

Molecules from the CSD

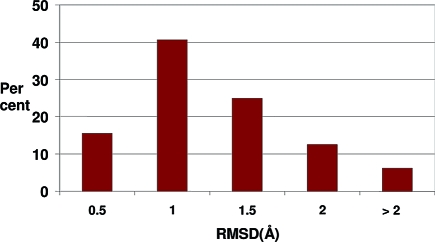
As mentioned previously, 492 molecules from the CSD were obtained from a previous publication, of which 480 survived the ligand filtering process (physicochemical and graph diversity filters). The mean pairwise similarity of this set using the LINGOS Tanimoto is 0.14, again indicating that the molecules are diverse at a graph level. It was hoped that these molecules from the CSD would represent a different set of challenges in conformer generation; the PDB structures are obtained in an aqueous environment, and the majority of CSD structures are obtained in nonpolar environments. Accordingly, using sets of high-quality structures from both sources will further challenge OMEGA’s abilities to reproduce solid-state structures. While there are large numbers of small molecule structures in the PDB and the CSD, the two databases show only a low level of overlap; a comparison of over 4000 druglike ligands from the PDB with over 57 000 druglike molecules in the CSD finds only 224 molecules in common (see Supporting Information for PDB and CSD codes). Of these 224 molecules, only 32 meet the quality criteria for PDB structures laid out previously (see Methods). The differences in the conformations of these 32 molecules (as measured by rmsd) found both in the PDB and the CSD sets are shown in Figure 6. The mean rmsd for this set is 1.02 Å, a figure close to that found in similar analyses.^17,36

Figure 6.

rmsd distribution for the same molecule found in both the CSD and the PDB (n = 32).

Clearly, the same molecule in the CSD and the PDB can sometimes adopt rather different conformations (over 7% have rmsd > 2 Å), while other protein-bound and uncomplexed conformations can be quite similar (16% have rmsd ≤0.5 Å). It is likely that at least some of these differences in conformation are due to the crystal packing forces often found in CSD structures. These can have a profound effect on the conformation of a molecule, sometimes enforcing a conformation not found in protein-bound structures.^14,32 The larger differences in conformation for the same molecule indicate that there could be several basins in a molecule’s energy hyper-surface in which solid-state structures are found, so sampling across a range of the hyper-surface could be useful.

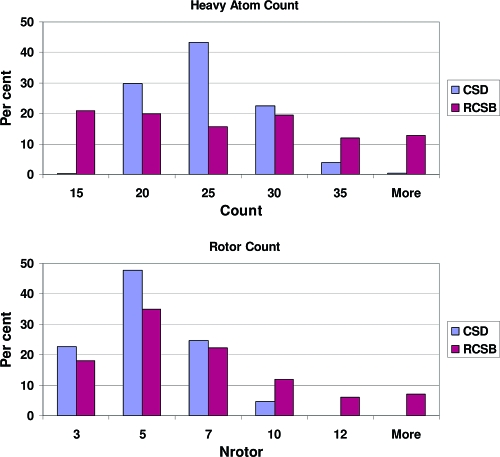
While the molecules from the CSD were selected to be druglike, they have somewhat different physicochemical properties than those from the PDB. Table 2 illustrates the differences between the CSD molecules and the PDB molecules for two simple properties, heavy atom count and rotatable bond count, and Figure 7 compares the distributions for these two properties. It can easily be seen that for both properties the molecules from the CSD occupy a smaller range than those from the PDB. Most importantly for this study, while the molecules from both sets are approximately equal in size (as judged by their heavy atom counts), the CSD-derived molecules are somewhat less flexible than the PDB derived set, having, on average, one fewer rotatable bond. Therefore, the CSD derived set is expected to be an easier test of conformer sampling and reproduction than the PDB set.

Table 2. Property Distributions for Molecules from the CSD and the PDB^a.

	rotor count (mean/median)	heavy atom count (mean/median)
PDB	6.3/5	24.4/23
CSD	4.7/4	23.1/22

^aGiven as mean/median.

Figure 7.

Property distributions for molecules from the CSD and the PDB.

Given the difference in rotatable bond count, the numbers of conformers produced by OMEGA2 for this set and for the PDB set are rather different; the median number of confomers per molecule was 47 for the CSD set and 123 for the PDB set.

In Figure 8 is shown OMEGA’s performance in reproducing these structures, as judged by rmsd and Tanimoto combo.

Figure 8.

Distribution of rmsds and Tanimoto combos between the closest conformer in a set and the experimental conformation for 480 molecules from the CSD.

As can be seen in Figure 8, 441/480 (84.5%) of the CSD structures are reproduced within 1 Å rmsd, while 400/480 (83.3%) are reproduced within 1.5 Tanimoto Combo. Table 3 shows the mean and median for the Tanimoto combo and rmsd metrics. Note that in the case of these structures from the CSD the positional uncertainty for the atoms is sufficiently small to be disregarded when calculating rmsds. The Spearman rank correlation for the two metrics in Table 3 is 0.89, and the Kendall tau is 0.72, in both cases slightly smaller than those found for the PDB set, again indicating that these two measures are assessing different aspects of OMEGA’s ability to reproduce the experimental conformation. The bootstrapping results on the CSD set are also shown in Table 3. As with the results from the PDB ligands, these small intervals imply that our results are not strongly dependent upon the exact composition of this data set and as such are reliable indicators of future performance on data sets of similar property distributions to the one used in this study. It can also be said with greater than 90% confidence that the CSD results, either for rmsd or for TC, are better than the PDB results since the 90% confidence intervals for either metric do not overlap.

Table 3. Reproduction of 480 Experimental Conformations from the CSD.

TC (mean/median)	rmsd (Å) (mean/median)	TC (5%/95%)	rmsd (Å) (5%/95%)
1.72/1.75	0.508/0.44	1.711/1.726	0.501/0.517

The results for “close” reproduction (rmsd < 1.25 Å) of the experimental conformations are much better than for the PDB; overall, 39% of the conformations generated for the CSD set are close to the experimental conformation. This is entirely consistent with the results from the CSD set relative to the PDB set for best pose reproduction (as judged by either Tanimoto combo or rmsd).

It is possible that the superior performance of OMEGA on the CSD set is not due to the lower average flexibility of the molecules but due to some consistent and unexpected difference in the nature of the molecules between the two sets. Therefore, a subset of the PDB ligands was derived to closely match relevant physical properties of the CSD set (heavy atom count and rotor count). The aggregate performance metrics on this subset are much closer, though not identical, to those seen from the CSD set, see Table 4.

Table 4. Reproduction of the Experimental Poses for a Subset of the PDB Ligands with Physical Properties Matching Those of the CSD Set.

TC (mean/median)	rmsd (Å) (mean/median)	TC (5%/95%)	rmsd (Å) (5%/95%)
1.637/1.680	0.54/0.47	1.628/1.646	0.526/0.551

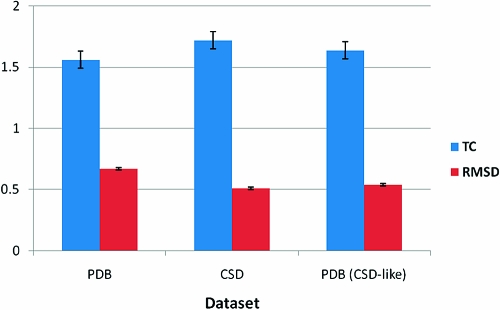
The performance of OMEGA on these three different sets is shown in Figure 9.

Figure 9.

Reproduction of three data sets by OMEGA, using both Tanimoto Combo (TC) and rmsd.

The 90% confidence intervals of the entire PDB set and the CSD-matched subset of the PDB set do not quite overlap, though they are very close (the difference could be entirely due to the physical property distributions of the two sets not being perfectly matched). Therefore, we cannot with complete assurance attribute the entire change in OMEGA’s performance to differences in the rotatable bond count between the two sets. However, we conclude that the superior performance of OMEGA on the CSD set derives to some large degree from the lower average flexibility of the CSD set compared to the PDB set and not from bias in the OMEGA knowledge base.

Effect of the Torsion Library

We used both the PDB- and CSD-derived test sets to investigate another possible source of bias in the results; the torsion library, which was assembled mostly by examination of ligand structures from the PDB. If there is significant overlap between the molecules used to arrive at specific angles in the torsion library and the molecules in the test sets used in this study, then the results will be artificially good (or artificially better for one test set over another). We investigated possible training set bias by eliminating all training set knowledge from the torsion library. In these experiments, the simplest possible torsion settings were used: every rotatable bond was sampled at 30 degree increments, and new conformer sets were produced using defaults for all other settings. Interestingly, OMEGA’s ability to reproduce the solid-state structures from the PDB or the CSD sets was not significantly changed (whether measured by rmsd or Tanimoto combo) when using this “naive” torsion library. Results for the PDB set using rmsd are shown in Table 5, where it can be seen that the 90% confidence intervals overlap substantially. Therefore, with 90% confidence, we can assert that OMEGA’s accuracy is not affected by the use of the knowledge-based torsion library. However, some other effects on performance were noted. For the PDB set, when the naive torsion library was used, the average number of conformations produced per molecule increased by almost 15% over using the default library (from 123.3 to 139.6 conformers/molecule), while the total run time increased by nearly 40%. It was also seen that the worst failures (highest rmsd, lowest TC) were less poor when the default, knowledge-based, torsion library was used than when the 30 degree library was used. Qualitatively similar results were obtained for the CSD data set (data not shown).

Table 5. Reproduction of 197 Structures from the PDB Using Two Torsion Libraries.

	mean rmsd (Å)	5% quantile	95% quantile
Default	0.668	0.647	0.688
Torlib30	0.685	0.663	0.704

Discussion

The object of this study was 2-fold: to arrive at reliable and challenging sets of solid-state structures to validate OMEGA and to examine its default parameters for their effectiveness on these well chosen solid-state structures (not to exhaustively evaluate a large number of combinations of parameters in OMEGA for their efficacy). The OMEGA algorithm presented here combines knowledge-based and first principles approaches to conformer generation, so it can be described as systematic and rule based. The knowledge-based part is the torsion library, while the fragment library, ensemble buildup, and sampling are all performed on a first principles basis.

We have developed a gold standard set of PDB ligand structures by paying particular attention to identifying structures that are good models for their electron density, an approach rarely taken in the literature. Many of the properties of a model that are used here are ignored or misinterpreted in other publications in this area. For example, based on the published literature, it is commonly believed that selecting a cocrystal structure with a resolution below some cutoff value (for example 2 Å) ensures a good quality ligand structure. That this is clearly mistaken can easily be seen by inspecting the ligand models for two structures, both of 2 Å resolution, 1NHU and 1IY7 (see Figure 10).

Figure 10.

Electron density for two ligands both solved at 2 Å resolution; 1NHU on the left, 1IY7 on the right.

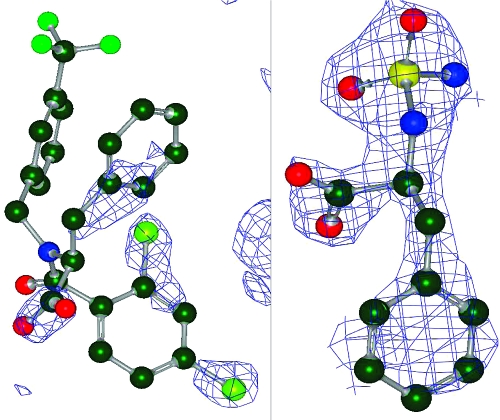
The 1IY7 ligand model is clearly a good model of complete density, while the 1NHU model is an interpretation of partial density that is obviously poor (the deposited ligand coordinates show severe atomic clashes). In two other cases at 2 Å resolution or better, 1ATL and 1ETA, there is no significant density for the ligand at all (even when viewed at 1σ) making the deposited coordinates at best highly speculative educated guesses. Therefore, resolution of the parent structure alone is no guide to the quality of a ligand’s conformation but should only be used as one criterion among many. Cases like 1NHU, 1ATL, and 1ETA also caution against using B-factors as a representation of thermal mobility in a structure. If there is no density for a set of atoms, what physical meaning is there in the B-factors for those atoms?

Models built from data collected to at least 2.7 Å resolution have a parameter to data point ratio of at least 1, allowing the model to be well constructed. The confidence in the fit of a model at the global level is increased if the difference in R and R_free is low (<0.05 herein), as a large difference in R and R_free is indicative of an overfit, though not necessarily poor, model. A low level of difference also means that the local measures of fit, RSCC and RSR, are meaningful, which is not the case for overfit models (good values of RSCC and RSR can be obtained for poor fits when R − R_free is large). By ensuring that the structures in the set all have low experimental error in their atomic coordinates (DPI), we can use atom-based metrics like rmsd, take appropriate account of this experimental error, and still generate meaningful measures of performance. The RSCC and RSR metrics often delineate ligands that show good fits to their local density from those that do not, and we thereby avoid many of the problems with structures from other publications. Cases like 1NHU and 1ATL are easily identified by these fit criteria as unsuitable for inclusion in conformation generator validation sets (or any other kind of validation set), as the coordinates are not supported by the experimental data. For example in 1NHU, the RSCCs for the two versions of the ligand in the unit cell are 0.768 and 0.744, and the RSRs are 0.27 and 0.25; while in 1ATL, the ligand RSCCs are 0.709 and 0.722, and the RSRs are 0.35 and 0.35, greatly exceeding the cutoffs used in this work. Unfortunately there are a number of poorly fit molecules like 1NHU in previously published data sets,(33) and their presence in these sets only weakens the conclusions that can be drawn therefrom. Any ligand conformation from the PBD that shows intramolecular atomic clashes is an error on the part of the crystallographer, and such structures are easily avoided by the use of the RSCC, RSR, and OWAB criteria used here. Further, by paying attention to the physicochemical properties and graph diversity of the ligands, we ensure a reasonable level of independence among the molecules in our data set. That this is a factor often ignored is easily seen by the example of the Kirchmair set,(17) which contains no less than 50 duplicate molecules. Such a level of duplication is likely to bias the results obtained from that data set.

While individually all the criteria we deploy seem reasonable and even relatively benign, when combined, they present a significant hurdle for a structure to surmount. Even though we began to assemble our validation set using three large data sets, two of which had already been selected for validation of conformer generators, we found it impossible to assemble a substantial set of well-solved structures. By applying relatively loose criteria for the quality of the crystallographic models at a global level, we removed around 75% of the starting structures. Overall, more than 90% of all the input structures failed our filtering criteria, a surprisingly high level. Figure 1 illustrates the attrition rates for each of the three databases used and shows that they are quite similar, which was unexpected. Given that the Kirchmair and Sadowski sets were selected with the explicit goal of testing conformer generators, we expected lower attrition rates for these two sets than for PDBBind, which is simply a collation of cocrystal structures for which there exists a published binding affinity. However, the percentages of surviving structures are quite similar: 5.3% for the Kirchmair set, 6.4% for PDBbind, and 8.1% for the Sadowski set. These very low levels of survival emphasize that the number of structures suitable for this sort of study in the PDB as a whole is very small, as has been seen in a study using PDB structures for docking validation.(37) However, given that recently the PDB has made deposition of structure factors along with coordinates a requirement, we hope that that this situation will improve quickly in the future.

The most commonly used metrics in conformer generation studies are based on comparing each conformer in the set to the experimental conformation, using some atom-based geometric measure such as rmsd. Metrics like rmsd are used almost without exception in conformer reproduction studies, probably because they are relatively easy to understand and require no specialized applications to calculate. There are, however, a number of objections to the use of rmsd as a metric of quality; it has no upper bound, it scales with molecular size (so that an rmsd of 2 Å for a molecule of 6 heavy atoms is much different than an rmsd of 2 Å for a molecule with 60 heavy atoms), and it can give an inaccurate picture of the overall quality of a prediction.(38) The most serious of the problems with rmsd may be that it does not directly compare a prediction with an experimental value but rather compares a prediction or model (the conformer set) with another model (the atomic positions in the crystal structure). This problem has been eloquently discussed in a paper by Yusuf et al.(39) in which the authors advocate comparison between the experimental data (electron density) with calculated density derived from a docking pose (or computed conformation) using the RSR metric (which is bounded by 0 and 1). These objections notwithstanding the large amount of published literature using rmsd militates against not using it as one metric of quality in a validation study, but it should not be the only one. A complementary approach, pace Yusuf et al., is to use a bounded metric that is not derived directly from the atom positions in the two conformers being compared. One recent approach in this vein has been the comparison of the overall shape of the experimental conformation to the shape of a docking pose using the shape Tanimoto metric employed by Warren et al.(40) We have extended their shape-based comparison to include an additional term (the color Tanimoto) that compares the alignment of functional groups between the conformers. The score representing this combination of shape matching (shape Tanimoto) and functional group matching (color Tanimoto) is known as the Tanimoto combo (TC). Since it represents the match of both shape and functional groups in space, TC allows for a greater discrimination between poses than using shape alone. Use of a metric like TC avoids some major problems with rmsd: while rmsd has no defined range, the range of TC is, by definition, 0−2; since TC is bounded by 0 and 2 comparisons using TC is independent of molecular size; large rmsds can arise from differences in the conformations of only small parts of the molecule, while TC is not as sensitive to these divergences; TC provides an extra weight for matching chemical functionality (the color Tanimoto term represents the matching of the chemical features only) while rmsd weights the matching of all atoms equally; the Gaussian representations of molecular properties used in the calculation of TC are “soft” so that the significance of results are not as affected by experimental uncertainties in atomic positions (though it is more difficult to quantitatively correct for their effect on TC). While any use of a cutoff value for good reproduction is difficult, we find that if TC is below 1.0 the reproduction of the experimental pose is always bad and if TC is above 1.5 the reproduction is almost always satiusfactory.

Another major issue with the common use of atom-based measures like rmsd, RDE, etc. is that no account is taken of experimental coordinate error in the structures being reproduced. To our knowledge, this is the first work in which reported rmsds are corrected for the atomic coordinate precision of the structure being reproduced. We have chosen to allow for coordinate error or uncertainty by the use of, as a metric of quality, either the maximum of the rmsd and the uncertainty or the difference between them. The second of these can be considered as an estimate of the level of computational noise introduced by the conformer generation process atop the existing experimental noise. While careful selection of our data set resulted in the corrected and uncorrected results not being significantly different, the correction of rmsds by coordinate uncertainty as outlined herein allows the future use of interesting structures with poorer coordinate precision than used in this study. There are clearly more sophisticated approaches that can be taken to this problem of experimental noise in PDB ligand structures, among which is to calculate a set of conformers that all fit the electron density equally well within some limit and compare these with the set computed by OMEGA. This more realistically reflects the fact that a crystal structure is an average over time and space, and so, a small molecule is likely to be found in a number of slightly different conformations in a solid-state structure.

The PDB-derived data set used here, while of good quality, is relatively small (197 structures), and so, a possible concern is that the results generated are not robust indicators of future performance. We have addressed this issue by performing bootstrapping on our two metrics. We find that in both cases the 5% and 95% quantiles are close and that the standard deviations of the bootstrap means are small. We infer that our results are quite stable to changes in the composition of the data sets used and, therefore, can be considered reliable indicators of future performance on molecule sets of similar physicochemical properties. The confidence interval has another, related, application in comparison between performance. The usual practice in this area has been to compare an aggregate statistic such as mean or median results, from a number of different tools or parameter sets and to declare one superior, without any account of the errors in these terms. However, by the use of confidence intervals, we can quantitatively assign a probability that one tool or parameter set actually is superior; for example based on data in this paper, it is over 90% likely that OMEGA with default parameters is better at reproducing small molecule structures from the CSD than from the PDB.

The torsion library in OMEGA is based upon analysis of a number of crystal structures from the PDB, coupled with analysis of energy profiles for certain torsions in the MMFF94 force field. Therefore, the problem of overtraining the torsion library arises if many of the structures used to derive the torsion library entries are also in the test sets used in this study. This problem was addressed by the use of a naive torsion library containing no torsion specific information at all. Comparison of the results from this naive library with the default one showed that the main impact of the torsion library is not to improve OMEGA’s ability to closely reproduce experimental structures but rather to reduce the size of the conformer ensemble required for good reproduction and the run time required. This result reduces any possible concern about the effect of “over-training” the torsion library so that it contains matches for many known structures. As above, the use of bootstrapping is key in interpreting the results; it is over 90% certain that the use of the default torsion library produces no improvement in reproduction of the PDB structures compared to the use of a naive torsion library.

While the purpose of this study was not to extensively compare parameter sets and versions of OMEGA, a comparison of previous versions of OMEGA with the current version (on the PDB ligand set) is provided in the Supporting Information.

Conclusion

We have presented OMEGA, an algorithm for rapid generation of conformers using a prebuilt library of fragments and a knowledge base of torsion angles and test sets of solid-state structures for its evaluation. The test sets of structures were obtained from both the PDB and the CSD. Identifying a set of small molecules from the PDB suitable for validation proved difficult, with the vast majority of ligand structures used in some previous validation sets for conformer generators proving unsuitable for this purpose. However, by applying a set of sequential quality filters to over 4500 structures from the PDB, a set of 197 ligands was found that were accurate and well fit to their electron density. Most of the structures failed due to insufficient nominal resolution, poor fits of the ligand to its density, and inappropriate physicochemical properties. It is hoped that the PDB data set used herein will be of general use to the community since it contains only highly reliable structures with well fit ligands, so conclusions based on this data set will be highly reliable. A set of 492 druglike molecules from the CSD was also subjected to a subset of these filters, and the surviving 480 molecules were tested against OMEGA. In contrast to most studies in this area, we have used two different metrics for success in reproducing these experimental structures, rmsd and the Tanimoto combo (which estimates overall similarity in three dimensions), as well as a metric of conformational coverage close to the experimental structure. We, thereby, obtained complementary information on OMEGA’s ability to satisfactorily sample the conformational space of molecules around their solid-state structures. OMEGA’s performance on both of the data sets was good when judged by any of the metrics used (performance was particularly good against the CSD structures, due to their lower flexibility). The use of bootstrapping has allowed us to determine confidence intervals for our results and to make quantitative discrimination between the performance of OMEGA on different data sets and with different amounts of information. In sum, we found that OMEGA was able to satisfactorily sample the conformational space around solid-state structures of druglike molecules, which is OMEGA’s design goal.

Supporting Information Available

The names of the 197 PDB and 480 CSD structures from which the ligands used in this study were extracted, comparative performance of previous versions of OMEGA with the current on the PDB set and interatomic clash distances derived from the CSD. This material is available free of charge via the Internet at http://pubs.acs.org.