Observations of Needle-Tissue Interactions

Abstract

Needles with asymmetric bevel tips naturally bend when they are inserted into soft tissue. In this study, we present an analytical model for the loads developed at the bevel tip during needle-tissue interaction. The model calculates the loads based on the geometry of the bevel edge and gel material properties. The modeled transverse force developed at the tip is compared to forces measured experimentally. The analytical model explains the trends observed in the experiments. In addition to macroscopic studies, we also present microscopic observations of needle-tissue interactions. These results contribute to a mechanics-based model of robotic needle steering, extending previous work on kinematic models.

I. Introduction

Percutaneous needle insertion is one of the most common minimally invasive clinical procedures. It is used for diagnosis, localized therapeutic drug delivery, and tissue sample removal from tumors deep within the body. For effective medical diagnoses and treatments, the needle must reach its intended target. However, tissue inhomogeneity and anisotropy, organ deformation, anatomy obstructing needle path, and physiological processes, such as respiration, flow of fluids, and edema, cause the needle to deviate from its intended path. A possible method to mitigate needle targeting error is to use a needle that can be robotically steered inside the body to reach the intended target (Fig. 1).

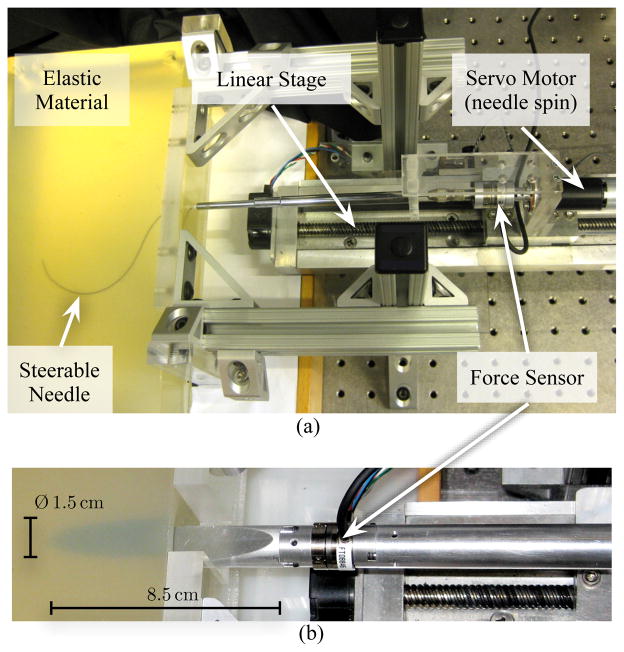
Fig. 1.

(a) Experimental setup used to robotically steer a flexible bevel-tipped needle though a soft elastic material. (b) Needle with 10° bevel angle and Ø 1.5 cm inserted into gel A (3:1 Plastisol gel) during the macroscopic experimental studies.

Several groups have examined the use of robotically steered flexible needles through tissue [1], [2], [3], [4], [5]. Abolhassani et al. [6] provide a summary of recent work in the area of robotic needle insertion in soft tissue. Planning such procedures requires an accurate model of the needle-tissue interaction. A general survey of surgical tool and tissue interaction models, which describes both physics- and non-physics-based interaction models, is provided in [7]. Webster et al. [2] presented a kinematic model specifically for bevel-tip needle steering, with parameters fit using experimental data. However, this model did not consider the interaction of the needle with an elastic medium. Misra et al. [8] developed a finite element model to simulate tissue cleavage that incorporated physical tissue parameters (rupture toughness and nonlinear material elasticity) and cohesive zone models to calculate the needle-tissue interaction forces at the bevel tip. A mechanics-based model was presented by Misra et al. [9], where the effects of tip forces on the whole needle was computed, but an analytical model for tip forces was not developed.

The current study extends the work developed in [8] and [9], and presents an analytical model that calculates the forces at the bevel tip of the needle. The developed forces are a function of the bevel geometry and the tissue material properties. Further, we conducted experimental studies with a physically scaled needle tip to validate the model. By capturing needle tip effects, our model attempts to provide a physics-based understanding of the needle-tissue interaction forces. We begin our analysis by exploring the variables that govern the deflection of a bevel-tipped steerable needle and their relative importance.

II. Dimensional Analysis

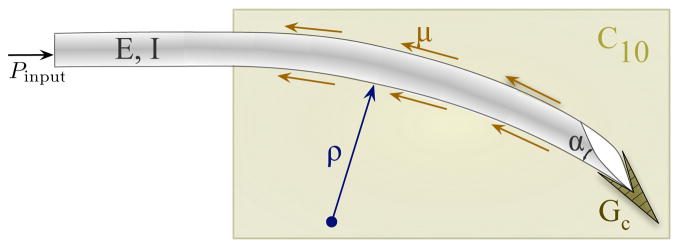
The deflection of a bevel-tip needle is a function of several parameters (shown in Fig. 2): the needle’s Young’s modulus (E, units: Pa), second moment of inertia (I, units: m⁴), and tip bevel angle (α); the tissue’s nonlinear (hypere-lastic) material property (C₁₀, units: Pa), rupture toughness (G_c, units: N/m), and coefficient of friction (μ); and input insertion force from the robot controller (P_input, units: N). The radius of curvature of the needle (ρ, units: m) can be written as a function, f, of these parameters:

$$\rho =f\left(\underset{\text{needle}}{\underbrace{E,I,\alpha }},\underset{\text{tissue}}{\underbrace{C_{10},G_c,\mu }},\underset{\text{input}\text{force}}{\underbrace{P_{\text{input}}}}\right).$$ (1)

Fig. 2.

Schematic of a bevel-tip needle interacting with a soft elastic medium. The two dimensional model incorporates tip forces generated by rupture, tissue properties (toughness: G_c, nonlinear elasticity: C₁₀) and needle properties (bevel angle: α and flexural rigidity: EI).

Performing dimensional analysis results in the following Π-groups, for primary variables E, I, C₁₀, and G_c: ${\mathrm{\Pi }}_1=\frac{{\rho EC}_{10}\sqrt[4]{I}}{G_c^2},{\mathrm{\Pi }}_2=\frac{P_{\text{input}}{EC}_{10}\sqrt[4]{I}}{G_c^3},{\mathrm{\Pi }}_3=\frac{{\alpha EC}_{10}\sqrt{I}}{G_c^2}$ and ${\mathrm{\Pi }}_4=\frac{{\mu EC}_{10}\sqrt{I}}{G_c^2}$. Thus, the non-dimensional form of (1), for some function, g, is given by

$$\frac{{\rho EC}_{10}\sqrt[4]{I}}{G_c^2}=g\left(\frac{P_{\text{input}}{EC}_{10}\sqrt[4]{I}}{G_c^3},\frac{{\alpha EC}_{10}\sqrt{I}}{G_c^2},\frac{{\mu EC}_{10}\sqrt{I}}{G_c^2}\right).$$ (2)

From (2), irrespective of the choice of the primary variables, it is observed that the radius of curvature is dimensionally scaled by both the tissue elasticity (global parameter) and also the tissue rupture toughness (local parameter), which tells us that in additon to α and μ, the effect of both of these parameters (C₁₀ and G_c) needs to be investigated. The remainder of this paper is aimed at understanding the needle tip and tissue interaction properties and characterizing the transverse needle tip force that enables needle steering.

III. Local Microscopic Tip Observations

Microscopic observations of needle and elastic medium interactions have been reported previously (e.g. [10]), but most of the literature focuses on observing damage to the gel or tissue surface after the needle has punctured the medium. Sections of the gel have also been observed, but again only after the needle has penetrated the medium. In order to observe the needle-tissue interaction within the gel as the needle is embedded in the medium, we used a Zeiss LSM 510 Meta laser scanning confocal microscope (Carl Zeiss AG, Oberkochen, Germany). The needle and gel were visualized with differential interference contrast (DIC), epifluorescence, and reflected light using the 488 nm line of an argon/ion laser and 0.3 NA Plan-Neofluar 10x objective lenses with pin hole diameter set at 9.33 Airy units.

The ratio of plastic to softener for Plastisol (M-F Manufacturing Co., Inc., Ft. Worth, TX, USA) gel was 4:1. The Plastisol gel (400 cm³) was doped with 20 μl of 10 mg/ml rhodamine green solution (Invitrogen, Carlsbad, CA, USA). This dye was added to facilitate epifluorescent confocal imaging of Plastisol gel. Since a very small amount of dye was used, we assume that it does not significantly change the material properties of the gel. Cubes of 0.5 cm³ were prepared and needles were manually inserted into the gel and viewed under the microscope. Observations were made in two configurations (axial and perpendicular), for needles of four different diameters and bevel angles. In the axial configuration, the laser light was along the needle axis, while in the perpendicular configuration the laser light was perpendicular to the needle axis. DIC and epifluorescent images were obtained for each configuration; one set is shown in Fig. 3.

Fig. 3.

Example DIC and epifluorescent images taken using a confocal microscope. The top row of images are in the axial configuration, while the bottow row of images pertain to the perpendicular configuration. Needle geometric properties: Ø 0.40 mm and α = 33.9°. Arrows in the DIC images indicate that rupture of the gel is observed close to the bevel edge of the needle, while arrows in the epifluorescent images indicate that the gel is compressed near the needle shaft (axial) and the bevel face of the needle tip (perpendicular).

For all the needles, opening and rupture are observed at the bevel edge. In the axial configuration, the needle cross-section appears crescent-shaped because of the bevel edge. Arrows in both the DIC and epifluorescent images in the axial configuration indicate regions where Mode-I crack (opening) of the gel is visible. In the perpendicular con-figuration, arrows point to the occurrence of Mode-II crack (rupture) near the bevel edge of the needle. Unlike brittle materials, crack propagation (classical Mode-I fracture) is not seen during the interaction of sharp needles and soft gels.

IV. Local Macroscopic Tip Observations

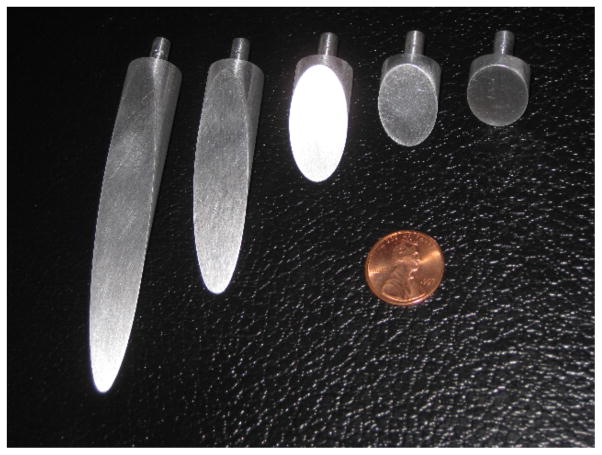
In order to understand the tissue cleavage process as the needle tip interacts with the medium, we performed experiments in which we physically magnified the bevel tip by machining “needles” of diameter Ø 1.5 cm. These needles had bevel angles ranging from 10° to 60°. Fig. 4 shows the needles with the five bevel angles used in the experiments. Three different types of Plastisol gel were used as the soft medium for the these studies. The ratio of plastic to softener for the Plastisol was set to 3:1 (gel A), 8:1 (gel B), and 4:1 (gel C). These experiments were performed using the experimental setup described in [11] and shown in Fig. 1.

Fig. 4.

Scaled needles of Ø 1.5 cm used to understand the interaction between the needle tip and medium. Needles of various bevel angles (10°, 15°, 30°, 45°, and 60°) were used in the study.

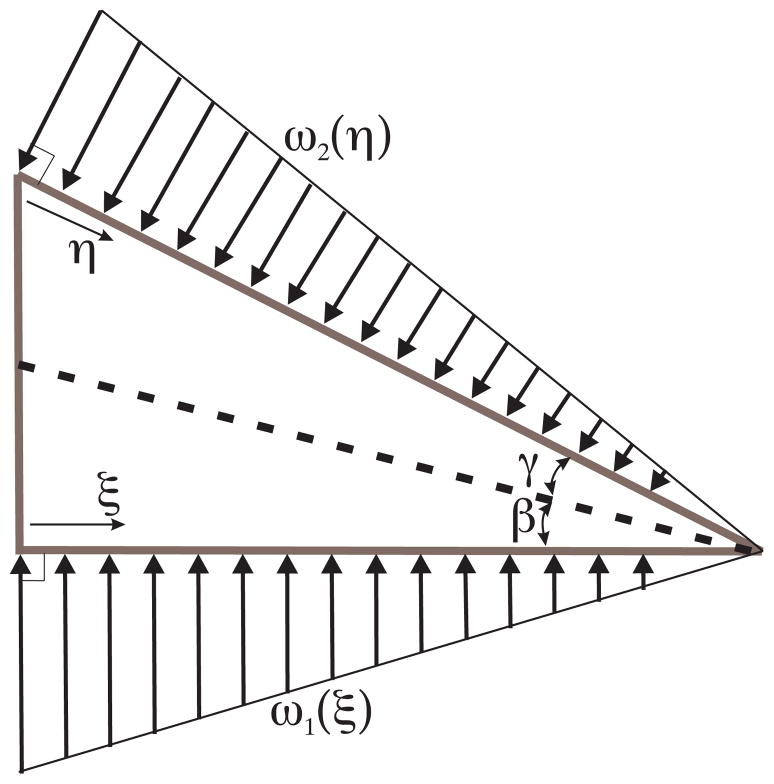
As the needle tip cuts through the soft solid, it moves material out of the way. The deformation of the material results in forces being developed along the needle tip edges. The material displacement as the needle tip progressively interacts with medium and moves forward results in a distributed load along the edge of the needle tip, which we model in Fig. 5. The model shown in Fig. 5 assumes angles, γ and β, which cut and displace material to accommodate the needle tip.

Fig. 5.

Displacement of material as the needle tip interacts with a soft solid and in order to accommodate the needle tip, results in a load distribution along the edges of the needle tip.

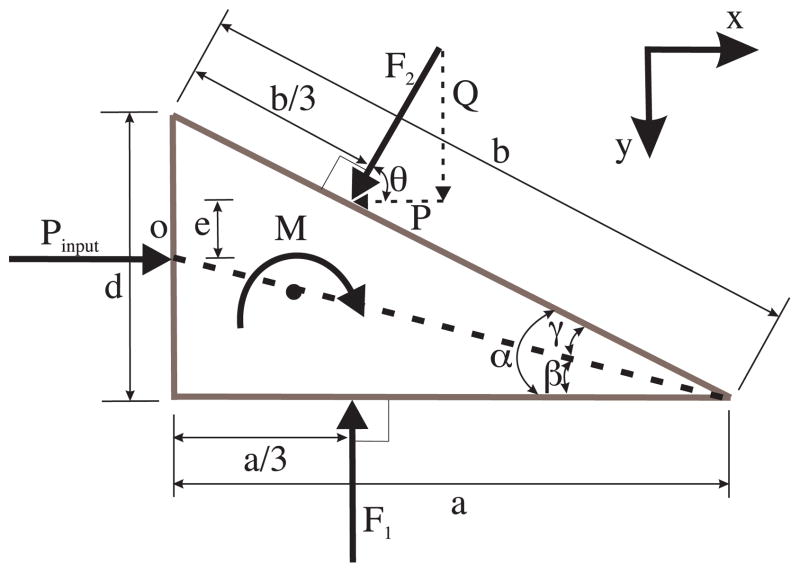
The load distribution along the edge of the needle is hypothesized to be triangular. Friction along the edges of the needle tip has been ignored in this calculation. The resultant forces and moments acting on the needle tip due to deformation of the medium and inclusion of the bevel tip are shown in Fig. 6. For d and α, the diameter of the needle and the bevel angle, respectively, we define the variables representing various dimensions in Fig. 6 as follows: α = γ + β, $a=\frac{d}{tan\alpha },b=\frac{d}{sin\alpha },e=d-asin\beta -\frac{b}{3}sin\alpha$, and θ = 90°−α.

Fig. 6.

Free-body diagram of the forces acting on the needle tip as it interacts with the medium.

Our objective is to derive expressions for the forces and moments developed at the bevel tip. In particular, we are interested in the transverse load, Q, which results from the tip asymmetry and causes the needle to bend. For δ₁ (ξ) being the displacement of the material along the bottom edge, the triangular load distribution along the bottom edge of the needle, ω₁ (ξ), has the following constraints:

$${\omega }_1(0)=K_T{\delta }_1(0)\text{and}{\omega }_{\text{1}}(a)=0,$$ (3)

where δ₁ (0) = a tan β and K_T is the stiffness of the medium per unit length. Similarly, for δ₂ (η) being the displacement of the material along the bevel edge, the triangular load distribution along the bevel edge of the needle, ω₂ (η), has the following constraints:

$${\omega }_2(0)=K_T{\delta }_2(0)\text{and}{\omega }_{\text{2}}(b)=0,$$ (4)

where δ₂ (0) = b tan γ. Thus, under the triangular load distribution assumption and using (3) and (4), the forces along the bottom and bevel edges of the needle tip are:

$$F_1={\int }_0^a{\omega }_1(\xi )d\xi =\frac{K_T{a}^2}{2}tan\beta ,$$ (5)

$$F_2={\int }_0^b{\omega }_2(\eta )d\eta =\frac{K_T{b}^2}{2}tan\gamma .$$ (6)

An input force, P_input, drives the needle into the medium. Using (5) and (6), the forces along the x and y directions, and moments about point o can be derived using static equilibrium balance. The expression for the resultant transverse force, Q, along the bevel edge is

$$\begin{array}{c}{\mathrm{\sum }F}_y=Q=-F_1+F_{2}sin\theta ,\\ \Rightarrow Q=\frac{K_T{b}^2}{2}tan\gamma cos\alpha -\frac{K_T{a}^2}{2}\left(\frac{tan\alpha -tan\gamma }{1+tan\alpha tan\gamma }\right).\end{array}$$ (7)

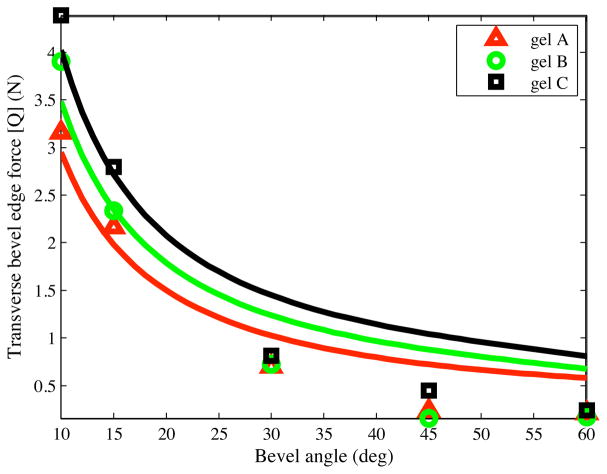
The inputs to the model are K_T and γ. K_T is a material property of the elastic medium, while γ depends both on the medium and the bevel angle. We compared the transverse tip force, Q, derived in (7) to the experimental results. Fig. 7 provides the maximum experimentally observed transverse force and analytically derived tip force for all bevel angles. The material property of the medium, K_T, is 4.83 kN/m², 9.21 kN/m², and 12.61 kN/m², for the gels A, B, and C, respectively. These values were measured using uniaxial compression tests, described in greater detail in [8] and [9]. In our model, the ratio $\frac{\gamma }{\alpha }$ was set to 0.97, 0.79, and 0.74, for gels A, B, and C, respectively. The optimized values for $\frac{\gamma }{\alpha }$ were obtained by minimizing the error between the experimentally derived normal force to the analytically derived Q, given in (7). As observed in Fig. 7, the experimental and analytical force values depict a similar trend. The analytically derived transverse tip forces qualitatively match the experimental values. The ideas resulting from this analysis could be applicable not just to bevel-tipped needles, but to any wedge embedded in an elastic medium.

Fig. 7.

Transverse tip load (Q) based on the analytical model and experiments, where the solid lines represent the analytical results.

V. Discussion

This study presented an analytical model to calculate needle-tissue interaction forces and moments at a bevel tip. The transverse tip load was compared to experimental data. The experiments used needle tips with a large diameter (Ø 1.5 cm) and varying bevel angle. The experimental results and analytical models exhibit a similar trend for the transverse tip loads. The model assumes a one-dimensional triangular load distribution, while the bevel face of the needle tip is an ellipse. This assumption along with neglecting the effects of friction and lack of accurate knowledge of $\frac{\gamma }{\alpha }$ are some of the reasons for variation between the model and experiments. Experimental evidence has shown that needles with smaller bevel angles have larger curvature and hence, greater steerability [11]. Both our analytical model and experiments also show that smaller bevel angles result in larger transverse tip forces, which is an indication of greater needle bending and thus, larger curvature. The results from this study would guide researchers in optimizing needle bevel design. In addition to macroscopic needle insertion studies, we also observed the needle-tissue interaction at a microscopic scale.

A possible extension to the current study is microscopic observations of needle insertion through tissue using a linear actuator. Such studies would help characterize the dynamic rupture of soft solids, which are different from the conventional and well understood fracture of brittle materials. The analytical model could be extended to include frictional effects. One of the primary goals within the domain of robotically steered bevel-tip needles is to have an analytical model that would predict the interaction forces and deflection of the needle. The inputs to this model would be needle geometry, and tissue and needle material properties. Building upon our previous work [8], [9], we aim to develop models of the bending needed to robotically steer needles through tissue, and also to choose feasible clinical applications and optimize needle design.