Abstract
Diffusion tensor imaging (DTI) is vulnerable to geometric distortions caused by subject-dependent susceptibility effects and diffusion-weighting direction-dependent eddy currents. Although the introduction of sensitivity encoding (SENSE) has reduced the overall distortions for the same imaging matrix size, this benefit is offset by the increasing demand for higher spatial resolution. Thus, significant distortions remain or are exacerbated in high-resolution SENSE DTI acquisitions. While the susceptibility-induced distortions cause global spatial misregistration, the direction-dependent eddy current-induced distortions cause misregistration among different diffusion-weighted images, leading to errors in the derivation of the diffusion tensor in virtually all voxels, and consequently in resulting diffusion parameters as well as in fiber tracking. Here, we apply a comprehensive approach that corrects for both susceptibility- and eddy current-induced distortions to high-resolution SENSE DTI acquisitions, and demonstrate its effectiveness, efficiency, and reliability in vivo as well as its advantages over a twice-refocused spin-echo sequence. This method should find increased use in modern DTI experiments where SENSE acquisitions are commonly used.[TKT1]
Keywords: Diffusion tensor imaging, SENSE, Distortion correction, Susceptibility, Eddy currents
INTRODUCTION
Diffusion tensor imaging (DTI), being sensitive to the anisotropic diffusion of water in biological tissues, is a powerful technique for the noninvasive characterization of the microstructure of normal and pathological tissue, and has found a wide range of applications in basic and clinical sciences (Basser and Pierpaoli, 1998; Le Bihan et al., 2001; Mori and Zhang, 2006). It involves the acquisition of at least one non-diffusion-weighted and six diffusion-weighted images with diffusion-weighting gradients applied along noncollinear directions. Fast imaging sequences such as echo planar imaging (EPI) are typically used to reduce scan time and minimize motion artifacts. However, because of the long readout duration, the acquired images suffer from severe geometric distortions due to magnetic field inhomogeneities, which are predominantly caused by susceptibility differences at air/tissue interfaces as well as eddy currents induced by the strong diffusion-weighting gradients. Furthermore, since the eddy current-induced distortions are dependent on the amplitude and direction of the diffusion-weighting gradients, the misregistration among different diffusion-weighted images leads to errors in the derivation of the diffusion tensor in virtually all voxels, and consequently in resulting maps of the apparent diffusion coefficient (ADC) or fractional anisotropy (FA), as well as in fiber tracking procedures. As such, it is desirable to correct for these direction-dependent distortions in all diffusion-weighted images before the derivation of the diffusion tensor.
A twice-refocused spin-echo (SE) sequence (Reese et al., 2003) has been proposed to effectively reduce the eddy currents, but requires a longer echo time (TE) than a conventional single SE sequence with identical diffusion-weighting, thus resulting in a lower signal-to-noise ratio (SNR). Other correction methods require the acquisition of eddy current-induced magnetic field profiles for each diffusion-weighting direction (Jezzard et al., 1998) or the acquisition of pairs of diffusion-weighted images with low and high diffusion-weighting (Haselgrove and Moore, 1996), with opposite phase-encoding directions (Andersson et al., 2003), or with opposite diffusion-weighting directions (Bodammer et al., 2004; Shen et al., 2004), all of which result in a substantially lengthened acquisition time. Post-processing methods based on cross-correlation (Haselgrove and Moore, 1996; Bastin, 1999) or mutual information (Horsfield, 1999; Rohde et al., 2004; Ardekani and Sinha, 2005) typically involve the coregistration of non-diffusion-weighted and diffusion-weighted images with highly variable contrasts and are generally computationally intensive. Furthermore, most existing methods only correct for either susceptibility- or eddy current-induced distortions. Chen et al. (2006) developed an efficient correction method that uses a non-diffusion-weighted magnetic field (B0) map acquired in vivo as well as diffusion-weighted B0 maps acquired on a phantom with the same diffusion-weighting scheme as the DTI acquisition to correct for the susceptibility- and eddy current-induced distortions, respectively. However, this initial implementation only accounted for the eddy current-induced linear gradients, whereas higher-order terms were neglected, as is the case with most other correction methods (Jezzard et al., 1998; Haselgrove and Moore, 1996; Andersson et al., 2003; Bastin 1999; Rohde et al., 2004; Papadakis et al., 2005; Zhuang et al., 2006).
The combination of parallel imaging techniques such as sensitivity encoding (SENSE) (Pruessman et al., 1999) with DTI acquisitions (Bammer et al., 2002; Jaermann et al., 2004) has reduced the overall distortions for the same imaging matrix size because of the shortened readout window. However, this benefit is offset by the increasing demand for higher spatial resolution. As such, significant distortions remain or are exacerbated at high resolution. In this report, we thus apply a comprehensive approach that corrects for both susceptibility-induced and high-order eddy current-induced distortions to high-resolution SENSE DTI acquisitions, and demonstrate its effectiveness, efficiency, and reliability in vivo as well as its advantages over the commonly used twice-refocused SE sequence.[TKT2]
METHODS
B0 Mapping
The B0 mapping is performed using a diffusion-weighted multi-echo SE sequence (Chen et al., 2006), wherein a train of gradient-echo images are acquired before and after the spin-echo with a short readout duration to avoid geometric distortions. This multi-echo method allows highly reliable one-dimensional phase unwrapping of the phase images along the echo dimension, followed by pixel-wise linear regression of the unwrapped phase images as a function of TE to derive accurate B0 maps. Because the echo train is acquired with readout gradients of alternating polarity, both the phase unwrapping and linear regression are performed separately on the odd and even echoes in order to avoid errors due to off-resonance effects, and the resulting B0 maps are subsequently averaged to yield the final maps.
A non-diffusion-weighted B0 map is acquired to measure and correct for the subject-dependent susceptibility-induced B0 inhomogeneities, whereas diffusion-weighted B0 maps are acquired with the same diffusion-weighting scheme as the DTI acquisition to measure and correct for the eddy current-induced B0 inhomogeneities. However, since the eddy currents only depend on the diffusion-weighting gradients but not on the subject being imaged, the diffusion-weighted B0 maps can be acquired on a phantom, provided that identical parameters are used. A non-diffusion-weighted B0 map of the phantom is then also acquired and subtracted from each diffusion-weighted B0 map to remove the common susceptibility-induced B0 inhomogeneities, thus yielding residual field maps representing the eddy current-induced magnetic fields. As such, only one B0 map needs to be acquired for each subject, which makes our method time efficient for in vivo studies.
Distortion Correction
For a given diffusion-weighting direction, the eddy current-induced magnetic field is typically expressed as the sum of a spatially invariant term (i.e., a B0 offset), linear gradients along the frequency-encoding, phase-encoding, and slice-selection directions, and higher-order terms, which are usually ignored. The B0 offset and the gradients along the frequency- and phase-encoding directions result in a shifting, shearing, and scaling (i.e., stretching or compression) of the images, respectively (Jezzard et al., 1998). These geometric distortions occur predominantly in the phase-encoding direction because of the low EPI readout bandwidth in that direction. The eddy current-induced gradient along the slice-selection direction does not result in geometric distortions but in a signal loss, which was experimentally found to be negligible and which will consequently not be further considered here.
In the method proposed by Chen et al. (2006), the eddy current-induced gradients along the frequency- and phase-encoding directions are computed by linear regression of the residual field maps, and converted to shearing and scaling factors, respectively, which are then used to correct for the distortions. In this first-order approach, the eddy current-induced magnetic fields are assumed to be well characterized by linear gradients, which may not always be the case. In the present work, no prior assumptions of linearity are made and higher-order terms are taken into account as well by fitting a two-dimensional polynomial to the residual field maps. To minimize blurring, the correction of both susceptibility-induced and high-order eddy current-induced distortions is performed in a single step by adding the non-diffusion-weighted B0 map acquired in vivo to each fitted residual field map. These combined field maps are then converted to maps of pixel displacements, and the distorted images are linearly interpolated at the shifted locations to generate the corrected images. In theory, the polynomial fitting is not needed, as the original residual field maps could be used directly for the distortion correction. However, these raw field maps are affected by noise, so the fitting procedure is important in that it helps smooth the data. An additional advantage is that it allows the magnetic field to be extrapolated outside of the phantom if needed, although more accurate results are obtained when using a phantom with a size comparable to or larger than a human head, as was the case in our studies.[TKT3]
Human Studies
A healthy volunteer, who provided written informed consent as approved by our Institutional Review Board, was studied on a 3 T Excite MRI scanner (GE Healthcare, Milwaukee, WI) using an eight-channel phased-array RF coil and a gradient system with 40 mT/m maximum amplitude and 150 T/m/s slew rate. Automatic whole-volume high-order shimming was used to minimize the global B0 inhomogeneity.
The SENSE DTI acquisition was performed using a single-shot diffusion-weighted SE EPI sequence with the following parameters: repetition time (TR) = 2000 ms, TE = 61.6 ms, field-of-view (FOV) = 25.6 cm, matrix size = 128×128 (interpolated to 256×256), slice thickness = 2 mm, and an axial slice orientation with right/left frequency-encoding direction. A SENSE reduction factor of 2, ramp sampling, and 5/8 partial Fourier encoding were used to minimize the readout window and TE, and hence the geometric distortions and signal loss due to T2 relaxation. Diffusion-weighting was applied along 15 noncollinear directions evenly distributed over a sphere with a b-factor of 1000 s/mm2, and 10 averages were used to increase the SNR. The B0 mapping was performed using identical TR, TE, FOV, slice thickness, and diffusion-weighting scheme, but with a matrix size of 64×64 (interpolated to 256×256) and 24 echoes. All B0 maps were acquired on a 20-cm diameter spherical uniform phantom, whereas only a non-diffusion-weighted B0 map was acquired in vivo.
Two additional scans were performed to demonstrate the effectiveness of our correction method. First, to validate the correction of susceptibility-induced distortions, high-resolution undistorted T2-weighted images were acquired using a fast spin echo (FSE) sequence with TR = 3000 ms, TE = 85 ms, FOV = 25.6 cm, matrix size = 256×256, and slice thickness = 2 mm. Second, to validate the correction of eddy current-induced distortions, another SENSE DTI acquisition was performed using a twice-refocused SE sequence (Reese et al., 2003) with identical parameters and diffusion-weighting scheme as in the single SE acquisition, except for a longer TE of 70.1 ms. While this dual SE sequence can reduce the eddy current-induced distortions, susceptibility-induced distortions remain and still need to be corrected for using the non-diffusion-weighted B0 map acquired in vivo. Finally, to demonstrate the robustness of our correction method, a second set of B0 maps was acquired on the phantom at a later time.
RESULTS
The residual field maps obtained on the phantom (Fig. 1A) show that the eddy current-induced magnetic fields are highly dependent on the 15 diffusion-weighting directions. Selected profiles along the frequency- and phase-encoding directions through the center of the phantom (Fig. 1B) are clearly nonlinear, but can be well characterized by a two-dimensional third-order polynomial. The coefficient of determination R2 (for all 15 diffusion-weighting directions) increases from 0.91 for a first-order polynomial fit to 0.97 for a second-order fit and 0.99 for a third-order fit. Further increasing the polynomial order does not result in a significant improvement, as the eddy current-induced magnetic fields are spatially slowly varying.[TKT4] The largest absolute B0 offset (zeroth-order polynomial coefficient) is equal to 1.1×10−7 T, which corresponds to a global shift of the image by 0.4 pixel for our choice of imaging parameters, whereas the largest linear gradients along the frequency- and phase-encoding directions (first-order polynomial coefficients) are equal to 1.3×10−6 and 4.6×10−6 T/m, which correspond to a shearing and scaling of the image by 1.2 and 4.2 pixels across the image, respectively. These results indicate that significant distortions remain in high-resolution SENSE DTI acquisitions, as confirmed by our human studies below.
Fig. 1.
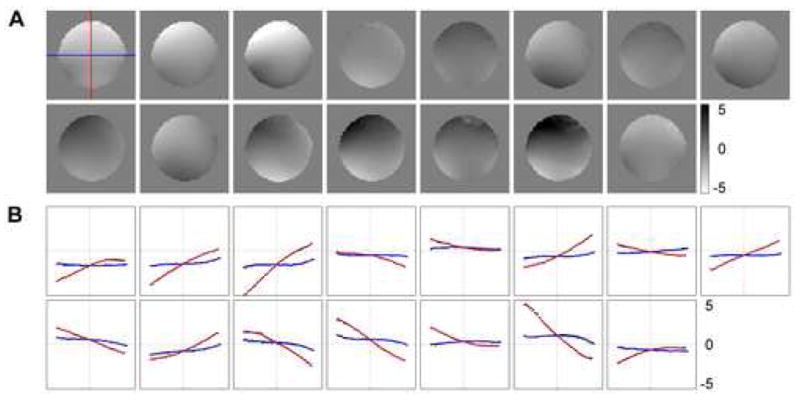
(A) Eddy current-induced residual magnetic field maps (in 10−7 T) corresponding to the 15 diffusion-weighting directions. (B) Central profiles along the frequency-encoding (right/left) and phase-encoding (anterior/posterior) directions (black dots) fitted with a two-dimensional third-order polynomial (blue and red lines, respectively).
Figure 2 shows in vivo results in a representative slice. Correction of susceptibility- and/or eddy current-induced distortions was applied to the single SE data, whereas only correction of susceptibility-induced distortions was applied to the dual SE data. First, to assess the effects of the susceptibility-induced distortions, contour lines were generated from the undistorted FSE images and overlaid on the non-diffusion-weighted images (Fig. 2A). Geometric distortions are clearly visible in both the single SE and dual SE images, most prominently in the frontal regions of the brain (arrows) as well as in the genu of the corpus callosum, which are displaced posteriorly and anteriorly with respect to the contour lines, respectively. These distortions are predominantly caused by large susceptibility-induced B0 inhomogeneities near air/tissue interfaces, as shown on the non-diffusion-weighted B0 map (Fig. 2D), and are effectively corrected for with our proposed method. Second, to assess the effects of the direction-dependent eddy current-induced distortions, maps of the variance of the diffusion-weighted images across all 15 diffusion-weighting directions were computed (Fig. 2B). Regions with artificially high variance are clearly visible at the anterior and posterior edges of the brain in the single SE map (arrows), but not in the dual SE map, as expected. These artifacts remain after correcting for the susceptibility-induced distortions only, but are effectively removed by applying the full correction. Third, to assess the influence of the direction-dependent distortions on parameters derived from the diffusion tensor, FA maps were computed and color-coded according to the direction of the first eigenvector (Fig. 2C). As expected, regions with artificially high FA values are seen at the anterior and posterior edges of the brain in the single SE map (arrows), and these artifacts are effectively suppressed with our correction method.
Fig. 2.
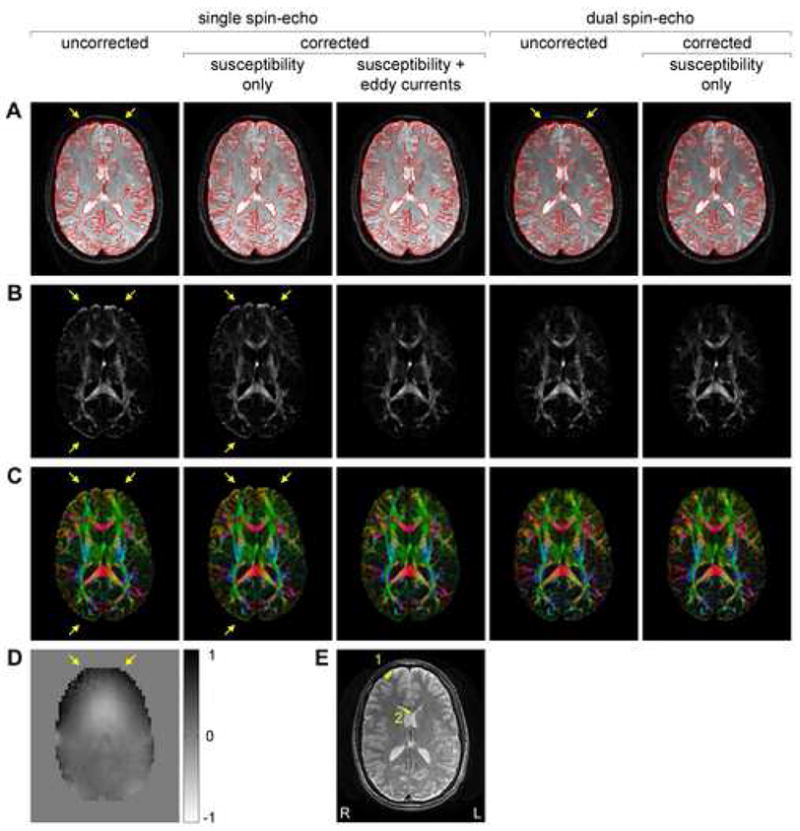
Non-diffusion-weighted images (A), variance of the diffusion-weighted images across all 15 diffusion-weighting directions (B), and color-coded FA maps (C) obtained with the single SE and dual SE sequences before and after correction of susceptibility- and/or eddy current-induced geometric distortions. (D) Non-diffusion-weighted B0 map (in 10−6 T). (E) Undistorted FSE image used to generate the contour lines in (A) with overlaid ROIs used in Table 1. The arrows in (A) and (B,C) show susceptibility- and eddy current-induced distortions, respectively. The images in (A) have the same scaling and show that the dual SE acquisition results in a lower SNR than the single SE acquisition. On the other hand, the variance maps in (B) are normalized to account for this difference in SNR. The FA maps in (C) are color-coded according to the direction of the first eigenvector (red = right/left, green = anterior/posterior, blue = superior/inferior).
To illustrate these effects more quantitatively, FA values were measured in regions-of-interest (ROIs) traced on the undistorted FSE image (Fig. 2E) near a gray/white matter interface in the right frontal lobe (ROI 1) and in the genu of the corpus callosum (ROI 2), where the distortions are particularly severe. Using the FA value computed from the corrected dual SE data as the “gold standard”, Table 1 shows that the FA values computed from the uncorrected dual SE data, the single SE data corrected for susceptibility-induced distortions only, and the uncorrected single SE data are largely overestimated or underestimated because of misregistration due to susceptibility-induced distortions, direction-dependent eddy current-induced distortions, or both, respectively. On the other hand, the FA values computed from the fully corrected single SE and dual SE data are very similar, thus demonstrating the effectiveness of our correction method. Furthermore, the FA values computed from the single SE data corrected using two separate sets of B0 maps acquired on the phantom are very consistent, demonstrating both the robustness of our correction method and the temporal stability of the eddy current-induced magnetic fields.
Table 1.
FA values (mean ± standard deviation) measured in the ROIs shown in Fig. 2E.
| ROI 1 | ROI 2 | |||
|---|---|---|---|---|
| Single SE, uncorrected | 0.361 ± 0.189 | (+19.4%)a | 0.687 ± 0.154 | (−9.15%) |
| Single SE, corrected, susceptibility only | 0.364 ± 0.096 | (+20.4%) | 0.748 ± 0.089 | (−1.03%) |
| Single SE, corrected, susceptibility and eddy currents (#1)b | 0.299 ± 0.077 | (−1.23%) | 0.755 ± 0.089 | (−0.09%) |
| Single SE, corrected, susceptibility and eddy currents (#2) | 0.303 ± 0.079 | (+0.33%) | 0.756 ± 0.084 | (+0.05%) |
| Dual SE, uncorrected | 0.191 ± 0.115 | (−36.7%) | 0.697 ± 0.150 | (−7.77%) |
| Dual SE, corrected, susceptibility only | 0.302 ± 0.090 | 0.756 ± 0.090 | ||
Percentage change with respect to the FA value computed from the corrected dual SE data.
(#1) and (#2) represent data corrected using two separate sets of B0 maps acquired on the phantom.
These two sets of B0 maps were acquired 8 hours apart. To demonstrate the temporal stability of the eddy currents over a longer time period, we acquired three additional sets of B0 maps on the phantom over a period of 15 days. The polynomial coefficients representing the eddy current-induced magnetic fields were derived for each data set, and their standard deviation was computed for all diffusion-weighting directions. The average standard deviation of the zeroth-order coefficient is 9.1×10−9 T, corresponding to a global shift of the image by only 0.03 pixel for our choice of imaging parameters, whereas the average standard deviation of the first-order coefficients are 8.3×10−8 and 1.6×10−7 T/m, corresponding to a shearing and scaling of the image by only 0.08 and 0.15 pixel across the image, respectively. These results thus demonstrate the temporal stability of the eddy current-induced magnetic fields over a time period of at least two weeks.[TKT5]
DISCUSSION AND CONCLUSIONS
Our studies have shown that high-resolution SENSE DTI acquisitions suffer from severe geometric distortions caused by subject-dependent susceptibility effects and diffusion-weighting direction-dependent eddy currents. This is especially true near air/tissue interfaces as well as in the basal ganglia where iron storage and calcifications may induce large B0 inhomogeneities.[TKT6] Moreover, the misregistration among different diffusion-weighted images can result in substantial errors in the estimation of local ADC and FA values, as well as in fiber tracking. Such errors have important implications in clinical applications of DTI, as artificially increased FA values could lead to inaccurate clinical diagnosis.[TKT7] Both the susceptibility- and eddy current-induced distortions can be effectively, efficiently, and reliably corrected for with our proposed method. The latter is as effective as the commonly used twice-refocused SE method (Reese et al., 2003) in correcting for eddy current-induced distortions. However, this dual SE sequence requires a longer TE than a single SE sequence with identical diffusion-weighting, resulting in a lower SNR. (In our studies, the single SE sequence allowed a 20% improvement in SNR as compared to the dual SE sequence.)[TKT8] Furthermore, susceptibility-induced distortions remain and still need to be corrected for.
In our proposed method, the eddy current-induced magnetic fields are measured on a phantom, so that only one B0 map needs to be acquired in vivo to measure the subject-dependent susceptibility-induced B0 inhomogeneities, which can be performed very efficiently. Furthermore, full characterization of the eddy current-induced magnetic fields is not required for every DTI acquisition, but can be performed on a much less frequent basis as long as the eddy currents remain temporally stable. As such, this method has an overall much improved efficiency as compared to several previously proposed correction methods (Jezzard et al., 1998; Haselgrove and Moore, 1996; Andersson et al., 2003; Bodammer et al., 2004; Shen et al., 2004). This is particularly advantageous when a large number of diffusion-weighting directions is used, such as in high angular resolution diffusion imaging.
In conclusion, our studies have shown that a comprehensive correction of both susceptibility-induced and high-order eddy current-induced geometric distortions can be applied to high-resolution SENSE DTI acquisitions, with only nominal time penalty in practice. It is anticipated that such an effective, efficient, and reliable method will allow improved delineation of ADC and FA maps, and enhance fiber tracking accuracy in modern DTI experiments where SENSE acquisitions are commonly used.
Acknowledgments
We thank Susan Music and Natalie Goutkin for their assistance with MRI scanning. This work was supported by grants RR 21382 and NS 50329 from the National Institutes of Health.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Andersson JLR, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage. 2003;20:870–888. doi: 10.1016/S1053-8119(03)00336-7. [DOI] [PubMed] [Google Scholar]
- Ardekani S, Sinha U. Geometric distortion correction of high-resolution 3 T diffusion tensor brain images. Magn Reson Med. 2005;54:1163–1171. doi: 10.1002/mrm.20651. [DOI] [PubMed] [Google Scholar]
- Bammer R, Auer M, Keeling SL, Augustin M, Stables LA, Prokesch RW, Stollberger R, Moseley ME, Fazekas F. Diffusion tensor imaging using single-shot SENSE-EPI. Magn Reson Med. 2002;48:128–136. doi: 10.1002/mrm.10184. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Pierpaoli C. A simplified method to measure the diffusion tensor from seven MR images. Magn Reson Med. 1998;39:928–934. doi: 10.1002/mrm.1910390610. [DOI] [PubMed] [Google Scholar]
- Bastin ME. Correction of eddy current-induced artefacts in diffusion tensor imaging using iterative cross-correlation. Magn Reson Imaging. 1999;17:1011–1024. doi: 10.1016/s0730-725x(99)00026-0. [DOI] [PubMed] [Google Scholar]
- Bodammer N, Kaufmann J, Kanowski M, Tempelmann C. Eddy current correction in diffusion-weighted imaging using pairs of images acquired with opposite diffusion gradient polarity. Magn Reson Med. 2004;51:188–193. doi: 10.1002/mrm.10690. [DOI] [PubMed] [Google Scholar]
- Chen B, Guo H, Song AW. Correction for direction-dependent distortions in diffusion tensor imaging using matched magnetic field maps. NeuroImage. 2006;30:121–129. doi: 10.1016/j.neuroimage.2005.09.008. [DOI] [PubMed] [Google Scholar]
- Haselgrove JC, Moore JR. Correction for distortion of echo-planar images used to calculate the apparent diffusion coefficient. Magn Reson Med. 1996;36:960–964. doi: 10.1002/mrm.1910360620. [DOI] [PubMed] [Google Scholar]
- Horsfield MA. Mapping eddy current induced fields for the correction of diffusion-weighted echo planar images. Magn Reson Imaging. 1999;17:1335–1345. doi: 10.1016/s0730-725x(99)00077-6. [DOI] [PubMed] [Google Scholar]
- Jaermann T, Crelier G, Pruessmann KP, Golay X, Netsch T, van Muiswinkel AMC, Mori S, van Zijl PCM, Valavanis A, Kollias S, Boesiger P. SENSE-DTI at 3 T. Magn. Reson Med. 2004;51:230–236. doi: 10.1002/mrm.10707. [DOI] [PubMed] [Google Scholar]
- Jezzard P, Barnett AS, Pierpaoli C. Characterization of and correction for eddy current artifacts in echo planar diffusion imaging. Magn Reson Med. 1998;39:801–812. doi: 10.1002/mrm.1910390518. [DOI] [PubMed] [Google Scholar]
- Le Bihan D, Mangin JF, Poupon C, Clark CA, Pappata S, Molko N, Chabriat H. Diffusion tensor imaging: concepts and applications. J Magn Reson Imaging. 2001;13:534–546. doi: 10.1002/jmri.1076. [DOI] [PubMed] [Google Scholar]
- Mori S, Zhang J. Principles of diffusion tensor imaging and its applications to basic neuroscience research. Neuron. 2006;51:527–539. doi: 10.1016/j.neuron.2006.08.012. [DOI] [PubMed] [Google Scholar]
- Papadakis NG, Smponias T, Berwick J, Mayhew JEW. k-space correction of eddy-current-induced distortions in diffusion-weighted echo-planar imaging. Magn Reson Med. 2005;53:1103–1111. doi: 10.1002/mrm.20429. [DOI] [PubMed] [Google Scholar]
- Pruessman KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42:952–962. [PubMed] [Google Scholar]
- Reese TG, Heid O, Weisskoff RM, Wedeen VJ. Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo. Magn Reson Med. 2003;49:177–182. doi: 10.1002/mrm.10308. [DOI] [PubMed] [Google Scholar]
- Rohde GK, Barnett AS, Basser PJ, Marenco S, Pierpaoli C. Comprehensive approach for correction of motion and distortion in diffusion-weighted MRI. Magn Reson Med. 2004;51:103–114. doi: 10.1002/mrm.10677. [DOI] [PubMed] [Google Scholar]
- Shen Y, Larkman DJ, Counsell S, Pu IM, Edwards D, Hajnal JV. Correction of high-order eddy current induced geometric distortion in diffusion-weighted echo-planar images. Magn Reson Med. 2004;52:1184–1189. doi: 10.1002/mrm.20267. [DOI] [PubMed] [Google Scholar]
- Zhuang J, Hrabe J, Kangarlu A, Xu D, Bansal R, Branch CA, Peterson BS. Correction of eddy-current distortions in diffusion tensor images using the known directions and strengths of diffusion gradients. J Magn Reson Imaging. 2006;24:1188–1193. doi: 10.1002/jmri.20727. [DOI] [PMC free article] [PubMed] [Google Scholar]


