On the relative magnitudes of photosynthesis, respiration, growth and carbon storage in vegetation

Abstract

Background and Aims

The carbon balance of vegetation is dominated by the two large fluxes of photosynthesis (P) and respiration (R). Mechanistic models have attempted to simulate the two fluxes separately, each with their own set of internal and external controls. This has led to model predictions where environmental change causes R to exceed P, with consequent dieback of vegetation. However, empirical evidence suggests that the R : P ratio is constrained to a narrow range of about 0·4–0·5. Physiological explanations for the narrow range are not conclusive. The aim of this work is to introduce a novel perspective by theoretical study of the quantitative relationship between the four carbon fluxes of P, R, growth and storage (or its inverse, remobilization).

Methods

Starting from the law of conservation of mass – in this case carbon – equations are derived for the relative magnitudes of all carbon fluxes, which depend on only two parameters: the R : P ratio and the relative rate of storage of carbon in remobilizable reserves. The equations are used to explain observed flux ratios and to analyse incomplete data sets of carbon fluxes.

Key Results

The storage rate is shown to be a freely varying parameter, whereas R : P is narrowly constrained. This explains the constancy of the ratio reported in the literature. With the information thus gained, a data set of R and P in grassland was analysed, and flux estimates could be derived for the periods after cuts in which plant growth is dominated by remobilization before photosynthesis takes over.

Conclusions

It is concluded that the relative magnitudes of photosynthesis, respiration, growth and substrate storage are indeed tightly constrained, but because of mass conservation rather than for physiological reasons. This facilitates analysis of incomplete data sets. Mechanistic models, as the embodiment of physiological mechanisms, need to show consistency with the constraints.

INTRODUCTION

The carbon balance of vegetation is dominated by two large fluxes: the inflow of carbon through photosynthesis and the outflow through respiration. The uptake of carbon as CO₂ in photosynthesis is the only significant process of carbon acquisition, because the uptake of carbon in organic form (such as soil amino acids) is small in comparison. On the other hand, although respiration is the dominant process of carbon loss, plants do lose biomass through senescence as well, and root exudation further contributes to carbon loss. Root exudation and senescence are not further discussed herein, as they do not affect the analysis we are presenting.

Net primary productivity (NPP) is defined as the difference between photosynthesis and autotrophic respiration. When NPP is positive, the plants are increasing their structural biomass and/or their pool of reserves. Modelling NPP has posed problems because of the presumed need to simulate the two large fluxes of photosynthesis and respiration separately (Ågren, 1996). Simulating the fluxes separately was considered necessary because they are subject to different internal and external controls (Amthor, 2000; Cannell and Thornley, 2000). However, models in which photosynthesis and respiration were indeed uncoupled often showed a lack of balance – with extreme responses of NPP to changes in the environment. For example, model predictions that much of the Amazonian rainforest may disappear this century because of global warming have been shown to depend in part on the assumption that respiration may increase independently of concomitant changes in photosynthesis (Huntingford et al., 2004; D. Galbraith et al., CEH-Edinburgh, UK, unpubl. res).

A few years ago, the work of Gifford (1995, 2003) seemed to provide a solution to such model instability. Gifford reasoned that respiration cannot be independent of photosynthesis because the substrate for respiration originates from photosynthesis, i.e. plants cannot respire what they did not photosynthesize before. Gifford proceeded by measuring photosynthesis and respiration of wheat plants over 24 h periods, under different temperature regimes ranging from 15 to 30 °C on average. He found that the ratio of respiration and photosynthesis (R : P) was relatively constant, 0·40–0·45, and independent of temperature. This was consistent with earlier work by Ryle et al. (1976), Winzeler et al. (1976) and Yamaguchi (1978), as reviewed by Monteith (1981). Dewar et al. (1999) showed that explicit incorporation of substrate dynamics could also constrain R : P in dynamic models. Further corroborating empirical evidence, for different plant species, was presented by various workers (Keith et al., 1997; Monje and Bugbee, 1998; Malhi et al., 1999; Cannell and Thornley, 2000). DeLucia et al. (2007), in a review of 60 forest studies, were able to account for 72 % of variation in NPP using a linear regression on gross primary productiviety (GPP) with a slope of 0·53. Remaining variation was attributed to differences between species and in tree age. Some mechanistic understanding of the constancy of R : P was provided by Atkin et al. (2005), who found that respiration and photosynthesis in most examined plant species acclimated similarly after temperature change. More recently, Atkin et al. (2007) confirmed homeostasis of R : P, in Plantago spp., but this was not maintained when plants were subjected to higher temperatures than usually experienced in their habitats. Differences between photosynthetic and respiratory acclimation to temperature have been reported by Campbell et al. (2007) and Hartley et al. (2006). Cheng et al. (2000) found that the R : P of sunflower was also insensitive to changes in atmospheric CO₂ concentration. Overall, the research confirms Monteith's (1981) assessment that the ratio may vary over short time periods but is constant over periods of weeks and longer. Gifford suggested that the constancy of the R : P ratio obviated the need for modellers to have separate calculations for respiration in their model.

All of the studies mentioned above proposed physiological explanations for observed values of the R : P ratio. In contrast, the aim of this study is to show that R : P is necessarily constrained between quite narrow bounds, albeit not for biological reasons but for mathematical ones. The possibility of such a mathematical analysis was suggested by the work of Amthor (2000), who analysed the role of respiration associated with growth and maintenance processes. We present a theoretical framework that relates photosynthesis and respiration to the other major fluxes of carbon in vegetation, i.e. growth, storage and remobilization. We show how consideration of the law of conservation of mass reveals constraints on the relative magnitudes of the different carbon-consuming processes. These constraints apply to any vegetation type and any time scale. As a corollary of our analysis, we show how grassland data sets that are incomplete with respect to the full carbon budget of vegetation can be extended with robust estimates of the missing processes.

The layout of this paper is as follows. Data on photosynthesis and respiration of grass swards are presented first. The theoretical analysis of the constraints on photosynthesis, respiration, growth and carbon storage in vegetation are then provided. In the subsequent section, it is shown what this implies for the values that are theoretically possible for respiration and storage. The analysis is then applied to the grass sward data, and the paper is concluded by a brief discussion.

MATERIALS AND METHODS

Data

Experiments were carried out under semi-controlled conditions in the Wageningen Rhizolab (Van de Geijn et al., 1994). In this facility, a 2 year experiment started in the autumn of 1993 with perennial ryegrass (Lolium perenne L., ‘Preference’) swards under enclosures at 350 and 700 ppm atmospheric CO₂ concentration with two replicates (Schapendonk et al., 1997). Only the data from the lower CO₂ concentration are used here. The surface area of the swards was 1·55 m². Each compartment had a separate drip irrigation system. Crop canopy photosynthesis, respiration and transpiration were measured simultaneously and continuously on half of the compartments at a time. Multiple sensors for measuring soil moisture status, electrical conductivity, temperature, soil respiration, trace gasses and oxygen were installed in spatial patterns in accordance with the requirements of the experiments. The rooting containers were filled with layers of loamy clay. Soil respiration was measured by forcing air from the canopy enclosures into the soil. The continuous flux was on average 30 m³ h⁻¹. The initial percentage organic matter in the soil was 4·7 % and the rooting profile was 1 m. The temperatures in the enclosures were controlled at set points that were equal to the measured outside temperature. Water shortage was prevented by irrigation. Respiration rates in the soil compartment, photosynthesis, evapotranspiration and dark respiration of the swards were monitored online at 6 min intervals in all compartments. The fluxes of water and carbon were calculated from the differences between CO₂ concentrations in the enclosures and in the air that was forced through the soil compartment into a drain at a depth of 15 cm. The actual depth of the air profile was 35 cm. Nitrogen (8 g m⁻²) was supplied after each harvest. The swards were cut at time intervals of 3 weeks at a clipping height of 0·05 m.

Theoretical analysis of the quantitative relationships between photosynthesis, respiration, growth and carbon storage in vegetation

Two types of respiration are distinguished, provisionally called growth respiration (R_g) and maintenance respiration (R_m):

1

where NPP is net primary productivity and P is photosynthesis. All terms of eqn 1 are in units of g C m⁻² d⁻¹. Ignoring senescence for the moment, NPP can also be written as:

2

where G is growth, i.e. the formation of structural biomass, and S is storage, i.e. the rate of increase of the plant storage pool of labile carbon (both again in units of g C m⁻² d⁻¹). Growth respiration R_g is proportional to growth G:

3

where Y_g is the growth yield, i.e. the amount of structural biomass formed per unit of photosynthates. Next, we introduce the symbol ‘ρ’ for the dimensionless R : P ratio:

4

Finally, we define a dimensionless allocation parameter ‘α’, defined as the ratio of storage to photosynthesis:

5

The five equations just given embody all the information we use in the following analysis of the plant carbon balance, which therefore will be time scale independent. The values of ρ and α might be quite constant in practice, but we will show examples of the carbon balance for different values of these two parameters. First we use the above equations to show that, if we know or assume a certain value for ρ, the respiration terms R_g and R_m cannot vary freely but are completely determined by the value of α. Moreover, if both ρ and α are known, we know exactly how photosynthates are allocated between growth, growth respiration, maintenance respiration and storage.

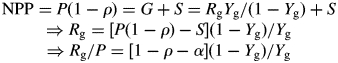6a

and

6b

The growth yield Y_g is independent of environmental conditions (Penning de Vries et al., 1974) and typically has a value of about 3/4 (Thornley and Cannell, 2000). This allows us to simplify the two equations for R_g/P and R_m/P further and brings us to the following set of four equations each only dependent on ρ and α:

7a

7b

7c

7d

So the complete carbon balance is determined by only knowing two parameters, ρ and α. If ρ is as constant as Gifford's work suggests, the above four equations can be simplified further. Then we only need to know the storage rate to tell us the relative magnitude of the four different photosynthate-consuming processes.

RESULTS

Implied constraints on carbon use parameters

Equation (7a) (or 7d) and eqn (7b) put constraints on the possible values of ρ and α, because respiration rates cannot be negative:

8

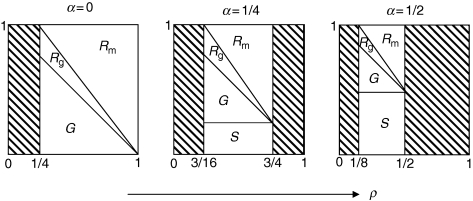
Figure 1 shows examples of the carbon balance, as determined by eqns (7) and (8) for three different storage rates (α = 0, 1/4, 1/2) and for the whole range of permitted values of the R : P ratio (ρ). If observations show that ρ is strongly constrained, say between 0·4 and 0·5, we can see in Fig. 1 that the carbon balance is tightly constrained too. Note that, over short periods of time, α can be negative – when plants remobilize their reserves. For example, when α = −0·5, the lower bound of ρ increases to 3/8 but its upper bound then exceeds unity. Figure 1 suggests that part of the empirically observed constancy of ρ is due to the fact that many values of ρ are not permitted (as indicated by the hatched areas of the graphs) because of the constraint quantified in eqn (8). It may therefore not be surprising that ρ is often about 0·4–0·5, given that lower or greater values tend to imply carbon use that cannot be sustained by photosynthesis.

Fig. 1.

Carbon balance as a function of the R : P ratio (ρ), for three different values of the ratio of storage to photosynthesis (α is 0, 1/4, 1/2). The graph shows carbon use in storage (S), growth (G), growth respiration (R_g) and maintenance respiration (R_m). All four flows are normalized with respect to P, so they sum to 1. The hatched parts of the graph indicate impossible values of ρ.

Equation (8) shows the constraints on ρ as a function of storage rate α. The equivalent constraint on α as a function of ρ is:

9

This relationship may be more helpful than eqn (8) in data analysis when respiration has been measured but storage rate has not. Furthermore, we would know exactly the value of α if the fraction of total respiration due to growth were known. One result that immediately follows from eqn (9) is that whenever ρ is <1/4, α has to be positive. This means that there can be no remobilization of reserves (negative α) in periods of low respiration rates.

Application of the analysis to the grass sward data

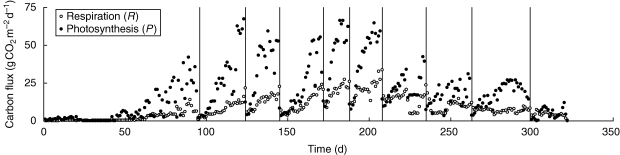
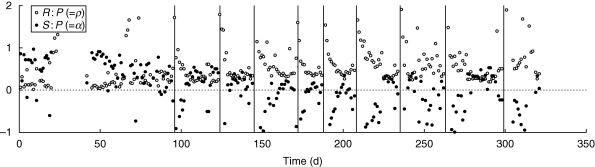
Here we analyse the grass sward data presented before by means of the theory derived above. The purpose of the data analysis is not that of testing the equations (which follow directly from mass conservation), but of demonstrating how the mathematical viewpoint may help extract hidden information from studies of carbon dynamics. The grassland data set is, as many such data sets are, incomplete in that only photosynthesis and respiration had been measured, but growth and storage had not. We use the equations to help fill these gaps. We begin by calculating the ratio of respiration and photosynthesis (=ρ) from the data presented in Fig. 2. The average values of ρ for 1994 and 1995 were 0·59 and 0·69, respectively. The variation over time was similar within both years – Fig. 3 shows the example of 1994. During the first 100 days of the year ρ tends to be <1/4, and above that value thereafter. Given the constraint expressed in eqn (9), we can conclude, unsurprisingly, that no remobilization occurs during the early winter months. To proceed with the analysis, we further assume that respiration consists of equal parts of growth and maintenance respiration, in which case α equals 1 – 2·5 ρ. This allows us to calculate the pattern of storage and remobilization of the sward throughout the year (Fig. 3). The analysis shows that cutting of the grass sward tends to be followed by periods of 3–11 d of remobilization of reserves. This conclusion is fairly robust to the partitioning of respiration. If growth respiration is half or double maintenance respiration, the calculated remobilization period is on average about 1 d shorter or 2 d longer, respectively. This information from calculation would have been difficult to establish by measurement on whole grass swards, but pot experiments have provided similar results (Donaghy and Fulkerson, 1997; Schnyder and de Visser, 1999).

Fig. 2.

Daily total photosynthesis and respiration in a grass sward (Lolium perenne), grown under the semi-controlled conditions of the Wageningen rhizolab in 1994. Vertical lines indicate the days at which the sward was cut.

Fig. 3.

Daily rates of respiration, R, and storage (or remobilization if negative), S, in a grass sward (Lolium perenne), grown under the semi-controlled conditions of the Wageningen rhizolab in 1994. The rates are non-dimensionalized by expressing them relative to daily gross photosymthetic rate, P. R : P was calculated from the data in Fig. 2, whereas S : P was calculated using the equations derived in the main text. Vertical lines indicate the days at which the sward was cut.

DISCUSSION

The analysis presented here has shown, without reliance on strong assumptions, that the various carbon-demanding processes in vegetation show quantifiable constraints on their relative magnitudes [Fig. 1, eqns (7)–(9)]. This may help explain observations of the conservative nature of the ratio of plant respiration to photosynthesis (Gifford, 1995, 2003). Because our equations are derived from the law of conservation of mass, they apply to any vegetation type and time scale, irrespective of the environmental conditions to which the plants are subjected. This explains, for example, why the constancy of R : P was not found to be affected by elevated CO₂ (Cheng et al., 2000). The equations also allow relatively robust estimates of unobserved processes to be made when our measurements are incomplete (Fig. 3). Such analysis is not affected by senescence and root exudation in so far as these are not active processes contributing to total respiration. However, they can affect measurement of G and S, and therefore the accuracy of the analysis in practice.

In periods of negative storage, i.e. remobilization of carbon reserves, eqns (7a)–(7d) are still valid, but the value of α then is negative. In such cases, the R : P ratio ‘ρ’ is no longer constrained to small values, and can even exceed unity. An extreme example is the carbon balance at night or in the winter when photosynthesis may be zero or very small and there may still be growth occurring. Another example is grassland shortly after cutting (as shown in this paper for the rhizolab data). However, the long-term value of α cannot be negative, because of mass conservation, and this explains why R : P is reported to be most constrained at longer time scales (Monteith, 1981). Under conditions of steady-state growth, α itself must be constant to maintain the proportions of the plant, and a value of the order of 0·2 may then be plausible (McDonald et al., 1986).

There are three ways in which the theoretical analysis may aid process-based modelling. First, the analysis shows how observations on the R : P ratio and allocation to storage of a system constrain its carbon balance, and we can use that information to quantify the different carbon flows in a model. Secondly, the analysis may help in calibration of process-based models by showing which values of carbon fluxes are more probable than others in the light of perhaps uncertain information on ρ and α. Finally, the analysis may help in testing models. Unbalanced carbon fluxes have been put forward as the major driver for model predictions of vegetation loss in response to global change. Our analysis shows that it would be prudent to verify that the simulated carbon balance does not violate the mathematical constraints on the relative magnitudes of fluxes.