A non-uniformly sampled 4D HCC(CO)NH-TOCSY experiment processed using maximum entropy for rapid protein sidechain assignment

Abstract

One of the stiffest challenges in structural studies of proteins using NMR is the assignment of sidechain resonances. Typically, a panel of lengthy 3D experiments are acquired in order to establish connectivities and resolve ambiguities due to overlap. We demonstrate that these experiments can be replaced by a single 4D experiment that is time-efficient, yields excellent resolution, and captures unique carbon-proton connectivity information. The approach is made practical by the use of non-uniform sampling in the three indirect time dimensions and maximum entropy reconstruction of the corresponding 3D frequency spectrum. This 4D method will facilitate automated resonance assignment procedures and it should be particularly beneficial for increasing throughput in NMR-based structural genomics initiatives.

Introduction

The development of non-uniform sampling (NUS) approaches to data collection in multidimensional NMR experiments represents the most fundamental change in the way that NMR data are collected since the development of Fourier transform (FT) NMR by Ernst and Anderson some 50 years ago.[1] Uniform sampling that is required by the discrete Fourier transform (DFT) prevents full realization of the benefits from costly ultra-high-field magnets because it is impractical to sample long evolution times, required for high resolution, in the indirect dimensions of multidimensional experiments. The use of non-uniform sampling is essential for making high-resolution 3D and 4D NMR experiments practical, especially for marginally soluble or transiently stable systems.

High-resolution multidimensional spectra are of particular interest in studies of complex biomolecules that are isotopically enriched with ¹³C and ¹⁵N.[2] These experiments are used both for resonance assignment of all ¹H, ¹³C and ¹⁵N atoms in the molecule and to extract interproton distance restraints from dipolar interactions. For proteins, this generally involves sequential assignment of backbone amide resonances followed by assignment of sidechain nuclei and, finally, extraction of distance and dihedral-angle restraints.

One of the most challenging steps in this process is the assignment of sidechain resonances. This process commonly involves the acquisition of two complementary 3D experiments, the H(CC)(CO)NH-TOCSY and (H)CC(CO)NH-TOCSY, which produce proton and carbon correlations respectively.[3] These experiments reveal correlations between the amide ¹H-¹⁵N pair of residue i and the aliphatic sidechain atoms of the previous residue, i-1. Thus, each spectrum contains roughly one resonance per aliphatic sidechain nucleus. These experiments, however, do not provide information about carbon-hydrogen connectivities, often leading to ambiguous assignments. This problem can be ameliorated using a 4D version of this experiment[4], but conventional uniform sampling of this experiment will require a prohibitively long acquisition time. In principle, it should be possible to reduce the experiment time through NUS.

A variety of methods have recently been introduced for processing NUS data with more than three dimensions.[5; 6; 7; 8; 9; 10] These methods are generally restricted to situations of high signal-to-noise ratio (S/N). The relatively low sensitivity of HCC(CO)NH-TOCSY type experiments (compared to HNCO, CBCA(CO)NH etc.) makes them poor candidates for these reconstruction methods. An alternative approach that works well in situations of low S/N is maximum entropy reconstruction (MaxEnt).[11; 12] However, an implementation capable of reconstructing three indirect dimensions simultaneously (i.e., 4D experiments) has not been available (note that very recently the FM approach was applied to a 4D-NOESY dataset[13], this method attempts to recover signal amplitudes accurately but suffers from very long processing times). Here, we use a new implementation of a previously-described MaxEnt algorithm[14; 15], applicable to 3D reconstruction in the indirect dimensions of a new 4D HCC(CO)NH-TOCSY experiments acquired using NUS (see Fig. 1).

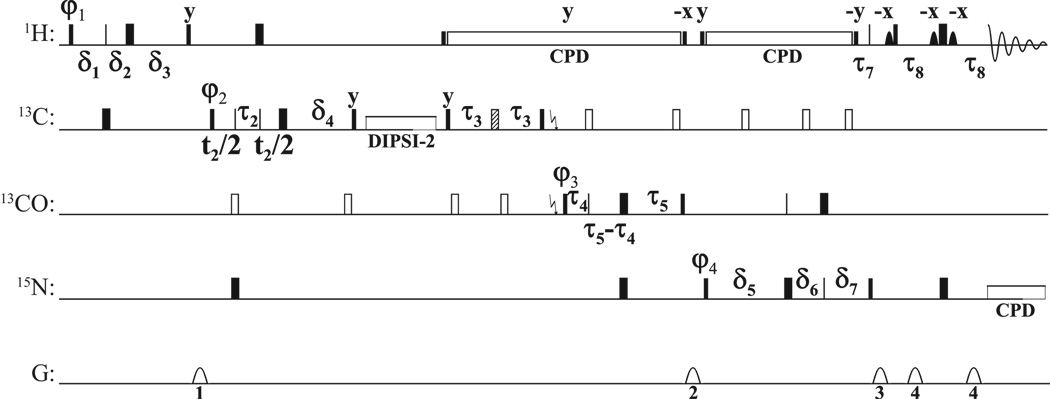
Figure 1.

For ¹H and ¹⁵N, narrow and wide rectangles represent 90° and 180° pulses (for hard pulses at 28.3 and 6.25 kHz) respectively. For ¹³C, solid narrow and wide rectangles denote on-resonance Q5 and Q3 pulses[27], while open rectangles represent pulses that are applied off-resonance by means of a phaseramp.[28] The hatched pulse represents a C_α-selective Q3 pulse. For ¹³C, every second 90° pulse is a time-reversed Q5. The pulse lengths are 274 µs for Q5/time-reversed Q5 pulses at a RF field strength of 16.7 kHz, 170 µs at 19.4 kHz for 180° pulses applied to all aliphatic carbons, and 667 µs at 4.95 kHz for the C_α-selective Q3 pulse. Solid shapes are selective pulses applied to the water magnetization (Sinc1 shape of 1 ms length at 425 Hz). The ¹H decoupling (DIPSI2[29] at 6.25 kHz) is flanked by 90° pulses given at the same power level. A DIPSI2[29] spinlock is applied for 11.5 ms at 10 kHz to achieve the CC TOCSY transfer. A garp4 supercycle is used for ¹⁵N decoupling during acquisition (1.39 kHz).[30] The delays are: τ₁ = 1/(4¹J_CH) (1.7 ms), τ₂ = 1/(6¹J_CH) (1.1 ms), τ₃ = 1/(4¹J_CαCO) (4.5 ms), τ₄ = 1/(4¹J_CαCO) (4.4 ms), τ₅ = 1/(4¹J_CON) (12.4 ms), τ₆ = τ₅, τ₇ = (1/(2¹J_NH) (5.5 ms), τ₈ = 2.3ms 1/(4¹J_NH) (2.3 ms; reduced to partially compensate for relaxation losses),ε₁ = τ_p (¹³C 180°) + initial setting of (1−κ₁)t₁/2, ε₂ = τ_p (¹H 180°) + initial setting of t₂, ε₃ = τ_p (¹³C 180°) + initial setting of (1−κ₃)t₃/2, δ₁=τ₁+t₁/2, δ₂=(1−κ₁)t₁/2, δ₃=τ₁−κ₁t₁/2+ε₁, δ₄=τ₂+ε₂, δ₅=τ₆−κ₃t₃/2+ε₃, δ₆=(1−κ₃)t₃/2, δ₇=τ₆+t₃/2. All pulses are along x except otherwise noted. The phase cycles are φ₁ = x, x, x, x, x, x, x, x, −x, −x, −x, −x, −x, −x, −x, −x; φ₂ = x, x, −x, −x; φ₃ = x, x, x, x, −x, −x, −x, −x; φ₄ = x, −x; φ_receive) = x, −x, −x, x, −x, x, x, −x, −x, x, x, −x, x, −x, −x, x. Gradients (1 ms) are sine-shaped with an amplitude of 25, 20, 30 and 15 G/cm respectively. Labeling of chemical shifts is performed in a semi-constant time fashion.[31; 32; 33] Phase sensitive spectra are obtained using the States-TPPI method[34] by either incrementing τ₁, τ₂ or decrementing τ₄ respectively in different experiments. Water suppression was achieved by using a soft pulse WATERGATE scheme.[35; 36]

Projections of a related 5D experiment[16] have recently been used to extract sidechain resonance frequencies. Such projections, however, have been shown to produce significant artifacts if the fully-dimensional spectrum is reconstructed.[17] Thus without further processing or analysis (e.g., APSY[16], PRODECOMP[18], etc.), the data are not sufficient to accurately determine the full spectrum. Similarly, non-uniform FT (also referred to as sparse multidimensional Fourier transform) processing of this 5D experiment has been reported, using a 1.5 mM sample of ubiquitin.[19] The advantages of MaxEnt reconstruction over non-uniform FT, particularly in situations of low S/N, have been extensively demonstrated.[12; 20]

We present here the first NUS 4D HCC(CO)NH-TOCSY spectrum, reconstructed using 3D MaxEnt, which we compare with corresponding conventional 3D spectra.

Results

The maximum entropy algorithm used here has been described in detail elsewhere[14; 15], and the formulae for the entropy and constraint readily generalize to multidimensional data. However, because MaxEnt reconstruction is nonlinear, MaxEnt must be the last time-to-frequency transformation applied. Thus, if MaxEnt is to be used in t₁, then the t₂ dimension must be transformed to the frequency domain first. If MaxEnt is to be used for both t₁ and t₂, then it must be applied to both dimensions simultaneously, rather than one at a time. The IDFT (inverse discrete Fourier transform) operation used and the corresponding sums can be applied along as many dimensions as desired, with concomitant scaling of processing and memory requirements.

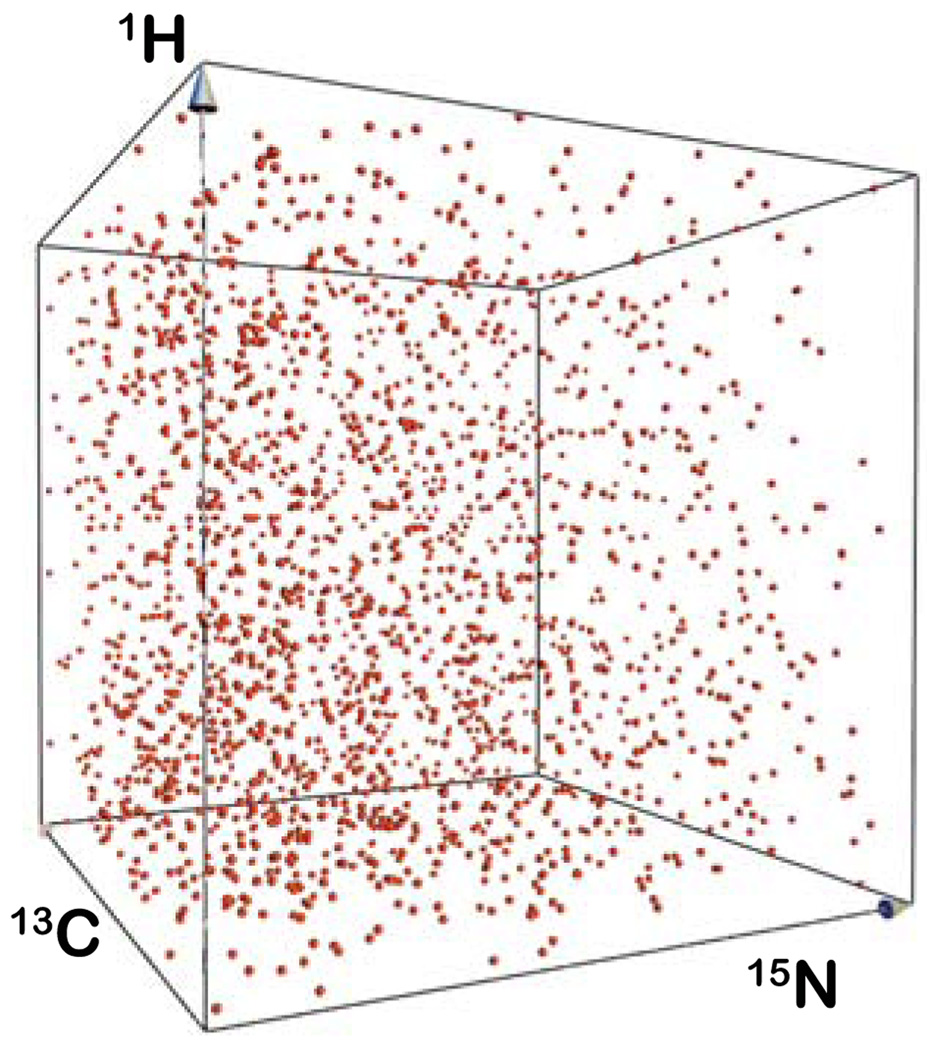
The experimental data consist of the 3D versions (uniformly sampled) and a 4D-NUS version of the HCC(CO)NH-TOCSY experiment, acquired using a 300 µM sample of a 4.5-kDa spider toxin known as PcTx1 (Fig. 2). The high-resolution 3D experiments were acquired in 1.5 days each to achieve resolution similar to the 4D experiment. The 3D data were processed using linear prediction extrapolation, apodization, zero-filling and discrete Fourier transform (DFT) in the indirect dimensions. The 4D experiment was acquired using 2000 hypercomplex samples distributed within a cube of 60×64×64 points in the ¹⁵N, ¹³C, and ¹H dimensions, respectively (Fig. 2); less than 1% of the complete (uniformly sampled) cube was sampled and the total acquisition time was 1.5 days.

Figure 2.

Distribution of sample points generated using the sched3d algorithm represented in 3D space, where the axes correspond to evolution time of ¹H, ¹⁵N and ¹³C nuclei.

The non-uniform sampling schedule was generated using an algorithm not yet applied to NMR data. In this approach, sample times are selected randomly without replacement so that the same sample point is not acquired more than once. The sample points are distributed using an exponentially decaying sampling density matched to the decay of the signal envelope; samples thus occur more densely at short times where the S/N is higher, for non-constant time (CT) dimensions. The algorithm differs from those previously described in that it is based on a one-pass approach described by Eframidis and Spirakis[21], who demonstrated that this is equivalent to weighted random selection without replacement. The algorithm is applicable to any dimensionality, but currently developed for up to three NUS dimensions in the program Sched3d. The algorithm calculates for each time point t(i) a weighting factor w(i), using the decay envelope of the signal, viz:

$$w(i)={{\displaystyle \prod _{k=1}^{\text{dim}}e}}^{\raisebox{1ex}{$-i_k\pi {\mathit{\text{lw}}}_k$}\!\left/ \!\raisebox{-1ex}{${\mathit{\text{sw}}}_k$}\right.}$$

where lw_k and sw_k are the linewidth and sweep width in the k^th dimension, respectively, dim is the number of dimensions and the equation may be further altered to include, for example, J modulation. The algorithm then calculates a rank for each point r(i) according to:

$$r(i)=x{(i)}^{1/w(i)}$$

where x(i) is a random number between 0 and 1 generated for each point. A subset of M points having the highest values of r(i) are then selected from N total points. This method is fast and it avoids sampling the same point multiple times.

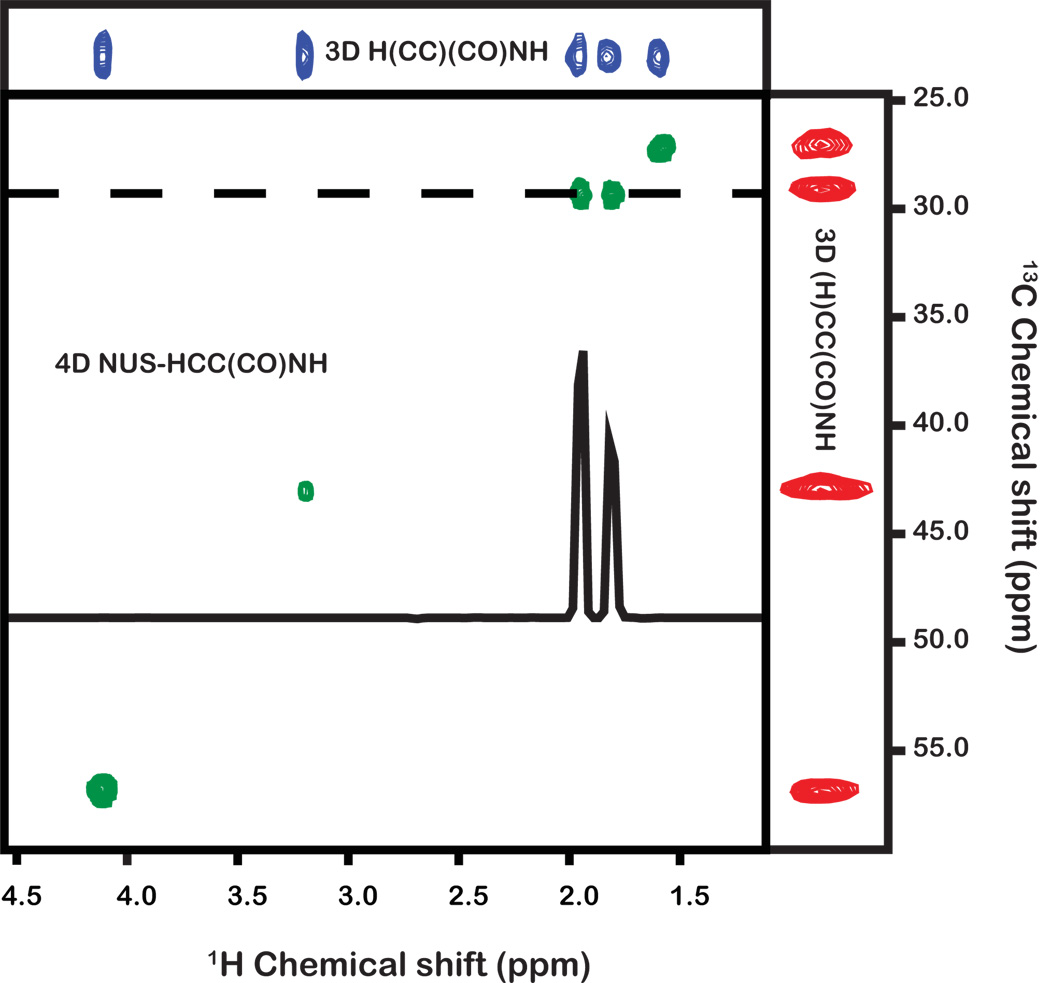
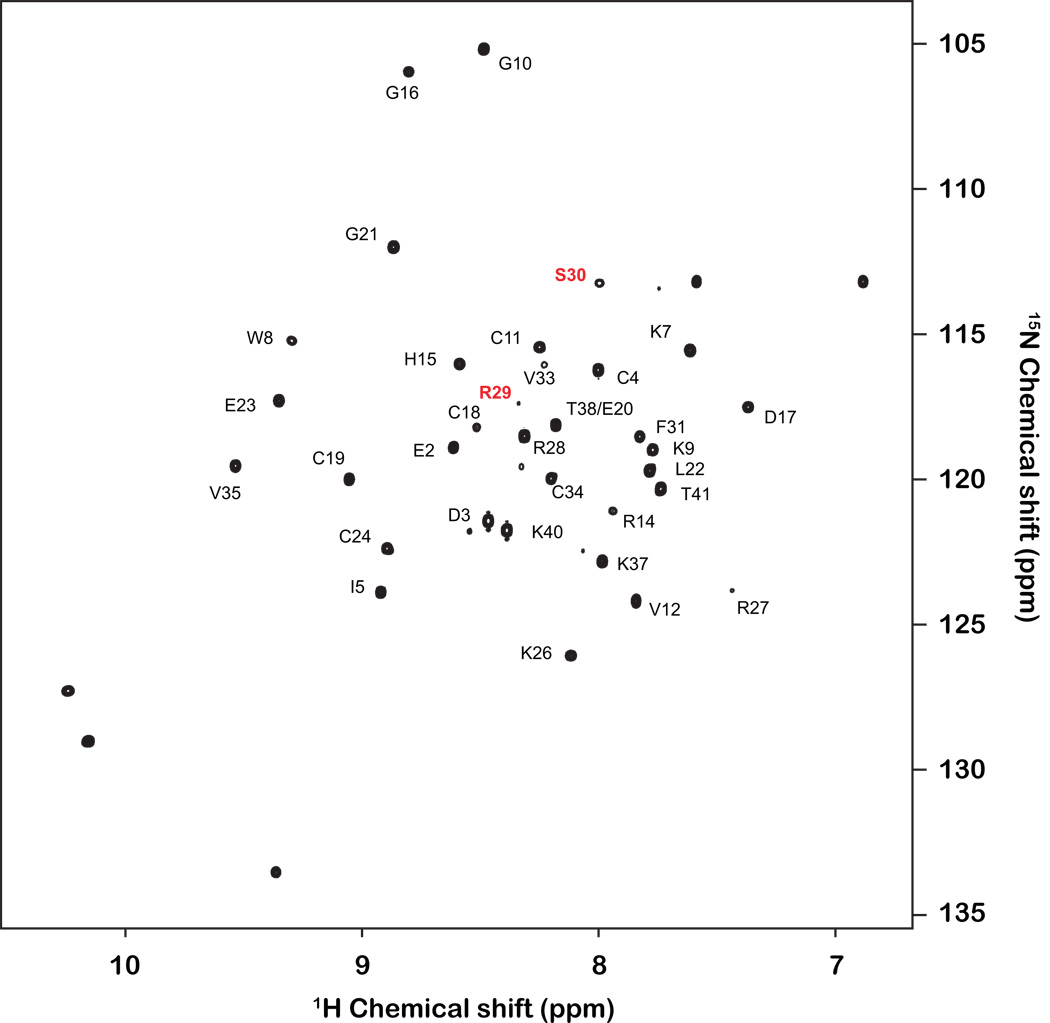
All data were processed using the Rowland NMR Toolkit (http://rnmrtk.uchc.edu). The 4D experiment was processed using the new 3D MaxEnt program (msa3d). The MaxEnt reconstruction parameters were determined using a previously reported approach (def=0.01, λ=0.02).[22; 23] Fig. 3 shows a 2D cross-section of the indirect ¹H and ¹³C dimensions, at the direct ¹H and indirect ¹⁵N frequencies corresponding to residue Ser30, revealing correlations from the sidechain protons of Arg29. This example illustrates: (i) the superb resolution of the 4D experiment, which is particularly useful for assigning complex sidechains; (ii) the excellent sensitivity of the 4D spectrum (note that Ser30 is one of the weakest peaks in the ¹H-¹⁵N HSQC spectrum; see Fig. 4); (iii) the ability to unambiguously determine which protons are attached to which carbons using the 4D experiment.

Figure 3.

Comparison of 2D planes from 3D (H)CC(CO)NH-TOCSY and H(CC)(CO)NH-TOCSY experiments and the 4D HCC(CO)NH-TOCSY experiment. Experiments were acquired using a cryogenically cooled probe on a Bruker Avance 900 MHz spectrometer using a 300 µM sample of the 4.5-kDa toxin PcTx1. The 3D experiments were sampled and processed using traditional methods. The 4D experiment was acquired using non-uniform sampling and processed using MaxEnt reconstruction; each experiment was acquired in ~1.5 days. All planes depict the same ¹H and ¹⁵N backbone-amide frequencies. The axes of the 3D experiments are the directly-detected ¹H dimension and either the ¹H or ¹³C indirectly-detected dimension. In the 4D experiment the axes are the indirect ¹H and ¹³C dimensions. The 1D trace shown in the 4D spectral plane is taken at the row indicated by the dashed line. All panels show sidechain resonances from residue Arg29.

Figure 4.

Annotated 2D ¹H-¹⁵N HSQC spectrum of PcTx1. Note the low S/N of the Arg29/Ser30 resonance (¹H and ¹⁵N chemical shifts of 7.99 and 113.0 ppm, respectively).

Discussion

The number of sample points required to faithfully reconstruct a spectrum depends on the complexity of the underlying data (e.g., the number of signals, dynamic range etc.), with the dimensionality of the experiment being of little consequence.[20] Since the number of unknowns (i.e., frequencies and phases of signals) in each of the two 3D experiments is roughly the same as in the 4D experiment, the number of data points required to obtain spectra with sufficient information content should be the same in all three experiments. The time required to carry out a 4D experiment would be about the same as the time required for two 3D experiments if all the hypercomplex components are collected (8 elements for 3D and 16 for 4D).

Crucially, however, in the two 3D experiments the signal acquired in one experiment does not contribute to the other whilst in the 4D all acquired data contribute to the sensitivity of the final reconstruction. This suggests that the 4D experiment will have the same overall sensitivity as both 3D experiments combined (neglecting losses due to differential relaxation), without incurring additional experiment time.

The 4D HCC(CO)NH-TCOSY experiment described here lends itself particularly well to rapid sidechain assignment in the context of structural genomics initiatives. The ability to unequivocally elucidate C–H correlations should facilitate automated assignment approaches, which currently suffer from the ambiguity present when the conventional experiments are used for aliphatic sidechain assignment.[16; 24] Furthermore, dispersion of resonances into an additional dimension significantly reduces the possibility of peak overlap; for example, in the conventional 3D H(CC)(CO)NH-TOCSY experiment it would not be possible to resolve two overlapping peaks from protons attached to carbon atoms resonating at different frequencies, whereas in the 4D experiment these would be resolved and unambiguously assigned.

Conclusions

In conclusion, we have described an approach for aliphatic sidechain assignment employing NUS and non-Fourier spectrum analysis that offers significant advantages over existing methods. This is an attractive alternative to existing fast methods as it is practical, simple to implement and applicable to most proteins routinely analysed by NMR, and is likely to benefit all proteins where sampling to an optimal evolution time of 1.6 × T₂ in all dimensions is unfeasible.[25; 26] Furthermore, the experiment yields results that can be readily analysed using either manual or automated approaches.

Experimental

The direct dimension was Fourier transformed. At each frequency point in the resulting interferogram, a 3D hyperplane (cube) was reconstructed using the MaxEnt approach. The time required to compute each cube using MaxEnt reconstruction varied and depends on the data in that cube. The example 2D plane of the 4D NUS experiment shown in Fig. 3 was taken from a cube processed on a laptop computer and converged after a total of 4 h; the average processing time per cube was ~2 h/CPU. Thus to reconstruct 512 pts would take ~1000 h on a single CPU or 128 h (5 days) on an 8 core computer. The full dataset presented here was processed on an Apple X-grid cluster consisting of 104 CPUs and converged overnight.

The 3D H(CC)(CO)NH-TOCSY experiment was acquired using 32 and 64 complex samples in the nitrogen and proton dimensions, respectively, while the 3D (H)CC(CO)NH-TOCSY experiment was acquired using 28 and 56 complex samples in the nitrogen and carbon dimensions, respectively. Both 3D experiments were acquired using 16 transients per time increment. The 3D data was processed using linear prediction extrapolation, shifted sine-bell apodization, zero-filling and discrete Fourier transform (DFT) in the indirect dimensions. The 4D experiment was collected using 8 scans per increment and processed using the new 3D MaxEnt algorithm (msa3d) to yield a digital resolution of 64×256×256 in the ¹⁵N, ¹³C, and ¹H dimensions, respectively. Each experiment (3Ds and 4D) was acquired in ~1.5 days.

Complete ¹H, ¹⁵N, and ¹³C chemical shifts for PcTx1 have been deposited in BioMagResBank (accession number 16468), while coordinates for both low-resolution and high-resolution structures are available from the Protein Data Bank (coordinate files 1LMM and 2KNI, respectively).