Of Bits and Wows: A Bayesian Theory of Surprise with Applications to Attention

Abstract

The amount of information contained in a piece of data can be measured by the effect this data has on its observer. Fundamentally, this effect is to transform the observer's prior beliefs into posterior beliefs, according to Bayes theorem. Thus the amount of information can be measured in a natural way by the distance (relative entropy) between the prior and posterior distributions of the observer over the available space of hypotheses. This facet of information, termed “surprise”, is important in dynamic situations where beliefs change, in particular during learning and adaptation. Surprise can often be computed analytically, for instance in the case of distributions from the exponential family, or it can be numerically approximated. During sequential Bayesian learning, surprise decreases like the inverse of the number of training examples. Theoretical properties of surprise are discussed, in particular how it differs and complements Shannon's definition of information. A computer vision neural network architecture is then presented capable of computing surprise over images and video stimuli. Hypothesizing that surprising data ought to attract natural or artificial attention systems, the output of this architecture is used in a psychophysical experiment to analyze human eye movements in the presence of natural video stimuli. Surprise is found to yield robust performance at predicting human gaze (ROC-like ordinal dominance score ∼ 0.7 compared to ∼ 0.8 for human inter-observer repeatability, ∼ 0.6 for simpler intensity contrast-based predictor, and 0.5 for chance). The resulting theory of surprise is applicable across different spatio-temporal scales, modalities, and levels of abstraction.

1. Introduction

The concept of information is central to science, technology, and many other human endeavors. While several approaches for quantifying information have been proposed, the most prominent one so far has been Claude Shannon's definition introduced over half a century ago [49, 1, 39, 7, 11]. According to this definition, the amount of information contained in a piece of data D is measured by −log₂ P(D) bits–a rare piece of data with small probability is considered more informative. Although eminently successful for the development of modern telecommunication and computer technologies, Shannon's definition does not capture all aspects of information. Here we look at information from a different angle. Starting from Bayes theorem, we notice that the fundamental effect that data has on a given observer is to change his/her/its prior beliefs into posterior beliefs. Thus we propose to measure the effect D has on the observer by the distance between his prior and posterior belief distributions. We call this facet of information surprise.

Surprise plays an important role in dynamic situations when the beliefs of the observer change significantly in time, as a result of consecutive applications of Bayes theorem. This can happen in at least two broad categories of situations: either when the beliefs keep changing all the time without converging to a stable value, or when the beliefs progressively converge to a stable value. The first case corresponds to tracking or adaption in a non-stationary environment. The second case corresponds to learning from a stationary data set, when beliefs evolve but finally converge to a stable value. In our framework, adaptation and learning are the results of the same fundamental operation: belief update using Bayes theorem. What distinguishes them is not the basic underlying mathematical operation, but rather the memory span and time scales involved.

In what follows, in Section 2 we first provide the mathematical definition of surprise. In Section 3, we show how surprise can be computed exactly or approximated efficiently in most common situations. In Section 4, we study how surprise changes during learning. In Section 5, we investigate the connections between surprise and other theories of information and novelty, including Shannon's theory of information. In Section 6, we describe a neural network architecture for computing surprise over image and video data in computer vision. Finally, in Section 7, we conduct psychophysical experiments and apply the surprise architecture to the problem of modeling attention and predicting rapid eye movements in humans watching natural stimuli.

The present paper builds on our previously published reports on the same theme [2, 24, 25, 26]. The two key new components here are: (1) a detailed and self-contained treatment of the theory with derivation of closed-form expressions for computing surprise in a number of important cases, analysis of the relationship between surprise and Bayesian learning, and comparison of surprise to other theories of information and novelty; and (2) a detailed presentation of the computational model of attention developed to investigate to which extent Bayesian surprise may predict what attracts human gaze while watching natural video clips. In addition, we also describe new experimental results comparing two variants of our computational model (using either Gaussian data and a Gaussian prior, or Poisson data and a Gamma prior; see below) on two open-access human gaze tracking datasets, and we develop a new temporal analysis that reveals a strong time contingency between the onset of a surprising event in a video clip and the execution of a human gaze shift towards such event. The reader is invited to explore our previous publications for more extensive discussions of the eye-tracking methodologies, general modeling of human saliency maps, and methodologies for comparing human gaze recordings to saliency maps generated by a number of different models available in the literature. All the data collected for the experiments have been made publicly available.

2. Mathematical Definition of Surprise

The definition we propose is best understood within the Bayesian or subjectivist framework of probability theory. In the subjectivist framework, degrees of belief or confidence are associated with hypotheses or models. It can be shown that under a small set of reasonable axioms, these degrees of belief can be represented by real numbers and that when rescaled to the [0,1] interval they must obey the rules of probability and in particular Bayes theorem [12, 48, 6, 31, 16, 32]. The amount of surprise in the data for a given observer can be measured by looking at the changes that take place in going from the prior to the posterior distributions.

Specifically, consider an observer with a prior distribution P(M) over a set 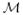of possible models or hypotheses. The collection of a piece of data D leads to a reevaluation of beliefs and the transformation of the prior probability into a posterior distribution according to Bayes theorem,

$$P(M\mid D)=\frac{P(D\mid M)}{P(D)}P(M)$$ (1)

¿From this equation, the effect of D is clearly to change P(M) to P(M∣D). In other words, we view the data D as an operator acting on the space of distributions over the space of models. Thus, one basic way of measuring information carried by D is to measure the distance between the prior and the posterior distributions. To distinguish it from Shannon's communication information, we call this notion of information the surprise information, or just surprise [2]:

$$S(D,ℳ)=d[P(M),P(M\mid D)]$$ (2)

where d is a distance or dissimilarity measure. There are different ways of measuring distance or dissimilarity between probability distributions. In what follows, for standard well-known theoretical reasons such as invariance with respect to reparameterizations, we use the relative entropy or Kullback-Liebler [34] divergence K

$$\begin{array}{l}S(D,ℳ)=K(P(M),P(M\mid D))\\ ={\int }_{ℳ}P(M)log\frac{P(M)}{P(M\mid D)}dM\\ =-H(P(M))-{\int }_{ℳ}P(M)logP(M\mid D)dM\\ =logP(D)-{\int }_{ℳ}P(M)logP(D\mid M)dM\end{array}$$ (3)

where H denotes the entropy.

The alternative version K(P(M∣D), P(M)) of the relative entropy may also be used (and may even be slightly preferable in settings where the “true” or “best” distribution is used as the first argument). While the basic principles in the following derivations apply to both forms, here we use the version in Equation 3 because in general it leads to slightly simpler analytical expressions. This is simply because the prior distribution, which occurs twice in Equation 3, in general has a simpler expression than the posterior distribution which contains additional data-dependent terms. Alternatively, the relative entropy might also be symmetrized by taking [K(P(M), P(M∣D)) + K(P(M∣D), P(M)]/2. Although the symmetric version is rarely used, the analytical formula to be derived could be applied to the symmetric version with the proper and obvious adjustments. The same applies to other variations, such as the Jensen-Shannon divergence [56, 37]. In considering the symmetric version, note, however, that there is no reason why the intuitive notion of surprise ought to be symmetric with respect to the distributions involved. In fact, introspection dictates that the contrary ought to be true. A broad prior distribution followed by a narrow posterior distribution corresponds to a reduction in uncertainty, while a narrow prior distribution followed by a broad posterior distribution corresponds to an increase in uncertainty, and both lead to different subjective experiences.

Equivalently, we can define the single-model surprise by the log-odd ratio

$$S(D,M)=log\frac{P(M)}{P(M\mid D)}$$ (4)

and the surprise by its average

$$S(D,ℳ)={\int }_{ℳ}S(D,M)P(M)dM$$ (5)

taken with respect to the prior distribution over the model class. In statistical mechanics terminology, surprise can also be viewed as the free energy of the negative log-posterior at a temperature t = 1, with respect to the prior distribution over the space of models [3].

A unit of surprise–the “wow”–can be defined for a single model M as the amount of surprise corresponding to a two-fold variation between the prior and the posterior, i.e., as −log₂ P(M)/P(M∣D). Note that unless we use absolute values, this ratio can be positive or negative depending on whether the observer's belief in model M increases or decreases. The total number of wows experienced when simultaneously considering all models is obtained by integrating over and, as a relative entropy, is always positive.

3. Analytical Computation or Approximation of Surprise

As a relative entropy, surprise can always be estimated, at least numerically. But for the concept to be really useful, one ought to be able to compute surprise analytically, at least in the most standard statistical cases.

More precisely, consider a data set D = {d₁, …, d_N} containing N points. For simplicity, although this does not correspond to any restriction in the general theory, we consider the case of conjugate priors, where the prior and the posterior have the same functional form. In addition to their theoretical interest, conjugate priors are also important for efficient implementations of iterative Bayesian learning where the posterior at iteration t becomes the prior for iteration t + 1. In order to compute surprise in Equation 3 with conjugate priors, we need only to compute general terms of the form

$$F(P_1,P_2)=\int P_{1}log{P}_{2}dx$$ (6)

where P₁(x) and P₂(x) are two distributions with the same functional form. The surprise is then given by

$$S=F(P_1,P_1)-F(P_1,P_2)$$ (7)

where P₁ is the prior and P₂ is the posterior. Note also that in this case the symmetric divergence can easily be computed using F(P₁, P₁) − F(P₁, P₂) + F(P₂, P₂) − F(P₂, P₁). Details for the calculation of F(P₁, P₂) in the following specific examples are given in the Appendix.

3.1. Discrete Data: Multinomial Model

Consider the case where d_i is binary. The simplest class of models for D is then M(p), the first order Markov model with a single parameter p representing the probability of emitting a 1. The conjugate prior on p is the Beta distribution (or Dirichlet distribution in the general multinomial case)

$$\begin{array}{l}{D}_1(a_1,b_1)=\frac{\mathrm{\Gamma }(a_1+b_1)}{\mathrm{\Gamma }(a_1)\mathrm{\Gamma }(b_1)}{x}^{a_1-1}{(1-x)}^{b_1-1}\\ =C_1{x}^{a_1-1}{(1-x)}^{b_1-1}\end{array}$$ (8)

with parameters a₁ ≥ 0, b₁ ≥ 0, and a₁ + b₁ > 0. The expectation is a₁/(a₁ + b₁). With n successes in the sequence D of N samples, the posterior is a Dirichlet distribution D₂(a₂, b₂) with [3]

$$\begin{array}{lll}{a}_2=a_1+n& \text{and}& b_2=b_1+(N-n)\end{array}$$ (9)

The surprise can be computed exactly

$$\begin{array}{l}S(D,ℳ)=K(D_1,D_2)\\ =log\frac{C_1}{C_2}+n[\mathrm{\Psi }(a_1+b_1)-\mathrm{\Psi }(a_1)]\\ +(N-n)[\mathrm{\Psi }(a_1+b_1)-\mathrm{\Psi }(b_1)]\end{array}$$ (10)

where Ψ is the derivative of the logarithm of the Gamma function (see Appendix). When N → ∞, and n = pN with 0 < p < 1 we have

$$S(D,ℳ)\approx N\text{K}(p,a_1)=NK\left((p,1-p),(\frac{a_1}{a_1+b_1},\frac{b_1}{a_1+b_1})\right)$$ (11)

where K(p, a₁) is a concise notation to represent the Kullback-Liebler divergence between the empirical distribution (p, 1 − p) and the expectation of the prior (a₁/(a₁ + b₁), b₁/(a₁ + b₁)). Thus asymptotically surprise grows linearly with the number of data points with a proportionality coefficient that depends on the discrepancy between the expectation of the prior and the observed distribution. The same relationship is true in the case of a multinomial model. When the prior is symmetric (a₁ = b₁), a slightly more precise approximation is provided by

$$S(D,ℳ)=K(D_1,D_2)\approx N\left[\sum _{k=a_1}^{2a_1-1}\frac{1}{k}-H(p)\right]$$ (12)

where H(p) denotes the entropy H(p) = −p log p − (1 − p) log(1 − p). For instance, when a₁ = 1 then K(D₁, D₂) ≈ N(1 − H(p)), and when a₁ = 5 then K(D₁, D₂) ≈ N[0.746 − H(p)].

3.2. Discrete Data: Poisson Model

As a second discrete example, consider the case where d_i is an integer. A simple class of models for D is the class of Poisson models parameterized by λ. The conjugate prior on λ is the Gamma prior

$${\mathrm{\Gamma }}_1(a_1,b_1)=\frac{b_1^{a_1}}{\mathrm{\Gamma }(a_1)}{x}^{a_1-1}{e}^{-b_{1}x}=C_1{x}^{a_1-1}{e}^{-b_{1}x}$$ (13)

with x ≥ 0, shape a₁ > 0, inverse scale b₁ > 0. The expectation is a₁/b₁. With N observations, the posterior is also a Gamma distribution Γ₂(a₂, b₂) with

$$\begin{array}{lll}{a}_2=a_1+N\overline{m}& \text{and}& b_2=b_1+N\end{array}$$ (14)

where m̄ is the sample mean. The surprise can be computed exactly

$$\begin{array}{l}S(D,ℳ)=K({\mathrm{\Gamma }}_1,{\mathrm{\Gamma }}_2)\\ =a_{1}log\frac{b_1}{b_1+N}-N\overline{m}log(b_1+N)\\ +log\frac{\mathrm{\Gamma }(a_1+N\overline{m})}{\mathrm{\Gamma }(a_1)}\\ +\frac{N{a}_1}{b_1}+N\overline{m}[log{b}_1-\mathrm{\Psi }(a_1)]\end{array}$$ (15)

When N → ∞, Stirling's formula yields the approximation

$$\begin{array}{l}S(D,ℳ)\approx N(\frac{a_1}{b_1}-\overline{m}[1-log\overline{m}\\ +\mathrm{\Psi }(a_1)-log{b}_1])\end{array}$$ (16)

Thus asymptotically surprise information grows linearly with the number of data points with a proportionality coefficient that depends on the difference between the mean a₁/b₁ of the prior and mean m̄ of the sample plus an offset.

3.3. Continuous Data: Unknown Mean/Known Variance

When the d_i are real, we can consider first the case of unknown mean with known variance. We have a family M(μ) of models, with a Gaussian prior $G_1({\mu }_1,{\sigma }_1^2)$. If the data has known variance σ², then the posterior distribution is Gaussian $G_2({\mu }_2,{\sigma }_2^2)$ with parameters given by [16]

$$\begin{array}{lll}{\mu }_2=\frac{\frac{{\mu }_1}{{\sigma }_1^2}+\frac{N\overline{m}}{{\sigma }^2}}{\frac{1}{{\sigma }_1^2}+\frac{N}{{\sigma }^2}}& \text{and}& \frac{1}{{\sigma }_2^2}=\frac{1}{{\sigma }_1^2}+\frac{N}{{\sigma }^2}\end{array}$$ (17)

where m̄ is the observed mean. In this case

$$\begin{array}{l}S(D,ℳ)=K(G_1,G_2)\\ =log\frac{\sigma }{\sqrt{{\sigma }^2+N{\sigma }_1^2}}+N\frac{{\sigma }_1^2}{2{\sigma }^2}+\frac{N^2{\sigma }_1^2{({\mu }_1-\overline{m})}^2}{2{\sigma }^2({\sigma }^2+N{\sigma }_1^2)}\\ \approx \frac{N}{2{\sigma }^2}[{\sigma }_1^2+{({\mu }_1-\overline{m})}^2]\end{array}$$ (18)

the approximation being valid for large N. In the special case where the prior has the same variance as the data σ₁ = σ then the formula simplify a little and yield

$$\begin{array}{l}S=K(G_1,G_2)\\ =\frac{N}{2}-\frac{1}{2}log(N+1)+\frac{N^2{({\mu }_1-\overline{m})}^2}{2(N+1){\sigma }^2}\\ \approx \frac{N}{2{\sigma }^2}[{\sigma }^2+{({\mu }_1-\overline{m})}^2]\end{array}$$ (19)

the last approximation being valid when N is large. In any case, surprise grows linearly with N with a coefficient that is the sum of the prior variance and the square difference between the expected mean and the empirical mean scaled by the variance of the data.

3.4. Continuous Data: Unknown Variance/Known Mean

When the d_is are real, we can also consider the case of unknown variance with known mean. We then have a family M(σ²) of models, with a conjugate scaled inverse gamma prior ([16])

$$\begin{array}{l}{\mathrm{\Gamma }}_1({\nu }_1,s_1)=\frac{{\left(\frac{{\nu }_1}{2}\right)}^{{\nu }_1/2}{s}_1^{{\nu }_1}}{\mathrm{\Gamma }\left(\frac{{\nu }_1}{2}\right)}{({\sigma }^2)}^{-(\frac{{\nu }_1}{2}+1)}{e}^{-\frac{{\nu }_1{s}_1^2}{2{\sigma }^2}}\\ =C_1{({\sigma }^2)}^{-(\frac{{\nu }_1}{2}+1)}{e}^{-\frac{{\nu }_1{s}_1^2}{2{\sigma }^2}}\end{array}$$ (20)

The posterior is then a scaled inverse gamma distribution [16] with

$$\begin{array}{lll}{\nu }_2={\nu }_1+N& \text{and}& s_2^2=\frac{{\nu }_1{s}_1^2+N{\overline{\sigma }}^2}{{\nu }_1+N}\end{array}$$ (21)

Here σ̄² = Σ(x_i − m)²/N is the observed variance, based on the known mean m. The surprise

$$\begin{array}{l}S(D,ℳ)=K({\mathrm{\Gamma }}_1,{\mathrm{\Gamma }}_2)=log\frac{C_1}{C_2}-\frac{N}{2}[\mathrm{\Psi }(\frac{\nu }{2})\\ +log\frac{2}{{\nu }_1{s}_1^2}]+\frac{N{\overline{\sigma }}^2}{2s_1^2}\end{array}$$ (22)

For large values of N,

$$\begin{array}{l}S=K({\mathrm{\Gamma }}_1,{\mathrm{\Gamma }}_2)\\ \approx \frac{N}{2}\left(\frac{{\overline{\sigma }}^2}{s_1^2}+log\frac{{\nu }_1{s}_1^2}{2{\overline{\sigma }}^2}-\mathrm{\Psi }(\frac{{\nu }_1}{2})\right)\end{array}$$ (23)

Thus surprise information scales linearly with N, with a coefficient of proportionality that typically depends mostly on the ratio of the empirical variance to the scale parameter $s_1^2$, which is roughly the expectation of the prior [the expectation of the prior is ${\nu }_1{s}_1^2/({\nu }_1-2)$ provided ν₁ > 2]. The effects of very large or very small values of σ̄ or ν₁ can also be seen in the formula above. In particular, surprise is largest when the empirical variance σ̄² goes to 0 or infinity, i.e., is very different from the prior expectation.

3.5. Continuous Data: Unknown Mean/Unknown Variance

Finally, we can consider the case of unknown mean with unknown variance. We have a family M(μ, σ²) of models, with a conjugate prior G₁Γ₁ = P(μ∣σ²)P(σ²) = G₁(μ₁, σ²/κ₁)Γ₁(ν₁, s₁), product of a normal with a scaled inverse Gamma distribution. Thus the prior has four parameters (μ₁, κ₁, ν₁, s₁), with κ₁ > 0, ν₁ > 0, and s₁ > 0. The conjugate posterior has the same form, with similar parameters (μ₂, κ₂, ν₂, s₂) satisfying (see for instance [16])

$$\begin{array}{l}{\mu }_2=\frac{{\kappa }_1}{{\kappa }_1+N}{\mu }_1+\frac{N}{{\kappa }_1+N}\overline{m}\\ {\kappa }_2={\kappa }_1+N\\ {\nu }_2={\nu }_1+N\\ {\nu }_2{s}_2^2={\nu }_1{s}_1^2+(N-1){\overline{\sigma }}^2+\frac{{\kappa }_{1}N}{{\kappa }_1+N}{(\overline{m}-{\mu }_1)}^2\end{array}$$

with m̄ = Σx_i/N and σ̄² = Σ(x_i − m̄)²/(N − 1). The surprise is

$$\begin{array}{l}S(D,ℳ)=K(G_1{\mathrm{\Gamma }}_1,G_2{\mathrm{\Gamma }}_2)\\ =\frac{1}{2}log\frac{{\kappa }_1}{{\kappa }_1+N}+\frac{N}{2{\kappa }_1}\frac{{\kappa }_1+N}{2}{\left[\frac{N(\overline{m}-{\mu }_1)}{({\kappa }_1+N)s_1}\right]}^2\\ +log\frac{C_1}{C_2}-\frac{N}{2}[\mathrm{\Psi }(\frac{{\nu }_1}{2})+log\frac{2}{{\nu }_1{s}_1^2}]\\ +\frac{(N-1){\overline{\sigma }}^2+\frac{{\kappa }_{1}N}{{\kappa }_1+N}{(\overline{m}-{\mu }_1)}^2}{2s_1^2}\end{array}$$ (24)

For large values of N,

$$\begin{array}{l}K(G_1{\mathrm{\Gamma }}_1,G_2{\mathrm{\Gamma }}_2)\approx \frac{N}{2}(\frac{1}{{\kappa }_1}+\frac{{\overline{\sigma }}^2}{s_1^2}+log\frac{{\nu }_1{s}_1^2}{2{\overline{\sigma }}^2}\\ -\mathrm{\Psi }(\frac{{\nu }_1}{2})+\frac{{(\overline{m}-{\mu }_1)}^2}{s_1^2})\end{array}$$ (25)

Surprise information is linear in N with a coefficient that is essentially the sum of the coefficients derived in the unknown mean and unknown variance partial cases.

3.6. Generalization: Exponential Families With Conjugate Priors

The previous examples can be generalized by considering a family M(θ) of models parameterized by the parameter vector θ with a likelihood function associated with the exponential family of distributions ([9])

$$P(d\mid M)=h(d)c(\theta )exp\left(\sum _{i=1}^k{w}_i(\theta )t_i(d)\right)$$ (26)

where h(d), c(θ), w_i(θ), and t_i(d) are known functions of the respective variables. With N independent data points (D = d₁, …, d_N)

$$\begin{array}{l}P(D\mid M)={[c(\theta )]}^{N}h(D)exp\left(\sum _{i=1}^k{w}_i(\theta )\sum _{j=1}^N{t}_i(d_j)\right)\\ ={[c(\theta )]}^{N}h(D)exp\left(\sum _{i=1}^k{w}_i(\theta )T_i(D)\right)\end{array}$$ (27)

where $h(D)={\prod }_{j=1}^{N}h(d_j)$, and $T_i(D)={\sum }_{j=1}^N{t}_i(d_j)$ are the sufficient statistics. The conjugate prior has a similar exponential form

$$P(\theta )=C_1(\theta )exp\left(\sum _{i=1}^k{A}_i^1{w}_i(\theta )\right)$$ (28)

parameterized by the $A_i^1$'s. Using Bayes theorem, the posterior has the same exponential form

$$P(\theta )=C_2(\theta )exp\left(\sum _{i=1}^k{A}_i^2{w}_i(\theta )\right)$$ (29)

parameterized by the $A_i^2$'s satisfying

$$A_i^2=A_i^1+T_i(D)$$ (30)

Calculation of surprise yields

$$S(D,ℳ)=log\frac{C_1}{C_2}-\sum _{i=1}^k{T}_i(D)E_{A^1}[w_i(\theta )]$$ (31)

where E_A¹[w_i(θ)] is the expectation of w_i(θ) with respect to the prior. Note that if surprise is defined by K(P(M∣D), P(M), the same calculation yields

$$S(D,ℳ)=log\frac{C_2}{C_1}+\sum _{i=1}^k{T}_i(D)E_{A^2}[w_i(\theta )]$$ (32)

Thus for members of the exponential family [9] of distributions, the posterior depends entirely on the sufficient statistics and therefore the surprise also depends crucially on them. The T_i(D) terms typically grow linearly with the data, and so does surprise.

4. Learning and Surprise

There is an immediate connection between surprise and computational learning theory. If we imagine that data points from a training set are presented sequentially, we can consider that the posterior distribution after the N-th point becomes the prior for the next iteration (sequential Bayesian learning). As a system learns from examples with a static distribution, new data points ought to become less and less surprising. Thus in this case we can expect on average surprise to decrease after each iteration. We shall compute the exact rate of decrease using examples taken from the distributions studied in the previous section.

4.1. Learning Curves: Discrete Data

Consider first a sequence of 0-1 examples D = (d_N). The learner starts with a Dirichlet prior D₀(a₀, b₀). With each example d_N, the learner updates its Dirichlet prior D_N(a_N, b_N) into a Dirichlet posterior D_N+1(a_N+1, b_N+1) with (a_N+1, b_N+1) = (a_N+1, b_N) if d_N+1 = 1, and (a_N+1, b_N+1) = (a_N, b_N + 1) otherwise. When d_N+1 = 1, the corresponding surprise is easily computed using Equations 56 and 59 (detailed in Appendix). For simplicity, and without much loss of generality, let us assume that a₀ and b₀ are integers, so that a_N and b_N are also integers for any N. Then if d_N+1 = 1 the relative surprise is

$$S(D_N,D_{N+1})=log\frac{a_N}{a_N+b_N}+\sum _{k=0}^{b_N-1}\frac{1}{a_N+k}$$ (33)

and similarly in the case d_N+1 = 0 by interchanging the role of a_N and b_N. By using the standard integral bound for series based on monotonically decreasing functions, we have

$$\sum _{k=0}^{b_N-1}\frac{1}{a_N+k}\le \frac{1}{a_N}+log\frac{a_N+b_N-1}{a_N}$$ (34)

By combining the last two equations we get

$$0\le S(D_N,D_{N+1})\le \frac{1}{a_N}+log(1-\frac{1}{a_N+b_N})$$ (35)

Asymptotically we have a_N ≈ a₀ + pN and b_N ≈ b₀ + (1 − p)N (this is exactly true in expectation). Therefore, by taking the first order expansion of log(1 − u) and substituting these approximate values, we see that asymptotically the bound gives

$$\frac{1}{a_N}+log(1-\frac{1}{a_N+b_N})\approx \frac{1-p}{pN}$$ (36)

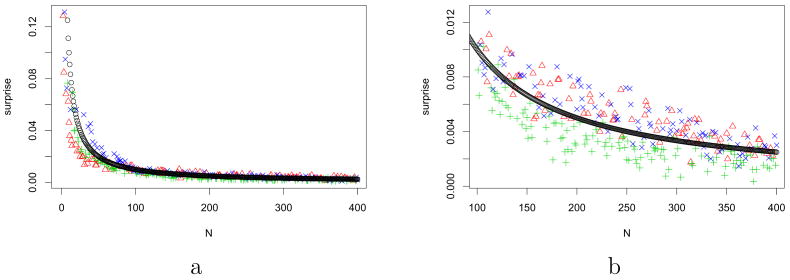
Thus surprise decreases in time with the number of examples as 1/N (Figure 1). A similar calculation can be done for the Poisson model.

Figure 1.

Simulation results corresponding to flips of a 3-sided (red, blue, green) die with a corresponding multinomial learning model. Curves are derived using 400 random samples, drawn from the distribution red = 0.3, blue = 0.3, and green = 0.4. x-axis correspond to learning iterations. y axis correspond to surprise. As predicted by the theory, during Bayesian learning, surprise decreases on average like 1/N (black curve) as learning progresses. (a) curve corresponding to epochs 1-400; (b) magnified view corresponding to epochs 100-400.

4.2. Learning Curves: Continuous Data

In the case of continuous Gaussian data with, for instance, known variance σ², the learner starts with a Gaussian prior $G_0({\mu }_0,{\sigma }_0^2)$ on the mean. With each example d_N, the learner updates its Gaussian prior $G_N({\mu }_N,{\sigma }_N^2)$ into a Gaussian posterior $G_{N+1}({\mu }_{N+1},{\sigma }_{N+1}^2)$ with

$$\begin{array}{lll}{\mu }_{N+1}=\frac{\frac{{\mu }_N}{{\sigma }_N^2}+\frac{d_{N+1}}{{\sigma }^2}}{\frac{1}{{\sigma }_N^2}+\frac{1}{{\sigma }^2}}& \text{and}& \frac{1}{{\sigma }_{N+1}^2}=\frac{1}{{\sigma }_N^2}+\frac{1}{{\sigma }^2}\end{array}$$ (37)

¿From Equation 18, the relative surprise is

$$\begin{array}{l}S(G_N,G_{N+1})=log\frac{\sigma }{\sqrt{{\sigma }^2+{\sigma }_n^2}}\\ +\frac{{\sigma }_N^2}{2{\sigma }^2}(1+\frac{{({\mu }_N-d_{N+1})}^2}{{\sigma }^2+{\sigma }_N^2})\end{array}$$ (38)

Asymptotically

$$E[S(G_N,G_{N+1})]\le \frac{{\sigma }_N^2}{2{\sigma }^2}$$ (39)

¿From Equation 17, we have $\frac{1}{{\sigma }_{N+1}^2}=\frac{1}{{\sigma }_0^2}+\frac{(N+1)}{{\sigma }^2}$, or ${\sigma }_{N+1}^2=\frac{{\sigma }_0^2{\sigma }^2}{{\sigma }^2+(N+1){\sigma }_0^2}$, which asymptotically behaves like σ²/N.

Combining this asymptotic form with Equation 39, we see that in this case surprise can be expected to decrease like 1/2N, again proportionally to the inverse of the number of data points.

Similar calculations can be done for the general exponential case (Equations 30 and 31) by noticing that, as N → ∞, in a stationary environment T_i(D) ≈ Nt̄_i(d), where t̄_i(d) is the average value of t_i.

5. Relations of Bayesian Surprise to Other Theories of Information and Surprise

5.1. Theories of Information

Several theories have been proposed over the years to try to capture the concept of information and entropy [49, 47, 1, 39, 7, 33, 11] and not all of them can be reviewed here. Shannon's theory has been by far the most successful one, and many of the other theories that have been proposed [47, 1] can be viewed as variations on Shannon's definition. Thus for conciseness here we focus on the relationship of Bayesian surprise to Shannon's definition and then separately on the relationship of Bayesian surprise to other specific definitions of surprise found in the literature.

Shannon theory of communication defines the information contained in D at the level of an individual model M by

$$I(D,M)=-logP(D\mid M)$$ (40)

with the corresponding entropy

$$\begin{array}{l}I(\mathcal{D},M)=H(P(D\mid M))\\ =-{\int }_{\mathcal{D}}P(D\mid M)logP(D\mid M)dD\end{array}$$ (41)

This entropy corresponds to an integral over data, whereas Bayesian surprise corresponds to an integral over models hence at this level surprise and information are dual facets of the data.

Shannon theory can also be applied at the level of the model class . In this case the information carried by D is

$$I(D)=I(D,ℳ)=-logP(D\mid ℳ)=-logP(D)$$ (42)

where P(D) = P(D∣) = ∫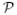(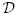∣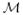)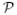()⌈ is also called the evidence and plays a key role in Bayesian analysis and model class comparison.

The corresponding entropy is given by

$$I(\mathcal{D},ℳ)=-{\int }_{\mathcal{D}}P(D\mid ℳ)logP(D\mid ℳ)dD$$ (43)

For a fixed data set D, the surprise is

$$\begin{array}{l}S(D,ℳ)=-I(D,ℳ)\\ +{\int }_{ℳ}P(M)I(D,M)dM\end{array}$$ (44)

and therefore it can also be viewed as the difference between the average Shannon information per model, taken with respect to the prior, and the Shannon information based on the evidence.

If we integrate the surprise with respect to the evidence

$$\begin{array}{l}{\int }_{\mathcal{D}}P(D)S(D,ℳ)dD=\\ ={\int }_{\mathcal{D},ℳ}P(D)P(M)log\frac{P(D)P(M)}{P(D,M)}\mathit{dDdM}\end{array}$$ (45)

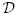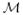we get the Kullback-Liebler divergence K(P(D)P(M), P(D, M)), which is the permuted version of the mutual information MI between and : MI(, ) = K(P(D, M), P(D)P(M)). If surprise is defined by K(P(M∣D), P(M)) then the integral of the surprise is equal to the mutual information between data and models. Note in contrast that the integral over models of the per-model entropy (Equation 41) is not equal to the mutual information, but related to it by a convex inequality, as shown by Equation 44.

In short, Bayesian surprise measures a facet of information that is different and complementary to Shannon's definition.

5.2. Theories of Surprise

The concepts of “surprise” and “surprising event” have also been raised multiple times in the statistical literature [54, 44, 5, 17, 35, 13].

One simple approach corresponds to outlier detection theory, whereby surprising events are defined as rare events, i.e. events having low probability. Such a definition of course is closely related to Shannon's theory of information since, by definition, rare events (P(D) small) have high Shannon information (I(D) = −log P(D) large). While it is easy to see that in many cases, Shannon's I(D) and the Bayesian surprise S(D) are closely related, there exist also specific situations where these two approaches provide clearly distinct answers, and Bayesian surprise matches intuition better. We illustrate here two somewhat extreme classes of examples corresponding to high Shannon information and low surprise, and vice versa.

Many Bits with Few Wows

The most simple example is obtained when 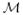contains a single model M. The prior is necessarily given by P(M) = 1, and the posterior distribution is always equal to the prior. Thus if there is data D satisfying P(D) = ε ≪ 1, the Shannon information log ε can be arbitrarily large, whereas the surprise is always zero. For a more complex and instructive example, let 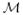= {M₁, …, M_N} with a uniform prior P(M_i) = 1/N for every i. Assume that for each model M_i, P(D∣M_i) = ε, and hence P(D) = ε; that is, a datum is observed which is unlikely for any of the models. By Bayes theorem, we have immediately P(M_i∣D) = P(M_i) = 1/N. Thus in this case Shannon's information −logε grows to infinity as we decrease the value of ε. On the other hand, the prior and the posterior distributions being identical, the surprise is zero. Thus while the number of wows is zero, the number of bits grows to infinity like −log ε. In this case, although D is a strong outlier, D is a false positive, in the sense that it carries no useful information for discriminating between the alternative hypotheses M_i. Therefore D carries no surprise as its observation leaves the observer's expectations unaffected.

Few Bits with Many Wows

Conversely, consider = {M₁, …, M_N} with a non-uniform prior given by P(M₁) = a and P(M_i) = (1 − a)/(N − 1) for i = 2, …, N. Consider data D with the likelihood P(D∣M₁) = (1 − a)/(N − 1) and P(D∣M_i) = a for i = 2, …, N. A simple calculation shows that P(D) = a(1 − a)N/(N − 1) while the posterior distribution is uniform and given by P(M_i) = 1/N for any i. Thus for large N, the Shannon information converges to the constant value I(D) = −log[a(a − 1)] bits, determined by the parameter a. For instance, if a = 0.5 the Shannon information converges to 2 bits. The surprise, however, is given by S(D) = a log Na + (1 − a) log[(1 − a)N/(N − 1)] which, for large values of N, converges to a log N + H(a). Thus while the number of bits is finite, the number of wows grows to infinity like a log N. A data with these properties would go undetected by standard outlier theory, but would be picked up by surprise since it is associated with a significant change from prior to posterior distribution.

Note that examples where D carries few bits but many wows do not require the number N of models to go to infinity. Consider the case N = 2 with P(M₁) = a and P(M₂) = 1 − a. Assume that P(D∣M₁) = b and P(D∣M₂) = c. We then have P(D) = ab + (1 − a)c, P(M₁∣D) = ba/P(D), and P(M₂∣D) = (1 − a)c/P(D). The surprise is equal to log[ab + (1 − a)c] − a log b − (1 − a) log c. By letting either b → 0 or c → 0, but not both, we can easily achieve a diverging amount of surprise in combination with a finite amount of Shannon information.

In any case, in the outlier detection approach, if all possible events or datasets have very low probability, then they are all very “surprising”, which is not very useful in practice. Thus it is clear that whether an event or data set is surprising or not cannot be decided on its probability alone. As a minimum, the probabilities of the other events must also be taken into consideration. Thus another approach, introduced in [54] and further developed in, for instance, [44, 17], tries to compare the probability of an event to the probabilities of all the other possible events by using a “surprise index”. Weaver [54] considers an experiment with n possible outcomes, with probabilities p₁, …, p_n and defines the Surprise Index by

$$SI=\frac{E(p)}{p_i}=\frac{{\sum }_{i=1}^n{p}_i^2}{p_i}$$ (46)

The SI measures “whether the probability realized, namely, p_i is small as compared with the probability that one can expect on the average to realize, namely, E(p). If this ratio is small and SI correspondingly large, then one has a right to be surprised.”[54]. Unlike simple outlier detection, the surprise index does consider an event in the context of other events. However, the surprise index does not consider explicitly prior and posterior distributions and is obviously quite different from the concept of Bayesian surprise described in this paper.

Perhaps closest in spirit to our work, but still different and derived completely independently, is the work of Evans [13, 14] which takes a Bayesian perspective and considers prior and posterior distributions and their ratios. More precisely, consider a family of models parameterized by θ, and a function T(θ) with a set of possible values t_i. Evans proposes to introduce a total ordering on the t_i and a surprise inference principle by considering that t₁ is strictly preferred to t₂ if “the relative increase in belief for t₁, from a priori to a posteriori, is greater than the corresponding increase for t₂.” In turn, this preference ordering is used to determine inferences and applied to estimation, hypothesis testing, and model checking procedures [13]. This statistical work, however, does not take an explicit information theoretic perspective, and does not define surprise as the relative entropy between the prior and posterior distributions.

6. A Neural Network Implementation of Surprise for Computer Vision

Here we describe a neural network architecture for processing and computing surprise over image and video data in bottom-up fashion. The architecture is inspired by the neurobiology of early visual processing in the primate brain [29, 24, 25, 26]. In this section we first describe the low-level, Hubel and Wiesel-like, visual feature detection front-end of the proposed system followed by two alternative surprise computation back-ends operating on the feature responses.

6.1. Low-level visual feature extraction

The proposed system employs a relatively mature and standard low-level feature extraction front-end [30, 28]. This front-end analyzes the incoming input images at several spatial resolutions and along several low-level feature dimensions, including color contrast, luminance contrast, oriented edges, and motion energy. In a manner inspired by how early visual processing is organized in the primate brain, the front-end processing thus decomposes the image into a number of sub-bands. Surprise is then computed at the level where the responses from the low-level feature detectors are integrated, as opposed to directly at the pixel level.

A schematic diagram of the system is given in Fig. 2. Input video frames are analyzed in dyadic image pyramids with 9 scales (from scale 0 corresponding to the original image, to scale 8 corresponding to the image reduced by a factor of 256 horizontally and vertically). The pyramids are constructed by iteratively filtering and decimating the input image. In the implementation used here, pyramids are computed for the following low-level visual features thought to guide human attention [55]: (1) luminance; (2) red-green color opponency; (3) blue-yellow color opponency; (4) four oriented edge filters (using Gabor kernels) spanning 180°; (5) luminance flicker (as computed from the difference between the previous image and the current one); and (6) four directions of motion spanning 360°. Additional details about the implementation of these image pyramids have been published previously [30, 27]. The final feature output is in the form of “feature maps” which are obtained by taking across-scale differences between pairs of levels within each feature pyramid. These differences coarsely approximate center-surround contrast enhancement mechanisms found in the early stages of biological visual processing [23, 51, 21]. Center-surround differences are computed for the following scale pairs: 2-5, 2-6, 3-6, 3-7, 4-7, 4-8. All feature maps are then resampled to scale 4 (where the final combined surprise map is later computed); for 640 × 480 input videos, these maps thus have 40 × 30 pixels. In total, 72 such feature maps are computed (6 for luminance, 12 for color opponencies, 24 for oriented Gabor edges, 6 for flicker, and 24 for motion). Fig. 2C shows all the feature maps computed for the example input image shown.

Figure 2.

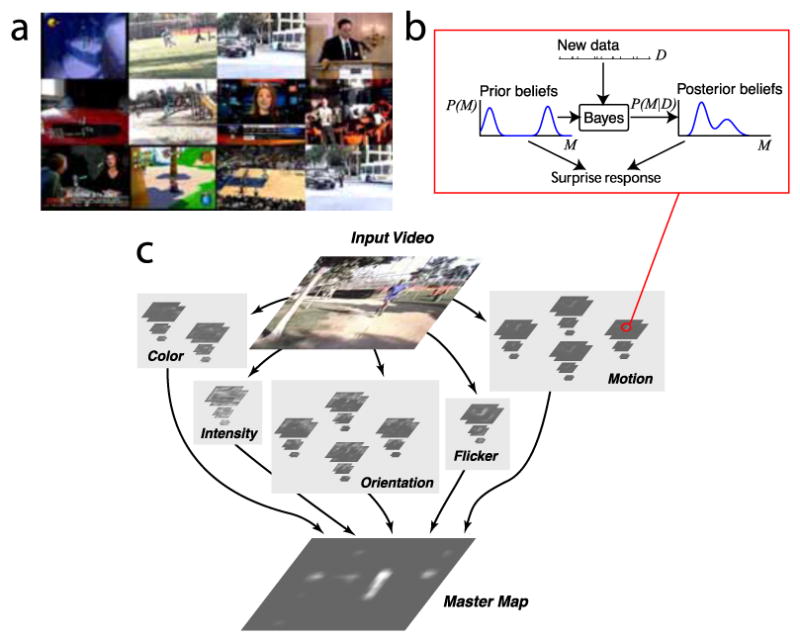
(a) Sample frames of video clips to be processed by the model and for which human eye movement recordings are available (see next section). (b) Computation of surprise at the single-neuron level, each time new data is received from a new video frame. (c) Architecture of the full computational system which analyzes video frames along the dimensions of color, intensity, orientation, flicker, and motion, computing surprise at multiple spatial and temporal scales within each of these feature channels. The surprise output from all feature channels finally gives rise to the master surprise maps. Higher (brighter) values in this map represent the system's prediction of where the strongest attractors of attention currently are in the video inputs (in the example shown, the man running towards the camera is most surprising).

6.2. Surprise computation in feature space

Surprise is computed for every pixel in each of the 72 center-surround feature maps. The underlying motivation is that simulated neurons in the feature maps may establish some very simple beliefs about the world as seen through their spatially- and feature-selective center-surround receptive fields. For instance, a neuron sensitive to red/green opponent contrast at a given location and scale may accumulate over time beliefs about the amount of red/green contrast present in the small portion of the world that is captured by the neuron's receptive field. When new data is observed with each new incoming video frame, the beliefs established thus far are used as prior, and Bayes' rule is applied to compute the posterior. The posterior at one video frame then becomes the prior for the next video frame. Using conjugate priors facilitates this process by ensuring that the posterior has the same functional form as the prior. The current implementation derives prior distributions at time t entirely from past inputs combined through Bayesian learning; however, the theory does not limit what may influence the prior distributions. Other sources such as top-down knowledge, behavioral states, or individual preferences could also influence the prior within the same general framework.

Here we explore two model classes to implement surprise: Gaussian (with a Gaussian conjugate prior) which is formally simple and parallels background adaptation techniques used in computer vision [19], and Poisson (with a Gamma conjugate prior) which may more accurately model incoming neural spike trains from the low-level feature extraction stages [50].

To accommodate for changing data and events at multiple temporal scales, we employ a chained cascade of surprise detectors at every pixel in every feature map, where the output of one surprise detector serves as input to the next detector in the cascade. Our implementation uses 5 such cascaded feature detectors at every pixel and for every feature. The first (fastest) is updated with feature map data from the low-level feature computations, and detector i + 1 samples from i, so that time constants increase exponentially with i. In total, the system thus comprises 72[maps] × (40 × 30) [pixels] × 5[time scales] = 432, 000 surprise detectors.

Finally, to account not only for temporally surprising events (e.g., sudden appearance of an object) but also for spatially surprising items (e.g., a red object among many green objects), we compute surprise both locally over time, and spatially in an instantaneous manner. For local temporal surprise, a single neuron in one of the feature maps is considered, and the prior is established over time from the observations received to date in the receptive field of that one neuron. For spatial surprise, a single neuron is also considered, but its prior is now derived from the compound instantaneous activity of surrounding neurons in the map, at the next faster time scale. For every video frame at time t, location (x, y), feature f, and time scale i, a neighborhood distribution of models is computed as the weighted combination of distributions from the next-faster local models, over a large neighborhood with two-dimensional Difference-of-Gaussians profile (σ₊ = 20 and σ₋ = 3 feature map pixels). As new data arrives, spatial surprise is the KL divergence between prior neighborhood distribution and the posterior after update by local samples from the neighborhood's center. For example, consider a neuron that observes a locally red image patch surrounded by a large green background. That neuron's neighbors would contribute a spatial prior that is strongly suggesting that the world is green. However, when that prior is combined with the local data received by the neuron of interest, which indicates that the world is red, a large difference between prior and posterior arises, and consequently a large spatial surprise (see Fig. 3 for pseudo-code).

Figure 3.

Simplified algorithm to compute surprise over space and time at multiple scales. This algorithm is applied to each of the 72 feature maps. The incoming data is the array of raw feature detector values for the feature map's feature type and center-surround spatial scale.

Our theory does not constrain how temporal and spatial surprises may combine. In previous work [24], we addressed this issue by turning to empirical single-unit recordings of complex cells in striate cortex of anesthetized monkey [40]. From fitting the neural data, total surprise S is given by:

$$S={\left[S_T+\frac{S_S}{20}\right]}^{\frac{1}{3}}$$ (47)

where S_T is the temporal and S_S the spatial surprise. This formulation resulted from a least-squares fit of a function of the form S = [a₁S_T + a₂S_S + a₃S_TS_S]^a₄ to the neural data. We further posit that surprise combines multiplicatively across time scales, such that an event is surprising only if at all relevant time scales, allowing the model to learn periodic stimuli of various frequencies. One caveat with this approach is that stimuli which may fully adapt the surprise detectors at one time scale and yield zero surprise at that scale may effectively zero out potentially surprising events at other time scales. To address this, we introduce below an additional step just before the prior is updated, whereby the variance of the prior is slightly relaxed (increased) prior to the arrival of every video frame. A parameter ζ regulates the amount of relaxation. With 0 < ζ < 1, the variance of the prior will not settle, even if, e.g., the data is stationary, resulting in surprise values that are always non-zero. We finally assume that surprise sums across features, such that a location may be surprising by its color, motion, or other. It is interesting to note that other alternatives may be more desirable, e.g., a max operation across features [36, 57]. However, for the datasets evaluated here, this alternative yields lower ordinal dominance scores (Fig. 5).

Figure 5.

Example maps generated by the computational systems tested. One video frame is shown (clip beverly08, frame 127) with the corresponding master map for each model. Current eye position of one human observer is indicated by the small cyan square (on the person running in the video clip). Ordinal dominance scores are indicated for each system, for both the original and MTV-style dataset. Higher scores indicate better systems, i.e. systems which predict high master map values near the locations selected by human gazes and low map values everywhere else.

The sum is then passed through a saturating sigmoidal nonlinearity to enforce plausible neuronal firing dynamics and yield the final master map used for comparison with human gaze behavior.

6.2.1. Gaussian data with Gaussian prior

With Gaussian models, the data from every low-level feature detector at every location in every video frame is assumed to have a Gaussian distribution with mean given by the feature detector's response to the current frame, and fixed variance which approximates the observation noise at the feature detection stage (which, in turns, reflects sensor noise and possibly neural noise inherent to the feature computation process).

Thus, for each of the 72 feature types (e.g., luminance, red-green opponency, etc), video frame, spatial center-surround feature scale, 2D image location in the rescaled feature map, and temporal scale, we here use the unknown mean / known variance formulation of section 3.3, eq. 17. With the addition of the prior relaxation term 0 < ζ < 1 (which here simply divides the prior's variance ${\sigma }_1^2$, we obtain:

$$\begin{array}{lll}{\mu }_2=\frac{\frac{{\mu }_1\zeta }{{\sigma }_1^2}+\frac{N\overline{m}}{{\sigma }^2}}{\frac{\zeta }{{\sigma }_1^2}+\frac{N}{{\sigma }^2}}& \text{and}& \frac{1}{{\sigma }_2^2}=\frac{\zeta }{{\sigma }_1^2}+\frac{N}{{\sigma }^2}\end{array}$$ (48)

We assume that N = 1 data samples are received for every new video frame, the data sample value (and m̄ since N = 1) are given by the feature detector's response to the current video frame, and the variance σ² of the data is fixed and reflects noise in the sensor and early stages of processing (we use s̄ = 5 given RGB pixel values in the [0 … 255]³ range). Our simulations use ζ = 0.7. Surprise is computed exactly per eq. 18 (without the approximation for large N).

6.2.2. Poisson data with Gamma prior

In a somewhat more neurally-plausible implementation, we model data received from feature map f at location (x, y) and time t as Poisson distributions M(λ) (which well describe cortical pyramidal cell firing statistics [50]), parameterized by firing rate λ ≥ 0. λ is trivially estimated over the duration of each video frame as simply the feature detector's response λ̅ = f(x, y, t). In contrast with the Gaussian case, here the variance of the sample is not arbitrarily fixed but directly determined by the assumed Poisson nature of the data samples, and thus is equal to the mean λ̅.

As detailed in Section 3.2, the prior P(M) satisfying the conjugate prior property on Poisson data is the Gamma probability density, eq. 13. With the addition of the ζ prior relaxation term (which here again divides the prior's variance, by multiplying both a₁ and b₁), we slightly modify Eq. 14 and obtain:

$$\begin{array}{lll}{a}_2=\zeta a_1+N\overline{m}& \text{and}& b_2=\zeta b_1+N\end{array}$$ (49)

We here again assume that N = 1 data samples are received at every video frame. Our simulations here again use ζ = 0.7. Surprise is computed exactly using Eq. 15.

7. An Application of Surprise to Psychophysics and Eye Movements

Developing an ability to rapidly detect surprising events is crucial in allowing living systems to quickly identify potential predators, preys, or mates and in ensuring survival. It is reasonable to postulate that surprising events ought to attract attention mechanisms in living systems, and that the same principle may be useful in the design of artificial systems, for instance in computer vision and surveillance. Indeed, it has been noted that events previously described as novel or salient tend to attract attention [43]. To test the surprise theory, we here present an application to finding surprising objects and events in natural video streams. Using eye-tracking experiments with human subjects, we quantitatively evaluate the extent to which surprising visual events occurring in natural video stimuli may indeed capture attention and gaze of human observers. The application presented here extends previous similar experimentations [24, 25, 26] by adding a new dataset, comparing two different model classes, Gaussian data with a Gaussian prior, and Poisson data with a Gamma prior, and introducing a new temporal analysis which demonstrates a strong time contingency between the onset of a surprising event in the stimuli and the initiation of a human eye movement towards that event.

7.1. Subjects, stimuli and gaze recording methods

Our experiments use the publicly available human eye movement dataset from the NSF-CRCNS data sharing project (crcns.org). This dataset contains two components.

In the first component, we recorded eye movements from eight naïve observers. Each watched a subset from 50 videoclips totaling over 25 minutes of playtime (“original” dataset). Clips comprised outdoors daytime and nighttime scenes of crowded environments, video games, and television broadcast including news, sports, and commercials. Right-eye position was tracked with a 240 Hz video-based device (see [25] for additional methodological details). To maintain interest, observers were instructed to follow the stimuli's main actors and actions, as simple questions would be asked to them at the end of the experiment to test their understanding of the contents of the clips. Here we only retain those clips for which gaze recordings from at least 4 observers were available (to allow for the establishment of an upper bound inter-observer correlation performance, below). Two hundred calibrated eye movement traces (10,192 gaze shifts or “saccades”) were analyzed, corresponding to four distinct observers for each of the 50 clips.

In the second component, the video clips were cut into 1-3s short “clippets” which were then re-assembled in random order into an “MTV-style” set of clips [10]. Another set of 8 observers watched the clips and we here again only retain clips for which recordings are available for at least 4 observers. The goal of the random shuffling of clippets was to abolish some of the long-term cognitive influences on attention and gaze, so that observer's gaze allocation would be more strongly short-term. Here, this dataset is of particular interest because it will help us gauge the extent to which past events beyond a few seconds may influence our modeled low-level vision priors, surprise, and human gaze. In total, 6,648 saccades were analyzed for the MTV-style dataset.

Informed consent was obtained from all subjects prior to the experiments. Each subject watched a subset of the collection of video clips, so that eye movement traces from four distinct subjects were obtained for each clip. Video clips were presented on a 22″ CRT monitor (LaCie, Inc.; 640 × 480, 60.27 Hz double-scan, mean screen luminance 30 cd/m², room 4 cd/m², viewing distance 80cm, field of view 28° × 21°). The clips comprised between 164 to 2,814 frames or 5.5s to 93.9s, totaling 46,489 frames or 25:42.7 playback time. Frames were presented on a Linux computer under SCHED_FIFO scheduling which ensured microsecond-accurate timing [15].

Right-eye position was tracked at 240 Hz using a video-based device (IS-CAN RK-464), which robustly estimates gaze from comparative real-time measurements of both the center of the pupil and the reflection of an infrared light source onto the cornea. Saccades were defined by a velocity threshold of 20°/s and amplitude threshold of 2°.

Sampling of master map values around human or random saccade targets used a circular aperture of diameter 5.6°, approximating the size of the fovea and parafovea. Saccade initiation latency was accounted for by subjecting the master maps to a temporal low-pass filter with time constant τ = 500ms. The random sampling process was repeated 100 times.

7.2. Gaze prediction results

We evaluate in Fig. 4 four different attention systems that predict human saccades: one using surprise with Gaussian data and prior (Section 6.2.1), one using surprise with Poisson data and Gamma prior (Section 6.2.2), a simple baseline control system which simply computes local pixel variance in small image patches, and a human inter-observer system — all further described below. In addition, in Fig. 5 we compare these systems with additional previously published systems and with variations on our surprise-based systems.

Figure 4.

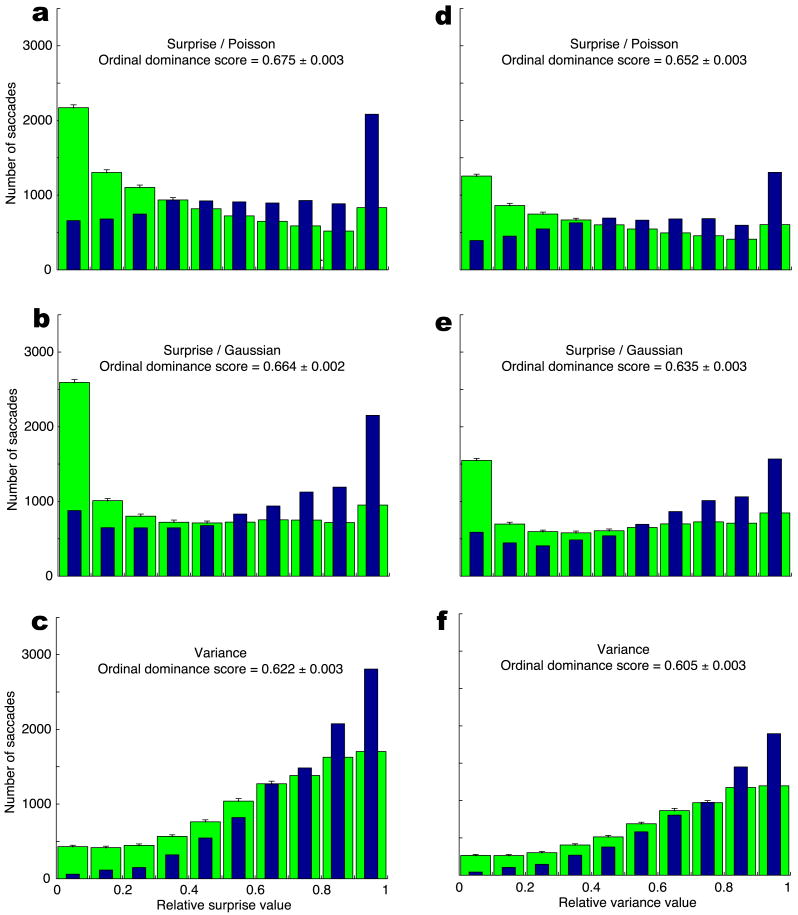
Histograms of master map values at saccade endpoints for random (wide green bars) and humans (narrow blue bars), for the “original” (a, b, c) and “MTV-style” (d, e, f) datasets. Human histograms particularly differ from the random ones in that humans gaze towards low master map values (leftmost bins in each histogram) less often than expected by chance, while they gaze towards high mastermap values (rightmost bins) more often than expected by chance. AUC scores indicate significantly different performance levels, and a strict ranking of chance < variance < Gaussian/Gaaussian surprise < Poisson/Gamma surprise < inter-observer.

The Gaussian/Gaussian and Poisson/Gamma surprise systems are as described above. The Variance system simply computes local variance of pixel luminance within 16 × 16 image patches. The resulting variance map has been suggested to already predict human gaze above chance [45]; hence we use this very simple system as a baseline or lower bound. The inter-observer system is built by plotting a Gaussian blob with σ = 3 master map pixels (4.5°), continuously at each of the eye positions of the three observers other than that under test, with some forgetting provided by the master map's temporal low-pass filter. High values on this map would hence be present only at the locations currently gazed at by some human observer. This system allows us to establish an upper bound for how well the other systems might be expected to predict human gaze.

To characterize image regions selected by our observers, we process the video clips through the different systems. Each system outputs a topographic dynamic master response map, assigning in real-time a response value to every input location. A good master map should highlight, more than expected by chance, locations gazed to by our human observers. Hence to score and compare each system, we sample, at the onset of every human saccade made, master map activity around the saccade's future endpoint, and around a uniformly random endpoint. Random sampling is repeated 100 times to evaluate variability. To quantify the extent to which humans may be attracted towards hotspots in the master maps, we use ordinal dominance analysis [4]. To this end, we first normalize master map values sampled at human and random saccade endpoints by the maximum activity in the master map at the time of the saccade. For each system, histograms of master map values at human and random saccade endpoints are then created (Fig. 4). In a manner similar to computing a Receiver Operating Characteristic (ROC) curve, we then sweep a threshold from 0 to 1; for each threshold value we count the percentage of eye positions and random positions which land above threshold (“hits”). The ordinal dominance curve is then created similarly to an ROC curve, with the difference that it plots human hits vs. random hits. This curve indicates how well a simple binary threshold is able to discriminate signal (master map values at human gaze locations) from noise (values at random locations). We finally score each system by computing the area under the curve (AUC) from the ordinal dominance curve. The process is repeated 100 times for the 100 random samples, which allows us to attach a confidence estimate to each AUC value.

An AUC value of 0.5 would indicate a system which is at chance in predicting where human observers looked. Our inter-observer system yields AUC scores of 0.805 ± 0.002 for the first (“original”) dataset and 0.827 ± 0.002 for the second (“MTV-style”) dataset. The surprise and variance systems are hence expected to score between 0.5 and 0.8, with higher scores indicating better ability to predict human gaze. Scores are shown in Fig. 4. All three systems perform significantly above chance level (AUC=0.5; t-test, p < 10⁻¹⁰ or better). Furthermore, both variants of the surprise-based system perform significantly better than the much simpler variance-based system (t-tests on the respective AUC scores, p < 10⁻¹⁰ or better). The Poisson/Gamma surprise system exhibits a small but significant advantage over the Gaussian/Gaussian surprise system in these experiments. These two surprise systems score about half-way between chance and inter-observer.

Fig. 5 shows an example video frame and corresponding master maps for the computational systems studied here, as well as for a few systems evaluated previously [26], and variations on the surprise systems described below. In particular, the Michelson contrast system, as in Mannan et al. [38], is an interesting alternative to our local variance system. However, we find that on these datasets it actually performs slightly below chance level (corresponding to a score of 0.5), indicating that observers tended to preferentially look towards locations with lower contrast than expected by chance. This is in agreement with the original results of Mannan et al., who conclude that a number of local features tested in their experiments (including Michelson contrast, edge density measures, and others) are poor predictors of human fixations. The Entropy and DCT-based information systems are very simplified measures of information in local image patches, and have been previously proposed as gaze predictors [30, 42, 26]. We find that they score above chance, but below surprise. Finally, we evaluated the hypothesis of Zhaoping and colleagues that salience signals may combine across different feature channels according to a maximum rule rather than a sum rule [36, 57]. To this end, we implemented variants of the surprise systems where color, intensity, orientation, flicker and motion sources of surprise combine with a max rule. With the datasets evaluated here, this alternative yields lower AUC scores (Fig. 5). The reason for the lower scores when taking the maximum across features is that this often yields lower gaze target to clutter signal-to-noise ratios. These intriguing results obtained with our free-viewing datasets should be evaluated further with future experiments aimed more directly at addressing the max vs. sum question.

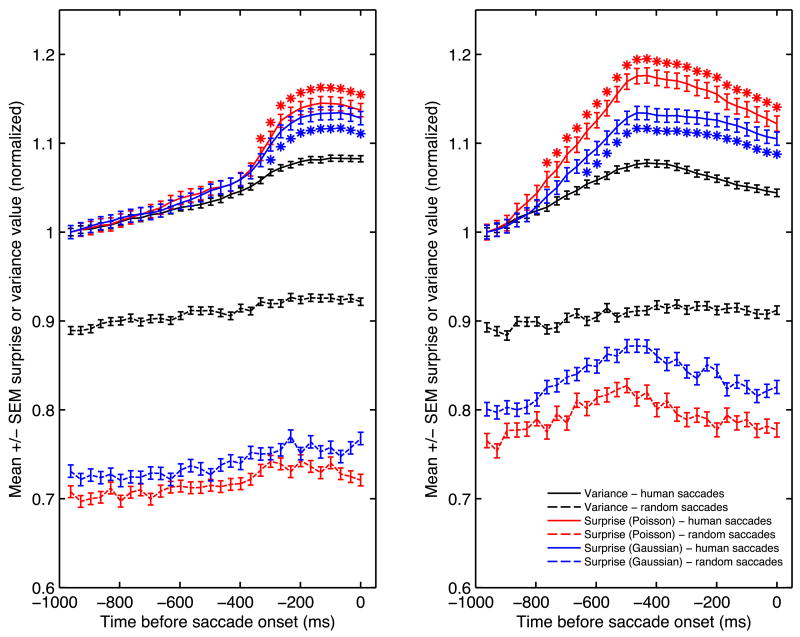
To further investigate the extent to which events detected as surprising by our systems might attract human gaze, we recorded, at the landing location of every saccade, the history of master map values for up to 1,000ms preceding the initiation of the saccade of interest (Fig. 6). In both datasets, a sudden surge of surprise is seen at saccade landing points shortly before saccades are initiated. A similar but weaker surge is observed also for the Variance system, indicating that the sudden appearance of textured objects might also have attracted saccades. However, the surge for the variance system is significantly weaker than for any of the surprise systems. In the MTV-style experiments, a surge of surprise is also observed for random saccades around 500ms prior to human saccades; this reflects the global surge of surprise which is observed at every abrupt jump-cut when the scene changes from one 1-3s clippet to the next. The surge in the random saccade data suggests that humans tended to execute saccades in a manner that was somewhat time-locked to jump-cuts in the stimuli. This is also reflected by the larger surge observed for human saccades in the MTV-style compared to the original dataset.

Figure 6.

History of master map values at locations selected by human saccades, for up to 1,000ms prior to the initiation of each saccade, for the “original” (left) and “MTV-style” (right) datasets. Curves are normalized in pairs (human saccades, solid lines, and random saccades, dashed lines) by the surprise value for human saccades at -1,000ms. This allows easy comparison between the curves for the different systems. Stars indicate time points where the surprise-based systems performed significantly differently from the variance-based system (t-tests, p < 0.05 after Bonferroni correction).

8. Discussion

Bayes theorem is the most fundamental theorem of learning and adaptation, quantifying how the prior distribution over the space of models or hypotheses ought to be revised into a posterior distribution as data is collected. Accordingly, the distance between the prior and posterior distributions is also bound to be a fundamental quantity, that may have escaped systematic attention. Here we have defined this quantity – surprise – and studied its properties systematically.

Surprise is different from Shannon's entropy, which it complements. Surprise is also different from several other definitions of information that have been proposed [1] as alternatives to Shannon's entropy. Most alternative definitions of entropy, such as Rényi's entropies, are actually algebraic variations on Shannon's definition rather than conceptually different approaches.

To measure the effect of data on the observer's prior and posterior distributions, one could envision using the difference between the entropy of the prior and the entropy of the posterior. However, such a difference would only quantify the difference in uncertainty between the prior and posterior distributions. Unlike surprise which is always positive, such a difference could be either positive or negative and therefore less appealing as a measure. More fundamentally, the posterior could, for instance, be very different from the prior, but retain a similar level of entropy. Thus data greatly affecting the observer could appear insignificant by this measure.

In many important cases related to the exponential family of distributions, surprise can be computed analytically and efficiently, both in terms of exact and approximate formula. The analytical results presented here could be extended in several directions including non-conjugate and other prior distributions as well as more complex multidimensional distributions (e.g., inverse Wishart). In general, however, the computation of surprise can be expected to require numerical techniques including Monte Carlo methods to approximate integrals over model classes. In this respect, the computation of surprise should benefit from ongoing progress in Markov chain and other Monte Carlo methods, as well as progress in computing power.

The concept of surprise has its own limitations. In particular, it does not capture all the semantic/relevance aspects of data. If, while surfing the web in search of a car to purchase one stumbles on a picture of Marilyn Monroe, the picture may carry a low degree of relevance, a high degree of surprise, and a low-to-high amount of Shannon information depending on the pixel structure. Thus, relevance, surprise, and Shannon's entropy are three different facets of information that can be present in different combinations. Although there have been several attempts (e.g. [33, 52]), defining relevance remains a central open challenge. Surprise, however, appears remarkable for its simplicity and generality which ought to result in its applicability to areas as diverse as learning, data mining and compression, and the design or reverse engineering of natural or artificial sensory systems.

We have only touched upon the connection between surprise and statistical learning theory [53, 22] by showing that surprise decreases as 1/N during sequential learning in simple cases. This analysis could be extended to more complex settings, such as artificial neural networks. At higher abstraction levels, informal ideas of novelty and surprise have been proposed that could capture attention and trigger learning [43, 20], which may now be formalized in terms of priors and posteriors. Highly surprising data could signal that learning is required and highly unsurprising data could signal that learning is completed, or adaptation no longer necessary.

A surprising training set is a prerequisite for learning. The amount of surprise in training data, however, should not be so excessive as to overwhelm the learning system. Thus information surprise in the training set ought to be calibrated to the capacity of the learning system. Furthermore, when the degree of surprise of the data with respect to the model class becomes low, the data is no longer informative for the given model class. This, however, does not necessarily imply that a good models of the data hase been learnt since the model class itself could be unsatisfactory and in need of a complete overhaul. The process by which a learning system realizes that a model class is unsatisfactory in an alternative free setting–the open-ended aspect of inference–has so far eluded precise formalizations and ought to be the object of future investigations.

As a side note, and to avoid any confusions, it is also worth noting that relative entropy has often been used as a training function for neural networks and other machine learning systems (e.g. [3] and references therein), but in a completely different sense. In a multinomial classification problem, for instance, model parameters can be adjusted in order to minimize the relative entropy Σt_i log t_i − Σt_i log p_i aggregated over all training examples. For a single training example, t_i is the 0-1 target representing membership in the i-th class and p_i is the probability of membership in the i-th class computed by the learning system. This relative entropy between the vectors t and p has little to do with the relative entropy between the prior and posterior distributions over the parameters of the model that is used to compute p.

In data mining applications, surprise could be used to systematically detect novelty in areas ranging from surveillance to information retrieval. In data compression applications, surprise could be used to guide dynamical encoding of information, allocating more bits to surprising data. For sensory systems, we have described an application of surprise to computer vision and the analysis of human attentional gaze shifts. Human attention is an exceedingly complex phenomenon, under the control of both bottom up and top down influences. Our results are not intended in any way to prove that human brains compute surprise to control eye movements. It is however encouraging to see that the simple bottom-up version of surprise outperforms other state-of-the-art metrics in predicting gaze shifts and that, in principle, top down influences could be incorporated into the surprise framework, simply by modulating the prior distribution. A number of additional theoretical frameworks and computational models have been proposed to explain attention guidance and eye movements, using information-theoretic principles in very restricted scenarios, such as discriminating shape silhouettes or searching for a known target in a noisy environment [46, 41]. While interesting, these approaches still need additional developments before they can be applied to the CRCNS eye-tracking datasets, or other kinds of “real data,” for the purpose of comparison with surprise or other theories. Indeed, such theories and approaches are not yet able to make useful predictions for arbitrary image or video stimuli and observer tasks. This is a fundamental difference between these very interesting but more specialized theories and our new approach: Our surprise theory and associated computational model are capable of making predictions (good or bad) for any set of image or video stimuli and any set of associated eye movement traces (human or other) acquired under any observer task.

Finally, in sensory systems and beyond the visual attention application studied here, surprise may be computed on auditory, olfactory, gustative, somatosensory, or other features, using exactly the same definition. Surprise may be computed at different temporal and spatial scales, and different levels of abstraction. Indeed, detecting surprise in neuronal spike trains or other data streams is a very general operation that does not require understanding the “meaning” carried by the data and therefore may be suitable for learning in deep architectures and other self-organization processes.

Appendix A: Discrete Case

Multinomial Case (Dirichlet prior)

In the two-dimensional case, consider two Dirichlet distributions D₁ = D(a₁, b₁)(x) = C₁x^a₁−1(1 − x)^b₁−1 and D₂ = D(a₂, b₂)(x) = C₂x^a₂−1(1 − x)^b₂−1, with C₁ = Γ(a₁ + b₁)/Γ(a₁)Γ(b₁), and similarly for C₂. To calculate the relative entropy in the two dimensional case, we use the formula ([18])

$${\int }_0^1{x}^{u-1}{(1-x)}^{v-1}log\mathit{xdx}=B(u,v)[\mathrm{\Psi }(u)-\mathrm{\Psi }(u+v)]$$ (50)

where B(u, v) is the beta function $B(u,v)={\int }_0^1{x}^{u-1}{(1-x)}^{v-1}dx=\mathrm{\Gamma }(u)\mathrm{\Gamma }(v)/\mathrm{\Gamma }(u+v)$ and Ψ(x) is the derivative of the logarithm of the gamma function Ψ(x) = d(log Γ(x))/dx. A cross term of the form

$$\begin{array}{l}F(D_1,D_2)=\\ {\int }_0^1{C}_1{x}^{a_1-1}{(1-x)}^{b_1-1}[log{C}_2+(a_2-1)logx\\ +(b_2-1)log(1-x)]dx\end{array}$$ (51)

is equal to

$$\begin{array}{l}F(D_1,D_2)=log{C}_2\\ +(a_2-1)[\mathrm{\Psi }(a_1)-\mathrm{\Psi }(a_1+b_1)]\\ +(b_2-1)[\mathrm{\Psi }(b_1)-\mathrm{\Psi }(a_1+b_1)]\end{array}$$ (52)

using the fact that C₁B(a₁, b₁) = 1. In particular, the entropy of a two-dimensional Dirichlet distribution such as D₁ is obtained by taking: −F(D₁, D₁).

With some algebra, the Kullback-Liebler divergence between any two Dirichlet distributions is finally given by:

$$\begin{array}{l}K(D_1,D_2)=log\frac{C_1}{C_2}\\ +(a_1-a_2)[\mathrm{\Psi }(a_1)-\mathrm{\Psi }(a_1+b_1)]\\ +(b_1-b_2)[\mathrm{\Psi }(b_1)-\mathrm{\Psi }(a_1+b_1)]\end{array}$$ (53)

With n successes in the sequence D, the posterior is a Dirichlet distribution D₂(a₂, b₂) with [3]

$$\begin{array}{lll}{a}_2=a_1+n& \text{and}& b_2=b_1+(N-n)\end{array}$$ (54)

Using this relation between the prior and the posterior, we get the surprise

$$\begin{array}{l}S(D_1,D_2)=log\frac{C_1}{C_2}+n[\mathrm{\Psi }(a_1+b_1)-\mathrm{\Psi }(a_1)]\\ +(N-n)[\mathrm{\Psi }(a_1+b_1)-\mathrm{\Psi }(b_1)]\end{array}$$ (55)

Using the general fact that $\mathrm{\Psi }(x)-\mathrm{\Psi }(y)={\sum }_{k=0}^{\infty }(\frac{1}{y+k}-\frac{1}{x+k})$, which implies $\mathrm{\Psi }(x+n)-\mathrm{\Psi }(x)={\sum }_{k=0}^{n-1}\frac{1}{x+k}$ when n is an integer, we get

$$\begin{array}{l}S(D_1,D_2)=log\frac{C_1}{C_2}+n(\sum _{k=0}^{\infty }\frac{1}{a_1+k}-\frac{1}{a_1+b_1+k})+\\ (N-n)(\sum _{k=0}^{\infty }\frac{1}{b_1+k}-\frac{1}{a_1+b_1+k})\end{array}$$ (56)

Now we have

$$\sum _{k=0}^{\infty }(\frac{1}{a_1+k}-\frac{1}{a_1+b_1+k})=\sum _{k=0}^{\lfloor b_1\rfloor -1}(\frac{1}{a_1+k})+\text{Rest}$$ (57)

where

$$\begin{array}{l}0\le \text{Rest}=\sum _{k=0}^{\infty }(\frac{1}{a_1+\lfloor b_1\rfloor +k}-\frac{1}{a_1+b_1+k})\\ \le (b_1-\lfloor b_1\rfloor )\sum _{k=0}^{\infty }\frac{1}{{(a_1+\lfloor b_1\rfloor +k)}^2}\end{array}$$ (58)

and similarly for the symmetric term. The rest is exactly 0 when a₁ and b₁ (and hence a₂ and b₂) are integers, and in general decreases with the size of a₁ and b₁. This yields the approximation

$$\begin{array}{l}S(D_1,D_2)\approx log\frac{C_1}{C_2}\\ +n(\sum _{k=0}^{\lfloor b_1\rfloor -1}\frac{1}{a_1+k})+(N-n)(\sum _{k=0}^{\lfloor a_1\rfloor -1}\frac{1}{b_1+k})\end{array}$$ (59)

This approximation is exact when a₁ and b₁ are integers. Now for x > 0 we have $log((x+n)/x)<{\sum }_{k=0}^{n-1}1/(x+k)<log((x+n-1)/x)+1/x$ or $0<{\sum }_{k=0}^{n-1}1/(x+k)-log((x+n)/x)<1/x$. Thus,

$$\begin{array}{l}S(D_1,D_2)\approx log\frac{C_1}{C_2}+nlog\frac{a_1+b_1}{a_1}\\ +(N-n)log\frac{a_1+b_1}{b_1}\end{array}$$ (60)

Now we have,

$$\begin{array}{l}log\frac{C_1}{C_2}=log\frac{\mathrm{\Gamma }(a_1+b_1)\mathrm{\Gamma }(a_2)\mathrm{\Gamma }(b_2)}{\mathrm{\Gamma }(a_1)\mathrm{\Gamma }(b_1)\mathrm{\Gamma }(a_2+b_2)}\\ =log\frac{(a_1+n-1)(a_1+n-2)\dots a_1(b_1+N-n-1)\dots b_1}{(a_1+b_1+N-1)(a_1+b_1+N-2)\dots (a_1+b_1)}\end{array}$$

We can use bounds of the form $loga+{\int }_{a_1}^{a_1+n1}log\mathit{xdx}<log{a}_1+\dots log(a_1+n-1)\le log{a}_1{\int }_{a_1+1}^{a_1+n}log\mathit{xdx}$ to estimate this term. Alternatively, one can assume that a₁ and b₁ are integers and use binomial coefficient approximations, such as those in [8]. In all cases, neglecting constant terms and terms of order log N, if we let n = pN (0 < p < 1) and N go to infinity we have

$$log\frac{C_1}{C_2}\approx -log\left(\begin{array}{c}N\\ n\end{array}\right)\approx -NH(p))$$ (61)

where H(p) is the entropy of the (p, q) distribution with q = 1 − p. Thus when N → ∞, and n = pN with 0 < p < 1 we have

$$\begin{array}{l}S(D_1,D_2)\approx N(plog\frac{a_1+b_1}{a_1}\\ +qlog\frac{a_1+b_1}{b_1}-H(p))\\ \approx N\text{K}(p,a_1)\end{array}$$ (62)

where K(p, a₁) is the relative entropy between the empirical distribution (p, q) and the expectation of the prior $\left(\frac{a_1}{a_1+b_1},\frac{b_1}{a_1+b_1}\right)$. Thus, asymptotically surprise grows linearly with the number of data points with a proportionality coefficient that depends on the discrepancy between the expectation of the prior and the observed distribution. The same relationship can be expected to be true in the case of a multinomial model.

Symmetric Prior (a₁ = b₁)

Consider now the case of a symmetric prior, then

$$S(D_1,D_2)=log\frac{C_1}{C_2}+N[\mathrm{\Psi }(2a_1)-\mathrm{\Psi }(a_1)]$$ (63)

Using formulas in [18], $\mathrm{\Psi }(2a_1)-\mathrm{\Psi }(a_1)={\sum }_{k=0}^{\infty }\frac{{(-1)}^k}{2a_1+k}+log2$, thus

$$\begin{array}{l}S(D_1,D_2))=log\frac{C_1}{C_2}\\ +N\sum _{k=0}^{\infty }\frac{{(-1)}^k}{2a_1+k}+log2\\ \approx N\left(\sum _{k=0}^{\infty }\frac{{(-1)}^k}{2a_1+k}+log2-H(p)\right)\end{array}$$ (64)

the approximation being in the regime n = pN and N → ∞. When a₁ is an integer, we also have $\mathrm{\Psi }(2a_1)-\mathrm{\Psi }(a_1)={\sum }_{k=1}^{2a_1-1}{(-1)}^{k+1}/k={\sum }_{k=a_1}^{2a_1-1}1/k$. Thus when a₁ is an integer

$$\begin{array}{l}S(D_1,D_2)=N[\sum _{k=a_1}^{2a_1-1}\frac{1}{k}]+\\ log\frac{(2a_1-1)\left(\begin{array}{c}2a_1-2\\ a_1-1\end{array}\right)}{(2a_1+N-1)\left(\begin{array}{c}N+2a_1-2\\ n+a_1-1\end{array}\right)}\end{array}$$ (65)

As N → ∞ with 0 < p < 1

$$\begin{array}{l}S(D_1,D_2)\approx N[\sum _{k=a_1}^{2a_1-1}\frac{1}{k}]-log\left(\begin{array}{c}N+2a_1-2\\ n+a_1-1\end{array}\right)\\ \approx N[\sum _{k=a_1}^{2a_1-1}\frac{1}{k}]-log\left(\begin{array}{c}N\\ n\end{array}\right)\end{array}$$ (66)

and therefore

$$S(D_1,D_2)\approx N[\sum _{k=a_1}^{2a_1-1}\frac{1}{k}-H(p)]$$ (67)

For instance, when a₁ = b₁ = 1, this gives:

$$S(D_1,D_2)=N-log(N+1)-log\left(\begin{array}{c}N\\ n\end{array}\right)$$ (68)

with the asymptotic form

$$\begin{array}{l}S(D_1,D_2)\approx N(1-H(p))+log\frac{\sqrt{2N\pi pq}}{N+1}\\ \approx N(1-H(p))\end{array}$$ (69)

With a uniform symmetric prior, the empirical distribution with maximal entropy brings the least information. When a₁ = b₁ = 5 this gives R(D₁, D₂) ≈ N[0.746 − H(p)]. As we increase a₁ + b₁, keeping a₁ = b₁, the constant ${\sum }_{a_1}^{2a_1-1}(1/k)$ decreases to its asymptotic value log 2 which corresponds to the asymptotic form S(D₁, D₂) ≈ NK(p, 0.5). The stronger the strength of the uniform prior (the larger a₁ + b₁), the smaller the surprise created by a die with maximum entropy.

Poisson Case (Gamma Prior)

We consider two Gamma distributions Γ₁ = Γ₁(a₁, b₁)x = C₁x^a₁−1e^−b₁x and Γ₂ = Γ₂(a₂, b₂)(x) = C₂x^a₂−1e^−b₂x with $C_1=b_1^{a_1}/\mathrm{\Gamma }(a_1)$, and similarly for C₂. To calculate the relative entropy, we use the formula ([18])

$${\int }_0^{\infty }{x}^{u-1}{e}^{-vx}log\mathit{xdx}=\frac{\mathrm{\Gamma }(u)}{v^u}[\mathrm{\Psi }(u)-logv]$$ (70)

A cross term F(Γ₁, Γ₂)

$$\begin{array}{l}F({\mathrm{\Gamma }}_1,{\mathrm{\Gamma }}_2)={\int }_0^{\infty }{C}_1{x}^{a_1-1}{e}^{-b_{1}x}[log{C}_2\\ +(a_2-1)logx-b_{2}x]dx\end{array}$$ (71)

is then equal to:

$$\begin{array}{l}F({\mathrm{\Gamma }}_1,{\mathrm{\Gamma }}_2)=a_{2}log{b}_2-log\mathrm{\Gamma }(a_2)-b_2\frac{a_1}{b_1}\\ +(a_2-1)[\mathrm{\Psi }(a_1)-log{b}_1]\end{array}$$ (72)

With some algebra, the KL divergence between two Gamma distributions is given by

$$\begin{array}{l}K({\mathrm{\Gamma }}_1,{\mathrm{\Gamma }}_2)=log\frac{b_1^{a_1}}{a_2^{b_2}}+log\frac{\mathrm{\Gamma }(a_2)}{\mathrm{\Gamma }(a_1)}+b_2\frac{a_1}{b_1}-a_1\\ +(a_1-a_2)[\mathrm{\Psi }(a_1)-log{b}_1]\end{array}$$ (73)

With N observations in D, the posterior is Gamma and satisfies

$$\begin{array}{ll}{a}_2=a_1+N\overline{m}& b_2=b_1+N\end{array}$$ (74)

With these values, this finally yields the surprise S(Γ₁, Γ₂)

$$\begin{array}{l}S(D,ℳ)=K({\mathrm{\Gamma }}_1,{\mathrm{\Gamma }}_2)=a_{1}log\frac{b_1}{b_1+N}\\ -N\overline{m}log(b_1+N)+log\frac{\mathrm{\Gamma }(a_1+N\overline{m})}{\mathrm{\Gamma }(a_1)}\\ +\frac{N{a}_1}{b_1}+N\overline{m}[log{b}_1-\mathrm{\Psi }(a_1)]\end{array}$$ (75)

When N is large, using Stirling's formula, the dominant terms in N log N cancel leaving the approximation

$$S(D,ℳ)\approx N\left(\frac{a_1}{b_1}-\overline{m}[1-log\overline{m}+\mathrm{\Psi }(a_1)-log{b}_1]\right)$$ (76)

Appendix B: Continuous Case

Unknown Mean/Known Variance

Consider now two Gaussians G₁(μ₁, σ₁) and G₂(μ₂, σ₂). Then, after some algebra, the cross term is given by

$$\begin{array}{l}F(G_1,G_2)={\int }_{-\infty }^{+\infty }{G}_{1}log{G}_{2}dx\\ =-\frac{1}{2}log(2\pi {\sigma }_2^2)-\frac{{\sigma }_1^2+{({\mu }_1-{\mu }_2)}^2}{2{\sigma }_2^2}\end{array}$$ (77)

here using for simplicity natural logarithms. $F(G,G)=\frac{1}{2}log[2\pi e{\sigma }^2]=H(G)$ is the entropy. The Kullback-Liebler divergence can then be obtained

$$K(G_1,G_2)=-\frac{1}{2}+log\frac{{\sigma }_2}{{\sigma }_1}+\frac{{\sigma }_1^2+{({\mu }_1-{\mu }_2)}^2}{2{\sigma }_2^2}$$ (78)

Consider now a data set with N points d₁, …, d_N with empirical mean m¯. If the data has known variance σ², then the posterior parameters are given by:

$$\begin{array}{lll}{\mu }_2=\frac{\frac{{\mu }_1}{{\sigma }_1^2}+\frac{N\overline{m}}{{\sigma }^2}}{\frac{1}{{\sigma }_1^2}+\frac{N}{{\sigma }^2}}& \text{and}& \frac{1}{{\sigma }_2^2}=\frac{\text{1}}{{\sigma }_1^2}+\frac{N}{{\sigma }^2}\end{array}$$ (79)

In the general case

$$\begin{array}{l}S(G_1,G_2)=log\frac{\sigma }{\sqrt{{\sigma }^2+N{\sigma }_1^2}}\\ +N\frac{{\sigma }_1^2}{2{\sigma }^2}+\frac{N^2{\sigma }_1^2{({\mu }_1-\overline{m})}^2}{2{\sigma }^2({\sigma }^2+N{\sigma }_1^2)}\\ \approx \frac{N}{2{\sigma }^2}[{\sigma }_1^2+{({\mu }_1-\overline{m})}^2]\end{array}$$ (80)

when N is large. In the special case where the prior has the same variance has the data σ₁ = σ then the formula simplifies a little and yields

$$\begin{array}{l}S(G_1,G_2)=\frac{N}{2}-\frac{1}{2}log(N+1)+\frac{N^2{({\mu }_1-\overline{m})}^2}{2(N+1){\sigma }^2}\\ \approx \frac{N}{2{\sigma }^2}[{\sigma }^2+{({\mu }_1-\overline{m})}^2]\end{array}$$ (81)

when N is large. In any case, surprise grows linearly with N with a coefficient that is the sum of the prior variance and the square difference between the expected mean and the empirical mean scaled by the variance of the data.

Unknown Variance/Known Mean

In the case of unknown variance and known mean, we have a family M(σ²) of models with a conjugate prior for σ² that is a scaled inverse gamma distribution ([16])

$$\begin{array}{l}{\mathrm{\Gamma }}_1({\nu }_1,s_1)=\frac{{\left(\frac{{\nu }_1}{2}\right)}^{{\nu }_1/2}{s}_1^{{\nu }_1}}{\mathrm{\Gamma }\left(\frac{{\nu }_1}{2}\right)}{({\sigma }^2)}^{-(\frac{{\nu }_1}{2}+1)}{e}^{-\frac{{\nu }_1{s}_1^2}{2{\sigma }^2}}d{\sigma }^2\\ =C_1{({\sigma }^2)}^{-(\frac{{\nu }_1}{2}+1)}{e}^{-\frac{{\nu }_1{s}_1^2}{2{\sigma }^2}}d{\sigma }^2\end{array}$$ (82)

with ν₁ > 0 degrees of freedom and scale s₁ > 0. F can be computed expanding the integrals and using the fact that ${\int }_0^{+\infty }{x}^{\nu /2-1}{e}^{-x}logx=\mathrm{\Gamma }(\frac{\nu }{2})\mathrm{\Psi }(\frac{\nu }{2})$. This yields:

$$\begin{array}{l}F({\nu }_1,s_1;{\nu }_2,s_2)=log\frac{{({\nu }_2/2)}^{{\nu }_2/2}{s}_2^{{\nu }_2}}{\mathrm{\Gamma }(\frac{{\nu }_2}{2})}\\ +(\frac{{\nu }_2}{2}+1)[\mathrm{\Psi }(\frac{{\nu }_1}{2})+log\frac{2}{{\nu }_1{s}_1^2}]-\frac{{\nu }_2{s}_2^2}{2s_1^2}\end{array}$$ (83)

The posterior is then a scaled inverse gamma distribution [16] with

$$\begin{array}{lll}{\nu }_2={\nu }_1+N& \text{and}& s_2^2=\frac{{\nu }_1{s}_1^2+N{\overline{\sigma }}^2}{{\nu }_1+N}\end{array}$$ (84)

where σ̄² is the empirical variance σ̄² = Σ_i(x_i − m²)/N, based on the known mean m. The surprise is given by

$$S({\mathrm{\Gamma }}_1,{\mathrm{\Gamma }}_2)=log\frac{C_1}{C_2}-\frac{N}{2}(\mathrm{\Psi }(\frac{{\nu }_1}{2})+log\frac{2}{{\nu }_1{s}_1^2})+\frac{N{\overline{\sigma }}^2}{2s_1^2}$$ (85)

For large values of N, taking only the leading terms

$$\begin{array}{l}S({\mathrm{\Gamma }}_1,{\mathrm{\Gamma }}_2)\approx \frac{N}{2}(\frac{{\overline{\sigma }}^2}{s_1^2}+log\frac{{\nu }_1{s}_1^2}{2}-\mathrm{\Psi }(\frac{{\nu }_1}{2}))\\ +log\mathrm{\Gamma }(\frac{{\nu }_1+N}{2})-\frac{{\nu }_1+N}{2}log\frac{{\nu }_1+N}{2}\\ -\frac{({\nu }_1+N)}{2}log\frac{{\nu }_1{s}_1^2+N{\overline{\sigma }}^2}{{\nu }_1+N}\end{array}$$ (86)

$$S({\mathrm{\Gamma }}_1,{\mathrm{\Gamma }}_2)\approx \frac{N}{2}\left(\frac{{\overline{\sigma }}^2}{s_1^2}+log\frac{{\nu }_1{s}_1^2}{2{\overline{\sigma }}^2}-\mathrm{\Psi }(\frac{{\nu }_1}{2})\right)$$ (87)

Thus surprise information scales linearly with N, with a coefficient of proportionality that typically depends mostly on the ratio of the empirical variance to the scale parameters $s_1^2$, which is roughly the expectation of the prior [the expectation of the prior is ${\nu }_1{s}_1^2/({\nu }_1-2)$ provided ν₁ > 2]. The effects of very large of very small values of σ̄, or ν₁ can also be seen in the formula above. In particular, surprise is largest when the empirical variance σ̄² goes to 0 or infinity, i.e. is very different from the prior expectation.

Unknown Mean/Unknown Variance

In the case of unknown mean and unknown variance, we have a family M(μ, σ²) of models with a conjugate prior of the form G₁ Γ₁ = P(μ∣σ²)P (σ²) = G₁(μ₁, σ²/κ₁)Γ₁(ν₁, s₁). Thus the prior has four parameters (μ₁, κ₁, ν₁, s₁), with κ₁ > 0, ν₁ > 0, and s₁ > 0. The conjugate posterior has the same form, with similar parameters (μ₂, κ₂, ν₂, s₂) satisfying (see for instance [16])

$$\begin{array}{l}{\mu }_2=\frac{{\kappa }_1}{{\kappa }_1+N}{\mu }_1+\frac{N}{{\kappa }_1+N}\overline{m}\\ {\kappa }_2={\kappa }_1+N\\ {\nu }_2={\nu }_1+N\\ {\nu }_2{s}_2^2={\nu }_1{s}_1^2+(N-1){\overline{\sigma }}^2+\frac{{\kappa }_{1}N}{{\kappa }_1+N}{(\overline{m}-{\mu }_1)}^2\end{array}$$ (88)

with m̄ = Σx_i/N and σ̄² = Σ(x_i − m̄)²/(N − 1). Computation of F = F(μ₁, κ₁, ν₁, s₁; μ₂, κ₂, ν₂, s₂) is similar to the two cases treated above and yields:

$$\begin{array}{l}F({\mu }_1,{\kappa }_1,{\nu }_1,s_1;{\mu }_2,{\kappa }_2,{\nu }_2,s_2)=\\ -\frac{1}{2}[log\frac{2\pi }{{\kappa }_2}\\ +\frac{{\kappa }_2}{{\kappa }_1}+log\frac{{\nu }_1{s}_1^2}{2}-\mathrm{\Psi }(\frac{{\nu }_1}{2})+{\kappa }_2{({\mu }_2-{\mu }_1)}^2{s}_1^{-2}]\\ +\frac{log{(\frac{{\nu }_2}{2})}^{{\nu }_2/2}{s}_2^{{\nu }_2}}{\mathrm{\Gamma }(\frac{{\nu }_2}{2})}+(\frac{{\nu }_2}{2}+1)[\mathrm{\Psi }(\frac{{\nu }_1}{2})+log\frac{2}{{\nu }_1{s}_1^2}]\\ -\frac{{\nu }_2{s}_2^2}{2s_1^2}\end{array}$$ (89)

¿From Equation 89, we can derive the surprise

$$\begin{array}{l}S(G_1{\mathrm{\Gamma }}_1,G_2{\mathrm{\Gamma }}_2)=\frac{1}{2}[log\frac{{\kappa }_1}{{\kappa }_2}-1+\frac{{\kappa }_2}{{\kappa }_1}\\ +{\kappa }_2{({\mu }_2-{\mu }_1)}^2{s}_1^{-2}]+log\frac{C_1}{C_2}+(\frac{{\nu }_1-{\nu }_2}{2})[\mathrm{\Psi }(\frac{{\nu }_1}{2})\\ +log\frac{2}{{\nu }_1{s}_1^2}]+\frac{{\nu }_2{s}_2^2-{\nu }_1{s}_1^2}{2s_1^2}\end{array}$$ (90)

Substituting the value of the posterior parameters

$$\begin{array}{l}S(G_1{\mathrm{\Gamma }}_1,G_2{\mathrm{\Gamma }}_2)=\frac{1}{2}log\frac{{\kappa }_1}{{\kappa }_1+N}\\ +\frac{N}{2{\kappa }_1}+\frac{{\kappa }_1+N}{2}{\left[\frac{N(\overline{m}-{\mu }_1)}{({\kappa }_1+N)s_1}\right]}^2\\ +log\frac{C_1}{C_2}-\frac{N}{2}[\mathrm{\Psi }(\frac{{\nu }_1}{2})+log\frac{2}{{\nu }_1{s}_1^2}]\\ +\frac{(N-1){\overline{\sigma }}^2+\frac{{\kappa }_{1}N}{{\kappa }_1+N}{(\overline{m}-{\mu }_1)}^2}{2s_1^2}\end{array}$$ (91)

For simplicity, we can consider the case where μ₁ = m̄. Then

$$\begin{array}{l}S(G_1{\mathrm{\Gamma }}_1,G_2{\mathrm{\Gamma }}_2)=\frac{1}{2}log\frac{{\kappa }_1}{{\kappa }_1+N}+\frac{N}{2{\kappa }_1}+log\frac{C_1}{C_2}\\ -\frac{N}{2}[\mathrm{\Psi }(\frac{{\nu }_1}{2})+log\frac{2}{{\nu }_1{s}_1^2}]+\frac{(N-1){\overline{\sigma }}^2}{2s_1^2}\end{array}$$ (92)

In all cases, for large values of N we always have the approximation

$$\begin{array}{l}S(G_1{\mathrm{\Gamma }}_1,G_2{\mathrm{\Gamma }}_2)\approx \frac{N}{2}(\frac{1}{{\kappa }_1}+\frac{{\overline{\sigma }}^2}{s_1^2}+log\frac{{\nu }_1{s}_1^2}{2{\overline{\sigma }}^2}\\ -\mathrm{\Psi }(\frac{{\nu }_1}{2})+\frac{{(\overline{m}-{\mu }_1)}^2}{s_1^2})\end{array}$$ (93)

Surprise is linear in N with a coefficient that is essentially the sum of the coefficients derived in the unknown mean and unknown variance partial cases.

Appendix C: Exponential Families With Conjugate Priors

Let A¹ and A² denote the parameters of two distributions P₁ and P₂ in the exponential family. Simple integration yields

$$F(P_1,P_2)=log{C}_2+\sum _{i=1}^k{A}_i^2{E}_{A^1}[w_i(\theta )]$$ (94)

where E_A¹ [w_i(θ)] denotes expectation with respect to P₁. Surprise S is then derived from F(P₁, P₁) − F(P₁, P₂).