Reference Free Structure Determination through Eigenvectors of Center of Mass Operators

Abstract

Recovering the three-dimensional structure of molecules is important for understanding their functionality. We describe a spectral graph algorithm for reconstructing the three-dimensional structure of molecules from their cryo-electron microscopy images taken at random unknown orientations.

We first identify a one-to-one correspondence between radial lines in three-dimensional Fourier space of the molecule and points on the unit sphere. The problem is then reduced to determining the coordinates of points on the sphere given a subset of their pairwise geodesic distances. To recover those coordinates, we exploit the special geometry of the problem, as rendered by the Fourier projection-slice theorem, to construct a weighted graph whose vertices are the radial Fourier lines and whose edges are linked using the common line property. The graph organizes the radial lines on the sphere in a global manner that reveals the acquisition direction of each image. This organization is derived from a global computation of a few eigenvectors of the graph's sparse adjacency matrix. Once the directions are obtained, the molecule can be reconstructed using classical tomography methods.

The presented algorithm is direct (as opposed to iterative refinement schemes), does not require any prior model for the reconstructed object, and is shown to have favorable computational and numerical properties. Moreover, the algorithm does not impose any assumption on the distribution of the projection orientations. Physically, this means that the algorithm is applicable to molecules that have unknown spatial preference.

1 Introduction

“Three-dimensional electron microscopy” [1] is the name commonly given to methods in which the three-dimensional structures of macromolecular complexes are obtained from sets of images taken by an electron microscope. The most widespread and general of these methods is single-particle reconstruction (SPR). In SPR the three-dimensional structure is determined from images of randomly oriented and positioned identical macromolecular “particles”, typically complexes 200 kDa or larger in size. The SPR method has been applied to images of negatively stained specimens, and to images obtained from frozen-hydrated, unstained specimens [2]. In the latter technique, called cryo-electron microscopy (cryo-EM) the sample of macromolecules is rapidly frozen in a thin (~ 100 nm) layer of vitreous ice, and maintained at liquid nitrogen temperature throughout the imaging process.

SPR from cryo-EM images is of particular interest because it promises to be an entirely general technique. It does not require crystallization or other special preparation of the complexes to be imaged, and in the future it is likely to reach sufficient resolution (~ 0.4 nm) to allow the polypeptide chain to be traced and residues identified in protein molecules [3]. Even at the present best resolutions of 0.9–0.6 nm, many important features of protein molecules can be determined [4].

Much progress has been made in algorithms that, given a starting three-dimensional structure, are able to refine that structure on the basis of a set of negative-stain or cryo-EM images, which are taken to be projections of the thee-dimensional object. Datasets typically range from 10⁴ to 10⁵ particle images, and refinements require tens to thousands of CPU-hours. As the starting point for the refinement process, however, some sort of ab initio estimate of the three-dimensional structure must be made. Present algorithms are based on the “Angular Reconstitution” method of van Heel [5] in which a coordinate system is established from three projections, and the orientation of the particle giving rise to each image is deduced from common lines among the images.

We propose Globally Consistent Angular Reconstitution (GCAR), a reconstruction algorithm that does not assume any ab initio model and establishes a globally consistent coordinate system from all projections. The special geometry of the problem rendered by the Fourier projection-slice theorem [6] is incorporated by GCAR into a weighted directed graph whose vertices are the radial Fourier lines and whose edges are linked using the common line property. Radial lines are viewed as points on the sphere and are networked through “spider-like” connections. The graph organizes the radial lines on the sphere in a global manner that reveals the projection directions. Such an organization is derived from the eigenvectors of the graph's sparse adjacency matrix. This global averaging property makes GCAR robust to both noise and false detections of common lines. GCAR is extremely fast because it requires only the computation of a few eigenvectors of a sparse matrix. Once the orientation of each projection is revealed by the eigenvectors, the reconstruction may be performed using any tomographic reconstruction method (see [6] for a review of the classical methods).

Many of the recent and successful algorithms for nonlinear dimensionality reduction of high-dimensional data, such as locally linear embedding (LLE) [7], Hessian LLE [8], Laplacian eigenmap [9] and diffusion maps [10, 11] involve the computation of eigenvectors of data-dependent sparse kernel matrices. However, such algorithms fail to solve the cryo-EM problem, because the reduced coordinate system that each of them obtains does not agree with the projection directions. On the other hand, GCAR finds the desired coordinate system of projection images, because it is tailored to the geometry of the problem through the Fourier projection-slice theorem. We have successfully applied similar graph-based approaches to the reconstruction of 2D structures, such as the Shepp-Logan phantom, from noisy 1D projection “images” taken at unknown random directions [12].

The organization of this paper is as follows. In Section 2 we introduce the structure determination problem in cryo-electron microscopy. This problem has a special underlying geometry, presented in Section 3 and exploited in Section 4 to construct the GCAR operator. We also prove in Section 4 that the eigenvectors of the GCAR operator reveal the projection orientations, and show its relation to the spherical harmonics. The algorithm for recovering the projection orientations is then summarized in Section 5, together with a few implementation details. Examples of applying our algorithm to simulated datasets are given in Section 6. We conclude in Section 7 with a summary and description of future work.

2 Problem setup

The goal in cryo-EM structure determination is to find the three-dimensional structure of a molecule given a finite number of its two-dimensional projection images, taken from unknown random directions. The intensity of pixels in each projection image corresponds to line integrals of the electric potential induced by the molecule along the path of the imaging electrons. The highly intense electron beam destroys the molecule, and it is therefore impractical to take projection images of the same molecule at known directions, as in the case of classical computerized tomography. In other words, a single molecule can be imaged only once. By using many copies of the same molecule, we obtain many projection images of the same underlying structure. However, there is usually no way of aligning all molecules in the same direction, as each molecule is free to move in the liquid medium until its orientation is fixed at the moment of freezing. Thus, every image is a projection of the same molecule but at an unknown random orientation. In this formulation, all molecules are assumed to have the exact same structure; they differ only by their spatial orientation.

The locations of the microscope (source) and the camera/film (detectors) are fixed, with different images corresponding to different spatial rotations of the molecule. Every image is thus associated with an element of the rotation group SO(3). If the electric potential of the molecule in some fixed reference coordinate system is ϕ(r), r = (x, y, z), then, rotating the molecule by g ∈ SO(3) results in the potential ϕ_g(r) = ϕ(g⁻¹r). We assume without loss of generality that the coordinate system of the microscope is given by the standard basis vectors $\overrightarrow{x},\overrightarrow{y},\overrightarrow{z}$. The projection image P_g(x, y) is formed on the $\overrightarrow{x}\overrightarrow{y}$ plane by integrating ϕ_g(r)along the $\overrightarrow{z}\text{-direction}$ (the source-detector direction)

$$P_g(x,y)={\int }_{-\infty }^{\infty }{\varphi }_g(x,y,z)dz.$$ (1)

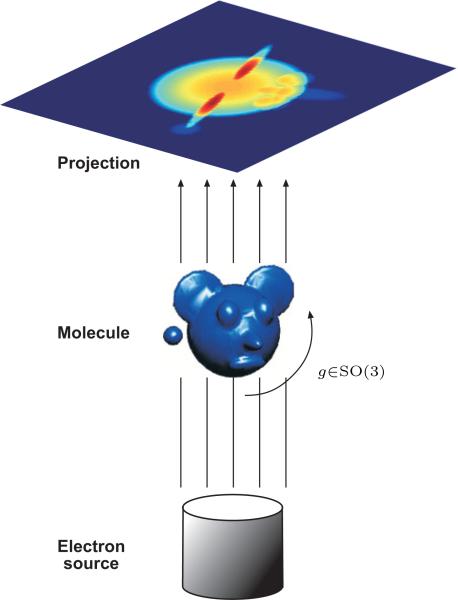
It is assumed that all integrals hereinafter exist, by requiring, for example that $\varphi \in L^1\left({\mathbb{R}}^3\right)$. Also, since ϕ represents a physical object, it must be band limited for all practical purposes. We denote the band limit by B, and in practice, it is determined by the characteristics of the imaging setup. After digitization, each projection image is a digital picture given as a p × p grid of pixels P_g(x_i,y_j), i, j = 1, . . . , p, where p is also determined by the characteristics of the imaging setup. The projection operator (1) is also known as the X-ray transform [6]. Figure 1 is a schematic illustration of the cryo-EM setting.

Figure 1.

Illustration of the cryo-EM imaging process: each projection image corresponds the line integrals of an unknown molecule rotated by an unknown three-dimensional rotation.

The cryo-EM problem is thus stated as follows: find ϕ(x, y, z) given a collection of K projections ${\left\{P_{g_k}\right\}}_{k=1}^K$, where g_k are unknown rotations. If the rotations ${\left\{g_k\right\}}_{k=1}^K$ were known, then the reconstruction of ϕ(x, y, z) could be performed by classical tomography methods. Therefore, the cryo-EM problem is reduced to estimating the rotations ${\left\{g_k\right\}}_{k=1}^K$ given the dataset ${\left\{P_{g_k}\right\}}_{k=1}^K$.

For convenience, we adopt the following equivalent point of view. Instead of having the microscope fixed and the molecule oriented randomly in space, we think of the molecule as being fixed, and the microscope being the one that is randomly rotated in space. The orientation of the microscope that corresponds to some rotation g ∈ SO(3) of the molecule is given by a beaming direction ${\tau }_g=g^{-1}\overrightarrow{z}\in S^2$, and an in-plane rotation angle α_g ∈ [0, 2π) of the camera. The image is then formed on the plane ${\tau }_g^{\perp }$. Using this convention, the projection operator in (1) becomes

$$P_g\left(u\right)={\int }_{{\tau }_g}\varphi (s+u)ds,u\in {\tau }_g^{\perp }.$$ (2)

3 Geometry of the problem – correspondence between Fourier rays and the unit sphere

For a fixed function ϕ, the operator in (2) defines a mapping from SO(3) into $L^1\left({\mathbb{R}}^2\right)$. Given the projection images, the structure determination problem is nothing else than the inverse problem of recovering the source in SO(3) of each projection image. We show that it is sufficient to consider a map from S² into ${\mathbb{C}}^n$ (n will be defined below), given that all projection images can be properly discretized. In this section we also review the Fourier projection-slice theorem, which relates the X-ray transform (2) with the Fourier transform. Using the Fourier projection-slice theorem, we determine the discretization of Fourier space and the mapping of Fourier space into S².

The two-dimensional Fourier transform of a projection image P_g(u) (see (2)) is given by the double integral

$${\widehat{P}}_g\left(\omega \right)=\frac{1}{{\left(2\pi \right)}^2}{\int }_{{\tau }_g^{\perp }}{e}^{-iu\cdot \omega }{P}_g\left(u\right)du,\omega \in {\tau }_g^{\perp }.$$ (3)

The three-dimensional Fourier transform of the molecule is given by the triple integral

$$\widehat{\varphi }\left(\xi \right)=\frac{1}{{\left(2\pi \right)}^3}{\int }_{{\mathbb{R}}^3}{e}^{-ir\cdot \xi }\varphi \left(r\right)dr,\xi \in {\mathbb{R}}^3.$$ (4)

One of the cornerstones of tomography is the Fourier projection-slice theorem, which states that the two-dimensional Fourier transform of a projection image is the planar slice ${\tau }_g^{\perp }$ (the slice perpendicular to the beaming direction τ_g) of the three-dimensional Fourier transform of the molecule (see, e.g., [6, p. 11]). Specifically, taking $\omega \in {\tau }_g^{\perp }$, combining (2) and (3) and writing an arbitrary point $r\in {\mathbb{R}}^3$ as

$$r=u+s,u\in {\tau }_g^{\perp },s\in {\tau }_g,$$ (5)

we get

$${\widehat{P}}_g\left(\omega \right)=\frac{1}{{\left(2\pi \right)}^2}{\int }_{{\tau }_g^{\perp }}du{\int }_{{\tau }_g}ds\varphi (u+s)e^{-ıu\cdot \omega }=\frac{1}{{\left(2\pi \right)}^2}{\int }_{{\mathbb{R}}^3}dr\varphi \left(r\right)e^{-ır\cdot \omega }=2\pi \widehat{\varphi }\left(\omega \right),$$ (6)

since by (5) we have that u · ω = r · ω. An immediate consequence of the Fourier projection-slice theorem (6) is that the Fourier transforms of any two projection images share a common line, i.e., the intersection line of the two planes; if η is a unit vector such that $\eta \in {\tau }_{g_1}^{\perp }\cap {\tau }_{g_2}^{\perp }$ then ${\widehat{P}}_{g_1}\left(\eta \right)={\widehat{P}}_{g_2}\left(\eta \right)$.

Note that the effect of rotating the camera (changing α_g) while fixing the beaming direction τ_g is an in-plane rotation of the slice without changing its position.

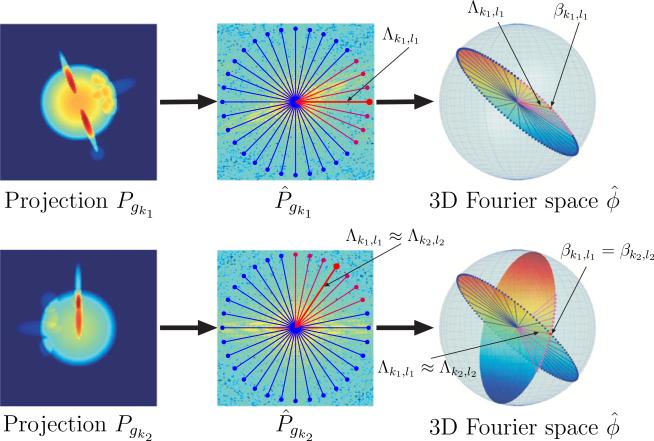
The Fourier transform of each projection image can be considered in polar coordinates as a set of planar radial lines in two-dimensional Fourier space. As a result of the Fourier projection-slice theorem, every planar radial line is also a radial line in the three-dimensional frequency space. This gives a one-to-one correspondence between those Fourier radial lines and points on the unit sphere S², by mapping each radial line to its direction vector in ${\mathbb{R}}^3$ (see (9) below). The radial lines of a single projection image correspond to a great circle (a geodesic circle) on S². Thus, to every projection image P_gk there corresponds a unique great circle ${\mathcal{C}}_k$ over S², and the common line property is restated as follows: any two different geodesic circles over S² intersect at exactly two antipodal points.

If the projection directions (the g_k's or the (τ_gk, α_gk)'s) are known, then the Fourier transform of the projection images gives the values of $\widehat{\varphi }\left(\xi \right)$ on different planes through the origin, as stated by (6). Inverting the Fourier transform $\widehat{\varphi }\left(\xi \right)$ would then reconstruct the molecule ϕ. In practice, however, inverting the Fourier transform on a non-regular grid is a subtle numerical process; due to space constraints, we do not include the details of this procedure. However, in the cryo-EM problem, the slices are unorganized. Neither their directions τ_gk nor their in-plane rotations α_gk are known.

We next explain the discretization of Fourier space and derive a mapping between the discretized Fourier space and points on the unit sphere S². Such a mapping would allow us to proceed by exploiting the geometry of S².

Let P_g1 (x, y), . . . , P_gK (x, y) be K projection images. Upon writing the Fourier transform in (3) in polar frequency coordinates, we obtain

$${\widehat{P}}_{g_k}(\rho ,\gamma )=\frac{1}{{\left(2\pi \right)}^2}\int \int P_{g_k}(x,y)e^{-i(x\rho \cos \gamma +y\rho \sin \gamma )}dxdy,k=1,\dots ,K.$$ (7)

For digital implementations we discretize ρ and γ, and compute (7) using a nonequally-spaced FFT [13, 14]. We denote by L the angular discretization of γ (angular resolution), and sample ρ in n equally-spaced points. That is, we split each transformed projection into L radial lines ${\Lambda }_{k,0},\dots ,{\Lambda }_{k,L-1}\in {\mathbb{C}}^n$, each represented by a set of n equispaced points

$${\Lambda }_{k,l}=\left({\widehat{P}}_{g_k}(B∕n,2\pi l∕L),{\widehat{P}}_{g_k}(2B∕n,2\pi l∕L),\dots ,{\widehat{P}}_{g_k}(B,2\pi l∕L)\right)\in {\mathbb{C}}^n,$$ (8)

1 ≤ k ≤ K, 0 ≤ l ≤ L − 1, where B is the band limit of the projection images. Note that the DC term (ρ = 0 in (7)) is shared by all lines independently of the image and is therefore ignored.

Let

$$\Lambda \left(\beta \right)=\left(2\pi \widehat{\varphi }(\beta B∕n),2\pi \widehat{\varphi }(2\beta B∕n),\dots ,2\pi \widehat{\varphi }(n\beta B∕n)\right)\in {\mathbb{C}}^n$$ (9)

be n samples from a ray through the origin in three-dimensional Fourier space, in a direction given by the unit vector β ∈ S². This defines a map $\Lambda :S^2\to {\mathbb{C}}^n$ that maps each unit vector in ${\mathbb{R}}^3$ to n samples of the Fourier ray in that direction. According to the Fourier projection-slice theorem, there exist β_k,l ∈ S², k = 1, . . . , K, l = 0, . . . , L−1 such that

$${\Lambda }_{k,l}=\Lambda \left({\beta }_{k,l}\right),$$ (10)

that is, the radial lines Λ_k,l in (8) are the evaluations of the function Λ(β) at the points β_k,l. The function Λ(β) is unknown, because so is $\widehat{\varphi }$. The point β_k,l ∈ S² is the orientation of the ray Λ_k,l in three-dimensional Fourier space. Our goal is to find the sources β_k,l of the overall KL radial lines. The L sources ${\left\{{\beta }_{k,l}\right\}}_{l=0}^{L-1}$ (k fixed) are equidistant points on the great circle ${\mathcal{C}}_k\subset S^2$, and the normal to their common plane is the projection orientation τ_gk corresponding to projection P_gk.

As mentioned earlier, the Fourier transforms of any two projections share a common line. After sampling the Fourier transform of each projection along a finite number L of rays, the true common line between P̂_gk1 and P̂_gk2 is not necessarily one of the L computed Fourier rays. However, since the frequency content of each projection is limited, if we choose L large enough, then the common line property asserts that for any k₁ and k₂ there exist l₁ and l₂ such that ∥Λ_k1,l1 − Λ_k2,l2∥ < ε. That is, for all practical purposes, for each k₁ and k₂, there exist l₁ and l₂ such that the pair (Λ_k1,l1, Λ_k2,l2) is the common line between projections k₁ and k₂. To denote that the common line between the Fourier transforms of projections k₁ and k₂ is the pair (Λ_k1,l1, Λ_k2,l2), we write Λ_k1,l1 ≈ Λ_k2,l2. Note that according to (8), each Fourier ray starts at a frequency with radial component B/n. Thus, any two projections share two common Fourier rays with antipodal directions (this is of course equivalent to one common line through the origin). See Fig. 2 for an illustration of the Fourier projection-slice theorem and the geometry induced on S². Although l₁ and l₂ are not guaranteed to be unique, it is unlikely that two different Fourier rays of the same projection will coincide. However, even if such non-uniqueness of common lines occurs in a few projections, it can be considered as noise and does not affect the outcome of the algorithm (see Section 6).

Figure 2.

Fourier projection-slice theorem and its induced geometry. The Fourier transform of each projection P̂_gk corresponds to a planar slice, at orientation determined by g_k, through the three-dimensional Fourier transform $\widehat{\varphi }$ of the molecule. The Fourier transforms of any two projections P̂_gk1 and P̂_gk2 share a common line Λ_k1,l1 ≈ Λ_k2,l2, which is also a ray of the three-dimensional Fourier transform $\widehat{\varphi }$. Each Fourier ray Λ_k1,l1 can be mapped to its direction vector β_k1,l1 ∈ S². The direction vectors of the common lines Λ_k1,l1 ≈ Λ_k2,l2 must coincide, that is, β_k1,l1 = β_k2,l2.

4 Orientation revealing operator

In this section we introduce the GCAR operator, whose eigenvectors reveal the orientation of each projection. The GCAR operator is a graph with each node representing a ray in Fourier space, and whose edges are determined by the common line property. The formal construction of this graph is presented in Section 4.1. The normalized adjacency matrix of the graph can be viewed as an averaging operator for functions defined on the nodes of the graph, as explained in Section 4.2. Analyzing the eigenvectors of this operator in Section 4.3 shows that they encode the projection orientations. We conclude the construction of the GCAR operator by showing in Section 4.4 that the eigenvectors of the GCAR matrix are intimately related to the spherical harmonics.

4.1 GCAR graph

Given K projection images, we denote by Λ_k,l, k = 1, . . . , K, l = 0, . . . , L − 1 the KL Fourier rays computed from the K projection images (see (8)). To construct the directed graph G = (V, E) associated with the set of radial lines {Λ_k,l}, we define the set of vertices V to be

$$V=\{(k,l):1\le k\le K,0\le l\le L-1\}.$$

The number of vertices is |V| = KL. In essence, we think of the radial lines as vertices of a graph, where each radial line Λ_k,l and its source β_k,l ∈ S² are identified with the vertex indexed by the pair (k, l). Once we specify the set of directed edges $E\subseteq V\times V$, the graph will be represented using a sparse adjacency matrix W of size KL × KL by

$$W_{(k_1,l_1),(k_2,l_2)}=\{\begin{array}{cc}1\hfill & \text{if}((k_1,l_1),(k_2,l_2))\in E\hfill \\ 0\hfill & \text{if}((k_1,l_1),(k_2,l_2))\notin E\hfill \end{array}\phantom{\}}.$$ (11)

For each radial line Λ_k,l (or alternatively, for each source β_k,l ∈ S²) there corresponds exactly one row in W. The edges in the graph are introduced according to the following rules:

1. For each vertex (k₁, l₁), 1 ≤ k₁ ≤ K, 0 ≤ l₁ ≤ L − 1, add to E the edges ((k₁, l₁), (k₁, l₁ + l)), −J ≤ l ≤ J, where J is some fixed constant (say 10) and addition is taken modulo L:

   $$\forall (k_1,l_1),\left\{((k_1,l_1),(k_1,l_1+l))\right\},-J\le l\le J\}\subseteq E.$$ (12)
2. Whenever Λ_k1,l1 and Λ_k2,l2 (k₁ ≠ k₂) are common radial lines, that is, Λ_k1,l1 ≈ Λ_k2,l2, add to E the edges ((k₁, l₁), (k₂, l₂ + l)), −J ≤ l ≤ J (again addition is taken modulo L):

   $${\Lambda }_{k_1,l_1}\approx {\Lambda }_{k_2,l_2}\Rightarrow \{((k_1,l_1),(k_2,l_2+l)),-J\le l\le J\}\subseteq E.$$ (13)

In general, the adjacency matrix W is not symmetric: ((k₁, l₁), (k₂, l₂)) ∈ E (for k₁ ≠ k₂) reflects the fact that the circle ${\mathcal{C}}_{k_2}$ containing (k₂, l₂) passes nearby the point (k₁, l₁). However, ${\mathcal{C}}_{k_1}$ does not necessarily passes nearby (k₂, l₂) so ((k₂, l₂), (k₁, l₁)) ∉ E. Symmetry occurs only within the same circle, that is, $((k,l_1),(k,l_2))\in E\iff ((k,l_2),(k,l_1))\in E$, which happens whenever |l₁ − l₂| ≤ J. Although the size of the matrix W is KL × KL, which is potentially computationally prohibitive, by choosing J << L we force it to be sparse. Its number of nonzero entries is only

$$\mid E\mid =(2J+1)KL+2K(K-1)(2J+1).$$ (14)

The first summand corresponds to the edges added according to rule 1 above, namely, 2J + 1 edges for each of the KL vertices. The second summand corresponds to edges between different images added according to rule 2. Any two circles intersect at exactly two antipodal points, so there are $2\left(\begin{array}{c}\hfill K\hfill \\ \hfill 2\hfill \end{array}\right)=K(K-1)$ intersection points. Every intersection point, that is, every common line Λ_k1,l1 ≈ Λ_k2,l2, contributes 2J + 1 nonzero elements to row (k₁, l₁) of W, and 2J + 1 nonzero elements to row (k₂, l₂). In practice, the number of edges in E is smaller than the number in (14), as explained in Section 5.

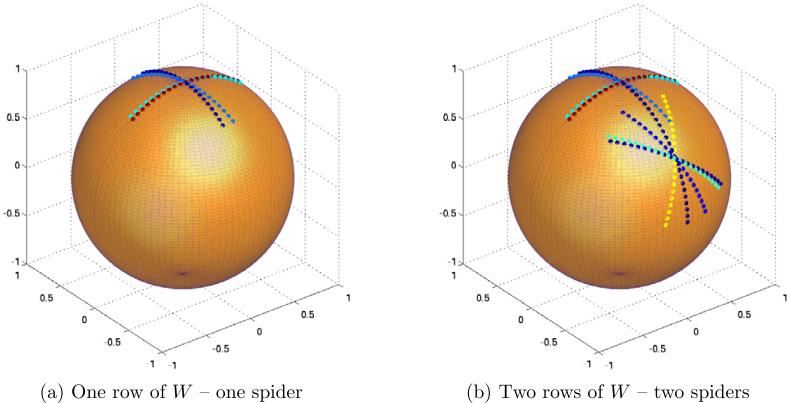
If we take row (k₁, l₁) from W and plot on S² all points β_k2,l2 ∈ S² for which W_{(k1,l1),(k2,l2)}, = 1, we get a “spider-like” picture as in Fig. 3a. To better understand this special geometry induced on S² by the matrix W, we now explain in detail how Fig. 3a was generated. To that end, we took K = 200 simulated electron-microscope projections of a known molecule, whose orientations were sampled from the uniform distribution over SO(3), and computed L = 100 Fourier rays in each projection. We then searched for the common line between each pair of Fourier-transformed images, and constructed the matrix W in (11) with J = 10. This corresponds to using K = 200 random geodesic circles on S², with L = 100 points on each geodesic circle, and J = 10. Since we know the projection orientation of each projection, we also know the positions β_k,l of each Fourier ray such that (10) holds. To produce Fig. 3a we set k₁ = 1, and plotted a small bead at each point β_k2,l2 ∈ S² for which W_{(k1,l1),(k2,l2)} = 1. Points β_k2,l2 that correspond to the same k₂ (come from the same projection image) are plotted with the same color. The reason for the “spider-like” structure can be seen in the bottom right part of Fig. 2 – each common line Λ_k1,l1 ≈ Λ_k2,l2 induces two intersecting arcs on S² centered at β_k1,l1. In light of Fig. 3a, we refer to each row of W as the “spider that corresponds to the point (k₁, l₁)”. The point β_k1,l1 is the head (center) of the spider. Figure 3b shows two rows of W plotted on S², from which we can see how different spiders interact. This interaction is essential for the global consistent assignment of coordinates explained below.

Figure 3.

Mapping the nonzero entries of rows of W to S².

4.2 Averaging operator

When constructing the matrix W, different spiders may have different number of legs, that is, different rows of W may have different row sums. We therefore normalize the adjacency matrix W to have constant row sums by dividing each row by its sum. Specifically, we define the outdegree d_k,l of the (k, l)'th vertex as the sum of its corresponding row in W

$$d_{k,l}=\sum _{(k^{\prime },l^{\prime })\in V}{W}_{(k,l),(k^{\prime },l^{\prime })}=\mid \{(k^{\prime },l^{\prime }):((k,l),(k^{\prime },l^{\prime }))\in E\}\mid ,$$ (15)

and divide the matrix W by the diagonal matrix D given by

$$D_{(k,l),(k,l)}=d_{k,l}.$$ (16)

This normalization results in the operator

$$A=D^{-1}W.$$ (17)

The operator $A:{\mathbb{C}}^{\mid V\mid }\to {\mathbb{C}}^{\mid V\mid }$ takes any discrete complex-valued function $f:V\to \mathbb{C}$ (realized as a vector in ${\mathbb{C}}^{KL}$) and assigns to the head of each spider the average of f over the entire spider

$$\left(Af\right)(k_1,l_1)=\frac{1}{d_{k_1,l_1}}\sum _{((k_1,l_1),(k_2,l_2))\in E}f(k_2,l_2).$$ (18)

To see that, consider an arbitrary vector $f\in {\mathbb{C}}^{KL}$. The (k₁, l₁) coordinate of the vector Af is given by the dot product of row (k₁, l₁) of A with the vector f. By construction, the only nonzero entries in row (k₁, l₁) of A are in columns (k₂, l₂) for which W_{(k1,l1),(k2,l2)} = 1, that is, ((k₁, l₁), (k₂, l₂)) ∈ E; the entries in these columns are $\frac{1}{d_{k_1,l_1}}$, due to the normalization (17). By definition, the set {((k₁, l₁), (k₂, l₂)) ∈ E} is exactly the spider neighborhood of (k₁, l₁). We therefore regard A as an averaging operator over ${\mathbb{C}}^{\mid V\mid }$.

The matrix A is row stochastic (the row sums of A all equal 1), and therefore, the constant function ψ₀(v) = 1 ∀v ∈ V is an eigenvector with λ₀ = 1: Aψ₀ = ψ₀. The remaining eigenvectors may be complex and come in conjugate pairs, because A is real but not symmetric: $A\psi =\lambda \psi \iff A\stackrel{‒}{\psi }=\stackrel{‒}{\lambda }\stackrel{‒}{\psi }$. As of the spectrum of A, λ₀ = 1 is the largest eigenvalue, and whenever the directed graph G is connected, the remaining eigenvalues reside inside the complex unit disk |λ| < 1, due to Perron-Frobenius theorem [15, Chapter 8].

4.3 Coordinate eigenvectors

The operator A has many interesting properties. For the cryo-EM problem, the most important property is that the coordinates of the sources β_k,l are eigenvectors of the averaging operator A, sharing the same eigenvalue. Explicitly, we have the following theorem.

Theorem. Let the matrix A be defined by (17). Let $e_x,e_y,e_z:{\mathbb{R}}^3\to \mathbb{R}$ be the coordinate functions in ${\mathbb{R}}^3$. Then, the vectors $x,y,z\in {\mathbb{R}}^{KL}$ defined by

$$x=e_x\left({\beta }_{k,l}\right),y=e_y\left({\beta }_{k,l}\right),z=e_z\left({\beta }_{k,l}\right),$$ (19)

k = 1, . . . , K, l = 0, . . . , L − 1 satisfy

$$Ax=\lambda x,Ay=\lambda y,Az=\lambda z,$$ (20)

where

$$\lambda =\frac{1}{2J+1}\sum _{l=-J}^J\cos \frac{2\pi l}{L}.$$ (21)

This remarkable fact is a consequence of the following observation: the center of mass of every spider is in the direction of the spider's head, because any pair of opposite legs balance each other. In other words, for any spider, the average of the coordinates of its points is a vector in the direction of the spider's head. For example, the center of mass of a spider whose head is located at the north pole lies just beneath it. We now give a formal proof of this theorem.

Proof. Suppose f(u, v, w) = a₁u + a₂v + a₃w = a · β is a linear function, where a = (a₁, a₂, a₃)^T and β = (u, v, w)^T ∈ S². Consider a spider whose head is at the point β₁ = (u₁, v₁, w₁)^T ∈ S², where the value of the function f is f(u₁, v₁, w₁) = a · β₁. Let β₂, β₃ be two unit vectors that complete β₁ into an orthonormal system of ${\mathbb{R}}^3$. In other words, the 3 × 3 matrix U whose columns are β₁, β₂, β₃ is orthogonal. We express any point β = (u, v, w)^T on the unit sphere as a linear combination β = u′β₁ + v′β₂ + w′β₃ = Uβ′, where β′ = (u′, v′, w′)^T are the coordinates of β in a rotated coordinate system. We apply a change of variable β → β′ in f to obtain the linear function f′(u′, v′, w′) = f(u, v, w) = a · β = a · Uβ′ = a′ · β′, where $a^{\prime }=U^{T}a={(a_1^{\prime },a_2^{\prime },a_3^{\prime })}^T$. The parametrization of a great circle going through β₁ is

$$\cos \theta {\beta }_1+\sin \theta \cos {\phi }_0{\beta }_2+\sin \theta \sin {\phi }_0{\beta }_3,$$

where θ ∈ (−π, π] and φ₀ is a fixed parameter that determines the normal to the plane of the circle. On that circle, f is a function of the single parameter θ

$$f\left(\theta \right)=f^{\prime }(\cos \theta ,\sin \theta \cos {\phi }_0,\sin \theta \sin {\phi }_0)=a^{\prime }\cdot {(\cos \theta ,\sin \theta \cos {\phi }_0,\sin \theta \sin {\phi }_0)}^T.$$

The average f̄ of f over the two discrete opposite legs of that circle is

$$\begin{array}{cc}\hfill \stackrel{‒}{f}(u_1,v_1,w_1)& =\frac{1}{2J+1}\sum _{l=-J}^{J}f\left(\frac{2\pi l}{L}\right)\hfill \\ \hfill & =\frac{a^{\prime }}{2J+1}\cdot \sum _{l=-J}^J{\left(\cos \frac{2\pi l}{L},\sin \frac{2\pi l}{L}\cos {\phi }_0,\sin \frac{2\pi l}{L}\sin {\phi }_0\right)}^T\hfill \\ \hfill & =\left[\frac{1}{2J+1}\sum _{l=-J}^J\cos \frac{2\pi l}{L}\right]a^{\prime }\cdot {(1,0,0)}^T,\hfill \end{array}$$

due to the linearity of the dot product and the fact that sin θ is an odd function. From

$$a^{\prime }\cdot {(1,0,0)}^T=U^{T}a\cdot {(1,0,0)}^T=a\cdot U{(1,0,0)}^T=a\cdot {\beta }_1=f(u_1,v_1,w_1),$$

we conclude that

$$\stackrel{‒}{f}(u_1,v_1,w_1)=\left[\frac{1}{2J+1}\sum _{l=-J}^J\cos \frac{2\pi l}{L}\right]f(u_1,v_1,w_1)$$ (22)

holds for all (u₁, v₁, w₁) and for any circle going through it. Therefore, linear functions are eigenvectors of the averaging operator A with eigenvalue $\lambda =\frac{1}{2J+1}{\sum }_{l=-J}^J\cos \frac{2\pi L}{L}$. This completes the proof.

4.4 Spherical harmonics

The eigenfunctions of the Laplacian on the sphere S² are known to be the spherical harmonics $Y_l^m$ [6, p. 195] (also known as the eigenstates of the angular momentum operator in quantum mechanics)

$${\Delta }_{S^2}{Y}_l^m=-l(l+1)Y_l^m,l=0,1,2,\dots ,m=-l,-l+1,\dots ,l,$$ (23)

where the Laplacian on S² is given by

$${\Delta }_{S^2}=\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial }{\partial \theta }\right)+\frac{1}{{\sin }^2\theta }\frac{{\partial }^2}{\partial {\phi }^2}.$$ (24)

The (non-normalized) spherical harmonics are given in terms of the associated Legendre polynomials of the zenith angle θ ∈ [0, π] and trigonometric polynomials of the azimuthal angle φ ∈ [0, 2π) by

$$\begin{array}{cc}\hfill Y_l^0(\theta ,\phi )& =P_l\left(\cos \theta \right),\hfill \\ \hfill Y_l^m(\theta ,\phi )& =P_l^{\mid m\mid }\left(\cos \theta \right)\cos m\phi ,1\le m\le l,\hfill \\ \hfill Y_l^{-m}(\theta ,\phi )& =P_l^{\mid m\mid }\left(\cos \theta \right)\sin m\phi ,1\le m\le l.\hfill \end{array}$$

The eigenspaces are degenerated so that the eigenvalue l(l + 1) has multiplicity 2l + 1. Alternatively, the l'th eigenspace corresponds to homogeneous polynomials of degree l restricted to S². In particular, the first three non-trivial spherical harmonics $Y_1^m$ share the same eigenvalue and are given by the three linear functions

$$Y_1^1=x,Y_1^{-1}=y,Y_1^0=z.$$

The spherical harmonics $Y_l^m$ are usually derived by separating variables in (23)–(24). However, the fundamental reason for which the spherical harmonics are eigenfunctions of the Laplacian is that the latter commutes with rotations. In fact, the classical Funk-Hecke theorem (see, e.g., [6, p. 195]) asserts that the spherical harmonics are the eigenfunctions of any integral operator $\mathcal{K}:L^2\left(S^2\right)\to L^2\left(S^2\right)$ that commutes with rotations. Such operators are of the form

$$\left(\mathcal{K}f\right)\left(\beta \right)={\int }_{S^2}k\left(\langle \beta ,{\beta }^{\prime }\rangle \right)f\left({\beta }^{\prime }\right)d{S}_{{\beta }^{\prime }},$$

where $k:[-1,1]\to \mathbb{R}$ is a kernel function that depends only on the angle between β and β′ (β, β′ ∈ S²). For such integral operators we have

$$\mathcal{K}{Y}_l^m={\lambda }_l{Y}_l^m,$$

where the eigenvalues λ_l depend on the specific kernel function k(·) and are given by

$${\lambda }_l=2\pi {\int }_{-1}^{1}k\left(t\right)P_l\left(t\right)dt.$$

For example, the spherical harmonics are the eigenfunctions of the operator that corresponds to averaging over spherical caps.

The averaging operator A defined in Section 4.2 usually does not commute with rotations, because every spider has different number of legs that go in different directions. The averaging operator A commutes with rotations only in the limit of infinite number of projection images corresponding to a uniform distribution over SO(3) (the Haar measure). Although A does not commute with rotations and the Funk-Hecke theorem is not guaranteed to hold, the coordinate vectors $x,y,z\in {\mathbb{R}}^{KL}$ span an eigenspace of A, due to the center of mass property. Nevertheless, numerical simulations demonstrate that the low-order spherical harmonics are present even for moderately small K (see example below), although this behavior is not guaranteed by the explanation above.

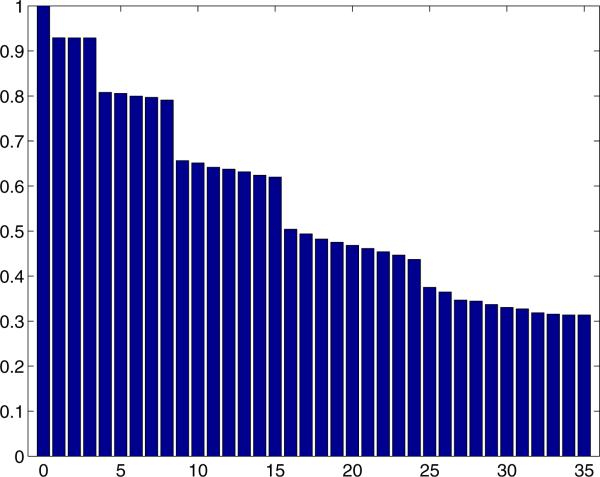
Figure 4 depicts the first 36 eigenvalues of the operator A constructed using K = 200 simulated projections, L = 100 points on each geodesic circle, and J = 10 samples on each leg of the spider, as explained in detail at the end of Section 4.1. The threefold multiplicity corresponding to the coordinate vectors is apparent in Fig. 4. Moreover, the observed numerical multiplicities of 1 ,3, 5, 7 and 9 are explained by the spherical harmonics.

Figure 4.

Numerical spectra of A: K = 200, L = 100, J = 10.

5 Algorithm

The fact that the coordinates x, y, z of the sources β_k,l, k = 1, . . . , K, l = 0, . . . , L − 1, form an eigenspace of A (see Section 4.2) enables to estimate the orientation of each Fourier ray by computing the first three non-trivial eigenvectors ψ₁, ψ₂, ψ₃ of the sparse matrix A. Taking a sufficiently small J ensures that x, y, z appear immediately after ψ₀ = 1 in the spectrum of A. However, due to the threefold multiplicity of the eigenvalue, the computed eigenvectors may be any linear combination of the coordinate vectors. This linear combination is easily determined (up to an orthogonal transformation) by using the fact that the coordinates correspond to points on the unit sphere, that is, β_k,l = (x(k, l), y(k, l), z(k, l)) is a point on S². To unmix x, y, z from the computed eigenvectors ψ₁, ψ₂, ψ₃, we need to find a 3 × 3 matrix M such that

$$X\equiv \left(\begin{array}{c}\hfill x^T\hfill \\ \hfill y^T\hfill \\ \hfill z^T\hfill \end{array}\right)=M\left(\begin{array}{c}\hfill {\psi }_1^T\hfill \\ \hfill {\psi }_2^T\hfill \\ \hfill {\psi }_3^T\hfill \end{array}\right)\equiv M\Psi .$$ (25)

The diagonal of the KL × KL matrix X^T X is given by

$${\left(X^{T}X\right)}_{ii}=x^2(k,l)+y^2(k,l)+z^2(k,l)={\Vert {\beta }_{k,l}\Vert }^2=1.$$

Since X^T X = Ψ^T M^T MΨ and Ψ is known (the computed eigenvectors), we get the overdetermined system of KL linear equations

$${\left({\Psi }^T{M}^{T}M\Psi \right)}_{ii}=1,$$ (26)

for the 9 entries of M^T M. The matrix M is then obtained from the least squares solution for M^T M by using SVD or Cholesky decomposition. We can recover M only up to an orthogonal transformation O ∈ O(3), because M^T O^T OM = M^T M. Thus, any reconstruction of the molecule is up to an arbitrary rotation and possibly a reflection (the chirality or handedness cannot be determined).

The locations of the radial lines can be further refined by using the fact that same image radial lines correspond to a great circle on S². In particular, such radial lines belong to the same plane (slice). Therefore, in the presence of misidentifications of common lines due to noise, we improve the estimation of the coordinates by using principal component analysis (PCA) for groups of L radial lines at a time. Furthermore, we equally space those radial lines on their corresponding great circle.

GCAR (Globally Consistent Angular Reconstitution) is summarized in Algorithm 1. Note that the algorithm assumes that the projection images are centered, for otherwise the Fourier projection-slice theorem no longer holds in the form (6), but instead, each projection P̂_g in (6) needs to be multiplied by phases that depend on the shift in the projection. These phase shifts alter the steps of finding common lines and three-dimensional reconstruction. The algorithm can be easily modified to handle non-centered projections. However, due to space limitations, we do not include here the details. The complexity of Algorithm 1 is completely dominated by finding common lines between projections. Using a naïve implementation, this requires O(nK²L²) operations.

Algorithm 1.

Outline of GCAR
Input: Projection images Pgk(x, y), k = 1, 2, ..., K.
Output: Coordinates vectors x, y, and z defined by (19).
1: Compute the polar Fourier transform P̂gk(ρ, γ) (see (7)).
2: Split each P̂gk(ρ, γ) into L radial lines Λk,l (see (8)).
3: Find common lines Λk1,l1 ≈ Λk2, l2.
4: Construct the sparse KL × KL weight matrix W with J << L (following Section 4.1).
5: Form the averaging operator A = D–1W (see (17)).
6: Compute the first three non-trivial eigenvectors of A: Aψi = λψi, i = 1, 2, 3.
7: Unmix x, y, z from ψ1, ψ2, ψ3.
8: Refinement: PCA and equally space same image radial lines.

The eigenvector computation is global and takes into account all the local pieces of information about common lines. Even if some common lines are misidentified, those errors are averaged out in the global eigenvector computation. Thus, GCAR should be regarded as a very efficient way of integrating the local cryo-EM geometry into a global orientation assignment.

The construction of the matrix W, as described in Section 4.1, uses all pairs of common lines. That is, for each pair of projection images k₁ and k₂, we find the Fourier lines Λ_k1,l1 and Λ_k2,l2 such that Λ_k2,l2 is closest to Λ_k1,l1, and use the pairs (k₁, l₁) and (k₂, l₂) to add edges to the set E according to (13). This corresponds to finding all geodesic circles on S² that pass though β_k1,l1. Note however, that the coordinate vectors are eigenvectors of A in (17) even if we use only a few of the geodesic circles that go through β_k1,l1. This corresponds to using fewer legs in each spider. Moreover, the resulting matrix W is sparser, and so requires less memory, and its eigenvectors can be computed faster. The key advantage of this observation is that we do not need to use all common lines determined by the $\left(\begin{array}{c}\hfill K\hfill \\ \hfill 2\hfill \end{array}\right)$ intersections of projection images. We can use only pairs of images for which the common line between projections k₁ and k₂ is reliable, e.g., whenever the correlation between Λ_k1,l1 and Λ_k2,l2 is above some threshold. This results in fewer misidentifications of common lines, and leads to a more accurate estimation of the orientations. This is demonstrated in the numerical examples in Section 6.

6 Numerical examples

In this section we demonstrate the performance of the GCAR algorithm using simulated data. Applying the algorithm to real datasets requires special considerations, due to the high levels of noise inherent to the imaging process. Practical considerations required for applying the algorithm to real cryo-EM datasets, which are beyond the scope of this paper, will be reported in a separate publication.

We implemented the algorithm in MATLAB, and tested it using simulated projections generated from a density map (three-dimensional volume) of the E. coli ribosome. Each simulated projection was computed by approximating the line integral (1) via the Fourier projection-slice theorem (6). Specifically, we computed the two-dimensional Fourier transform (3) of each projection on a Cartesian grid by accurately resampling the three-dimensional Fourier transform (4) of the molecule on a plane perpendicular to the projection orientation. This was implemented using a three-dimensional extension of [13, 14]. Once the two-dimensional discrete Fourier transform (DFT) of each projection was computed, the projection was obtained by a two-dimensional inverse DFT. Four noiseless simulated projections of the E. coli ribosome at random orientations are shown at the top row of Fig. 5. All projection orientations in our experiments were sampled from the uniform distribution on SO(3). The common line between each pair P̂_gk1 and P̂_gk2 of Fourier-transformed projections was detected by computing the correlations between all Fourier rays Λ_k1,l1 and Λ_k2,l2, and taking the pair (l₁, l₂) with the highest correlation as the common line.

Figure 5.

Simulated projections of the E. coli ribosome. Top row: Noiseless projections. Bottom row: Same projections as in the top row with additive Gaussian white noise with SNR=1/3.

All tests were executed on a quad core Xeon 2.33GHz running Linux. No knowledge of the orientations nor their distribution was used by the algorithm. Once the orientations were determined, the molecule was reconstructed by interpolating the KL Fourier lines into the three-dimensional pseudo-polar grid, by using nearest-neighbor interpolation, followed by an inverse three-dimensional pseudo-polar Fourier transform, implemented along the lines of [16, 17].

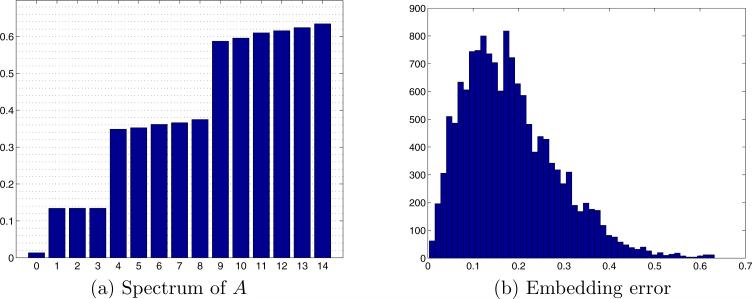
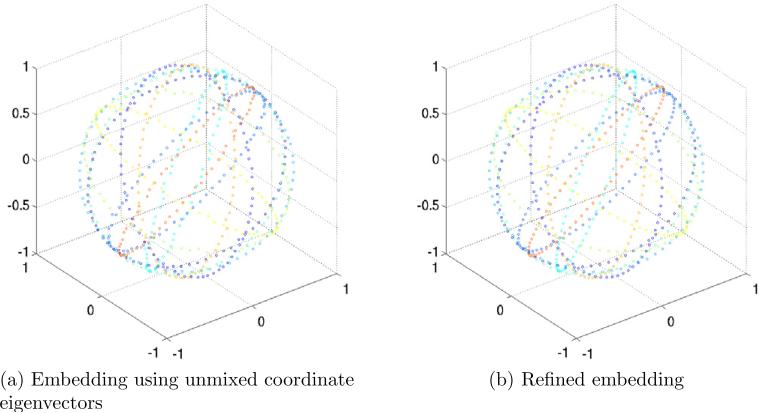
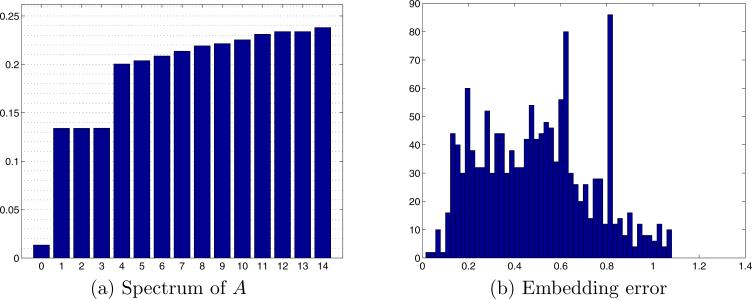
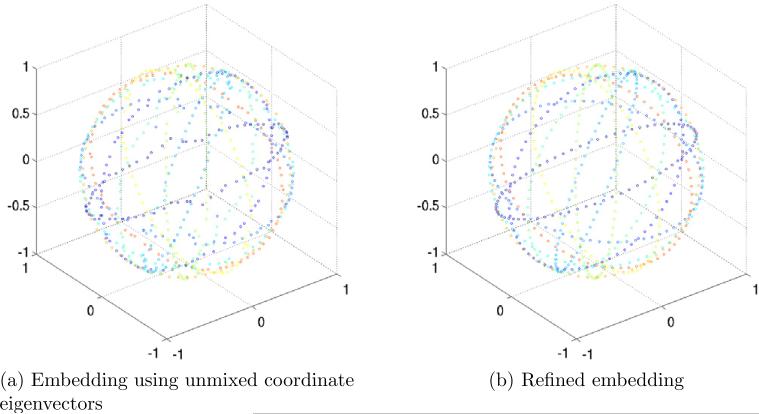
In the first experiment, we generated K = 200 projections, and computed L = 72 Fourier rays for each projection. This corresponds to an angular resolution of 5°. We then constructed the operator A in (17) using J = 10 and computed its spectrum (all eigenvalues and eigenvectors were computed using MATLAB's eigs function). Figure 6a shows the inverted spectrum of A, that is |1 − λ_i| for i = 1, . . . , 15. As expected, due to the row stochastic normalization of A, the first eigenvalue is one (zero in the bar plot). The eigenspace of dimension three is apparent, and its corresponding eigenvalue agrees with (21). The orientations β_k,l of each Fourier ray were then estimated by un-mixing the eigenvectors corresponding to this eigenspace, as explained in Section 5. We thus estimate each β_k,l as (x(k, l), y(k, l), z(k, l)), where x, y, and z are the unmixed coordinate eigenvectors. Figure 7a shows the estimated direction vectors β_k,l of the Fourier rays that correspond to the first 10 projections. Each estimated orientation is a point on S², and points that correspond to Fourier rays from the same projection are displayed in the same color. Figure 7b shows the refined embedding of the same Fourier rays (see Section 5 for details on the unmixing and refinement procedures). It is clear that even without refinement, same image Fourier rays are embedded to the same plane.

Figure 6.

Applying the GCAR algorithm on K = 200 simulated projections, with L = 72 Fourier rays in each projection, and J = 10. (a) Inverted spectrum of A (bar plot of |1 − λ_i|). The first bar (corresponding to eigenvalue 1) is of height 0, and was pulled above zero only for display purposes. (b) Embedding error (in degrees) – histogram of the angle between the true direction vector in ${\mathbb{R}}^3$ of each Fourier ray and its refined estimated direction.

Figure 7.

Embedding the first 10 projections out of K = 200 projections on S². (a) Estimated coordinates of Fourier rays that correspond to the first 10 projections, as obtained from the eigenvectors of the operator A after unmixing. (b) Refined embedding of the first 10 projections.

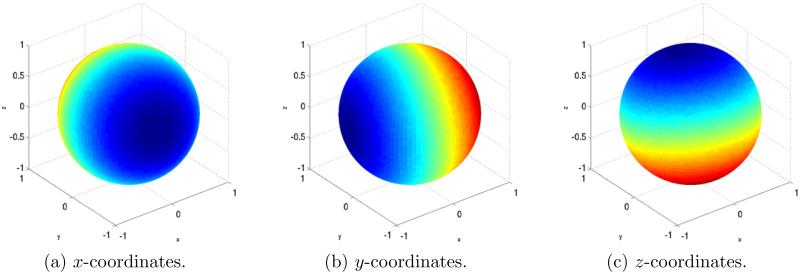
Figure 8 shows a plot of the estimated coordinate eigenvectors x, y, and z on S². Figure 8a was generated by coloring each point β_k,l ∈ S² (the true orientation of the (k, l) Fourier ray) by the value x(k, l). Figures 8b and 8c were generated in a similar way using y(k, l) and z(k, l), respectively. It is clear from Fig. 8 that the eigenvectors x, y, and z vary along three perpendicular axes, that is, they are indeed coordinates in an orthogonal coordinate system. We thus define the direction of variation of x in Fig. 8a as the x axis. Similarly, we define the direction of variation of y and z as the y and z axes, respectively. Note however, that these axes do not align with the canonical x, y, and z axes, illustrated by the overlaid grid, due to the arbitrary O(3) transformation inherent to the unmixing procedure.

Figure 8.

Unmixed eigenvectors of the operator A plotted of S². After computing the coordinate vectors x, y, and z by solving (25), we color each point β_k,l ∈ S² (the true orientation of the (k, l) Fourier ray) on the spheres in (a), (b), and (c), by the value of x(k, l), y(k, l), and z(k, l), respectively.

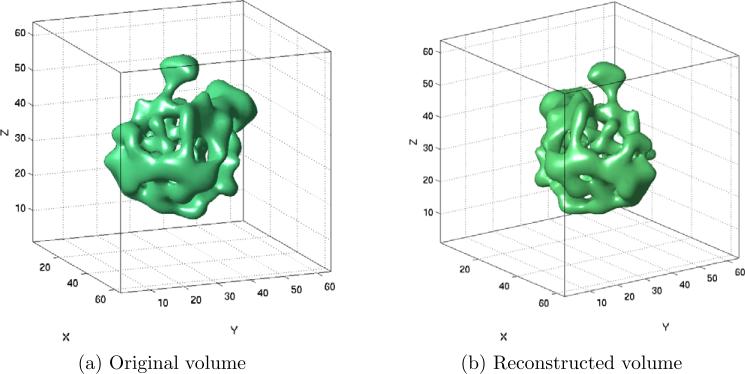
To demonstrate the accuracy of the algorithm, we show in Fig. 6b the histogram of the angles estimation error, that is, the histogram of the angle (in degrees) between the true orientation β_k,l and its refined embedding for each Fourier ray. Finally, Fig. 9 shows a two-dimensional view of the original and reconstructed volumes.

Figure 9.

(a) Two-dimensional view of the original volume. (b) View of the volume reconstructed using K = 200 projections and the refined estimated orientations.

Next, in order to demonstrate that the algorithm is independent of the number of projections K, we repeated the previous experiment with K = 20 projections, and with L = 72 and J = 10 as before. The spectrum of the operator A is shown in Fig. 10a. Again, the eigenspace of dimension three is apparent, and its eigenvalue is as predicted by (21). Note however, that while the second eigenspace in Fig. 6a is of dimension 5, the second eigenspace in Fig. 10a is no longer of dimension 5, as the convergence of the eigenspaces of dimensions 5 and up to the spherical harmonics does depend on K. The embedding errors for the case K = 20, shown in Fig. 10b, are roughly the same as those for K = 200, shown in Fig. 6b. In both cases the error is way below 2.5° (half the angular resolution), which can be thought of as the roundoff error inherent to the embedding due to the angular discretization. According to (20) and the averaging properties of A, each coordinate is obtained as the average of its neighboring coordinates. Thus, the error in each coordinate is reduced by averaging out the errors of its neighbors. The larger K the more neighbors get averaged, and so the error decreases. This is the reason for the slight difference between the histograms for K = 200 and K = 20 (Figs. 6b and 10b, respectively).

Figure 10.

Applying the GCAR algorithm on K = 20 simulated projections, with L = 72 Fourier rays in each projection, and J = 10. See Fig. 6 for a detailed description.

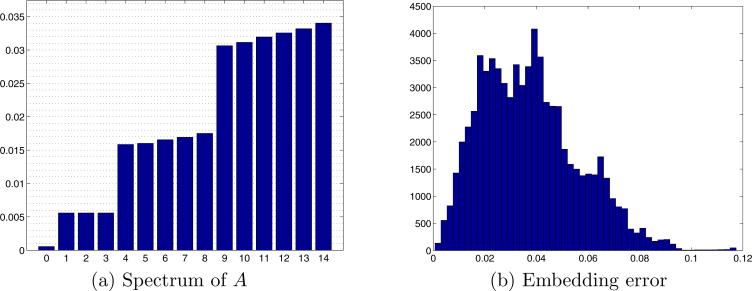
To further demonstrate this point, we show in Fig. 11 the results of using K = 200 projections, with L = 360 Fourier rays per projection, and J = 10. Figure 11a shows that the eigenvalue corresponding to the eigenspace of dimension three has changed according to (21), and Fig. 11b shows that the embedding error has decreased. The optimal value for L is determined by the frequency content of the projections. In practice, due to noise, there is no point in choosing L too large, as the high frequencies contain mostly noise. Reducing L, however, means faster detection of common lines, as fewer correlations need to be computed for each pair of projections.

Figure 11.

Applying the GCAR algorithm on K = 200 simulated projections, with L = 360 Fourier rays in each projection, and J = 10. See Fig. 6 for a detailed description.

We next demonstrate the robustness of our algorithm to noisy projections. To that end, we generated K = 200 projections to which we added additive white Gaussian noise with SNR=1/3, that is, the energy of the noise is three times larger than the energy of the signal. Several noisy projections are illustrated at the bottom row of Fig. 5. We then applied the same algorithm as in the previous experiments, with L = 72 and J = 10, obtaining the results in Figs. 12–14. The only difference in the current experiment is that instead of using all common lines, we constructed the operator A using only common lines whose correlation is among the 50% of highest correlations. The advantage of this pruning procedure is explained in Section 5.

Figure 12.

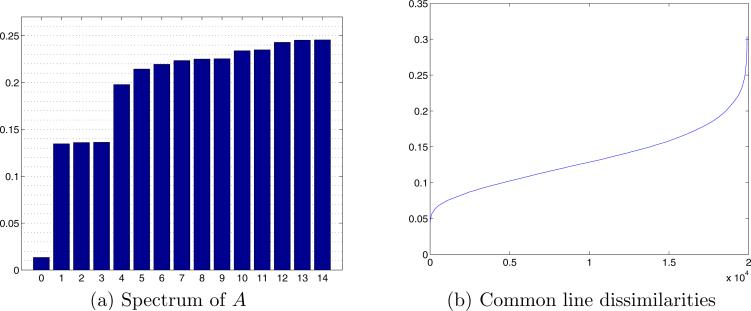
K = 200 noisy simulated projections with SNR=1/3. (a) Inverted spectrum of the operator A. The first bar (corresponding to eigenvalue 1) is of height 0, and was pulled above zero only for display purposes. (b) Sorted dissimilarities between all pairs of common lines (the dissimilarity is defined as the absolute value of one minus the correlation).

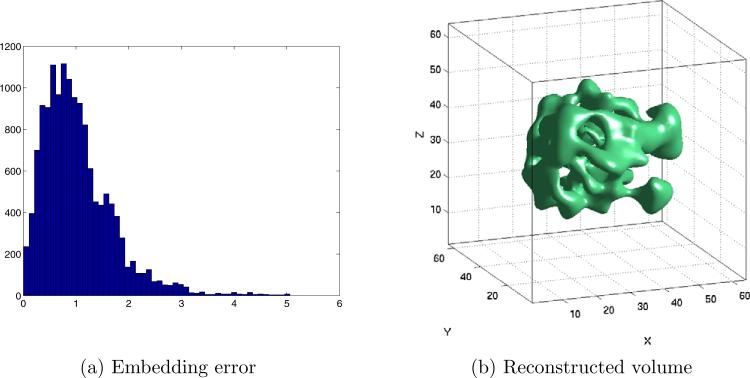
Figure 14.

K = 200 noisy simulated projections with SNR=1/3. (a) Histogram of the embedding error (in degrees). The embedding error is small in spite of the noisy projections, due to the averaging properties of the eigenvector computation. (b) View of the volume reconstructed using the K = 200 noisy projections and the refined estimated orientations.

Figure 12a shows the spectrum of the operator A constructed using the noisy projections. The noise in the projections results in misidentifications of common lines, which is translated into errors in the matrix A. Those errors cause slight deviation from the threefold degeneracy of the second eigenspace, as can be observed in Fig. 12a. Also, the next eigenspace is no longer of dimension 5. To illustrate the pruning procedure of Section 5, we plot in Fig. 12b the dissimilarity between each pair of common lines Λ_k1,l1 and Λ_k2,l2, for each pair of images k₁ and k₂, sorted from the smallest (most similar) to the largest (most different). Such a plot allows us to pick the threshold for filtering the GCAR matrix, thus using trustworthy common lines.

The errors in the matrix A obviously result in perturbation of the coordinate eigenvectors. This is demonstrated in Fig. 13a, which shows the embedding on S² of all Fourier rays corresponding to the first 10 projections. This embedding is noisier than the embedding in Fig. 7a, as for example, same image rays no longer lie exactly on the same plane, and the spacing between them is less regular. This noise, however, is removed by refining the embedding using PCA, as shown in Fig. 13b. The resulting embedding errors are depicted in Fig 14a, showing that even in the presence of noisy projections with SNR=1/3, most embedding errors are concentrated around 1°. Finally, we used the refined orientations estimated by the algorithm together with the noisy projections to reconstruct the three-dimensional volume. A view of the reconstructed volume is shown in Fig. 14b. This reconstructed volume is rotated compared to the original volume in Fig. 9a, due to the arbitrary O(3) transformation inherent to the unmixing procedure, as explained in Section 5.

Figure 13.

K = 200 noisy simulated projections with SNR=1/3. (a) Linear eigenvectors of A after unmixing. The resulting embedding is noisy due to the errors in A. (b) Refined embedding.

7 Summary and future work

We introduced a new algorithm for three-dimensional cryo-EM structure determination. Our GCAR algorithm incorporates the Fourier projection-slice theorem into a novel construction of a graph, followed by an efficient calculation of a few eigenvectors of its normalized sparse adjacency matrix. The resulting eigenvectors reveal the projection orientations in a globally consistent manner, as was demonstrated using simulated projection images.

Although the construction of the GCAR operator seems tightly coupled to the cryo-EM problem, the underlying idea of encoding geometrical information using center-of-mass relations is quite general. For example, a similar approach is used in [18] for solving the localization problem of scattered points in Euclidean space given a subset of their noisy distances.

Handling real cryo-EM projections is non-trivial due to the noise inherent to the imaging process. The noise in real cryo-EM projections is not only very high (SNR ~ 1/100), but also has special properties, due to, for example, the contrast transfer function of the microscope.

Detecting common lines between projections is the main challenge in the presence of noise: out of all detected common lines, only a small percentage is actually true common lines. Whenever the percentage of correctly detected common lines is too small, the resulting embedding found by the GCAR algorithm is distorted and cannot be used directly to reveal the orientations. However, it can be iteratively improved using geometrical considerations, until convergence to a globally consistent embedding is obtained. In each iteration, we ignore common lines that do not agree with the previously obtained embedding. This iterative procedure, which resembles well known procedures in robust estimation, such as the iterative weighted least squares procedure, cleans up the noisy graph and enables successful reconstructions.

Due to space constraints, it is impossible to include here all the extensions and implementation details required for dealing with real cryo-EM projections. Those details, including the iterative refinement procedure and the translational alignment of non-centered projections will be reported in a subsequent publication.