GENERATING OSCILLATORY BURSTS FROM A NETWORK OF REGULAR SPIKING NEURONS WITHOUT INHIBITION

Abstract

Avian nucleus isthmi pars parvocellularis (Ipc) neurons are reciprocally connected with the layer 10 (L10) neurons in the optic tectum and respond with oscillatory bursts to visual stimulation. Our in vitro experiments show that both neuron types respond with regular spiking to somatic current injection and that the feedforward and feedback synaptic connections are excitatory, but of different strength and time course. To elucidate mechanisms of oscillatory bursting in this network of regularly spiking neurons, we investigated an experimentally constrained model of coupled leaky integrate-and-fire neurons with spike-rate adaptation. The model reproduces the observed Ipc oscillatory bursting in response to simulated visual stimulation. A scan through the model parameter volume reveals that Ipc oscillatory burst generation can be caused by strong and brief feedforward synaptic conductance changes. The mechanism is sensitive to the parameter values of spike-rate adaptation. In conclusion, we show that a network of regular-spiking neurons with feedforward excitation and spike-rate adaptation can generate oscillatory bursting in response to a constant input.

1 INTRODUCTION

Oscillatory bursts play an important role in stimulus encoding (Gabbiani et al. 1996; Lesica, Stanley 2004; Oswald et al. 2004; Reinagel et al. 1999) and in the communication between neurons (Izhikevich et al. 2003; Lisman 1997; Sherman 2001). Mechanisms of oscillatory burst generation (Coombes and Bressloff 2005) range from the interaction of fast and slow currents in single neurons (Izhikevich 2007; Krahe and Gabbiani 2004; Rinzel and Ermentrout 1998; Wang and Rinzel 2003) to the interaction of neurons in networks typically consisting of excitatory and inhibitory connections (Buzsaki 2006; Traub et al. 2004). Here, we investigate oscillatory burst generation in a recurrently connected network of spiking neurons with excitatory synapses, where activity-dependent adaptation replaces the stabilizing role of inhibition.

The avian isthmo-tectal system (Fig. 1) plays a key role in visual information processing (Cook 2001; Maczko et al. 2006; Marin et al. 2007; Wang 2003). It consists of three key anatomical elements. A subpopulation of tectal layer 10 (L10) neurons receive retinal inputs and project to the ipsilateral nucleus isthmi pars parvocellularis (Ipc) and the nucleus isthmi pars magnocellularis (Imc) in a topographic fashion (Wang et al. 2004, 2006). The cholinergic Ipc neurons form topographic reciprocal connections with the tectum, where their axons terminate in a columnar manner ranging from layer 2 to 12 (Wang et al. 2006). The GABAergic Imc neurons consist of two cell types. One type projects broadly to the Ipc, whereas the other type projects upon tectal layers 10 to 13 (Wang et al. 2004).

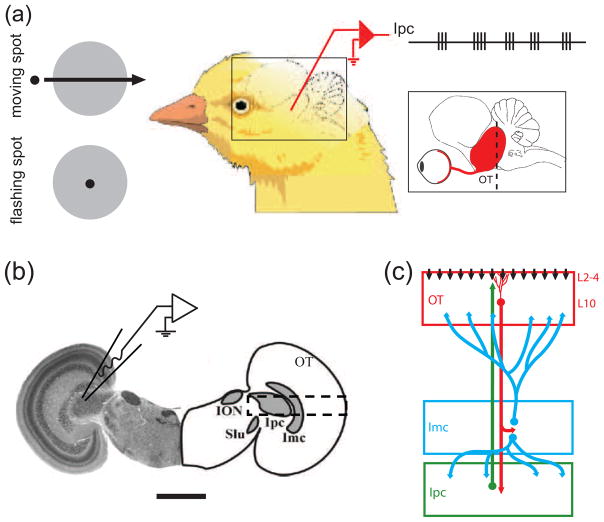
Fig. 1.

Schematic drawings of in vivo and in vitro recording set-ups. (a) Recordings in vivo showed that nucleus isthmi pars parvocellularis (Ipc) neurons responded to moving dots and flashing dots with oscillatory bursts (Marin et al. 2005). The rectangle inset shows a schematic lateral view of the chick brain with the retina, optic nerve, and optic tectum (OT) in red. The dashed line indicates the approximate location of the transverse slicing. (b) A transverse slice of the chick midbrain both in histological image and corresponding outlines (scale bar = 2 mm). The nucleus isthmo-opticus (ION) and the nucleus semilunaris (SLu) are not considered in this study. The patch-electrode schematic indicates a typical recording location from an Ipc neuron. The dashed rectangle indicates the location of the schematic circuitry described in (c). (c) Schematic drawings of the isthmo-tectal circuitry consisting of the retinal ganglion cells axons (vertical black arrows), the tectal layer 10 (L10) neurons (red), the Ipc neurons (green), and the nucleus isthmi pars magnocellularis (Imc) neurons (blue).

Ipc neurons respond with fast oscillatory bursts to flashing or moving visual stimulations (Fig. 1(a); Marin et al. 2005). Because of the extensive arborisation of Ipc axons in upper tectal layers (Wang et al. 2006), the Ipc oscillatory bursts (Marin et al. 2005) are also detected in extracellular recordings from superficial and intermediate tectal layers (Knudsen 1982; Neuenschwander and Varela 1993; Neuenschwander et al. 1996). Thus, as pointed out by Marin and coworkers, oscillatory burst recordings in the tectum may falsely be interpreted as oscillatory bursts originating in the tectum (Marin et al. 2005). The oscillatory bursts in tectal recordings disappear after injecting micro-drops of lidocaine into the corresponding area of the Ipc nucleus (Marin et al. 2005), thus confirming the role of the Ipc neurons in the oscillatory burst generation. The Ipc nucleus receives two inputs (Fig. 1(b), (c)). It receives glutamatergic (Hellmann et al. 2001; Marin et al. 2007) and possibly cholinergic (Britto et al. 1992; Wang et al. 2006) inputs from a subpopulation of tectal L10 neurons, characterized by unusual “shepherd’s crook” axons that arise from the apical dendrite and then make a U-turn to leave the tectum through deeper layers (Wang et al. 2006). It receives GABAergic input from the adjacent Imc nucleus (Wang et al. 2004). Importantly, the Ipc oscillatory burst responses persist when the Imc nucleus is inactivated via local application of CNQX (see Fig. 6D in Marin et al. 2007). Further, the retinal inputs to L10 neuron dendrites in upper tectal layers (Fig. 1(c)) show no evidence of bursting; rather in vivo recordings seem to suggest that spots of light produce continuous and long-lasting evoked potentials in superficial tectal layers (Holden 1980; Letelier et al. 2000). These observations narrow down the possible mechanisms for the observed Ipc oscillatory burst generation to the reciprocally connected L10 and Ipc neurons. For instance, the delays in the reciprocal connection (Meyer et al. 2008) could imply the involvement of delayed feedback in the induction of oscillatory dynamics (Brandt et al. 2006; Brandt and Wessel 2007; Brandt et al. 2007; Chacron et al. 2005; Doiron et al. 2003; Laing and Longtin 2003; Milton 1996).

To investigate the mechanisms of the observed oscillatory bursting in Ipc, we conducted whole-cell recordings from L10 and Ipc neurons combined with synaptic stimulations in chick brain slice preparations (Fig. 1(b)). Based on the in vitro experimental results, we built a model network consisting of reciprocally connected leaky integrate-and-fire neurons, representing L10 and Ipc neurons, and tested under what conditions this experimentally constrained model network reproduces the observed bursting activity in Ipc.

2 METHODS

2.1 Experiments

White Leghorn chick hatchlings (Gallus gallus) of less than 3 days of age were used in this study. All procedures used in this study were approved by the local authorities and conform to the guidelines of the National Institutes of Health on the Care and Use of Laboratory Animals. Animals were injected with ketamine (40 mg per kg, i.m.). Brain slices of the midbrain were prepared following published protocols (Dye and Karten 1996; Luksch et al. 2001). Briefly, preparations were done in 0°C, oxygenated, and sucrose-substituted saline (240 mM sucrose, 3 mM KCl, 5 mM MgCl₂, 0.5 mM CaCl₂, 1.2 mM NaH₂PO₄, 23 mM NaHCO₃, and 11 mM D-glucose). After decapitation, the brains were removed from the skull, and the forebrain, cerebellum, and medulla oblongata were discarded. A midsagittal cut was used to separate the tectal hemispheres. The tectal hemispheres were sectioned at 500 μm on a tissue slicer (Vibroslice, Campden or VF-200, Precisionary Instruments) in either the transverse or the horizontal plane. Slices were collected in oxygenated saline (120 mM NaCl, 3 mM KCl, 1 mM MgCl₂, 2 mM CaCl₂, 1.2 mM NaH₂PO₄, 23 mM NaHCO₃, and 11 mM D-glucose) and kept submerged in a chamber that was bubbled continuously with carbogen (95% oxygen, 5% CO₂) at room temperature. The slice was then transferred to a recording chamber (RC-26G, Warner Instruments) mounted on a fixed-stage upright microscope equipped with differential interference contrast optics (BX-51WI, Olympus). The slice was held gently to the bottom of the chamber with an anchor of nylon threads, and the chamber was perfused continuously with oxygenated saline at room temperature. The potential effects of temperature or age on measured cellular and synaptic properties were not addressed in this study. The L10 and Ipc neurons are visible with DIC optics.

Local electrical stimulation was achieved by inserting bipolar tungsten electrodes under visual control into either the tectal layers 10/11, or the Ipc nuclei with a three-axis micromanipulator (U-31CF, Narishige). Electrodes were custom-built from 50-μm diameter, insulated tungsten wires (California Fine Wire) that were glued together with cyanoacrylate and mounted in glass micro capillaries for stabilization. The wires protruded several hundred μm from the capillaries, and the tips were cut at an angle. Stimulus isolators (Isolated Pulse Stimulator 2100, AM Systems) generated biphasic current pulses (20 – 200 μA, 500 μs).

Whole-cell recordings were obtained with glass micropipettes pulled from borosilicate glass (1.5 mm OD, 0.86 mm ID, AM Systems) on a horizontal puller (P-97, Sutter Instruments or DMZ Universal Puller, Zeitz Instruments) and were filled with a solution containing 100 mM K-Gluconate, 40 mM KCl, 10 mM HEPES, 0,1 mM CaCl₂, 2 mM MgCl₂, 1.1 mM EGTA, 2 mM Mg-ATP, pH adjusted to 7.2 with KOH. Electrodes were advanced through the tissue under visual guidance with a motorized micromanipulator (MP-285, Sutter Instruments) while constant positive pressure was applied and the electrode resistance was monitored by brief current pulses. Once the electrode had attached to a membrane and formed a seal, access to the cytosol was achieved by brief suction. Whole-cell recordings were performed with the amplifier (Axoclamp 2B, Axon Instruments or SEC-05L, npi-electronic) in the bridge mode (current clamp). The liquid junction potential was measured and estimated to be approximately −10 mV. This correction was ignored, i.e., the real membrane potentials are more negative than the stated values. The series resistance was estimated by toggling between the bridge and the DCC (discontinuous current clamp) mode, and subsequently compensated with the bridge balance. Depolarizing and hyperpolarizing currents were injected through intracellular electrodes. Analog data were low-pass filtered (4-pole Butterworth) at 1 kHz, digitized at 5 kHz, stored, and analyzed on a PC equipped with a PCI-MIO-16E-4 and LabView software (both National Instruments).

Labeling of a subset of recorded neurons was carried out as described previously (Luksch et al. 1998; Mahani et al. 2006). In brief, whole-cell patch recordings were obtained as described above. Additionally, the electrode solution contained 0.5% Biocytin (w/v) to label the recorded neurons. Individual cells were filled intracellularly with 2 nA of positive current injection over 3 minutes through the patch electrode. After recording and labeling, slices were kept in oxygenated ACSF for an additional 30 minutes and subsequently fixed by immersion in 4% paraformaldehyde in PB for at least 4 hours. Slices were then washed in phosphate buffer (PB, 0.1 M, pH 7.4) for at least 4 hours, immersed in 15% sucrose in PB for at least 4 hours and then immersed in 30% sucrose in PB for 12 hours, and resectioned at 60 μm on a freezing microtome. The sections were collected in PB and the endogenous peroxidase blocked by a 15-minute immersion in 0.6% hydrogen peroxide in methanol. The tissue was washed several times in PB, and then incubated in the avidin-biotin complex solution (ABC Elite kit, Vector Labs) and the reaction product visualized with a heavy-metal intensified DAB protocol. Following several washes in PB, the 60 μm-thick sections were mounted on gelatin-coated slides, dried, dehydrated, and coverslipped. Sections were inspected for labeled neurons, and only data from cells that could unequivocally be classified according to published criteria (Wang et al. 2004, 2006) were taken for further analysis. Cells were reconstructed at medium magnification (10x or 20x) with a camera lucida on a Leica microscope and projected onto the 2D plane.

2.2 Two-Neuron Model

We investigated the network dynamics of two reciprocally connected model neurons, representing the L10 and the Ipc neuron in the avian isthmotectal system. Each model neuron is of the leaky integrate-and-fire type with spike-rate adaptation. The dynamic of the membrane potentials V_L10 and V_Ipc are determined by two coupled differential equations:

$${\tau }_{m,L10}\frac{{dV}_{L10}}{dt}=E_{r,L10}-V_{L10}-R_{m,L10}(I_{\mathit{sra},L10}+I_{\mathit{Ipc}\to L10}-I_{e,L10})$$ (1)

$${\tau }_{m,\mathit{Ipc}}\frac{{dV}_{\mathit{Ipc}}}{dt}=E_{r,\mathit{Ipc}}-V_{\mathit{Ipc}}-R_{m,\mathit{Ipc}}(I_{\mathit{sra},\mathit{Ipc}}+I_{L10\to \mathit{Ipc}})$$ (2)

where E_r,L10 denotes the resting membrane potential of the L10 neuron, R_m,L10 is the membrane input resistance, andτ_m,L10 is the membrane time constant. The measured membrane time constants (Table 1) are larger than the measured axonal delays (Meyer et al. 2008). Thus delays in synaptic voltage responses of leaky integrate-and-fire model neurons are dominated by the membrane time constants. Therefore, we did not explicitly include axonal delays in the network model. When the membrane potential V_L10 reaches the threshold V_θ,L10 it is reset to V_reset,L10 instantaneously. This is interpreted as the occurrence of a spike. The external current input I_e,L10 to the L10 neuron represents the stimulus from the retinal ganglion cell. The spike-rate adaptation current,

TABLE 1.

Single neuron parameters.

Neuron	τm(ms)	Rm(MΩ)	Er(mV)	Vθ(mV)	Vreset(mV)	τsra(ms)	Δgsra(nS)	Esra(mV)
L10	104	480	−55	−39	−50	50	1.25	−70
Ipc	25	135	−61	−40	−50	60	8.15	−70

Abbreviations: τ_m = membrane time constant, R_m = membrane input resistance, E_r = resting membrane potential, V_θ = threshold for spiking, V_reset = reset voltage, τ_sra = spike-rate adaptation time constant, Δg_sra = spike-rate adaptation conductance increment, E_sra = spike-rate adaptation reversal potential.

$$I_{\mathit{sra},L10}=g_{\mathit{sra},L10}(t)(V_{L10}-E_{\mathit{sra},L10})$$ (3)

has the adaptation reversal potential E_sra,L10, and the time varying adaptation conductance g_sra,L10(t), which evolves according to the differential equation

$${\tau }_{\mathit{sra},L10}\frac{{dg}_{\mathit{sra},L10}}{dt}=-g_{\mathit{sra},L10}$$ (4)

Whenever the neuron fires a spike, the adaptation conductance changes according to

$$g_{\mathit{sra},L10}(t^{+})\to g_{\mathit{sra},L10}(t^{-})+{\mathrm{\Delta }g}_{\mathit{sra},L10}$$ (5)

The synaptic current

$$I_{\mathit{Ipc}\to L10}=g_{\mathit{Ipc}\to L10}{P}_{\mathit{Ipc}\to L10}(t)(V_{L10}-E_{\mathit{Ipc}\to L10})$$ (6)

from the Ipc neuron to the L10 neuron projection is proportional to the open probability P_Ipc→L10(t) of the synaptic conductance, where g_Ipc→L10 is the maximum synaptic conductance and E_Ipc→L10 is the synaptic reversal potential. The open probability P_Ipc→L10(t) of the synaptic conductance from the Ipc to the L10 neuron has the form

$$P_{\mathit{Ipc}\to L10}(t)=B_{\mathit{Ipc}\to L10}\sum _k\left(exp(-\frac{t-t_{\mathit{Ipc}}^k}{{\tau }_{1,\mathit{Ipc}\to L10}})-exp(-\frac{t-t_{\mathit{Ipc}}^k}{{\tau }_{2,\mathit{Ipc}\to L10}})\right)$$ (7)

where the normalization factor

$$B_{\mathit{Ipc}\to L10}={\left({\left(\frac{{\tau }_{2,\mathit{Ipc}\to L10}}{{\tau }_{1,\mathit{Ipc}\to L10}}\right)}^{{\tau }_{\mathit{rise},\mathit{Ipc}\to L10}/{\tau }_{1,\mathit{Ipc}\to L10}}-{\left(\frac{{\tau }_{2,\mathit{Ipc}\to L10}}{{\tau }_{1,\mathit{Ipc}\to L10}}\right)}^{{\tau }_{\mathit{rise},\mathit{Ipc}\to L10}/{\tau }_{2,\mathit{Ipc}\to L10}}\right)}^{-1}$$ (8)

ensures that the peak value of P_Ipc→L10(t) generated by a single spike equals to 1, the variable $t_{\mathit{Ipc}}^k$ represents the time at which the Ipc neuron generates the kth spike, and a summation is performed over all spikes generated by the Ipc neuron. The time constant τ_1,Ipc→L10 and τ_2,Ipc→L10 (τ_1,Ipc→L10 > τ_2,Ipc→L10) determine the time course of the synaptic conductance change. The synaptic rise time is ${\tau }_{\mathit{rise},\mathit{Ipc}\to L10}=\frac{{\tau }_{1,\mathit{Ipc}\to L10}{\tau }_{2,\mathit{Ipc}\to L10}}{{\tau }_{1,\mathit{Ipc}\to L10}-{\tau }_{2,\mathit{Ipc}\to L10}}$, while τ_1,Ipc→L10 represents the fall time. The variables and parameters of the Ipc model neuron in Eq. (2) are all analogous to those of the L10 model neuron. The Ipc model neuron does not receive an external current input.

The Ipc steady-state response (taken to start 100 ms after stimulus onset) is represented by the “burst score” (Fig. 5). A spike preceded by an inter-spike-interval (ISI) of more than 10 ms and followed by an ISI of less than 4 ms is classified as the beginning of a burst. Subsequent spikes with ISIs of less than 4 ms are part of the burst. All other spikes are classified as isolated (Sillito and Jones 2002). The burst score is defined by the number of bursts divided by the sum of the number of bursts and the number of isolated spikes in the steady-state response. The score equals 1 when all spikes belong to bursts and equals 0 when all spikes are isolated. When the firing rate exceeds 1000 Hz the Ipc response is classified as diverging.

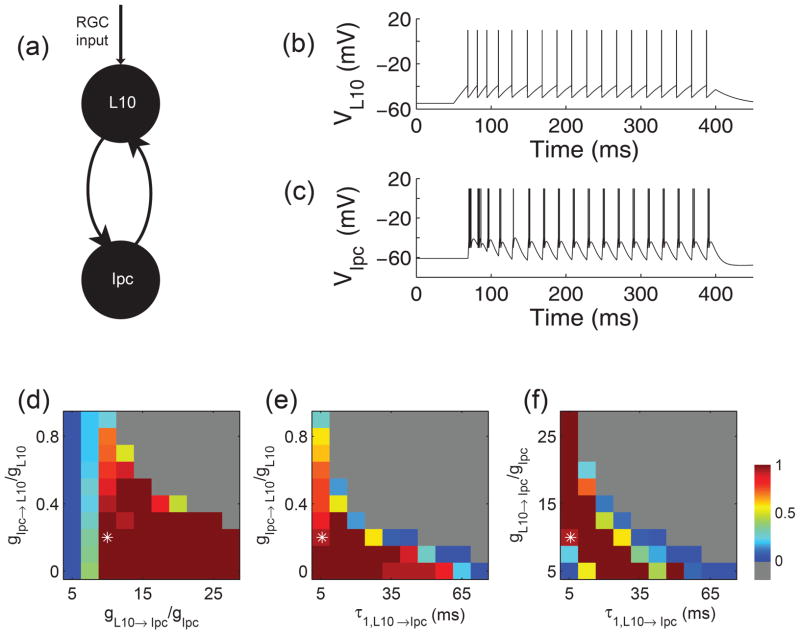
Fig. 5.

Generation of oscillatory bursting in a pair of model neurons with recurrent excitation. (a) Schematic drawing of the reciprocally coupled pair of L10 and Ipc model neurons with retinal (RGC) inputs to the L10 model neuron. (b) and (c) Responses of the reciprocally coupled L10 and Ipc model neurons to depolarizing current injection into the L10 model neuron. The injected current had a duration of 350 ms (starting at time = 50 ms) and an amplitude of 0.2 nA. The cellular and synaptic parameter values were chosen as described in the text and Table 1. The maximum synaptic conductances relative to the membrane conductance were g_L10→Ipc/g_Ipc = 10 and g_Ipc→L10/g_L10 = 0.2. The Ipc burst score (see Methods) for this trace equals14/15 ≅ 0.93. (d), (e), (f) Ipc responses for three cross sections through the 3-dimensional parameter space spanned by the maximum synaptic conductances g_L10→Ipc/g_Ipc and g_Ipc→L10/g_L10, and by the feedforward synaptic fall times τ_1,L10→Ipc. The three cross sections intersect the point (asterisk) 10, 0.2, 5.6 ms, respectively, which is also the parameter set chosen for the sample trace in (b) and (c). The Ipc responses are represented in pseudo color by the burst score. When all spikes belong to bursts the score is 1 (red), when all spikes are isolated the score is 0 (blue), when the firing rate exceeds 1000 Hz the Ipc response is classified as diverging (gray).

2.3 Population model with uncorrelated noise

For the population model of L10 and Ipc neurons (Fig. 6a) each individual neuron is of the leaky integrate-and-fire type with spike-rate adaptation as described above. Each population consists of 400 neurons. When referring to an individual neuron, we use the subscript i for L10 neurons and the subscript j for Ipc neurons. The dynamics of the membrane potentials V_i (L10 neuron i) and V_j (Ipc neuron j) are determined by the coupled differential equations:

$${\tau }_{m,L10}\frac{{dV}_i}{dt}=E_{r,L10}-V_i-R_{m,L10}(I_{\mathit{sra},i}+I_{\mathit{Ipc}\to i}-I_{e,i}+{\chi }_i)$$ (9)

$${\tau }_{m,\mathit{Ipc}}\frac{{dV}_j}{dt}=E_{r,\mathit{Ipc}}-V_j-R_{m,\mathit{Ipc}}(I_{\mathit{sra},j}+I_{L10\to j}+{\chi }_j)$$ (10)

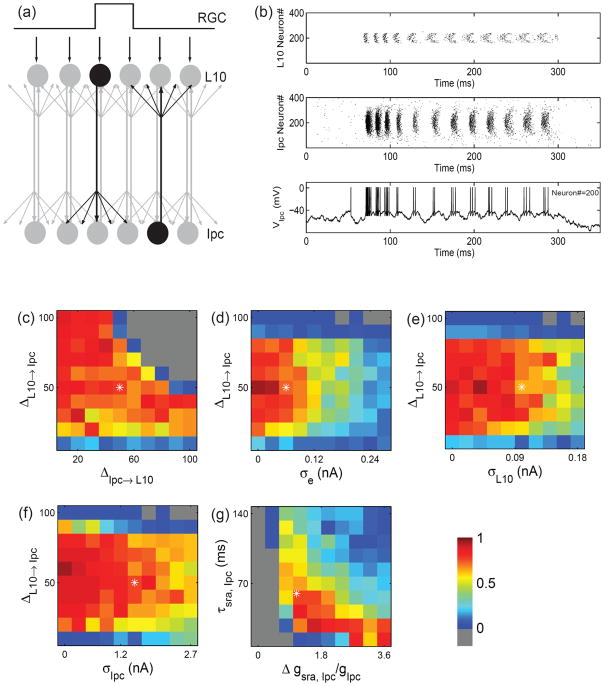
Fig. 6.

Generation of oscillatory bursts in a population model with recurrent excitation and uncorrelated noise. (a) Schematic drawing of the reciprocally coupled populations of L10 and Ipc model neurons with local RGC inputs to a small group of L10 neurons. The projections are topographic, but have a certain width as indicated by the spread of arrows. (b) Sample L10 and Ipc population responses (raster plot of spikes) to a stimulus current step delivered to 80 neurons centered on L10 neuron #200. The concurrent voltage response of Ipc neuron #200 is shown in the bottom trace. Single neuron parameters are listed in Table 1. The stimulus, synaptic, and noise parameters are: I₀ = 0.18 nA, g_L10→Ipc = 1.85 nS, g_Ipc→L10 = 4.69×10⁻³ nS, Δ_L10→Ipc = 50, Δ_Ipc→L10 = 50, σ_e = 0.06 nA, σ_Ipc = 1.5 nA, σ_L10 = 0.1 nA. The stimulus current is turned on at t = 50 ms and lasts for 250 ms. (c) to (f) Ipc responses for four cross sections through the 5-dimensional parameter space spanned by the spatial width of the synaptic weight distributions Δ_L10→Ipc and Δ_Ipc→L10, and the white noise standard deviations σ_e, σ_Ipc, and σ_L10. The four cross sections intersect the point (asterisk) 50, 50, 0.06 nA, 1.5 nA, 0.1 nA, respectively, which is also the parameter set chosen for the sample trace in (b). The Ipc responses are represented in pseudo color (see Fig. 5) by the “average burst score”, which is the burst score (see Methods) averaged over 5 trials. (g) Ipc responses for different values of the Ipc spike-rate adaptation increment,Δg_sra,Ipc, and the decay time constant, τ_sra,Ipc. All other parameters are as in (b).

The synaptic currents, I_{L10→ j} and I_Ipc→i, are similar in form to the one described above, Eq. (7), but now include contributions from a population of presynaptic neurons. For instance, the synaptic current in Ipc neuron j

$$I_{L10\to j}=\sum _i{g}_{L10\to \mathit{Ipc}}{P}_{ji}(t)W_{ji}(V_j-E_{L10\to \mathit{Ipc}})$$ (11)

includes contributions from all L10 synaptic inputs to Ipc neuron j. The synaptic conductance is the product of the maximum synaptic conductance, g_L10→Ipc, and the weight distribution

$$W_{ji}=exp\left(-\frac{{(i-j)}^2}{{2\mathrm{\Delta }}_{L10\to \mathit{Ipc}}^2}\right)$$ (12)

of width Δ_L10→Ipc. The latter reflects the narrow topographic projection from L10 to Ipc (Wang et al. 2006). The open probability of the synaptic conductance from L10 neuron i to Ipc neuron j has the form

$$P_{ji}(t)=B_{L10\to \mathit{Ipc}}\sum _k\left(exp(-\frac{t-t_i^k}{{\tau }_{1,L10\to \mathit{Ipc}}})-exp(-\frac{t-t_i^k}{{\tau }_{2,L10\to \mathit{Ipc}}})\right)$$ (13)

The time constants and the normalization factor are the same as described above. The variable $t_i^k$ represents the time at which the L10 neuron i generates the kth spike. The total synaptic current received by Ipc neuron j is therefore a sum of all the synaptic currents from the population of L10 neurons. The expression for the synaptic current I_Ipc→i received by L10 neuron i has a similar form.

The external current input, I_e,i = (I₀ + η_e,i)H (i − 160)H (240 − i), to L10 neuron i represents the stimulus from the retinal ganglion cell. This external current input has a constant component I₀ and a noise component η_e,i. The Heaviside step function, H, expresses that the current to L10 neurons is non-zero between neuron #160 and #240 and zero elsewhere. The noise component,η_e,i, is modeled as uncorrelated white noise of standard deviation σ_e, i.e., $\langle {\eta }_{e,i}(t){\eta }_{e,i^{\prime }}(t^{\prime })\rangle ={2\sigma }_e^2\delta (t-t^{\prime }){\delta }_{{ii}^{\prime }}$.

To allow for spontaneous activity, each L10 and Ipc neuron receives an uncorrelated noise current, χ_i and χ_j, respectively. The noise currents are modeled as uncorrelated white noise, i.e. $\langle {\chi }_i(t){\chi }_{i^{\prime }}(t^{\prime })\rangle ={2\sigma }_{L10}^2\delta (t-t^{\prime }){\delta }_{{ii}^{\prime }}$ and $\langle {\chi }_j(t){\chi }_{j^{\prime }}(t^{\prime })\rangle ={2\sigma }_{\mathit{Ipc}}^2\delta (t-t^{\prime }){\delta }_{{jj}^{\prime }}$ of standard deviation σ_L10 and σ_Ipc, respectively.

In one set of simulations, we implemented an after-depolarization to the Ipc leaky integrate-and-fire model neurons using a phenomenological description (Doiron et al. 2007). When an Ipc spike occurs, an after-depolarizing current I_ADP = Ax(t) is evoked after a time delay τ_ADP. Here x(t) evolves according to the set of two differential equations $\frac{dx}{dt}=y$ and $\frac{dy}{at}=-{\alpha }^{2}x-2\alpha y+{\alpha }^2{\displaystyle \sum _i}\delta (t-t_i-{\tau }_{\mathit{ADP}})$, where t_i is the time at which the Ipc neuron spikes, α is the inverse of the time constant of the depolarization current and A is the current amplitude. The ADP current parameters (A= 0.7 nA, τ_ADP = 0.5 ms, α= 4.5 s⁻¹) were chosen for the simulated after-depolarization to match a large recorded after-depolarization.

The source code for the model is accessible at https://senselab.med.yale.edu/ModelDB/showmodel.asp?model=120783.

3 RESULTS

3.1 Cellular and synaptic properties of L10 and Ipc neurons

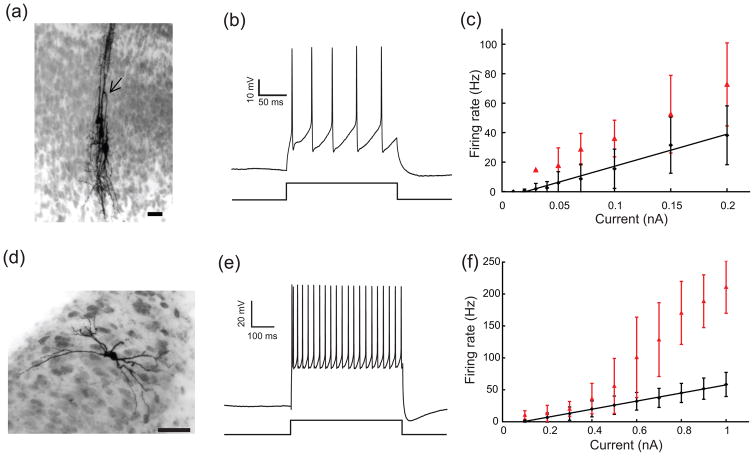
The Ipc nucleus receives glutamatergic inputs from a subpopulation of L10 neurons with the characteristic shepherd’s crook axon (Wang et al. 2006). A total of 12 neurons located in tectal layer 10 were recorded and were sufficiently labeled for unequivocal identification as shepherd’s crook neurons. This type of neuron consists of an apical dendrite, several basal dendrites, and an axon originating from the apical dendrite with a characteristic U-turn before it courses towards the deep tectal layers (Fig. 2(a)). The average resting membrane potential was −59 ± 8 (mean ± SD, n = 12) mV, the average input resistance was 349 ± 198 MΩ, and the average membrane time constant was 105 ± 77 ms. We analyzed the cellular properties of the L10 neurons with depolarizing somatic current injections from 0.01 to 0.2 nA. The recorded L10 neurons responded with a regular series of action potentials (Fig. 2(b)). The average firing rates, determined from the total number of spikes divided by the duration of the current pulse, increased approximately linearly with current amplitude (Fig. 2(c)). The average instantaneous onset firing rates, determined from the inverse of the first interspike intervals in response to the onset of the current pulse, were larger than the average firing rates (Fig. 2(c)), thus indicating some level of spike-rate adaptation.

Fig. 2.

Morphological and electrophysiological properties of L10 and Ipc neurons. (a) Intracellular biocytin fills of three tectal L10 neurons. The U-shaped axon (arrow head) characterizes the center neuron as a shepherd’s crook neuron, which projects to the nucleus isthmi. A U-shaped axon is also visible for the left neuron. Scale bar = 20 μm. (b) Response of a representative L10 neuron to a 0.1 nA current step. (c) Average firing rate (black diamonds) and instantaneous firing rate (the inverse of the first interspike intervals, red triangles) vs. current for the population of recorded L10 neurons. The black line represents a linear fit (F(I)= 217.86 × I − 4.61; r² = 0.9821) of the firing rate, F, as a function of the injected current, I, to the measured average firing rate data points. (d) Intracellular biocytin fill in an Ipc neuron (scale bar = 50 μm). (e) Response of a representative Ipc neuron to a 0.5 nA current step. (f) Average firing rate (black diamonds) and instantaneous firing rate (the inverse of the first interspike intervals, red triangles) vs. current for the population of recorded Ipc neurons. The black line represents a linear fit (F(I) = 63.427× I − 5.73; r² = 0.9988) of the firing rate as a function of the injected current to the measured average firing rate data points.

A total of 45 cells were recorded in the Ipc nucleus and 27 of them were labeled sufficiently to allow for the attribution to the Ipc nucleus. The filled Ipc neurons were round or oval in shape and had a bipolar dendritic structure (Fig. 2(d)). The efferents from Ipc neurons terminate in the optic tectum in “paintbrush” terminal fields in a columnar manner (Wang et al. 2006). The average resting membrane potential was −61 ± 7 mV, the input resistance was 114 ± 37 MΩ, and the average membrane time constant was 35 ± 15 ms. The recorded Ipc neurons responded with a regular sequence of spikes to depolarizing current injections in the range from 0.1 to 1.0 nA injected into the soma (Fig. 2(e)). The average firing rates increased approximately linearly with current amplitude (Fig. 2(f)). For current amplitudes above ~0.5 nA, the average instantaneous onset firing rates were larger than the average firing rates (Fig. 2(f)), thus indicating some level of spike-rate adaptation.

For completeness, we tested the possibility of intrinsic bursting from hyperpolarized levels, such as the T current-mediated bursting in thalamic relay neurons (McCormick and Huguenard 1992; Sherman 2001; Wang 1994; Zhan et al. 1999). We observed regular spiking in response to depolarizing current steps from hyperpolarized levels of −90 mV in L10 and Ipc neurons (Supplementary Fig. 1).

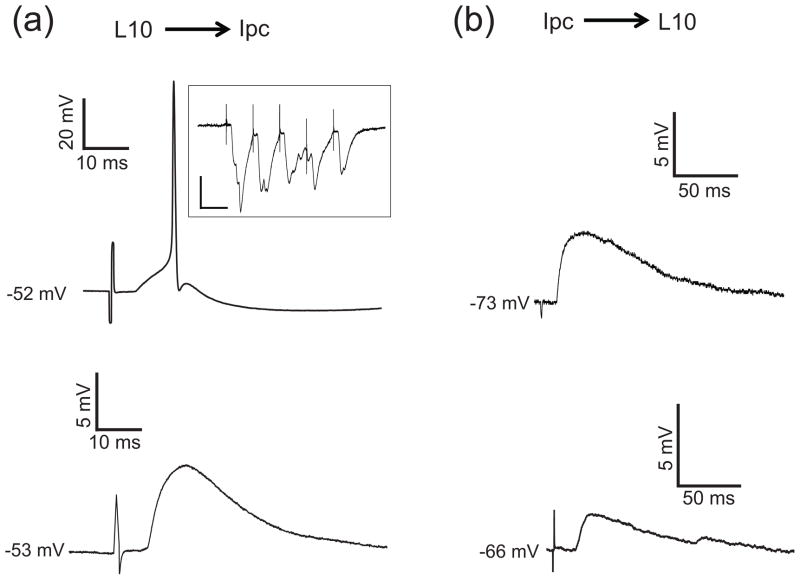
To measure the amplitude and time courses of the reciprocal synaptic connections between L10 and Ipc neurons, we positioned an extracellular stimulus electrode in either structure and recorded the response to local extracellular electrical stimulation in the other one. Recorded Ipc neurons responded to the stimulation in tectal layer 10 with fast and strong EPSPs that could generate one to three action potentials for sufficiently strong stimulation (Fig. 3(a)). The synapse showed little depression (Fig. 3(a) inset). From seven recorded L10 → Ipc connections we estimated the values for the synaptic time constants, τ_1,L10→Ipc = 7.2± 4.7 ms and τ_2,L10→Ipc = 0.47± 0.16 ms, by matching the time course of model neuron synaptic responses (Sec. 2.2) to the recorded subthreshold EPSPs. The feedback connection was qualitatively different. Recorded L10 neurons responded to brief electrical stimulation within the Ipc nucleus with small and long lasting EPSPs (Fig. 3(b)). The large L10 membrane time constant of approximately 100 ms precludes a reliable estimation of the synaptic time constant for the Ipc → L10 connection from the voltage response. Therefore, we limited the quantification of the synaptic responses to the time course of the EPSPs. The recorded EPSPs dropped to 37 % of their peak value after 87 ± 8 ms (n = 3 cells). These observations indicate that in the avian isthmo-tectal system the synaptic conductance change is strong and brief in the feedforward direction, L10 → Ipc, and weak and long-lasting in the feedback direction, Ipc → L10.

Fig. 3.

Synaptic properties of the L10 → Ipc and the Ipc → L10 connections. (a) Brief electrical stimulation with a biphasic current pulse (200 μA, 500 μs) in tectal layer 10 evoked an EPSPs plus spikes or just EPSPs in the recorded Ipc neurons. Inset: Synaptic current recorded from an Ipc neuron in voltage clamp in response to electrical stimulation in tectal layer 10 with a train of 5 pulses of 20 ms interval. The membrane potential was held at −70 mV (scale bars = 20 ms, 200 pA). (b) Brief electrical stimulation in the Ipc nucleus evoked long-lasting EPSPs in recorded L10 neurons. Note the different scale bars in (a) and (b).

3.2 Determining experimentally constrained model parameters

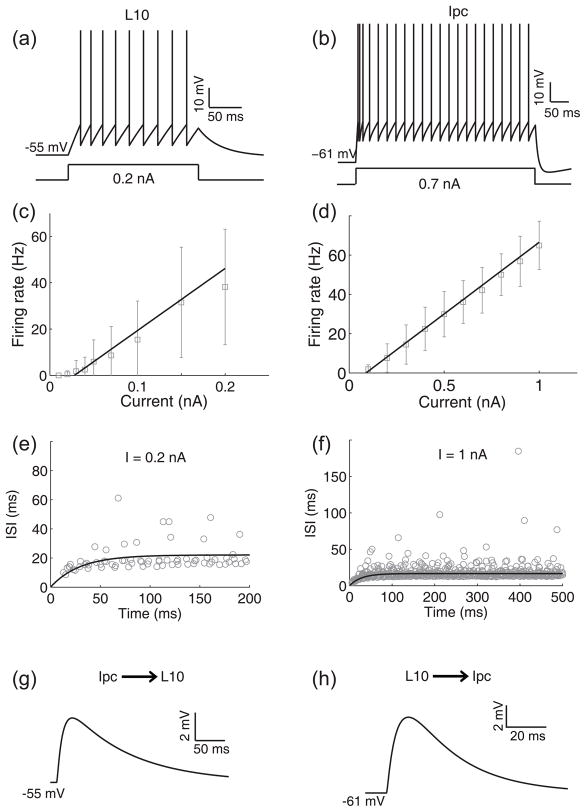
For our model investigation into the mechanisms of oscillatory burst generation, we considered leaky integrate-and-fire model neurons, representing the L10 and the Ipc neuron in the avian isthmotectal system. The cellular properties of a model neuron (Eq. (1) to (5)) are specified by 8 parameters. We constrained the parameters by comparing the simulated responses of the L10 and Ipc model neurons (Eq. (1) and (2)) to depolarizing current injections (Fig. 4) with the experimental results (Fig. 2). A L10 (Fig. 4(a)) or Ipc (Fig. 4(b)) model neuron responds with a regular spike train to an injected current pulse. Because of the spike-rate adaptation (Eq. (3) to (5)), a model neuron responds with a short inter-spike-interval (ISI) between successive spikes at the onset of a current pulse. The ISI then increases with time t after the current pulse onset and reaches a steady state within the duration of the current pulse. From the simulated spike train, we calculated the average firing rate, dividing the number of spikes by the duration of the current pulse. We repeated this procedure for different current amplitudes. We then derived the model F-I curve by fitting a linear function through the calculated average firing rates (Fig. 4(c), (d)). We also calculated the inter-spike-interval (ISI) between successive spikes in the simulated spike train and fitted an exponential function to the calculated values (Fig. 4(e), (f)). All 8 cellular parameter values (Table 1) were tuned within their experimental constraints until the model F-I curve and the ISI functions for all current amplitudes (Table. 2 and 3) matched the experimental data (Fig. 4(c) to (f)). The 8 cellular parameter values for each neuron were then kept fixed for all the simulations presented in the paper.

Fig. 4.

Cellular and synaptic properties of L10 and Ipc model neurons. (a) The response of the L10 model neuron to an injected current pulse of 0.2 nA amplitude. (b) The response of the Ipc model neuron to an injected current pulse of 0.7 nA amplitude. (c) The fitted F-I curve of the L10 model neuron, F(I) = 268.4 × I − 7.5; r² = 0.9883. The experimental data (average firing rates from Fig. 2(c)) of the recorded real L10 neurons in response to current injections are shown for comparison (gray squares). (d) The fitted F-I curve of the Ipc model neuron, F(I) = 73.0 × I − 6.5; r² = 0.9992. The experimental data (average firing rates from Fig. 2(f)) of the recorded real Ipc neurons in response to current injections are shown for comparison (gray squares). (e) The fitted ISI curve, ISI(t) = A(1 − exp(−t/B)), of the L10 model neuron for a current injection of 0.2 nA (see Table 2). The experimental data from 9 recorded real L10 neurons in response to the same current injection are shown for comparison (gray circles). (f) The fitted ISI curve, ISI(t) = A(1 − exp(−t/B)), of the Ipc model neuron for a current injection of 1.0 nA (see Table 3). The experimental data from 18 recorded real Ipc neurons in response to the same current injection are shown for comparison (gray circles). (g) The synaptic response of the L10 model neuron to a single pre-synaptic action potential. The synaptic parameters were g_Ipc→L10 = 2.08 nS, τ_1,Ipc→L10 = 10 ms, τ_2,Ipc→L10 = 1 ms and the cellular parameters were the same as described in the text and Table 1. (h) The synaptic response of an Ipc neuron to a single pre-synaptic action potential. The synaptic parameters were g_L10→Ipc = 5.2 nS, τ_1,L10→Ipc = 5.6 ms, τ_2,L10→Ipc = 0.3 ms, and the cellular parameters were the same as described in the text and Table 1. The synaptic input caused the Ipc neuron to spike two times in a short period of time. The number of spikes depends on the chosen value of the maximum synaptic conductance.

TABLE 2.

Fitting ISI curves, ISI(t) = A(1 − exp(−t/B)), to calculated ISI points from recorded and simulated spike trains for L10 neurons.

Current (nA)	A (ms)		B (ms)		r2
	Exp	Theo	Exp	Theo	Exp	Theo
0.1	31.53	51.37	22.35	48.57	0.092	0.996
0.15	24.74	30.97	27.13	35.90	0.046	0.998
0.2	22.78	22.11	26.55	29.33	0.089	0.980

The small r² values for the experimental data are due to the large variations of ISI values between cells, which are also reflected in the large SD of the measured firing rates (Fig. 2). The values of A, B and r² for 0.2 nA correspond to Fig. 4(e)

TABLE 3.

Fitting ISI curves, ISI(t) = A(1 − exp(−t/B)), to calculated ISI data points from recorded and simulated spike trains for Ipc neurons.

Current (nA)	A (ms)		B (ms)		r2
	Exp	Theo	Exp	Theo	Exp	Theo
1	17.47	16.68	20.47	27.48	0.36	0.97
0.9	19.36	18.73	20.85	28.56	0.25	0.97
0.8	22.62	21.37	22.04	30.15	0.25	0.96
0.7	27.22	24.84	24.21	31.94	0.24	0.96
0.6	32.44	28.68	29.55	34.68	0.15	0.95
0.5	42.67	36.82	33.81	38.30	0.089	0.95
0.4	52.22	48.49	34.09	44.42	0.027	0.91

The small r² values for the experimental data are due to the large variations of ISI values between cells, which are also reflected in the large SD of the measured firing rates (Fig. 2). The values of A, B and r² for 1 nA correspond to Fig. 4(f)

The model contains two types of synapses (Eq. (6) to (8)), each of which is described by 4 parameters. We adopted the synaptic reversal potential from the literature. The L10 → Ipc projection is mediated in part by glutamate receptor subtypes GluR1 or GluR2/3 (Hellmann et al. 2001) and is blocked by CNQX (Marin et al. 2007). Therefore, we assume a standard value of E_L10→Ipc = 0 mV for the synaptic reversal potential of the glutamate receptor channel complex (Koch 1999). Ipc neurons also show a strong somatic staining for the α7 subunit of nicotinic acetylcholine receptors (nAChR) (Britto et al. 1992; Wang et al. 2006). Since the reversal potential for the nAChR channel complex of −5 mV (Koch 1999) is close to the synaptic reversal potential of 0 mV, we did not add the nAChR channel complex as a separate pathway in the model L10 → Ipc projection. Ipc neurons project with dense cholinergic axonal terminals across many tectal layers (Bagnoli et al. 1992; Hellmann et al. 2001; Medina and Reiner 1994; Sorenson et al. 1989; Wang et al. 2006). Therefore, for the Ipc → L10 projection, we assumed E_Ipc→L10 = −5 mV, which is a typical reversal potential for the nAChR channel complex (Koch 1999). The time course of the synaptic conductance change is determined by two time constants (Eq. (7)). For the Ipc model neuron with AMPA synaptic conductances (Hellmann et al. 2001; Marin et al. 2007) typical rise time values, τ_{rise,L10→Ipc} = 0.32 ms, and fall time values, τ_1,L10→Ipc = 5.6 ms, were taken from the literature (Destexhe et al. 1994) and are consistent with the estimates based on our recordings (Fig. 3a). Matching L10 model neuron synaptic response to the recordings (Fig. 3b) led to a synaptic rise time of τ_{rise,Ipc→L10} = 1.1 ms and a fall time of τ_1,Ipc→L10 = 10 ms. With the chosen values for the synaptic time constants, the time courses of the model synaptic responses (Fig. 4(g), (h)) reproduce slow EPSPs in the L10 neuron (Fig. 3(b)) and fast EPSPs in the Ipc neuron (Fig. 3(a)). Note that the maximum synaptic conductance is not constrained by the in vitro measurement. The extracellular stimulation was not limited to single-axon stimulation, rather the number of stimulated synaptic inputs depended on the chosen stimulus current and the position of the stimulus electrode relative to the presynaptic axons.

3.3 Mechanisms of oscillatory bursting in a reciprocally coupled pair of L10 and Ipc model neurons

Armed with the biologically plausible and experimentally constrained description of the cellular and synaptic properties of individual L10 and Ipc model neurons, we next investigated whether a reciprocally coupled pair of neurons (Fig. 5(a)) could generate oscillatory bursting in the Ipc model neuron in response to a plausible representation of a retinal flash of light. Since a brief flash of light generates long-lasting evoked potentials in tectal superficial layers in vivo (Holden 1980; Letelier et al. 2000), we simulated the retinal input by a depolarizing current pulse of 0.2 nA amplitude and 350 ms duration into the L10 model neuron. For the chosen values of a strong L10 → Ipc and a weak Ipc → L10 maximum synaptic conductance, the current injection generates a regular sequence of spikes with an average firing rate of 51 Hz in the L10 model neuron (Fig. 5(b)). Concurrently, the Ipc model neuron responds with a short burst of spikes to every presynaptic L10 spike, thus generating oscillatory bursting in the Ipc model neuron (Fig. 5(c)).

Our model simulation shows that the recorded oscillatory bursts in Ipc neurons in response to a flash of light (Marin et al. 2005) can be mediated by feedforward mechanisms alone. Qualitatively, the following sequence of events causes Ipc oscillatory bursts. The retina and its tectal projection transform a brief flash of light into a long-lasting L10 synaptic current (approximated as an external current input in the model), which in turn causes the L10 neuron to spike. The L10 neuron spike generates a large depolarizing synaptic current in the Ipc neuron. The synaptic current is sufficiently strong to generate a spike and to push the membrane potential repeatedly from the reset value to the threshold for spiking, thus generating a burst of multiple spikes with ISIs of less than 4 ms. A synaptic and a cellular mechanism jointly contribute to the termination of the burst; the short duration of the synaptic current, determined by the synaptic fall time, τ_1,L10→Ipc, and the activation of the spike-rate adaptation current with every Ipc spike. The arrival of the next L10 spike, approximately 20 ms after the previous one in the displayed simulation (Fig. 5(b)), evokes the next burst in the Ipc neuron. Since the L10 neuron responds to the flash-induced long-lasting L10 synaptic current with a regular spike train, the Ipc neuron also responds with a regular sequence of bursts. In short, regular sequences of L10 spikes are transformed into regular sequences of Ipc bursts.

This mechanism of Ipc oscillatory burst generation is valid for the parameter area that represents a strong feedforward L10 → Ipc and a weak feedback Ipc → L10 maximum synaptic conductance (Fig. 5(d)). For reduced L10 → Ipc maximum synaptic conductance, only sequences of Ipc spikes rather than bursts are generated. Interestingly, the Ipc → L10 feedback can render the L10 spike train more irregular, but is not necessary for the Ipc burst generation. Rather, for increased Ipc → L10 feedback maximum synaptic conductance, the two neurons excite each other continuously and the system transitions into a diverging regime. Another important parameter is the feedforward synaptic fall time, τ_1,L10→Ipc, which contributes to the termination of the burst. For increasing values of τ_1,L10→Ipc, significant temporal summation of EPSPs occurs in the Ipc neuron, the Ipc spike-rate adaptation is not enough to terminate the bursts, and the system transitions into a diverging regime (Fig. 5(e), (f)). The numerical value of τ_1,L10→Ipc at which the transition to divergence occurs decreases with decreasing ISI of the L10 neuron, which of course depends on the chosen value of the retinal input; 0.2 nA for the simulation results shown in Fig. 5. For decreasing values of the feedforward synaptic fall time, τ_1,L10→Ipc, the time for burst generation is too short and only isolated Ipc spikes occur. Thus, there is a limited range of parameter values for burst generation (Fig. 5(f)). With decreasing τ_1,L10→Ipc values the burst generation becomes more robust to the value of the feedforward maximum synaptic values, g_L10→Ipc.

3.4 A population of L10 and Ipc neurons with spontaneous activity

Does the mechanism of oscillatory bursting in a reciprocally coupled pair of L10 and Ipc model neurons extend to populations of neurons? Because of the finite width of the L10→Ipc projection (Wang et al. 2006), an Ipc neuron, embedded within the isthmo-tectal system, receives synaptic inputs from more than one L10 neuron. Further, because of the high level of spontaneous activity (Maczko et al. 2006; Sherk 1979), the Ipc neuron may receive uncorrelated inputs at such a high frequency that it will spike tonically, not burst. This raises an important question: Under what conditions does this simple mechanism of oscillatory burst generation break down in a population of L10 and Ipc neurons with spontaneous activity when each Ipc neuron receives inputs from many L10 neurons?

To address this question we investigated a population model of L10 and Ipc neurons with topographic reciprocal excitation (Fig. 6(a)) and spontaneous activity. Important model parameters are the widths, Δ_L10→Ipc and Δ_Ipc→L10, of the projections, which determine the strength of synaptic inputs from other neurons, and the standard deviations, σ_e, σ_L10 and σ_Ipc, of the noise currents, which determine the uncorrelated activity of neurons. For a set of parameters within the bursting regime, a stimulus current step delivered to a group of L10 neurons (centered around L10 neuron #200) generates oscillatory bursts in Ipc neuron #200 (Fig. 6(b)). Because of the width and the strength of the L10 → Ipc projection, the spiking activity spreads to numerous Ipc neurons beyond the group of Ipc neurons that correspond to the topographic projection of the directly stimulated group of L10 neurons. In contrast, the feedback projection, Ipc → L10, of the same width, is too weak to generate L10 spikes beyond the group of directly stimulated L10 neurons. The feedback projection does however cause dispersion in the timing of L10 spikes, i.e., because of the larger summation of excitatory feedback, L10 neurons in the center spike earlier than L10 neurons away from the center. The uncorrelated L10 activity introduces variability in the Ipc burst duration.

For narrow feedback, i.e., Δ_Ipc→L10 is small, the number of correlated L10 inputs to an Ipc neuron increases with increasing width, Δ_L10→Ipc, of the feedforward projection and thus the Ipc neuron generates more bursts rather than isolated spikes (Fig. 6(c)). However, for broad feedback, L10 spike trains from neurons away from the center are less correlated. Thus, with increasing width of the feedforward projection, Ipc burst generation increases only over a narrow range then the Ipc activity diverges. In this parameter region, the adaptation current is not sufficient to prevent the system from diverging.

Because of the strong feedforward synapse, Ipc burst generation is very sensitive to uncorrelated noise in L10 neurons. The mechanism of feedforward burst generation breaks down when the value of the standard deviations, σ_e or σ_L10, of the noise currents approach the chosen mean value, 0.18 nA, of the stimulus current (Fig. 6(d) and (e)). Because of the weak feedback connection and suppressive effect of adaptation current, Ipc burst generation is much less sensitive to uncorrelated noise current into Ipc neurons (Fig. 6(f)).

In contrast, Ipc burst generation is less sensitive to noise in L10 neurons when the noise is correlated. Because of common inputs to adjacent L10 neurons, noise correlations in the L10 input currents are likely to exist. Given the potential importance of noise correlations for burst generation and stimulus representation in sensory systems (Chacron and Bastian 2008), we investigated the role of noise correlations in the isthmo-tectal system. We simulated the population model with correlated noise, η_e,i, in the external current input, I_e,i = (I₀ + η_e,i), to the subset of L10 neurons, labeled i=160 to i= 240. The noise correlation in the external current input to two L10 neurons, i and i′, decreases with distance as described by $\langle {\eta }_{e,i}(t){\eta }_{e,i^{\prime }}(t^{\prime })\rangle ={2\sigma }_e^{2}exp(-\mid i-i^{\prime }\mid /\lambda )\delta (t-t^{\prime })$, where λ represents a correlation length (Abbott and Dayan 1999). In the limit of λ → 0, we recover the case of uncorrelated noise, $\langle {\eta }_{e,i}(t){\eta }_{e,i^{\prime }}(t^{\prime })\rangle ={2\sigma }_e^2\delta (t-t^{\prime }){\delta }_{{ii}^{\prime }}$. It is instructive to start the simulation with uncorrelated noise with a large standard deviation, σ_e = 0.2 nA, comparable to the value of the constant component, I₀. In this case, L10 neurons produce largely uncorrelated spike trains and Ipc neurons do not burst (burst score below 0.3; Fig. 6(d)). However, with increasing noise correlation, spike trains of stimulated L10 neurons become more correlated and Ipc bursting resumes. For instance, with a correlation length of λ= 30 the burst score reaches 0.9 (Supplementary Fig. 2).

The Ipc spike-rate adaptation conductance is determined by the decay time constant, τ_sra,Ipc, and the conductance increment, Δg_sra,Ipc. Interestingly, the two-dimensional parameter space reveals a narrow region for Ipc burst generation (Fig. 6(g)). For the conductance increment decreasing from this region, the Ipc neuron activity diverges as expected, since spike-rate adaptation is the only activity-dependent regulatory mechanism in this network of reciprocal excitation. For the conductance increment increasing from this region, the Ipc neuron produces isolated spikes, rather than bursts, to synaptic inputs. Similarly, Ipc activity diverges with decreasing decay time constant and transitions to tonic spiking when the time constant increases.

Since some Ipc recordings displayed a spike after-depolarization (ADP) and since in general ADPs can provide a mechanism for bursting (Higgs and Spain 2009), the potential role of ADPs in the case of Ipc bursting was evaluated. We implemented ADPs in the Ipc model neuron using a simple formalism (Doiron et al. 2007), where each Ipc spike triggers a delayed depolarizing current (see Sec. 2.3). Simulation results with the ADP included indicate that the ADP is not necessary for Ipc burst generation; however the ADP slightly enlarges the region of parameter space for burst generation (Supplementary Fig. 3) compared to Ipc model neurons without ADPs (Fig. 6(g)).

4 DISCUSSION

We measured the cellular and synaptic properties of avian L10 and Ipc neurons in vitro. We found regular spiking neurons with spike-rate adaptation. We also found reciprocal excitation, with a strong and brief feedforward L10 → Ipc and a weak and long-lasting feedback Ipc → L10 synaptic conductance change. Our simulation of an experimentally constrained excitatory neural network reveals that Ipc oscillatory burst generation in response to simulated retinal inputs to L10 neurons can be mediated by regular L10 neuron spiking combined with Ipc burst responses to an L10 spike. The mechanism requires a strong and brief feedforward synaptic conductance change and is aided by Ipc spike-rate adaptation. The measured weak and long-lasting feedback synaptic conductance change is not necessary for Ipc oscillatory burst generation. Increasing components of uncorrelated Ipc inputs force a transition from oscillatory bursting to irregular tonic spiking.

4.1 Excitatory neural networks with adaptation

The mechanisms of oscillatory burst generation typically have in common a fast excitatory current causing a train of spikes and an activity-dependent slow inhibitory current that interrupts the spike train (Izhikevich 2007; Marder and Calabrese 1996). However, purely excitatory neural networks can produce oscillatory bursts as well (Feller 1999; O’Donovan 1999; Smith et al. 1991). In these networks, recurrent excitation mediates episodes of activity, which is terminated by activity-dependent depression or adaptation (Hansel et al. 1995; Nesse et al. 2008; Tabak et al. 2000; Tabak and Rinzel 2005; Van Vreeswijk and Hansel 2001; Vladimirski et al. 2008) rather than inhibitory synaptic currents.

Adaptation affords a rich repertoire of neurophysiological effects (Kohn 2007). Our model simulations indicate that the Ipc spike-rate adaptation current plays an important role in terminating the burst. The oscillatory bursts in Ipc neurons are evoked by the strong projection from periodically firing L10 neurons. Without the adaptation current, the burst duration is largely determined by the synaptic fall time,τ_1,L10→Ipc. For increasing values of τ_1,L10→Ipc, a small increase in maximum synaptic conductance, g_L10→Ipc and g_Ipc→L10, would push the system from bursting to diverging. In contrast, when the Ipc spike-rate adaptation current is present, it provides an activity-dependent negative feedback that terminates the bursts after a few spikes. Ipc spike-rate adaptation thus enlarges the volume for bursting in the three-dimensional parameter space (Fig. 5(d), (e), (f)). Two parameters, the decay time constant, τ_sra,Ipc, and the conductance increment, Δg_sra,Ipc, specify the Ipc spike-rate adaptation conductance. The population model investigation reveals a narrow area for bursting in this two-dimensional parameter space (Fig. 6(g)).

Spike-rate adaptation is often mediated by potassium currents with slow inactivation (Brown et al. 1990; Brownstone 2006; Lewis et al. 1986; Storm 1990). In the phenomenological description chosen for our model, the parameter values for the spike-rate adaptation (Table 1) are experimentally constrained by the measured F (I) and ISI (t) curves (Fig. 4). The fact that the ISI (t) curves for model and real neurons are well matched for all current injection values considered (Fig. 4(e), (f) and Table 2, 3), indicates that the leaky integrate-and-fire model provides a good approximation for the real L10 and Ipc neurons.

4.2 Brief feedforward synaptic conductance changes

Even with the experimentally constrained spike-rate adaptation included, oscillatory burst generation requires the synaptic fall time, τ_1,L10→Ipc, to be well below 100 ms (Fig. 5(e), (f)). With increasing synaptic fall times the excitatory synaptic potentials in the Ipc neuron sum. As a result the system activity transits into the diverging regime even for small synaptic conductances. This model result is consistent with the observation that the L10 → Ipc projection is mediated by AMPA-type glutamate receptors (Hellmann et al 2001; Marin et al. 2007) and possibly by nicotinic acetylcholine receptors (Britto et al. 1992; Wang et al. 2006); both of which have the required short synaptic fall times (Destexhe et al. 1994).

4.3 Neuronal noise produces variable burst durations

The consequences of neuronal noise and correlations on the integrative properties of neural systems have received increasing attention in recent years (Averbeck et al. 2006; Chance et al. 2002; Destexhe and Contreras 2006; Destexhe and Rudolph 2009; Fox et al. 2006; Wolfart et al. 2005). Ipc bursts in vivo have variable burst durations (Marin et al. 2005). Our population model provides a simple explanation. Uncorrelated L10 activities, mediated by noise currents, add variability to the Ipc burst duration (Fig. 6(b)). With increasing noise levels the Ipc response transitions from bursting to irregular spiking (Fig. 6(d), (e)). Because of the weak feedback connection and the suppressive effect of adaptation current, the mechanism of Ipc burst generation is less sensitive to noise currents into Ipc neurons (Fig. 6(f)).

4.4 The cholinergic feedback is weak

We recorded a slow and long-lasting Ipc → L10 synaptic potential change (Fig. 3(b)). This observation is consistent with, but does not test, the previously-discussed hypothesis that the cholinergic feedback to the optic tectum might be mediated by a paracrine mode of synaptic transmission (Gruberg et al. 1994; Sargent et al. 1989; Sereno and Ulinski 1987; Wang et al. 2006).

Our model simulations indicate that the Ipc → L10 feedback is not necessary for the Ipc oscillatory burst generation (Fig. 5(d)). However, these model results can not exclude the possibility that feedback may contribute to the oscillatory burst generation in vivo via mechanisms not included in the simple model. For instance, cholinergic feedback may control the excitability (Kawai et al. 2007) of RGC axons, the calcium influx into RGC axon terminals (Dudkin and Gruberg 2003) and thus synaptic transmission, or may activate GABAergic tectal circuits (Luksch and Golz 2003) with potentially inhibitory effect on L10 neurons.

Feedback in our model can affect the oscillatory burst pattern. With increasing feedback strength the L10 spike train pattern, and thus the Ipc oscillatory burst pattern, becomes more irregular. Interestingly, the related concept of spike-triggered feedback currents has previously been included in leaky integrate-and-fire models to provide more realistic model responses (Jolivet et al. 2004; Paninski et al. 2004 Pillow et al. 2005).

When the Ipc → L10 feedback increases above a critical value, the L10 and Ipc neuron excite each other continuously and the system transitions into a diverging regime (Fig. 5(d)). The latter observation is consistent with the ‘no-strong-loops hypothesis’ (Crick and Koch 1998), which states that a strong excitatory loop formed between two cortical areas would lead the system into uncontrolled oscillations (Schnitzler and Gross 2005).

Although the Ipc → L10 feedback is apparently weak and is not required for the oscillatory burst generation, cholinergic feedback is involved in tectal visual processing. For instance, cholinergic feedback enhances calcium influx into optic nerve fiber terminals in frog (Dudkin and Gruberg 2003) and inactivation of cholinergic feedback prevents visual responses in the ascending visual pathway to the nucleus rotundus in birds (Marin et al. 2007). Bursts facilitate synaptic transmission across unreliable synapses via increased transmitter release (Izhikevich et al. 2003; Lisman 1997; Sherman 2001). We expect this effect to be significant for paracrine transmission in the cholinergic feedback as well. In conclusion, delivering the cholinergic feedback via oscillatory bursting Ipc axon terminals in the tectum is likely to be of great importance for the population coding of visual information in the intricate retino-tecto-rotundal pathway (Khanbabaie et al. 2007; Luksch et al. 1998, 2001, 2004; Mahani et al. 2006; Marin et al. 2003).