Summary
Automatic modeling methods using cryo-electron microscopy (cryoEM) density maps as constrains are promising approaches to building atomic models of individual proteins or protein domains. However, their application to large macromolecular assemblies has not been possible largely due to computational limitations inherent to such unsupervised methods. Here we describe a new method, EM-IMO, for building, modifying and refining local structures of protein models using cryoEM maps as a constraint. As a supervised refinement method, EM-IMO allows users to specify parameters derived from inspections, so as to guide, and as a consequence, significantly speed up the refinement. An EM-IMO-based refinement protocol is first benchmarked on a data set of 50 homology models using simulated density maps. A multi-scale refinement strategy that combines EM-IMO-based and molecular dynamics (MD)-based refinement is then applied to build backbone models for the seven conformers of the five capsid proteins in our near-atomic resolution cryoEM map of the grass carp reovirus (GCRV) virion, a member of the aquareovirus genus of the Reoviridae family. The refined models allow us to reconstruct a backbone model of the entire GCRV capsid and provide valuable functional insights that are described in the accompanying publication. Our study demonstrates that the integrated use of homology modeling and a multi-scale refinement protocol that combines supervised and automated structure refinement offers a practical strategy for building atomic models based on medium- to high-resolution cryoEM density maps.
Keywords: cryo-electron microscopy, density fitting, homology modeling, structure refinement, protein structure prediction
Introduction
Macromolecular assemblies that consist of tens to hundreds of components play crucial roles in most biological processes. Due to the difficulties in applying X-ray crystallography and NMR spectroscopy to the structure determination of such large assemblies, cryo-electron microscopy (cryoEM) has become increasingly important in structural biology.1-3 Recent advances in cryoEM techniques have made it possible to determine the three-dimensional (3D) structures of macromolecular assemblies to near-atomic resolution.4-6 However, in most cases, cryoEM maps are still limited in resolution and cannot be used directly to build models. In some cases, the atomic structures of individual components of the macromolecular assembly are known and can be fitted into the cryoEM map of the assembly to produce a “pseudo-atomic” model for the entire assembly. It has been suggested that the precision of such models can be better by several fold than the nominal experimental resolution.7,8 In principle, both experimentally determined structures9,10 and homology models11 can be used in the cryoEM fitting procedure. Programs based on different fitting techniques are available for this purpose.12-19
A variety of approaches have been developed for the refinement of structures once they have been fitted into cryoEM maps. These include real-space refinement methods10,20-23 that were originally developed in X-ray crystallography, normal mode analysis (NMA)-based methods that are particularly useful for function-related conformational changes24-26 and methods that exploit structure prediction tools.27-33 Recently, two gradient-based refinement methods were introduced: a heuristic optimization that combines Monte Carlo search, energy minimization and rigid-body molecular dynamics34 and standard molecular dynamics which uses the cryoEM map as a component of the force field (MDFF).35 Most methods developed so far were validated using simulated data and then used in a small number of applications. For example, the Moulder-EM protocol of Topf et al27 was benchmarked on 20 homology models using simulated maps and then applied to the refinement of a homology model built for the upper domain of the P8 capsid protein of rice dwarf virus (RDV) within a 6.8Å-resolution cryoEM map. An improvement of RMSD from 8.7 to 5.3 Å was reported. More recently, Topf et al34 applied their gradient-based method, Flex-EM, to the refinement of the GroEL monomer and EF-Tu within previously determined medium-resolution maps. For both proteins, the refined structures were significantly more accurate than the initial models in terms of Cα RMSD. The GroEL monomer together with Poliovirus 135S cell entry intermediate, for which a 8.7Å-resolution map has been determined, was used in the validation of S-flexfit by Carazo and coworkers,29 while RDV P8 and GroEL were used in a recent study to test the performance of the modified Rosetta program in refining protein structures constrained by low-resolution density maps.33
To date the primary focus of methodological developments has been a global, brute-force refinement approach of an entire structure, which avoids human input or intervention in the refinement process. However, discrepancies between the model and the map are often localized to certain regions of the structure and can be readily recognized through visual inspection. Moreover, when homology modeling is used to generate initial models, uncertainties in alignment as well as genuine structural differences between the protein and the template will inevitably lead to errors in the initial model that are difficult to identify, or to fix, with automated, global refinement procedures. More importantly, since unsupervised, automatic refinement methods are based on brute-force search of conformational space, they can generate numerous intermediate models and waste significant computation time to regions where there is already a good agreement between the experimental structure and the initial model. The computation time of such approaches is often prohibitively long, making it impractical for applications in modeling large assemblies. Indeed, to date, none of these unsupervised methods has been reported to successfully build a structural model for an entire macromolecular assembly.
In order to address these issues, we report a supervised method that combines automated refinement with input obtained from human inspection. Rather than embark at the outset on global refinement, which can degrade some regions of a structure so as to refine others, we first carry out local refinement only on problematic regions of a model that have been identified, through visual inspection, as not fitting well into the cryoEM density map. This new local refinement method, termed EM-IMO, also incorporates a technique that searches for low-energy conformations of protein segments containing rigid secondary structure elements connected by flexible loops (the Iterative Modular Optimization – IMO procedure).36 Iterative refinement of different local regions that deviate from the density map is carried out with the EM-IMO method until a matching between the cryoEM map and the model of the entire molecule is achieved as indicated by the convergence of cryoEM density fitting score. As a final step, the MD-based refinement method (MDFF)35 is applied to further adjust structural details of the model.
Following validation using simulated maps, the utility of the full refinement approach in real applications is demonstrated by applying it to the model building of the grass carp reovirus (GCRV) virion based on a near-atomic resolution cryoEM reconstruction. We have derived backbone models for the seven conformers of the five capsid proteins of GCRV. Initial models were constructed from homologous proteins from mammalian Reovirus (MRV),37,38 which share sequence identities with GCRV proteins ranging from only 14 to 31%39. Refinement against our cryoEM maps yielded significant improvements in these models and has allowed us to reconstruct a full model for the entire GCRV capsid, thus providing the first high-resolution description of molecular interactions among the over 1000 molecules in this enormous macromolecular machine.
Results
In this section, we first evaluate the performance of the EM-IMO-based refinement protocol (See detailed implementation of the protocol in Materials and Methods) using a set of CASP models and simulated maps. We then describe the application of the method to building a backbone model for the entire GCRV virion using our experimentally determined cryoEM map at near-atomic resolution. For GCRV proteins, our refinement approach involves: initial construction of homology models and their fitting into cryoEM maps; application of a refinement protocol that employs EM-IMO as its core component in the iterative refinement of local regions so as to generate a high-quality model; application of an MD-based method35 that derives energy and gradients from the cryoEM map to further refine the structural details.
Overall performance on the CASP data set
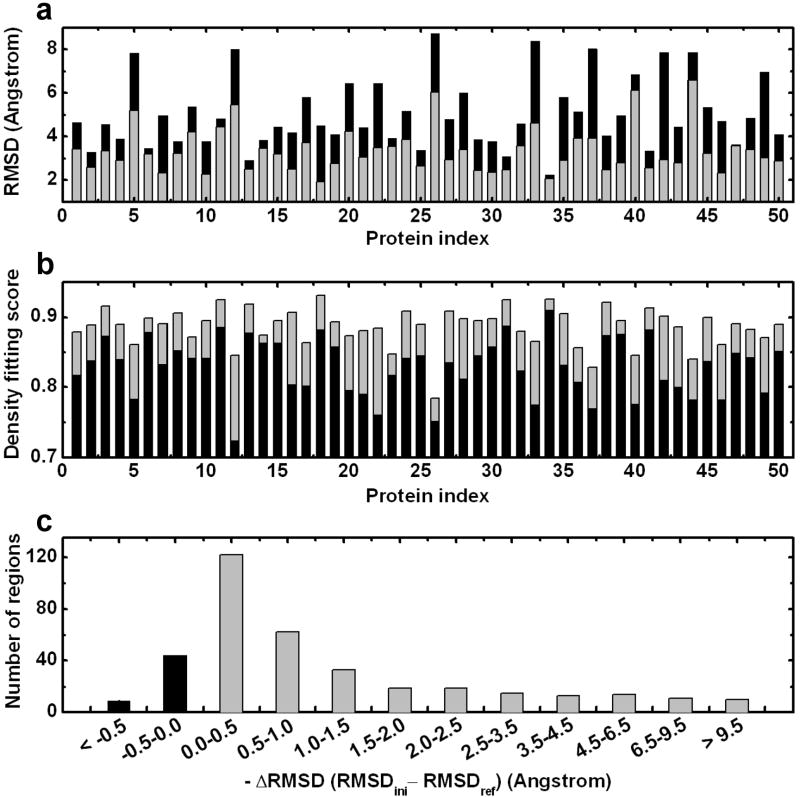
We first tested the robustness of the EM-IMO-based refinement protocol using simulated density maps from the CASP data set. The results obtained at a simulated resolution of 7 Å, which is typical for medium-resolution cryoEM maps, are used to illustrate the overall performance of the method. As can be seen in Fig. 1a, for each of the 50 proteins the backbone RMSD was reduced after one iteration of refinement, giving an average improvement of 1.7 Å. For 36 proteins the RMSD of the final model was at least 1.0 Å lower than that of the starting model. In 13 cases where the starting model was more than 5.0 Å away from the native structure, the RMSD was improved by an average of 2.5 Å. As shown in Fig. 1b, the density fitting score measured by cross-correlation coefficient (CCC) was improved by an average of 0.057. In Fig. 1c the distribution of the 371 regions that were refined using EM-IMO is plotted against the RMSD change during refinement. For 85% of the regions, the local RMSD decreased after refinement by an average of 1.5 Å. For 92% of the regions, the CCC increased after refinement, with an average improvement of 0.009. EM-IMO was found to be very effective in refining secondary structure elements (SSEs) within cryoEM maps. For 125 cases where α-helices were remodeled, the average RMSD improvement was 2.0 Å. For 25 cases where β-sheets were refined by applying distance restraints, RMSD was improved on average by 2.5 Å. For 6 cases where the positional restraint was applied, the RMSD was improved by 3.8 Å. For the remainder of the cases where no SSE change or restraint was applied, the average RMSD improvement was 1.1 Å. Further, the size of the locally refined regions ranges from 4 to 71 amino acid residues with an average size of 19 residues and we found the region size had little effect on the effectiveness of the refinement. Overall, the refinement was very effective in improving the structural quality and density fitting both globally and locally. For T0159, T0217, T0293, T0345 and T0370, whose RMSD remained above 5 Å after one iteration of refinement, a second iteration was carried out. This resulted in an improvement in RMSD by an average of 1.7 Å, suggesting that additional iterations, as implemented in the EM-IMO-based protocol, would further improve the structures.
Figure 1.
Performance of EM-IMO-based refinement protocol on 50 CASP proteins using simulated density maps. (a) Backbone RMSD (N, Cα and C) of the homology model with respect to the experimental structure before (in black) and after (in grey) one iteration of refinement using the EM-IMO-based protocol. (b) Density fitting score of the homology model before (in black) and after (in grey) refinement. (C) Distribution of 371 regions against the RMSD change during refinement.
The effect of the cryoEM density constraint was investigated by comparing the results of applying different weighting factors (w1) to the cryoEM term in the scoring function. Overall the performance reaches a plateau when w1 is between 4.0 and 8.0 with a value of 8.0 giving the best results. Since the DFIRE40 score is normalized and the density fitting score is scaleless, the optimal ratio between two terms, w1, once determined, should be transferable between systems of different size. The effect of map resolution was investigated by performing the refinement under two other conditions, one using maps simulated at a resolution of 4 Å and the other at 10 Å, which covers the range for which cryoEM maps can provide meaningful constraints for refining atomic models. Although the best performance was obtained at a resolution of 7 Å, the refinement appeared not to be sensitive to the resolution. At 7 Å the global RMSD was improved for all 50 models with an average improvement of 1.7 Å, while at 4 and 10 Å, a total of 46 and 49 models were refined with an average RMSD change of 1.3 and 1.6 Å, respectively. In terms of local RMSD, 85%, 86% and 83% of the 371 regions were improved after refinement with an average RMSD change of 1.3, 1.5 and 1.4 Å at resolutions of 4, 7 and 10 Å, respectively. We speculate that the high-resolution maps, although providing more constraints, require precise positioning of atoms into their densities. As a result, more trial conformations need to be sampled to yield a notable increase in the density fitting score. This explains why using the same number of conformations in sampling, the refinement performance at 4 Å results in slightly degraded performance compared to 7 Å. Overall, our results on the CASP data set indicate that EM-IMO can be applied to cryoEM maps with a broad range of resolutions.
Two examples of EM-IMO refinement from the CASP data set
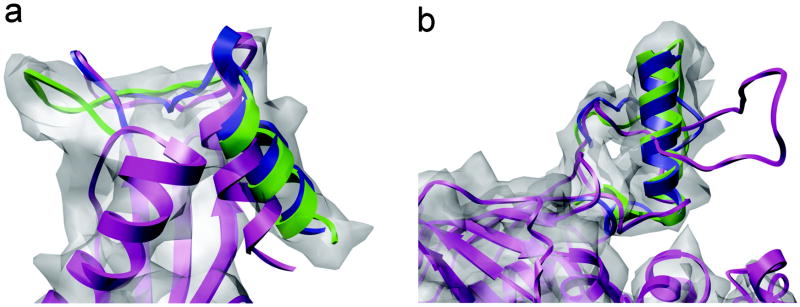
Fig. 2 illustrates two simple but typical scenarios in cryoEM refinement. As shown in Fig. 2a, the C-terminal helix in the original homology model (in magenta) of T0132 deviates from a cylindrically shaped density, which is characteristic of helical structures. In order to move the helix, residues 138-151, into its corresponding density, an adjacent loop, residues 125-137, was used as the driver region during refinement. After 10 cycles of EM-IMO refinement, the helix moved into the cylindrical density (in blue) and overlapped well with the crystal structure (in green). For the entire region, the local RMSD was reduced from 4.6 to 3.9 Å while the CCC increased from 0.817 to 0.839. The 3.9 Å RMSD reflects errors in the loop region, which can be refined afterwards if desired. As will be shown later for the GCRV protein, the simple strategy illustrated here can be applied to the refinement of large terminal domains with hundreds of residues.
Figure 2.
Two examples of EM-IMO refinement from the CASP data set using density maps simulated at 7 Å. (a) C-terminus of T0132 (125-151). (b) Segment of T0298 (159-197) with a missing helix (165-179). The initial model is shown in magenta, while the refined region is shown in blue and the native structure in green.
A second example is shown in Fig. 2b, where a 16-residue α-helix in T0298 appears as a random loop in the homology model, which was constructed using a template with a sequence identity of 21.4%. However, secondary structure prediction by PSIPRED41 clearly indicates a helix in this region, although the predicted helix length is slightly shorter than in the actual structure. After visual inspection, a 39-residue length segment was identified for refinement. The region, residues 165-179, was specified as a helix according to PSIPRED and was treated as a rigid body during refinement. For the helical region, the backbone dihedral angles ϕ and φ were set to the helical angles of 65° and 40°, respectively. During 20 EM-IMO cycles the step size of local sampling decreased from 25 to 5° and in this process a helix with standard geometry was built and then fitted into the density map through extensive search. After refinement, the local RMSD was reduced from 13.0 to 2.7 Å with an accompanying increase of CCC from 0.812 to 0.855. This example bears general implications for refining homology models within cryoEM maps, because secondary structure elements in a homology model often differ in length, position and orientation from the actual structure. In the most extreme case, an entire secondary structure element can be missing. To deal with such problems, a refinement method should be capable of not only searching for the optimal fit of an existing secondary structure element in the cryoEM map but also building and modifying their structures during refinement.
Model construction of GCRV virion
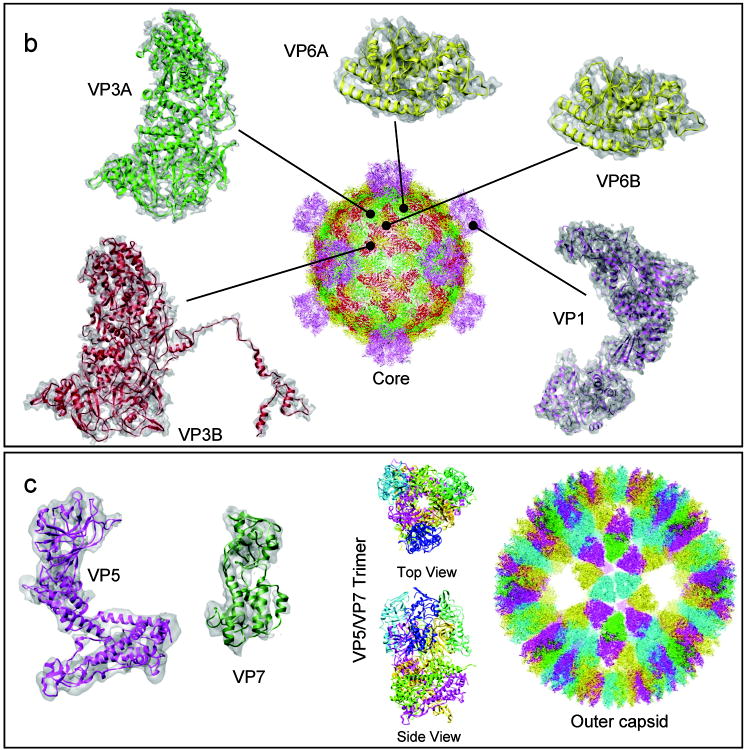
In order to build a backbone model for the entire GCRV virion, homology models for GCRV proteins were first constructed from corresponding Reovirus templates.37,38 Then, the homology models were subjected to five iterations of refinement using the EM-IMO-based protocol. Table 1 lists the information used in the homology modeling and structure refinement of all GCRV proteins along with the results after refinement. The refined models of the seven conformers of the five GCRV proteins are shown superimposed with their cryoEM maps in Fig. 3. The details of these structures and their structural and functional roles in GCRV assembly are presented in a companion paper by Cheng et al. Briefly, our GCRV capsid structure is composed of 1500 protein molecules organized into two layers: a turreted core enclosed by an outer capsid shell. The core consists of three proteins, VP1, VP3 and VP6 (Fig. 3a). 120 copies of VP3 in two distinct conformations (VP3A and VP3B) form a complete icosahedral shell, which is stabilized by 120 copies of the clamping protein, VP6, also in two distinctive conformations (VP6A and VP6B). 12 turret pentamers of VP1 project from this shell (Fig. 3a, center). Each outer shell is made up of 200 trimers of VP5/VP7 dimers (Fig. 3b), in which VP5 is the membrane-penetration protein and VP7 is the protector protein. Striking differences were observed between different conformers of the same protein (c.f. VP3A and VP3B in Fig. 3a), which could have not been predicted using the sequence-based homology modeling technique alone. The biological implications of such conformational differences are described in the companion paper by Cheng et al. Below, we provide examples of GCRV protein structures to illustrate applications of EM-IMO refinement to various scenarios that might be encountered in other applications. In particular, we focus on scenarios that involve domain movement and complications caused by errors in homology modeling. These examples shall offer general guidelines for cryoEM-constrained model building and refinement of proteins.
Table 1.
Homology modeling and structure refinement of grass carp reovirus (GCRV) proteins. a
| Target | Template | Chain ID | SEQID (%) | NRES b | NREG | CCCini | CCCref-mod | CCCref-mdff | ΔRMSD |
|---|---|---|---|---|---|---|---|---|---|
| Virus core | |||||||||
| VP3A | λ1A | B | 29.3 | 1027 | 29 – 42 | 0.441 | 0.485 | 0.507 | 1.78 |
| VP3B | λ1B | C | 31.3 | 1196 | 22 – 50 | 0.402 | 0.476 | 0.497 | 4.32 |
| VP6A | σ2-i | D | 19.9 | 412 | 9 – 19 | 0.467 | 0.524 | 0.552 | 2.19 |
| VP6B | σ2-ii | E | 19.9 | 412 | 8 – 18 | 0.480 | 0.541 | 0.567 | 2.53 |
| VP1 | λ2 | A | 27.3 | 1299 | 51 – 59 | 0.439 | 0.540 | 0.568 | 5.72 |
| Membrane-penetration complex | |||||||||
| VP5 | μ1 | A, B | 25.3 | 639 | 18 – 25 | 0.356 | 0.429 | 0.448 | 3.47 |
| VP7 | σ3 | G | 14.9 | 276 | 11 – 15 | 0.343 | 0.526 | 0.563 | 10.84 |
The information used in the homology modeling and structure refinement of GCRV proteins are listed together with the results from five iterations of EM-IMO-based refinement and MDFF refinement. Target and Template refer to the names of GCRV proteins and MRV proteins, respectively. Chain ID refers to the chain identifiers of the template structures as they appear in the PDB files (1EJ6 and 1JMU). SEQID (%) is the sequence identity between target and template. NRES is the number of residues in the initial model. NREG is the number of problematic regions identified for the EM-IMO refinement. CCCini, CCCref-mod, and CCCref-mdff refer to the density fitting scores of the initial model, the model refined using the EM-IMO-based protocol, and the final model after the MDFF refinement. ΔRMSD is the Cα RMSD between initial model and final model.
The regions that cannot be recognized from the cryoEM map were not included in the refinement. Specifically, the first 187 residues in VP3A, the first 18 residues in VP3B, and the first 9 residues in VP5 were removed from the initial models.
Figure 3.
Near-atomic resolution cryoEM map of GCRV virion and the seven refined backbone models of all five GCRV structural proteins present in the virion. (a) Protein structures of the core. Five distinct structures/conformers of the three core proteins (two conformers of VP3: VP3A and VP3B; two conformers of the clamping protein VP6: VP6A and VP6B; and turret protein VP1) exist in inner capsid core. The cryoEM density is shown in semi-transparently gray and the final refined model is shown in ribbon. The full model of the core is shown in the center with each of the seven unique protein structures shown in a different color. (b) Proteins of the outer shell. The outer shell is made up of trimers of VP5/VP7 dimer. On the left two panels are the cryoEM density maps of VP7 and VP5 (semi-transparently gray) superimposed with the final refined models shown in ribbon. Top and side views of the ribbon model of the trimer are shown in the middle. The full model of the outer shell is shown at the right with each of the seven unique protein structures shown in a different color.
Scenario 1: Local regions that deviate from the density map
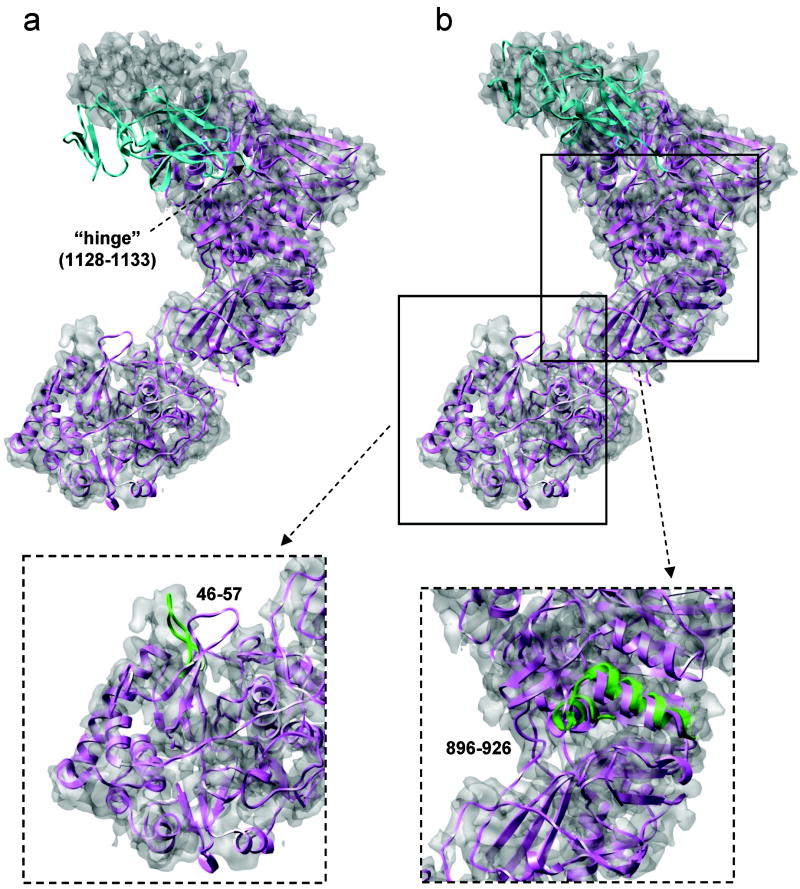
Local structural deviation is the simplest and also most common scenario encountered in EM-IMO refinement. In such scenario, such as VP3A, VP6A and VP6B, the overall structure of the homology models fits the cryoEM map, local regions that deviate from the cryoEM map are the main problems to be dealt with during refinement. In general, regions such as secondary structure elements and loops that differ from the density map after fitting were identified with visual inspection and refined using the EM-IMO method. Several examples of local refinement are shown for VP1 (Fig. 4, inserted figures) and VP5 (Fig. 5, inserted figures). For example, the loop 46-57 in the initial model of VP1 is completely outside the density but fits into the density after a thorough EM-IMO refinement. Similar result can be found for the region 896-926, where two helices move as rigid bodies during EM-IMO refinement.
Figure 4.
Refinement of the VP1 C-terminal domain (1128-1299). (a) Initial homology model. (b) Homology model after a short EM-IMO refinement of the head domain. In a and b the protein body is shown in magenta and the C-terminal domain in cyan. Two inserted figures show the EM-IMO refinement for a loop region (46-57) and a double-helical region (896-926), with the refined structure in green.
Figure 5.
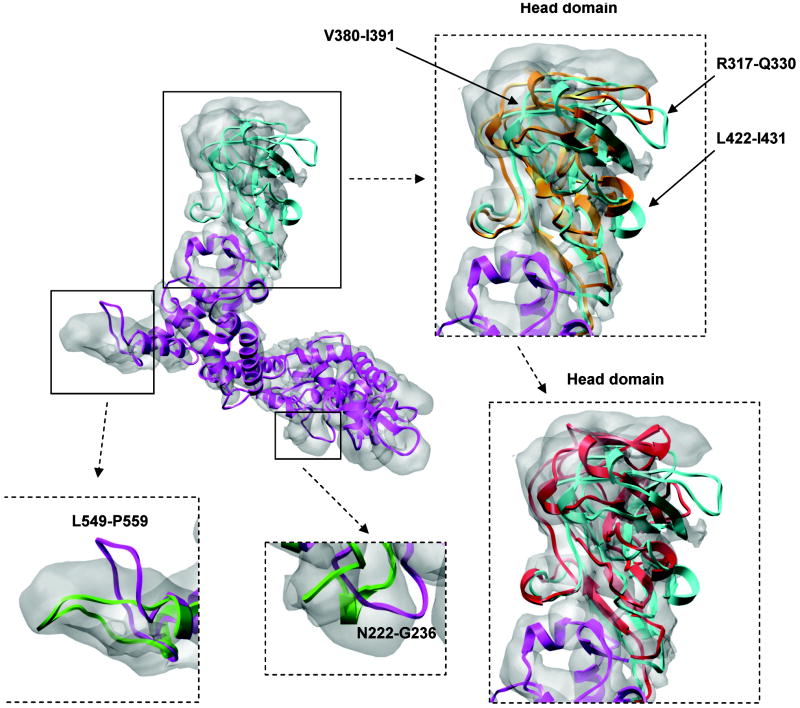
Refinement of the VP5 head domain (287-473). Initial homology model (up-left corner) is in magenta and the head domain is marked in cyan. Two inserted figures on the right show the head domain after a single EM-IMO refinement (in orange) and after the subsequent 5 iterations of refinement using the EM-IMO-based protocol (in red). Two inserted figures on the bottom show the EM-IMO refinement for loop regions 222-236 and 549-559, with the refined structure in green.
Scenario 2: Terminal domains that deviate from the map
Often, a terminal region or domain of a protein undergoes a rigid-body type of movement as compared to the homology model, as is the case for VP1. After fitting the homology model into the cryoEM map, the C-terminal domain of VP1, consisting of a total of 172 residues, was found to adopt a different conformation compared to that of the MRV λ2 structure, as shown in Fig. 4a. Thus, prior to detailed local refinement of the VP1 model, a region consisting of 6 residues (1128 to 1133) was used as a “hinge” to move the C-terminal domain, which was treated as rigid body during refinement. The same parameters used in the refinement of C-terminal helix of T0132 (Fig. 2a) were used to refine the C-terminal domain of VP1. After 5 cycles of EM-IMO refinement, the density fitting score (See Materials and Methods) was improved from 0.439 to 0.484. As shown in Fig. 4b, the refined structure of the C-terminal domain agrees with the cryoEM map.
Scenario 3: Mid-chain domains that deviate from the map
A more difficult scenario in domain refinement is when the discrepancies between the homology model and the experimental map involve a domain located in the middle of the protein chain and refinement requires that the orientation of this domain with respect to other domains be altered. Such an example can be found in the refinement of VP5. After fitting the template structure, μ1, into the VP5 map, we found that a large portion of the head domain was outside the density as shown in Fig. 5, suggesting that VP5 may adopt a conformation different from that of μ1. A comparison between the VP5 model and the density map revealed further detail: the entire head domain shifts slightly from the density and a number of regions within the domain also move relative to each other.
Similar to the case of VP1, the head domain of VP5 was moved into the density prior to any detailed refinement. However, for VP5 we adopted a more complex refinement protocol due to the intra-domain movement. Specifically, the head domain 287-473 was divided into seven rigid-body segments connected by flexible linkers. During 10 cycles of EM-IMO refinement, the step size of local sampling decreased from 5 to 1° in order to gently adjust the position of the head domain and the rigid-body segments within. After refinement, the density fitting score was improved from 0.356 to 0.376 and the structure of the head domain became more consistent with the density map. This can be seen from two turn regions 317-330 and 422-431, which both are largely exposed in the initial model but now only require minor adjustment to fit in the corresponding density.
After domain refinement, the VP1 model was relaxed within the cryoEM map using the EM-IMO-based protocol. During the five iterations of refinement, 18 to 25 regions were identified through visual inspection and refined using the EM-IMO method. The density fitting score of the final model is 0.4291, which is 7.5% higher than that of the initial model, indicating a significantly better fit of the final refined model within the experimental cryoEM map (Fig. 5).
Scenario 4: Alignment errors and template gaps
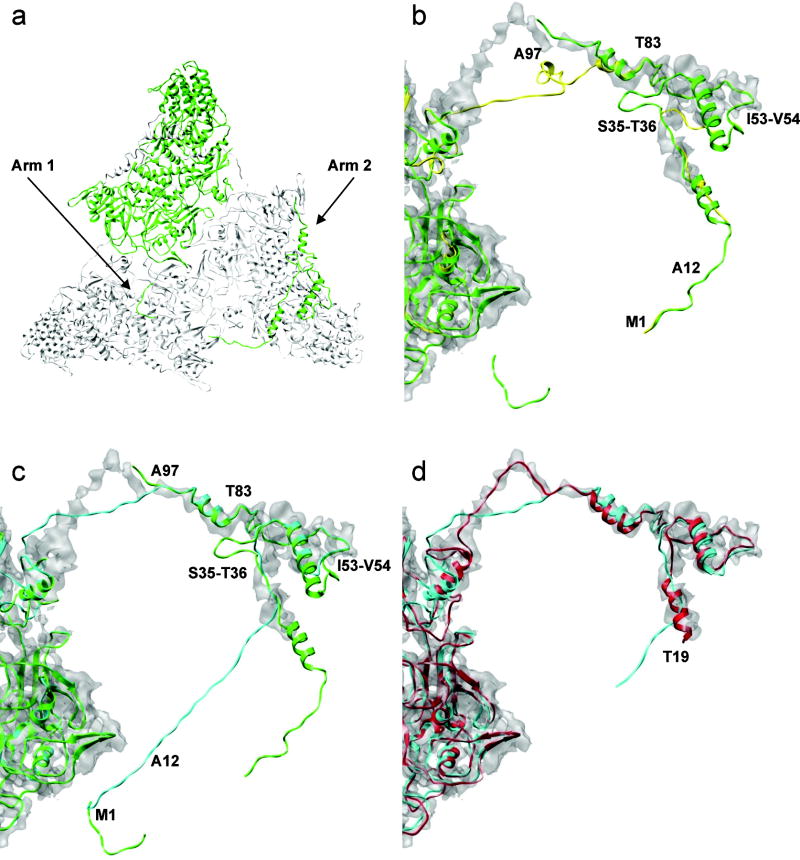
Two common problems in homology modeling, alignment errors and structural gaps in the template, can cause serious flaws in the resulting model, which need to be fixed before detailed local refinement. Alignment errors may be alleviated by adjustment of sequence alignment while the errors caused by structural gaps have to be refined explicitly using the EM-IMO method. One example is provided by the VP3B N-terminus. This region, 1–175, corresponds to the first 240 residues in the λ1B structure of MRV, which contains three arms extending to the other two λ1B subunits related by three-fold symmetry37 (Fig. 6a). Comparison between the N-terminus of the VP3B model and the cryoEM map indicates that there are structural errors arising from two sources: first, there are alignment errors between GCRV VP3B and MRV λ1B, resulting from the relatively low sequence homology at their N-terminal regions, and second the homology model deviates significantly from the map due in part to the missing linkers between three arms in the template structure.
Figure 6.
Refinement of the VP3B N-terminus. (a) λ1B structure (green) in the three-fold symmetry. (b) Initial homology model (yellow). (c) Homology model built based on the tuned sequence alignment (cyan). In b and c the template structure is shown in green and the key residues used in the alignment tuning are marked. (d) Final model after five iterations of refinement using the EM-IMO-based protocol (red), with the first 18 residues truncated.
Our approach to alignment-induced structural errors is to optimize sequence alignment by trial and error. Specifically, the region 1-12 of VP3B was aligned to arm one of λ1B assuming that VP3B possesses arm one. Two gaps were inserted into the VP3B sequence between S35 and T36 and between I53 and V54, and the region 83-97 of VP3B was realigned. The N-terminus of the VP3B model before and after alignment tuning is shown together with the N-terminus of the λ1B structure in Fig. 6b and 6c, respectively. Clearly, the model built based on the tuned alignment is more consistent with the cryoEM map and, correspondingly, the density fitting score is improved from 0.402 to 0.414. This result indicates that a cryoEM map with sufficient resolution can provide useful guidelines in the homology modeling process to help generate an optimal starting model for refinement.
During 5 iterations of refinement, the N-terminus of the VP3B model was divided into regions and refined using the EM-IMO method. For example, the following segments – 19-37, 39-58, 72-77, 79-96, 98-122, 124-142, 144-157, 160-167 and 170-188 – were used in the first iteration of refinement. Fig. 6d shows the N-terminus structure before and after refinement within the cryoEM map. For the region 19-37, a helix was first built using the standard geometry for helical structure and then fitted into the cryoEM density during EM-IMO refinement. For the region 39-58, a helix in the initial model that deviates from the density was relaxed and further fitted into the density map. During refinement, large structural changes occurred in a number of regions, leading to significantly more consistent fit between the final model and the cryoEM map. For example, significant structural changes can be found in the region 98-122, which corresponds to a missing linker in the λ1B structure; in the region 124-142, which is a Zinc finger that binds mRNA, and in the region 144-157, which corresponds to another missing linker in the λ1B structure.37 After refinement, the density fitting score of the final model is improved by 7.4% compared to that of the starting model. The resulting model was then further relaxed in the MD-based refinement (See below).
Scenario 5: Remote sequence homology
Model quality declines rapidly when the sequence relationship between the protein to be modeled and the template is remote. In such cases, the resulting model may contain serious alignment errors and sometime topological errors, which have to be fixed in order to generate a reasonable model for effective refinement. VP7, the outermost protein on the outer shell, provides a good example for this scenario.
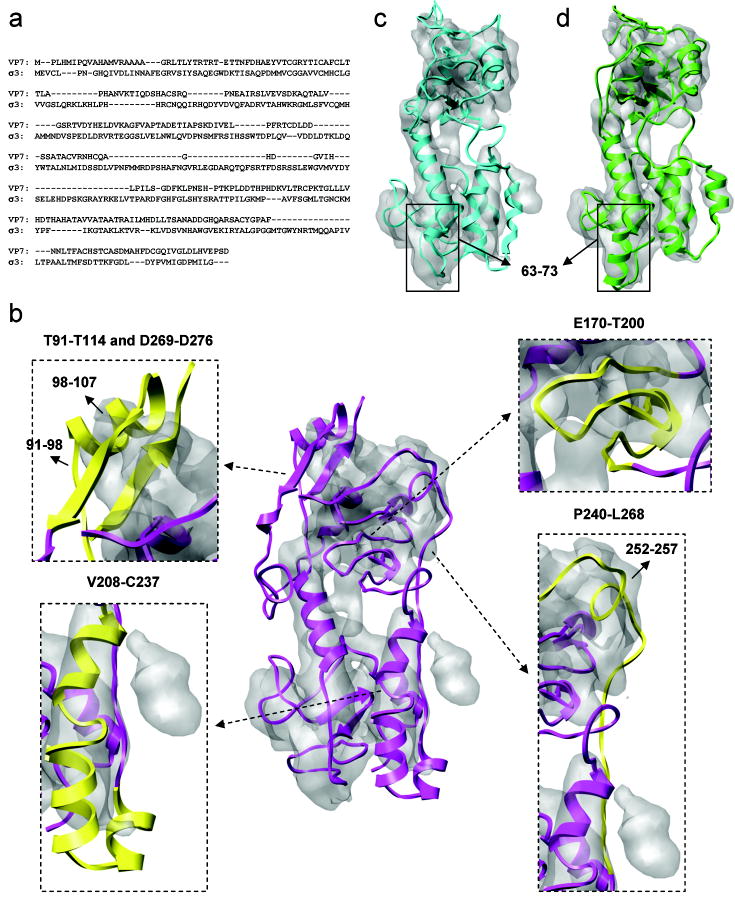
The sequence identity between GCRV VP7 and MRV σ3 is about 14.9% and the alignment contains numerous gaps, insertions and deletions as shown in Fig 7a. As a result, the initial model of VP7 built based on the σ3 structure has a low quality and overall is not as consistent with the cryoEM map as other GCRV proteins, as can be seen from Fig. 7b. In order to generate a reasonable model for refinement, the sequence alignment was manually adjusted in the β-sheet region, residues 170-200, and helical region, residues 208-237, based on secondary structure prediction and the cryoEM map. For the former, alignment gaps within strands were removed to maintain the β-sheet geometry, and for the latter, helical boundaries were adjusted to be consistent with secondary structure prediction. After alignment tuning, the density fitting score was improved by 2.3%. Two obvious discrepancies between the VP7 model and the cryoEM map are the strained helix 98-107, for which the adjacent loop 91-98 is nearly straight and does not correspond to any density, and the non-local β-sheet formed by strands 112-114 and 269-271, which is partly exposed and in an apparently incorrect orientation. Based on the cryoEM map, we speculate that the region 98-107 contains a strand that forms an anti-parallel β-sheet with the other two strands. A three-strand β-sheet was constructed and rotated by ~ 90° counterclockwise around the long axis of the VP7 model. In addition, a helix was constructed for the region 252-257 in order to be more consistent with the map and to anchor the adjacent loops, residues 240-251 and 258-268 to the protein body. After these adjustments, the density fitting score was improved by 8.3% and the resulting model is shown in Fig. 7c.
Figure 7.
Refinement of the VP7 model. (a) Sequence alignment of GCRV VP7 and MRV σ3. (b) Initial homology model (center, magenta) with four inserted figures showing regions subjected to the manual adjustment of sequence alignment and topology (yellow). (c) Homology model built after adjustment. (d) Final model after 5 iterations of refinement using the EM-IMO-based protocol.
In each of five iterations of EM-IMO-based refinement, the VP7 model was broken down into about 15 regions which were refined in parallel using the EM-IMO method. For example, residues 50-74 in the initial model appear as a random loop protruding from a cylinder-like density, which seems to suggest a helix. However, secondary structure prediction in this region is ambiguous. To explore all the possibilities, a helix with standard geometry was built with different lengths and fitted into the density in a number of trial EM-IMO refinements. After trial and error, we found that when residues 63-73 were treated as helical the refined structure was most consistent with the map both visually and as judged by the density fitting score. After five iterations of detailed refinement, the final density fitting score was 0.5261, which is 18.3% higher than that of the initial model built directly based on the sequence alignment. The final model is shown superimposed with the cryoEM map in Fig. 7d.
Molecular dynamics refinement of GCRV proteins
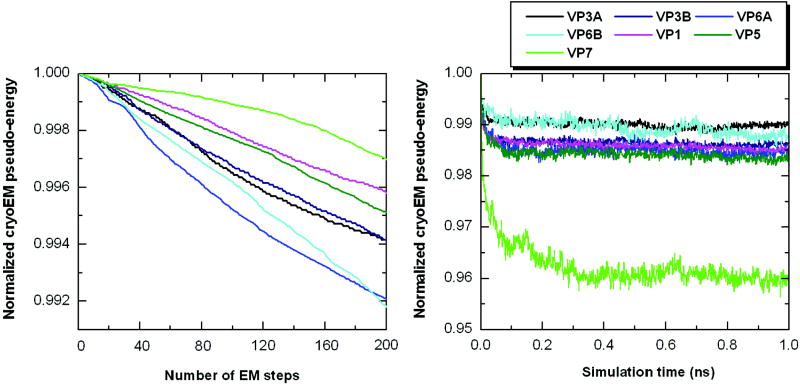
The seven conformers of five GCRV proteins were further refined by energy minimization and 1- ns simulation using the MDFF algorithm35 that we implemented in the GROMOS96 MD program.42 A slightly higher threshold than used by Trabuco et al,35 Φthr=2.5, was used for GCRV proteins in the pseudo-energy function to eliminate the effect of noise and ambiguous density. Similarly, a higher scaling factor, ξ=3.5, was used in the same energy function so as to impose a strong cryoEM constraint on the models during MDFF refinement. The pseudo-energy, after normalization using the initial energy, is plotted in Fig. 8 for all GCRV proteins. As shown in Fig. 8a and 8b, the pseudo-energy decreased to different extents for different proteins during refinement using the MDFF algorithm. The structures previously refined using the EM-IMO-based protocol were relaxed during the MDFF refinement.
Figure 8.
MDFF refinement of GCRV proteins. (a) Plot of normalized cryoEM pseudo-energy (ref. 35) during 200-step energy minimization (b) Plot of normalized cryoEM pseudo-energy (ref. 35) during 1-ns MDFF simulation.
As shown in Table 1, the MDFF refinement provided an average improvement of 2.6% in CCC score for GCRV proteins, while the EM-IMO-based refinement yielded an improvement ranging from 4.4% for the easiest case (VP3A) to 18.3% for the most difficult case (VP7). The comparison of structures before and after refinement reveals that MDFF appeared to be most effective in adjusting structural details, which is consistent with the local nature of the cryoEM map-derived gradient. This can be seen from the improved twist of β-sheets, geometry of helical turns and some conformations of bulky side chains in VP3A and VP3B, for which the map quality is good enough to derive the gradient accurately. Note that in a number of cases EM-IMO was applied again following MDFF refinement to correct local deviations from the cryoEM map caused by the MDFF refinement. These regions mainly corresponded to surface loops where densities usually contain more noise.
We have used our implementation of the MDFF method35 to refine the VP1 C-terminal domain without first using the EM-IMO method. MDFF was found to be quite effective but also several orders of magnitude slower than EM-IMO (3 days as compared to 0.5 seconds). Thus, the multi-scale strategy used here, that relies on EM-IMO for refinement problems involving large structural changes and MDFF for finer-grained refinement, offers an approach that builds on the strengths of both methods.
Discussion
CryoEM is at a stage where medium-resolution maps can be obtained routinely and where near-atomic resolution maps are possible for samples with high level of structural homogeneity and symmetry.3 Fitting atomic models into cryoEM maps is obviously an important goal that can benefit from the techniques that have been developed for homology modeling and from the large number of potential templates for refinement that it offers. In this study, we have implemented a new approach to use homology models in cryoEM refinement and applied it to the reconstruction of the entire capsid structure of grass carp reovirus (GCRV) using a near-atomic resolution cryoEM map. The structures and their biological implications are considered in the accompanying paper. In the following, we discuss issues that are crucial to cryoEM refinement and summarize features of EM-IMO that we believe are uniquely suited to address a wide range of problems associated both with the fitting of homology models into cryoEM maps and the concomitant refinement of the models themselves.
CryoEM-constrained homology modeling
The quality of homology models depends critically on the quality of the sequence alignment that is used. In actual structure prediction applications, alignments are often corrected manually and then subjected to computational refinement. We have shown here that when a cryoEM map is available, the measured mass densities can be used directly to improve the alignment and hence to generate a higher-quality initial model for refinement. The approach we have used is to identify regions that do not fit well into the map by visual inspection and then to improve the quality of the fit through an iterative alignment-tuning/model-building process. Automatic procedures that explore alternative alignments27 can also be used for this purpose, however the exhaustive search required poses severe computational demands and may be unnecessary in cases where the alignment appears optimal except in a few regions. In cases where alignment errors are too severe or where the location of secondary structure elements is clearly inconsistent with the experimental cryoEM map, direct structure refinement may be more effective than alignment tunning. Secondary structure prediction can play a vital role in guiding alignment tunning and structure refinement, as we have demonstrated throughout this study. In our study, GRASP243 which presents and analyses sequence, secondary structure and three-dimensional models in the same graphic interface facilitated our model tuning as well as input preparation process in refinement.
EM-IMO: versatility, efficiency and localized refinement
While EM-IMO was designed primarily for refining local structures within cryoEM maps, it offers a variety of functionalities for model building such as rebuilding individual secondary structure elements and assembling fragments of structures from different templates. This versatility is due in large part to its torsion-space local sampling algorithm36 that can move secondary structure elements and connect loops in a single step, which facilitates the manipulation of protein structures in various ways. Moreover, the combined use of a local sampling algorithm and a statistical potential enables EM-IMO to generate thousands of conformations in a few seconds and to evaluate their energies within the same time scale. Another important feature of EM-IMO is its focus on local as opposed to global refinement. Most existing methods were developed primarily for “global refinement” which can yield a good overall fit but, in general, the fit in some regions will be improved at the price of degrading others. The refinement protocol that uses EM-IMO to refine multiple regions of protein models in an iterative fashion provides an alternative strategy for global refinement that does not sacrifice detail in individual regions.
Supervised vs. unsupervised refinement
Unsupervised, fully automatic refinement methods implicitly assume that errors are distributed homogeneously throughout the structure and that a single functionality can deal with most problems encountered in refinement. Neither of these assumptions is true in real applications. For example, in the case of VP3B, the homology model fits the cryoEM map well except in the N-terminus, which contains serious errors such as a missing helix and misplaced loops. Refining the VP3B structure as a whole, can only result in low efficiency in the sense that much computational power will be devoted to the protein body that already fits the map quite well. As for the second assumption, the use of a single functionality will necessarily limit the refinement to a subset of cases for which that functionality is appropriate. For example, most automatic methods will fail to refine VP3B N-terminus simply because they do not have the ability to remodel a missing helix. For the MDFF35 method used in our final refinement, generating a helix would require the ab initio folding of a peptide.
In our EM-IMO method, human supervision plays a crucial role in guiding the automatic refinement. As has been demonstrated throughout our study, reconstructing the model for the GCRV virion could not have been accomplished with entirely automatic methods and, rather, requires a dynamic interplay between automatic refinement and human supervision. Of particular importance in our approach is the ability to use the cryoEM maps as a constraint in the construction of homology models and in local refinement, as demonstrated for the GCRV proteins. In our study, human supervision was based on the integration of various sources of information such as secondary structure analysis and the experimentally determined cryoEM map. Two approaches have been applied to systematically reduce the risk of human bias. First, in the EM-IMO-based protocol multiple iterations of refinement are performed and, in each iteration, regions to be refined are defined with different anchor residues. This can effectively eliminate the bias associated with a single refinement and the arbitrary definition of the region boundary. Second, in the final stage of the protocol, an automatic refinement method, MDFF,35 is applied to minimize the effects of decisions made at earlier stages.
In summary, we have introduced a new method which has allowed us to report a full-backbone model derived from homology models for an entire macromolecular assembly, GCRV. The biological implications of the structure are reported in the accompanying publication. The EM-IMO method itself, the EM-IMO-based refinement protocol and the MDFF refinement method offer an integrated set of tools that should be widely applicable in the construction of cryoEM-derived structural models of macromolecular assemblies.
Materials and Methods
Software implementation and usability
Details about software implementation, installation, input preparation, execution, and download instruction of the EM-IMO refinement and related tools are provided in the Supplementary Information and at the WWW site: http://wiki.c2b2.columbia.edu/honiglab_public/index.php/Software:cryoEM.
CASP data set
All target proteins in CASP5, 6 and 7 were processed using an in-house structure prediction pipeline (http://luna.bioc.columbia.edu/honiglab/pudge/cgi-bin/pipe_int.cgi), in which template selection and sequence alignment were performed using HMAP44 and SP3,45 and homology models were constructed using NEST.46 A list of 50 proteins was manually selected with one homology model for each protein (see Supplementary Table 1). The selection was done in such a way that protein size, sequence identity and backbone RMSD would cover a broad range of values. Density maps were simulated for the crystal structures of all 50 proteins using the EMAN47 program “pdb2mrc” at 7.0 A resolution with a sampling of 1.75 Å/pixel.
Modeling of GCRV proteins
In our work, the five proteins in MRV for which crystal structures have been determined for both virus core (PDB entry code: 1EJ637) and membrane-penetration complex (PDB entry code: 1JMU38) were used as templates to model their counterparts in GCRV. Sequence alignment and model building were performed using the same programs as for the CASP proteins. As shown in Table 1, the sequence identity between GCRV proteins and their templates ranges from 31.3%, a typical value for homology modeling, to 14.9%, which is generally viewed as in the “twilight zone” for structure prediction. The structural quality of initial models measured by backbone geometry and side chain packing is reasonably good for most proteins except for the N-terminus of VP3B and VP7, where poor alignments led to more structural errors. The cryoEM maps used for model fitting and refinement were obtained from a near-atomic reconstruction of GCRV virion, which is described in an accompanying paper.
Local structure refinement using a cryoEM map as a constraint the EM-IMO method
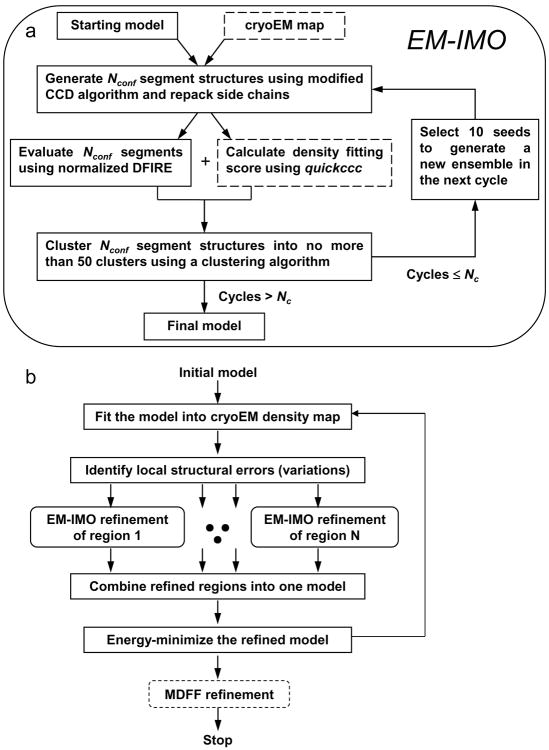
IMO is a method developed previously for local structure refinement of homology models.36 The EM-IMO method is a new atomic modeling method that uses cryoEM density maps as constraints. EM-IMO adapts the basic IMO framework but has enhanced features for protein structure manipulation. A flowchart of the EM-IMO procedure is shown in Fig. 9a. The basic idea is to move protein segments as rigid bodies through a torsion-space sampling procedure that uses backbone dihedral angles of residues in connecting regions as variable. After repacking side chains,48 the sampled conformations are evaluated and clustered based on a scoring function that combines a pairwise statistical potential and a density fitting score.
Figure 9.
Flow charts of local and global refinement. (a) Flow chart of the EM-IMO program, which is a local refinement method. (b) Typical steps involved in refining full protein structure. Our procedure is basically a global refinement protocol using EM-IMO as a core component, thus termed EM-IMO-based refinement protocol.
The sampling algorithm used here provides more modeling functions in addition to those described in the original IMO procedure.36 Briefly, after the backbone dihedral angles of driver residues in the region to be refined are perturbed, a modified cyclic coordinate descent (CCD) algorithm36,49 is used to close the C-terminal gap between the variable and fixed parts of the protein chain as well as to generate a new conformation for the entire region. In this perturbation-closure procedure, regions within the local structure to be refined can be treated as rigid bodies and move along with the residues being perturbed. Alternative conformations can be specified for the rigid-body regions using their backbone dihedral angles. This function is particularly useful for refining regions with missing secondary structure elements or to assemble parts of a protein taken from different models into a new model. For extended, terminal regions (or domains), the sampling algorithm is simply a perturbation procedure without chain closure.
The scoring function we formulated in this work is a linear combination of a density fitting score, a normalized DFIRE score40 and a restraint score:
where w1, w2 and w3 are weighting factors. The ratio of w1 to w2 is 8 for the results reported for both CASP and GCRV proteins, while the value of w3 was determined by trial and error when restraints were applied. The density fitting score is measured by a cross-correlation coefficient (CCC) between the experimental map and the map simulated from the atomic model. In the original IMO procedure, an all-atom pairwise statistical potential based on the distance-scaled, finite ideal-gas reference state, DFIRE40, was used to evaluate the structural quality (e.g. atomic packing and clashes) of conformations sampled during refinement. In EM-IMO, this atomic potential was converted to a normalized, residue-based potential and the score was further normalized using the number of residues in the structure to be refined. The combined used of a normal energy function (DFIRE) and a density fitting score ensures that the refined structure not only fits cryoEM map better but also has a reasonable structural quality. The positional restraint and distance restraint are implemented using a harmonic function:
where d denotes the Cα-Cα distance, r denotes the Cα position, and the subscript 0 denotes the desired distance or position. Note that the weight of constraint term, w3, was not parameterized in our study since by nature is not transferable between systems and varies case to case in real applications. Given the starting structure and the geometric constraint to be imposed, w3 can be determined by trial and error.
An EM-IMO-based refinement protocol
The final refinement protocol is summarized in the flowchart shown in Fig. 9b. Each step in this protocol is carried out using a stand-alone, modular program. The refinement is carried out in an iterative manner and can be terminated based on a user-specified criterion. The individual steps are as follows.
1) An atomic model is fitted into the cryoEM map with either graphics programs such as UCSF Chimera50 or automatic fitting programs such as foldhunter.51 For CASP proteins, since the experimental structures are known, we used a simplified fitting procedure in which homology models were superimposed onto the native structures using Cα atoms of the secondary structure elements. For GCRV proteins, we manually fitted the homology models into the cryoEM maps using Chimera’s Fit-Model-in-Map function. 2) Two graphic programs, GRASP243 and Chimera,50 were used together to identify problematic regions in the homology model. Regions that involve sequence alignment errors or discrepancies in secondary structure elements were identified using GRASP2 and then compared to the cryoEM map using Chimera. Similarly, regions that are inconsistent with the cryoEM map in position, orientation or other geometric characteristics are recognized using Chimera and then checked for alignment errors and secondary structure errors using GRASP2. This step takes less than a few hours for a large protein with more than a thousand amino acids such as VP1. 3) All the problematic regions identified are refined in parallel with the EM-IMO method. 4) Regions with improved density fitting scores are merged into a new structural model using a Perl script. 5) The model is energy minimized using the program minimize.x in the TINKER package.52 The non-hydrogen backbone atoms were restrained during minimization using a force constant of 100 kcal/mol/Å2. The final model is used as the initial model for the next iteration of refinement if the density fitting score (CCC) of the entire protein model is not converged. In the current study, 5 iterations of refinement were performed to ensure that the difference of CCC between two consecutive runs is less than 0.01.
MD-based refinement method
We implemented the MDFF algorithm35 in the GROMOS96 MD program42 and used it to finalize all seven models of the five GCRV proteins. In our program, the GROMOS96 43a1 force field was used in conjunction with the mAGB implicit solvation model53,54 and a cryoEM term that derives energy and forces from the grid representation of cryoEM map using linear interpolation.35 We used up to 200 steps of conjugate gradient energy minimization to relax the models previously refined using the EM-IMO-based protocol. A 1-nanosecond MDFF simulation was then performed to further adjust the structural details guided by the physical energy function and the cryoEM map. Unlike the protocol used by Trabuco et al,35 no secondary structure constraint was applied. After refinement, the density fitting scores measured by cross-correlation coefficient (CCC) were calculated for all the snapshots generated during the MDFF simulation and the snapshot with the best score was selected as the final model.
Supplementary Material
Acknowledgments
This research was supported in part by grants from the National Institutes of Health (GM071940 and AI069015 to ZHZ, GM30518 to BH), the National Science Foundation (HRD-0420407 to ZHZ and MCB-0416708 to BH), National Basic Research Program of China (973 Program #2009CB118701 to QF), National Natural Scientific Foundation of China (30671615 and 30871940 to QF) and the Chinese Academy of Sciences (KSCX2-YW-N-021 to QF).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Chiu W, Baker ML, Almo SC. Structural biology of cellular machines. Trends in Cell Biology. 2006;16:144–150. doi: 10.1016/j.tcb.2006.01.002. [DOI] [PubMed] [Google Scholar]
- 2.Mitra K, Frank J. Ribosome dynamics: Insights from atomic structure modeling into cryo-electron microscopy maps. Annual Review of Biophysics and Biomolecular Structure. 2006;35:299–317. doi: 10.1146/annurev.biophys.35.040405.101950. [DOI] [PubMed] [Google Scholar]
- 3.Zhou ZH. Towards atomic resolution structural determination by single-particle cryo-electron microscopy. Current Opinion in Structural Biology. 2008;18:218–228. doi: 10.1016/j.sbi.2008.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jiang W, et al. Backbone structure of the infectious epsilon 15 virus capsid revealed by electron cryomicroscopy. Nature. 2008;451:1130–U12. doi: 10.1038/nature06665. [DOI] [PubMed] [Google Scholar]
- 5.Zhang X, et al. Near-atomic resolution using electron cryomicroscopy and single-particle reconstruction. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:1867–1872. doi: 10.1073/pnas.0711623105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yu XK, Jin L, Zhou ZH. 3.88 angstrom structure of cytoplasmic polyhedrosis virus by cryo-electron microscopy. Nature. 2008;453:415–U73. doi: 10.1038/nature06893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Baker TS, Johnson JE. Low resolution meets high: Towards a resolution continuum from cells to atoms. Current Opinion in Structural Biology. 1996;6:585–594. doi: 10.1016/s0959-440x(96)80023-6. [DOI] [PubMed] [Google Scholar]
- 8.Rossmann MG. Fitting atomic models into electron-microscopy maps. Acta Crystallographica Section D-Biological Crystallography. 2000;56:1341–1349. doi: 10.1107/s0907444900009562. [DOI] [PubMed] [Google Scholar]
- 9.Rossmann MG, Morais MC, Leiman PG, Zhang W. Combining x-ray crystallography and electron microscopy. Structure. 2005;13:355–362. doi: 10.1016/j.str.2005.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fabiola F, Chapman MS. Fitting of high-resolution structures into electron microscopy reconstruction images. Structure. 2005;13:389–400. doi: 10.1016/j.str.2005.01.007. [DOI] [PubMed] [Google Scholar]
- 11.Topf M, Sali A. Combining electron microscopy and comparative protein structure modeling. Current Opinion in Structural Biology. 2005;15:578–585. doi: 10.1016/j.sbi.2005.08.001. [DOI] [PubMed] [Google Scholar]
- 12.Wriggers W, Milligan RA, McCammon JA. Situs: A package for docking crystal structures into low-resolution maps from electron microscopy. Journal of Structural Biology. 1999;125:185–195. doi: 10.1006/jsbi.1998.4080. [DOI] [PubMed] [Google Scholar]
- 13.Wriggers W, Birmanns S. Using Situs for flexible and rigid-body fitting of multiresolution single-molecule data. Journal of Structural Biology. 2001;133:193–202. doi: 10.1006/jsbi.2000.4350. [DOI] [PubMed] [Google Scholar]
- 14.Wriggers W, Chacon P. Modeling tricks and fitting techniques for multiresolution structures. Structure. 2001;9:779–788. doi: 10.1016/s0969-2126(01)00648-7. [DOI] [PubMed] [Google Scholar]
- 15.Chacon P, Wriggers W. Multi-resolution contour-based fitting of macromolecular structures. Journal of Molecular Biology. 2002;317:375–384. doi: 10.1006/jmbi.2002.5438. [DOI] [PubMed] [Google Scholar]
- 16.Tama F, Wriggers W, Brooks CL. Exploring global distortions of biological macromolecules and assemblies from low-resolution structural information and elastic network theory. Journal of Molecular Biology. 2002;321:297–305. doi: 10.1016/s0022-2836(02)00627-7. [DOI] [PubMed] [Google Scholar]
- 17.Volkmann N, Hanein D. Quantitative fitting of atomic models into observed densities derived by electron microscopy. Journal of Structural Biology. 1999;125:176–184. doi: 10.1006/jsbi.1998.4074. [DOI] [PubMed] [Google Scholar]
- 18.Volkmann N, Hanein D. Docking of atomic models into reconstructions from electron microscopy. Macromolecular Crystallography, Pt D. 2003;374:204–225. doi: 10.1016/S0076-6879(03)74010-5. [DOI] [PubMed] [Google Scholar]
- 19.Roseman AM. Docking structures of domains into maps from cryo-electron microscopy using local correlation. Acta Crystallographica Section D-Biological Crystallography. 2000;56:1332–1340. doi: 10.1107/s0907444900010908. [DOI] [PubMed] [Google Scholar]
- 20.Chapman MS. Restrained Real-Space Macromolecular Atomic Refinement Using a New Resolution-Dependent Electron-Density Function. Acta Crystallographica Section A. 1995;51:69–80. [Google Scholar]
- 21.Chen LF, Blanc E, Chapman MS, Taylor KA. Real space refinement of acto-myosin structures from sectioned muscle. Journal of Structural Biology. 2001;133:221–232. doi: 10.1006/jsbi.2000.4321. [DOI] [PubMed] [Google Scholar]
- 22.Chen JZ, Furst J, Chapman MS, Grigorieff N. Low-resolution structure refinement in electron microscopy. Journal of Structural Biology. 2003;144:144–151. doi: 10.1016/j.jsb.2003.09.008. [DOI] [PubMed] [Google Scholar]
- 23.Gao HX, et al. Study of the structural dynamics of the E-coli 70S ribosome using real-space refinement. Cell. 2003;113:789–801. doi: 10.1016/s0092-8674(03)00427-6. [DOI] [PubMed] [Google Scholar]
- 24.Ma JP. Usefulness and limitations of normal mode analysis in modeling dynamics of biomolecular complexes. Structure. 2005;13:373–380. doi: 10.1016/j.str.2005.02.002. [DOI] [PubMed] [Google Scholar]
- 25.Tama F, Brooks CL. Symmetry, form, and shape: Guiding principles for robustness in macromolecular machines. Annual Review of Biophysics and Biomolecular Structure. 2006;35:115–133. doi: 10.1146/annurev.biophys.35.040405.102010. [DOI] [PubMed] [Google Scholar]
- 26.Tama F, Miyashita O, Brooks CL. Flexible multi-scale fitting of atomic structures into low-resolution electron density maps with elastic network normal mode analysis. Journal of Molecular Biology. 2004;337:985–999. doi: 10.1016/j.jmb.2004.01.048. [DOI] [PubMed] [Google Scholar]
- 27.Topf M, Baker ML, Marti-Renom MA, Chiu W, Sali A. Refinement of protein structures by iterative comparative modeling and cryoEM density fitting. Journal of Molecular Biology. 2006;357:1655–1668. doi: 10.1016/j.jmb.2006.01.062. [DOI] [PubMed] [Google Scholar]
- 28.Velazquez-Muriel JA, Valle M, Santamaria-Pang A, Kakadiaris IA, Carazo JM. Flexible fitting in 3D-EM guided by the structural variability of protein superfamilies. Structure. 2006;14:1115–1126. doi: 10.1016/j.str.2006.05.013. [DOI] [PubMed] [Google Scholar]
- 29.Velazquez-Muriel JA, Carazo JM. Flexible fitting in 3D-EM with incomplete data on superfamily variability. Journal of Structural Biology. 2007;158:165–181. doi: 10.1016/j.jsb.2006.10.014. [DOI] [PubMed] [Google Scholar]
- 30.Baker ML, et al. Ab initio modeling of the herpesvirus VP26 core domain assessed by CryoEM density. Plos Computational Biology. 2006;2:1313–1324. doi: 10.1371/journal.pcbi.0020146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.DePristo MA, de Bakker PIW, Johnson RJK, Blundell TL. Crystallographic refinement by knowledge-based exploration of complex energy landscapes. Structure. 2005;13:1311–1319. doi: 10.1016/j.str.2005.06.008. [DOI] [PubMed] [Google Scholar]
- 32.Furnham N, et al. Knowledge-based real-space explorations for low-resolution structure determination. Structure. 2006;14:1313–1320. doi: 10.1016/j.str.2006.06.014. [DOI] [PubMed] [Google Scholar]
- 33.DiMaio F, Tyka MD, Baker ML, Chiu W, Baker D. Refinement of protein structures into low-resolution density maps using rosetta. J Mol Biol. 2009;392:181–90. doi: 10.1016/j.jmb.2009.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Topf M, et al. Protein structure fitting and refinement guided by cryo-EM density. Structure. 2008;16:295–307. doi: 10.1016/j.str.2007.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Trabuco LG, Villa E, Mitra K, Frank J, Schulten K. Flexible fitting of atomic structures into electron microscopy maps using molecular dynamics. Structure. 2008;16:673–683. doi: 10.1016/j.str.2008.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhu J, Xie L, Honig B. Structural refinement of protein segments containing secondary structure elements: Local sampling, knowledge-based potentials, and clustering. Proteins-Structure Function and Bioinformatics. 2006;65:463–479. doi: 10.1002/prot.21085. [DOI] [PubMed] [Google Scholar]
- 37.Reinisch KM, Nibert M, Harrison SC. Structure of the reovirus core at 3.6 angstrom resolution. Nature. 2000;404:960–967. doi: 10.1038/35010041. [DOI] [PubMed] [Google Scholar]
- 38.Liemann S, Chandran K, Baker TS, Nibert ML, Harrison SC. Structure of the reovirus membrane-penetration protein, mu 1, in a complex with its protector protein, sigma 3. Cell. 2002;108:283–295. doi: 10.1016/s0092-8674(02)00612-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cheng L, Fang Q, Shah S, Atanasov IC, Zhou ZH. Subnanometer-resolution structures of the grass carp reovirus core and virion. J Mol Biol. 2008;382:213–22. doi: 10.1016/j.jmb.2008.06.075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhou HY, Zhou YQ. Distance-scaled, finite ideal-gas reference state improves structure-derived potentials of mean force for structure selection and stability prediction. Protein Science. 2002;11:2714–2726. doi: 10.1110/ps.0217002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Jones DT. Protein secondary structure prediction based on position-specific scoring matrices. Journal of Molecular Biology. 1999;292:195–202. doi: 10.1006/jmbi.1999.3091. [DOI] [PubMed] [Google Scholar]
- 42.van Gunsteren WF, B SR, Eising AA, Hunenberger PH, Kruger P, Mark AE, Scott WRP, Tironi IG. Groningen Molecular Simulation (GROMOS) System. University of Groningen; the Netherlands; ETH Zurich; Switzerland: 1996. [Google Scholar]
- 43.Petrey D, Honig B. GRASP2: Visualization, surface properties, and electrostatics of macromolecular structures and sequences. Macromolecular Crystallography, Pt D. 2003;374:492–+. doi: 10.1016/S0076-6879(03)74021-X. [DOI] [PubMed] [Google Scholar]
- 44.Tang CL, et al. On the role of structural information in remote homology detection and sequence alignment: New methods using hybrid sequence profiles. Journal of Molecular Biology. 2003;334:1043–1062. doi: 10.1016/j.jmb.2003.10.025. [DOI] [PubMed] [Google Scholar]
- 45.Zhou HY, Zhou YQ. Fold recognition by combining sequence profiles derived from evolution and from depth-dependent structural alignment of fragments. Proteins-Structure Function and Bioinformatics. 2005;58:321–328. doi: 10.1002/prot.20308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Petrey D, et al. Using multiple structure alignments, fast model building, and energetic analysis in fold recognition and homology modeling. Proteins-Structure Function and Genetics. 2003;53:430–435. doi: 10.1002/prot.10550. [DOI] [PubMed] [Google Scholar]
- 47.Ludtke SJ, Baldwin PR, Chiu W. EMAN: Semiautomated software for high-resolution single-particle reconstructions. Journal of Structural Biology. 1999;128:82–97. doi: 10.1006/jsbi.1999.4174. [DOI] [PubMed] [Google Scholar]
- 48.Canutescu AA, Shelenkov AA, Dunbrack RL. A graph-theory algorithm for rapid protein side-chain prediction. Protein Science. 2003;12:2001–2014. doi: 10.1110/ps.03154503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Canutescu AA, Dunbrack RL. Cyclic coordinate descent: A robotics algorithm for protein loop closure. Protein Science. 2003;12:963–972. doi: 10.1110/ps.0242703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Pettersen EF, et al. UCSF chimera - A visualization system for exploratory research and analysis. Journal of Computational Chemistry. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 51.Jiang W, Baker ML, Ludtke SJ, Chiu W. Bridging the information gap: Computational tools for intermediate resolution structure interpretation. Journal of Molecular Biology. 2001;308:1033–1044. doi: 10.1006/jmbi.2001.4633. [DOI] [PubMed] [Google Scholar]
- 52.Ponder JW. TINKER-software tools for molecular design, version 3.7. Washington University; St. Louis, MO: 1999. [Google Scholar]
- 53.Gallicchio E, Levy RM. AGBNP: An analytic implicit solvent model suitable for molecular dynamics simulations and high-resolution modeling. Journal Of Computational Chemistry. 2004;25:479–499. doi: 10.1002/jcc.10400. [DOI] [PubMed] [Google Scholar]
- 54.Zhu J, Alexov E, Honig B. Comparative study of generalized Born models: Born radii and peptide folding. Journal Of Physical Chemistry B. 2005;109:3008–3022. doi: 10.1021/jp046307s. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.