Abstract
The ability to measure proton exchange rates in tissue using MRI would be very useful for quantitative assessment of magnetization transfer properties, both in conventional MT imaging and in the more recent chemical exchange saturation transfer (CEST) approach. CEST is a new MR contrast mechanism that depends on several factors, including the exchange rate of labile protons in the agent in a pH-dependent manner. Two new methods to monitor local exchange rate based on CEST are introduced. The two MRI-compatible approaches to measure exchange are quantifying exchange using saturation time (QUEST) dependence and quantifying exchange using saturation power (QUESP) dependence. These techniques were applied to poly-l-lysine (PLL) and a generation-5 polyamidoamine dendrimer (SPD-5) to measure the pH dependence of amide proton exchange rates in the physiologic range. Data were fit both to an analytical expression and to numerical solutions to the Bloch equations. Results were validated by comparison with exchange rates determined by two established spectroscopic methods. The exchange rates determined using the four methods were pooled for the pH-calibration curve of the agents consisting of contributions from spontaneous (k0) acid catalyzed (ka), and base catalyzed (kb) exchange rate constants. These constants were k0 = 68.9 Hz, ka = 1.21 Hz, kb = 1.92 × 109 Hz, and k0 = 106.4 Hz, ka = 25.8 Hz, kb = 5.45 × 108 Hz for PLL and SPD-5, respectively, showing the expected predominance of base-catalyzed exchange for these amide protons.
Keywords: CES, pH, chemical exchange rate, magnetization transfer, saturation transfer, PLL, SPD-5, poly-l-lysine, polyamidoamine dendrimer
Chemical exchange saturation transfer (CEST) has recently been proposed as a new imaging contrast mechanism (1) in which the radiofrequency-induced saturation of labile protons in the agent is transferred to water protons. The resulting MRI signal intensity depends on a multitude of parameters, including agent concentration, number of exchangeable protons, proton exchange rate, T1, T2, saturation time, and saturation efficiency (1–8). Of these, the chemical exchange rate is often the parameter of interest that reflects tissue pH and the molecular environment, such as salt or metal content. During saturation, labile protons of the low-concentration solute are saturated and exchange multiple times with unsaturated protons of the large water pool, resulting in a fractional reduction of the water line. If this exchange rate and the T1 of water are sufficiently large, there is an amplification of the MR sensitivity with respect to the agent concentration (1). Recently, we showed that macromolecules with multiple amide groups (2) or imino groups (5) can give a CEST effect within the micromolar range. The exchange rates of these proton types have a strong pH dependence in the physiologic range (9,10) and may be useful as pH reporters. Measurement of these rates would be a powerful means for pH calibration (3,4,11–15), but existing technologies for this, such as the water exchange (WEX) sequence (16) and measurement of linewidths, are spectroscopy (MRS) based. As a consequence, they are time consuming for the lower rates because of the low contrast agent concentration and not suitable for measuring the faster rates at high pH because of signal loss due to line broadening. If such rates could be measured through the water resonance, it would be possible to have higher acquisition speeds and use the approach for MRI. We here present two techniques to measure fast chemical exchange rates via water detection by exploiting the effect of exchange rate on signal intensity as a function of saturation time and saturation power. These techniques were tested on 5-mm tubes containing samples of two polyamide-based CEST agents, poly-l-lysine (PLL, 705.8 kDa) and generation-5 polyamidoamine dendrimer (SPD-5, 28.6 kDa) using 1D NMR spectra.
To establish suitability of these agents as pH markers, their pH-sensitivity was measured and fitted to existing equations for catalyzed exchange to determine the baseline mechanism.
Theory
Chemical exchange processes can be described by modified Bloch equations (4,6,17–22) with exchange terms. Comprehensive solutions have been presented elsewhere (21). In a recent paper (6) we derived concise expressions for the signal intensities of the exchangeable protons of the contrast agent (solute:SS in the WEX experiment and for water protons (Sw) in the saturation transfer experiment. These equations are valid for saturation transfer experiments under the assumptions of sufficiently separate resonances for these two types of protons (i.e., no direct saturation of the other resonance when saturating one). Here we evaluate the applicability of these expressions for measuring the single-proton solute–water exchange rate (kSw) for the typical exchange rates encountered in CEST studies (i.e., kSw > 30 Hz). This applicability will be judged through comparison with well-established spectroscopic measures of this rate and through fitting of the results using the exact Bloch equations (see the Appendix).
MRS Measures of Exchange Rate
The most simple spectroscopic measure of large exchange rates is through assessment of the linewidth of the solute protons (LWS), which in the slow exchange regime is directly related to the exchange rate and the transverse relaxation rate via (23,24):
| [1] |
In addition, exchange rates can also be measured spectroscopically using methods in which magnetization is transferred from water to the solute. One such approach is the so-called WEX sequence (16,25,26). The pulse sequence for this experiment is shown in Fig. 1a, with the water suppression modified from previous studies. Water magnetization is selectively excited by the first 90°–G1–180 ° (water selective)–G1 combination and is either inverted to −z or put back to the z axis (scan 2) by the second 90 ° pulse. Subsequently, longitudinal water magnetization is allowed to exchange during the mixing time tm, followed by detection of the exchangeable proton signals. Water suppression was performed using a double echo consisting of a hard 180 ° pulse and a water-selective 180 ° pulse (27), with the purpose of not exciting water while refocusing amide proton evolution. Any water excited due to small RF pulse deviations is suppressed by the gradients. By measuring magnetization transfer of the exchangeable protons as a function of mixing time, the exchange rates with water can be quantified. The solute signal intensity (Ss) as a function of tm is (6,16)
FIG. 1.
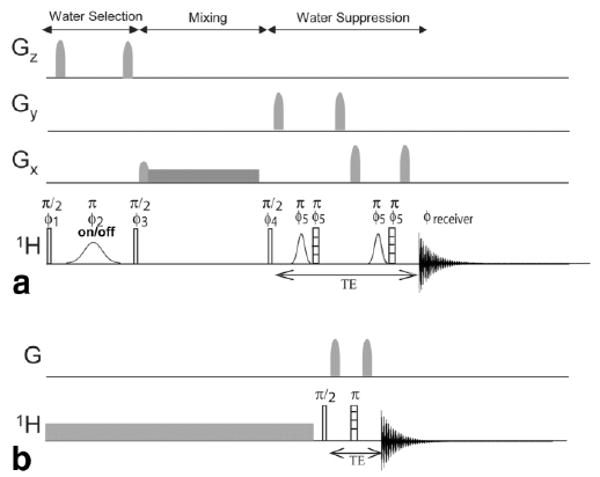
(a) Modified WEX experiment used for spectroscopic exchange rate determination. The shaped pulses are water-selective Gaussians 180° pulses, open boxes are 90° pulses, and hatched boxes are 180° pulses. During water selection, the Gaussian was 16 ms and during water suppression 2-ms Gaussians were used. The phase cycle was four steps with φ1 = 1313, φ 2 = 1, φ 3 = 1, φ 4 = 31, φ 5 = 1, φ receiver = 1313, with the 16-ms Gaussian switched off for scans 3 and 4. (b) Saturation transfer experiment utilized for power and time dependence measurements, with the open box a 90° pulse and the hatched box a 180° pulse.
| [2] |
in which S0S is the equilibrium magnetization. This equation can be used to determine ksw, provided the longitudinal relaxation rates (1/T1) for water (R1w ∼ 0.248 s−1) and the agent (R1s ∼ 0.71 s−1) are known at the particular field strength (11.7 T). For the amide protons of interest here, ksw is larger than 30 Hz and dominates the terms ksw + R1s − R1w and ksw + R1s, providing two major advantages. First, even substantial errors (e.g., 10–20%) in R1s and R1w do not produce significant errors in ksw. Second, the coefficient before the bracketed expression can be approximated by S0s and can be determined from the time point with the maximal signal, which is convenient for fitting experimental data to the exchange rate:
| [3] |
Notice that WEX experiments are less suitable when exchange rates become very high (order of 300–400 Hz or more). This is because the maximum intensity of the signal will be reached in several milliseconds, requiring the use of very short mixing times. This may become a problem for measuring exchange rates in vivo due to the finite duration of the water labeling pulse.
MRI Measures of Exchange Rate
Saturation transfer experiments from the solute to water (Fig. 1b) are obviously also sensitive to chemical exchange, the quantification of which is described by the same Bloch equations as used for the WEX experiments. Assuming that a steady state is reached instantaneously upon saturation of the solute (notice that this is not the same as complete saturation), the following equation applies for the measured CEST effect or proton transfer ratio (PTR) (6),
| [4] |
in which xCA is the fractional concentration of exchangeable protons of the contrast agent, tsat is the saturation time, α is the saturation efficiency, and the term kswxCA accounts for back exchange of saturated water protons to the solute, which will occur when the exchange rate and/or the concentration of exchangeable protons for the CEST agent are very high. Notice that this expression is equivalent to the one given previously (2,5) and reaches the same maximum reduction as predicted by Sherry and co-workers and also Aime and co-workers assuming complete saturation (4,7) and can be related to the proton transfer enhancement for the particular agent, which depends on the number of protons per molecular weight unit (NCA) and the molecular weight (MCA) of the agent:
| [5] |
The water signal intensity depends on the pulse power (ω1 = γB1) via (6):
| [6] |
in which
Because of the low solute concentration, the longitudinal and transverse rates for water can be measured using conventional inversion-recovery and spin-echo approaches, respectively, while R1s ≪ ksw and can be neglected for the CEST agents. The transverse rate for the solute cannot be directly measured due to interference of the exchange, but because 1H relaxation in proteins is dominated by dipolar interactions with other protons within 5 Å (28), it can be approximated by the R2 of the nearby protons (Hα for PLL). Thus, using Eqs. [4] and [6], two experiments can be designed to quantify exchange rates from the water intensity, namely quantification of exchange as a function of saturation time (QUEST) and saturation power (QUESP).
As mentioned above, the working equations were derived under the assumption of negligible direct saturation of the water protons. However, especially at lower fields, the bandwidth of the saturation is generally not narrow enough to avoid this. Fortunately, in these simple water solutions the drop in water intensity due to direct saturation can be measured by applying a saturation pulse at the same frequency difference with water as for the exchangeable protons, but on the opposite side (−Δωsw) of the water resonance.
| [7] |
in which S0 and are, respectively, the water signals without saturation and with saturation at −Δωsw, to correct for spillover (29–32). The amount of direct saturation depends on the ratio of the strength of the saturation pulses with respect to the chemical shift difference between irradiation frequency and water. For sufficiently low B1 fields (<2.5μ T ∼ 100 Hz) due to the large separation between the amide protons and water (∼1800 Hz at 11.7 T), the direct saturation as measured by Eq. [7] is only about 1%, which is quite negligible compared to the PTR effects for the present CEST agents at the concentrations studied, which range from 15 to 60%. In addition to the irradiation field strength and offset, direct saturation is also affected by R2w through its relationship to the water linewidth. As will be described further in the Discussion, for the present amide protons at 11.7 T the Bloch equations including direct saturation will have to be used when R2w > ∼6 Hz. However, as a first approximation, it is common to measure PTR by applying a zero-order correction using the asymmetry in the magnetization transfer ratio (MTR) via (31,33)
| [8] |
Notice that compared to Eq. [4], S0w here is replaced by .
This definition of PTR corrects for the missing direct saturation that is present experimentally and is equivalent provided that the direct saturation (Eq. [7]) is less than ∼20%. In this paper, we measure PTR in this way and fit the results as a function of saturation time and pulse power to determine the exchange rate. The results will be compared with measures from the solute proton linewidth and the WEX approach, as well as by fitting of using the complete six Bloch equations (see the Appendix). This will be used to establish guidelines for the use of the above expressions for quantifying the exchange rates of CEST agents.
Materials and Methods
Sample Preparation
All samples were prepared using 0.01 M phosphate-buffered saline buffer. PLL (705.8 kDa by viscosity; purchased from Sigma, Catalog No. P1524) was diluted to an initial concentration of 0.05 mM from which five samples of 500 μL each were prepared. These were supplemented with 10 μL of D2O and then titrated to the following pH values: 7.9, 7.7, 7.3, 6.5, 6.0. The ratio of amide protons to water protons was determined from the NMR spectra using the ratio of the Hε to the H2O peak (Hε is the narrowest resonance in PLL). In addition, a sample of 30 kDa PLL was initially prepared at a concentration of 1 mM and titrated to pH 6.72 (molar ratio was measured by NMR to be 1:958). The measured concentrations expressed in terms of the proton fraction, xCA, which were used in the data analysis, are shown in Table 1. A SPD-5 dendrimer, purchased from Dendritech, Inc., was initially prepared at 1 mM and then titrated to pH 8.11, 7.6, 7.0, 6.7, 6.3, and 5.6. A total of 10 μL of D2O was also added and again the final concentration was determined by NMR by comparing the integral under the total amide peak to water, with the molar ratios all about 1:700, corresponding to about 0.6 mM (Table 1).
Table 1.
Exchange Constants for the Various pH's for PLL and the G5 PAMAM Dendrimer Obtained from Linewidth, WEX, QUEST, and QUESP
| pH | xCA (×103) exp. | LW ksw (Hz) | WEX kswa (Hz) | QUEST kswa (Hz) | QUESP kswa (Hz) | ||
|---|---|---|---|---|---|---|---|
| Numerical | Analytical | Numericalc | Analytical | ||||
| G5 PAMAM | |||||||
| 8.1 | 1.368 | 580 | — | 521 ± 24 | 454 ± 13 | 550 + 200/−150 | 436 + 268/−131 |
| 7.6 | 1.307 | 382 | 305 + 98/−73 | 415 + 85/−104 | 316 + 54/−41 | 350 ± 50 | 300 + 73/−54 |
| 7.0 | 1.488 | 165 | 202 + 59/−48 | 161 ± 17 | 155 ± 17 | 175 ± 25 | 151 ± 26 |
| 6.7 | 1.456 | 115 | 128 + 37/−31 | 153 ± 15 | 133 ± 15 | 150 ± 25 | 132 ± 20 |
| 6.3 | 1.634 | 90 | 83 ± 13 | 78 ± 6 | 74 ± 6 | 75 ± 25 | 64 ± 11 |
| 5.6 | 1.346 | 27 | 39 ± 4 | 45 ± 3 | 41 ± 2 | 37 ± 12.5 | 37 ± 3 |
| PLL | |||||||
| 7.9 | 0.656 | 1211 | — | 1257 + 500/−400 | 782 ± 47 | 1250 ± 550 | 788 + 482/−378 |
| 7.7 | 0.579 | 639 | — | 660 + 143/−100 | 552 ± 17 | 650 ± 150 | 534 + 186/−124 |
| 7.3 | 0.674 | 398 | 404 + 153/−106 | 410 ± 70 | 379 ± 14 | 450 ± 150 | 379 + 98/−77 |
| 6.7b | 1.044 | 133 | 122 ± 15 | 151 ± 24 | 140 ± 8 | 125 ± 50 | 121 ± 11 |
| 6.5 | 1.035 | 71 | 89 ± 10 | 81 ± 10 | 83 ± 7 | 75 ± 25 | 79 ± 6 |
| 6.0 | 0.907 | 39 | 48 ± 1 | 49.8 ± 4 | 52 ± 3 | 50 ± 12.5 | 45 ± 8 |
NMR Experiments
All experiments were performed at 37 ± 0.1°C on an 11.7 T Bruker Avance system using a triple-channel, triple-axis gradient high-resolution NMR probe. For each sample, the probe was tuned, the magnet shimmed using gradient shimming, and ω1/2π power determined using a 2π pulse. The water linewidth (with probe detuned to prevent radiation damping) was <1 Hz. All samples were locked using D2O.
Simple excite–detect experiments (64 scans, π/2 = 10 μs, TR = 6 s, dwell time = 60 μs) were performed to measure the linewidths of the exchangeable amide peaks and to measure the ratio of these peaks to water.
The WEX sequence (16) shown in Fig. 1a used a 16-ms Gaussian pulse for water selection, which has a 99% bandwidth of ±115 Hz. This sharp bandwidth was necessary for water selective labeling on PLL as the coupled Hα line was only 160 Hz away from water. Water suppression employed a double echo consisting of a 2-ms Gaussian water refocusing pulse and a 20-μs hard refocusing pulse. The Gaussian pulses were calibrated by maximizing the water suppression on one scan using a single echo WATERGATE sequence (34). In the WEX sequence, amide buildup was monitored as a function of mixing time. To suppress unwanted multiple quantum transitions, the water selective pulse was turned off for two shots, and these two scans were subtracted from the two with the pulse turned on. The recycle predelay was 6 s with tm = 2, 6, 11, 16, 21, 26, 41, 51, 71, 91, 101, and 151 ms. For faster exchange rates, more points were acquired below 10 ms (3, 3.5, and 5 ms) to better characterize the magnetization transfer. For water suppression, TE was 6 ms, which produced a TR of 6–6.16 s. The total data collection times for the 16 scans of 12 different time points took ∼20 min.
QUEST experiments used the saturation-transfer pulse sequence shown in Fig. 1b, consisting of a saturation pulse with variable offset followed by a spin echo acquisition with TE = 6 ms. Data were collected by varying the saturation time and keeping the power constant. The maximum duration of the saturation pulse was 11 s, with a 6-s recycle predelay, yielding TR values of 6–17 s. This time series was collected at two frequencies, one on resonance with the exchangeable protons (+Δωsw) and a second on the opposite side (−Δωsw) of the water line, which for 11 time points resulted in 4.5 min of data collection. QUEST data were taken at two saturation powers (ω1/2π), 100 or 200 Hz. For data where the linewidth-based estimate of the exchange rate was <400 Hz (Table 1), we carried out the magnetization transfer experiment using a saturation field strength of 100 Hz. For rates larger than 400 Hz, we used a saturation field strength of 200 Hz (ω1/2π). This choice was justified by our preliminary simulations, which indicated that optimum transfer of saturation occurs with saturation fields of ∼200–250 Hz for exchange rates between 400 Hz and 2 kHz and was ∼100–125 Hz for exchange rates below 400 Hz as long as R2w < 2 Hz. Since the water linewidth (<1 Hz for all samples) was much smaller than either on-resonance saturation field used, additional shimming of the water line should not have any impact on the results.
QUESP data were collected using the same pulse sequence in Fig. 1b, by varying the saturation power while keeping the saturation time constant. For all of the QUEST data collected above, PTR reached a steady state by ∼10 s, which we therefore used for the saturation time. TR was then 16 s and TE was 6 ms. Similar to QUEST, QUESP data were collected at two frequencies (±Δωsw). The saturation field strengths used were 50, 75, 100, 150, 200, and 250 Hz, which resulted in a total data collection time of just over 3 min.
Data Fitting and Modeling
Linewidths and peak integrals in the excite–detect and WEX spectra were determined using a mixed Gaussian/Lorentzian deconvolution as implemented in Xwinnmr3.5 (Bruker). For the SPD-5 dendrimer there were three amide lines. All lines were fit to a Lorentzian peakshape, except the right-most peak. For this peak the best fit (lowest χ2) was obtained by using a 70% Lorentzian, 30% Gaussian peak, which was cross-checked for pH 6.3, 6.7, and 7.0 where the three peaks could be seen prominently. For PLL, we fit the single peak to a Lorentzian lineshape. The mixing-time-dependent (WEX), saturation-time-dependent (QUEST), and saturation-power-dependent (QUESP) signal intensity curves were fit using Matlab 6.5's (The Mathworks, Inc.) nonlinear fitting routines. Errors (95% confidence limits) were estimated using the F statistic.
The linewidths of the excite–detect spectra were related to the exchange rate using Eq. [1]. The WEX data were fit to Eq. [2] with the Levenburg–Marquardt routine. This expression was normalized by setting S0 = 1 and scaling the maximal signal via Eq. [3] to remove S0 from the fitting. For SPD-5, the deconvolution of the three peaks not baseline resolved introduced an additional error into the peak measurement. Therefore, the maximum signal was determined by averaging the data at the three longest mixing times.
The QUEST and QUESP data were fit both analytically using Eq. [4] and numerically using Eqs. [10–15]. For the analytical fits, we fit our experimental data collected at both frequencies (±Δωsw) using Eq. [8] to relate MTRasym to PTR. Numerical solutions to the six Bloch equations including direct saturation (Eqs. [10–15] in the Appendix) were obtained using the ordinary differential equation solver. These were solved using the initial conditions of [0, 0, M0s/M0w, 0, 0, 1] for [Mxs, Mys, Mzs, Mxw, Myw, Mzw], respectively, and with an error tolerance for each integration step of 10−6. Since these coupled equations are linear, they could also be solved using the Matlab expm function (22), which should increase speed. The results were fed into the least squares nonlinear fitting routine in Matlab. Fitting MTRasym would be too time consuming for the numerical fits, because we would have to solve at least 12 equations (6 for +Δωsw and 6 for −Δωsw). Therefore, for QUEST, we fit the data collected at one frequency, +Δωsw, to Mzw, obtained by solving the 6 equations for as a function of time. For QUESP data, the fits were even more time consuming because for each dataset we must numerically solve the 12 equations for a 10-s saturation time at six different saturation powers (70 equations). Therefore, instead of iteratively fitting the data, we computed MTRasym as a function of saturation power for a grid of exchange rates between 50 and 1300 Hz in steps of 25 Hz and then estimated the exchange rate by finding the best fit between experiment and the grid. There are six parameters in the Bloch equations: ksw, xCA, R1s, R2s, R1w, and R2w. Since R1 and R2 of both bulk water and solute should not change much from sample to sample, we measured these separately. R1w was determined to be 0.248 Hz by using an inversion-recovery experiment with a weak gradient to remove effects of radiation damping (27) and crosschecked by floating it between 0.240 and 0.260 Hz and fitting the experimental MTRasym for the QUEST datasets. R1s was estimated to be 0.71 Hz from the same inversion recovery experiment by looking at the other protons in the solute and then crosschecked by allowing this to float between 0.5 and 1.0 Hz and fitting the experimental MTRasym for the QUEST datasets. This compares well to literature values for proteins (35). R2w was estimated from the direct saturation of water in the saturation transfer experiment to be 0.6 ± 0.1 s−1 by comparing the water line with saturation at to no saturation (S0w). In addition, R2s was approximated by R2 of Hα in PLL (39 s−1) because the proton–proton dipole couplings will dominate the relaxation (28), and this is the nearest proton to HN. xCA = M0s/M0w was measured for all samples using a 64-scan excite–detect experiment (Table 1).
To evaluate the range over which the analytical solution (Eq. [4]) is valid for the QUEST and QUESP experiments as a function of frequency offset from water and water linewidth, we generated synthetic data for a series of exchange rates using Eqs. [10–15] in the Appendix, under the same conditions as our experiments. The offset Δωsw was varied from 4 kHz to 1077 Hz, which is equivalent to the amide splitting from 26 to 7 T fields. Relaxation parameters were kept the same as determined previously, and xCA = 1/1400 was used. For QUEST, saturation times of 4, 8, and 10 s were used. The saturation power was 100 Hz for exchange rates less than 400 Hz and 200 Hz for exchange rates that were higher as was the case for the experiments, except for the curves with R2w = 10, 20 Hz where a 100-Hz saturation field was used throughout because of the large spillover occurring by 200 Hz. Synthetic QUESP data sets were generated with ω1 = 50, 100, 150, 200, and 300 Hz. The saturation time was 10 s.
To calibrate the pH dependence of the amide proton exchange rates for PLL and SPD-5, we followed the example in Gregory et al. (36) and fit the function
| [9] |
in which k0 (spontaneous exchange), ka (acid catalyzed exchange), kb (base catalyzed exchange) are used as fitting constants. The exchange rates were averaged over the four methods (linewidth, WEX, QUEST, QUESP) and fit using the Levenburg–Marquardt algorithm as implemented in Matlab 6.5 (The Mathworks, Inc.) to Eq. [9].
Results
Linewidth and WEX Experiments
Figures 2a and b show the pH dependence of the amide resonances for SPD-5 and PLL, respectively. The dendrimer spectrum consists of three amide lines, which converge at low pH. The middle peak is small in all cases and tough to separate, while the right peak is characterized by a slow exchange rate (∼30 Hz) and limited pH dependence. The broader left peak responds sensitively to pH and will therefore be of most influence on the z-spectra used in the QUEST and QUESP experiments. Therefore, this peak was used to extract the exchange rates using the fits shown in Fig. 2 (dashed lines).
FIG. 2.
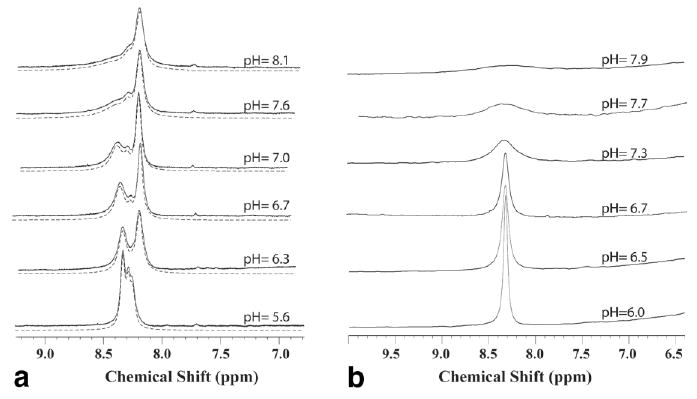
Amide region of the 1D 1H NMR spectra for the contrast agents over the range of pH's studied. All spectra were aquired using π/2-acquire without water suppression. (a) The 28.8-kDa G5 PAMAM dendrimer (SPD-5). Spectra are solid lines; fits as described under Materials and Methods are dashed. (b) The 708-kDa poly-l-lysine
Figures 3a and b show the pH dependence of the experimental WEX buildup curves for PLL and SPD-5, respectively, along with the best fits from the model (Eq. [2]). In all cases, the first 30 ms of data define the buildup quite well and provide good fits of the buildup curves. However, for higher pH, where the exchange rates are more than a few hundred Hertz, very small changes in the buildup curves have a large effect on the fit and are less accurate. For example for pH 7.3 for PLL in Fig. 3b, the peak builds up to 80% of the maximum intensity within 5 ms. In agreement with this, the WEX and linewidth rates are comparable for lower exchange rates (<300 Hz) but deviate for higher values. From Fig. 3, it is clear that the equation produces reasonable fits with the data. For SPD-5, the agreement is not so good at pH 5.6. However, this is not unexpected, because it can be seen in Fig. 2a that the deconvolution of the peaks is particularly challenging at this pH, so the linewidth measurement should be less reliable. All other exchange rates are in good accord with linewidth data and, consequently, these two approaches can be used as standard for the newly developed QUEST and QUESP approaches. This is true even for the pH 6.7 PLL (30 kDa PLL), the separate sample composed of a smaller polymer.
FIG. 3.
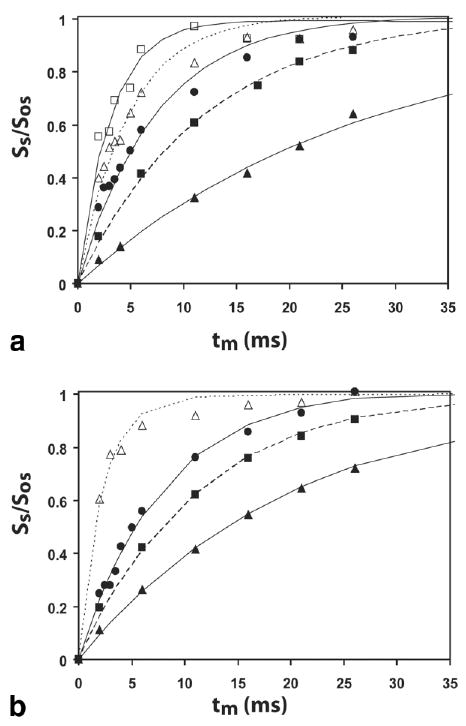
Experimental solute signal intensities for the WEX experiment as a function of pH, along with best fit using Eq. [7]. (a) SPD-5 experimental data were obtained at ▲ pH 5.6, ■ 6.3, ● 6.7, △ 7.0, and □ 7.6. (b) PLL experimental data were obtained at ▲ pH 6.0, ■ 6.5, ● 6.7, and △ 7.3.
Saturation Transfer Experiments
Figure 4 shows the frequency dependence of the saturation transfer effect on water (z-spectra, Figs. 4a and c) and the calculated MTRasym (Figs. 4b and d) for the two contrast agents. The MTRasym dependence on the saturation time (QUEST data) is shown as a function of saturation time at various pH values in Fig. 5 for SPD-5 (Fig. 5a) and PLL (Fig. 5b). For exchange rates slower than 400 Hz, ω1/2π = 100 Hz, the best fits shown are the analytical solutions (Eq. [4]), which fit the data reliably in this range. This equation can be used successfully at this power level because the spillover is less than 1%, and the weak RF saturation field approximation holds. For exchange rates faster than 400 Hz, the experimental data were collected with a 200-Hz saturation field. The analytical fits in Fig. 5 are still excellent for these exchange rates. However, this is misleading because the determined rates are incorrect above about 500 Hz, as judged from comparison with the numerical and linewidth results in Table 1. This discrepancy will be discussed further below. In addition, for the fastest exchange rate, PLL at pH 7.9, there is very little change in MTRasym with exchange rate at 1200 Hz or higher using Eqs. [10–15]. As such, the 95% confidence interval for this exchange rate determination is much broader than the lower exchange rates and also that obtained using Eq. [4].
FIG. 4.
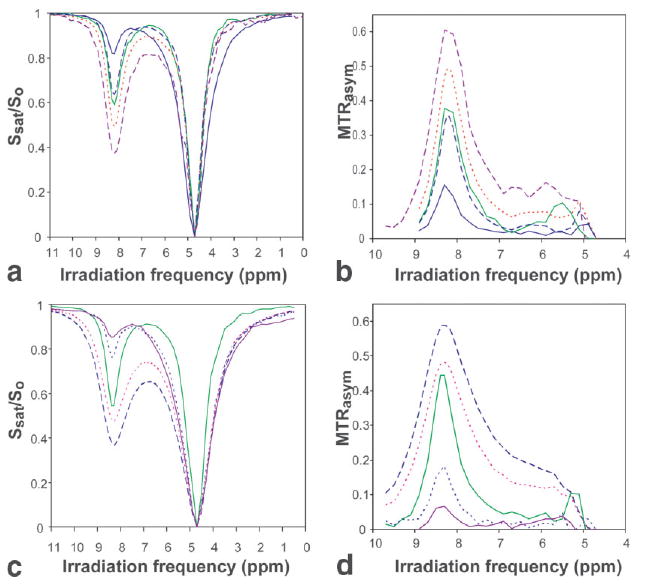
Saturation transfer as a function of saturation frequency (z-spectra) at 37°C and resulting MTRasym spectra calculated using Eq. [8]. (a) z-spectra of SPD-5 as a function of pH: 5.6 (—), 6.7 (--), 7.0 (—), 7.6 (⋯) and 8.1(--). (b) MTRasym for SPD-5 as a function of pH, frequency. (c) Experimental z-spectra of PLL as a function of pH: 6.0 (--), 6.5 (⋯), 7.3 (—), 7.7 (⋯) and 7.9 (--). (d) Resulting MTRasym for PLL as a function of pH and frequency.
FIG. 5.
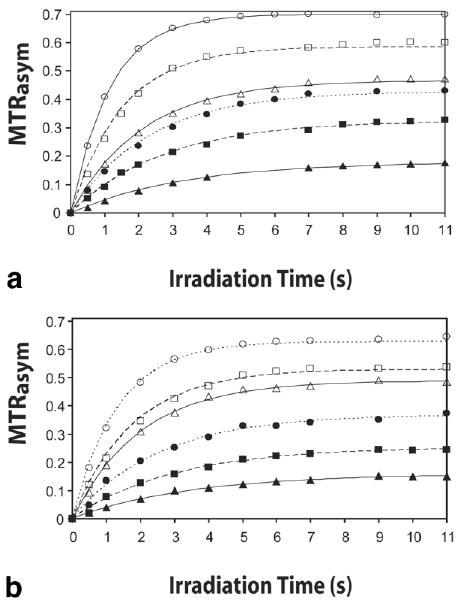
QUEST results. Plot of MTRasym as a function of saturation time at various pH values together with best fits to the Eq. [4]. (a) SPD-5 data: ▲ pH 5.6, ■ 6.3, ● 6.7, △ 7.0, □ 7.6, ○ 8.1. (b) PLL data: ▲ pH 6.0, ■ 6.5, ● 6.7, △ 7.3, □ 7.7, ○ 7.9.
In Fig. 6, the analytical QUESP fits are shown for both SPD-5 (Fig. 6a) and PLL (Fig. 6b). Again, the determined exchange rates are not correct for the 500-Hz and higher range, as judged from comparison with the linewidth and numerical results. In addition, for the fastest exchange rates, i.e., PLL, pH 7.7, 7.9, and SPD-5, pH 8.1, Eq. [4] substantially overestimates the MTRasym occurring at lower saturation powers (50, 75, 100 Hz), due to a breakdown in this approximation, as will be mentioned in the Discussion. As a result, the first several points on the graph aren't in good agreement.
FIG. 6.
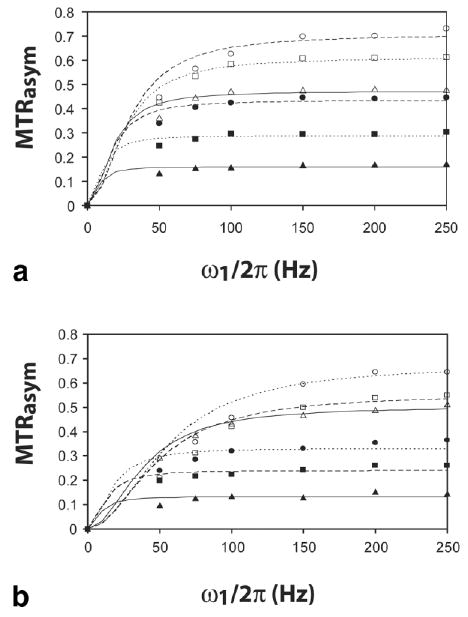
QUESP results. Plot of saturation power dependence of MTRasym at various pH values together with best fits to the Eq. [4]. (a) SPD-5 data: ▲ pH 5.6, ■ 6.3, ● 6.7, △ 7.0, □ 7.6, ○ 8.1. (b) PLL data: ▲ pH 6.0, ■ 6.5, ● 6.7, △ 7.3, □ 7.7, ○ pH 7.9.
Validity of Analytical Solution for QUEST, QUESP
Figures 7a and b compare exchange rates obtained from the QUEST analytical and numerical fits as a function of water–solute frequency offset and water linewidth, respectively by fitting QUEST simulated datasets obtained by solving Eqs (10–15) to Eq. [4]. The analytical equation produces errors of lower than 10% for all exchange rates below 200 Hz. Above 200 Hz, errors for the analytical fit accumulate quickly and depend primarily on Δω and R2w, parameters that effect the direct saturation of the water line. For the 11.7 T amide–water frequency difference (Δω = 1800 Hz, R2w = 0.6 Hz), there is only a 10% deviation at 500 Hz. The error is produced by the lack of terms accounting for direct saturation in Eq. [4] and increases with exchange rate. This occurs because the change in MTRasym with ksw drops as ksw increases for a fixed saturation field. The error is reduced by using the Eq. [8] definition of MTRasym, as opposed to dividing by S0w, but not completely eliminated. For the Δω = 4000 Hz curve, Fig. 7a, the spillover contribution to the error is reduced to 0.7%, allowing accurate predictions of exchange rates up to ∼600 Hz. In Fig. 7b, the agreement between the analytical and numerical solutions is shown as a function of R2w, setting Δω = 1800 Hz. For R2w < 2 Hz, the analytical model underestimates the exchange rate by 10% or less for exchange rates <300 Hz. The agreement deteriorates more rapidly for increasing R2w, already producing errors of 18% for R2w = 10 Hz by the time the exchange rate is 300 Hz. Direct saturation increases as R2w increases and is the primary source of this error.
FIG. 7.
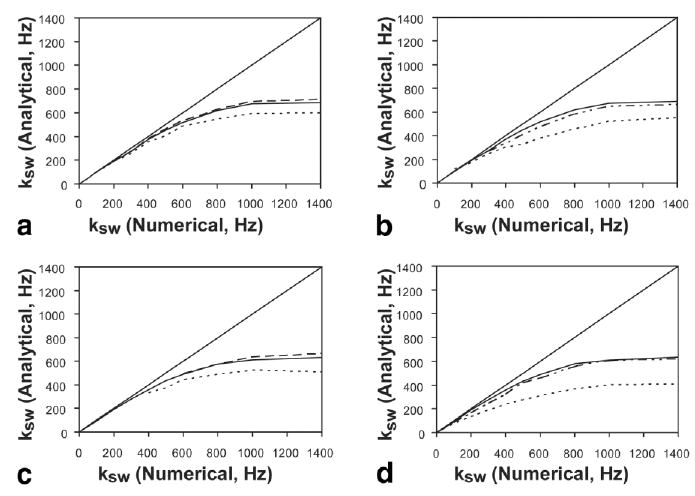
Comparison of analytical versus. numerical models for simulated QUEST (a and b) and QUESP (c and d) data as a function Δω (a and c) and R2w (b and d). (a) QUEST comparison as a function of Δω. (b) QUEST comparison as a function of R2w. (c) QUESP comparison as a function of Δω. (d) QUESP comparison as a function of R2w. The Δω-values simulated were 4000 (– –), 1800 (–), 1077 Hz(---), while the dependence on R2w used values of 0.6 (–), 2.0 (−●, ●), and 10.0 Hz (---).
Figures 7c and d compare the analytical and numerical solutions for the QUESP experiment. This experiment produces a slightly poorer agreement, because the analytical solution is less accurate for saturation fields (ω1) lower than the exchange rate. As the QUEST experiment keeps ω1 at a high value, the error is reduced. Another problem occurs for the higher ω1/2π data points, which produce more direct saturation of the water line. This can be seen by comparing the R2w = 2, 10 Hz curves in Fig. 7d with those in Fig. 7b. Since such spillover is ignored in Eq. [4], the result is an underestimation of the exchange rate.
pH Dependence of the Exchange Rate
Figure 8 compares the measured exchange rates as a function of pH to the pH calibration curve produced using Eq. [9] for PLL and SPD-5. The best fit was k0 = 68.9 Hz, ka = 1.21 Hz, kb = 1.92 × 109 Hz for PLL and k0 = 106.4 Hz, ka = 25.8 Hz, kb = 5.45 × 108 Hz for SPD-5. As can be seen, the base-catalyzed term dominates this fitting for both agents, and the exchange rate is highly responsive to pH changes.
FIG. 8.
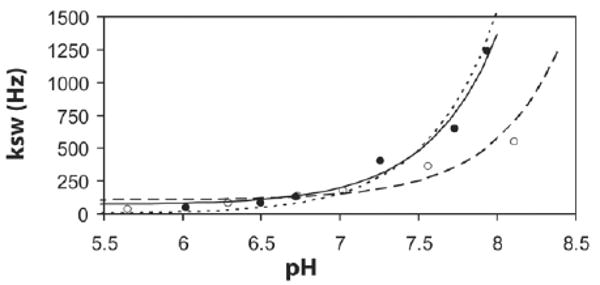
Dependence of the proton exchange constant on pH at T = 37°C for the two different contrast agents: PLL, SPD-5. Exchange rates are the average of those obtained by the four different measurements, and lines are the best fits using Eq. [9]. For PLL the solid line represents our fit (–), and the dashed line(---) represents the fit using constants found in Bai et al. (40) translated to 37°C as described in this reference. For SPD-5 the line (– –) is our best fit.
Discussion
MRI Methodology for Measuring Exchange Rates
The methods used to measure exchange rates in this paper fall under two classes. In the first class exchangeable peaks were detected directly (WEX and Linewidth), and in the second chemical exchange was indirectly detected by observing changes in the water peaks (QUEST and QUESP). Both direct detect methods suffer from the sensitivity of this exchangeable peak due to the low concentrations of the contrast agent, which is reduced further at high exchange rates due to broadening of the resonance. The WEX experiment has been shown previously to reliably measure exchange rates of amide protons in proteins (16,25), with potential errors occurring from spin diffusion and the appearance of pure CαH-NH NOE peaks. The present data were acquired with a narrow-banded Gaussian refocusing pulse (Fig. 1a) to minimize the latter, and for these CEST agents, the exchange rate is fast enough to ignore spin diffusion effects and use Eq. [2] to model the magnetization transfer. However, using the WEX experiment to measure exchange rates more than a few hundred Hertz suffers from several drawbacks. Small changes in the buildup curves collected have a large effect on the fit at these rates, which are therefore less accurate. In addition, the intensity of the exchangeable peak after water suppression will be reduced due to fast exchange with saturated water protons, which produces errors in the integrated peak area.
The data in Table 1 and Figs. 2, 3, 5, and 6, obtained through 1D NMR experiments on the water resonance, show that QUEST and QUESP, which take advantage of the high sensitivity of the water signal and can be used with any MRI pulse sequence, provide exchange rates that are on the same order of magnitude as those determined by established spectroscopic methods. For SPD-5 in the pH range from 5.7 to 7.6, the agreement with linewidth and WEX estimates is well within experimental error. Even though the exchange rates produced by the analytical fits are systematically lower than those obtained numerically, the overall agreement between the exchange rates obtained numerically and analytically is quite acceptable between pH 5.6 and 7.0. For PLL, the pH range from 6.0 to 7.3 has sufficiently slow rates to show good agreement among all methods, while for the larger exchange rates at higher pH, the rates are correct only for the numerical fits, but underestimated for the analytical ones. We expect that the main source of error in the QUEST and QUESP determinations of ksw must be an error in the experimental determination of xCA. For this reason, we chose the sharpest resonance for PLL (Hε) to measure xCA experimentally. In addition, for the higher exchange rates such as PLL at pH 7.7 the error is asymmetric. This occurs because the change in MTRasym with exchange rate drops as this rate approaches the chemical shift separation between the exchangeable peak and water.
It is clear from the above results that, even though the QUEST MRI technique is suitable for estimating proton exchange rates for CEST agents, care must be taken in the interpretation of these rates. When using the analytical approach, the determined exchange constants are correct until they reach about 400–500 Hz. Above that, the numerical approaches must be used. The main problem with respect to quantification occurs when competing processes saturate the water signal in addition to the CEST effect. For the present in vitro examples, direct water saturation is the only effect, but, when working in vivo, conventional magnetization transfer (MT) effects would also contribute. The magnitude of direct water saturation depends on the relationship between the frequency difference between the solute proton and water (Δωsw), the exchange rate (ksw), the saturation bandwidth, and the water linewidth (proportional to the transverse relaxation rate, R2w). The effects of R2w, ksw, and Δωsw are shown in Fig. 7. The simulations carried out to analyze our experimental data revealed three things: (a) the analytical solution for MTRasym is accurate with these relaxation measurements at 11.7 T for exchange rates lower that 500 Hz, (b) the reliability of the analytical solution degrades as R2w increases, and (c) the effect the exchange rate has on MTRasym levels off as it approaches Δω. Additionally, the proper choice of saturation field for measuring exchange rates is influenced by R2w. Having R2w ≥ 2 Hz will dictate using a lower saturation field to reduce the amount of spillover, with the optimal field ∼125 Hz for R2w = 20 and ksw = 1400 Hz. This is important to realize when carrying these experiments out in vivo. Even though no CEST agents have yet been tested in vivo, CEST-like experiments are feasible, as has been demonstrated for endogeneous proteins/peptides by Zhou et al. (29,37). Even though all effects interfere, the larger exchange rate of the PLL and SPD-5 compounds should allow us to use this approximation.
In addition to these arguments based on the simulation results, it should be realized that a proper choice of ω1 field is particularly important for the QUEST experiment. For exchange rates of 600 Hz or higher, 100-Hz saturation fields will not allow us to measure the exchange rate accurately because the rate of MTRasym change with change in exchange rate drops and for exchange rates higher than 800 Hz, the MTRasym decreases with increasing exchange rate. Therefore, ω1/2π must be raised to measure these exchange rates. If a 200-Hz saturation field is used, the MTRasym increases at 10 s saturation all the way up to 1400 Hz and thus allows measurement of higher exchange rates.
In summary, for QUEST, the numerical fits provide a reliable estimate of the exchange rates in all cases. The exchange rate for SPD-5 at pH 7.6 is higher than that measured by QUESP, WEX, and linewidth, but this deviation falls within the 95% confidence limits of the measurement. For PLL, the exchange rate agrees quite well with the rate measured by WEX, linewidth, and QUESP as expected. The main source of error for this experiment is expected to be the measurement of xCA, which the other methods are not dependent on. As can be seen in Eq. [4], MTRasym depends on ksw × xCA, and so it is difficult to decouple these effects, and so an accurate measure of xCA is important to measure the exchange rate.
The QUESP technique has a few more pitfalls. For exchange constants below 300 Hz, there is a large change in MTRasym with saturation power, and this experiment is relatively robust, although it degrades more rapidly with increasing R2w than QUEST, with 10% errors in ksw at 100 Hz with R2w = 2 Hz. For 300- to 800-Hz exchange rates, there is almost no change in MTRasym with saturation powers of 100 Hz or lower. Therefore, the data taken using the higher power saturation fields (above 100 Hz) define the exchange rate obtained from the fits. In addition, Eq. [4] isn't accurate when ω1/2π < ksw, leading to MTRasym being overestimated compared to Eqs. [10–15]. This is worse than for QUEST, where we pick an optimal power for the measurements and all time points contribute. Separately the numerical fits to Eqs. [10–15] required to fit the QUESP dataset are much more computationally expensive than QUEST and, experimentally, there are also limitations on the saturation power due to probe breakdown and SAR considerations with R1w = 0.248 Hz. Because of this, we did not explore using higher power saturation pulses than 250 Hz. As for QUEST, the PLL data at pH 7.7 and 7.9 and the SPD-5 data at pH 8.1 give large errors in the ksw due to the reduced change in MTRasym as a function of exchange rate for large exchange rates.
In summary, the fitting QUESP data to the numerical solutions to the Bloch equations produce exchange rates that are consistent with linewidth, WEX, and QUEST measurements. As in QUEST, MTRasym depends on ksw × xCA, and so it is difficult to decouple these effects without explicitly measuring xCA separately. However, this experiment is less desirable to carry out in vivo than QUEST.
In order to estimate whether the Eq. [4] can be used for a given experiment, there are several assumptions that must be met: (1) ksw ≪ ω1 (2) ksw ≪ Δω, and (3) arctan (ω1/Δω) < 30°, which can be derived from Sun et al. (38) and Baguet et al. (39). The ω1/2π = 50, 75, 100 Hz data points of the QUESP experiment for PLL pH 7.9, 7.7 don't meet condition 1, causing a breakdown in Eq. [4]. Condition 2 can be seen in Table 1, where at ∼Δω/3 the error exceeds 10%. In addition, the equivalency of MTRasym to PTR in Eq. [8] links the relative values for Δω, R2w, and ω1 to the accuracy of Eq. [4]. For example, if Δω = 4kHz (instead of 1.8 kHz, as might be the case for a ParaCEST agent), exchange rates up to 1 kHz can be measured with ω1/2π ∼ 500 Hz. If then R2w = 6 Hz (instead of 0.6 Hz), the direct saturation increases at higher power, so the maximum exchange rate drops to 600 Hz, which is best measured with a ω1/2π ∼ 300 Hz. Here the direct saturation is ∼12% about the maximum allowable direct saturation for the equivalence of Eq. (8) to hold, which corrects for direct saturation. Proper choice of power has been described elsewhere (38).
For in vivo measurements, where R2w may be 10–20 Hz depending on field strength, caution must be exercised when interpreting QUEST data using the analytical expression due to the direct saturation. In this case, the exchange rates should be reliably estimated as long as they are less than 100–200 Hz, depending on the tissue and field strength. The QUESP experiment is less suited for in vivo measurements than QUEST due to the collection of higher ω1/2ω data with higher direct saturation.
pH Dependence of the Exchange Rate
The results show that both SPD-5 and PLL can be used as pH contrast agents in the physiologic range. Each compound may have specific advantages, but PLL, which has a single resonance and a faster exchange rate, may be the most practical for in vivo applications. Equation [9] was used to calibrate the dependence of exchange rate on pH for these agents. This expression is nice, because it can be translated to different temperatures, as mentioned by Bai et al. (40). The pH 6.7 PLL data were taken on a smaller polymer (30 kDa versus 705.8 kDa), but as can be seen this exchange rate falls on top of the fit, implying that for PLL the size change doesn't affect this rate. Bai et al. (40) used a set of peptides (including PLL) at low salt conditions to obtain a general pH calibration for amide protons with k0 = 0.004 Hz, ka = 0.965 Hz, kb = 2.28 × 109 Hz. Even though he used different salts/concentrations, the agreement is quite reasonable with our PLL data and only starts to really deviate below pH 6.7. This could be due to the presence of phosphates in our buffer, which also catalyze proton exchange (11).
If these agents were to be used in vivo, their effect would compete with MT effects and with the amide proton transfer (APT) effects of endogenous mobile proteins and peptides. For these latter compounds, which have not yet been identified, Zhou et al. (29) used just the base-catalyzed term and found kb = 3.28 × 108 (adjusting kb so that pKw = 14.17, the value we used). Even neglecting the other two terms, for PLL our best fit was obtained with kb = 2.13 × 109, which is a factor of ∼6.5 higher. However, a different exchange rate is not sufficient to separate out these compounds from the background, because there is no internal reference for the endogenous effects. Therefore, a control measurement in a normal tissue (other animal/human) must be performed as reference. This would constitute comparison with normal controls, which is quite common in the clinic. Using these expressions, we could map the pH for CEST agents using either the QUEST or the QUESP experiments proposed. Because of these extra proton pools from the semi-solid lattice (conventional MT) and endogenous mobile proteins/peptides (APT), the simple two pool model is only a first-order approximation. However, using the definition of MTRasym in Eq. [8] to partially correct for tissue MT effects and using a calibration curve for the agent to determine the pH, reasonable results should be attainable.
Conclusions
We have developed two new methods for measuring proton exchange rates of solutes using the water signal and carried out a systematic study of the pH dependence of the exchange rate for two poly cationic CEST contrast agents. The set of exchange constants determined above from the four types of measurements are all self-consistent within the error ranges. The QUEST method appears to be the best method to measure the exchange rate for high exchange rates, due to the fitting being computationally less expensive, and the contribution of all the data toward measuring the exchange rate. In addition, for the two experiments proposed QUEST and QUESP, care must be taken in the interpretation of these rates via the analytical solution, which depends on the relationship between the parameters involved, i.e., the frequency difference between the solute proton and water, the exchange rate, the irradiation power, and the water linewidth (proportional to the transverse relaxation rate).
We found the amide proton exchange contrast for these compounds to be highly dependent on pH, making them potential pH indicators for use in vivo, with the benefit of being biodegradable molecules, unlike other conventional metal-based contrast agents. From the modeling of the contrast in the MT experiment with chemical exchange rate we found that the power and saturation time effects can be modeled reliably using the Bloch equations and is consistent with the MR measurements. Thus, this type of modeling can assist future adjustment of experimental parameters, in order to optimize MR studies using these agents.
Acknowledgments
NIH; Grant number: R21 EB005252
Appendix
Assuming a small pool of solute protons (s), a large pool of water protons (w) while applying B1 along the x axis, the Bloch equations for a two-pool proton exchange model are (6)
| [10] |
| [11] |
| [12] |
| [13] |
| [14] |
| [15] |
in which ω0 = γB0 and ω1 = γB1; Δωs and Δωw are the chemical shift differences between the saturation pulse and the solute and water resonance frequencies, respectively; M0 is the equilibrium magnetization; proton exchange between the two pools occurs with rates ksw (solute [rtarrow] water) and kws (water [rtarrow] solute) and kswM0s = kwsM0w at equilibrium. For low power fields of 5–100 Hz, spillover of saturation between the two pools is quite negligible (only 1% loss as measured by Eq. [7]) at 11.7 T, because the separation between the amide protons and water is about 1800 Hz. For fields as large as 200 Hz, there is a larger loss (∼3%) due to spillover. These effects, not included in Eq. [4], become significant as the exchange rates increase, although they are partially offset by defining MTRasym using Eq. [8]. When experimental data are fit to Eq. [4], the fit produces a lower exchange rate than the actual one as mentioned in the Discussion. In addition to the saturation field, the relaxation parameter R2w also affects the spillover as discussed in the Discussion. This is due to the relationship between R2w and the water linewidth, with the spillover increasing with this width.
References
- 1.Ward K, Aletras A, Balaban R. A new class of contrast agents for MRI based on proton chemical exchange dependent saturation transfer (CEST) J Magn Reson. 2000;143:79–87. doi: 10.1006/jmre.1999.1956. [DOI] [PubMed] [Google Scholar]
- 2.Goffeney N, Bulte JW, Duyn J, Bryant LH, Jr, van Zijl PC. Sensitive NMR detection of cationic-polymer-based gene delivery systems using saturation transfer via proton exchange. J Am Chem Soc. 2001;123:8628–8629. doi: 10.1021/ja0158455. [DOI] [PubMed] [Google Scholar]
- 3.Aime S, Delli Castelli D, Terreno E. Novel pH-reporter MRI contrast agents. Angew Chem Int Ed Engl. 2002;41:4334–4336. doi: 10.1002/1521-3773(20021115)41:22<4334::AID-ANIE4334>3.0.CO;2-1. [DOI] [PubMed] [Google Scholar]
- 4.Zhang S, Merritt M, Woessner DE, Lenkinski RE, Sherry AD. PARACEST agents: modulating MRI contrast via water proton exchange. Acc Chem Res. 2003;36:783–790. doi: 10.1021/ar020228m. [DOI] [PubMed] [Google Scholar]
- 5.Snoussi K, Bulte JW, Gueron M, van Zijl PC. Sensitive CEST agents based on nucleic acid imino proton exchange: detection of poly(rU) and of a dendrimer-poly(rU) model for nucleic acid delivery and pharmacology. Magn Reson Med. 2003;49:998–1005. doi: 10.1002/mrm.10463. [DOI] [PubMed] [Google Scholar]
- 6.Zhou J, Wilson DA, Sun PZ, Klaus JA, van Zijl PCM. Quantitative description of proton exchange processes between water and endogenous and exogenous agents for WEX, CEST, and APT experiments. Magn Reson Med. 2004;51:945–952. doi: 10.1002/mrm.20048. [DOI] [PubMed] [Google Scholar]
- 7.Terreno E, Castelli DD, Cravotto G, Milone L, Aime S. Ln(III)-DOTA-MGIY complexes: a versatile series to assess the determinants of the efficacy of paramagnetic chemical exchange saturation transfer agents for magnetic resonance imaging applications. Invest Radiol. 2004;39:235–243. doi: 10.1097/01.rli.0000116607.26372.d0. [DOI] [PubMed] [Google Scholar]
- 8.Aime S, Calabi L, Biondi L, De Miranda M, Ghelli S, Paleari L, Rebaudengo C, Terreno E. Iopamidol: Exploring the potential use of a well-established x-ray contrast agent for MRI. Magn Reson Med. 2005;53:830–834. doi: 10.1002/mrm.20441. [DOI] [PubMed] [Google Scholar]
- 9.Englander SW, Kallenbach NR. Hydrogen exchange and structural dynamics of proteins and nucleic acids. Q Rev Biophys. 1984;16:521–655. doi: 10.1017/s0033583500005217. [DOI] [PubMed] [Google Scholar]
- 10.Roder H, Wagner G, Wuthrich K. Individual amide proton exchange rates in thermally unfolded basic pancreatic trypsin inhibitor. Biochemistry. 1985;24:7407–7411. doi: 10.1021/bi00346a056. [DOI] [PubMed] [Google Scholar]
- 11.Liepinsh E, Otting G. Proton exchange rates from amino acid side chains–implications for image contrast. Magn Reson Med. 1996;35:30–42. doi: 10.1002/mrm.1910350106. [DOI] [PubMed] [Google Scholar]
- 12.Mori S, Eleff SM, Pilatus U, Mori N, van Zijl PC. Proton NMR spectroscopy of solvent-saturable resonances: a new approach to study pH effects in situ. Magn Reson Med. 1998;40:36–42. doi: 10.1002/mrm.1910400105. [DOI] [PubMed] [Google Scholar]
- 13.Ward K, Balaban RS. Determination of pH Using Water Protons and Chemical Exchange Dependent Saturation Transfer (CEST) Magn Reson Med. 2000;44:799–802. doi: 10.1002/1522-2594(200011)44:5<799::aid-mrm18>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
- 14.van Zijl PCM, Goffeney N, Duyn JH, Bryant LH, Jr, Bulte JWM. The use of starburst dendrimers as pH contrast agents. Proceedings of the 9th Annual Meeting of ISMRM; Glasgow, Scotland. 2001. p. 878. [Google Scholar]
- 15.Aime S, Barge A, Delli Castelli D, Fedeli F, Mortillaro A, Nielsen FU, Terreno E. Paramagnetic lanthanide(III) complexes as pH-sensitive chemical exchange saturation transfer (CEST) contrast agents for MRI applications. Magn Reson Med. 2002;47:639–648. doi: 10.1002/mrm.10106. [DOI] [PubMed] [Google Scholar]
- 16.Mori S, Abeygunawardana C, Pv Zijl, Berg J. Water exchange filter with improved sensitivity (WEX II) to study solvent-exchangeable protons. application to the consensus zinc finger peptide CP-1. J Magn Reson B. 1996;110:96–101. doi: 10.1006/jmrb.1996.0015. [DOI] [PubMed] [Google Scholar]
- 17.Jeener J, Meier BH, Bachmann P, Ernst RR. Investigation of exchange processes by 2-dimensional NMR-spectroscopy. J Chem Phys. 1979;71:4546–4553. [Google Scholar]
- 18.Forsen S, Hoffman RA. Study of moderately rapid chemical exchange reactions by means of nuclear magnetic double resonance. J Chem Phys. 1963;39:2892–2901. [Google Scholar]
- 19.McConnell HM. Reaction rates by nuclear magnetic resonance. J Chem Phys. 1958;28:430–431. [Google Scholar]
- 20.McConnell BM, von Hippell PH. Hydrogen exchange as a probe of the dynamic structure of DNA: I. General acid-base catalysis. J Mol Biol. 1970;50:297–316. doi: 10.1016/0022-2836(70)90194-4. [DOI] [PubMed] [Google Scholar]
- 21.Kingsley PB, Monahan WG. Effects of off-resonance irradiation, cross-relaxation, and chemical exchange on steady-state magnetization and effective spin–lattice relaxation times. J Magn Reson. 2000;143:360–375. doi: 10.1006/jmre.2000.2018. [DOI] [PubMed] [Google Scholar]
- 22.Woessner DE, Zhang S, Merritt ME, Sherry AD. Numerical solution of the Bloch equations provides insights into the optimum design of PARACEST agents for MRI. Magn Reson Med. 2005;53:790–799. doi: 10.1002/mrm.20408. [DOI] [PubMed] [Google Scholar]
- 23.Gutowsky HS, McCall DW, Slichter CP. Nuclear magnetic resonance multiplets in liquids. J Chem Phys. 1953;21:279–292. [Google Scholar]
- 24.Gutowsky HS, Saika A. Dissociation, chemical exchange, and the proton magnetic resonance in some aqueous electrolytes. J Chem Phys. 1953;21:1688–1694. [Google Scholar]
- 25.Mori S, Berg JM, van Zijl PCM. Separation of intramolecular NOE and exchange peaks in water exchange spectroscopy using spin-echo filters. J Biomol NMR. 1996;7:77–82. doi: 10.1007/BF00190459. [DOI] [PubMed] [Google Scholar]
- 26.van Zijl PC, Zhou J, Mori N, Payen JF, Wilson D, Mori S. Mechanism of magnetization transfer during on-resonance water saturation. A new approach to detect mobile proteins, peptides, and lipids. Magn Reson Med. 2003;49:440–449. doi: 10.1002/mrm.10398. [DOI] [PubMed] [Google Scholar]
- 27.van Zijl PCM, Moonen CT. Solvent Suppression Strategies for In Vivo Magnetic Resonance Spectroscopy. NMR Basic Princ Progr. 1992;26:67–108. [Google Scholar]
- 28.Cavanagh J, Fairbrother WJ, Palmer AG, III, Skelton NJ. Protein NMR spectroscopy : principles and practice. San Diego: Academic Press; 1996. p. 271. [Google Scholar]
- 29.Zhou J, Payen JF, Wilson DA, Traystman RJ, van Zijl PC. Using the amid proton signals of intracellular proteins and petides to detect pH effects in MRI. Nat Med. 2003;9:1085–1090. doi: 10.1038/nm907. [DOI] [PubMed] [Google Scholar]
- 30.Kingsley PB, Monahan WG. Corrections for off-resonance effects and incomplete saturation in conventional (two-site) saturation-transfer kinetic measurements. Magn Reson Med. 2000;43:810–819. doi: 10.1002/1522-2594(200006)43:6<810::aid-mrm6>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
- 31.Spencer RGS, Horska A, Ferretti JA, Weiss GH. Spillover and incomplete saturation in kinetic measurements. J Magn Reson B. 1993;101:294–296. [Google Scholar]
- 32.Horska A, Spencer RGS. Correctly accounting for radiofrequency spillover in saturation transfer experiments: application to measurement of the creatine kinase reaction rate in human forearm muscle. MAGMA. 1997;5:159–163. doi: 10.1007/BF02592247. [DOI] [PubMed] [Google Scholar]
- 33.Guivel-Scharen V, Sinnwell T, Wolff SD, Balaban RS. Detection of proton chemical exchange between metabolites and water in biological tissues. J Magn Reson. 1998;133:36–45. doi: 10.1006/jmre.1998.1440. [DOI] [PubMed] [Google Scholar]
- 34.Piotto M, Saudek V, Sklenar V. Gradient-tailored excitation for single-quantum NMR spectroscopy of aqueous solutions. J Biomol NMR. 1992;2:661–665. doi: 10.1007/BF02192855. [DOI] [PubMed] [Google Scholar]
- 35.Grzesiek S, Bax A. The importance of not saturating H2O in protein NMR. Application to sensitivity enhancements and NOE measurements. J Am Chem Soc. 1993;115:12593–12594. [Google Scholar]
- 36.Gregory RB, Crabo L, Percy AJ, Rosenburg A. Water catalysis of peptide hydrogen isotope exchange. Biochemistry. 1983;22:910–917. doi: 10.1021/bi00273a031. [DOI] [PubMed] [Google Scholar]
- 37.Zhou J, Lal B, Wilson DA, Laterra J, van Zijl PC. Amide proton transfer (APT) contrast for imaging of brain tumors. Magn Reson Med. 2003;50:1120–1126. doi: 10.1002/mrm.10651. [DOI] [PubMed] [Google Scholar]
- 38.Sun PZ, van Zijl PCM, Zhou J. Optimization of the irradiation power in chemical exchange dependent saturation transfer experiments. J Magn Reson. 2005;175:193–200. doi: 10.1016/j.jmr.2005.04.005. [DOI] [PubMed] [Google Scholar]
- 39.Baguet E, Roby C. Off-resonance irradiation effect in steady-state NMR saturation transfer. J Magn Reson. 1997;128:149–160. doi: 10.1006/jmre.1997.1230. [DOI] [PubMed] [Google Scholar]
- 40.Bai Y, Milne JS, Mayne L, Englander SW. Primary structure effects on peptide group hydrogen exchange. Protein Struct Funct Genet. 1993;17:75–86. doi: 10.1002/prot.340170110. [DOI] [PMC free article] [PubMed] [Google Scholar]


