Image Guidance of Flexible Tip-Steerable Needles

Abstract

Image guidance promises to improve targeting accuracy and broaden the scope of medical procedures performed with needles. This paper takes a step toward automating the guidance of a flexible tip-steerable needle as it is inserted into human tissue. We build upon a previously proposed nonholonomic model of needles that derive steering from asymmetric bevel forces at the tip. The bevel-tip needle is inserted and rotated at its base in order to steer it in six degrees of freedom. As a first step for control, we show that the needle tip can be automatically guided to a planar slice of tissue as it is inserted. Our approach keeps the physician in the loop to control insertion speed. The distance of the needle tip position from the plane of interest is used to drive an observer-based feedback controller which we prove is locally asymptotically stable. Numerical simulations demonstrate a large domain of attraction and robustness of the controller in the face of parametric uncertainty and measurement noise. Physical experiments with tip-steerable Nitinol needles inserted into a transparent plastisol tissue phantom under stereo image guidance validate the effectiveness of our approach.

I. Introduction

Successful outcomes for needle-based interventions such as interventional brachytherapy, fine needle aspiration biopsy, thermal ablation critically depend on accurate targeting [2], [3]. Improving needle targeting accuracy, and expanding the applicability of needle interventions, in general, involves actively steering a needle as it is inserted into tissue. Physicians often rely on pre- or intra-operative medical imaging to guide a needle to its target. Several factors limit performance, including the amount of steering that a needle affords after it is inserted, noisy sensors, imperfect actuators, and tissue deformations. Furthermore, navigation in 3D under image guidance by manipulating the needle at its base (from outside the patient) requires profound spatial reasoning skills and extensive training. Efforts to overcome these limitations focus on developing new needles and their placement devices [4]–[8], improving imaging modalities for building pre- and intra-operative models [9], developing models that capture tissue-needle interaction [10]–[12], and improved path planning [13]–[18]; refer to Abolhassani et al. [19] for a recent survey on needle insertions.

Building on these recent improvements in needle placement, imaging, and planning, we propose to use model-based feedback control theory for the first time, to the best of our knowledge, for real-time image-based needle guidance. This approach relies on models of needle steering amenable to systems theory (as opposed to, say, finite element models). Recent efforts make progress towards such “plant models” for manipulating a needle from outside the patient. DiMaio and Salcudean [10] show that needles that are stiff relative to the surrounding tissue can be steered by moving the base of the needle to deflect the tissue as the needle is inserted; they model this effect as a kinematic control system with a numerically determined Jacobian matrix that relates base motions to needle-tip motions. Glozman and Shoham [11] model the interaction between a flexible needle and surrounding tissue using virtual springs to compute local deformations. In [14] Glozman and Shoham plan a needle path that avoids obstacles in the work space and then at every time step they invert their virtual spring model to obtain the translation and orientation of the needle base (the inputs) in order to drive the needle back to the planned path in one step.

Webster et al. consider flexible bevel-tip needles that follow a curved path due to asymmetric cutting forces at the needle tip [12]; they model this effect using a nonholonomic, kinematic system, and the present work builds directly on this model. In both the rigid and flexible cases described above, the inputs at the needle base are treated as inputs to a kinematic control system. Among these needle insertion models, the one by Webster et al. seems to be the most amenable to a systems-theoretic approach for control, and is the only such model that has been experimentally validated for tip-steerable needles [12]. We build on this model and apply observer-based feedback control to achieve a desired task. This enables us to articulate analytical performance limits of our controller, such as the domain of attraction. Moreover, our approach only requires the extraction of the needle tip position from images, rather than the entire needle curve, thereby simplifying image segmentation.

Problem statement

A flexible bevel-tip needle [12], [20] can be steered by rotation and insertion at the base of the needle (outside the patient). As the needle is inserted, the asymmetry of the bevel creates a moment at the needle tip, deflecting the needle and causing it to follow a circular arc. As the needle base is rotated, the bevel tip is reoriented in space, so that subsequent insertion follows an arc in a new plane.

As the needle is pushed through tissue, there is a small amount of tissue deformation and the needle must be steered to avoid bones and other sensitive organs through which it cannot or should not pass. To address this problem, Alterovitz et al. propose planning algorithms to generate desired needle trajectories within a 2D plane [17], for the same type of needles used in the present study. The output of these 2D planners is a path that can be followed by alternating between forward insertion (without rotation) of the needle into the tissue and 180° rotation (without insertion) of the needle base. The planners assume that during the process the needle stays in a known (nominal) 2D plane. However, our numerical tests indicate that small errors of only a few degrees in needle tip orientation cause the needle to deviate rapidly from the nominal 2D plane. The goal of this paper is to ensure that the needle tip is stabilized to the desired 2D plane.

Contribution

In the current work we design and demonstrate a nonlinear image-based observer–controller pair to drive a flexible bevel-tip needle to a desired 2D plane. We base our plant model on the nonholonomic kinematic model presented in [12]. We assume that the position (but not orientation) of the needle tip can be measured in the operation room by a 3D imaging modality such as biplane fluoroscopy or 3D ultrasound or by stereo cameras in the laboratory setting, and present an asymptotic observer for estimating needle orientation needed to achieve the control task.

As detailed in [21], the controller presented in this paper operates in conjunction with the 2D planners previously developed [17]. Whenever there is a 180° rotation, the controller is employed to ensure that the needle stays close to the nominal plane, as required for the planning algorithm to work effectively. We believe that this paper presents a crucial step towards automated needle guidance in human tissue. Our controller also allows us to validate the efficacy of the kinematic model described in [12].

II. System Overview

We use the setup shown in Figure 1, which is similar to that described in [12], for image-guided needle steering experiments. In the setup, transparent tissue phantoms made from plastisol, which is a mixture of liquid PVC plastics and the plasticizer adipate (M-F Manufacturing Co., Inc., Fort Worth, TX) simulate human tissue. An overhead stereo pair of XCD-X710 firewire cameras (Sony Corporation, Tokyo, Japan) capture images of the needle as it is inserted into the phantom by a two-degree-of-freedom needle insertion device. The insertion device is comprised of a stepper-motor-driven linear stage that drives the insertion degree of freedom and a DC servo motor that axially rotates the needle shaft. The rotary stage is attached to the base of the needle shaft, and as the linear stage drives the rotary stage forward, the needle advances into the tissue. A telescoping support sheath around the needle shaft prevents the needle from buckling outside of the tissue. The needle itself is a 0:7mm nitinol wire (Nitinol Devices and Components, Fremont, CA), cut with an approximately 45° bevel tip, and pre-bent by 10° at 9mm from the needle tip to enhance steerability.

Fig 1.

The needle steering device inserts the needle into the tissue phantom while the needle tip position is tracked using two overhead cameras.

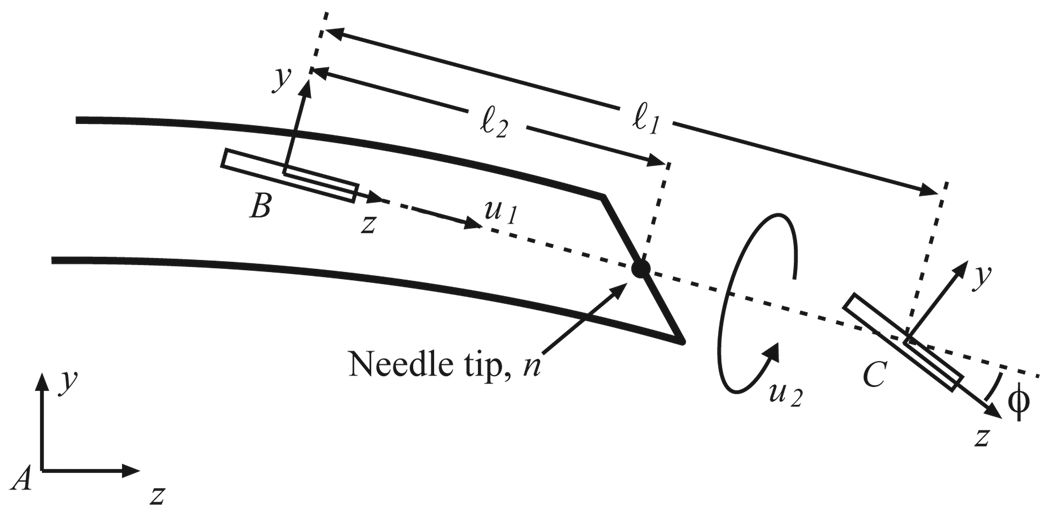
The insertion and rotation speeds comprise two inputs to the kinematic model for bevel-tip flexible needle steering developed by Webster et al. [12]. The model is a generalization of the nonholonomic bicycle model, and neglects torsional compliance of the needle shaft. This model, depicted in Figure 2, is reproduced here for reader convenience.

Fig 2.

Kinematic bicycle model: Frame A is the inertial world reference frame. Frames B and C are attached to the two wheels of the bicycle. This figure is reproduced from [12] with permission from the authors.

In the model, ℓ₁, ℓ₂ determine the location of bicycle wheels with respect to the needle tip. Parameter ϕ is the fixed front wheel angle relative to the rear wheel. Frame A is the inertial world reference frame and frames B and C are attached to the two wheels of the bicycle. In homogeneous coordinates, the rigid body transformation between frames A and B is given by the rigid body transformation matrix

$$g=\left[\begin{array}{cc}\hfill R\hfill & \hfill \mathit{p}\hfill \\ \hfill 0^T\hfill & \hfill 1\hfill \end{array}\right]\in \text{SE}(3),\text{where}R\in \text{SO}(3)\text{ and }\mathit{p}\in {ℝ}^3.$$ (1)

We assume in this paper that the imaging system measures p, the 3D location of frame B. In the non-generic case that ℓ₂ = 0 (the unicycle model discussed in [12]), p coincides with the needle tip.

Let υ,ω ∈ ℝ³ denote, respectively, the linear and angular velocities of the needle tip written relative to frame A, and let V = [υ^T,ω^T]^T ∈ ℝ⁶. Webster et al. use Lie-group theory to find a “coordinate-free” differential kinematic model on the special Euclidean group, SE(3):

$$\mathbf{V}={(g^{-1}\dot{g})}^{\vee }={\mathbf{V}}_1{u}_1+{\mathbf{V}}_2{u}_2,$$ (2)

where ∨ and ^ denote the usual isomorphism between 𝔰𝔢(3) and ℝ⁶ (see Appendix), u₁ is the insertion speed, u₂ is the rotation speed of the needle, and the control vector fields are given by V₁ = [0, 0, 1, κ, 0, 0]^T (which corresponds to insertion) and V₂ = [0,…0, 1]^T (which corresponds to needle rotation). Here, κ = tan ϕ/ℓ₁ is the curvature that the needle follows. Insertion of the needle, u₁, causes the needle to move in the body-frame z-axis direction, but also to rotate (due to the bevel tip) about the body-frame x-axis. Rotation of the needle shaft, u₂, causes pure rotation of the needle tip about the body-frame z-axis. Note that this model is only valid for forward insertions of the needle into the tissue; during the removal of the needle from the tissue, there are no cutting forces on the needle tip and hence the needle follows the path (in reverse) it followed during the forward insertion into the tissue.

III. Reduction And Control For Plane Tracking

A. Reduced-Order Plant Model

We use Z-Y-X fixed angles as generalized coordinates to parameterize R, the rotation matrix between frames A and B. Let γ be the roll of the needle, β be the pitch of the needle out of the plane and α be the yaw of the needle in the plane. Let the position of the origin of frame B be p = [x, y, z]^T ∈ ℝ³ relative to the inertial frame A. We assume that an imaging system measures the location of the origin of frame B. Note that by driving the origin of frame B to the y-z plane the needle tip will also be stabilized to the y-z plane.

Using this notation, q = [x, y, z, α, β, γ]^T ∈ 𝒰 ⊂ ℝ⁶ forms a (local) set of generalized coordinates for the configuration of the needle tip. The coordinates are well defined on

$$𝒰=\{\mathit{q}\in {ℝ}^6:\alpha ,\gamma \in ℝ\text{ mod }2\pi ,\beta \in (-\pi /2,\pi /2)\}.$$ (3)

The body frame velocity is given by V = Jq̇, where

$$J=\left[\begin{array}{cc}\hfill R^T\hfill & \hfill 0_{3\times 3}\hfill \\ \hfill 0_{3\times 3}\hfill & \hfill J_{22}\hfill \end{array}\right],J_{22}=\left[\begin{array}{ccc}\hfill \text{cos}\beta \text{cos}\gamma \hfill & \hfill \text{sin}\gamma \hfill & \hfill 0\hfill \\ \hfill -\text{cos}\beta \text{sin}\gamma \hfill & \hfill \text{cos}\gamma \hfill & \hfill 0\hfill \\ \hfill \text{sin}\beta \hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right].$$

The kinematic model (2) of the bevel tip flexible needle reduces to

$$\dot{\mathit{q}}=J^{-1}{\mathbf{V}}_1{u}_1+J^{-1}{\mathbf{V}}_2{u}_2=\left[\begin{array}{cc}\hfill \text{sin}\beta \hfill & \hfill 0\hfill \\ \hfill -\text{cos}\beta \text{sin}\alpha \hfill & \hfill 0\hfill \\ \hfill \text{cos}\alpha \text{cos}\beta \hfill & \hfill 0\hfill \\ \hfill \kappa \text{cos}\gamma \text{sec}\beta \hfill & \hfill 0\hfill \\ \hfill \kappa \text{sin}\gamma \hfill & \hfill 0\hfill \\ \hfill -\kappa \text{cos}\gamma \text{tan}\beta \hfill & \hfill 1\hfill \end{array}\right]\left[\begin{array}{c}\hfill u_1\hfill \\ \hfill u_2\hfill \end{array}\right].$$ (4)

Due to the introduction of generalized coordinates, there are singularities at β = ±π/2 that cause det J = cos β = 0.

To stabilize the needle to the y-z plane, the states y, z, and α need not be controlled. Also, these states do not affect the dynamics of the remaining states, x, β, and γ. Let r = [r₁, r₂, r₃]^T = [x, β, γ]^T denote the state vector of the “reduced” order system. Tracking the needle tip with an imaging systems typically enable us to measure only the position of the needle and not its orientation (without performing any differentiation), which in reduced coordinates is just the distance from the y-z plane, namely x. We then reparameterize the reduced-order system in terms of insertion distance, l, enabling the physician to control the insertion speed. With a slight abuse of notation, we write ṙ where we mean dr/dl, and interpret the insertion distance as “time” for convenience of exposition; this is equivalent to setting u₁ = 1 in (4). This system can be represented as:

$$\begin{array}{c}\dot{\mathit{r}}=\left[\begin{array}{c}\hfill \text{sin}{r}_2\hfill \\ \hfill \kappa \text{sin}{r}_3\hfill \\ \hfill -\kappa \text{cos}{r}_3\text{tan}{r}_2\hfill \end{array}\right]+\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right]u\hfill \\ w=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]r=r_1.\hfill \end{array}$$ (5)

Note that r = 0 corresponds to the desired equilibrium state of remaining within the y-z plane to which we wish to stabilize the needle.

Using judiciously chosen generalized coordinates, we reduced the plant model to a third order nonlinear system (5). This system can be feedback linearized (see, e.g. [22]) via a transformation of state and input coordinates:

$$\mathit{s}={[r_1,\text{ sin}{r}_2,\kappa \text{cos}{r}_2\text{sin}{r}_3]}^T,$$ (6)

$$\upsilon =-{\kappa }^2\text{sin}{r}_2+\kappa \text{cos}{r}_2\text{cos}{r}_{3}u.$$ (7)

The state equations in the feedback linearized form are:

$$\begin{array}{c}\dot{\mathit{s}}=A\mathit{s}+B\upsilon =\left[\begin{array}{ccc}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\mathit{s}+\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right]\upsilon \hfill \\ w=C\mathit{s}=[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}]\mathit{s}.\hfill \end{array}$$ (8)

The system (A,B,C) is completely controllable and observable.

B. Observer-Based Feedback Control

Note that even though the change of coordinates from the nonlinear system (5) to the feedback linearized system (8) is nonlinear, the first state—and, importantly, the output—is identical for both systems. In other words the system is completely observable in both coordinate systems based on the sensory measurement w = s₁ = r₁. Hence, simple control system design techniques from linear system theory can be used to control this system. A full state Luenberger observer with the following dynamics estimates all the states from the output:

$$\begin{array}{c}\dot{\tilde{\mathit{s}}}=A\tilde{\mathit{s}}+B\upsilon +L(w-\tilde{w})\hfill \\ \tilde{w}=C\tilde{\mathit{s}}.\hfill \end{array}$$ (9)

The control input to the system is then given by full-state feedback, using the state estimate:

$$\upsilon =-K\tilde{\mathit{s}}.$$ (10)

Because the system is linear and time-invariant, the separability principle allows us to select the observer gain matrix, L, and proportional gain matrix, K, independently as we do in our experiments. Since there are only three states to estimate, and we expect to have reasonable estimates of sensor noise, the observer can be quickly and effectively tuned using the Linear Quadratic Gaussian framework, leading to successful simulations and laboratory experiments (Section IV).

In the present framework, there are singularities at β = ±π/2 due to the introduction of generalized coordinates. In addition, the nonlinear transformation from r to s also introduces singularities at γ = ±π/2. This limitation seems inescapable: global linearization is mathematically impossible for dynamical systems on the space of rigid transformations. Fortunately, our feedback linearization scheme works for all needle positions and orientations except when the needle is orthogonal to the plane to which we are trying to stabilize. We believe that this scenario is not of clinical significance; such large errors in orientation should be addressed at the level of planning, not with low-level servo control. That said, it is important for the above described controller never to take the system—or even the state estimate—to these singularities.

Note that one theoretical difficulty arises because we must compute u from (7), which requires exact knowledge of r. However, we do not know s nor r exactly, so we must use s̃ to compute an estimate of r by plugging s̃ into the inverse of (6). This implies that the estimator dynamics will have an input error. But locally near the goal, r ≈ 0, and therefore υ ≈ κu. This allows us to show local asymptotical stability through linearization of the system given by (8) and (9). Fortunately, both simulations and experiments suggest that the domain of attraction is quite large; analytically proving this remains work in progress. It is useful to find an invariant domain that avoids β = ±π/2 and γ = ±π/2. In general, this is challenging because of the nonlinear change of coordinates from u to υ, and the lack of full state knowledge needed for that coordinate transformation. However, if we assume that the error computing u is negligible, Lyapunov stability analysis can be used to approximate this region; for details on this computation, see [23].

IV. Results

A. Numerical simulations

Extensive simulations were conducted in MATLAB to test our proposed controller. We used a discrete-time implementation of the system and the controller-observer pair, to reflect our physical implementation as closely as possible. The plant model was discretized assuming constant insertion by 1mm of the needle into the tissue between samples. We assumed measurement noise of up to ±1mm with a uniform distribution; this seems clinically reasonable given that 3D ultrasound imaging can be accurate to within 0:8mm [24], and is approximately the same or slightly higher than the noise of our tracking system. The parameter value for the model was taken to be 1/κ = 12:2cm, which is the radius of curvature of the needle used in laboratory trials.

In our simulations, we observed that if the entry point was too far away from the desired plane, the estimator states (which are in the feedback-linearized coordinates) left the region in which the inverse of the change of coordinates in (6) is well defined. To avoid such singularities, we performed estimator saturation, namely if the estimator states left this region, they were projected to the closest point in that region. For example, if [s̃₁, s̃₂, s̃₃]^T = [0, 1:5, 0]^T, then it is projected to [s̃₁, s̃₂, s̃₃]^T = [0, 1, 0]^T. Since we used state feedback control in the feedback-linearized space, this pull-back affects only the magnitude of the input and not the sign of the input. Our numerical tests suggested that this saturated nonlinear observer worked quite well, although formal analysis of the saturation remains work in progress.

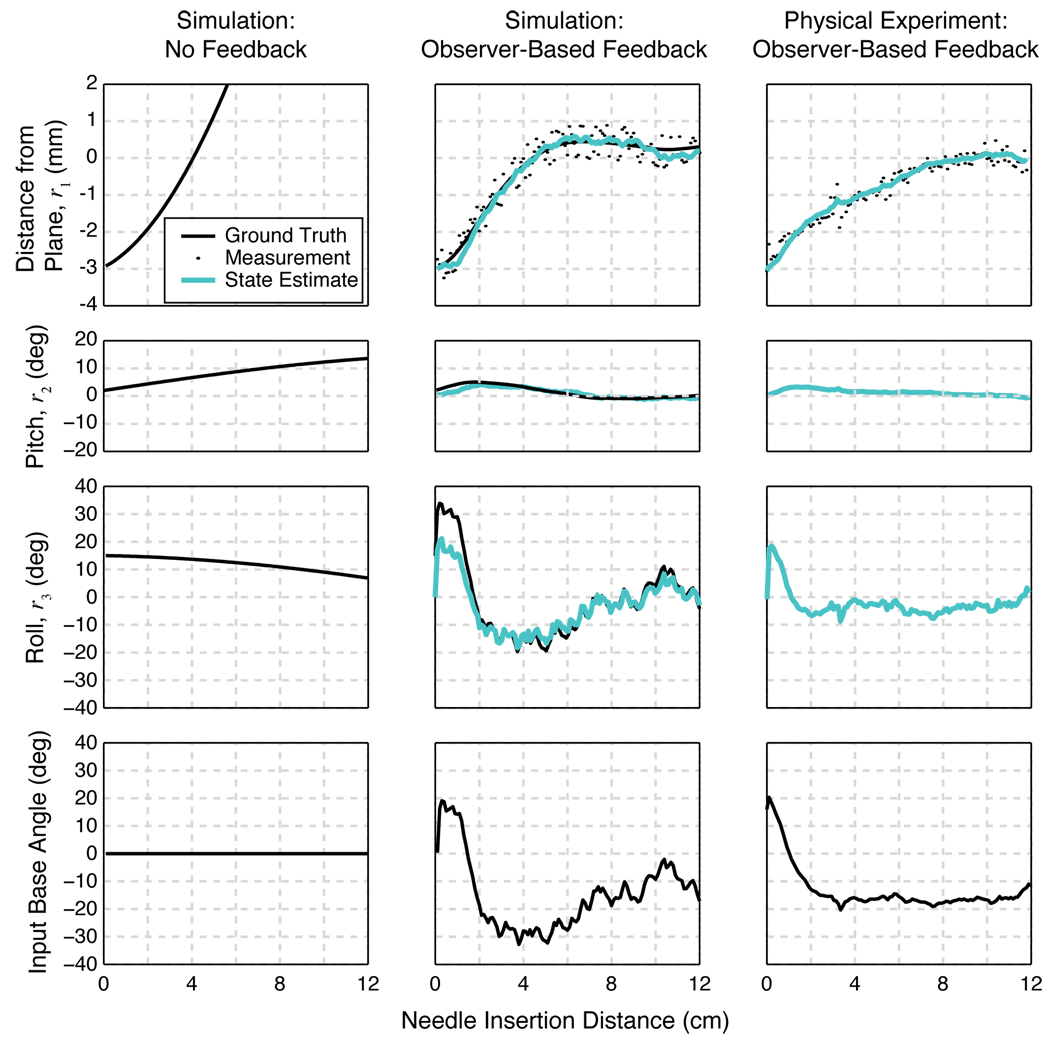
Two characteristic simulations are presented in Figure 3, with the same initial conditions. In the first case, we tested the system without any feedback control, and it rapidly diverged from the desired plane despite relatively small errors in roll, pitch and depth. In the second simulation, our observer-based controller drove the needle to the desired plane within about 5 cm of needle insertion.

Fig 3.

Comparison amongst a simulation with no feedback control (first column), a simulation with feedback control (second column), and an experimental trial (third column). The first three rows of plots show the three states (r₁, r₂, _r3), respectively. In the two simulations, the simulated ground truth state is known (solid black line), whereas in the physical experiment, only its estimate (solid teal line) is known. In the feedback control simulation and physical experiment, the first state is measured at each time step (small black circles). The fourth row is the cumulative rotational input given to the system. First column: Open-loop simulation with initial conditions of r = [−3mm, 2°, 15°]. With no control, the needle tip diverges the needle from the desired plane. Second column: Closed-loop simulation with the same initial conditions. Noise in the needle tip position is modeled as a random variable with a uniform distribution between ±0:5mm. With the feedback control, the needle converges to the desired 2D plane within the noise levels. Third column: One of the nine experimental trials, with approximately the same initial conditions as the simulations (ground truth is not known). With the feedback control, the needle tip converges to the desired 2D plane.

We tested our controller over a uniform grid (10 × 10 × 10) of 1000 initial conditions of up to ±3mm error in depth from the plane, and up to ±10° initial error in “pitch” (r₂) and up to ±30° initial error in “roll” (r₃). In all cases, we seeded the initial condition of the observer to s̃₂ = s̃₃ = 0°, and for the first state, s̃₁ = z₁ + noise of up to 1mm. Each initial condition was simulated 10 times with noise, for a total of 10,000 simulations. Each insertion was to a length of 12cm. We found that 98:56% of initial conditions converged to within ±1mm (the sensor noise floor); upon closer inspection of the remaining 144 runs in which the states did not converge to within this tight tolerance in the finite needle insertion distance, we found that they did not diverge.

We tested the controller using an incorrect value of κ (up to 20% error) and found that the controller always converged, albeit slower than it would have if the correct κ was given. Thus the system appeared to be robust to parametric uncertainty; for an analytic proof we refer to [25].

B. Experimental validation

Experiments were conducted on the needle steering device described in Section II. The tissue used in the experiments was approximately 35mm thick, and it was sufficiently transparent for visual tracking purposes. We captured the images of the needle inside the tissue using XVision [26]. This tissue phantom had a refractive index of 1:3. Refraction was accounted for in our calculations by assuming that tissue’s top surface was horizontal. The needle used for the experiments had a radius of curvature of 12:2cm when inserted into the tissue. The needle follows a circle of radius 1/κ when it is inserted into the tissue without any rotation at the base, so we collected needle-tip position data during pure insertion to estimate κ using least-squares. Following the observation of Webster et al. [6], we assume that this parameter does not change as a function of insertion speed.

In the experiments the goal was to reach the y − z plane that was 3mm above from the initial x-position. The pitch was approximately zero, but neither the pitch nor the roll of the needle tip were precisely known. The needle was inserted into the tissue for 12cm, which is about the radius of curvature of the needle inside the tissue. Nine trials were conducted on this experimental setup with varying pitch and roll initial conditions. Figure 3 shows a comparison of a typical trial with our simulation results, and Figure 4 summarizes all nine experimental trials. In each of the trials, the needle tip converged to the desired plane within the noise levels of the position measurement. As with the simulations, these experiments validate the efficacy of our controller–observer pair and the experiments further support the nonholonomic model for flexible bevel-tip needle insertion developed by Webster et al. [12]. It was interesting to note, however, that while the physical and numerical results were qualitatively quite similar, the physical system exhibited a consistently more sluggish response, which we suspect was due to neglected torsional damping due to friction between the tissue and the needle shaft.

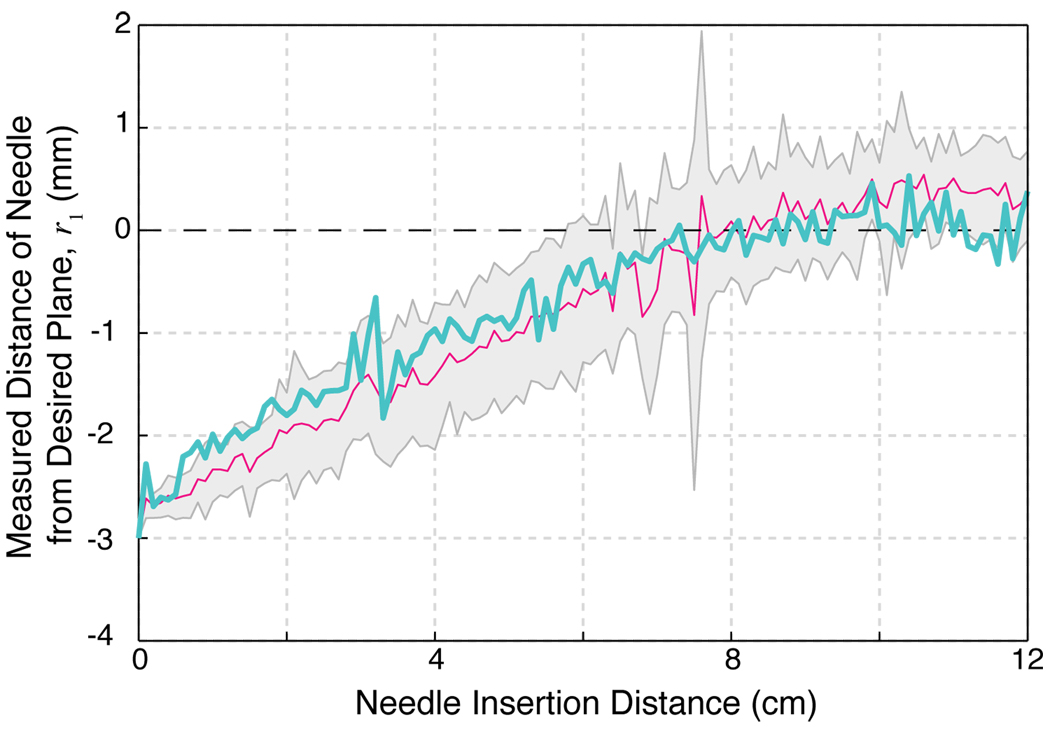
Fig 4.

Nine experimental trials validate the controller. The mean value of r₁ of the nine trials is plotted against the insertion distance of the needle into the tissue (solid magenta line; gray region indicates mean ± standard deviation). The specific trial shown in Figure 3 is reproduced here (solid teal line). All trials control approach the desired 2D plane (r₁ = 0, dashed black line) and stay within the noise levels of the position measurements of approximately 1mm.

V. Discussion

We present a feedback controller that stabilizes a flexible tip-steerable needle to a desired 2D plane. We show that considering a reduced 3-DOF system is sufficient to achieve this goal. The task of driving the needle tip to a desired 2D plane only required us to keep track of three of the six degrees of freedom of the needle tip, which greatly simplifies controller–observer design. We recently generalized this idea of “task-induced” reduction for other tasks and kinematic systems on Lie groups [25].

In this paper, we assume that only the 3D position (but not orientation) of the needle tip can be measured using an imaging system, and present a linear observer to recover the reduced-order needle-tip state. Another approach may be to enhance our sensory measurement, for example by measuring the pitch, r₂, if needle shaft orientation can be segmented in both images in a neighbhorhood of the needle tip. In this case, we can use a reduced-state Luenberger observer (instead of the full state observer) to estimate only the roll, r₃. Measuring the roll itself may be more challenging due to very small size of the bevel-tip.

Irrespective of the measurement (either just position, or position and pitch), alternative estimation schemes could be used. For example, in an Extended Kalman Filter (EKF) the system is (approximately) linearized around the current state estimate to propagate covariance and the Kalman gain matrices. In contrast our approach uses an exact change of coordinates to obtain the controller and estimator with the trade-off being the use of state estimates to obtain u from υ and, as discussed, exhibits local asymptotic stability. As with EKFs and other schemes such as particle filters [27], we have no formal global characterization of the domain of attraction for our observer–controller pair. However, our scheme is relatively simple and performs well in practice.

An important next step is to evaluate the performance of this controller by conducting tests on a variety of tissues (phantom, ex vivo, and animal cadaver) using ultrasound or fluoroscopy imaging systems. Due to tissue inhomogeneity, implementing control on real tissue might benefit from an adaptive version of our controller that would “learn” the model parameters while stabilizing the needle to a 2D plane, or a scheme that is insensitive to variations in steering curvature, as proposed in [23]. Our ultimate goal is to incorporate automatic needle steering with pre- and intra-operative planning to greatly enhance the effectiveness of percutaneous therapies.

Appendix

Special Euclidean Group, SE(3)

The special Euclidean Group in thee dimension, SE(3), is the group of rigid-body transformations. It is the cross product of ℝ³ and the space of rotation matrices, SO(3). SE(3) can also be used to represent configuration of a rigid body, as we do in this work. The space of skew-symmtric matrices in three dimensions, 𝔰𝔬(3), is the Lie algebra of SO(3). The “wedge/hat” isomorphism ℝ³ ≃ 𝔰𝔬(3) is defined by

$${\wedge }_{:}\left[\begin{array}{c}\hfill {\mathit{\omega }}_1\hfill \\ \hfill {\mathit{\omega }}_2\hfill \\ \hfill {\mathit{\omega }}_3\hfill \end{array}\right]\leftrightarrow \left[\begin{array}{ccc}\hfill 0\hfill & \hfill -{\mathit{\omega }}_3\hfill & \hfill {\mathit{\omega }}_2\hfill \\ \hfill {\mathit{\omega }}_3\hfill & \hfill 0\hfill & \hfill -{\mathit{\omega }}_1\hfill \\ \hfill -{\mathit{\omega }}_2\hfill & \hfill {\mathit{\omega }}_1\hfill & \hfill 0\hfill \end{array}\right]{:}^{\vee }$$

where 𝔰𝔬(3) is the Lie algebra of SO(3). The Lie algebra of SE(3) is denoted by 𝔰𝔢(3). In a standard abuse of notation, we use the wedge/hat isomorphism ℝ⁶ ≃ 𝔰𝔢(3) to relate translational υ and angular ω velocities to “twists” ξ ∈ 𝔰𝔢(3) via

$${\xi }^{\vee }=\left[\begin{array}{c}\hfill \mathit{\upsilon }\hfill \\ \hfill \mathit{\omega }\hfill \end{array}\right],\text{ and }{\left[\begin{array}{c}\hfill \mathit{\upsilon }\hfill \\ \hfill \mathit{\omega }\hfill \end{array}\right]}^{\wedge }=\left[\begin{array}{cc}\hfill \widehat{\mathit{\omega }}\hfill & \hfill \mathit{\upsilon }\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right]=\xi .$$

For more detail, refer to [28].