Allosteric mechanism of Ca²⁺ activation and H⁺-inhibited gating of the MthK K⁺ channel

Abstract

MthK is a Ca²⁺-gated K⁺ channel whose activity is inhibited by cytoplasmic H⁺. To determine possible mechanisms underlying the channel’s proton sensitivity and the relation between H⁺ inhibition and Ca²⁺-dependent gating, we recorded current through MthK channels incorporated into planar lipid bilayers. Each bilayer recording was obtained at up to six different [Ca²⁺] (ranging from nominally 0 to 30 mM) at a given [H⁺], in which the solutions bathing the cytoplasmic side of the channels were changed via a perfusion system to ensure complete solution exchanges. We observed a steep relation between [Ca²⁺] and open probability (Po), with a mean Hill coefficient (n_H) of 9.9 ± 0.9. Neither the maximal Po (0.93 ± 0.005) nor n_H changed significantly as a function of [H⁺] over pH ranging from 6.5 to 9.0. In addition, MthK channel activation in the nominal absence of Ca²⁺ was not H⁺ sensitive over pH ranging from 7.3 to 9.0. However, increasing [H⁺] raised the EC₅₀ for Ca²⁺ activation by ∼4.7-fold per tenfold increase in [H⁺], displaying a linear relation between log(EC₅₀) and log([H⁺]) (i.e., pH) over pH ranging from 6.5 to 9.0. Collectively, these results suggest that H⁺ binding does not directly modulate either the channel’s closed–open equilibrium or the allosteric coupling between Ca²⁺ binding and channel opening. We can account for the Ca²⁺ activation and proton sensitivity of MthK gating quantitatively by assuming that Ca²⁺ allosterically activates MthK, whereas H⁺ opposes activation by destabilizing the binding of Ca²⁺.

INTRODUCTION

MthK is a Ca²⁺-gated K⁺ channel that has served as a model to aid in our understanding of K⁺ channel gating and modulation of gating by intracellular ligands (Jiang et al., 2002a,b). MthK channels bind Ca²⁺; in turn, Ca²⁺ binding likely induces a series of conformational changes that facilitate channel opening (Jiang et al., 2002a; Zadek and Nimigean, 2006; Li et al., 2007). Structural studies of MthK by x-ray crystallography have yielded a model of its fourfold symmetrical pore and tethered assembly of RCK domains, which form an eight-member “gating ring” at the cytoplasmic side of the channel in the Ca²⁺-bound open conformation (Jiang et al., 2002a). The combination of this structure and the x-ray structure of an unliganded MthK gating ring (Ye et al., 2006) yields remarkable insight toward the mechanism of MthK gating. By sequence comparison and alignment, at least one apparent RCK-like domain can be found within the large cytoplasmic tail region of the mammalian large-conductance Ca²⁺-activated K⁺ (BK) channel, and consequently MthK has served as a model to provide insight toward BK channel structure and gating mechanism (Jiang et al., 2001; Brelidze et al., 2003; Niu et al., 2004; Krishnamoorthy et al., 2005; Kim et al., 2006).

Previous electrophysiological studies of MthK gating have demonstrated a steep dependence of opening on [Ca²⁺], with open probability (Po) versus [Ca²⁺] relations described by Hill coefficients (n_H) of ∼8 (Zadek and Nimigean, 2006). In addition, MthK gating was observed to be inhibited by H⁺ at the cytoplasmic side of the channel (Li et al., 2007). Although H⁺ is known to affect the oligomeric stability of RCK domain subunits of “soluble” (i.e., channel-free) MthK RCK gating rings, the relation of this phenomenon to MthK gating is not clear, and the quantitative nature of relation between Ca²⁺ activation and proton-sensitive gating in MthK is not yet fully understood (Dong et al., 2005; Ye et al., 2006; Kuo et al., 2007).

To gain insight toward the relation between Ca²⁺ and H⁺ modulation of MthK gating, we recorded current through reconstituted MthK channels in planar lipid bilayers over a wide range of pH and [Ca²⁺]. We observed that at pH ranging from 6.5 to 9.0, MthK opening displayed a steep Ca²⁺ dependence, consistent with a strong energetic coupling between Ca²⁺ binding and opening, and positive intersubunit cooperativity. Neither the maximal Po nor n_H changed significantly as a function of pH over pH ranging from 6.5 to 9.0, and MthK channel opening in the nominal absence of Ca²⁺ showed no apparent H⁺ sensitivity over pH ranging from 7.3 to 9.0. However, increasing [H⁺] (i.e., decreasing pH) raised the EC₅₀ for Ca²⁺ activation over the entire range of pH studied (6.5–9.0). Collectively, these results suggest that H⁺ binding does not directly modulate either the channel’s closed–open equilibrium or the allosteric coupling between Ca²⁺ binding and channel opening. We present a quantitative working hypothesis that accounts for the Ca²⁺ activation and proton sensitivity of MthK gating by assuming that the binding of Ca²⁺ allosterically activates MthK through relative stabilization of the open state, whereas H⁺ opposes (inhibits) activation by destabilizing the binding of Ca²⁺.

MATERIALS AND METHODS

Channel purification and reconstitution

MthK cDNA (provided by C. Miller, Brandeis University, Waltham, MA) was obtained in the pQE-70 vector and subcloned into the pQE-82L vector (QIAGEN) between the SphI and BglII restriction sites, and then modified by inserting a thrombin-cleavable 6xHis-tag at the C-terminal end of the gene and deleting the N-terminal 6xHis-tag from the pQE-82L vector. Channel protein was expressed and purified essentially as described previously (Parfenova et al., 2006). In brief, MthK was expressed in Escherichia coli XL-1 Blue cells on induction with 0.4 mM IPTG. Bacteria were harvested and resuspended in 20 mM Tris and 100 mM KCl, pH 7.6 (Buffer A), and lysed by sonication in the presence of PMSF and a protease inhibitor cocktail (Complete EDTA-free; Roche). The protein was solubilized by 2-h incubation in Buffer A with 50 mM decyl maltoside (DM; Affymetrix), followed by centrifugation at 16,000 rpm for 45 min. The supernatant was loaded onto a Co²⁺-charged HiTrap metal affinity column (GE Healthcare) and washed with 20 mM imidazole and 5 mM DM in Buffer A. The channel protein was eluted using 400 mM imidazole and 5 mM DM in Buffer A. The 6xHis-tag was cleaved immediately after elution by incubating with 2.0 U of thrombin/3.0 mg eluted protein for 2 h at room temperature. Protein was concentrated using an Amicon Ultra filter (50,000 MWCO; Millipore) and further purified on a Superdex 200 gel filtration column, and then concentrated again to ∼5 mg/ml. The protein was then reconstituted into liposomes composed of E. coli lipids (Avanti Polar Lipids, Inc.), essentially as described previously (Heginbotham et al., 1998), which were then rapidly frozen in liquid N₂ and stored at −80°C until use. Protein concentrations in liposomes ranged from 10 to 50 µg of protein per mg lipid.

Lipid bilayer recording and solution changes

Recordings were obtained using planar lipid bilayers of POPE/POPG (3:1) in a horizontal bilayer chamber at 22–24°C. In these experiments, solution in the cis (top) chamber contained 200 mM KCl and 10 mM HEPES, pH 7.0; solution in the trans (bottom) chamber contained 200 mM KCl, 10 mM of pH buffer, which was either HEPES (pH 6.9–8.5), Mes (pH 6.5), or 2-[N-cyclohexylamino]ethanesulfonic acid (CHES; pH 9.0–9.5), and CaCl₂ at the indicated concentrations. Ca²⁺ buffers were not used in the recording solutions, except in experiments that used 5 mM EGTA to reduce the free [Ca²⁺] to nominal levels. We estimated the concentration of contaminating Ca²⁺ in our solutions (introduced mainly in the KCl salt) to be ∼10 µM, as measured with a Ca²⁺-sensitive electrode (Orion Research). All of the recordings analyzed for this paper were obtained at −100 mV.

The solution bathing the cis side of the membrane, at pH 7.0 and with no added Ca²⁺, suppressed the activity of MthK channels that were incorporated with their cytoplasmic face toward the cis chamber to nominal levels, resulting in the activation only of MthK channels with their cytoplasmic end facing the trans chamber (depending on the pH and [Ca²⁺]). This orientation of MthK channels was confirmed by changing the transmembrane voltage to observe the intrinsic inward rectification properties of the channels (Jiang et al., 2002a; Parfenova et al., 2006; Zadek and Nimigean, 2006; Li et al., 2007).

Within each bilayer, multiple solution changes were performed using a gravity-fed perfusion system to measure the relation between [Ca²⁺], pH, and channel activity. The capability of multiple solution changes enabled the assessment of the number of MthK channels in each bilayer throughout the course of an experiment. Monitoring the number of channels was a critical component of these analyses because of the possibility of additional MthK channels occasionally incorporating or becoming active and, conversely, active channels becoming inactive during the course of a long (>30 min) experiment. Changes such as these can introduce errors in the estimation of the numbers of channels in a bilayer, which consequently can lead to errors in Po values estimated from multichannel patches.

The numbers of active channels in each bilayer were typically reassessed several times during the courses of experiments by exchanging the solution in the trans chamber to high Ca²⁺ solutions, which would activate MthK channels in the bilayer and allow quantification of all open-channel current levels. To ensure completeness of solution changes, the trans chamber was washed with a minimum of 10 chamber volumes of solution before recording under a given set of conditions.

In experiments designed to record from >10 active channels in a single bilayer, liposomes were fused to form large vesicles by adding 1 vol of 1.5 M KCl to a thawed liposome suspension containing 25 µg of protein per mg lipid, and then refreezing the suspension at −80°C for 30 min. After thawing, the addition of these liposomes to the bilayer chamber resulted in a relative increase in channel incorporation.

Electrophysiological data analysis

Single-channel currents were amplified using a patch clamp amplifier (PC-ONE; Dagan Corp.) with low-pass filtering to give a final effective filtering of 1 kHz (dead time of 0.18 ms) and sampled by computer at a rate of 10 kHz. Currents were analyzed by measuring durations of channel openings and closings at each current level by 50% threshold analysis using pClamp9. These were used to calculate NPo as:

$$NPo={\displaystyle \sum _{i=1}^{n}i{P}_i},$$ (1)

where i is the open level and P_i is probability of opening at that level. The mean single-channel Po is obtained by dividing NPo by N, which is the number of channels in the bilayer, determined by recording under conditions where the maximum level of channel opening can be observed. In initial experiments, N for each bilayer was determined by recording current in the presence of 10 mM Ca²⁺, pH 7.7. In later experiments, it was determined that channels could be activated to Po ≈ 0.93 at all pHs ranging from 6.5 to 9.0 in the presence of sufficient Ca²⁺ at the cytoplasmic side of the channel. In these cases, N was determined by recording at a given pH with [Ca²⁺] ranging from 2 mM (at pH 9.0) to 30 mM (at pH 6.5).

For datasets containing a single active channel, or multiple channels that opened to a single current level with no superimposed openings, gating was analyzed further by exponential fitting of open and closed dwell-time distributions. Dwell-time distributions (histograms) were generated using log-binning at a resolution of 10 bins per log unit, and distributions were fitted with sums of exponential components using the maximum likelihood method. Intervals with durations less than two times the dead time were excluded from fitting (McManus et al., 1987). The minimum number of exponential components required to describe a given dwell-time distribution was determined by the likelihood ratio test, as described previously (McManus and Magleby, 1988). Assuming that MthK channels gate independently and homogeneously, open-time distributions obtained from multichannel bilayers in which channels opened to a single current level (with no superimposed openings) should be indistinguishable from open-time distributions obtained from single-channel bilayers; this appears to be the case (Fig. 7). In the case of closings, durations of long closings (mostly gaps between bursts of openings) will be inversely proportional to the number of active channels in the bilayer, whereas durations of brief closings (flickers within bursts) from single-channel or multichannel bilayers are indistinguishable from one another. The closed-time distributions in Fig. 8 are presented “as measured” from both single-channel and multichannel bilayers, with no corrections applied to the measured durations.

Figure 7.

Representative open dwell-time distributions at different cytoplasmic pH and [Ca²⁺]. Smooth curves represent fits of these data with a single-exponential component with the indicated time constant (τ). Distributions from bilayers containing more than one active channel (n > 1) were generated from data that showed only a single open current level. The number of fitted intervals in the distribution were: pH 6.5, 5 mM, 84 events; pH 6.5, 10 mM, 4,024 events; pH 6.5, 30 mM, 5,695 events; pH 7.3, 2 mM, 231 events; pH 7.3, 3 mM, 2,451 events; pH 7.3, 30 mM, 5,527 events; pH 8.1, 0.7 mM, 1,203 events; pH 8.1, 1 mM, 2,570 events; pH 8.1, 10 mM, 7,386 events.

Figure 8.

Representative closed dwell-time distributions at different cytoplasmic pH and [Ca²⁺]. Smooth curves represent fits of these data with mixtures of one to four exponential components (with indicated time constants [τ] and fractional areas). Distributions from bilayers containing more than one active channel (n > 1) were generated from data that showed only a single open current level; thus, for n > 1, the true durations of long closings are “N” times the observed durations. These data illustrate that closed times are typically comprised of one or more long lifetime components and one or more brief lifetime components (“flickers”); the durations of flickers appear independent of [Ca²⁺] and pH ([H⁺]), whereas the durations and frequency of longer closings decrease with higher [Ca²⁺] and higher pH (i.e., lower [H⁺]). The number of fitted intervals in the distribution were: pH 6.5, 5 mM, 83 events; pH 6.5, 10 mM, 4,024 events; pH 6.5, 30 mM, 5,696 events; pH 7.3, 2 mM, 230 events; pH 7.3, 3 mM, 2,453 events; pH 7.3, 30 mM, 5,528 events; pH 8.1, 0.7 mM, 1,202 events; pH 8.1, 1 mM, 2,569 events; pH 8.1, 10 mM, 7,386 events.

Burst analysis

Analysis of burst of openings was performed as described previously (Magleby and Pallotta, 1983; Nimigean and Magleby, 1999). In brief, distributions of closed interval durations were fitted with the sums of two or more exponential components. The closed intervals from the components with time constants >10 msec were defined as gaps between bursts; closed intervals from briefer components were defined as intraburst closings. The time constants and relative areas of the distributions were then used to calculate a critical time, which was used to classify the measured closed intervals so that the numbers of misclassified gaps and misclassified intraburst closings were equal to one another. This analysis was restricted to datasets with Po < ∼0.7 because of the low occurrence of obvious gaps in data with higher channel activity. Burst kinetics were quantified as burst duration (summed durations of consecutive openings and closings in a burst) and openings/burst.

Gap durations presented in Fig. 3 D have been corrected for the number of channels by multiplying the measured gap durations by the number of active channels in the patch; for these experiments, the number of active channels was determined from currents recorded in the presence of 2 mM Ca²⁺ at pH 9.0, which yields maximal activation of MthK.

Figure 3.

MthK channel gating in the nominal absence of Ca²⁺. (A) MthK currents recorded from a single bilayer at pH 9.0; these currents are representative of several minutes of continuous recording at each of the indicated conditions. Here, in the presence of 5 mM EGTA, no openings were observed in 10 min of continuous recording, with the exception of the burst opening at the beginning of the second “5 mM EGTA” period (right). In addition, no openings were observed in 10 min of continuous recording with 0 added Ca²⁺ (no EGTA). Similar results were observed in two additional bilayers at pH 9.0 in the presence of 5 mM EGTA, and in six additional experiments at pH 9.0 with no added Ca²⁺ (no EGTA). (B) Po in the nominal absence of Ca²⁺, plotted as a function of pH. The dashed line represents a regression line fit with these data, which had a slope of 0.00017/pH unit and y intercept of −0.00098. These data are consistent with pH having little effect on Po in the absence of Ca²⁺. (C) Mean burst duration in the nominal absence of Ca²⁺, plotted as a function of pH. Increasing pH over the range of 7.3–9.0 did not yield a corresponding change in burst duration. The pooled burst durations over this pH range yielded a mean of 252 ± 46 ms (dotted horizontal line). (D) Mean gap duration in the nominal absence of Ca²⁺, plotted as a function of pH. Pooled gap durations over this pH range yielded a mean of 13.1 ± 4.7 min (dotted horizontal line).

Kinetic modeling

MthK gating was analyzed further by the global fitting of single-channel Po versus [Ca²⁺] data obtained at seven different pHs by incorporating both pH dependence and Ca²⁺ dependence within the framework of allosteric gating models. A starting point for these models is based on previous work (Zadek and Nimigean, 2006) that used a basic 18-state scheme, in which closed states can bind 0–8 Ca²⁺, and the binding of Ca²⁺ biases the equilibrium constant toward the corresponding open state. Gating in this model is thus described by:

$$Po=\frac{Po\max }{1+\frac{{(1+K)}^8}{L{(1+KC)}^8}},$$ (2)

where K = [Ca²⁺]/K_C. Here, Pomax is the maximum single-channel Po (i.e., within a burst), K_C is the effective dissociation constant for Ca²⁺, L is the equilibrium constant for gate movement in the absence of Ca²⁺, and C is the allosteric factor for coupling between Ca²⁺ binding and opening. Gating was also analyzed with a dual allosteric model in which Ca²⁺ and H⁺ may activate the channel independently of one another, and Ca²⁺-dependent gating may allosterically modulate H⁺-dependent gating, similar to models previously developed for BK channels (Horrigan and Aldrich, 2002):

$$Po=\frac{Po\max }{1+\frac{{(1+K+H+KHE)}^8}{L{(1+KC+HD+KHCDE)}^8}},$$ (3)

where H = [H⁺]/K_H. Here, K_H is the effective dissociation constant for H⁺, and D and E are the allosteric factors for coupling between H⁺ binding and opening (D), and between Ca²⁺ binding and H⁺ binding (E).

Po data predicted by the models were calculated from a starting set of kinetic parameters, predicted Po values from the models were then compared with the experimental data, and kinetic parameters were optimized using an iterative χ2 minimization routine implemented in Origin 8 (GE Healthcare).

Analytical size exclusion chromatography

Effects of Ca²⁺ and pH on apparent molecular size of purified, detergent-solubilized MthK were determined by size exclusion chromatography using an AKTA FPLC system (GE Healthcare). MthK samples (300 µg) were diluted into buffer containing 200 mM KCl with 10 mM pH buffer (HEPES for pH 6.8 and CHES for pH 9.0), 2 mM nitrilotriacetic acid, and CaCl₂ to yield the indicated free [Ca²⁺] (estimated using WEBMAXC; Patton et al., 2004). Samples were loaded onto a Superdex 200 10/30 (GE Healthcare) column that was previously equilibrated with the same buffer. Protein was eluted at a flow rate of 0.5 ml/min and monitored via absorbance at 280 nm. Fractions were collected via an automated fraction collector. For experiments involving serial reloading, the appropriate fractions were pooled and concentrated to a volume of 500 µl using an Amicon Ultra filter (10,000 MWCO; Millipore) before reloading into the Superdex 200 column. Protein standards used for molecular weight calibration were as follows: thyroglobulin, 670 kD; catalase, 250 kD; γ-globulin, 158 kD; bovine serum albumin, 66 kD; ovalbumin, 44 kD; myoglobin, 17 kD.

RESULTS

MthK opening displays a steep Ca²⁺ dependence

Previous studies of MthK function have established that the channel is activated by Ca²⁺ at its cytoplasmic side, although the steepness of its Ca²⁺ dependence is less well established, with Hill coefficients ranging from ∼4 to 8 (Zadek and Nimigean, 2006; Li et al., 2007). In addition, Hill coefficients for Ca²⁺ gating of MthK were reported to be sensitive to the pH (i.e., protons, H⁺) at the cytoplasmic face of the channel (Li et al., 2007). To establish the relation between Ca²⁺ activation and proton sensitivity of MthK gating, we recorded current through purified, reconstituted MthK channels in planar lipid bilayers. The use of a horizontal bilayer chamber enabled us to incorporate a mechanically stable, semi-automated, gravity-fed perfusion system, which facilitated experiments involving multiple complete solution changes for each bilayer. Importantly, this capability made it possible to test for reversibility of the effects of solution changes, and thus to quantify any changes in the number of active channels that might occur over the course of a single experiment (due to incorporation of additional active channels or, conversely, irreversible inactivation).

The effects of Ca²⁺ on MthK gating are summarized in Fig. 1. These data illustrate a steep relation between [Ca²⁺] and MthK Po, as exemplified in the representative current traces in Fig. 1 A. In this example, a doubling in [Ca²⁺] from 1 to 2 mM at pH 7.7 resulted in a 900-fold increase in Po, nearly equivalent to a 10th power relation between Po and [Ca²⁺] (900 = 2^9.8).

Figure 1.

Ca²⁺-dependent opening of MthK. (A) Representative channel currents recorded over a range of [Ca²⁺] at −100 mV. These currents are from the same bilayer, which contained two active channels. (B) P_O over a range of cytoplasmic [Ca²⁺] and pH. Symbols represent the mean Po at particular pH (down triangle, pH 6.5; diamond, pH 6.9; square, pH 7.3; circle, pH 7.7; up triangle, pH 8.1; left triangle, pH 8.5; star, pH 9.0). These symbols corresponding to each pH are used in subsequent figures, as applicable. Solid lines represent fits with Hill equations for data at a given pH. Increasing pH over the range of 6.5–9.0 resulted in roughly parallel shifts of Po versus [Ca²⁺] relations toward lower [Ca²⁺]. (C) Logarithmic plot of fitted EC₅₀(Ca²⁺) values versus pH shows an approximately linear relation. The solid line represents a linear fit to these data points. (D) Variation in fitted Hill coefficients does not correlate with pH. In B–D, all error bars represent standard errors of the means (n ≥ 4).

Results from additional bilayer experiments, in which Po versus [Ca²⁺] relations were determined at seven different pHs ranging from 6.5 to 9.0, are summarized in Fig. 1 B. By fitting mean Po versus [Ca²⁺] from pooled experiments at each pH, we observe two properties. First, Ca²⁺ can fully activate MthK channels over the entire range of pH tested in our experiments to a maximum Po of 0.93 ± 0.005 (n = 36 complete datasets). Previous work has suggested that Ca²⁺ cannot fully activate the channel at near-neutral pH (∼7.0) (Zadek and Nimigean, 2006; Li et al., 2007). However, the previous studies did not analyze MthK gating at [Ca²⁺] > 10 mM, and we observe that maximal channel activation at near-neutral pH can require [Ca²⁺] > 10 mM. Second, we observe that decreasing pH (i.e., increasing [H⁺]) results in a shift of the Po versus [Ca²⁺] relation toward higher [Ca²⁺], without a systematic change in the steepness of this relation.

To analyze these properties further, we measured Po in individual bilayers at four to six different [Ca²⁺] and fitted these data with Hill equations to estimate EC₅₀ and n_H and determine the relation between these parameters and pH. These results are summarized in Fig. 1 (C and D). We observed that the relation between log(EC_50,Ca²⁺) and pH is approximately linear over pH ranging from 6.5 to 9.0, with EC_50,Ca²⁺ increasing 4.7-fold per tenfold increase in [H⁺] (n = 4–7 datasets at each pH). In addition, although some variability in estimated Hill coefficients was apparent, we observe no systematic relation between Hill coefficient and pH over the range of 6.5–9.0.

Under the assumption that H⁺ does not systematically alter the Hill coefficient for the Po versus [Ca²⁺] relation, we pooled the individual estimates to calculate a mean Hill coefficient of 9.9 ± 0.9 (n = 36). This is consistent with the previous observation of a steep Hill coefficient for Ca²⁺-dependent gating of MthK at a single pH (Zadek and Nimigean, 2006). Structural and biochemical studies have demonstrated that each MthK channel contains eight RCK domains, with each RCK domain containing one Ca²⁺-binding site (Jiang et al., 2002a; Dong et al., 2005). The mean Hill coefficient of 9.9 ± 0.9 is, within error, consistent with the eight Ca²⁺ per channel stoichiometry; thus, it is possible that observed Hill coefficients >8 could arise from stochastic variability. It is alternatively possible that these paradoxically steep Hill coefficients could arise from additional, overlapping Ca²⁺-dependent gating processes (Zadek and Nimigean, 2006).

MthK opening in the presence of Ca²⁺ is proton sensitive

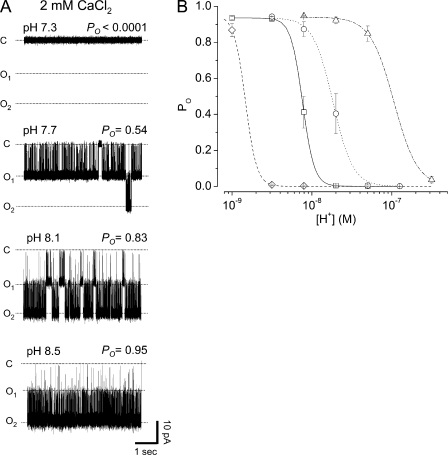
The effects of H⁺ on gating of MthK channels in the presence of Ca²⁺ are summarized by the representative current traces in Fig. 2 A. These currents illustrate that at 2 mM Ca²⁺, decreasing pH (i.e., increasing [H⁺]) results in a steep decrease in Po. To gain further insight toward possible mechanisms underlying H⁺-sensitive gating, we plotted Po data obtained at several [Ca²⁺] as a function of [H⁺] and fitted these data with Hill equations to estimate a lower limit on the stoichiometry of H⁺ modulatory sites. Based on these data, we estimated Hill coefficients ranging from 2.9 to 6.1, consistent with a minimum of three to six H⁺ modulation sites in the channel. If, as with Ca²⁺, the MthK channel contains one H⁺ modulation site per RCK domain, this would give rise to eight H⁺ modulation sites per channel. Alternatively, it is possible that H⁺ modulation sites are located outside of the RCK domains, i.e., near the transmembrane domains, which could give rise to four (or more) H⁺ modulation sites per channel.

Figure 2.

Inhibition of MthK activation by H⁺. (A) Representative channel currents recorded over a range of pH at −100 mV. Each of these currents was from different bilayers, which each contained two active channels. For the top of A, no channel activity was observed for 10 min of recording. (B) Po versus [H⁺] at four different [Ca²⁺]: 0.5 mM (open diamond and dash line), 1 mM (open square and solid line), 2 mM (open circle and dotted line), and 10 mM (open triangle and dash-dotted line). Smooth curves represent fits of data at each [Ca²⁺] with Hill equations. Parameters (±SE) for 0.5 mM Ca²⁺ fit: EC₅₀ = 1.47 × 10⁻⁹ ± 1.8 × 10⁻¹⁰ M (pH = 8.8), n_H = 6.1 ± 1.9, and Pomax = 0.95 ± 0.01; for 1 mM Ca²⁺ fit: EC₅₀ = 7.6 × 10⁻⁹ ± 5.9 × 10⁻¹⁰ M (pH = 8.1), n_H = 5.9 ± 10.0, and Pomax = 0.94 ± 0.04; for 2 mM Ca²⁺ fit: EC₅₀ = 1.84 × 10⁻⁸ ± 2.0 × 10⁻⁹ M (pH = 7.7), n_H = 3.5 ± 2.1, and Pomax = 0.94 ± 0.07; for 10 mM Ca²⁺ fit: EC₅₀ = 1.06 × 10⁻⁷ ± 1.3 × 10⁻⁸ M (pH = 7.0), n_H = 2.9 ± 0.45, and Pomax = 0.94 ± 0.02.

Relation between Ca²⁺ activation and proton sensitivity

We have observed that increasing H⁺ (i.e., decreasing pH) shifts the EC₅₀ for Ca²⁺-dependent activation of MthK toward higher [Ca²⁺]. A critical experimental test of whether H⁺ binding is directly coupled to MthK channel gating is to determine whether gating can be modulated by changing pH in nominally 0 Ca²⁺.

We first attempted to activate MthK channels at pH 9.0 in the nominal absence of Ca²⁺; we reasoned that if H⁺ binding directly inhibited channel gating, Po in 0 Ca²⁺ would be higher at pH 9.0 than at lower pH. The results are exemplified by the experiment presented in Fig. 3 A. Here, a single MthK channel is fully activated in the presence of 1 mM Ca²⁺ at pH 9.0 at the cytoplasmic side of the channel, with a Po of ∼0.94. The solution at the cytoplasmic side (trans chamber) was then replaced by perfusion of 10 chamber volumes with a solution containing 5 mM EGTA (with no added Ca²⁺). During 10 min of continuous recording in this solution, no channel openings were observed. The trans chamber was then reperfused with Ca²⁺-containing solutions (0.4 mM, followed by 1 mM; both without EGTA) to reveal opening of the channel. The solution was then exchanged again with the 5-mM EGTA solution; one burst of openings was observed at the end of the solution exchange, followed by no channel activity during 10 min of continuous recording. The solution was then exchanged with an identical solution without EGTA, but again with no added Ca²⁺; no openings were observed in 10 min of continuous recording. This was then followed by 0.4 mM Ca²⁺, which again maximally activated the channel. The absence of channel opening in the nominal absence of Ca²⁺ during long (10-min) stretches of continuous recording was observed in similar experiments in seven additional bilayers at pH 9.0 in the presence of 5 mM EGTA, and in eight additional bilayers at pH 9.0 in the absence of EGTA but with [Ca²⁺] < 125 µM (22 channels total), as well as in five bilayers at pH 8.5 (13 channels).

Because the apparent frequency of openings in nominally 0 Ca²⁺ was <1/10 min, we resorted to using large liposomes containing high levels of reconstituted MthK to increase the likelihood of incorporation of liposomes with 10 or more active MthK channels (see Materials and methods). Using this technique, we were able to observe apparent MthK gating in nominally 0 Ca²⁺, which is summarized in Fig. 3 B. In these bilayers that contained many channels, Po at nominally 0 Ca²⁺ occasionally displayed sudden variability with time, which could be attributed to instances of modal gating (see below); thus, we restricted our analysis to periods of stable channel activity, which accounted for ∼96% of the total recording time. In recordings from five different bilayers containing typically ∼10 channels per bilayer, Po at nominally 0 Ca²⁺ ranged from 2.3 × 10⁻⁴ (±0.00015) at pH 7.3 to 4.2 × 10⁻⁴ (±0.00017) at pH 9.0. Datasets from individual bilayers obtained at two or more pH were fit with regression lines; these yielded a mean slope of −0.00076 ± 0.0014 Po units per 10-fold increase in [H⁺], which was not significantly different from a slope of 0 (P = 0.61; t test).

A regression line fitted with all Po data obtained with 5 mM EGTA (no added Ca²⁺) at pH 7.3, 8.1, 8.5, and 9.0 predicts that Po decreases by 1.7-fold per 10-fold increase in [H⁺] (Fig. 3 B). This H⁺ inhibition is small compared with the greater than sixth power relation between Po and [H⁺] in the presence of 2 mM Ca²⁺ (Fig. 2), and suggest that the steep relation between Po and [H⁺] arises primarily from a combined action of H⁺ and Ca²⁺ on MthK gating, rather than direct, Ca²⁺-independent coupling between H⁺ binding and gating. A viable mechanism that may account for proton sensitivity of MthK gating without direct coupling between H⁺ binding and gating could include H⁺ modulation of Ca²⁺ sensing, which will be explored later.

By analyzing bilayers containing 10 or more MthK channels using long stretches of continuous recording, we were able to further analyze the intrinsic (i.e., apparent Ca²⁺-independent) gating of these channels. The gating consisted of bursts of openings separated by long gaps of inactivity. Even with apparently minimal activation in nominally 0 Ca²⁺, these channels gated in bursts with a mean duration of 252 ± 46 ms (Fig. 3 C). These were separated by long closed periods with a mean duration of 13.1 ± 4.7 min for each channel (Fig. 3 D); the durations of these gaps of inactivity was consistent with observations in single-channel bilayers (Fig. 3 A), which typically showed no channel activity in the nominal absence of Ca²⁺ during several minutes of continuous recording. The burst and gap durations provide estimates of the intrinsic closing and opening rates of MthK with no Ca²⁺ bound (3.97 s⁻¹ and 0.00127 s⁻¹, respectively), which in turn can be used to constrain potential quantitative gating mechanisms.

MthK channels may enter a high-activity mode at high pH

Over the course of many MthK bilayer experiments conducted at pH ≥ 8.1, we observed occasional channels displaying paradoxically high levels of activity. Two examples are presented in Fig. 4. Fig. 4 A shows a current trace from a bilayer at pH 9.0 that contained three active channels, with one MthK-like channel that was constitutively active in the nominal absence of Ca²⁺. Fig. 4 B shows currents from a bilayer at pH 8.5 that contained two active channels; both channels displayed apparently normal gating during recordings at several [Ca²⁺], and one of these channels displayed paradoxical high-activity gating in the presence of 0 added Ca²⁺. In every case where we have observed high-activity gating in bilayers containing several MthK channels, we have never observed superimposed openings of high activity, consistent with their relatively low frequency of occurrence. Based on observations in 23 different bilayers, the probability of observing high-activity gating in nominally 0 Ca²⁺ was 4.0% (11 out of 272 active channels). When observed, the duration of the apparent high activity ranged from ∼4 min to >10 min; thus, this activity may represent a gating mode that occurs in a minority of channels, although the frequency of reverting to normal gating is not clear because reversion to normal gating was sometimes not observed.

Figure 4.

Appearance of a high-activity gating mode among MthK channels at high pH. (A) Representative trace showing that one out of the three channels in this bilayer was fully active at pH 9.0 with [Ca²⁺] ≤ 0.25 mM Ca²⁺, at which channels are typically closed most of the time. (B) Representative trace showing one out of two channels in a bilayer that showed high activity at pH 8.5 with no added Ca²⁺ ([Ca²⁺] ≈ 10 µM), at which channels are typically closed most of the time. In this example, Po for the two channels had decreased at 0.5 mM Ca²⁺, followed by the appearance of high-activity gating at 0 Ca²⁺. Similar paradoxical high-activity gating was observed in 11 out of 272 active channels from among 23 different bilayers at pH ≥ 7.7.

Based on our observations, the high-activity gating mode seems more likely to occur at high pH (≥8.1) and at low Ca²⁺. We have not observed the high-activity mode at pH < 8.1, even with nominally 0 Ca²⁺ (5 mM EGTA with no added Ca²⁺). Because it was shown previously that pH can alter the oligomeric stability of the MthK gating ring (Dong et al., 2005; Kuo et al., 2007), we hypothesized that in the nominal absence of Ca²⁺, high pH (i.e., low [H⁺]) may destabilize MthK channels, resulting in dysregulated gating. To test this idea, we analyzed the oligomeric stability of purified, detergent-solubilized MthK channels at pH 6.8 and 9.0 in the presence and nominal absence of Ca²⁺ by size-exclusion chromatography (Fig. 5). We observed that at pH 6.8, MthK eluted primarily as a single peak centered at ∼10.5 ml (corresponding to ∼200 kD) either with or without Ca²⁺ (Fig. 5 A, blue and red traces, respectively), with a relatively small peak at ∼15 ml (indicated by arrow) corresponding to monomeric RCK domain (∼26 kD). In contrast, at pH 9.0, with 20 mM Ca²⁺ (Fig. 5 B, blue trace), MthK eluted primarily as a single peak centered at ∼11 ml, whereas with nominally 0 Ca²⁺ (red trace), MthK eluted with a major peak centered at ∼10.5 ml and a peak at ∼15 ml that was larger than that observed at pH 6.8. This illustrates that non-tethered (monomeric) RCK domains show increased dissociation from MthK channels at high pH.

Figure 5.

Exposure of detergent-solubilized MthK channels at pH 9.0 in the nominal absence of Ca²⁺ results in gradual depletion of docked RCK domains from the channel complex. (A) Elution profile of purified detergent-solubilized MthK at pH 6.8 from a Superdex 200 size-exclusion column. Solutions contained 200 mM KCl, 5 mM DM, 10 mM HEPES, 2 mM nitrilotriacetic acid, and either 0 or 20 mM of added Ca²⁺. Under these conditions, MthK eluted primarily as a single peak centered at ∼10.5 ml either with or without Ca²⁺ (blue and red traces, respectively), with a relatively small peak at ∼15 ml (indicated by arrow) corresponding to monomeric RCK domain. (B) Elution profile of purified detergent-solubilized MthK at pH 9.0. Solutions were identical to those in A, except that 10 mM CHES was used instead of HEPES. With 20 mM Ca²⁺ (blue trace), MthK eluted primarily as a single peak centered at ∼11 ml. With nominally 0 Ca²⁺ (red trace), MthK eluted with a major peak centered at ∼10.5 ml and a peak at ∼15 ml that was larger than that observed at pH 6.8. (C) A series of size-exclusion chromatography runs at pH 9.0 with nominally 0 Ca²⁺, in which fractions eluting between 9 and 14 ml were pooled, concentrated, and reloaded. With each successive run, the peak at ∼15 ml is diminished, consistent with depletion of dissociated RCK domains. In addition, two peaks are resolved from the original single peak at ∼10.5 ml (a) and 12 ml (b). (D) Analysis of pooled fractions eluting between 9 and 14 ml from the first and fourth successive chromatography runs by SDS-PAGE, stained with Coomassie blue. Fractions from the first run show bands at ∼200 and 26 kD, consistent with elution of a channel complex containing transmembrane and soluble RCK subunits, as shown previously (Jiang et al., 2002a; Parfenova et al., 2006). Fractions from peaks (a) and (b) in the fourth run contain the ∼200-kD band but are depleted of the 26-kD band. This is consistent with peaks (a) and (b) each being comprised primarily of transmembrane subunits of the MthK channel that are depleted of “soluble” RCK subunits.

The dissociation of RCK domains from MthK channels at high pH is further illustrated in Fig. 5 C. Here, fractions corresponding to the ∼200-kD peak were collected and serially refractionated by size-exclusion chromatography. The pooled fractions from each of the serial chromatography runs were then separated by SDS-PAGE to analyze their components. We observe (Fig. 5 D) that although the ∼200-kD peak in the initial sample contained full-length channel subunits and non-tethered RCK domains (200- and 26-kD bands, respectively; 1st lane), non-tethered RCK domains are depleted from subsequent (refractionated) samples (4^th lanes a and b). Because each size-exclusion experiment lasts ∼45 min, these results are consistent with the idea that at high pH, non-tethered (i.e., “soluble”) RCK domains may dissociate from the MthK channel complex over a relatively slow time scale (i.e., minutes). Whether this phenomenon alone might account for the high-activity gating mode is unclear.

Effects of Ca²⁺ and H⁺ on MthK open and closed times

To further identify whether Ca²⁺ and H⁺ affect Po through effects on channel opening or closing rates, we measured mean open and mean closed times in individual bilayer experiments (Fig. 6). Fig. 6 A illustrates that closed times decreased steeply as a function of Ca²⁺, and lower pH shifted closings toward longer durations. The decrease of closed times was ∼100-fold per doubling of [Ca²⁺] in the linear range of the effect, which was shifted toward higher [Ca²⁺] with decreasing pH, consistent with the inhibitory effect of H⁺ on Po. In contrast, mean open times displayed a nominal increase with [Ca²⁺] at pH ranging from 6.5 to 9.0. These results suggest that Ca²⁺ and H⁺ affect gating transitions primarily by increasing effective opening rates, with little effect on effective closing rates.

Figure 6.

Effects of Ca²⁺ and H⁺ on mean open and closed times. Symbols corresponded to pH as indicated in Fig. 1. (A) Mean closed times as a function of [Ca²⁺] and pH. Closed times decreased steeply as a function of [Ca²⁺], ∼100-fold per doubling of [Ca²⁺], consistent with an approximately sixth power relationship. Increasing [H⁺] (decreasing pH) leads to longer mean closed times. (B) In contrast, mean open times increased less than twofold with a 100-fold increase in [Ca²⁺], over pH ranging from 6.5 to 9.0. Thus, Ca²⁺ appears to increase Po by decreasing mean closed time, while H⁺ increases mean closed time, with little effect on open times.

To determine classes of gating transitions that might be modulated by Ca²⁺ and H⁺, we measured dwell times from bilayers under conditions that yielded a single open current level (i.e., no superimposed openings). We then generated dwell-time histograms, which in turn were fitted with sums (mixtures) of exponential components (a) to estimate the minimum numbers of kinetic states over a wide range of pH and [Ca²⁺], and (b) to determine the effects of H⁺ and Ca²⁺ on classes of gating events. The effect of Ca²⁺ and H⁺ on open dwell times is illustrated in the representative distributions in Fig. 7. These histograms illustrate that H⁺ and Ca²⁺ have little effect on open dwell times over a wide range of pH and [Ca²⁺], and over an ∼1,200-fold range of Po. In addition, for the data included in these analyses, the open dwell-time distributions were typically best described with a single-exponential component (131 out of 137 datasets). Collectively, these observations are consistent with MthK channels gating in a single open state whose mean lifetime does not change substantially over a wide range of pH or [Ca²⁺].

In contrast, Ca²⁺ can have large effects on closed dwell times, as can H⁺ in the presence of Ca²⁺. The representative closed-time distributions in Fig. 8 illustrate that increasing Po through increasing [Ca²⁺] or increasing pH in the presence of Ca²⁺ resulted in a decrease in the frequency and duration of long closings (“gaps”), whereas having little effect on the durations of brief closings (“flickers”). This is in contrast to the observation that the duration and frequency of gaps show no apparent change with increasing pH at nominally 0 Ca²⁺ (Fig. 3 D). Thus, the observations that gaps decrease in frequency and duration with increasing [Ca²⁺], and increase in frequency and duration with increasing [H⁺] in the presence of Ca²⁺, are consistent with an increase in the frequency and duration of bursts of openings, which in turn underlies observed Ca²⁺-dependent increases in MthK Po.

Increasing [Ca²⁺] increases the durations of bursts of openings

The observation that increasing [Ca²⁺] resulted in decreases in the frequencies and durations of gaps and increasing [H⁺] in the presence of Ca²⁺ resulted in increases in the frequencies and durations of gaps, while having little effect on the durations of individual open events or brief flicker closings, predicts that Ca²⁺ acts to increase both the frequencies and the durations of bursts of openings, whereas H⁺ acts to decrease the frequencies and the durations of bursts. To test this, we analyzed the effects of pH and [Ca²⁺] on the number of openings per burst and on burst duration (see Materials and methods).

We observed that the distributions of the number of openings per burst and of burst duration were typically best described by a single geometric or exponential component, respectively, consistent with the idea that MthK channels gate primarily through a single open state (Fig. 9, A and C). In addition, we observed that over pH 6.5–9.0, doubling [Ca²⁺] increased the number of openings per burst a maximum of 6.6-fold (± 1.7-fold) and the burst duration a maximum of 7.7-fold (± 2.3-fold), and increasing pH in the presence of Ca²⁺ resulted in a leftward shift in the relation between [Ca²⁺] and the number of openings per burst as well as the relation between [Ca²⁺] and burst duration (Fig. 9, B and D). In contrast, increasing pH at nominally 0 Ca²⁺ resulted in no increase in burst duration (Fig. 3 C).

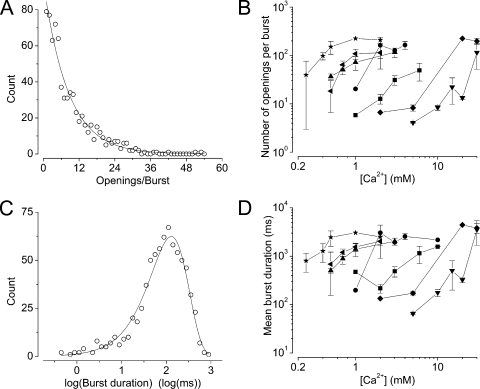
Figure 9.

Burst analysis of MthK gating over a range of pH and [Ca²⁺]. Bursts of openings were classified by calculation of a critical closed interval duration (see Materials and methods), and the number of openings per burst and durations of bursts was analyzed over a range of experimental conditions. (A) Representative distribution of the number of openings per burst from data at 15 mM Ca²⁺, pH 6.5. Data were binned at a resolution of one opening/burst per bin. The solid line represents a fit of the data with a geometric distribution (N(r)=N(1) b^r-1), with mean number of openings per burst (given by 1/1-b) = 9. (B) Increasing [Ca²⁺] increases the number of openings per burst, whereas increasing [H⁺] (decreasing pH) decreases the number of openings per burst. The number of openings per burst increased 6.6-fold per twofold increase in [Ca²⁺], indicating that the frequency of gaps between bursts decreased by that amount to increase channel Po. In general, increasing H⁺ increased the [Ca²⁺] required to reach a given burst length. (C) Representative distribution of burst durations from data at 15 mM Ca²⁺, pH 6.5. The solid line represents a fit of the data with a single-exponential component, with τ = 130 ms. (D) As with the number of openings/burst, increasing [Ca²⁺] increases burst duration, whereas increasing [H⁺] decreases burst duration. Burst duration increased 7.7-fold per twofold increase in [Ca²⁺], and increasing [H⁺] increased the [Ca²⁺] required to reach a given burst duration. Symbols in B and D represent mean ± SEM.

Modified allosteric models cannot account for both the Ca²⁺ activation and H⁺ inhibition of MthK gating

To describe MthK gating as a function of [Ca²⁺] and [H⁺] and, consequently, to provide estimates of the energetics of individual gating steps, quantitative kinetic models were developed. The observations of (a) a steep relation between Po and [Ca²⁺] that is consistent with at least eight Ca²⁺-dependent steps in the activation pathway (Fig. 1, A and B), and (b) a single detectable open state over a wide range of [Ca²⁺] (Fig. 7) have been accounted for in previous kinetic modeling (Zadek and Nimigean, 2006). Using these constraints as a starting point, the Ca²⁺- and H⁺-dependent gating model will need to further account for (a) the steep inhibitory relation between [H⁺] and Po in the presence of Ca²⁺ (Fig. 2), which predicts at least six H⁺-dependent gating steps; (b) the lack of substantial H⁺-dependent gating in the nominal absence of Ca²⁺ (Fig. 3), which suggests that direct allosteric coupling between H⁺ binding and channel opening is very weak; and (c) the lack of an apparent relation between pH and the Hill coefficient for Ca²⁺-dependent activation (Fig. 1 D).

If H⁺ binding does not inhibit the opening of MthK independent of Ca²⁺, then we must assume, in the framework of a model, that H⁺ inhibits MthK gating through an effect on the functional action of Ca²⁺. In principle, this could occur through an effect on (a) the allosteric coupling between Ca²⁺ binding and channel opening, or (b) an effect on the equilibrium constant of the Ca²⁺-dependent gating transitions.

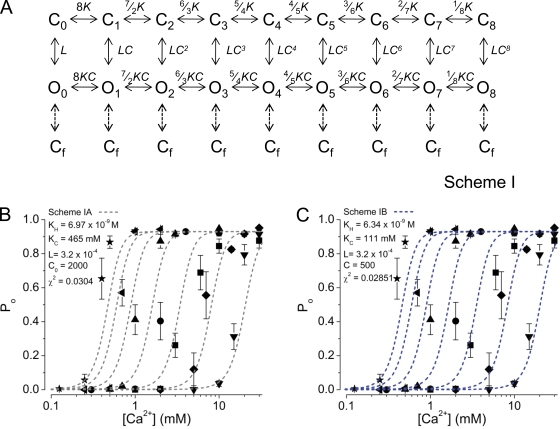
In BK channels, Mg²⁺ has been proposed to facilitate channel gating through enhancement of the allosteric coupling between voltage sensing and channel opening (Horrigan and Ma, 2008). To explore whether H⁺ inhibits MthK solely by decreasing the allosteric coupling between Ca²⁺ binding and channel opening, we developed a modified Monod-Wyman-Changeux (MWC)-type allosteric model (Monod et al., 1965) (Fig. 10 A, Scheme I), described by a modified form of Eq. 2. In the context of this modified model, Scheme IA, the allosteric coupling factor between Ca²⁺ binding and channel opening, C, is modulated by [H⁺], such that C = C₀ (K_H /(K_H + [H⁺])), where C₀ is the theoretical C factor at 0 H⁺ and K_H is the apparent H⁺ dissociation constant.

Figure 10.

Allosteric model describing the Ca²⁺ activation of MthK. (A) Scheme I, in which eight Ca²⁺ bind to the channel, with each bound Ca²⁺ biasing the gating equilibrium toward the open states. (B) Po versus [Ca²⁺] relations predicted by Scheme IA (gray dashed lines) that incorporate H⁺ dependence with C = C₀(K_H/(K_H+[H⁺])), as described in Results. Parameter values were: K_H = 6.97 × 10⁻⁹ M H⁺; K_C = 465 mM Ca²⁺; L = 3.2 × 10⁻⁴; C₀ = 2,000. (C) Po versus [Ca²⁺] relations predicted by Scheme IB (blue dashed lines) that incorporate pH dependence with K = ([Ca²⁺]/K_C)(K_H/(K_H+[H⁺])), as described in Results. Parameter values were: K_H = 6.34 × 10⁻⁹ M H⁺; K_C = 111 mM Ca²⁺; L = 3.2 × 10⁻⁴; C = 500. In B and C, symbols correspond to mean Po at each [Ca²⁺] at pH 9.0, 8.5, 8.1, 7.7, 7.3, 6.9, and 6.5 (as described in previous figures).

A set of parameters for Scheme IA was estimated by global fitting of Po data at [Ca²⁺] ranging from 10 µM to 30 mM and pH ranging from 6.5 to 9.0 (209 data points) with Eq. 2 (see Materials and methods) with C = C₀ (K_H /(K_H + [H⁺])). For these fits, the value of L was fixed by using an estimate derived from our experimental data at nominally 0 Ca²⁺; for a mean duration of 252 ms and mean gap duration of 13.1 min (7.86 × 10⁵ ms), L = 3.2 × 10⁻⁴ (252/7.86 × 10⁵). Simulated Po versus [Ca²⁺] relations using the best-fit parameters are shown in Fig. 10 B. We observe that although Scheme IA can qualitatively describe the pH-dependent shift in Po versus [Ca²⁺] relations (Fig. 10 B), this scheme quantitatively predicts that with increasing pH (decreasing [H⁺]), the size of the shift decreases compared with the shifts observed at lower pH, which is inconsistent with the experimental data (Fig. 1 C). Consistent with the idea that H⁺ may not act solely through effects on allosteric coupling between Ca²⁺ binding and gating, isolated MthK RCK domain complexes undergo apparent pH-dependent conformational changes, even when physically uncoupled from the transmembrane domain of MthK (Ye et al., 2006). This is in contrast to the mechanism of Mg²⁺ action on BK channels, which requires proximity between apparent Mg²⁺ binding residues in the cytoplasmic RCK domain and transmembrane voltage sensor (Hu et al., 2003; Yang et al., 2007).

If H⁺ does not inhibit MthK channels solely by decreasing the allosteric coupling between Ca²⁺ binding and channel opening, an alternative possibility to account for H⁺ inhibition of MthK channels is that H⁺ could affect the equilibrium constant of the Ca²⁺-dependent gating transitions. Physically, this could arise from H⁺ binding either destabilizing the Ca²⁺-bound states or stabilizing the Ca²⁺-free states of the channel. In a kinetic framework, the relative stabilization of Ca²⁺-free states can be achieved either by (a) introducing a H⁺-dependent equilibrium constant that directly modulates each Ca²⁺-dependent equilibrium constant, or (b) introducing direct allosteric coupling between H⁺ binding and Ca²⁺ binding.

To test the possibility that the Ca²⁺- and H⁺-dependent equilibrium constants govern the same gating transitions, we tested an additional modified MWC-type allosteric model. In this modified MWC-type model, Scheme IB, the equilibrium constant K = ([Ca²⁺]/K_C) (K_H/(K_H + [H⁺])); thus, Ca²⁺-dependent gating transitions are driven forward by increasing [Ca²⁺] and decreasing [H⁺]. Physically, this could arise from H⁺ binding that directly excludes Ca²⁺ binding, and vice versa (direct competitive inhibition). We observe that Scheme IB qualitatively describes a pH-dependent shift in Po versus [Ca²⁺] relations (Fig. 10 C), although (as with Scheme IA) Scheme IB predicts that with increasing pH (decreasing [H⁺]), the size of the shift decreases compared with the shifts observed at lower pH, which is inconsistent with the experimental data (Fig. 1 C).

A dual allosteric model can account for both the Ca²⁺ activation and H⁺ inhibition of MthK gating

A second means of incorporating H⁺ modulation of Ca²⁺-dependent gating transitions is through introducing direct allosteric coupling between H⁺ binding and Ca²⁺ binding. This type of allosteric coupling has been incorporated previously to describe gating of BK channels, in which there is evidence for relatively weak, direct allosteric coupling between Ca²⁺ sensing and voltage sensing (Horrigan and Aldrich, 2002). To do this, starting from Scheme I (Fig. 10 A), we assumed that each of the nine possible closed and open states, each with 0–8 Ca²⁺ bound, could each in turn exist in nine possible closed and open states, each of those with 0–8 H⁺ bound. This gives rise to a 162-state model (not depicted, of course), which we summarize with an abbreviated diagram that shows the elementary gating transitions, as done previously in representations of the dual allosteric gating model for BK channels (Horrigan and Aldrich, 2002).

The proposed Ca²⁺- and H⁺-dependent gating mechanism is summarized in Scheme II (Fig. 11 A). In the context of this model, gating is modulated by the binding of H⁺, described by the equilibrium constant H, with eight modulatory sites per channel. H⁺ binding is coupled to the Ca²⁺-dependent gating steps, which are described by the equilibrium constant K; the coupling between H and K is described by the parameter E. In turn, the Ca²⁺-dependent gating steps are positively coupled to channel opening, described by L; the coupling between K and L is described by C. H⁺-dependent gating steps, in principle, could also be coupled to gating; the coupling between H and L is described by D. Finally, the open channel can also undergo brief closings that are outside of the activation pathway (C_f).

Figure 11.

Working hypothesis of Ca²⁺ activation and proton-sensitive gating of MthK. (A) Abbreviated model describing Ca²⁺ activation and proton-sensitive gating of MthK (Scheme II; see Results and Discussion for explanation of the model). (B) Po versus [Ca²⁺] relations predicted by Scheme II with the parameters: K_H = 2.78 × 10⁻⁹ M H⁺; K_C = 7.71 mM Ca²⁺; L = 3.2 × 10⁻⁴; C = 50.6; D = 1.0; E = 0.00930 (Scheme IIA, black dashed lines); and K_H = 4.53 × 10⁻⁹ M H⁺; K_C = 19.1 mM Ca²⁺; L = 3.2 × 10⁻⁴; C = 132; D = 0.0381; E = 1.0 (Scheme IIB, red dashed lines). Symbols correspond to mean Po at each [Ca²⁺] at pH 9.0, 8.5, 8.1, 7.7, 7.3, 6.9, and 6.5 (as described in previous figures). (C) Log(EC₅₀) versus pH relation predicted by Schemes IIA and IIB (black and red dashed lines, respectively), estimated from analysis of the predicted curves using the Hill equation. Experimental data (filled circles) are superimposed. (D) Hill coefficient versus pH as predicted by Schemes IIA and IIB (black and red dashed lines, respectively), also estimated from analysis of the predicted curves using the Hill equation, with experimental data (filled circles) superimposed. The higher Hill coefficients observed in the experimental data imply strong positive cooperativity or additional Ca²⁺-binding sites not included in Scheme II.

In the context of Scheme II, H⁺ binding could result in inhibition either through direct (but negative) coupling to the closed–open transition (described by D) or through direct (but negative) coupling to Ca²⁺ binding (described by E), or both. To develop the most parsimonious model, we simplified Scheme II by testing these two possibilities separately; first, by neutralizing coupling between H⁺ binding and channel opening by setting D = 1 (Scheme IIA), and second, by neutralizing coupling between H⁺ binding and Ca²⁺ binding by setting E = 1 (Scheme IIB).

A set of parameters for Scheme IIA was estimated by the global fitting of Po data at [Ca²⁺] ranging from 10 µM to 30 mM and pH ranging from 6.5 to 9.0 (209 data points) with Eq. 3 (see Materials and methods), again with L = 3.2 × 10⁻⁴. The coupling between H and L was constrained to be energetically neutral (D = 1). Simulated Po versus [Ca²⁺] relations using the best-fit parameters are shown in Fig. 11 B (black dashed lines). These relations begin to capture the major features of the data reasonably well, most notably the size of the pH-dependent shift in Po versus [Ca²⁺] curves over pH ranging from 6.5 to 9.0 (Fig. 11 C, black dashed line), as well as the Hill coefficients of the curves as a function of pH, although the individual experimental Hill coefficients were generally higher (Fig. 11 D, black dashed line).

We next tested Scheme IIB, which assumes, instead, that H⁺ binding is directly coupled to gating and not directly coupled to Ca²⁺ binding, by constraining coupling between H and K to be energetically neutral (E = 1) and allowing D to be estimated as a free parameter. At first glance, these predicted curves appear similar to the curves predicted by Scheme IIA (Fig. 11, B–D, dashed red lines). However, a key difference is revealed when the predicted Po values are displayed on a logarithmic scale (Fig. 12 A). In Scheme IIA, the minimum Po values at all pHs are the same, whereas in Scheme IIB these minimum Po values are predicted to increase with increasing pH.

Figure 12.

Distinguishing between Scheme IIA (H⁺ binding inhibits Ca²⁺ binding) and Scheme IIB (H⁺ binding inhibits gating). (A) Scheme IIA (black dashed lines) predicts that at low to nominally 0 Ca²⁺, the minimum Po does not change with pH, whereas Scheme IIB (red dashed lines) predicts that the minimum Po decreases by >10-fold per 0.5-unit decrease in pH (i.e., an approximate threefold increase in [H⁺]). (B) Po measured at nominally 0 Ca²⁺ plotted as a function of pH (filled circles), superimposed on the predicted Po at nominally 0 Ca²⁺ for Scheme IIA (black dashed line) and Scheme IIB (red dashed line). These data illustrate that Scheme IIA, in which H⁺ binding inhibits Ca²⁺ binding with no direct coupling between H⁺ binding and channel gating, is consistent with the experimental data.

To distinguish between the two models, we exploited the strong prediction that to achieve the experimentally observed spacing among Po versus [Ca²⁺] relations as a function of pH in Scheme IIB, the minimum Po (at nominally 0 Ca²⁺) must change >10-fold for a change of 0.5 pH units. Fig. 12 B illustrates that at nominally 0 Ca²⁺, the experimentally measured Po values do not differ by 10-fold, even over 1.7 pH units. Thus, Scheme IIB, which lacks direct coupling between H⁺ binding and Ca²⁺ binding, cannot on its own account for these essential features of MthK gating. We cannot rule out that some small level of direct coupling between H⁺ binding and channel opening may contribute to MthK gating, but this would have to be in addition to a mechanism that incorporates coupling between H⁺ binding and Ca²⁺ binding.

Features and limitations of Scheme IIA

The generally higher steepness of the experimental Po versus [Ca²⁺] relations compared with that predicted by Scheme IIA (Fig. 11 D) suggests that some form of positive cooperativity in the Ca²⁺-dependent transitions may occur. Previous work has incorporated a cooperativity factor into Scheme I to account for this effect at a single pH (Zadek and Nimigean, 2006). To explore whether a form of cooperativity in the Ca²⁺-dependent transitions may underlie the steepness of the Po versus [Ca²⁺] relations over a range of pH, we incorporated a similar form of cooperativity in the Ca²⁺-dependent transitions in Scheme IIA. Despite introducing an additional free parameter, a modified form of Scheme IIA with this type of cooperativity yielded only nominal improvement in the reduced χ² for the fit compared with the same model with no cooperativity (0.01776 without cooperativity vs. 0.01710 with cooperativity). This nominal effect suggests either (a) that the form of cooperative interactions underlying the steep Ca²⁺-dependence is more complex than what we have explored in the context of Scheme II, or (b) that the mechanism underlying the steepness is through another mechanism aside from cooperativity in the Ca²⁺-dependent transitions.

Analysis of the fitted parameters from Scheme IIA suggests that Ca²⁺ binding is tightly coupled to channel opening. Based on the parameter estimates for Scheme IIA, the binding of each Ca²⁺ biases the gating equilibrium 50.6-fold toward the open state, for an increase in the effective gating equilibrium constant of 4.3 × 10¹³ with the binding of 8 Ca²⁺ (50.6⁸). In addition, the binding of H⁺ is strongly coupled to biasing of Ca²⁺-dependent transitions toward Ca²⁺-free states; each H⁺ bound decreases the effective forward Ca²⁺-dependent equilibrium constant (K_C) by ∼100-fold (1/E). This could be explained in physical terms as either a decrease in the effective Ca²⁺-binding rate or an increase in the effective Ca²⁺ dissociation rate at lower pH, in which Ca²⁺ and H⁺ do not compete for the same binding site. Alternatively, H⁺ binding may act by inhibiting a conformational change in the RCK domain that would occur subsequent to Ca²⁺ binding, but before opening of the channel.

DISCUSSION

Mechanism of H⁺ inhibition of MthK gating

As a ligand-gated K⁺-selective channel whose structure is known at the atomic level, an understanding of the functional mechanisms underlying gating of MthK stands to provide insight toward mechanism in other ligand-gated K⁺ channels. Here, we sought to understand the relation between the processes underlying modulation of MthK by two ligands, Ca²⁺ and H⁺, through analysis of channel gating kinetics and development of a quantitative working hypothesis of the gating mechanism. Our results suggest, principally, that Ca²⁺ binds to and stabilizes the open state of the MthK channel, and H⁺ binding does not on its own inhibit opening of the channel, but instead inhibits opening through the relative destabilization of Ca²⁺-bound states that subsequently drive the channel toward the open state, as described by Scheme IIA (Fig. 12).

We observe that H⁺ binding inhibits MthK opening, and that this inhibition can be completely overcome by increasing the [Ca²⁺] (Fig. 1). This behavior is a hallmark of competitive inhibition. Thus, the relation between Ca²⁺ binding and H⁺ binding in Scheme IIA may be viewed as a form of allosteric competitive inhibition, in which the binding of H⁺ allosterically inhibits Ca²⁺ binding, and vice versa (Fig. 13). This type of inhibition has been described previously in glycine and ACh receptors (Bertrand et al., 1992; Lynch et al., 1995).

Figure 13.

Apparent allosteric competitive inhibition of Ca²⁺ binding by H⁺ in MthK channels. H ([H⁺]/K_H) and K ([Ca²⁺]/K_C) represent the equilibrium constants for H⁺ and Ca²⁺ binding, respectively. E represents the allosteric coupling factor between H⁺ binding and Ca²⁺ binding (E < 1). The binding of H⁺ drives the Ca²⁺-dependent equilibrium constant away from the Ca²⁺/H⁺-bound states; likewise, the binding of Ca²⁺ drives the H⁺-dependent equilibrium constant away from the Ca²⁺/H⁺-bound states. Because Ca²⁺ binding is coupled to channel opening (not depicted here), this action of H⁺ effectively inhibits MthK opening. Although the binding sites for H⁺ and Ca²⁺ are depicted separately here, we cannot rule out the possibility that the binding sites for H⁺ and Ca²⁺ partially overlap.

An alternative possibility to explain the competitive inhibitor-like behavior of H⁺ would be to assume that binding of a H⁺ can exclude binding of a Ca²⁺ to its binding site on the RCK domain. This type of mechanism is described by Scheme IB (Fig. 10 A). We observe that Scheme IB cannot account quantitatively for the pH-dependent shifts in Po versus Ca²⁺ relations over pH ranging from 6.5 to 9.0 (Fig. 10 C), whereas Scheme IIA provides the best description of these data out of the models tested. This suggests that H⁺ binding is not likely to completely exclude Ca²⁺ binding. However, we cannot rule out the possibility that the binding site for H⁺ partially physically overlaps the Ca²⁺-binding site; it is possible that protonation of a Ca²⁺-coordinating side chain in the RCK domain (D184, E210, or E212; Dong et al., 2005) may destabilize Ca²⁺ binding, while not completely excluding Ca²⁺ binding. It is also possible that destabilization of Ca²⁺ binding occurs through protonation of a completely separate site.

In previous work it was hypothesized that H⁺ binding (i.e., low pH) leads to disruption of the eight-member cytoplasmic gating ring of the MthK channel. Although disruption of soluble MthK RCK domain octamers is observed at pH < 7.0, H⁺ clearly affects MthK gating at concentrations that do not result in a major loss of gating ring integrity (Fig. 1) (Dong et al., 2005; Kuo et al., 2007). Perhaps in intact MthK channels, H⁺ binding has more subtle effects on gating ring conformation, which may either (a) promote release of Ca²⁺ from binding sites on the RCK domains, or (b) inhibit a Ca²⁺-dependent conformational change by binding to a H⁺-titratable site on the RCK domain.

Relation to previous experimental observations

The work of Zadek and Nimigean (2006) provided a kinetic framework that suggested that Ca²⁺ activates MthK in a highly cooperative manner, giving rise to steep Hill coefficients (∼8). To account for the steep Ca²⁺ dependence, they incorporated a cooperativity factor that had the effect of increasing the Ca²⁺-dependent forward equilibrium constants in their model. This, combined with a high allosteric coupling factor (of ∼200), yielded a predicted Hill coefficient of 7.5 ± 0.5 (Zadek and Nimigean, 2006). Without incorporating a cooperativity factor, Scheme IIA yields Hill coefficients of 5.4 for simulated data over pH ranging from 6.5 to 9.0, which is within the range of Hill coefficients we have observed in experimental data for the present studies. Collectively, the present and previous models are consistent with the idea that some form of positive cooperativity does occur, and its incorporation into a suitable model should lead to a more complete description of MthK gating.

We have observed that MthK gating activity in the nominal absence of Ca²⁺ is relatively low (Po of ∼10⁻⁴) and showed essentially no pH sensitivity (Fig. 3), which appears qualitatively at odds with a previous report that MthK can be substantially activated in nominally 0 Ca²⁺ in a pH-sensitive manner (Po of ∼0.3 at pH 9.0) (Li et al., 2007). We suspect that these observations can be partly reconciled if we assume that the activation observed at high pH in the previous report could be accounted for by high activity modal gating (Fig. 4). However, the levels of modal gating we observe cannot account for the previous report entirely because in our recordings, in the presence of 5 mM EGTA, fewer than 5% of active channels displayed this activity, which is too small to account for the levels of activity observed at high pH by Li et al. (2007). It is conceivable that differences in the methods used to change the pH during the course of experiments may be an additional factor contributing to different levels of modal gating (i.e., we used complete solution exchange via a gravity-fed perfusion system, whereas Li et al. used a titration technique). It will be important to resolve these discrepancies as more features of MthK gating (e.g., gating modes and sensitivity to other experimental conditions) become clear.

Because of the difficulty in clearly distinguishing between “very brief sojourns into modal gating” and “normal low-activity gating” in our recordings at nominally 0 Ca²⁺, it is possible that error in Po measurements could be introduced in datasets due to inclusion of modal gating in the analysis. Because instances of the high-activity mode were observed more frequently at higher pH (>8.1), we would expect the contribution of this error to lead to overestimates of Po at higher pH in the data presented in Fig. 3 B. If this error were significant, the true relation between Po and pH at nominally 0 Ca²⁺ may be weaker than the already small degree that we have estimated (Fig. 3).

Conclusions

The present studies provide support for a testable working hypothesis for Ca²⁺ activation and proton-sensitive gating of MthK over a wide range of conditions (Scheme IIA). This scheme provides a framework that may be useful for understanding the effects of targeted mutations on MthK gating energetics, which may further our understanding of the allosteric mechanisms that underlie channel gating. Just as our current hypothesis is built on earlier work, we anticipate that additional studies will rigorously test assumptions implicit in Scheme II, such as the assumptions of (a) equivalence among Ca²⁺ binding sites in modulation of gating and (b) equivalence among H⁺ binding sites in modulation of gating, and may further account for the apparent cooperativity in Ca²⁺-dependent gating over a range of pH.