Asymmetric Image-Template Registration

Abstract

A natural requirement in pairwise image registration is that the resulting deformation is independent of the order of the images. This constraint is typically achieved via a symmetric cost function and has been shown to reduce the effects of local optima. Consequently, symmetric registration has been successfully applied to pairwise image registration as well as the spatial alignment of individual images with a template. However, recent work has shown that the relationship between an image and a template is fundamentally asymmetric. In this paper, we develop a method that reconciles the practical advantages of symmetric registration with the asymmetric nature of image-template registration by adding a simple correction factor to the symmetric cost function. We instantiate our model within a log-domain diffeomorphic registration framework. Our experiments show exploiting the asymmetry in image-template registration improves alignment in the image coordinates.

1 Introduction

Dense spatial correspondences among multiple images can be established by either directly registering pairs of images [1,2], or through a common coordinate system, where each image is aligned with a template [3,4,5]. Standard off-the-shelf pairwise registration algorithms are commonly used by both approaches. Yet, as we discuss in this paper, the two formulations are inherently different. In particular, we show that employing an algorithm designed for pairwise image registration can be sub-optimal if one of the images is a template.

In pairwise image registration, we seek a bi-directional mapping between the spatial coordinates of two images. It is therefore natural to assume that both coordinate systems should play equivalent roles in the algorithm. This symmetry of the pairwise image registration problem is exploited by inverse consistent algorithms [1,6,7,8,9,10,11]. These methods use the gradients of both images in the optimization while constraining the warps between the images to be inverses of each other, either explicitly or by construction. Empirically this strategy yields more robust and accurate alignment results [7,11].

In contrast, the problem of image alignment to a template is fundamentally asymmetric: registration must be unidirectional for the template to represent a valid probabilistic model [12,13]. In this paper, we further argue that this asymmetry is important in the context of atlas-based segmentation because the alignment quality should be measured in the image coordinate frame, rather than that of the atlas. To the best of our knowledge, this paper includes the first practical demonstration of this argument.

We present an energy-based formulation of the asymmetric image-template registration. Many of the derivations we include have previously appeared, cf. [8,10], but only in the context of symmetric pairwise image registration. The main point of the present paper is to demonstrate that accounting for the asymmetry in image-template registration will lead to improved segmentation. We develop an algorithm that employs a stationary velocity field parametrization of diffeomorphisms [11] to solve the proposed optimization problem. We include two sets of experiments on images from the OASIS [14] and Brainweb [15] datasets.

2 Problem Formulation

Given two images I, J: ℝ³ ↦ ℝ, the transformation Φ: ℝ³ ↦ ℝ³ that aligns the images is commonly determined via a regularized optimization problem, such as:

$$\widehat{\mathrm{\Phi }}=\underset{\mathrm{\Phi }}{\text{argmin}}{\left|\right|I-J\circ \mathrm{\Phi }\left|\right|}_2^2+\text{Reg}(\mathrm{\Phi }),$$ (1)

where [J ◦ Φ](x) = J (Φ(x)) and ${\left|\right|f\left|\right|}_2^2={\int }_{{\mathbb{R}}^3}{(f(x))}^{2}dx$ for any f: ℝ³ ↦ ℝ.

While we only consider the L₂ norm in this paper, the following discussion extends to other image dissimilarity measures. It can be shown that the L₂ norm is not symmetric with respect to spatial transformation, and the optimization problem of Eq. (1) depends on which image is warped [8,1,10]. In the absence of a preference, it makes sense to symmetrize the dissimilarity measure either by using a symmetric differential form as in [10] or by seeking

$$\widehat{\mathrm{\Phi }}=\underset{\mathrm{\Phi }}{\text{argmin}}{\left|\right|I-J\circ \mathrm{\Phi }\left|\right|}_2^2+{\left|\right|I\circ {\mathrm{\Phi }}^{-1}-J\left|\right|}_2^2+\text{Reg}(\mathrm{\Phi })+\text{Reg}({\mathrm{\Phi }}^{-1}).$$ (2)

Eq. (2) is the basis of many inverse consistent image registration approaches [6,7,8,9,11]. The use of symmetry results in robust and accurate optimizers that employ gradients of both images.

As discussed in [12], a true probabilistic formulation requires the model (template) to be warped and thus registration of an image should be formulated uni-directionally. This argument can be extended to energy-based approaches. In segmentation, for example, one estimates an anatomical label for each voxel in image I. A typical approach involves registering the image I with template T, which might represent the average of training images. The goal is to bring the underlying hidden labels of the image into spatial agreement with the labels of the training data. Segmentation quality depends heavily on this accordance.

Since segmentation accuracy is measured as the agreement between estimated and ground truth labels in the spatial coordinates of the image I, using a dissimilarity term measured in the image coordinates should improve label alignment. This points to the “forward” formulation, where the template T is warped:

$$\widehat{\mathrm{\Phi }}=\underset{\mathrm{\Phi }}{\text{argmin}}{\int }_{{\mathbb{R}}^3}{[I(x)-T(\mathrm{\Phi }(x))]}^{2}dx+\text{Reg}(\mathrm{\Phi }).$$ (3)

By introducing y = Φ(x), we arrive at an equivalent formulation:

$$\widehat{\mathrm{\Phi }}=\underset{\mathrm{\Phi }}{\text{argmin}}{\int }_{{\mathbb{R}}^3}{[I({\mathrm{\Phi }}^{-1}(y))-T(y)]}^{2}det(\nabla {\mathrm{\Phi }}^{-1}(y))dy+\text{Reg}(\mathrm{\Phi }),$$ (4)

where ∇Φ⁻¹ denotes the Jacobian matrix of transformation Φ⁻¹ with respect to the spatial coordinates. Eq. (4) involves warping the image I, and hence can be viewed as a “backward” formulation. Combining Eq. (3) and Eq. (4), we achieve a “bi-directional” formulation for image-template registration:

$$\widehat{\mathrm{\Phi }}=\underset{\mathrm{\Phi }}{\text{argmin}}\frac{1}{2}{\int }_{{\mathbb{R}}^3}{[I(x)-T(\mathrm{\Phi }(x))]}^2+{[I({\mathrm{\Phi }}^{-1}(x))-T(x)]}^{2}det(\nabla {\mathrm{\Phi }}^{-1}(x))dx+\text{Reg}(\mathrm{\Phi }).$$ (5)

Note that Eqs. (3), (4) and (5) are theoretically identical in the continuous domain, but may yield different numerical solutions after discretization. In particular, solving the bi-directional optimization problem of Eq. (5) will involve the gradients of both the image and template. Thus, we expect that similar to inverse consistent approaches, this formulation will enjoy robust and accurate performance. If we use an inverse consistent warp regularization, i.e., Reg(Φ) = Reg(Φ⁻¹), the only difference between Eq. (5) and the symmetric formulation of Eq. (2) is the Jacobian weighting term that encodes local areal distortion due to the warp. Specifically, det(∇Φ⁻¹(x)) is larger than 1 in regions where an area in image I is mapped to a smaller area in template T and less than 1 elsewhere. This weighting reflects the asymmetry in the objective function that evaluates alignment in image coordinates.

3 Log-Domain Diffeomorphic Registration

We demonstrate and compare the algorithms that solve Eq. (3), Eq. (4) and Eq. (5) in the log-domain diffeomorphic registration framework [11], which employs a Demons-style approach [16] to decouple the optimization of the similarity measure and of the regularization term, by introducing an auxiliary transformation Γ. In each iteration, the algorithm minimizes the following energy:

$$E(I,T,\mathrm{\Phi },\mathrm{\Gamma })=\text{Dissim}(I,T,\mathrm{\Phi })+\lambda \text{Dist}{(\mathrm{\Phi },\mathrm{\Gamma })}^2+\text{Reg}(\mathrm{\Gamma }),$$ (6)

where λ > 0 and Dist(Φ, Γ) encodes the distance between the two transformations. Reg(Γ) + λ Dist(Φ, Γ)² replaces Reg(Φ) from the previous section. In each iteration, the Demons algorithm optimizes Eq. (6) in two steps. First, we fix Γ and estimate Φ that minimizes the first two terms. Then, we fix Φ and minimize the last two terms with respect to Γ. The second step searches for a smooth approximation to the current warp Φ and typically reduces to smoothing Φ.

In the log-domain diffeomorphic Demons framework [11], a warp Γ is parameterized with a smooth, stationary velocity field v: ℝ³ ↦ ℝ³ via an ODE: $\frac{\partial \mathrm{\Gamma }(x,t)}{\partial t}=v(\mathrm{\Gamma }(x,t))$ and an initial condition Γ (x, 0) = x. The solution of the ODE, Γ (x) = exp(v)(x), can be computed efficiently using scaling and squaring [17] and inverted by using the negative of the velocity field: Γ⁻¹ = exp(−v). An update velocity field u computed in the first step of the current iteration, can be then combined with the previous warp estimate Γ = exp(v) to compute the current warp Φ = exp(v′) ≈ exp(v + u) [11]. The distance between the two warps Dist(Φ, Γ) is defined as ${\left|\right|u\left|\right|}_2^2$.

We now derive the update formula for the asymmetric bi-directional dissimilarity cost of Eq. (5). For a fixed deformation Γ = exp(v), the first step of the Demons algorithm seeks u that minimizes the following objective function:

$$\sum _{x\in \mathrm{\Omega }}\left[{\left[I(x)-T(exp(v+u)(x))\right]}^2+{\left[I(exp(-v-u)(x))-T(x)\right]}^{2}det(\nabla exp(-v)(x))\right]+2\lambda {\left|\right|u(x)\left|\right|}^2,$$

where, for simplicity, we approximate det(∇exp(−v − u)(x)) ≈ det(∇exp(−v)(x)) for a small u, removing dependencies between the voxels at each update and replace the integral with a discrete sum. This non-linear least squares problem can be efficiently solved using the Gauss-Newton method, which requires finding the gradient of the terms with respect to the stationary velocity field u at u = 0 and solving a linearized least-squares problem. We define: g_T (x) = ∇T (exp(v)(x)), g_I (x) = ∇I (exp(−v)(x)), c_v (x) = det(∇ exp(−v)(x)), and

$$H(x)=\left[{\mathit{g}}_T(x){\mathit{g}}_T{(x)}^T-c_v(x){\mathit{g}}_I(x){\mathit{g}}_I{(x)}^T+4\lambda {\text{Id}}_{3\times 3}\right].$$

The image gradients are column vectors, c_v (x) is a scalar, H (x) is a 3×3 matrix, (·)^T denotes the transpose and Id_3×3 is the 3 × 3 identity matrix. Solving the linearized least-squares problem yields the update for each voxel x

$$u(x)=H{(x)}^{-1}\left[\left(I(x)-T(\mathrm{\Gamma }(x)\right){\mathit{g}}_T(x)-\left(I({\mathrm{\Gamma }}^{-1}(x))-T(x)\right)c_v(x){\mathit{g}}_I(x)\right].$$ (7)

Since the cost function in Eq. (5) is the average of the ones in Eq. (3) and Eq. (4), corresponding updates can be similarly derived. Furthermore, the symmetric formulation used by inverse-consistent registration algorithms for pairwise image alignment can be obtained by setting the Jacobian determinant term c_v (x) = 1 in our framework. The following is a summary of the algorithm. ★ K_σK denotes spatial convolution with an isotropic Gaussian with standard deviation σ_K.

Asymmetric bi-directional log-domain image-template registration

• – Initialize Γ = exp(0)

• – Iterate until convergence:

  • Given current Γ = exp(v), compute update u(x) based on Eq. (7).

  • Update: v ← v + u

  • Regularize: v ← v ★ K_σK

The algorithm has two input parameters: λ that controls the step size taken in the update (via H(x)) and σ_K that controls the warp smoothness.

4 Experimental Results

Using two experiments, we compare five algorithms:

1. Template Warp: Optimize Eq. (3).

2. Image Warp: Optimize Eq. (4).

3. Asymmetric Bi-directional: Optimize Eq. (5).

4. Image Warp without Jacobian: Ignore the Jacobian term in the Image Warp Algorithm and treat the template as a second image.

5. Symmetric Bi-directional: Ignore the Jacobian term in the Asymmetric Bi-directional Algorithm.

For each ordered pair of images, we ran all five algorithms, treating the first image as the image I and the second image as the template T. The only algorithm invariant to the ordering of the two images is the symmetric Algorithm 5.

We quantify the quality of alignment in the image coordinates using: (1) image mean square error (MSE), obtained by averaging the squared differences between the image intensities and the interpolated template intensities over the image voxels, and (2) the Dice score [18] to measure overlap of regions of interest. Dice scores were computed in the image coordinates by measuring the overlap between the image labels and the transferred template labels obtained through nearest neighbor interpolation. Dice scores vary from 0 to 1 with higher values indicating better alignment. Both MSE and Dice have been extensively used in the literature to evaluate registration results, cf. [19]. Yet, it is important to note that different applications might require different evaluation metrics.

Due to the arbitrary tradeoff between the image-based term and regularization in the objective function, comparisons between registration algorithms are fair only when considered over a range of harmonic energy of the warps [20]. Harmonic energy measures the non-linearity of the warp, defined to be the average Frobenius norm of the Jacobian of the displacement field associated with the warp. A wider kernel used to estimate Φ (larger σ_K) results in smoother warps, yielding a lower harmonic energy.

We ran each algorithm on each ordered pair of images ten times with σ_K values at equally spaced intervals from one to ten voxels and λ = 10⁻³. For each ordered pair of subjects and each algorithm, we thus obtained 10 alignment scores with corresponding harmonic energies. We then computed the mean and standard error across trials for a particular harmonic energy.

In the two experiments, we provide a pairwise comparison of the Image Warp and Aysmmetric Bi-directional Algorithms (Algs. 2, 3) to their counterparts that ignore the Jacobian term (Algs. 4, 5). This pairwise comparison aims to investigate the effect of ignoring the Jacobian term in the cost function.

4.1 Oasis Experiment

In the first experiment, we employed pre-processed (skull stripped and gain-field corrected) MRI volumes (176 × 208 × 176, 1 mm isotropic) of 6 subjects from the OASIS database [14]. The subjects represent a wide spectrum of the population, both in terms of age and dementia score. Axial slices are shown in Fig. 1, demonstrating large anatomical variability across the six subjects. We applied the five algorithms to all thirty ordered pairings of these subjects.

Fig. 1.

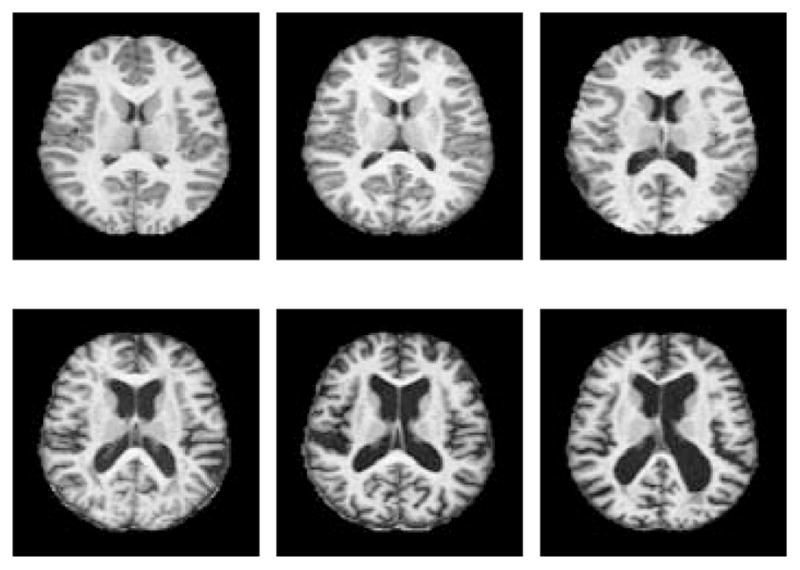
OASIS: Brain MRIs of six subjects

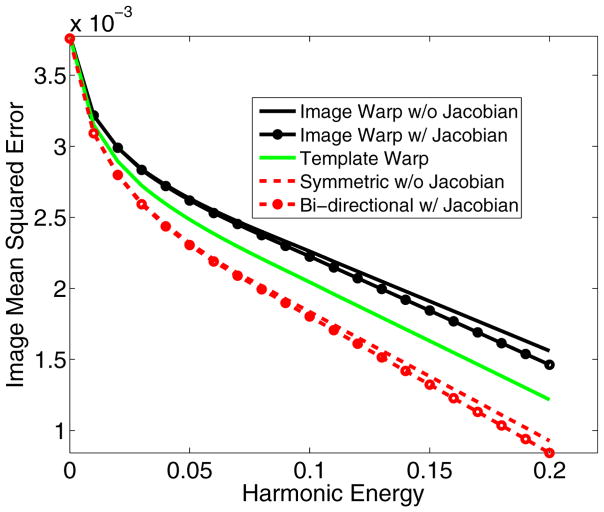
Fig. 2 shows the image mean squared errors (MSE) over a range of harmonic energy values averaged across all pairings. Error bars are not included to avoid clutter. It is clear that the bi-directional methods (Algs. 3 and 5) outperform the unidirectional methods (Algs. 1, 2, and 4).

Fig. 2.

OASIS: Average Image Mean Squared Error (MSE). The dynamic range of image intensities is [0, 1].

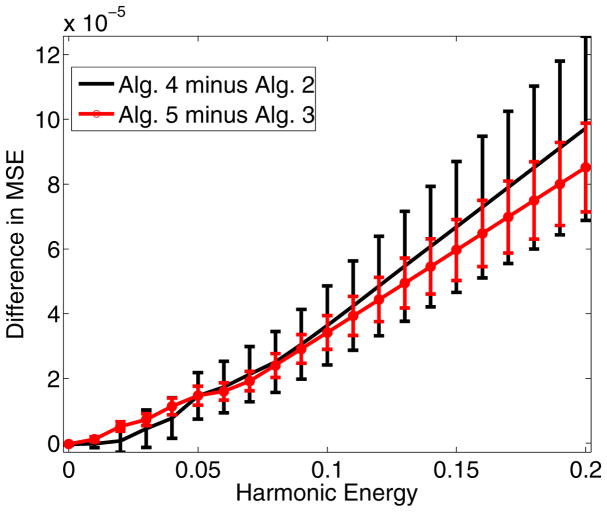
Furthermore, taking into account the asymmetry of image-template registration outperforms the respective algorithms that treat both images the same way (Algs. 2 vs 4 and Algs. 3 vs 5). Fig. 3 highlights this comparison. For each ordered pair of images and each harmonic energy value, we subtracted the MSE value of Alg. 2 (3) from Alg. 4 (5) and averaged across all pairings. Positive values indicate that the former algorithm outperforms the latter. It is clear that the algorithms incorporating the Jacobian term are statistically significantly better than the corresponding algorithms that do not. Moreover, the difference between the algorithms grows with increasing harmonic energy because under more nonlinear warps, certain regions shrink or grow more, resulting in an increased asymmetry due to substantial variations in the Jacobian map over space.

Fig. 3.

OASIS: Average Image Mean Square Error (MSE) Difference. Positive values indicate that ignoring the Jacobian term increases the average error in registration.

4.2 Brainweb Experiment

We used ten synthetic scans obtained from Brainweb [15]. Each scan contained a simulated T1-weighted MRI volume (256 × 256 × 181, 1 mm isotropic) with corresponding tissue label maps for CSF, gray and white matter. We ran the five algorithms on 20 random ordered pairings of the subjects. A comparison of the image mean squared error (MSE) values over a range of harmonic energy values (not shown) revealed a ranking of the algorithms consistent with the OASIS dataset: bi-directional methods outperform uni-directional methods, and taking into account the asymmetry of image-template registration improves alignment.

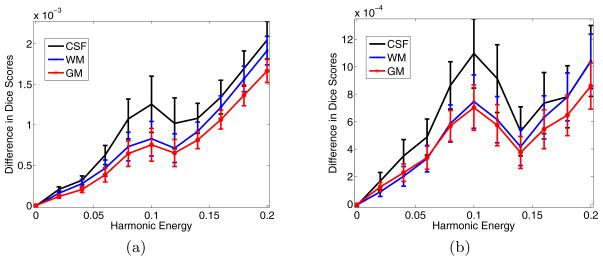
To further evaluate the algorithms, we used the tissue labels to quantify the overlap between the underlying tissue map of the image and interpolated tissue map of the warped template. Fig. 4a compares the Dice scores for the three tissue types of the Image Warp (Alg. 2) with its counterpart that ignores the Jacobian term (Alg. 4). Similar to the previous experiment, positive values indicate that taking the Jacobian term into account yields significantly improved alignment of the underlying tissue labels, suggesting better segmentation quality in a template-based segmentation application. Moreover, the difference between the two methods grows with increasing harmonic energy. Fig. 4b shows that this conclusion is also true for the bi-directional Algorithms (Algs. 3 and 5). Note that a Dice score difference of 10⁻³ roughly corresponds to 100 voxels in white matter, 600 voxels in grey matter and 1000 voxels in CSF.

Fig. 4.

Brainweb. Dice Score Differences between: (a) Image Warp with Jacobian (Alg. 2) minus Image Warp without Jacobian (Alg. 4). (b) Asymmetric (Alg. 3) minus Symmetric Bi-directional (Alg. 5).

5 Conclusions

This paper investigates the asymmetry in image-template registration. Due to this asymmetry, our analysis and experiments suggest that a straightforward application of off-the-shelf pairwise registration algorithms may be sub-optimal in the context of image-template registration. We present a bi-directional objective function that takes the asymmetry into account by introducing a correction factor: the Jacobian that quantifies the deformation of the spatial grid. This correction factor can be used to modify virtually any symmetric registration algorithm into an asymmetric bidirectional one.

Our experiments confirm that bi-directional methods yield improved results compared to unidirectional algorithms since the use of both image gradients in the optimization improves robustness against local minima. Furthermore, incorporating the Jacobian weighting term to account for the asymmetry produces significantly improved alignment scores in the image coordinates. This improvement becomes more pronounced under more nonlinear warps.