Fast LROC Analysis of Bayesian Reconstructed Emission Tomographic Images Using Model Observers

Abstract

Lesion detection and localization is an important task in emission computed tomography. Detection and localization performance with signal location uncertainty may be summarized by a scalar figure of merit, the area under the Localization Receiver Operating Characteristic (LROC) curve, A_LROC. We consider model observers to compute A_LROC for two-dimensional maximum a posteriori (MAP) reconstructions. Model observers may be used to rapidly prototype studies that use human observers. We address the case background-known-exactly (BKE) and signal known except for location. Our A_LROC calculation makes use of theoretical expressions for the mean and covariance of the reconstruction and, unlike conventional methods that also use model observers, does not require computation of a large number of sample reconstructions. We validate the results of the procedure by comparison to A_LROC obtained using a gold-standard Monte Carlo method employing a large set of reconstructed noise samples. Under reasonable simulation conditions, our theoretical calculation is about one to two orders of magnitude faster than the conventional Monte Carlo method.

1. INTRODUCTION

Image Quality in a PET or SPECT reconstruction is measured by how well the reconstruction supports a task, such as lesion detection. A figure of merit (FOM) summarizing detection task performance could be used to optimize the parameters of a reconstruction algorithm. Such FOM’s can be obtained via human observer studies, e.g. Receiver Operating Characterisitic (ROC) studies, but these are time consuming and quickly become impractical if many reconstruction parameters are to be optimized. One can substitute a model observer chosen to emulate human performance (Barrett et al 1993), and apply this observer to a test set of sample reconstructions. Even in this case, the computational requirements of generating a sufficient number of sample reconstructions can be daunting. A third alternative is to develop theoretical formulae to rapidly compute the desired FOM’s. In this paper, we focus on the third alternative.

The key to using theoretical methods is to have available rapidly computable expressions for the reconstruction covariance and mean. For linear reconstructions such as Filtered Backprojection (FBP), these are easy to compute, and expressions have also been developed for general iterative (Qi 2003), Maximum Likelihood - Expection Maximization (ML-EM) (Barrett et al 1994) and Bayesian MAP reconstructions (Fessler 1996), (Wang and Gindi 1997), (Qi and Leahy 1999), (Qi and Leahy 2000), (Xing et al 2001), (Xing et al 2003), and (Stayman and Fessler 2004). Previous work has used these theoretical expressions to calculate FOM’s for the case of SKE/BKE (signal known exactly/background known exactly) detection tasks. Such SKE/BKE FOM’s have been developed for the Hotelling and non-prewhitening observers (Qi and Huesman 2001) as applied to FBP and MAP reconstructions, and for the Channelized Hotelling Observer (CHO) as applied to MAP reconstructions (Xing et al 2003, Fessler and Yendiki 2002). In (Bonetto et al 2000, Yendiki and Fessler 2004b), theoretical tools for FOM calculation in a SKE/BKS (background known statistically) task with a limited form of background variability were also introduced. In Qi (2004), the model was extended to include forms of signal and background variability, but not signal location variability. However, the tasks mentioned above did not include a search task where the signal location was unknown. Since human performance is affected by a search task, it is desirable to include signal location variability in our theoretical computations of an appropriate FOM.

In our work, we are given a reconstruction method, a model observer, a fixed two-dimensional (2D) background and a signal known except for location. Under this context, we show how to rapidly compute the relevant FOM, A_LROC, or area under the LROC curve. In (Gifford et al 2002, Gifford et al 2003b), model observers for the LROC task were proposed. Their performance was compared, using sample methods, to that of human observers. Here, our aim is to incorporate the LROC model observers of (Gifford et al 2002, Gifford et al 2003b) into our theoretical methods. In any task-based performance evaluation, we need to limit our attention to a few promising strategies and appropriate ranges for the various parameters of interest before sample methods or human observer studies are employed. Our computational techniques would allow such prototyping to be rapidly performed.

We have previously (Khurd and Gindi 2005) presented a method for rapid computation of A_LROC. However, as described later, this method made certain approximations. In this paper, we remove some of the restrictive assumptions in Khurd and Gindi (2005). Initial work on our new theoretical method was presented in Khurd and Gindi (2004). A similar method was proposed independently and simultaneously in Qi and Huesman (2004), and in section 4, we discuss differences between the two methods. A related problem was addressed by Yendiki and Fessler (2004a) and is also discussed in section 4.

2. Methods

2.1. The ROC and LROC curves

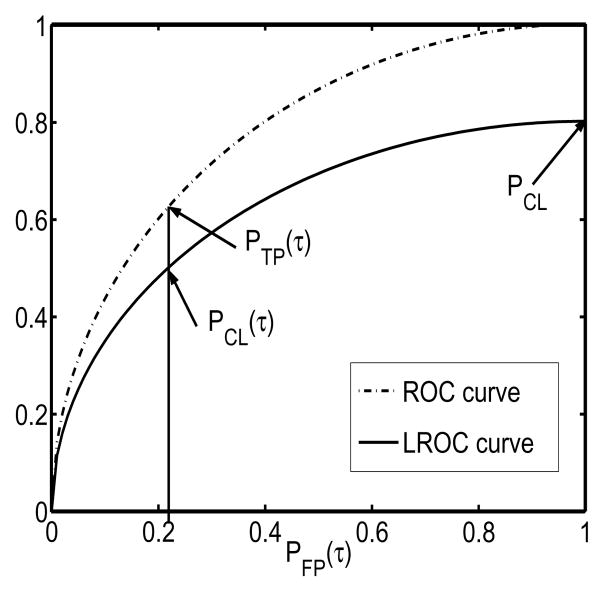
We consider model observers that compute a scalar observer response λ when applied to the reconstruction. The response λ is compared to a decision threshold τ and signal present/absent is decided based on λ ≷ τ. Let “+” or “−” designate a signal present or absent in the reconstruction. We define λ|+ as the response for signal present and λ|− for signal absent. The ROC curve is generated as a plot of the true-positive (TP) rate vs. the false positive (FP) rate, where these are defined as P_TP (τ) = Pr(λ|+ > τ) and P_FP (τ) = Pr(λ|− > τ). The area under the resulting curve, A_ROC, is a widely accepted measure of detectability, but does not measure an observer’s ability to correctly localize a signal.

The LROC curve is more subtle. Again we consider the signal present/absent case, but for signal present, the signal may appear with probability Pr(loc) at a location loc from a set Ω of N_Ω locations in the 2D image. We assume that the signal is compact. We define the observer response λ_loc to be the local observer response at location loc, and given the set of local observer responses, we take λ = max_loc λ_loc. This form of a “max detector” for λ has been commonly used for detection tasks (Swensson 1996, Gifford et al 2002) with location uncertainty. Define λ_loc|(+, loc′) as the local observer response at loc when the signal is centered at loc′. It follows then that λ|− = max_loc∈Ω λ_loc|− and that λ|(+, loc′) = max_loc∈Ω λ_loc|(+, loc′). The abscissa of the LROC curve, the false-positive rate P_FP (τ) = Pr(λ|− > τ), is defined as before. The ordinate of the LROC curve, P_CL(τ), is the probability of correct detection and localization. There is a notion of search tolerance T involved in deciding whether correct localization has occurred. We decide that the signal has been correctly localized if λ|(+, loc′) > τ and if the location at which the maximum occurs is within a radius T around the true signal location loc′.

With these definitions, the LROC curve is defined as a plot of P_CL(τ) vs. P_FP (τ). The ROC curve plots P_TP (τ) vs. P_FP (τ). Figure 1 shows examples of both curves. The quantity P_CL = P_CL(τ = −∞) is the probability of correct localization given that the observer always decides “signal-present” when the image indeed contains a signal. The area under the LROC curve, A_LROC, is an important FOM for the detection task with signal location uncertainty. In this paper, we focus on the computation of A_LROC because it jointly measures detection and localization performance. We note that P_CL and A_ROC can also be easily calculated using our proposed methods.

Figure 1.

The ROC and LROC curves

2.2. Object and Reconstructions: Definitions

Consider an N-dim lexicographically ordered object vector f, a (fixed) N-dim background vector b and an N-dim signal vector s_loc centered at loc. Thus f has components f_n, n = 1, ···, N as do b and s_loc. Note that s_loc is known except for location. We model image formation by a simple Poisson model g ~ Poisson(ℋf), where ℋ is the system matrix whose element ℋ_mn is proportional to the probability of receiving a count in detector bin m that emanates from pixel n, and g is the data vector (sinogram) whose elements are g_m, m = 1, ···, M. (The Poisson model is easily extended to include randoms, for PET, and scatter, for PET and SPECT, by the inclusion of an affine term, and this expansion can be easily included in the ensuing analysis.) For a signal-present object, we may append subscripts to write f_+,loc = b + s_loc and for a signal-absent object, f₋ = b.

We append a caret superscript to quantities to denote their reconstructions (e.g. f̂₋ = b̂ is the reconstruction of the background). We shall use the symbol f̂ as a notational convenience to denote either b̂, ŝ_loc or $\widehat{\mathbf{b}+{\mathbf{s}}_{\mathit{loc}}}$ as needed. We denote the reconstruction covariance by the N × N matrix K_f̂. We also append a bar superscript or use <···> to indicate quantities averaged over data noise, so that $\overline{\widehat{\mathbf{f}}}=<\widehat{\mathbf{f}}>$. We assume that $\overline{\widehat{\mathbf{f}}}$ is well estimated by a noiseless reconstruction (Fessler 1996). For small signals, it is also a reasonable approximation to assume that

$$K_{\widehat{\mathbf{b}+{\mathbf{s}}_{\mathit{loc}}}}\approx K_{\widehat{\mathbf{b}}}$$ (1)

We define

$${\overline{\widehat{\mathbf{s}}}}_{\mathit{loc}}\equiv \overline{\widehat{\mathbf{b}+{\mathbf{s}}_{\mathit{loc}}}}-\overline{\widehat{\mathbf{b}}}$$ (2)

We note that we have made a slight departure from our notational conventions in our definition in equation (2), in that ${\overline{\widehat{\mathbf{s}}}}_{\mathit{loc}}$ does not denote the direct noiseless reconstruction of s_loc. The form of equation (2) accounts for object-dependent resolution (Fessler and Rogers 1996) in nonlinear MAP reconstruction.

2.3. Affine Observer Model

Following (Gifford et al 2002, Gifford et al 2003b), we take the form of our local model observer as an affine model observer ${\lambda }_{\mathit{loc}}={\mathbf{w}}_{\mathit{loc}}^T(\widehat{\mathbf{f}}-\overline{\widehat{\mathbf{b}}})$. Note that this has the form of a template applied to a background-subtracted reconstruction. The familiar inner-product form w^Tf̂ is a widely used model observer in SKE tasks. The need for background subtraction becomes evident if we consider a signal present in a cold region of the object. The max detector will yield a much higher response in a hot region of the object (where there is no signal) unless some form of background subtraction is included.

We now consider four common local observers. Each of the template expressions in equations (3)–(6) makes use of equation (2). The local non-prewhitening (NPW) observer (Barrett et al 1993) corresponds to:

$${\mathbf{w}}_{\mathit{loc},\mathit{NPW}}=(\overline{\widehat{\mathbf{b}+{\mathbf{s}}_{\mathit{loc}}}})-\overline{\widehat{\mathbf{b}}}={\overline{\widehat{\mathbf{s}}}}_{\mathit{loc}}.$$ (3)

The local Hotelling (HO) observer (Barrett et al 1993) corresponds to:

$${\mathbf{w}}_{\mathit{loc},HO}={\mathbf{K}}_{\widehat{\mathbf{f}}}^{-1}{\overline{\widehat{\mathbf{s}}}}_{\mathit{loc}}.$$ (4)

Psychophysical studies (Myers and Barrett 1987) indicate that the the human visual system processes the retinal image by a feature reduction step in which the image (here f̂) is operated on by a series of bandpass channels t_k to form N_C features. Define T_loc as a N × N_c matrix of the channels. The sub-script loc indicates that the channels have been centered at loc. Channelized versions (Gifford et al 2003b) of the local NPW and HO observers, denoted by CNPW and CHO, are then given by:

$${\mathbf{w}}_{\mathit{loc},\mathit{CNPW}}={\mathbf{T}}_{\mathit{loc}}{\mathbf{T}}_{\mathit{loc}}^T{\overline{\widehat{\mathbf{s}}}}_{\mathit{loc}}$$ (5)

$${\mathbf{w}}_{\mathit{loc},\mathit{CHO}}={\mathbf{T}}_{\mathit{loc}}{({\mathbf{T}}_{\mathit{loc}}^T{\mathbf{K}}_{\widehat{\mathbf{f}}}{\mathbf{T}}_{\mathit{loc}})}^{-1}{\mathbf{T}}_{\mathit{loc}}^T{\overline{\widehat{\mathbf{s}}}}_{\mathit{loc}}.$$ (6)

We note that in (Gifford et al 2002, Gifford et al 2003b), good correlation with human performance was found for the CNPW and CHO observers. We now make further definitions so that we may write observer responses in a compact form. Denote the vector of all local observer responses λ_loc′, loc′ = 1, ···, N_Ω by Λ. Define Λ|− as the response vector when there is no signal present and Λ|(+, loc) as the response vector when the signal is present at loc. From the previous definition of λ|− and λ|(+, loc), we may write λ|− = max Λ|− and λ|(+, loc) = max Λ|(+, loc). We define the N × N_Ωmatrix W to be one whose loc^th column comprises the local observer templates w_loc. Then from the definitions of Λ, Λ|−, Λ|(+, loc), we obtain:

$$\mathbf{\Lambda }={\mathbf{W}}^T(\widehat{\mathbf{f}}-\overline{\widehat{\mathbf{b}}})$$ (7)

$$\mathbf{\Lambda }\mid -={\mathbf{W}}^T({\widehat{\mathbf{f}}}_{-}-\overline{\widehat{\mathbf{b}}})$$ (8)

$$\mathbf{\Lambda }\mid (+,\mathit{loc})={\mathbf{W}}^T({\widehat{\mathbf{f}}}_{+,\mathit{loc}}-\overline{\widehat{\mathbf{b}}})$$ (9)

2.4. Monte Carlo Computation of A_LROC

In section 1, we mentioned that A_LROC could be computed using a Monte Carlo (MC) method that employs a large set of sample reconstructions. We describe this method in detail since it will aid in explaining our new theoretical method in section 2.5 and also, we will use it in section 3 for validation studies. The MC method comprises five steps: Step 1: We begin by generating N_samp noisy sinograms from a signal-absent object and N_samp,loc ∝ Pr(loc) noisy sinograms from an object with the signal present at location loc. The numbers of samples N_samp and N_samp,loc are chosen so that the sample error in the MC-estimated A_LROC is small enough for validation purposes. Step 2: Reconstructions are then performed on each sinogram. Thus, we compute a total of N_samp + Σ_loc N_samp,loc reconstructions. Step 3: Compute observer templates using equations (3)–(6). Further details on template calculation are given in section 3. Step 4: The observer response vector Λ is computed for each reconstruction. Step 5: The max detector then results in N_samp values of λ|− and N_samp,loc values of λ|(+, loc) ∀ loc ∈ Ω. If the reported location, i.e. location at which the maximum λ|(+, loc) occurs, leads to an incorrect localization, it is discarded. In order to plot the LROC curve, we determine a set of N_T thresholds from the range of values of λ|(+, loc) and λ|−. For each threshold τ, the probability of correct localization P_CL(τ) and the false-positive rate P_FP (τ) is determined by computing the fraction of observer responses that exceed the threshold, and the LROC curve is plotted. Note that in computing P_CL(τ), one divides the number of correctly localized λ|+’s that exceed τ by the total number of λ|+’s (including the discarded incorrectly localized λ|+’s). Then A_LROC is obtained by simple trapezoidal integration of the LROC curve.

2.5. Theoretical Method for A_LROC computation

Our basic assumption is that Λ has a multivariate Gaussian (normal) distribution, i.e. Λ ~ 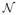(Λ̄, K_Λ) under both the signal-absent and signal-present hypotheses. Here, Λ̄ is the mean of Λ and K_Λ is its N_Ω × N_Ω covariance matrix. This assumption will hold if f̂ itself has a multivariate Gaussian distribution, and may hold approximately even if f̂ is not normal. For linear reconstructions such as filtered backprojection, f̂ is approximately multivariate normal on account of the Central Limit Theorem (CLT) as discussed in section 15.2.6 of Barrett and Myers (2003). The ML-EM reconstruction has an approximately multivariate log-normal distribution (Barrett et al 1994), but under a wide range of conditions, this may be approximated as a multivariate Gaussian distribution (Wilson 1994, Soares et al 2000). Other algorithms such as penalized weighted-least-squares reconstructions can be shown to lead to an f̂ that is normal. Imposition of a positivity constraint results in a skewed (non-normal) distribution for extremely low values of f̂_n’s. However, if all the signals are located in a region where the background values are not too low, this skewness (and non-normality) of the distribution of f̂ will not affect our normality assumption for Λ significantly. Note also, that the components of Λ, i.e. the local observer responses λ_loc, are themselves approximately normally distributed again on account of the CLT (Abbey 1998). In section 3, we show that use of normality assumptions leads to good agreement with MC results.

We now calculate Λ̄, K_Λ for the signal-absent and signal-present cases. We denote these as Λ̄|−, K_Λ|−, Λ̄|(+, loc) and K_Λ|(+,loc). It is easily seen that

$$\overline{\mathbf{\Lambda }}\mid -=\mathbf{0}.$$ (10)

where 0 is a vector of N_Ω 0’s. Similarly,

$$\overline{\mathbf{\Lambda }}\mid (+,\mathit{loc})={\mathbf{W}}^T{\overline{\widehat{\mathbf{s}}}}_{\mathit{loc}}$$ (11)

since $\overline{\mathbf{\Lambda }}\mid (+,\mathit{loc})=<{\mathbf{W}}^T(\widehat{\mathbf{f}}-\overline{\widehat{\mathbf{b}}})>={\mathbf{W}}^T(<\widehat{\mathbf{f}}>-\overline{\widehat{\mathbf{b}}})={\mathbf{W}}^T{\overline{\widehat{\mathbf{s}}}}_{\mathit{loc}}$. Note that the mean vector in equation (11) can have non-zero contributions in the neighborhood of loc. The covariance of Λ can be easily seen to be K_Λ = W^TK_f̂W. The covariances K_Λ|− and K_Λ|(+,loc) are hence given by:

$${\mathbf{K}}_{\mathbf{\Lambda }\mid -}={\mathbf{W}}^T{\mathbf{K}}_{{\widehat{\mathbf{f}}}_{-}}\mathbf{W}={\mathbf{W}}^T{\mathbf{K}}_{\widehat{\mathbf{b}}}\mathbf{W}$$ (12)

$${\mathbf{K}}_{\mathbf{\Lambda }\mid (+,\mathit{loc})}={\mathbf{W}}^T{\mathbf{K}}_{{\widehat{\mathbf{f}}}_{+,\mathit{loc}}}\mathbf{W}$$ (13)

For the remainder of the paper, we shall use the approximation from equation (1), K_b̂ = K_f̂+,loc, and use the symbol K_f̂ to indicate either quantity. Hence, we may write:

$${\mathbf{K}}_{\mathbf{\Lambda }\mid -}={\mathbf{K}}_{\mathbf{\Lambda }\mid (+,\mathit{loc})}={\mathbf{W}}^T{\mathbf{K}}_{\widehat{\mathbf{f}}}\mathbf{W}$$ (14)

We shall henceforth use the symbol K_Λ to denote both K_Λ|− and K_Λ|(+,loc).

Given these assumptions, we can replace the MC generation of Λ’s in section 2.4 by sampling from the multivariate normal distributions for Λ|− and Λ|(+, loc). To do this, we decompose K_Λ = DD^T by the Cholesky factorization (Golub and Van Loan 1989). To generate samples of Λ|−, we obtain samples from 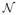(0, I), where I is the N_Ω × N_Ω identity matrix and then multiply each sample by D. As in section 2.4, we generate N_sampT such samples for the signal-absent case. (Here, we have used suffix T in sampT to indicate that the number of samples generated in this theoretical procedure could differ from the number of samples generated in the MC procedure.) To generate signal-present samples of Λ|(+, loc), we simply add Λ̄|(+, loc) to samples of Λ|−. As in section 2.4, we generate N_sampT,loc ∝ Pr(loc) such samples. Armed with these samples, we simply follow the remaining MC procedure (Step 5) in section 2.4. We have avoided the laborious reconstructions needed by Step 2 of the MC method in section 2.4. The central rationale for our theory method is thus achieved.

To summarize, we can list the three main steps involved in the theory computation. These three steps may be compared to the five steps of the MC method in section 2.4. The three steps are: Step 1: Compute Λ̄|−, K_Λ|−, Λ̄|(+, loc) and K_Λ|(+,loc) using equations (10), (11) and (14). Step 2: Use the quantities from Step 1 to generate multivariate Gaussian samples of Λ|− and Λ|(+, loc). Step 3: Using these samples, follow Step 5 of the MC procedure to obtain A_LROC.

2.6. Application of Theory to MAP reconstruction

Our theory so far will apply to any scenario in which ${\overline{\widehat{\mathbf{s}}}}_{\mathit{loc}}$ and K_f̂ can be rapidly calculated. Specifically, for the theory in section 2.5, we need ${\overline{\widehat{\mathbf{s}}}}_{\mathit{loc}}$ and K_f̂ in equations (11), (14) and furthermore, in the expressions for w_loc in equations (3)–(6). However, we have yet to specify a particular reconstruction algorithm. We are interested in MAP reconstructions given by f̂ = arg max_{f ≥0} Ψ_L(g|f)−βΨ_P(f), where Ψ_L is a Poisson log-likelihood and Ψ_P is a smoothing regularizer (a prior) with weight β. We will assume a quadratic regularizer, given by: ${\mathrm{\Psi }}_P(\mathbf{f})={\sum }_n{\sum }_{n^{\prime }\in \mathcal{N}(n)}{w}_{n{n}^{\prime }}{(f_n-f_{n^{\prime }})}^2=\frac{1}{2}{\mathbf{f}}^T\mathcal{R}\mathbf{f}$. The term 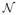(n) is a local neighborhood about n. The weights are symmetrical w_nn′ = w_n′n and positive. For a 2D problem, the neighborhood 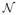(n) could comprise the eight nearest neighbors of n. The neighborhood structure is invariant with position (except for edge effects), so that ℛ is an (approximate) doubly block-circulant matrix (Wang and Gindi 1997). The weight β > 0 controls a crucial resolution-noise trade-off that could affect A_LROC. In section 3, we study the behavior of A_LROC vs. β for the observers in equations (3)–(6).

For this class of reconstruction algorithms, it turns out (Fessler 1996) that K_f̂ is approximated by:

$${\mathbf{K}}_{\widehat{\mathbf{f}}}\approx {(\mathcal{F}+\beta \mathcal{R})}^{-1}\mathcal{F}{(\mathcal{F}+\beta \mathcal{R})}^{-1}$$ (15)

where ℱ denotes the Fisher information matrix, given by $\mathcal{F}={\mathscr{H}}^T\text{diag}\left(\frac{1}{\overline{\mathbf{g}}}\right)\mathscr{H}$. Here, we take ḡ to be the mean sinogram for a signal-absent object with ḡ_m = [ℋb]_m. The other quantity we need is ${\overline{\widehat{\mathbf{s}}}}_{\mathit{loc}}$, which may be approximated using an expression for the local impulse response (Fessler and Rogers 1996). The object-dependent local impulse response due to e_i, a point source at location i, is given by ${\overline{\widehat{\mathbf{e}}}}_i\approx {(\mathcal{F}+\beta \mathcal{R})}^{-1}\mathcal{F}{\mathbf{e}}_i$. Then for the small, compact signal s_loc, our approximation of equation (2) is given by:

$${\overline{\widehat{\mathbf{s}}}}_{\mathit{loc}}\approx {(\mathcal{F}+\beta \mathcal{R})}^{-1}\mathcal{F}{\mathbf{s}}_{\mathit{loc}}$$ (16)

The N × N matrices ℱ and ℛ are formidably large and calculation of the inverses in equations (15) and (16) appears intractable. However, in some cases (Qi and Leahy 1999, Qi and Leahy 2000), we can use Fourier diagonalization to obtain efficient expressions for equations (15) and (16). We shall focus on the simple case of a 2D space-invariant imaging system with only geometrical effects. This is discussed in Qi and Leahy (1999), although such expressions have also been developed for space-variant imaging systems in PET (Qi and Leahy 2000) and SPECT (Xing et al 2003, Stayman and Fessler 2004). In particular, these developments for space-variant imaging systems would allow one to incorporate more complex imaging models (e.g. non-uniform attenuation in SPECT) into accurate expressions for K_f̂ and ${\overline{\widehat{\mathbf{s}}}}_{\mathit{loc}}$. For our space-invariant system, ℋ^Tℋ, like ℛ, is also doubly block circulant and is Fourier diagonalizable. In this case, it can be shown (Qi and Leahy 1999) that equation (16) can be approximated as:

$${\overline{\widehat{\mathbf{s}}}}_{\mathit{loc}}\approx {\mathcal{Q}}^{-1}\text{diag}(\frac{{\zeta }_n}{({\zeta }_n+\frac{\beta }{{\kappa }_{\mathit{loc}}^2}{\eta }_n)})\mathcal{Q}{\mathbf{s}}_{\mathit{loc}}$$ (17)

Here, 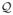denotes a 2D Discrete Fourier Transform (DFT) matrix. The vector ζ comprises the eigenvalues of ℋ^Tℋ and the vector η comprises the eigenvalues of ℛ. The quantity κ is calculated according to the formula: ${\kappa }_n^2=\frac{{\sum }_m{\mathscr{H}}_{mn}^2/{\overline{g}}_m}{{\sum }_m{\mathscr{H}}_{mn}^2}$. (Technically, we need κ_n, n ∈ Ω, but the full backprojection will add negligible additional computation.) For a detailed discussion of the quantities κ, ζ and η, the interested reader is referred to (Qi and Leahy 1999, Qi and Leahy 2000, Xing et al 2003). It turns out (Qi and Leahy 1999) that equation (15) may be similarly approximated as:

$${\mathbf{K}}_{\widehat{\mathbf{f}}}^{\mathit{loc}}\approx {\kappa }_{\mathit{loc}}^{-2}{\mathcal{Q}}^{-1}\text{diag}(\frac{{\zeta }_n}{{({\zeta }_n+\frac{\beta }{{\kappa }_{\mathit{loc}}^2}{\eta }_n)}^2})\mathcal{Q}$$ (18)

The approximation in equation (18) is one that applies locally at location loc, that is, the approximation is accurate only when computing matrix-vector products of the form ${\mathbf{K}}_{\widehat{\mathbf{f}}}^{\mathit{loc}}{\mathbf{a}}_{\mathit{loc}}$, where a_loc is a compact vector centered at loc. Now, we may use equations (17) and (18) to re-write the expressions for the observer templates in equations (3)–(6). Here, we give the expression for equation (6), though the others follow similarly:

$$\begin{array}{c}{\mathbf{w}}_{\mathit{loc},\mathit{CHO}}={\kappa }_{\mathit{loc}}^2{\mathcal{Q}}^{-1}{\stackrel{\sim }{\stackrel{\sim }{\mathbf{T}}}}_{\mathit{loc}}{\left[{\stackrel{\sim }{\stackrel{\sim }{\mathbf{T}}}}_{\mathit{loc}}^H\text{diag}(\frac{{\zeta }_n}{{({\zeta }_n+\frac{\beta }{{\kappa }_{\mathit{loc}}^2}{\eta }_n)}^2}){\stackrel{\sim }{\stackrel{\sim }{\mathbf{T}}}}_{\mathit{loc}}\right]}^{-1}\\ {\stackrel{\sim }{\stackrel{\sim }{\mathbf{T}}}}_{\mathit{loc}}^H\text{diag}(\frac{{\zeta }_n}{({\zeta }_n+\frac{\beta }{{\kappa }_{\mathit{loc}}^2}{\eta }_n)})\mathcal{Q}{\mathbf{s}}_{\mathit{loc}}\end{array}$$ (19)

Here, $\stackrel{\sim }{\stackrel{\sim }{\mathbf{T}}}$ is a matrix obtained by taking the DFT of each channel (column vector) in T and the superscript H denotes the conjugate transpose.

It appears that we have all the necessary expression to plug into equations (11) and (14) to compute A_LROC via sampling. However, [K_Λ]_ij involves two locations i and j and ${\mathbf{K}}_{\widehat{\mathbf{f}}}^{\mathit{loc}}$ holds only at one location loc. Hence, we use the following averaging scheme:

$${[{\mathbf{K}}_{\mathbf{\Lambda }}]}_{ij}=\frac{1}{2}{\mathbf{w}}_i^T{\mathbf{K}}_{\widehat{\mathbf{f}}}^i{\mathbf{w}}_j+\frac{1}{2}{\mathbf{w}}_i^T{\mathbf{K}}_{\widehat{\mathbf{f}}}^j{\mathbf{w}}_j$$ (20)

Thus, in order to evaluate A_LROC for MAP reconstruction for a given local observer template w_loc, we first substitute the appropriate Fourier expressions for w_loc, ${\overline{\widehat{\mathbf{s}}}}_{\mathit{loc}}$ and ${\mathbf{K}}_{\widehat{\mathbf{f}}}^{\mathit{loc}}$ into equations (11) and (20), generate samples from the multivariate normal distributions for Λ|− and Λ|(+, loc) ∀ loc ∈ Ω and use these samples to compute A_LROC following Step 5 of the MC procedure in section 2.4, but without the need for sample reconstructions as in Step 2 of the MC procedure.

3. Results

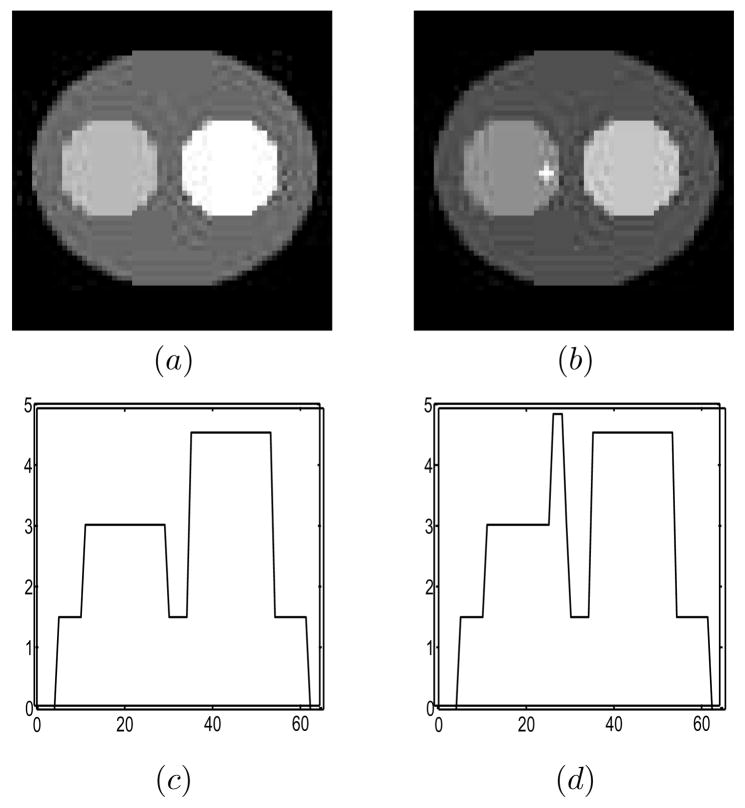
In this section, we validate our theory results using MC methods. Our fixed background b (figures 2a, 2c) was a two-dimensional 64 × 64 elliptical phantom with two circles, scaled to produce 300K counts over 64 angles. The simple piecewise-constant nature of the phantom adequately serves our validation purposes. This is because the model observer has the exact knowledge of the background, and the subtraction step in equation (7) compensates for the form of the background. Indeed, in Khurd and Gindi (2005), we used a phantom whose spatial profile was Gaussian. The signal, 5 pixels in the shape of a cross was placed on one of N_loc = 81 possible signal locations. The array of locations constituted a square grid with a 3-pixel separation. Figure 3 shows the grid of signal locations superimposed on the background along with the cross-shaped signal at one particular grid point. The search grid Ω was a square array of 27 × 27 pixels that included all the pixels in the grid of signal locations and their neighbors. Figures 2b, 2d show the signal placed on the background.

Figure 2.

(a) The 64×64 background (b) Background+signal at location (33,27) for signal contrast 0.4 (c) Background profile (d) Background+signal profile. Both profiles are taken through the central row of the signal. Note (a) and (b) use different grey scales for clarity.

Figure 3.

Sampling grid with signal at one grid point.

Note that the signal appears on a sub-sampled (9 × 9) grid of the larger (27 × 27) search grid Ω. Our general rationale in choosing such grids is that (a) the search grid Ω should constitute a reasonable fraction of the non-zero reconstructed image (or else there is no challenging search problem.) (b) the signal grid can be a sub-sampled version of the search grid, corresponding to a particular form of Pr(loc). The type of sub-sampling in (b) does not affect our validation results for A_LROC, adequately emulates conditions for a corresponding human observer study, and facilitates MC validation by allowing several sample reconstructions per signal location. We note that this form of sub-sampling does not reduce the computation of the theory method, which depends on N_Ω only, but does reduce MC computation time slightly.

SPECT sinograms were generated with an analytical projector modelling geometrical effects and by addition of Poisson noise to the noiseless sinogram. Depth-dependent detector response, and attenuation and scatter effects were not modelled in the analytical projector. Iterative MAP reconstructions using the same analytical projector (and its corresponding backprojector) were done for β = 0.01, 0.1, 1.0 and 10.0 and for a signal contrast of 0.4. Here, signal contrast was defined as (amplitude of s)/(maximum of b). Figure 4 shows anecdotal signal-present reconstructions at each β. We used a positivity-constrained regularized ordered-subset convergent MAP algorithm (Hsiao et al 2002) for the reconstruction. Note that we chose a low contrast (0.4) such that the signals are difficult to see in figure 4. This choice is discussed further below.

Figure 4.

Anecdotal reconstructions of background+signal for signal contrast 0.4 at (a) β = 0.01, (b) β = 0.1, (c) β = 1 and (d) β = 10. Arrows show signal location.

The MC procedure in section 2.4 was followed. At each β, N_samp = 500 signal-absent reconstructions were done and N_samp,loc = 20 signal-present reconstructions were done at each of the 81 locations. Thus, for each of the 4 values of β, 2120 reconstructions were done. We used the observer templates for all 4 observers in equations (3)–(6). We used N_T = 1000 thresholds in determining the LROC curve. For the channelized observers, we used four dyadic channels (Abbey 1998, Myers and Barrett 1987) with square profiles and a starting cutoff frequency of 0.0441 cycles per pixel. We note that even in this MC validation, we computed observer templates using analytical formulae as in equation (19). In a conventional MC test, one would use sample reconstructions to compute the templates. Since our MC validations were intended to test the approximations of the theory, we wanted to use the same templates for theory and MC, thus avoiding unwanted additional sample error in the template estimation. This strategy incidentally leads to a speedup for the MC methods.

Error bars on the MC estimates of A_LROC for each observer and each β were obtained by the following procedure: using the bootstrap (Zoubir and Boashash 1998), 2000 re-sampled sets of 500 values for λ|− and 1620 values of λ|+ along with the reported location were obtained. For each set, the values of A_LROC were obtained using the MC procedure described earlier. We then determined 95% confidence intervals from histograms of these 2000 values.

In the theory computations, we followed the steps described in section 2.5. We generated N_sampT = 500 samples of Λ|− and N_sampT,loc = 500 samples of Λ|(+, loc) ∀ loc. We once again used N_T = 1000 thresholds in obtaining the LROC curve.

We coded the MC and theory calculations in C using a gcc compiler, and ran the programs on a Pentium IV 2.0 GHz, 2GB RAM Linux desktop. The reconstructions were carried to a high number (50) of iterations to ensure effective convergence to the MAP solution. Under these conditions, the MC method took a total of 5.5 hrs., almost all of which was devoted to the reconstructions. The theory method took 90 sec., leading to a speedup by a factor of about 200. In using a MC method to calculate A_LROC and not purely as a validation tool, one could tolerate a small error by terminating at about 10 iterations, in which case the theory speedup is about 40. This speed advantage should hold for 128× 128 images with proportionally larger N_Ω.

We note that the theory speed is handicapped by the exhaustive calculations in equation (20) wherein the terms ${\mathbf{w}}_i{\mathbf{K}}_{\widehat{\mathbf{f}}}^j{\mathbf{w}}_j$ are computed for i far from j even though these terms have negligible contributions. We are investigating further speedup strategies.

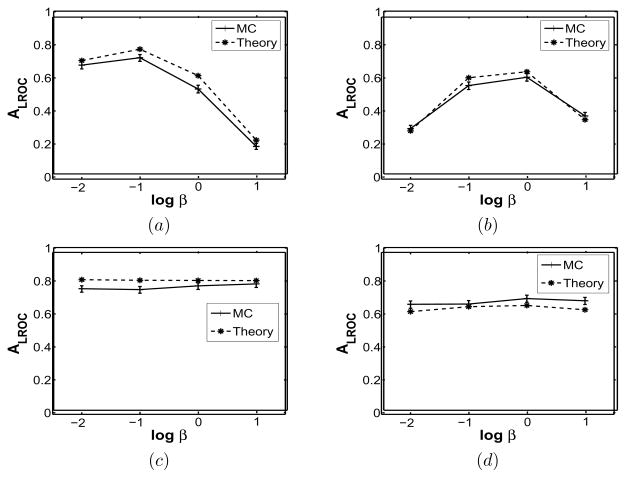
Figure 5 shows A_LROC vs. β for each of the four observers. The MC and theory curves match closely indicating that the theory is quite accurate. Here, we used a search tolerance of 1.5 pixels, i.e. localization was deemed correct if any one of the 9 pixels in the 3 × 3 square centered at the true location were reported. We may note that the observers that include some form of pre-whitening are relatively less sensitive to β, the amount of regularization, in the reconstruction.

Figure 5.

A_LROC vs. β at a search tolerance of 1.5 for (a) NPW, (b) CNPW, (c) HO and (d) CHO observers. All 4 plots have 2 curves corresponding to Theory and Monte Carlo (MC).

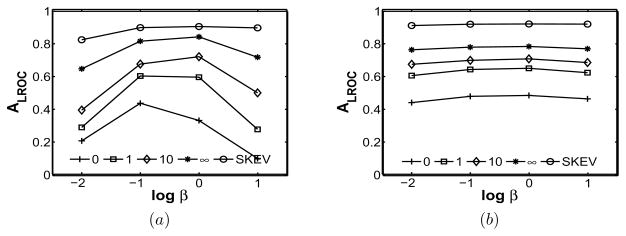
In figure 6, we have explored the effect of the search tolerance on the CNPW and CHO observers. (We note that the curves in figure 6 match their Monte Carlo (MC) validations closely, so the MC curves are suppressed here for clarity.) As expected, A_LROC increases with search tolerance. Note that the increase in the values of A_LROC when the search tolerance is increased from 0.0 pixels to 1.0 pixels is much greater than when the search tolerance is increased from 1.0 to 10.0 pixels. This indicates that the reported location is frequently one of the four neighbors of the true location. However, this property may be characteristic of our simple simulations and may not be observed in more realistic SPECT simulations (Gifford et al 2002). The spatial resolution of SPECT reconstruction using more realistic simulations is typically worse than in our simplified simulations. As a result, A_LROC would grow more gradually as search tolerance increases. We may observe that the shape of the A_LROC vs. β curve depends on the search tolerance for the CNPW observer, but the shape is fairly invariant to the search tolerance for the CHO observer. Similar results were observed for the non-channelized versions of these observers.

Figure 6.

A_LROC vs. β at search tolerances of 0.0; 1.0; 10.0 and ∞ pixels, along with a SKEV AUC (top curve) at signal contrast = 0.2 for (a) CNPW and (b) CHO observers.

One might question whether the more easily performed SKEV task (Barrett et al 1995, Eckstein et al 2003, Eckstein and Abbey 2001) (signal known exactly but variable) in which the signal location is varied, but the observer is given knowledge of the location, might replace the LROC task for image quality studies. The top curves in figure 6 show a SKEV result. This curve was generated by applying the CNPW and CHO observers at each signal location and calculating the A_ROC corresponding to an SKE/BKE problem. The A_ROC’s were then averaged over location to obtain the curve. At high search tolerance, the A_LROC result is similar to the SKEV A_ROC curve. Thus depending on an acceptable search tolerance, a user might elect to perform the easier SKEV task. Note that in figure 4, the signals at 0.4 contrast are difficult to see. However, for the SKEV case, where the observer was given knowledge of signal location, detection using model observers was nearly perfect with A_ROC near unity. We were forced to lower contrast to 0.2 to obtain reasonable values of SKEV A_ROC. For the 0.4 contrast in the A_LROC experiments in figure 6, we observe an interesting variation in the shape and level of the A_LROC vs. β curve as search tolerance varied. These effects would be difficult to observe in our simulations with a contrast much greater than 0.4.

4. Discussion and Conclusions

In Khurd and Gindi (2005), we developed an alternate, purely analytic means of calculating A_LROC that did not require sampling from a normal distribution. However, the theory in Khurd and Gindi (2005), unlike our present theory, required an assumption of independence of local observer responses. This assumption can break down in practice, as we demonstrated in Khurd and Gindi (2004), where we showed improved agreement to MC with our current theory vs. the one in Khurd and Gindi (2005). In Qi and Huesman (2004), a method similar to our current theory was proposed to rapidly compute A_LROC. Their method lent insight into the problem of joint detection and localization, showing how A_LROC approached A_ROC as the search tolerance increased. However, in Qi and Huesman (2004), the problem was restricted so that the signal was at a single fixed location and the observer was required to search for it in a search radius around this single true location. This restriction allowed mathematical simplifications in which the form of the template w_loc did not change with location, and allowed the use of an unique doubly-block-circulant approximation to K_f̂ in the computation of K_Λ. This allowed rapid generation of samples of Λ. To model our more realistic case in which the true location of the signal was allowed to vary over a large region, we could not make use of the above simplifications, and our method is therefore somewhat slower. Both our method and the one in Qi and Huesman (2004) require obtaining samples of Λ. An attempt to replace this step with an approximate analytical calculation (that still modelled local observer correlation) was made in Yendiki and Fessler (2004a). Using an analytical formula for the tail distribution of λ under an MVG assumption for the distribution of Λ, it was demonstrated that the initial part of the ROC curve corresponding to large thresholds could be rapidly evaluated. However, this work did not address the computation of A_LROC and the proposed technique could only be used for a small local search region.

Our theory has been applied to A_LROC. We note, however, that the corresponding A_ROC problem, in which signal location is unknown, but only detection is required, is of importance. For rapid calculation of A_ROC, only a small modification of our procedure is needed: simply include correctly detected but incorrectly localized observer responses to plot and integrate an ROC curve.

We have demonstrated a fast theoretical means for LROC analysis of 2D MAP reconstructed images in emission computed tomography. We note that LROC model observers have been extensively used in optimizing SPECT reconstruction (Bruyant et al 2004, Farncombe et al 2004, Gifford et al 2002). Our theoretical A_LROC computation could potentially replace the laborious MC-based A_LROC computation in such studies. As further psychophysical research on the signal-location-unknown problem progresses, it is likely that the recommended observer models in (Gifford et al 2002, Gifford et al 2003b) will be modified and include internal noise effects (Barrett and Myers 2003). In addition, application of model observers to multislice LROC studies (Gifford et al 2003a) would entail further modifications. We plan to investigate incorporation of these advances into our theory methods.