Abstract
In emission tomography, anatomical side information, in the form of organ and lesion boundaries, derived from intra-patient coregistered CT or MR scans can be incorporated into the reconstruction. Our interest is in exploring the efficacy of such side information for lesion detectability. To assess detectability we used the SNR of a channelized Hotelling observer and a signal-known exactly/background known exactly detection task. In simulation studies we incorporated anatomical side information into a SPECT MAP (maximum a posteriori) reconstruction by smoothing within but not across organ or lesion boundaries. A non-anatomical prior was applied by uniform smoothing across the entire image. We investigated whether the use of anatomical priors with organ boundaries alone or with perfect lesion boundaries alone would change lesion detectability relative to the case of a prior with no anatomical information. Furthermore, we investigated whether any such detectability changes for the organ-boundary case would be a function of the distance of the lesion to the organ boundary. We also investigated whether any detectability changes for the lesion-boundary case would be a function of the degree of proximity, i.e. a difference in the radius of the true functional lesion and the radius of the anatomical lesion boundary. Our results showed almost no detectability difference with vs without organ boundaries at any lesion-to-organ boundary distance. Our results also showed no difference in lesion detectability with and without lesion boundaries, and no variation of lesion detectability with degree of proximity.
1. Introduction
In emission tomography (ET) one tries to determine the underlying radiotracer distribution of radiopharmaceutical within the patient body. This tracer concentration has high correlation with the underlying anatomy. The high correlation is due to the fact that different anatomical structures have different physiological function and hence we expect to see a difference in tracer uptake between these anatomical regions. A common assumption on anatomy-function correlation is that activity uptake tends to be slowly varying within an organ or anatomical region, but can suffer a discontinuity at a region boundary. This general observation is borne out in high resolution autoradiographic images in which functional images also clearly reveal the morphology of the underlying structures (Gindi et al 1993). In some cases, lesion boundaries can also be observed in the anatomical scan (Bruyant et al 2004a), and so lesion boundary information can be used to aid in determining whether there is a significant uptake in the lesion versus its surround. This high correlation with anatomy would lead one to expect an improvement in the functional image quality with the use of this anatomical “side-information” in the image reconstruction process. Such anatomical side information can be made available from coregistered MR (for brain) and from CT (whole body) images. Furthermore, the advent of PET/CT and SPECT/CT increase the availability of coregistered anatomical images. Many ways of improving the ET reconstruction by incorporating anatomical side information have been proposed, but the improvement in the ET images must be evaluated based on the performance with respect to a chosen task, in our case, a detection task.
As discussed below, one might intuitively expect lesion detectability to be improved by anatomical side information if the lesion were proximate to an anatomical boundary; and less improved if the lesion was distant from the boundary. To address this question, we use an SKE/BKE (signal-known-exactly/background-known-exactly) detection task, and a CHO (channelized Hotelling observer) which is a numerical observer whose detection performance emulates that of humans for this task. To investigate lesion proximity effects, we therefore vary lesion and boundary locations and calculate an SNR, a scalar figure of merit for detection.
Though there are many ways to impose anatomical information, we choose a MAP (maximum a posteriori) reconstruction method in which a simple uniform smoothing prior can be modified by not smoothing across organ and/or anatomical lesion boundaries. Such a method lends itself to very rapid calculation of the SNR by using analytic methods, and so allows us to perform many more experiments than we could using sample methods. In addition, the imposition of smoothness only within boundaries is a strategy shared by many proposed reconstruction schemes that use anatomical information.
Previous work can be categorized based on the use of the side-information either in the image reconstruction step or in post-processing the reconstructed image. A limited survey follows. In Videen et al (1988), Meltzer et al (1990), Muller-Gartner et al (1992) and Rousset et al (1990) a post-processing method for brain imaging using a convolution-based approach was discussed. The approaches in the former category use Bayesian estimation techniques to introduce the anatomical side-information into the reconstruction processes. Gindi et al (1993), Leahy and Yan et al (1991), Lipinski et al (1997) and Ouyang et al (1994) used an edge-preserving Gibbs prior where the anatomical boundary information was used to control the formation of discontinuities in the emission reconstruction. In more recent work in Comtat et al (2002) and Bruyant et al (2004a), segmented anatomical labels were used to manipulate the weighting of a quadratic prior. Baete et al (2004a) have developed an anatomy-based MAP algorithm for PET brain imaging. The “AMAP” scheme uses an edge-preserving concave prior (Nuyts et al 2002) for the grey matter and Gaussian priors for white matter and CSF. Ardekani et al (1996) proposed an minimum cross-entropy reconstruction algorithm that incorporates multi-spectral MR data into a cross-entropy prior, which performs edge preserving smoothing based on the anatomical information. An interesting MAP approach by Hsu and Leahy (1997) used a segmented anatomical image to impose a graded form of smoothing in inter-region areas where partial volume effects limit one’s ability to impose sharp continuity breaks. A more elaborate hierarchical Bayesian approach was proposed by Bowsher et al (1996). Sastry and Carson (1997) suggested a label-based tissue composition model to impose a Gaussian distribution within a tissue region. The exact tissue fractions for each pixel were provided from segmented MR brain images. Rangarajan et al (2000) used a joint-mixture framework to incorporate anatomical information. Much of the previous work reports improvement with anatomical priors in terms of ROI quantitation tasks. In more recent work, discussed in detail in section 5.2, several authors have addressed improvements in detection tasks.
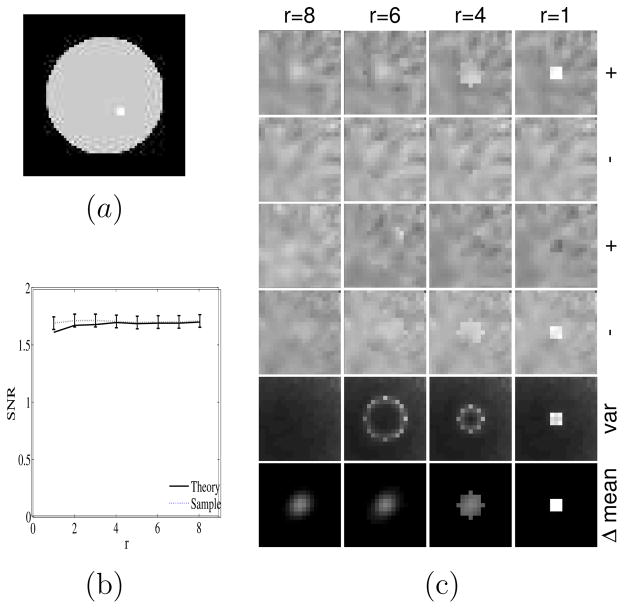
To motivate our interest in the question of lesion proximity, consider the following: Intuitively, one might expect that for a case in which a small hot spherical lesion in a weaker background is enveloped precisely by continuity-suspending boundaries, these boundaries might be helpful in detection. The intuition comes from the fact that the suspension of smoothness across boundaries prevents the blurring of the lesion into the surrounding tissue, thus possibly enhancing detection. (Any reconstruction will have a noise-resolution tradeoff, leading to a somewhat blurred reconstructed lesion.) See figure 1 for an example using noiseless reconstructions. If the boundary were distant or absent, we’d intuitively expect the detectability to not be enhanced. In fact, in our study, our results show that these intuitions are incorrect for an SKE/BKE detection task using a CHO and our SPECT MAP reconstruction.
Figure 1.
(a) Phantom with lesion present. Lesion contrast is 1.333:1 (b) Noiseless lesion-present MAP reconstruction without anatomical boundary information. (c) Noiseless lesion present MAP reconstruction with anatomical boundary information placed precisely along the lesion boundary. The figure supports the intuition that with the presence of lesion boundary information, we expect the detectability of the lesion to be enhanced.
In section 2, we review MAP reconstruction and present a simple way to incorporate anatomical information into the prior. We also review some relevant details of the CHO. In section 3 we show how to rapidly calculate detection performance using analytic methods. Our simulation results are shown in section 4. In the discussion section 5.1, we summarize our work. In our discussion in section 5.2, we place our work in the context of efforts by others to improve lesion detectability using anatomical information.
2. Background
2.1. MAP Reconstruction With Anatomical Priors
Define an N-voxel 3D emission object as the N-dim lexicographically ordered vector f, {fn; n = 1,…, N }. A MAP reconstruction is given by the following optimization: f̂ = argmaxf≥0 (ΦL(g; f) + βΦP (f)) where g, {gm; m = 1, …, M} is the M-element sinogram, ΦL the log of the Poisson likelihood, and ΦP a quadratic prior. The scalar β > 0 controls the degree of smoothing. For Poisson data, the log likelihood term is where ℋ is the system matrix whose element ℋmn is proportional to the probability that an emission from pixel n reaches detector bin m. (The likelihood term used here excludes affine terms sometimes used to model scatter in SPECT or randoms and scatter in PET.).
We assume the anatomical information to be present in the form of a tissue label map, where label ln is the tissue class of voxel n. We use a quadratic prior to capture anatomy-function correlation by smoothing within an organ or lesion boundary while suspending smoothing across boundaries. The prior, similar to ones used in Bruyant et al (2004a) and Comtat et al (2002), is given by
| (1) |
where 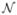 (n) defines neighbors of pixel n, dnj is the Euclidean distance between voxels n and j, and the penalty weight ωnj (ln, lj) is dependent on the anatomical labels of voxels n and j as follows:
(n) defines neighbors of pixel n, dnj is the Euclidean distance between voxels n and j, and the penalty weight ωnj (ln, lj) is dependent on the anatomical labels of voxels n and j as follows:
| (2) |
Thus, if n and j belong to different anatomical regions, ωnj is set to 0, thus “breaking continuity” between voxels n and j. Note that if want to turn off anatomical information, we simply set ω(ln, lj) = 1 unconditionally and thus obtain a uniform space-invariant quadratic prior.
The anatomical prior would reduce noise by smoothing within anatomical regions and preserve edges by not blurring across different anatomical regions. It will be convenient to re-express the prior, ΦP (f) as a quadratic form , where the N × N matrix ℛ is the Hessian of −ΦP (f) with matrix elements given by
| (3) |
The anatomical prior we use described above is idealized in two ways. We assume that the anatomical label map is in perfect register with the reconstruction volume, and that the label maps, derived from high resolution CT or MR, occur on voxels whose size is the same as that of an emission reconstruction voxel. Thus in our scheme each reconstruction voxel gets a unique label. In actuality, since anatomical images are usually of higher resolution than functional images, each functional image voxel contains many anatomical voxels with possibly heterogeneous labels. Hence instead of a unique label for each fn, various label mixture schemes are more realistic. Indeed, misregistration and mismatched resolution effects are important and have been addressed in Gindi et al (1993), Sastry and Carson (1997), Comtat et al (2002), Baete et al (2004a,2004b) and elsewhere. However, we assume that if boundary proximity effects are significant, they should show up in the idealized case where both effects are absent.
So far, we have implied a model in which different anatomical regions have different activity. But to complicate matters, there may be an emission lesion boundary with no corresponding anatomical lesion boundary. For example, a tumor avid lesion in an organ may not have an anatomical signature. In the same vein, an anatomical lesion boundary may not correspond to an emission hot-spot, e.g. a necrotic lesion that shows up in CT may not show up in SPECT. To assess the efficacy of anatomical priors, we must consider both cases of false boundaries.
2.2. Channelized Hotelling Observer
To evaluate the performance for a detection task one would have to perform a human observer study and use a figure of merit, such as the area under the ROC curve, to assess performance. The experiments we describe below involve many lesion locations and boundaries, and each would require a human observer study. Since the amount of labor involved would be unrealistic, we used numerical observers that emulate human performance. The channelized Hotelling observer (CHO) (Barrett and Myers 2003) is found to be a good predictor of human performance in detecting lesions in correlated noisy backgrounds such as those in SPECT reconstruction (Gifford et al 2000, Abbey and Barrett 2001, Narayanan et al 2002, Wollenweber et al 1999). The CHO uses the first- and second-order statistics of the reconstructed images and delivers a scalar figure of merit, the SNR. The use of an SNR requires an assumption that the CHO observer responses are approximately Gaussian distributed under both signal-present and signal-absent hypotheses, a requirement satisfied in our case.
SNR calculations typically require sample methods as discussed in section 3.3. For each of the many cases we will consider, the calculation of SNR using sample methods requires a few hundred sample reconstructions. This is a formidable amount of computation. The SNR is applied to an SKE/BKE detection task since such a task can clearly elicit the effects of boundary proximity. In addition, SKE/BKE tasks lend themselves to rapid evaluation of SNR for the CHO using the theoretical methods described in section 3.
As does a human, the CHO observes a 2D slice image extracted from the 3D reconstruction. Let ℒ be a linear slice extraction operator which is an N2D × N matrix with N2D the number of pixels in the extracted image. The CHO applies anthropomorphic bandpass channels to reduce the N2D-dim image into Nc channel responses (features). The feature reduction step is carried out by the dot product of the image with each of the Nc channel templates. Since Nc is usually around 3–6, the number of features is far less than the number of pixels N2D. If the vector ti is the ith channel template centered at the lesion center, then the corresponding ith channel response is ûi = (ti)T ℒf̂. (Here, the T exponent means “transpose”.) The feature vector is given by û =  ℒf̂, where ti is the ith column of
ℒf̂, where ti is the ith column of  , and
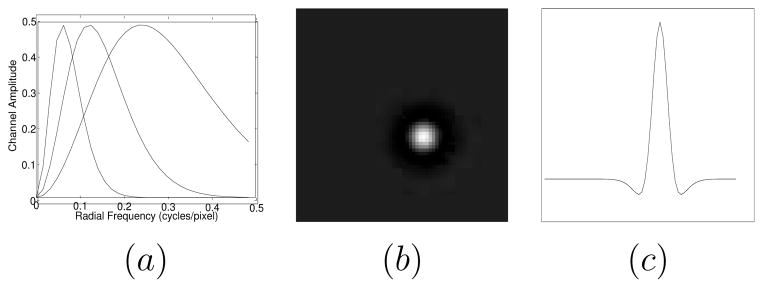
, and 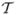 is an N2D × Nc matrix. In this study we use radially symmetric channels. Figure 2(a) displays the radial channel profiles in the frequency-domain, showing three difference-of-Gaussian (DOG) kernels (Abbey 1998, Abbey and Barrett 2001) of dyadically increasing widths. Figure 2(b) shows the 2-D spatial version of the first channel template and figure 2(c) its central profile. The CHO applies an optimal linear discriminant to these channel responses to get a scalar observer response.
is an N2D × Nc matrix. In this study we use radially symmetric channels. Figure 2(a) displays the radial channel profiles in the frequency-domain, showing three difference-of-Gaussian (DOG) kernels (Abbey 1998, Abbey and Barrett 2001) of dyadically increasing widths. Figure 2(b) shows the 2-D spatial version of the first channel template and figure 2(c) its central profile. The CHO applies an optimal linear discriminant to these channel responses to get a scalar observer response.
Figure 2.
(a) Radial profile of channels in frequency space. (b) 2D space domain channel template (corresponding to the first channel) displayed here as a 64 × 64 grey scale image. (c) Central profile of the channel template in (b).
Let b be a fixed background and s be a fixed signal. Define f1 = b and f2 = b + s as signal-absent and signal-present objects, respectively. Let
and
represent the mean (over data noise) reconstructions and
and
the mean feature vectors of f̂1 and f̂2, respectively. Denote the average of the signal-present and signal-absent covariance of the reconstruction by 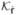 . Let
. Let 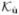 be the average of the lesion-absent and lesion- present channel response covariance matrices. The channel covariance matrix is thus
be the average of the lesion-absent and lesion- present channel response covariance matrices. The channel covariance matrix is thus 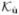 =
= 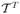 ℒ
ℒ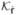 ℒT
ℒT 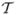 . Then a measure of detectability, the CHO SNR, is given by (Abbey 1998)
. Then a measure of detectability, the CHO SNR, is given by (Abbey 1998)
| (4) |
Note that 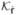 is an average covariance, but for the low contrast signals that we will use, it is a good approximation to use
is an average covariance, but for the low contrast signals that we will use, it is a good approximation to use 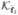 for
for 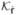 . We can justify this approximation because our analytically calculated SNR’s (which use
. We can justify this approximation because our analytically calculated SNR’s (which use 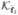 ) are validated by sample-method SNR’s (computed using
). The mean channel responses become
and
. The covariance of these extracted 2D images is ℒ
) are validated by sample-method SNR’s (computed using
). The mean channel responses become
and
. The covariance of these extracted 2D images is ℒ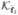 ℒT and the corresponding covariance of the channel responses,
ℒT and the corresponding covariance of the channel responses, 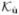 , becomes
, becomes 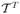 ℒ
ℒ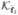 ℒT
ℒT 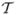 . With the inclusion of slice extraction and the approximation
. With the inclusion of slice extraction and the approximation 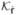 ~
~ 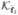 , the CHO SNR becomes
, the CHO SNR becomes
| (5) |
We shall base our sample-method calculation of SNR on (4) and our analytic methods on (5).
3. Methods
In this section, we focus on the theoretical methods used to rapidly obtain SNR. We perform two types of studies. In the first, termed the “organ boundary experiment”, we place a lesion at varying distances from an organ boundary and evaluate the SNR vs. distance for the case of an anatomical prior and for an ordinary smoothing prior (no anatomy). In the second, termed a “lesion boundary experiment”, there were no organ boundaries, only a uniform background with a single lesion. We fix the functional lesion size and location but vary the anatomical boundary about the lesion so that its radius increases beyond the functional lesion. At its minimum radius, the anatomical boundary exactly encloses the lesion boundary. The maximum radius corresponds to no lesion boundary information at all. The lesion boundary experiment is motivated by the following consideration: A perfect anatomical lesion boundary is the extreme case of isotropic boundary information at minimal proximity in all directions. We relax this “ultimate” anatomical information by increasing the radius of the boundary until there is no boundary, and then we assess the effects on SNR vs. radius to gain insight.
3.1. Organ Boundary Experiment
Let sj denote a lesion centered at j. Then, f2j = b + sj is the signal-present 3D object. Let
be the the mean reconstruction of the object with sj. Denote 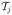 as the channel template matrix centered at j. From (5) the detectability of the lesion centered at j is given by
as the channel template matrix centered at j. From (5) the detectability of the lesion centered at j is given by
| (6) |
The quantities
and
are well approximated by noiseless reconstructions. The main theoretical computation is in the terms (
) in (6). This involves the difficult-to-compute covariance matrix 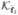 . For our MAP case, a theoretical expression for the covariance in (6) is approximated by (Fessler 1996)
. For our MAP case, a theoretical expression for the covariance in (6) is approximated by (Fessler 1996)
| (7) |
where is an N × N matrix that approximates the Fisher information matrix.
For uniform quadratic priors with no continuity breaking, the Hessian of the prior, ℛ, is triply block circulant (shift invariant), hence ( ) in (6) can be evaluated using a local shift invariance assumption and Fourier approximations (Qi and Leahy 2000). But with the incorporation of continuity breaking, the matrices ℛ become shift variant and hence we cannot use the Fourier tricks. Instead we use the following alternate method. Substituting (7) in ( ) we get
| (8) |
| (9) |
where Xj ≡ (ℱ + βℛ)−1 ℒT 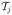 is an N × Nc matrix. The ith column of matrix Xj, given by vector
, can be obtained by solving the following linear system
is an N × Nc matrix. The ith column of matrix Xj, given by vector
, can be obtained by solving the following linear system
| (10) |
where is the ith channel template centered at j.
Equation (10) must be solved for all i = 1, …, Nc channels and j = 1, …, J locations. We can solve this matrix-vector equation for a given using a preconditioned conjugate-gradient (PCG) method with a diagonal preconditioner (Trefethen and Bau 1997). Solving for one is computationally equivalent to a few reconstructions. Thus (10) would involve an order of JNc reconstructions. In (9), the matrix is obtained by projecting each column of Xj. (In this notation , the projection of is the lth column of ℋXj). Thus ℋXj entails Nc projections. Given ℋXj, each mnth element of the Nc × Nc matrix can be calculated by the dot product of and weighted by diagonal elements of diag . That is . Thus in (9) we have shown how to compute the crucial Nc × Nc matrix . Since Nc is small, the inversion of this Nc × Nc matrix is rapidly accomplished.
The terms and in (6) can each be evaluated by a noiseless reconstruction (Fessler 1996) for each lesion location plus one noiseless reconstruction for a signal-absent case, requiring a total of J + 1 reconstructions. Since (10) requires ~JNc reconstructions, our theory method to calculate the CHO SNR at locations j = 1, ···, J with varying proximity to a fixed boundary thus entails an order of J(Nc + 1) + 1 reconstructions, where Nc is typically 3–5. Sample methods as discussed below would take (J +1)Nsamp reconstructions, where Nsamp is the number of sample reconstructions for a given object. Since Nsamp should 10 ~100 times Nc (Abbey et al 1997), the net computational savings using theory vs. sample methods is thus roughly two orders of magnitude.
3.2. Lesion Boundary Experiment
In this scenario, we take r = 1, ···, R spherical anatomical lesion boundaries with varying radii circumscribing the fixed-location functional lesion s of fixed radius. (The quantity r is not the radius; it indexes the lesion boundary radius as will be shown in figure 3 below.) Our intent is to relax the lesion boundary confinement (proximity) of the fixed functional lesion by surrounding it with continuity-breaking lesion boundaries of increasing radii. To study the effects of r = 1, …, R different lesion boundaries on the detectability of the lesion, we have to calculate the CHO SNR for the rth lesion boundary given by
Figure 3.
2D cross-section of 3D spherical anatomical lesion boundaries of increasing radii centered on a fixed small functional lesion. The radii are indexed by r. Note r = 1 corresponds to an anatomical lesion boundary coincident with the fuctional lesion boundary and r = 8 to no anatomical lesion boundary. Dark pixels are inside the anatomical lesion boundary.
| (11) |
where and are the reconstructions of f2 and f1 using the rth lesion boundary information in the prior. Figure 3 shows an example of varying anatomical lesion boundaries for r = 1, …, 8.
As in section 3.1, the main computation is in the terms (
) in (11). Following (7), (8), (9), (10) in section 3.1 but for given r instead of a given j, we can again compute (
). Note that in (7), ℛ becomes ℛr, i.e. the ℛ prior matrix indexed by r, and ℱ becomes ℱr, given by
. Furthermore since the lesion is now centered at a single location, the channel matrices 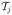 becomes a single matrix
becomes a single matrix  . With this reindexing, and for R lesion boundaries and Nc channels, we obtain the following computational burden for the lesion boundary case. It takes ~RNc reconstructions to obtain (
) for r = 1, ···, R. For a single boundary,
and
can be calculated using 2 noiseless reconstructions. Therefore, for R different boundaries, the theory method takes on the order of RNc + 2R reconstructions, while sample methods would involve 2RNsamp reconstructions. The net computational savings is again about two orders of magnitude.
. With this reindexing, and for R lesion boundaries and Nc channels, we obtain the following computational burden for the lesion boundary case. It takes ~RNc reconstructions to obtain (
) for r = 1, ···, R. For a single boundary,
and
can be calculated using 2 noiseless reconstructions. Therefore, for R different boundaries, the theory method takes on the order of RNc + 2R reconstructions, while sample methods would involve 2RNsamp reconstructions. The net computational savings is again about two orders of magnitude.
3.3. Sample Methods
We can also calculate the CHO SNR with sample methods. First we reconstruct an ensemble of noisy reconstructions and , where k = 1, ···, Nsamp indexes sample number. Then we obtain the channel response and by applying the channel matrix on the extracted slice. The sample means of the signal-present and -absent channel responses are given by
| (12) |
and the sample covariance of the channel responses is given by
| (13) |
Since 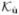 is Nc × Nc, calculating its inverse is easy. As mentioned, to get a good estimate of
is Nc × Nc, calculating its inverse is easy. As mentioned, to get a good estimate of 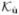 and its subsequent inverse, Nsamp should 10 ~100 times Nc (Abbey et al 1997). We can then substitute (12) and (13) into (4) to obtain the sample SNR. We shall use sample methods to validate the analytic methods.
and its subsequent inverse, Nsamp should 10 ~100 times Nc (Abbey et al 1997). We can then substitute (12) and (13) into (4) to obtain the sample SNR. We shall use sample methods to validate the analytic methods.
4. Results
We conducted 3D SPECT simulations to explore the effects of anatomical information. In all cases, we used Nc = 3 DOG bandpass channels in the radially symmetric CHO as shown in figure 2. The center frequencies of the 3 DOG channels were 0.0625 cycles/pixel, 0.1250 cycles/pixel and 0.250 cycles/pixel. These channel parameters were chosen according to criteria described in Oldan et al (2004). We used the theoretical methods of section 3 to calculate SNR and validated the theory methods with sample methods.
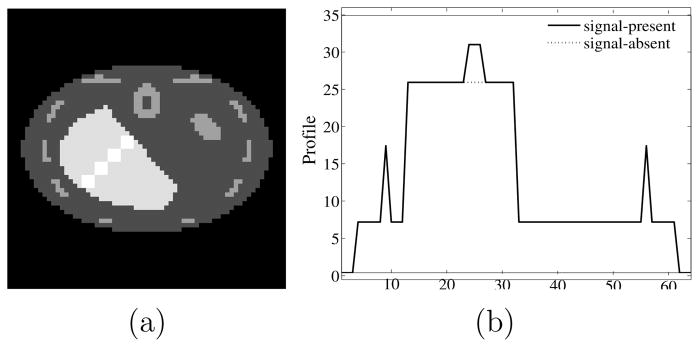
We performed the organ boundary experiment with a 3D MCAT 64 × 64 × 16 phantom with cubic voxels of size 0.625cm and an attenuation map at 140 KeV. The 16 slices comprised a region around the liver (The slices start where the lungs end and contain most of the liver). A depth-dependent collimator response was modeled as a Gaussian psf whose σ was modeled as σ (cm) = 0.013 d (cm) + 0.0392 cm where d is depth measured from the collimator face. No scatter was simulated. Figure 4 shows the 9th slice of the phantom with four prospective lesion locations in the liver at varying distances from the (inner edge) straight liver boundary. We used 10 lesion locations across the liver from one edge to the other. The lesion is a 3 × 3 × 3 cube with the 8 corner voxels deleted and with a low-contrast lesion-to-background ratio of 6:5. We note that for SKE/BKE studies in ET, low-contrast lesions are required to avoid unacceptably high SNR’s. Each camera face comprised 96 × 32 square bins of size 0.625 cm and was placed at a distance of 30 cm from the center of rotation. We simulated a parallel-beam geometry with 65 equispaced projection angles. The total number of counts was 4.8M. The reconstructions with a regularization weight of β = 0.001 used the COSEM-MAP (Hsiao et al 2002) algorithm with 16 subsets and was run till convergence. The smoothing parameter β was chosen to obtain a reasonable noise-resolution trade-off. Organ boundary information was applied using (2) in the reconstructions.
Figure 4.
(a) The 9th slice of the phantom through the lesion center. The figure shows four of the ten prospective lesion locations. (b) Horizontal profile plot through center of second lesion from top. In the profile plot the lesion is easily seen, centered at pixel 25.
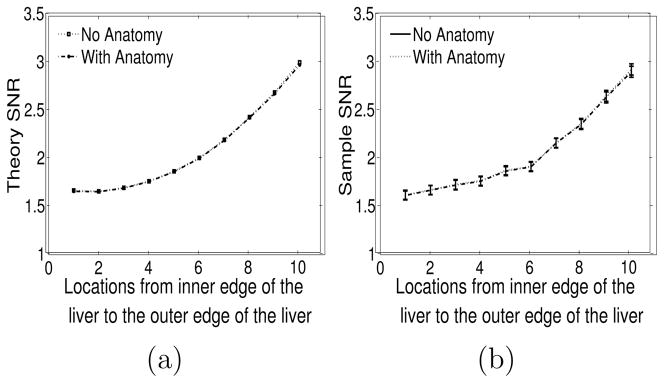
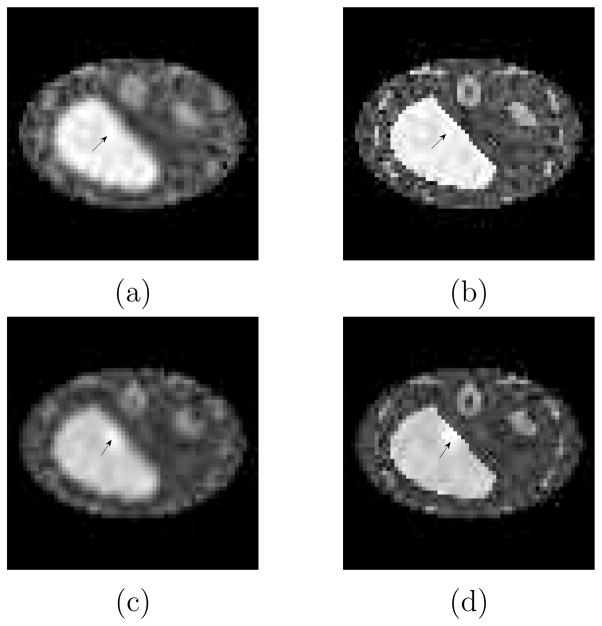
Figure 5(a) plots SNR vs. lesion location from the inner edge to the outer edge of the liver boundary for the cases with/without anatomy. The CHO SNR’s were calculated using the theoretical expressions for SNR in (6). There is no visible difference in the anatomy/no anatomy curves. One thousand two hundred lesion-present and lesion-absent reconstructions were used for the sample validation of the SNR using (12),(13) and (4). The sample SNR curves are shown in figure 5(b). They show close correspondence with the theory curves in figure 5(a). Error bars calculated using a jackknife procedure (Zoubir and Boashash 1998) and displayed in figure 5(b) represent a 68% confidence interval. As seen, there is no visible anatomy vs. no-anatomy difference in the SNR (for either sample or theory methods) even when the lesion is adjacent to either edge of the liver. Figures 6(a)(b) show signal-present anecdotal reconstructions with no anatomy information and with anatomy information, respectively. Figures 6(c)(d) are anecdotal signal-present reconstructions with the signal contrast enhanced for display purposes.
Figure 5.
Organ boundary experiment (a) Theory SNR plotted as a function of location ranging from the inner edge of the liver to the outer edge. “Location” is proportional to distance from the inner edge. (b) Sample SNR along with error bars plotted as a function of location ranging from the inner edge of the liver to the outer edge. In each case, the curves for the anatomy and no-anatomy cases coincide almost exactly, so the plots appear as a single curve.
Figure 6.
Slice from anecdotal signal-present reconstructions (a) without organ boundaries (b) with organ boundaries. Signal-present reconstructions with a signal contrast increased for visualisation (c) without and (d) with anatomical boundary discontinuities. Note (a)(b) share a common gray scale and (c)(d) share a common grey scale.
The bowing of the SNR curves is due to attenuation effects. The voxel corresponding to the location # 1 in figure 5 is near the object center while that at location # 10 is near the edge of the object. Pixels near the center will suffer lower SNR relative to those near the edge, hence the bowing. When attenuation is removed, the SNR curves in figures 5(a)(b) become nearly flat, but remain coincident.
One might suspect that our main conclusion for the organ boundary experiment, i.e. no separation of the anatomy and no-anatomy curves in figure 5, would be altered with the inclusion of internal noise (Barrett and Myers 2003) in the CHO. To address this we used an internal noise model (Oldan et al 2004) summarized by the following transformation of the diagonal of 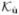 :
: 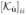 →
→ 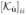 + α1
+ α1 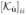 + α2 maxj
+ α2 maxj 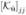 where α1, α2 were positive scalars. We tried 441 combinations of (α1, α2). In each case, the curves in figure 5 were lowered, but they remained coincident, so that internal noise did not affect our main conclusion.
where α1, α2 were positive scalars. We tried 441 combinations of (α1, α2). In each case, the curves in figure 5 were lowered, but they remained coincident, so that internal noise did not affect our main conclusion.
We performed the lesion boundary experiment using a 64 × 64 × 16 object with cubic voxels of size 0.625cm. Here, as seen in figure 7(a), the background was uniform and the lesion was placed near the center of the object volume. The lesion, a 3 × 3 × 3 cube with the 8 corner voxels removed, had a contrast of 1.345 relative to background. All other imaging and reconstruction parameters were as before except that a smoothing parameter β = 0.002 was used. The smoothing is reasonable in reducing the noise in the reconstruction without over-smoothing the reconstructed signal. Anatomical information in the form of R spherical anatomical lesion boundaries indexed by r = 1, ···, R was used in the reconstructions. Anatomical information is indexed by a parameter r, with r = 1 implying perfect knowledge of the functional lesion boundary, r = 2 imperfect knowledge where the radius of the surrounding anatomical lesion boundary is enlarged slightly, r = 3, 4, 5, 6, 7 even more imperfect knowledge with even larger radii as shown in figure 3, and with r = 8 corresponding to no lesion boundary. MAP reconstructions with and without anatomical information were evaluated using our theoretical expressions for the SNR in (11). The observer is applied at the lesion site and evaluated vs. r. Nine hundred lesion-present and lesion-absent reconstructions for each r were used for the sample validation of the SNR using (12), (13) and (4). Error bars calculated using a jackknife procedure (Zoubir and Boashash 1998) and displayed in figure 7(b) represent a 68% confidence interval.
Figure 7.
Effects of increasingly inaccurate boundary information about the lesion. (a) 9th slice of the phantom through center of the lesion (b) SNR versus proximity of boundary with r=1 a perfect boundary and r=8 no boundary. Plot shows that SNR versus r is relatively flat, with theory and sample methods in agreement. (c) Each column corresponds to a boundary indexed by r. The first two rows show anecdotal reconstructions with the lesion present (+) and absent (−). The next two rows show another such set of anecdotal reconstructions. Each image in the four rows shares a common gray-scale. The fifth row plots variance at each pixel and the sixth row is the difference of mean signal present and absent reconstructions. The fifth row images share a common gray and the sixth row images share a common gray scale.
From figure 7(b) we see that the SNR does not significantly vary with r and that the theory and sample methods correspond well. This result belies the intuition discussed in figure 1. That the SNR vs. r curve is indeed flat is borne out by the anecdotal signal-present (+) and -absent (−) reconstructions shown in the first four rows of figure 7(c). Note that even in the signal-absent cases, the lesion boundaries can induce false lesions as seen in the 4th row of figure 7(c). For signal-present cases, the lesion boundaries can induce reverse contrast (cold) lesions in place of the hot-lesion signal. The fifth row of figure 7(c) comprises the variance images (at a common gray scale) of the 9th slice. The sixth row shows the 9th slice of the noiseless reconstructions of the signal, given by . Note that the variance level along the perimeter of the anatomical lesion boundary increases as the lesion boundary becomes more confining. This accounts for a typical result of a false positive lesion as seen in the fourth row, column r=1 and the cold lesion as seen in the third row, column r = 1. The high variance can also lead to false negative reports as seen in the images in row 3, columns r = 4, 6 and 8. The last row illustrates that the anatomical lesion boundary restricts the spread of the mean reconstructed lesion and yields for noiseless images a higher contrast with more restricting lesion boundaries. One would expect this latter effect to increase SNR as r is reduced. However, tight lesion boundaries also increase variance (row 5), and this decreases SNR. The trade-off of these two effects results in the slow variation of SNR with r seen in figure 7(b). We note that increased variance within a lesion boundary was also observed by Comtat et al (2002).
We repeated the lesion boundary experiment of figure 7(b), but with a smaller 1 × 1 × 3 pixel lesion whose size in the plane of observation was less than the system resolution. We added one additional lesion boundary, indexed by r = 0, that exactly encompassed the smaller functional lesion. The resulting SNR vs r curve was again invariant with r.
We again tested whether the inclusion of internal noise would affect our main conclusion - the invariance of SNR with r. As before, we used 441 combinations of (α1, α2) in the internal noise modification of 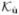 . We observed that inclusion of internal noise lowered the overall SNR(r) curve, but did not change the invariance with r. Internal noise, therefore, did not alter our conclusions.
. We observed that inclusion of internal noise lowered the overall SNR(r) curve, but did not change the invariance with r. Internal noise, therefore, did not alter our conclusions.
Though the results in figures 5 and 7 were for a single β, we found that using higher or lower β’s (10β and 0.1β) simply shifted the curves up (for 10β) and down (for 0.1β) without altering the basic shape of the curve for the lesion boundary experiment and without changing the agreement of the anatomy and no-anatomy cases for the organ boundary experiment.
5. Discussion
5.1. Summary
We studied the effects of anatomical information on lesion detectability using anatomical and non-anatomical MAP priors, an SKE/BKE task, a CHO observer and a scalar figure of merit SNR. We investigated, in this context, whether SNR would be improved with the incorporation of organ boundary information. We further investigated whether this improvement in SNR would be a function of proximity of the lesion to an organ boundary. We concluded that SNR was unchanged with the addition of organ boundary information, and in particular, we found no change in SNR at any proximity.
We also investigated whether the incorporation of anatomical lesion boundaries coincident with the assumed functional lesion boundary (our r = 1 case) would improve SNR relative to no anatomical information (our r = 8 case). We further investigated whether SNR improvements, if any, would vary if the anatomical lesion boundary was less proximate (our 1 < r < 8 case) to the assumed functional lesion boundary. We concluded that SNR was unaffected by the inclusion of perfect (r = 1) lesion boundaries. In particular, SNR was insensitive to r. This insensitivity may be due to the fact that for the low lesion contrast necessary for an SKE/BKE task, the detection performance is limited by the appearance of false positive and false negative lesions within anatomical lesion boundaries. This is caused by an increase in variance within the lesion boundary as seen in figure 7(c).
In sum, we found that anatomical boundary information did not affect SNR in our context, and that SNR was unaffected as proximity was varied. We note that related studies by others, discussed in section 5.2, do not include proximity effects. Hence any comparisons to our work involve only perfect (r = 1) lesion boundary information. In addition, comparisons involving organ boundaries do not take into account lesion location with respect to the organ boundary.
One can gain some insight into our negative results by noting that, for our reconstruction method an optimal linear observer, the Hotelling observer (HO), would yield no SNR difference with anatomy versus without anatomy. Therefore any difference in our anatomy versus no-anatomy results must be due to the inclusion of channels. Note that the CHO is a Hotelling observer applied to channel responses instead of directly to pixels. The HO is a limiting form of the CHO as we increase the number of channels so that a unit-weight channel template is applied to each pixel. Note that . (We verified this numerically for simple 2D organ boundary experiments.) Qualitatively, the smoothing prior without anatomy acts as a linear information-preserving slowly-varying smoothing filter in the reconstruction domain, and the HO is insensitive to this smoothing if the reconstruction step does not remove information. When we adjust ℛ to incorporate anatomical information, it simply induces a form of smoothing on the reconstruction that yields sudden changes along anatomical loci and the HO is again insensitive to this form of smoothing. Indeed, it is possible for the SKE/BKE case, given that ℱ and (ℱ + βℛ) are invertible, to calculate using only sinogram quantities (Qi and Huesman 2001, Abbey 1998) having nothing to do with ℛ.
Our selection of a 3-DOG channel scheme does not seem especially important and we have observed similar results with different channel schemes. For any reasonable β, the anatomy/no anatomy SNR curves remain in close agreement. We also observed that the inclusion of internal noise did not alter our conclusions. Our CHO used radially symmetric channels even near organ boundaries where a non-symmetric channel might be more appropriate. The use of radially symmetric channels is justified (Abbey and Barrett 2001) when the signal profile and noise covariance is radially symmetric around the lesion. This is true for our lesion boundary experiment. But for the organ boundary experiments, the signal spread and the covariance are anisotropic and the use of anisotropic channels might give different performance. Partly to address this problem, we designed our somewhat artificial lesion boundary experiment to be completely isotropic in 3D. We again observed little difference in SNR as the anatomical lesion boundary radius was expanded to the point where the boundary disappeared.
Finally, this work should obviously be extended to human observer testing. Preliminary results using human experiments with a 2AFC methodology (Barrett and Myers 2003) to measure SNR showed agreement of human and model observer for our lesion boundary experiment, but far more work is needed.
5.2. Related Work
Any comparison of our results to other work must be couched in the context of the components of a generalized detection task. Thus one must specify the task (detection or detection plus localization or localization). The object model including signal (size, contrast, shape, location known or unknown) and background (variable or fixed) must be stated. The imaging modality (PET or SPECT) and imaging model (Monte Carlo vs analytical projector, modeling of scatter or other effects) must also be stated. One must consider the nature of the anatomical boundary information (the particular type of lesion and or organ boundary) and the reconstruction method (MAP with some anatomical or non-anatomical prior, post smoothed ML). To measure image quality, one must specify the observer + scalar figure of merit (CHO+SNR, NPW+SNR, scanning CNPW+ALROC, human+ALROC, human+localization accuracy.) Finally many studies focus on the variation of the figure of merit with some regularization parameter (smoothing weight β in MAP, post smoothing kernel for ML, number of iterations).
It will be useful in our comparisons below to be more specific about our anatomical boundary taxonomy. We will consider 4 types of boundary: (i) organ boundaries (ii) perfect lesion boundaries as in our r = 1 case (we shall refer to these as “tight lesion boundaries”) (iii) organ + tight lesion boundaries (iv) hybrid boundaries, in which functional lesions are surrounded by complex anatomies that do not correspond to any of the cases (i)–(iii).
Others have assessed the effects of anatomical priors in PET and SPECT for pure detection, pure localization, and for detection plus localization tasks. None of these directly addressed our question of boundary proximity effects, but some of these works had conclusions that bore relation to our work. We first consider previous work that involved detection only.
The work most similar to ours is found in Nuyts et al (2005). Nuyts et al (2005) considered the detection of hypometabolic regions in brain PET using an SKE/BKE task and CHO+SNR. They compared SNR performance for their brain-specific AMAP anatomical reconstruction versus a non-anatomical post-smoothed ML (psML) reconstruction. Like our anatomical MAP prior, the prior in AMAP breaks continuity across anatomical boundaries but applies different forms of smoothing within grey matter, white matter and CSF. In phantom studies incorporating tight lesion boundaries, organ boundaries and hybrid boundaries, they found that AMAP at a variety of smoothing parameters β outperformed psML at a variety of Gaussian post-smoothing kernels with standard deviation σps. A related study by Baete et al (2004a,2004b) assessed SNR of hypometabolic brain regions in PET but used an NPW (Non-prewhitening) observer (Barrett and Myers 2003) rather than a CHO. Again AMAP was compared to psML. The brain phantom used here involved hybrid boundaries only. No significant difference was found between the optimal NPW SNR of AMAP and the optimal NPW SNR of psML. In further work by Baete et al (2004a), they again addressed the same PET problem using an NPW observer, but this time compared the performance of AMAP versus that of a MAP algorithm using a relative difference prior (Nuyts et al 2002). The NPW SNR was greater for AMAP than that of MAP-RD.
Since for our MAP with SKE/BKE and CHO+SNR, anatomical information essentially had no advantage, and since, in the various contexts listed above, AMAP did often show an advantage, one is motivated to reconcile these differences. In (Nuyts 2005) AMAP did indeed outperform psML using a CHO and SKE/BKE detection task. However, the study was incommensurate with ours in that AMAP differed from our anatomical MAP and psML differed from our non-anatomical MAP. In Baete et al (2004a) the MAP-RD prior is of interest because it is the natural non-anatomical Bayesian counterpart of AMAP. However, that study was again incommensurate with ours since the observer was an NPW. Despite incommensurabilities, one might well infer that a prior (such as AMAP) highly tuned to the anatomical correlates of the underlying radiotracer distribution might lead to improved performance in a detection-only task.
We now consider previous work (Bruyant et al (2004a,2003,2004b) and Lehovich et al 2006) involving a detection plus localization task for a Ga-67 SPECT torso simulation. The projection data were generated using a Monte Carlo package. These tasks involve model observers and a figure of merit radically different than ours and also necessarily involve lesion contrasts much higher than those required by SKE/BKE. The figure of merit was the area under the LROC curve (ALROC). These works used either human observers or a numerical scanning channelized NPW (CNPW) observer (Gifford et al 2003). The observer was required to correctly detect the signal while also localizing it within a search tolerance. They addressed the case of SPECT with an imaging model similar to ours. They encoded anatomical information using a MAP objective identical to ours. Their lesion contrasts were high ranging from 12:1 to 30:1. They considered organ boundaries but with the lesion location, if the lesion was present, distributed uniformly throughout a search region. The results in Bruyant et al (2004a), using their numerical observers, showed that the use of organ-boundary information did not increase ALROC relative to that obtained with non-anatomical psML. While scatter was not modeled in Bruyant et al (2004a), it was included in Bruyant et al (2003, 2004b). In Bruyant et al (2003), organ boundary information led to a mild increase in ALROC for the numerical observer relative to that of non-anatomical psML. In a human observer study in Lehovich et al (2006), they used, in addition to a non-anatomical psML reconstruction, a non-anatomical MAP reconstruction identical to the one in this paper. Scatter was included. An interesting conclusion was that for MAP reconstructions organ boundaries alone did not significantly improve ALROC. These papers also considered the case of organ + tight lesion boundaries. All four papers found significant ALROC increases with respect to their non-anatomical counterparts for this organ + tight lesion boundary case. In sum, organ boundaries alone did not help much, but organ + tight lesion boundaries were of significant help in detection plus localization studies. In a separate work by a PET brain group, Baete et al (2004b) used a pure localization task (signal always present but location unknown), human observers, and a figure of merit given by percent correctly localized signals in an MAFC study. They used a brain phantom whose hypometabolic lesions were surrounded by hybrid boundaries. The lesion contrast ranged from 5% –100%. In this context it was found that AMAP outperformed the non-anatomical psML reconstruction.
While none of the studies involving higher-order tasks, such as detection plus localization, directly addressed boundary proximity effects, it would be interesting to investigate these. For example, since the ALROC metric involves an aggregate detectability over all locations in a search region, it is not clear whether lesions nearer to boundaries contributed more to ALROC than other lesions.
Finally, we point out that previous studies discussed in this section have not included the important feature of statistically variable backgrounds. Aside from their realism, the inclusion of background variability might lead to a change in conclusions regarding the efficacy of anatomical priors in some task contexts.
Acknowledgments
This work was supported by National Institute of Health (NIH)-NIBIB grant R01 EB02629 and in part by grants NSC94-2320-B-182-014 NSC Taiwan and CMRPG34005 from Chang Gung Research Fund, Taiwan
References
- Abbey CK, Barrett HH, Eckstein M. Practical issues and methodology in assessment of image quality using model observers. Conf. Rec. SPIE Med. Imaging; 1997. pp. 182–94. [Google Scholar]
- Abbey C. PhD Thesis, Graduate Interdisciplinary Program in Applied Mathematics. University of Arizona; Tuscon, AZ, USA: 1998. Assessment of reconstructed images. [Google Scholar]
- Abbey C, Barrett HH. Human- and model-observer performance in ramp-spectrum noise: effects of regularization and object variability. J Opt Soc Am A. 2001;18(3):473–88. doi: 10.1364/josaa.18.000473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ardekani BA, Braun M, Hutton BF, Kanno I, Iida H. Minimum cross-entropy reconstruction of PET images using prior anatomical information. Phys Med Biol. 1996;41(11):2497–517. doi: 10.1088/0031-9155/41/11/018. [DOI] [PubMed] [Google Scholar]
- Baete K, Nuyts J, Van Paesschen W, Suetens P, Dupont P. Anatomical-based FDG-PET reconstruction for the detection of hypo-metabolic regions in epilepsy. IEEE Trans on Medical Imaging. 2004a;23(4):510–9. doi: 10.1109/TMI.2004.825623. [DOI] [PubMed] [Google Scholar]
- Baete K, et al. Evaluation of anatomy based reconstruction for partial volume correction in brain FDG-PET. NeuroImage. 2004b;23:305–17. doi: 10.1016/j.neuroimage.2004.04.041. [DOI] [PubMed] [Google Scholar]
- Barrett HH, Myers KJ. Foundations of Image Science. Wiley Interscience; 2003. [Google Scholar]
- Bowsher J, Johnson V, Turkington T, Jaszczak R, Floyd C, Jr, Coleman R. Bayesian reconstruction and use of anatomical a priori information for emission tomography. IEEE Trans Med Imaging. 1996;15(5):673–86. doi: 10.1109/42.538945. [DOI] [PubMed] [Google Scholar]
- Bruyant P, Gifford H, Gindi G, King M. Numerical observer study of MAP-OSEM regularization methods with anatomical priors for lesion detection in Ga-67 images. IEEE Trans Nucl Sci. 2004a;51(1):193–7. [Google Scholar]
- Bruyant P, Gifford H, Gindi G, King M. Investigation of observer performance in MAP-EM reconstruction with anatomical priors and scatter correction for lesion detection in 67Ga images. Conf. Rec. IEEE Nuc. Sci. Symp. Med. Imaging Conf.; 2003. pp. 3166–9. [Google Scholar]
- Bruyant P, Gifford C, Gindi G, Pretorius P, King M. Human and numerical observer studies of lesion detection in Ga-67 images obtained with MAP-EM reconstructions and anatomical priors. Conf. Rec. IEEE Nuc. Sci. Symp. Med. Imaging Conf.; 2004b. pp. 4072–5. [Google Scholar]
- Comtat C, Kinahan P, Fessler J, Beyer T, Townsend D, Defrise M, Michel C. Clinically feasible reconstruction of 3D whole-body PET/CT data using blurred anatomical labels. Phys Med Biol. 2002;471:1–20. doi: 10.1088/0031-9155/47/1/301. [DOI] [PubMed] [Google Scholar]
- Fessler J. Mean and variance of implicitly defined biased estimators (such as penalized maximum likelihood): applications to tomography. IEEE Trans Image Processing. 1996;5(3):493–506. doi: 10.1109/83.491322. [DOI] [PubMed] [Google Scholar]
- Gifford HC, King MA, de Vries DJ, Soares EJ. Channelized hotelling and human observer correlation for lesion detection in hepatic SPECT imaging. J Nucl Med. 2000;41(3):514–21. [PubMed] [Google Scholar]
- Gifford HC, Pretorius PH, King MA. Comparison of human- and model-observer LROC studies. Conf. Rec. SPIE Med. Imaging; 2003. pp. 112–22. [Google Scholar]
- Gindi G, Lee M, Rangarajan A, Zubal G. Bayesian reconstruction of functional images using anatomical information as priors. IEEE Trans Med Imaging. 1993;12:670–80. doi: 10.1109/42.251117. [DOI] [PubMed] [Google Scholar]
- Hsu CH, Leahy R. PET image reconstruction incorporation anatomical information using segmented regression. Conf. Rec. SPIE Med. Imaging; 1997. pp. 381–92. [Google Scholar]
- Hsiao IT, Rangarajan A, Gindi G. A new convergent MAP reconstruction algorithm for emission tomography using ordered subsets and separable surrogates. Conf. Rec. IEEE Int. Symp. Biomed. Imaging; 2002. pp. 409–12. [Google Scholar]
- Lipinski B, Herzog H, Rota Kops E, Oberschelp W, Muller-Gartner HW. Expectation maximization reconstruction of positron emission tomography images using anatomical magnetic resonance information. IEEE Trans Med Imaging. 1997;16(2):129–36. doi: 10.1109/42.563658. [DOI] [PubMed] [Google Scholar]
- Leahy R, Yan X. Incorporation of anatomical MR data for improved functional imaging with PET. Information Processing in Medical Imaging: 12th International Conference; Wye, UK. 1991. pp. 105–20. [Google Scholar]
- Lehovich A, Bruyant PP, Gifford HC, Gindi G, Schneider PB, Squires S, King MA. Human-observer LROC study of lesion detection in Ga-67 SPECT images reconstructed using MAP with anatomical priors. Conf. Rec. IEEE Nuc. Sci. Symp. Med. Imaging Conf.; 2006. p. M03-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meltzer C, Leal JP, Mayberg HS, Wagner HN, Frost JJ. Correction of PET data for partial volume effects in human cerebral cortex by MR imaging. J of Comp Assisted Tomography. 1990;14(4):561–70. doi: 10.1097/00004728-199007000-00011. [DOI] [PubMed] [Google Scholar]
- Muller-Gartner HW, Links JM, Prince JL, Bryan RN, Mcveigh E, Leal JP, Davatzikos C, Frost JJ. Measurement of radiotracer concentration in brain gray matter using positron emission tomography: MRI-based correction for partial volume effects. J Cereb Blood Flow Metab. 1992;12(4):571–83. doi: 10.1038/jcbfm.1992.81. [DOI] [PubMed] [Google Scholar]
- Narayanan M, Gifford H, King M, Pretorius P, Farncombe T, Bruyant P, Wernick M. Optimization of iterative reconstructions of 99mTc cardiac SPECT studies using numerical observers. IEEE Trans Nuc Sci. 2002;49:2355–60. [Google Scholar]
- Nuyts J, Beque D, Dupont P, Mortelmans L. Concave prior penalizing relative differences for Maximum-a-Posteriori reconstruction in emission tomography. IEEE Trans Nucl Sci. 2002;49(1):56–60. [Google Scholar]
- Nuyts J, Baete K, Beque D, Dupont P. Comparison between MAP and postprocessed ML for image reconstruction in emission tomography when anatomical knowledge is available. IEEE Trans Med Imaging. 2005;24(5):667–75. doi: 10.1109/TMI.2005.846850. [DOI] [PubMed] [Google Scholar]
- Oldan J, Kulkarni S, Xing Y, Khurd P, Gindi G. Channelized Hotelling and human observer study of optimal smoothing in SPECT MAP reconstruction. IEEE Trans Nucl Sci. 2004;51(3):733–41. [Google Scholar]
- Ouyang X, Wong WH, Johnson VE, Hu X, Chen CT. Incorporation of correlated structural images in PET image reconstruction. IEEE Trans Med Imaging. 1994;13(4):627–40. doi: 10.1109/42.363105. [DOI] [PubMed] [Google Scholar]
- Rangarajan A, Hsiao IT, Gindi GR. A Bayesian joint mixture framework for the integration of anatomical information in functional image reconstruction. J Math Imaging and Vision. 2000;12(3):199–217. [Google Scholar]
- Rousset OG, Ma Y, Evans AC. Correction partial volume effects in PET: principle and validation. J Nucl Med. 1998;39(5):904–11. [PubMed] [Google Scholar]
- Sastry S, Carson RE. Multimodality Bayesian algorithm for image reconstruction in PET: a tissue composition model. IEEE Trans Med Imaging. 1997;16(6):750–61. doi: 10.1109/42.650872. [DOI] [PubMed] [Google Scholar]
- Trefethen LN, Bau D. Numerical Linear Algebra (SIAM) 1997 [Google Scholar]
- Qi J, Leahy R. Resolution and noise properties of MAP reconstruction for fully 3-D PET. IEEE Trans Med Imaging. 2000;19(5):493–506. doi: 10.1109/42.870259. [DOI] [PubMed] [Google Scholar]
- Qi J, Huesman R. Theoretical study of lesion detectability of MAP reconstruction using computer observers. IEEE Trans Med Imaging. 2001;20(8):815–22. doi: 10.1109/42.938249. [DOI] [PubMed] [Google Scholar]
- Videen O, Perlmutter J, Mintun M, Raichle M. Regional correction of positron emission tomography data for the effects of cerebral atrophy. J Cereb Blood Flow Metab. 1998;8(5):662–70. doi: 10.1038/jcbfm.1988.113. [DOI] [PubMed] [Google Scholar]
- Wollnweber SD, Tsui BMW, Lalush DS, Frey DS, LaCroix KJ, Gullberg GT. Comparision of Hotelling observer models and human observers in defect detection from myocardial SPECT imaging. IEEE Trans Nucl Sci. 1999;46(6):2098–103. [Google Scholar]
- Zoubir AM, Boashash The bootstrap and its application in signal processing. IEEE Signal Processing Magazine. 1998;15(1):56–76. [Google Scholar]