Speckle attenuation in optical coherence tomography by curvelet shrinkage

Abstract

We describe an algorithm based on shrinkage in the curvelet domain to attenuate speckles in optical coherence tomography (OCT) images. The algorithm exploits the curvelet transform’s sparse representation of edge discontinuities that are common in OCT images and its ability to map signals and noise into different areas in the curvelet domain. The speckle attenuation is controlled by a single parameter that determines the threshold in the curvelet domain. Applying the algorithm to OCT images shows significant improvement of image quality.

Recent years have seen increasing interest in the use of optical coherence tomography (OCT) for a variety of imaging applications, especially in the field of biomedical imaging [1]. Many issues remain to be addressed in order for OCT to be widely used in clinical applications. One of these is the degradation of OCT image quality owing to speckles [2]. Speckles make it particularly challenging to perform further quantitative image analysis such as edge detection, segmentation, and pattern recognition. Consequently, much research has been carried out to develop methods to reduce speckles. The methods developed include spatial compounding [2,3], frequency compounding [2], and digital filtering such as an enhanced Lee filter [4], median filter [4], a symmetric nearest neighbor filter [4], an adaptive Wiener filter [4], an I-divergence regularization [5], as well as filtering in a transform domain such as the wavelet [4,6-9]. Among them, filtering in a transform domain is one of the most promising approaches.

The basic principle of transform domain filtering is to shrink transformed coefficients according to some threshold values. This method is based on the assumption that, in the transform domain, signals are usually more concentrated and represented by some large coefficients, while noise is more spread out and coded in small ones. As a result, by zeroing out small coefficients and keeping large ones, it is possible to effectively attenuate noise without significantly damaging signal components. Two elements are therefore essential for the method: a domain that provides sparse representation of signals and an optimal threshold value. The wavelet is one such domain. It provides a sparse representation for signals containing singularities that satisfy a variety of local smoothness constraints including, for example, piecewise smoothness [10]. Different thresholding strategies in the wavelet domain have been applied for OCT images previously [6,8,11].

OCT images, however, are usually characterized by edge discontinuities rather than individual point discontinuities as many biological tissues have layered structures. The wavelet representation of this kind of feature is not optimally sparse and therefore limits the application of the thresholding strategy. Recently, another multiscale method called curvelet transform was developed [12]. The basis functions of the curvelet transform, so called curvelets, can represent curved edges much more efficiently than wavelets. This concept is illustrated in Fig. 1, which shows that, for the same image, the signal energy is concentrated in a fewer number of curvelet coefficients than of wavelet coefficients. Importantly, the error of reconstructing original signals based on curvelet coefficients as a function of the largest coefficients decays rapidly, which makes denoising via coefficient thresholding quite robust. Curvelets are also directionally sensitive, which offers many degrees of freedom to manipulate signals along certain directions. In contrast, the 2D wavelet transform decomposes data in only three directional subbands. Given the many superior properties of curvelets, we present in this work a method based on the curvelet transform to attenuate speckle noise in OCT images. Our results indicate that image quality is significantly improved.

Fig. 1.

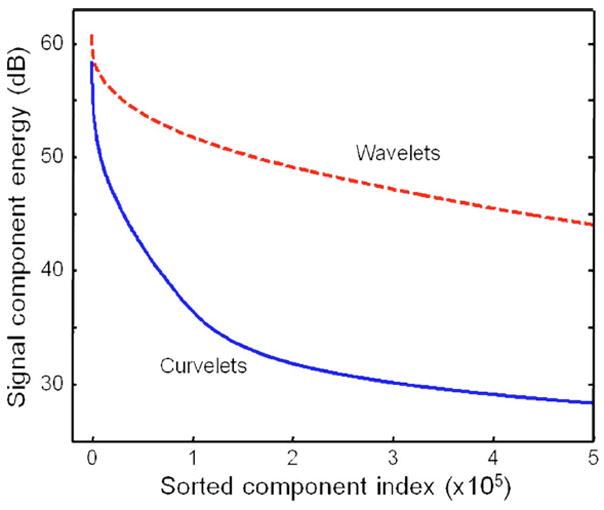
(Color online) Energies of the curvelet and wavelet coefficients of the OCT image shown in Fig. 2(a). The coefficients are sorted in descending order of energy from left to right. Curvelets provide a sparser representation of the image, as the signal energy is concentrated in fewer curvelet coefficients than wavelet coefficients.

There are several software implementations of curvelet transform. We use the wrapping method of fast discrete curvelet transform to perform both the forward and inverse transformations [13]. The forward transformation involves several steps, and one of the major steps is to partition the frequency plane into dyadic annuli and trapezoidal regions. The dyadic annuli provide scale information, and trapezoidal regions provide the orientation information of image features. The curvelets are localized in both frequency plane and space domain, and hence the transformed coefficient is a function of the scale j, the orientation l, and the spatial coordinates p and q.

The denoising procedure of our algorithm closely mimics those in the wavelet domain and consists of four steps: logarithm transformation, forward curvelet transform, thresholding, and inverse curvelet transform. As speckles are usually well modeled as multiplicative noises, a logarithm transformation is first applied to convert them to additive noises: log(s) = log(x) + log(z), where s is the acquired data, x is the noise-free signal to be recovered, and z is the speckle. Then a forward curvelet transform is performed on the converted data to produce curvelet coefficients S_j,l,p,q = X_j,l,p,q + Z_j,l,p,q, where S, X, and Z are the coefficients for measured data, noise-free signals, and speckle noise, respectively. Following that, a hard threshold T_j,l is applied to each curvelet coefficient S_j,l,p,q so that S̄_j,l,p,q = S_j,l,p,q when |S_j,l,p,q| > T_j,l, and S̄_j,l,p,q = 0, otherwise. Then an inverse curvelet transform is performed to S̄_j,l,p,q to reconstruct the denoised image, and a simple exponential calculation of base 10 would convert the denoised image in the logarithm scale back to the original linear scale.

To obtain the threshold, we use a method called k sigma [14]: T_i,j = kσ₁σ₂. Here k is an adjustable parameter, σ₁ is the standard deviation of speckles in a background region, and σ₂ is the standard deviation of speckles in the curvelet domain at a specific scale j and orientation l. By choosing a background region, which contains only speckles, one can compute the mean value and the standard deviation σ₁. Based on those values, σ₂ is computed using the Monte Carlo simulation method [14]. We note that, in the computation of σ₂, speckles after logarithm operation are assumed to have a Gaussian distribution, but extensive data analysis shows that they generally do not fully satisfy this assumption, so the computed value will be theoretically slightly off. However, since k is adjustable, that effect turns out not to be critical. The value of k can be scale and orientation dependent. It is usually obtained by trial and error.

Figure 2 shows a Fourier domain OCT image of the optical nerve head (a) before and (b) after curvelet denoising. The details of the OCT instrument and image acquisition have been previously described [15]. Much of the speckle in the original image has been reduced, making some image features hidden in the original image more obvious, as shown at the places, for example, indicated by the two white arrows in (b). To better appreciate the performance of the algorithm, Fig. 2(c) shows a cross section of the images at the indicated dashed line in Figs. 2(a) and 2(b). The denoised signal is much cleaner than the original one: the noise fluctuation at the beginning of the original signal is attenuated to close to zero and the noise superimposed on the signal components is also attenuated significantly. Most importantly, all of those are achieved when the image features and the edge sharpness of the original signal are both well maintained, demonstrating the ability of the algorithm to preserve signal while attenuating noise.

Fig. 2.

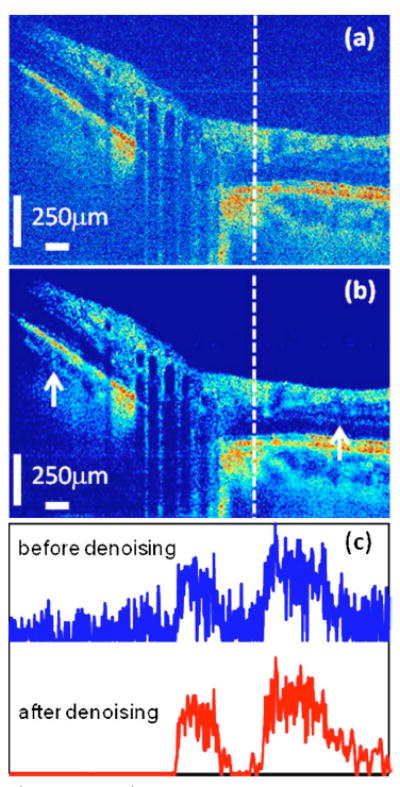
(Color online) Fourier domain OCT images of the optical nerve head (a) before and (b) after curvelet despeckling. For direct comparison, the images are shown on the same color scale. The SNR, CNR, and ENL are all increased, with a high similarity between the images before and after denoising, as detailed in Table 1. The two white arrows in (b) indicate the places where features hidden in the original image are more obvious in the denoised image. (c) shows the cross section signal along the white dashed lines in (a) and (b), and they are vertically offset for clarity. The edge sharpness of the original image is well preserved in the denoising process, as can be seen in (c). The curvelet transform parameters are: the number of scales is 3 and the number of orientations at the second coarsest scale is 16. A universal threshold is used for all directions, and the value of k is 0.7.

To quantify the performance of the algorithm, four quality metrics are computed: contrast-to-noise ratio (CNR) [6], which measures the contrast between image features and noise; average equivalent number of looks (ENL) [6], which measure the smoothness of homogeneous areas; peak-signal-to-noise ratio (SNR), defined as SNR = 20 log₁₀{[max(X)]/σ}, where X is the amplitude data and σ is the noise variance; and cross correlation (XCOR), which measures the similarity between the images before and after denoising and is defined as $\mathrm{XCOR}={\mathrm{\sum }}_{m,n}{s}_{m,n}{y}_{m,n}/({\mathrm{\sum }}_{m,n}{s}_{m,n}^2{y}_{m,n}^2)$, where s is the intensity data before denoising, y is the intensity data after denoising, and m and n are the indices of the images. Both CNR and ENL are computed using logarithmic scale data, while SNR and XCOR are computed using linear scale data. The value of XCOR is smaller than 1, and the larger is the XCOR, the closer the denoised image is to the original image.

Table 1 lists the results of the quality metrics for different thresholds. With a small increase in the threshold, as expected, the cross correlation decreases, since more data are zeroed, while the values of SNR, CNR, and ENL all increase. For comparison, we have also performed wavelet-based thresholding. The wavelet filtering is based on undecimated discrete wavelet transform and the threshold is chosen to be 4.2 times the noise variance, obtained from the robust median estimator of the highest subband of the transform [16], with the number 4.2 obtained by trial and error to give the best results. Comparing curvelet- with wavelet-based methods, for a similar cross-correlation value, our curvelet method (k = 0.7) further improves the SNR by 7.84 dB.

Table 1.

Image Quality Metrics

Image	XCOR	SNR (dB)	CNR (dB)	ENL
Original	1	33.67	3.38	6.84
Curvelet, k = 0.65	0.932	57.89	5.31	18.07
Curvelet, k = 0.70	0.926	61.34	5.43	20.08
Curvelet, k = 0.75	0.920	64.50	5.53	21.99
Wavelet	0.927	53.50	4.91	17.79

While the curvelet transform provides an optimally sparse representation of OCT images, it is still unavoidable that image features can be attenuated in the process of thresholding. This can be the result of setting too large a threshold and/or some image noise may have curvelet coefficients that are comparable to those of signals. To minimize the impact, one can take advantage of the direction selectivity of the curvelets. For example, when signals are mainly along certain directions, a small threshold should be used for those directions to preserve signals and a large threshold can be used for other directions to attenuate more noise. This property of the curvelet transform makes it superior to wavelets, as it can distinguish image events in more directions than the 2D wavelet transform, which only decomposes data into three directions: horizontal, vertical, and diagonal. Another advantage is that here the whole process is computationally very efficient, taking only a few seconds in a typical dual-processor laptop computer; by contrast, while many simple wavelet filters take about a few seconds, the spatially adaptive wavelet filter takes about 7 min [6].

To summarize, a curvelet based algorithm is demonstrated that significantly suppresses speckles in OCT images. The image quality is significantly improved: the SNR is increased by 27.7 dB, and the contrast ratio as well as smoothness measure are enhanced, with a small 7.4% loss of similarity. These results highlight the power of the curvelet transform in OCT image analysis and processing. We anticipate that this approach can be applied to other problems in biophotonic and biomedical imaging where noise poses a serious challenge.