Computational Modeling of the Nitrile Stretching Vibration of 5-Cyanoindole in Water

Abstract

The bandwidth of the nitrile (C≡N) stretching vibration of 5-cyanotryptophan shows a significant broadening upon hydration. Thus, it has been proposed to be a useful infrared probe of the local hydration environment of proteins. However, the molecular mechanism underlying this hydration-induced spectral broadening is not known, making interpretation of the experimental results difficult. Herein, we investigate how interactions of water with various sites of 5-cyanoindole, the sidechain of 5-cyanotryptophan, affect its C≡N stretching vibration via a combined electronic structure/molecular dynamics approach. It is found that, besides those interactions with the nitrile group, interactions of water with the indole ring also play a significant role in mediating the C≡N stretching frequency. Thus, this study provides a molecular basis for understanding how hydration affects the C≡N stretching band of 5-cyanotryptophan. In addition, an empirical model, which includes interactions of water with both the nitrile and indole groups, is developed for predicting the C≡N stretching vibrational band via molecular dynamics simulations.

It is well known that the C≡N stretching vibration of a nitrile group is sensitive to its environment.^1–4 Thus, several nitrile-derivatized, non-natural amino acids, including p-cyanophenylalanine, cyanoalanine, and cyanylated cyteine, have been used as infrared (IR) reporters of local conformation and/or electrostatics of peptides^5–9 and proteins.^10–12 These applications are primarily based on the premise that the C≡N stretching frequency shifts upon a change in the immediate environment of the corresponding non-natural amino acid. However, recently we have shown that in the case of 5-cyanotryptophan it is the bandwidth of the C≡N stretching vibrational band, instead of its peak frequency, that is more sensitive to the hydration status of the IR reporter.¹³ In fact, the bandwidth of the C≡N stretching vibrational band of 5-cyanoindole (Figure 1), which is the sidechain of 5-cyanotryptophan, is increased from ∼8.7 cm⁻¹ to ∼15.6 cm⁻¹ when the solvent is changed from tetrahydrofuran (THF) to water, whereas the band frequency shows only a slight blue shift (∼4 cm⁻¹). In addition, the C≡N stretching band of 5-cyanoindole in water is also significantly broader than those of other model nitrile compounds (i.e., acetonitrile^1,2,5, p-tolunitrile⁵, and methyl cyanate^14,15).

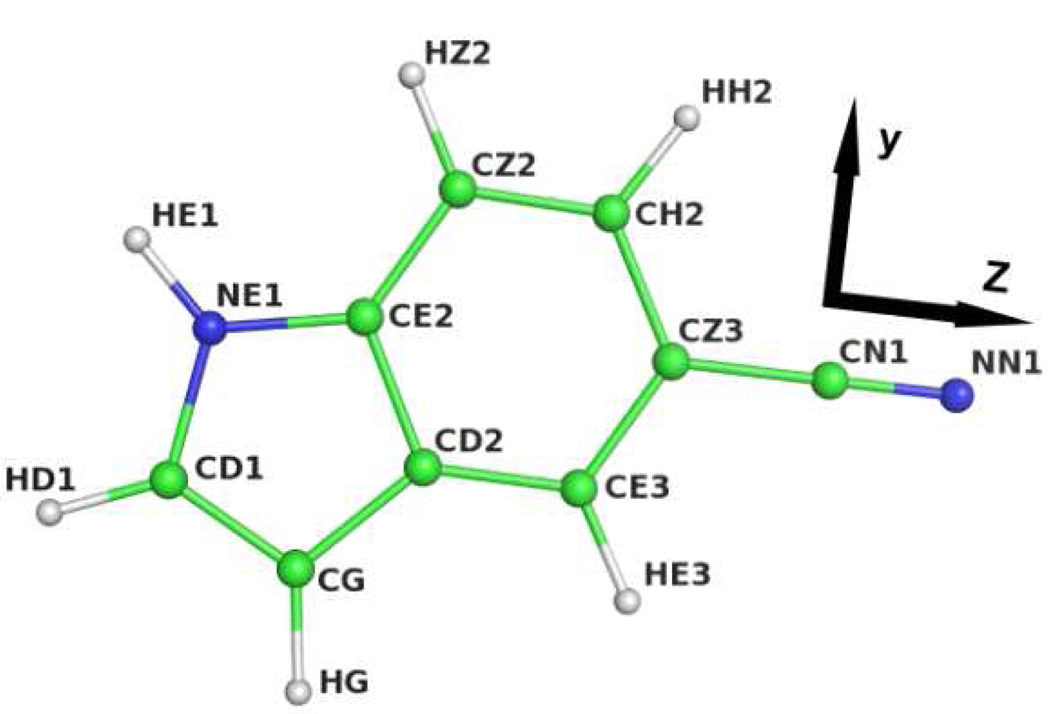
Figure 1.

Atom names in 5-cyanoindole and definition of molecular coordinate system. The x unit vector (not shown) is pointing out of the molecular plane, towards the reader.

Given the range of lifetimes (∼1–5 ps) measured for the C≡N stretching vibration of several related nitrile compounds,^16,17 it seems unlikely that lifetime broadening plays a dominant role in the broadening of the C≡N stretching band of 5-cyanoindole. Instead, it seems more likely that the broadening is caused by the heterogeneous interactions between the bulky indole ring and water molecules. Such a picture is supported by the studies of the groups of Eaton, Reimers, and Cho, which showed that even for acetonitrile (CH₃CN) the C≡N stretching frequency is determined by the precise configuration of water molecules surrounding the nitrile group.^1,2,15,18 For example, a linear arrangement of CH₃CN--HOH (termed σ-bonding with nitrogen lone-pair) results in a blue-shift of the C≡N stretching frequency as compared to its gas phase value, whereas interactions of water molecules with the π-orbital of the C≡N group (termed π-bonding) lead to a red-shift. However, for 5-cyanoindole, besides those interactions between water molecules and the C≡N group, one might expect that the solvation status of the parent molecule, which is comparatively much larger than a methyl group and also contains an extended π-electron system that is electronically coupled to the triple bond of the nitrile group, also plays an important role in determining the peak frequency and band shape of the C≡N stretching vibration. In order to provide a more quantitative description, herein we carry out a theoretical investigation of how interactions of water molecules with 5-cyanoindole influence its C≡N stretching vibration.

The details of the frequency calculations, which are based on methods used in similar studies,^3,15,18–30 are described in the Supporting Information. Briefly, a molecular mechanics (MM) model of 5-cyanoindole was first developed, and subsequently used in a molecular dynamics (MD) simulation of 5-cyanoindole in water. The Born-Oppenheimer potentials of the C≡N stretch were then determined for a set of 5-cyanoindole-water clusters, which were randomly selected from a MD trajectory. These potentials were then fitted to a Morse potential function in order to obtain their quantum mechanical (QM) vibrational frequencies. Finally, an empirical model, which relates the C≡N stretching frequency to its electrostatic environment, was developed.

Specifically, the atomic charges of 5-cyanoindole (Figure 1) were parameterized by achieving a satisfactory agreement between the MM and QM solvent-solute interaction energies. To do so, the internal parameters of 5-cyanoindole (i.e., bond-, angle-, and dihedral-force constants, as well as Urey-Bradley parameters) were based on those of its structural analogs, indole³¹ and 3-cyanopyridine.³² Its bond lengths were determined based on the MPW1B95/6−31++G(d,p) optimized 5-cyanoindole molecule, while its Lennard-Jones parameters were taken from those of indole and acetonitrile.³³ Using the Gaussian 03 software package³⁴, the initial MM atomic charges were then obtained via a CHelpG³⁵ analysis of the electron density of 5-cyanoindole at the MPW1B95/6−31++G(d,p) level of theory, under the constraint that the atomic charges are to reproduce the QM permanent dipole moment of the molecule. The results are summarized in Table S1 (Supporting Information).

To further optimize the initially obtained atomic charges so that the MM interaction energies agree with the QM interaction potentials, a fitting procedure using the following harmonic penalty function³⁶ was then carried out.

$${\chi }^2={\chi }_{inter}^2+{\chi }_{penalty}^2={\displaystyle \sum _{\alpha }{(I{E}_{\alpha }^{MM}-I{E}_{\alpha }^{QM})}^2}+\rho {\displaystyle \sum _i{(q_i^{MM}-q_i^{QM})}^2}$$ (1)

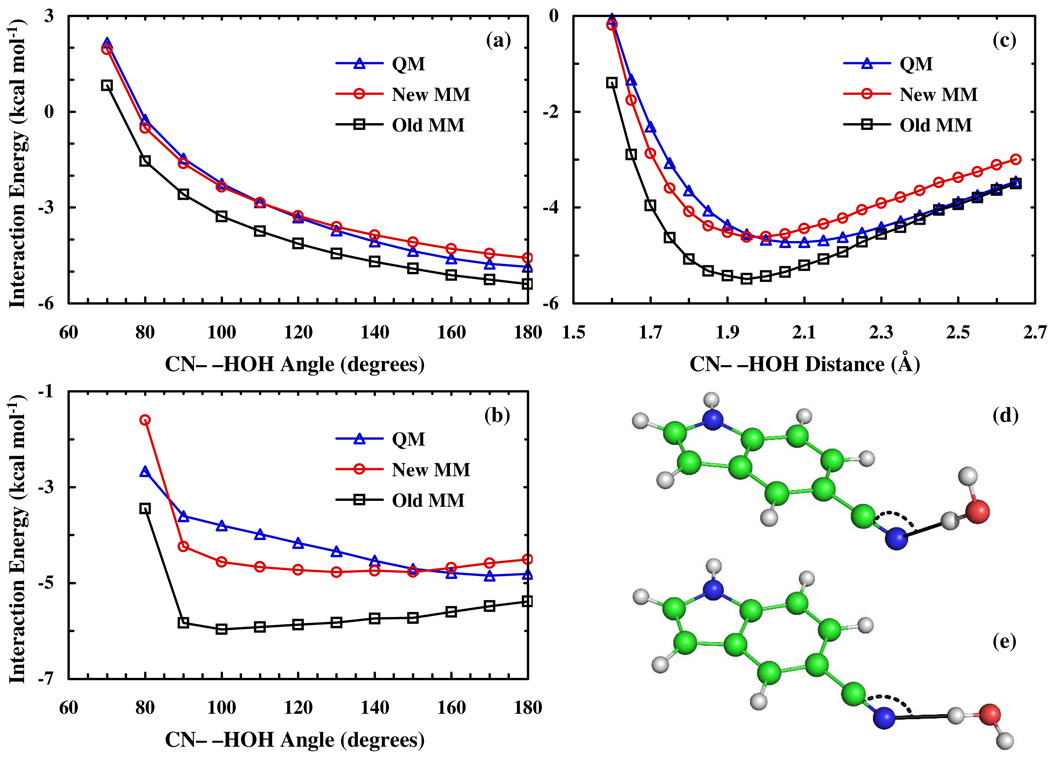
Where $I{E}_{\alpha }^{MM}$ and $I{E}_{\alpha }^{QM}$ represent the MM and QM interaction energies at geometry α of the interaction potential and $q_i^{MM}$ and $q_i^{QM}$ are the MM charge of atom i and the corresponding CHelpG reference charge, respectively. The weighting factor, ρ, of the penalty function was set to a value of 15. Three QM interaction potentials, defined as IE = E(complex) – E(5-cyanoindole) – E(water), were calculated at the MPW1B95/6−311++G(3df,2dp) level of theory. Specifically, the optimization was achieved by considering the following three interaction potentials: (A) A water molecule was placed 2.0 Å away from the nitrile nitrogen with one H–O bond pointing towards the C≡N bond and the other pointing out of the indole ring plane (Figure 2d). The C≡N--H angle was then stepped in 10° increments, moving the water out of the indole ring plane. (B) A water molecule was placed 2.0 Å away from the nitrile nitrogen, within the plane defined by the indole ring (Figure 2e) and with one H–O bond pointing towards the C≡N bond. The C≡N--H angle was then stepped in 10° increments, moving the water within the indole ring plane. (C) A water molecule was placed 1.6 Å from the nitrile nitrogen with one H–O bond pointing towards the C≡N bond and the other pointing out of the indole ring plane. The C≡N--HOH distance was than stepped in 0.05 Å increments from 1.60 to 2.65 Å.

Figure 2.

(a) QM and MM interaction energies between water and 5-cyanoindole as a function of the CN--H angle when the water is bent out of the indole plane (b) and when the water is kept in the indole ring plane. (c) QM and MM interaction energies as a function of the CN--HOH distance with one of the H–O bonds aligned with the nitrile group. Example geometries (CN--H angle = 130°) corresponding to the scans in (a) and (b) are shown in panels (d) and (e), respectively.

Once the charges on the water molecule (O = −0.834 e; H = 0.417 e) and the Lennard-Jones term are given, the Coulomb part of the interaction potential can be optimized by adjusting the MM atomic charges of 5-cyanoindole via minimization of the χ² (eq. 1). As shown (Figure 2), the new MM interaction energies of the optimized force field match the QM interaction potential significantly better than the CHelpG based force field energies, while the optimized charges deviate only slightly from those obtained via QM calculations (Table S1, Supporting Information). Thus, this optimization procedure (i.e., eq. 1) produced a set of charges that is expected to better describe the interactions between water and the C≡N moiety, a pivotal requirement for the correct prediction of its stretching frequency shift upon hydration.^15,18,29,30

Having developed a MM model of 5-cyanoindole, we next sought to establish an empirical model that allows us to determine the localized C≡N stretching frequency in water from MD simulations based on the notion that the vibrational frequency of a localized vibrational mode is related to the local electric field (or potential).^15,18–28 Specifically, we employed a computational procedure that is similar to those used by Skinner and coworkers^21–23 as well as by Corcelli and coworkers.^29,30 First, we randomly selected 40 5-cyanoindole-water clusters from a 1 ns MD simulation at 300 K and 1 atm (details of the NAMD simulation³⁷ are given in the Supporting Information). As shown (Figure S1, Supporting Information), these clusters contain 5–17 water molecules (12 on average) and were further divided into two subsets, Set-A and Set-B. For Set-A, wherein the indole ring is considered dehydrated, only those water molecules that have at least one atom located within 4.5 Å of the NN1 atom of the indole ring are included in each cluster. On the other hand, the clusters in Set-B are composed of water molecules that have at least one atom located within 3.5 Å of the NN1, NE1, or CD2 atom of the indole ring (atom names are given in Figure 1). Thus, the indole ring in Set-B is regarded as partially hydrated. In the following we will consider Set-A and Set-B as a common set. Second, DFT calculations were carried out on these clusters using the Zhao-Truhlar hybrid meta functional MPW1B95³⁸ in conjunction with the 6−31++G(d,p) basis set. It has been shown that this level of theory adequately describes the weak interactions between water and the indole ring.³⁹ For each cluster, the potential energy of the system as a function of the C≡N bond length (from 1.0 to 1.4 Å in increments of 0.05 Å) was determined via DFT calculations wherein all other atomic coordinates were fixed. Third, the obtained potential energy curves were then fitted to a Morse oscillator model, allowing analytical determination of the underlying anharmonic frequencies. Fourth, an empirical model relating the vibrational frequency to the electrostatic field components on the nitrile group was obtained by least-square fitting the following equation to the ab initio frequencies: ${\omega }_{emp}={\displaystyle {\sum }_{a,i}{c}_i^a{E}_i^a}+{\omega }_{gas}$, where $E_i^a$ is the Cartesian electric field component i at a site a on the molecule, $c_i^a$ is a constant of proportionality, and ω_gas corresponds to the gas phase value of the C≡N stretching frequency of 5-cyanoindole, which was calculated to be 2392.3 cm⁻¹ using an isolated 5-cyanoindole molecule and the procedure described above. Finally, the electric fields arising from the partial charges of water were calculated using an in-house written code within the VMD software environment,⁴⁰ and the proportionality constants $(c_i^a)$ were determined by the multivariate least-square fitting method.

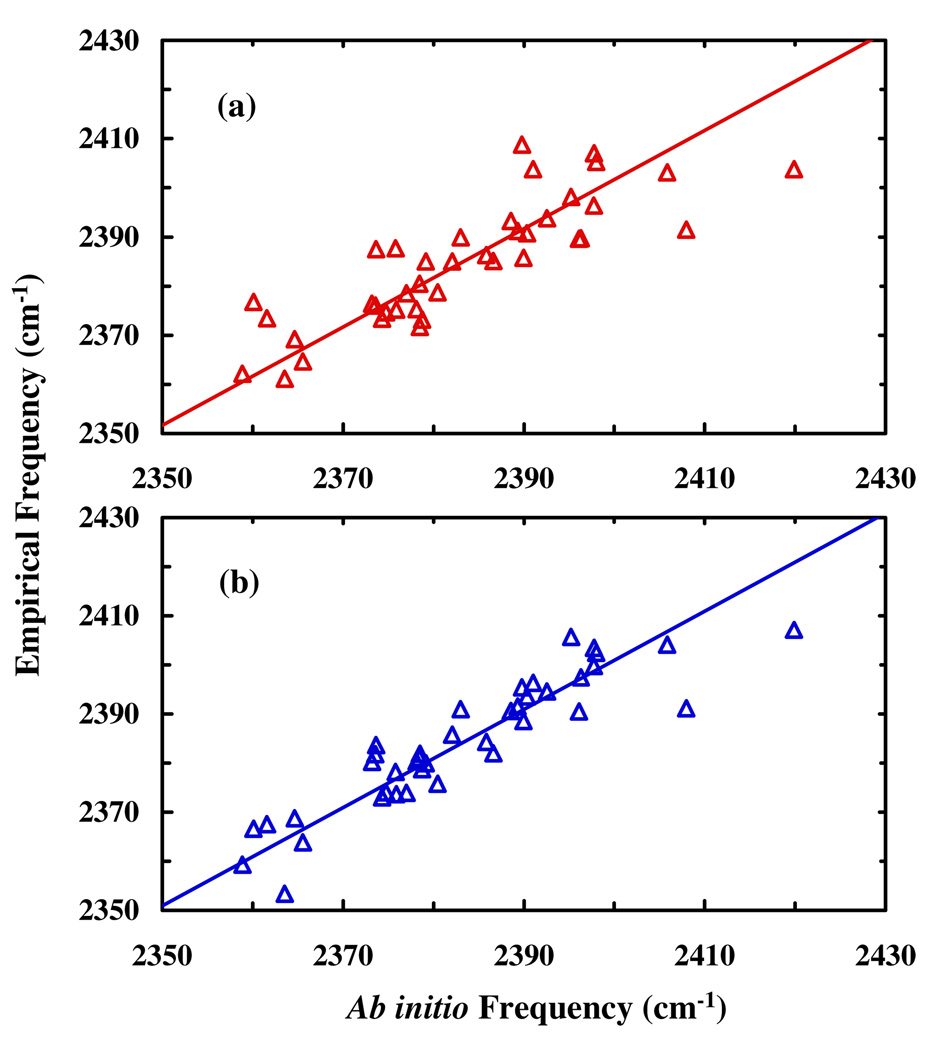
As shown (Figure 3a), fitting the 40 ab initio frequencies obtained from the vibrational analysis of the clusters with a model that only includes the electric field components on the nitrile group in the direction of the vibrational transition dipole, i.e.,

$${\omega }_{emp}=c_z^{CN1}{E}_z^{CN1}+c_z^{NN1}{E}_z^{NN1}+{\omega }_{gas}$$ (2)

yields a relatively poor correlation coefficient (R²) of 0.64 and a root mean square deviation (rmsd) of 7.6 cm⁻¹ between empirical and ab initio frequencies. However, when the model was refined to include the z-component of the electric field at the center of the six-membered ring, $E_z^{6m}$, i.e.,

$${\omega }_{emp}=c_z^{CN1}{E}_z^{CN1}+c_z^{NN1}{E}_z^{NN1}+c_z^{6m}{E}_z^{6m}+{\omega }_{gas}$$ (3)

the resultant correlation (Figure 3b) is significantly improved, yielding a correlation coefficient of 0.81 and a rmsd of 5.8 cm⁻¹ with $c_z^{CN1}=4554.4{\text{cm}}^{-1}/\mathrm{a}.\mathrm{u}.$, $c_z^{NN1}=-1652.2{\text{cm}}^{-1}/\mathrm{a}.\mathrm{u}.$, and $c_z^{6m}=1989.7{\text{cm}}^{-1}/\mathrm{a}.\mathrm{u}.$ Taken together, these results indicate that the electric field component at a point on the ring but distant from the nitrile group could have a significant effect on its vibrational frequency. While a model including only the electric field localized at the C≡N group could also yield a good correlation, it requires at least six electric field components to produce a comparable correlation (Table S2, Supporting Information). Thus, these findings show that by considering the electric field away from the C≡N group it is possible to fit the ab initio frequencies with a minimum number of parameters.

Figure 3.

Ab initio frequency versus the empirical frequency determined from (a) the two-component and (b) the three-component empirical models. The correlation coefficients (R²) are 0.64 and 0.81 for the data presented in (a) and (b), respectively.

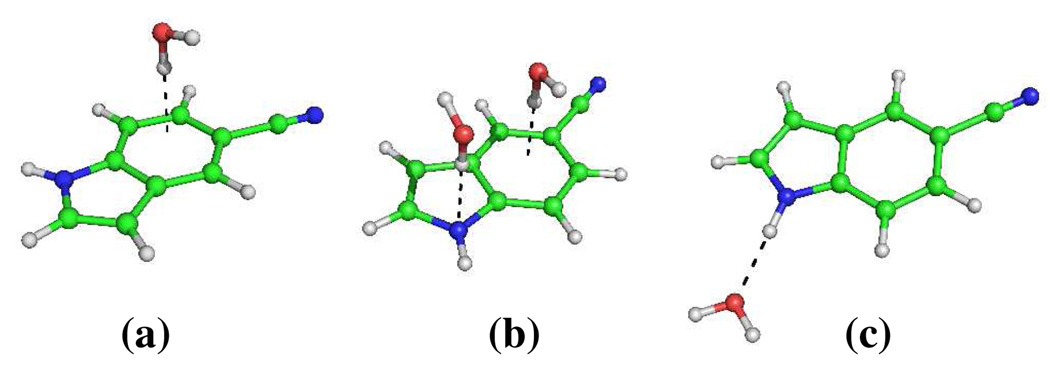
To further verify that the indole ring indeed plays a significant role in mediating the stretching frequency of the nitrile group, we have investigated the specific effect of one or two water molecules placed at different positions with respect to the ring, as shown in Figure 4. As expected, we found that the C≡N stretching frequency of all three clusters shows a significant shift (i.e., Δω = ω_cluster −ω_gas ≠ 0) from that of the unsolvated ring with Δω = 3.9, 8.8 , and −4.0 cm⁻¹ for (a), (b) and (c), respectively. Thus, these results, which indicate that Δω is sensitive to the position and orientation of the water molecule(s), corroborate the notion that the solvent-indole interaction is a significant determinant of the C≡N stretching frequency.

Figure 4.

Three model 5-cyanoindole-water clusters. In (a) and (b), the distance between the closest water hydrogen and the indole ring plane is 2.4 Å, whereas in (c) the H₂O--HN distanceis 2.0 Å.

Having determined a set of parameters $(c_i^a)$, eq. 3 was then used to calculate the C≡N stretching frequency of individual snapshots along the 1 ns MD trajectory of 5-cyanoindole in water. The resultant frequencies show a Gaussian distribution with a standard deviation of 13.5 cm⁻¹ and a mean that is −9.7 cm⁻¹ red-shifted with respect to ω_gas. The latter suggests that the current model correctly predicts the trend of the frequency shift of the C≡N stretching vibration upon hydration as the nitrile stretching frequency is typically red-shifted with respect to the gas-phase value. For example, the C≡N stretching frequency of benzonitrile is ∼2244 cm⁻¹ in the gas-phase,⁴¹ which shifts to ∼2235 cm⁻¹ in water.¹⁶ Unfortunately, for the present case a more quantitative assessment of the predicted shift cannot be made at this time because an experimental value for ω_gas for 5-cyanoindole is currently not available.

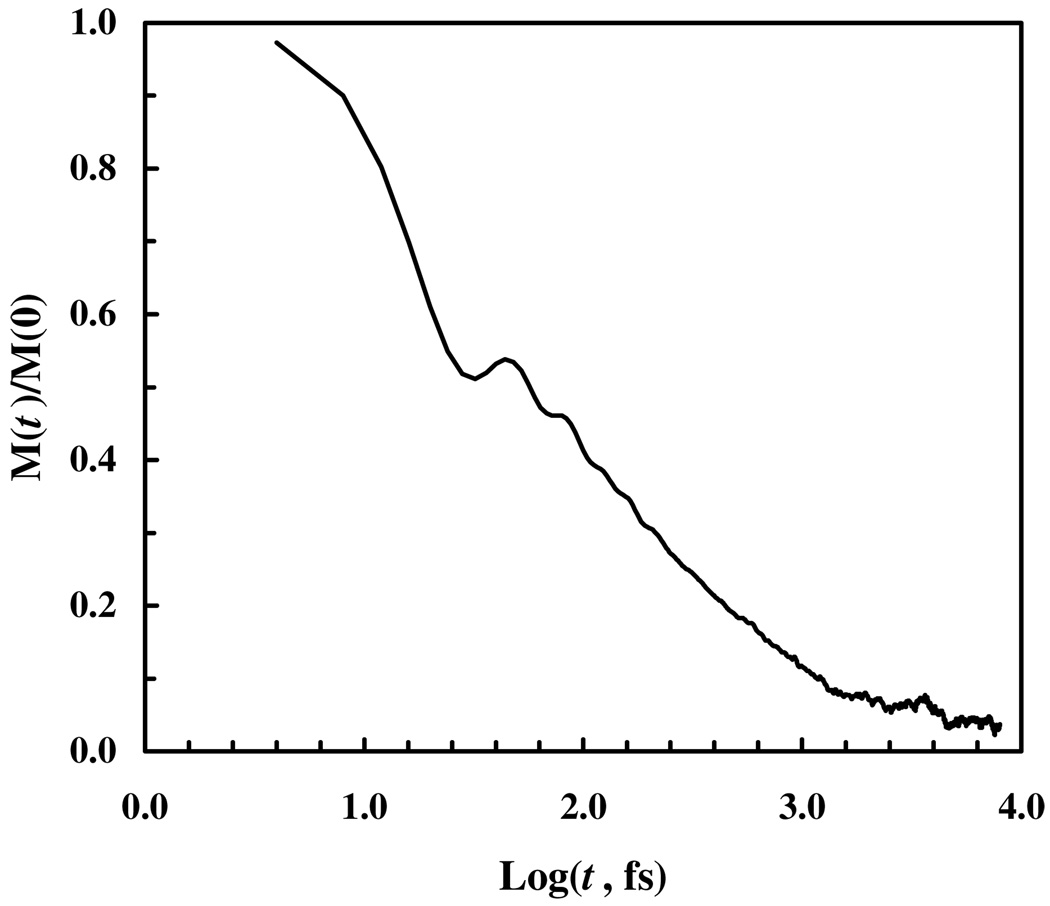
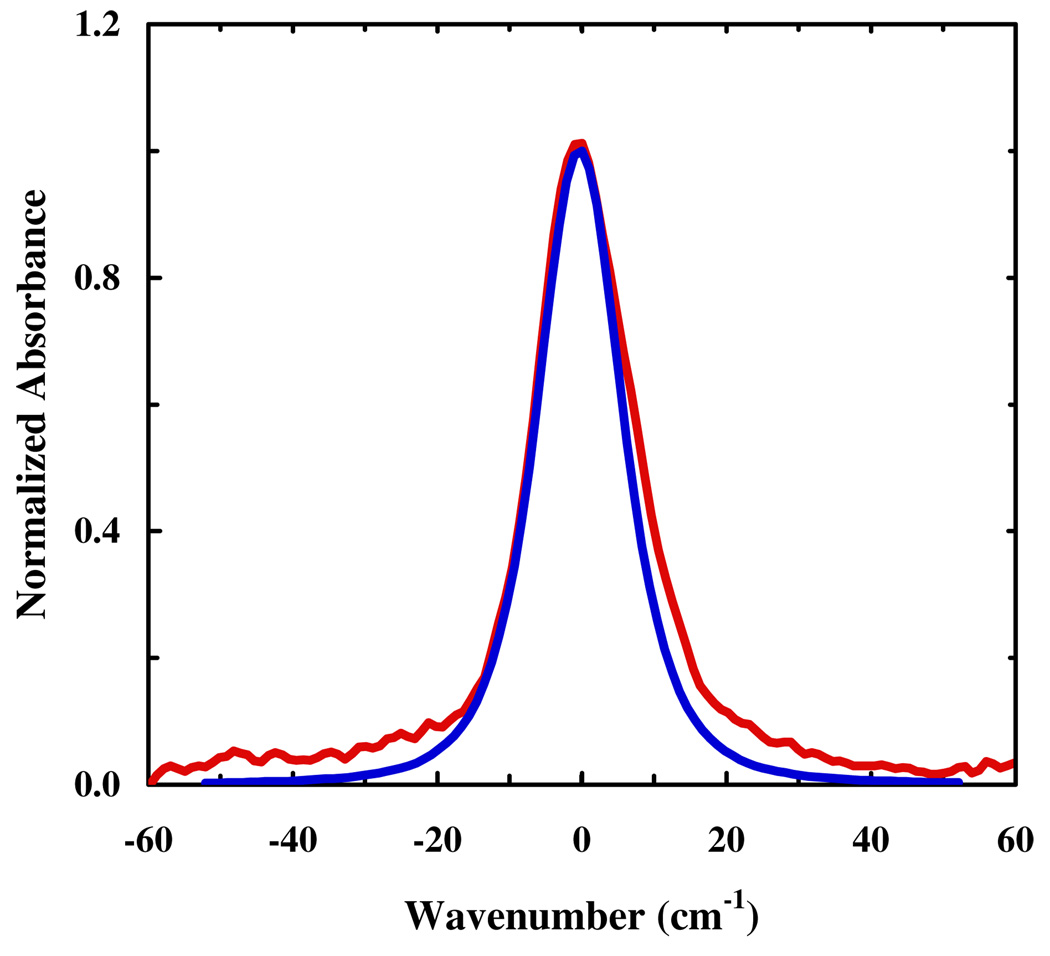
Finally, we calculated the IR band of the C≡N stretching vibration from the frequency-frequency correlation function, $M(t)=\langle \delta \text{Ω}(t)\delta \text{Ω}(0)\rangle$ with $\delta \text{Ω}(t)=2\pi c\left\{\delta \tilde{v}(t)-\langle \delta \tilde{v}\rangle \right\}$. As shown (Figure 5), the (normalized) autocorrelation function decays rapidly in a bimodal fashion, similar to that observed for other nitrile compounds.^15,16,17,30 The vibrational pure dephasing constant, $T_2^{*}=1/{\displaystyle {\int }_0^{\infty }dtM(t)}$, was estimated to be 0.25 ps. The variance, $\text{Δ}\equiv \sqrt{M(0)}$, and correlation time, $\tau \equiv {\displaystyle {\int }_0^{\infty }dtM(t)/M(0)}$, of the C≡N stretching frequency fluctuations of 5-cyanoindole were found to be 2.53 ps⁻¹ and 0.61 ps, respectively. Thus, the spectrum is neither in the homogeneous nor in the inhomogeneous regime. Therefore, the vibrational spectrum was calculated using a semiclassical approximation^42–44 to $I(\omega )\sim {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}dt{e}^{i\omega t}\langle \mu (t)\cdot \mu (0)\rangle }$, where μ is the quantum mechanical dipole operator (see Supporting Information for details). As shown (Figure 6), the bandwidth of the simulated spectrum is in very good agreement with that determined experimentally. However, this agreement must be cautiously interpreted. First, the vibrational lifetime of 5-cyanoindole is currently not available. Thus, we have assumed a vibrational lifetime of 5 ps. Second, the production run of the simulation was carried out in the NPT ensemble, which may adversely affect the quality of the frequency-frequency time correlation function.

Figure 5.

Normalized frequency-frequency correlation function, calculated from the C≡N frequency trajectory.

Figure 6.

Comparison between the experimentally measured (red) and simulated (blue) C≡N stretching bands of 5-cyanoindole.

Moreover, it is worth noting that the present electrostatic map may not be applicable to 5-cyanotryptophan, especially when it locates in a heterogeneous environment of proteins or membranes, as this map incorporates interactions that are specific to water. Although such “solvent-specific” maps have been used within the context of peptides,⁴⁵ alternative approaches such as those developed by the groups of Corcelli,^29,30 Mukamel,^24–26 , Jansen²⁸ and Kurnikova⁴⁶ may be more appropriate.

In conclusion, we demonstrate that interactions between water and the indole ring make an important contribution to the broadening of the C≡N stretching band of 5-cyanoindole in aqueous solution. Thus, this study provides a molecular basis to support the notion that 5-cyanotryptophan is a useful IR probe of local hydration status of proteins, and also indicates that the chemical moiety to which the C≡N group is attached may need to be considered in the development of electrostatic maps for calculation of the C≡N stretching frequencies.