Robotic Motion Compensation for Beating Heart Intracardiac Surgery

Abstract

3D ultrasound imaging has enabled minimally invasive, beating heart intracardiac procedures. However, rapid heart motion poses a serious challenge to the surgeon that is compounded by significant time delays and noise in 3D ultrasound. This paper investigates the concept of using a one-degree-of-freedom motion compensation system to synchronize with tissue motions that may be approximated by 1D motion models. We characterize the motion of the mitral valve annulus and show that it is well approximated by a 1D model. The subsequent development of a motion compensation instrument (MCI) is described, as well as an extended Kalman filter (EKF) that compensates for system delays. The benefits and robustness of motion compensation are tested in user trials under a series of non-ideal tracking conditions. Results indicate that the MCI provides an approximately 50% increase in dexterity and 50% decrease in force when compared with a solid tool, but is sensitive to time delays. We demonstrate that the use of the EKF for delay compensation restores performance, even in situations of high heart rate variability. The resulting system is tested in an in vitro 3D ultrasound-guided servoing task, yielding accurate tracking (1.15 mm root mean square) in the presence of noisy, time-delayed 3D ultrasound measurements.

1. Introduction

Real-time 3D ultrasound (3DUS) imaging has enabled new surgical procedures within the beating heart that are not possible with current endoscopic technology (Cannon et al. 2003; Suematsu et al. 2005). These procedures eliminate the need for cardiopulmonary bypass and its attendant side effects, such as increased stroke risk, decline in cognitive performance, delay of neural development in children, and damage to the major vessels (Zeitlhofer et al. 1993; Bellinger et al. 1999; Murkin et al. 1999). Beating heart procedures also make the realtime evaluation of structural modifications possible while the heart continues to function. The benefits of such procedures are clear; however, the rapid motion of the heart poses serious challenges to the surgeon. This is especially true of procedures involving intracardiac structures such as the mitral valve, which recoils rapidly with every heartbeat. In order to realize the potential of minimally invasive beating heart mitral valve procedures, the difficulty of manipulating tissues undergoing fast motion must be addressed.

One appealing approach to the beating heart repair of intracardiac structures is robotic assistance to the surgeon. In this setting, the surgeon uses a handheld robotic instrument that tracks the fast motion of the heart so that the operation is performed on an effectively stopped heart (i.e. as if the heart were not beating). This is similar to previously proposed motion compensation systems in which the surgeon could interact with the heart on a supported moving platform (Trejos et al. 1999) or teleoperate on a “virtually” stopped heart (Nakamura et al. 2001; Ortmaier et al. 2005; Ginhoux et al. 2006; Bebek and Cavusoglu 2007). This approach should be distinguished from the recent clinical application of commercial surgical robots in performing minimally invasive mitral valve repair, with a stopped heart and cardiopulmonary bypass (Reichenspurner et al. 2005; Woo et al. 2006). Prior work on beating heart motion compensation has largely focused on the development of robust tracking controllers intended for multi-degree-of-freedom (DOF) robot manipulators and extracardiac procedures. However, implementing a full six-DOF robot for intracardiac applications has a number of challenges, including the development of a manipulator with sufficient mechanical bandwidth, creating a wrist that can operate in the restricted workspace within the beating heart, and ensuring safety for a complex manipulator system. These requirements are far beyond the capabilities of current commercial surgical robots.

Another major consideration for beating intracardiac procedures is guidance inside of the heart, which requires imaging tissue through blood in real-time. Currently, 3DUS is the only technology that has these capabilities: endoscopic systems are obscured by blood, and computed tomography and magnetic resonance imaging are not yet able to image at the speeds necessary for beating heart surgery. 3DUS also eases the difficulties in spatial perception experienced with traditional 2D ultrasound (Cannon et al. 2003). However, for all of its advantages, the acquisition and processing of 3DUS volumes introduces a substantial time delay, during which time the annulus can recoil over the majority of its trajectory (Novotny 2007). Servoing a robot with these measurements directly would result in large errors that could damage the valve and nearby structures.

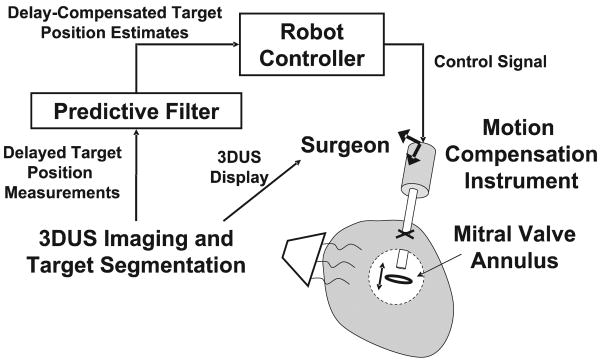
In this paper we describe a robotic motion compensation system that is compatible with the space limitations inside the heart and also counteracts the delays and noise in 3DUS imaging. The system comprises an actuated one-DOF instrument commanded by a predictive filter (Figure 1). The surgeon can use this system in procedures where the motion of the cardiac tissue is largely in a single direction. As will be shown shortly, this includes the motion of the mitral valve annulus, and thus the system can be used for beating heart mitral annuloplasty: the most frequently performed element of mitral valve repair. The instrument consists of a linear actuator capable of following the major component of the annulus motion. The filter that is used to command the actuator, an extended Kalman filter (EKF), can accurately track and predict annulus motion in the presence of noise by exploiting quasiperioidicity in its motion. It is used to feed-forward the trajectory of a cardiac target to the instrument controller for accurate synchronization despite time delays.

Fig. 1.

Motion compensation system. Time-delayed position measurements of the target are provided to a filter which uses prediction to compensate for delay. These are fed-forward to the controller of the one-DOF MCI to synchronize with the target motion. The surgeon holds the instrument and navigates its end-effector to the target using 3DUS imaging.

In the following, we first characterize the motion of the mitral annulus to determine the tracking performance requirements of the system. Next, we present the design of the actuated one-DOF motion compensation instrument (MCI). We then describe the EKF and several other predictive filtering methods and compare them in simulation. Two subsequent user studies evaluate the efficacy of the robotic motion compensation system against traditional non-tracking tools in a simulated in vitro surgical task. Furthermore, they validate the robustness of the system in situations of high noise, time delay and heart rate variability. Finally, we measure the position tracking accuracy of the system in a series of 3DUS-guided motion synchronization experiments.

2. Motion Analysis of the Mitral Valve Annulus

To guide the development of the motion compensation system, the motion of the mitral valve annulus was analyzed using ultrasound image data such as that available in surgery for real-time guidance. A transthoracic 3DUS image-volume sequence of the mitral annulus was acquired¹ at 24 Hz (SONOS 7500, Philips Medical Systems, Andover, MA, USA). This raw 3DUS data was manually segmented to extract mitral annulus trajectory information. For each 3D volume sample, a minimum of 50 data points were selected from the mitral valve annulus and used to locate the annulus centroid. Repeated for each time-stamped data frame, this process generated a record of the annulus centroid position over the cycle of the heartbeat. As this manual segmentation process was extremely labor intensive, only data from two patients were analyzed.

In order to specify hardware design constraints for the motion compensation instrument, position, velocity, and acceleration along the major axis of the valve's motion were extracted from these data. Using singular value decomposition (SVD), a line was fit to each data set. The relative sizes of the singular value associated with each orthonormal basis vector generated by SVD (i.e. 21.75, 5.49, 2.97) suggest that the valve's motion is strongly constrained to a principal axis (Figure 2). Furthermore, working with sheep, Gorman et al. (1996) generated tracking data which indicates that rotational movements around this primary axis are also negligible. Subsequent analysis presented here will therefore focus on the component of motion along this primary axis.

Fig. 2.

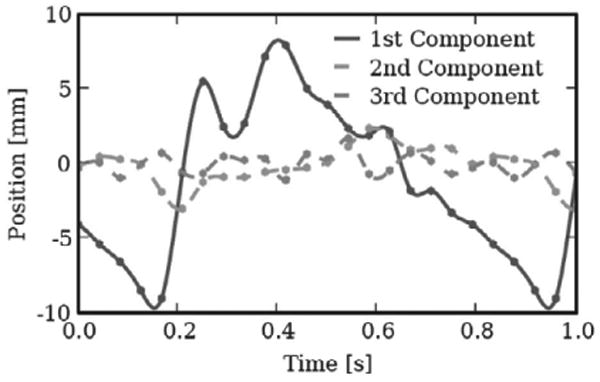
Orthogonal views of 3DUS tracking data centroid positions plotted in principal component axes. The axes are scaled in millimeters. Note the dominance of motion in the first component.

Velocity and acceleration were estimated by considering the relative motion between 3DUS data samples. This method provided mitral valve velocity and acceleration maxima of approximately 210 mm s⁻¹ and approximately 3.8 m s⁻², respectively, with a total travel of approximately 20 mm at a heart rate of 76 beats per minute (bpm). While only two subjects were analyzed in this fashion, work by Kamigaki and Goldschlager (1972) on the mitral valve leaflets reports similar velocity and amplitude results.

The major frequency components of motion were also reviewed using spectral decomposition (Figure 3). This analysis indicates major motion components at 1.3, 2.6, and 5.2 Hz with further components of decreasing amplitude at higher frequencies. This is consistent with the findings of Nakamura et al. (2001) which show dominant frequency components of 1.5 and 3.0 Hz in the motion of porcine epicardium. Ginhoux et al. (2006) found the same major frequency components in the motion of porcine epicardium. This paper also noted higher-frequency transients that it deemed significant and concluded that a 25 Hz sampling rate would be insufficient to track the motion of the epicardium with high precision (Ginhoux et al. 2006). Bebek and Cavusoglu (2007) found similar frequency components, but concluded that the motion could be adequately characterized using lower sampling frequencies, i.e. 26 Hz.

Fig. 3.

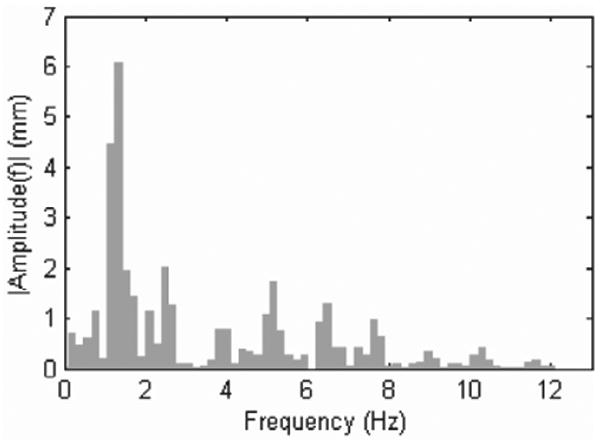
3DUS tracking data spectral decomposition. Motion amplitudes decrease quickly with increasing frequency.

3. Motion Compensation Instrument Design

The MCI developed here is an actuated handheld or robot-mounted minimally invasive tool to aid surgeons in working on the moving mitral valve. Rather than attempting to correct for motion components in all three dimensions, the objective was to develop a device that could compensate for the major component of motion and allow surgeons and passive tissue compliance to counter the slow or relatively minor motions along the remaining two axes. The surgical procedure that we are developing for this purpose is a modification of a minimally invasive beating heart procedure for the repair of atrial–septal defects (Vasilyev et al. 2006). In the new procedure, the instrument will be inserted through the left atrial appendage and controlled by a pursestring suture. A custom annuloplastry ring will be inserted through an adjacent incision and positioned over the mitral annulus (Figure 4). The actuated instrument will be tipped with a modified 14 gauge needle (OD = 0.083 in) that will deploy anchors to “staple” the annuloplasty ring to the annulus (Wagner et al. 2006). The surgeon will then maneuver the ring and anchor driver to the appropriate locations over the annulus and repeatedly fire the anchor driver to attach the ring and reshape the annulus.

Fig. 4.

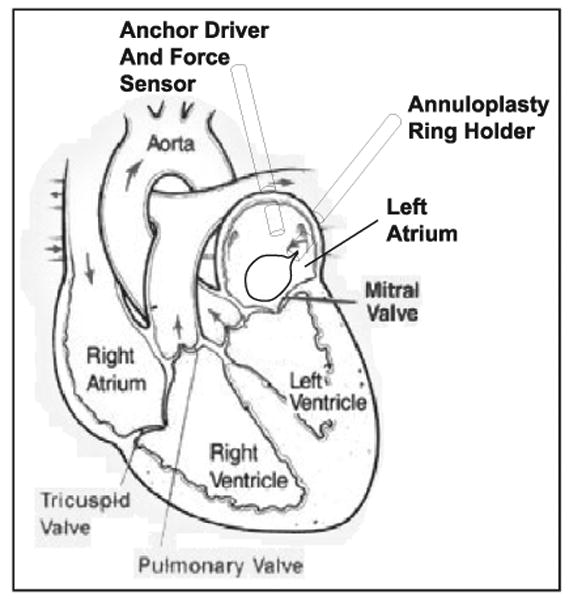
Diagram of proposed surgical procedure. The anchor driver approaches along the valve's axis, which corresponds to the valve's major component of motion.

The selection of the mechanical mechanism to follow the linear motion component of the mitral valve annulus was guided by the clinical 3DUS trajectory analysis from Section 2. The high velocity and acceleration requirements lead to a linear motor-based design which benefits from low friction and low moving mass (Figure 5). This design format also produces a surgical tool similar in design and function to typical endoscopic tools, supported by a port and maneuvered by hand. Consequently, the MCI will be intuitive to operate for trained endoscopic surgeons.

Fig. 5.

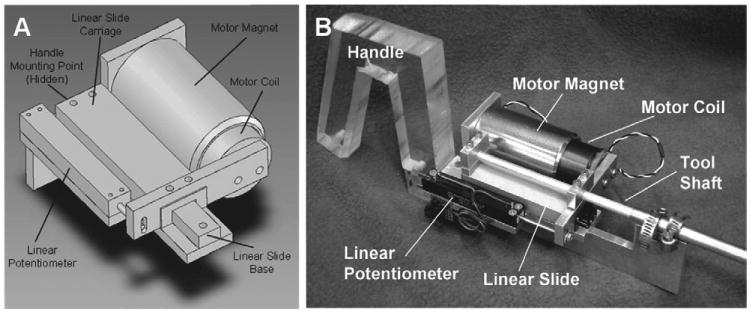
MCI design and prototype. A, MCI actuation package. The MCI may be mounted by its base (at the upper left of the image) to a robot or handle. The surgical anchor driver is mounted on the linear slide carriage. B, MCI hardware prototype.

The MCI uses a voice coil motor (NCC20-18-020-1X, H2W Technologies, Inc., Valencia, CA, USA) and a high linearity potentiometer (P3 America, San Diego, CA, USA) for position sensing. These components are mounted on a linear ball-bearing stage (BX4-3, Tusk Direct, Inc., Bethel, CT, USA). The MCI prototype has a 5.4 cm range of motion and is powered by a linear power amplifier (BTA-28V-6A, Precision MicroDynamics, Victoria, BC, Canada). PID servo control is implemented in a 1 kHz servo loop on a personal computer under Windows XP The MCI is interfaced to this computer through a data acquisition card (PCI-60-40E, National Instruments, Corp., Austin, TX, USA).

The resulting system has the characteristics required to track the mitral valve. The MCI has demonstrated velocities and accelerations as high as approximately 290 mm s⁻¹ and approximately 17.5 m s⁻², respectively. Controller gains were hand tuned to achieve good stiffness and response. To avoid potentially dangerous overshoot and instability, the system is overdamped. The tool has a static stiffness of 0.23 N mm⁻¹ and a friction force less than 0.009 N. The system's frequency response is similarly adequate for the tracking task (Figure 6). The system has a −3 dB point of 20.6 Hz and roll-off rate of 40 dB per decade. The potentiometer on the MCI is capable of measuring position with a root mean square error (RMSE) of less than 0.01 mm. The system is capable of maintaining stationary at a commanded position with a RMSE of 0.009 mm.

Fig. 6.

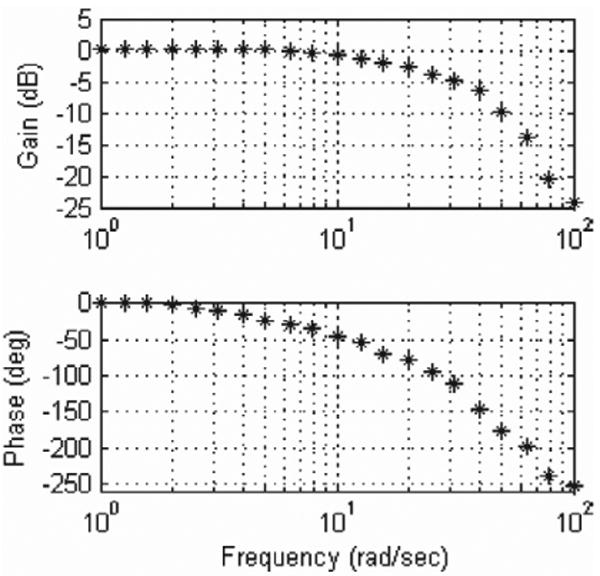
Frequency response of the MCI. The system is overdamped and has a −3 dB point of 20.6 Hz.

The tracking abilities of the MCI were demonstrated by commanding the system to follow the motion of a mitral valve at 60 bpm (Figure 7). Mitral motion was determined from the 3DUS data above (Figure 2). The MCI reliably replicated the motion profile of the valve with an effective delay of 14 ms.

Fig. 7.

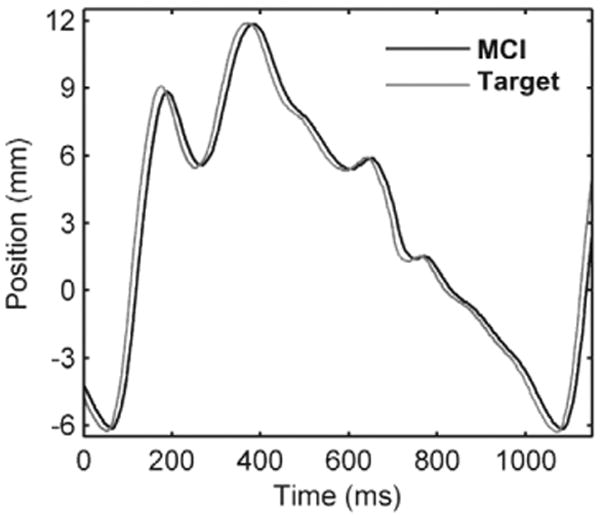
The MCI tracking a simulated mitral valve trajectory. The MCI motion profile closely mimics that of the target with an approximately 14 ms delay.

4. Time Delay Compensation

The time delay that is intrinsic to 3DUS makes direct servoing of the MCI from this signal potentially dangerous. A previous characterization of the acquisition, transmission, and computation times for 3DUS estimated delays of approximately 70 ms, a sufficient amount of time for the mitral valve annulus to traverse the majority of its path (Novotny 2007). For the purposes of illustration, an example of the error for MCI tracking a mitral valve target with a 75 ms measurement delay is shown in Figure 8. The rapid recoil of the valve associated with ventricular relaxation (100–200 ms in Figure 8) results in a large (approximately 14 mm) tracking error that would cause the instrument to pierce and damage the tissue target.

Fig. 8.

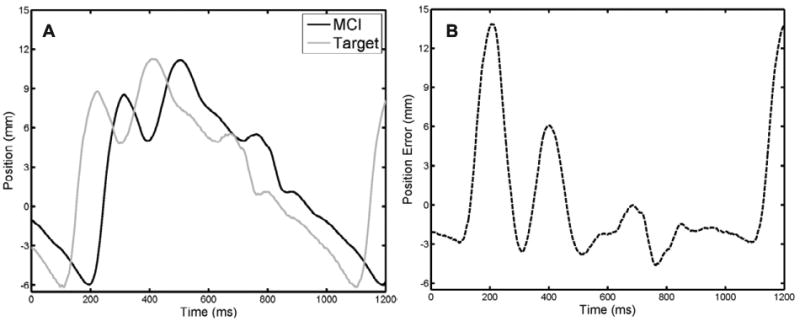
MCI tracking of a mitral valve target with 75 ms measurement delay. A, MCI and target positions. B, Tracking error. Note that the additional 14 ms response time of the MCI yields an effective delay of 89 ms. Maximum and RMS tracking errors are 14.49 and 4.60 mm, respectively.

4.1. Predictive Filters

To avoid this outcome, we exploit the near periodicity of the mitral valve trajectory to predict its path and hence compensate for time delay. However, such predictions must be made in the presence of measurement noise and a potentially variable heart rate. Here we describe and evaluate several predictive filtering methods that can be employed for delay compensation in this setting: an autoregressive (AR) filter, a fading memory AR filter, and an EKF with a quasiperiodic motion model. The AR filter has previously been applied by Nakamura et al. (2001) in a spectral analysis of heart motion for motion compensation in coronary artery bypass graft (CABG) procedures. In principle, this method is equivalent to the adaptive harmonic filter bank used by Ginhoux et al. (2006) for CABG and has its attendant assumption of a fixed heart rate. The fading memory AR filter overcomes this limitation despite using the same model by exponentially discounting the measurements supplied to the filter, thereby allowing it to adjust to more recent information. This approach has been used for motion synchronization in CABG by Franke et al. (2007). In contrast, the EKF permits variations to heart rate by directly accounting for it in a time-varying Fourier series model. A similar model was employed by Riviere et al. (1998) in the weighted Fourier linear combiner (WFLC) estimator for CABG; however, unlike the EKF, this method does not explicitly model noise. Ortmaier et al. (2005) has evaluated other non-linear prediction techniques for CABG such as artificial neural networks and an estimator based on Takens theorem.

4.1.1. AR Model with Least Squares Estimator

Fixed-rate mitral valve motion can be modeled as an n -order AR model

$$y\left[k\right]=\text{∑}_{i=1}^n{a}_{i}y\left[k-i\right],$$ (1)

where α_i, i ∈ {1,…, n}, are the model coefficients and y[k] is the target position at time sample k. Note that rather than explicitly assuming periodicity in the target motion, this model predicates that the kth position can be expressed as a linear combination of the previous n positions.

In order to predict the target position, the model coefficients and order must be estimated. The first can be achieved in realtime using the recursive covariance method estimator. Denoting z[k] = y[k]+ν[k] as the noise-corrupted position measurement at time sample k with $\nu [k]\sim \mathcal{N}(0,{\sigma }_R^2)$, this estimator is expressed compactly in matrix form as

$$\begin{array}{l}\mathit{\text{Z}}[k]=[z[k-n-1],\dots ,z[k-1]],\\ \mathit{\text{R}}[k]=\mathit{\text{R}}[k-1]+\mathit{\text{Z}}{[k]}^{\text{T}}\mathit{\text{Z}}[k],\end{array}$$ (2)

$$\begin{array}{l}\widehat{\mathit{\alpha }}[k]=\widehat{\mathit{\alpha }}[k-1]+\mathit{\text{R}}{[k]}^{-1}\mathit{\text{Z}}{[k]}^{\text{T}}\times (z[k]-\mathit{\text{Z}}\widehat{\mathbf{\alpha }}[k-1]),\end{array}$$ (3)

with initial conditions R[0] = 0 and α̂[0] = 0. An appropriate AR model order was determined using the Akaike information criteria on the mitral valve annulus trajectory in Figure 2, yielding n = 30. Predicted target locations, ŷ[k], can be obtained through evaluation of (1). In addition, the target trajectory can be interpolated from its inherent measurement rate (i.e. 28 Hz, a typical 3DUS frame rate) to the higher control rate of the robot using the Whittaker–Shannon interpolation formula.

4.1.2. AR Model with Fading Memory Estimator

Imperfect periodicity can cause the AR model coefficients to change over time. In this situation, it can be useful to preferentially weight recent measurements over those in the past: otherwise the filter becomes progressively less responsive to new data and (3) does not update α̂ because R[k]⁻¹ Z^T → 0 as k → ∞. Exponential weighting of previous measurements in the iterative least squares estimator is achieved through a simple modification of (2):

$$\mathit{\text{R}}[k]=f\mathit{\text{R}}[k-1]+\mathit{\text{Z}}{[k]}^{\text{T}}\mathit{\text{Z}}[k],$$

where 0 < f ≤ 1 is the so-called fading factor. Choosing f = 1 recovers the estimator of Section 4.1.1 while choosing f → 0 increases the speed by which previous measurements are discounted. To distinguish between the two estimators, we term the former the AR filter and the latter the fading AR filter for the remainder of this section. As can be imagined, reducing the contribution of previous measurements (f < 1) can be desirable if the trajectory evolves through time, although doing so incurs increased estimation error when the trajectory is not time varying.

4.1.3. Time-varying Fourier Series Model with EKF

The spectral analysis of mitral valve annulus motion from Section 2 suggests that its motion may be approximated by a limited number of harmonics. Consider a perfectly periodic motion model obtained by an m-order Fourier series with a constant offset

$$y(t)=c+\sum _{i=1}^m{r}_{i}sin(i\omega t+{\phi }_i),$$ (4)

where y(t) is the position in ultrasound coordinates, ω is the heart rate, c is the constant offset, and r_i and ϕ_i are the harmonic amplitudes and phases, respectively. Accurate modeling of quasiperiodicity requires a more flexible model in which the heart rate and signal morphology can evolve over time. Using the parametrization of Parker and Anderson (1990), the trajectory can be expressed as the following time-varying Fourier series

$$y(t)=c(t)+\sum _{i=1}^m{r}_i(t)sin{\theta }_i(t),$$ (5)

where ${\theta }_i(t)=i{\int }_0^t\omega (\tau )d\tau +{\phi }_i(t)$ and all other parameters are the time-varying equivalents to those in (4).

Defining the state vector x(t) ≜ [c(t), r_i(t), ω(t), θ_i(t)]^T, i ∈ {1,…, m} and assuming that c(t), r_i (t), ω(t), and ϕ_i (t) evolve through a random walk, the state space model for this system is

$$\begin{array}{l}\mathit{\text{x}}(t+\Delta t)=\mathit{\text{F}}(\Delta t)\mathit{\text{x}}(t)+\mathit{\mu }(t)\\ z(t)=h(\mathit{\text{x}}(t))+\nu (t),\end{array}$$

where

$$\mathit{\text{F}}(\Delta t)=\left[\begin{array}{cccccc}{\mathit{\text{I}}}_{m+1}& & & & \mathbf{0}& \\ & 1& & & & \\ & \Delta t& 1& & & \\ \mathbf{0}& 2\Delta t& 0& 1& & \\ & ⋮& & & \ddots & \\ & m\Delta t& & & & 1\end{array}\right],$$

h(x(t)) ≜ y(t) from (5), $\nu (t)\sim \mathcal{N}(0,{\sigma }_R^2)$ is zero mean Gaussian measurement noise, and μ(t) ∼ 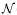(0, Q) is the random step of the states assumed to be drawn from a zero mean multivariate normal distribution with covariance matrix Q.

Prediction with this model requires estimation of the 2m+2 parameters in x(t); a non-linear estimation problem owing to the measurement function, h(x(t)). We employ the EKF, a non-linear filtering method that approximates the Kalman filter through linearization about the current state estimate x̂(t|t). The EKF can be computed in real-time using the recursion

$$\begin{array}{l}\mathit{\text{P}}(t+\Delta t|t)=\mathit{\text{F}}\mathit{\text{P}}(t|t){\mathit{\text{F}}}^{\mathrm{T}}+\mathit{\text{Q}}\\ S={\sigma }_R^2+\mathit{\text{H}}\mathit{\text{P}}(t+\Delta t|t){\mathit{\text{H}}}^{\mathrm{T}}\\ \mathit{\text{K}}=\mathit{\text{P}}(t+\Delta t|t){\mathit{\text{H}}}^{\mathrm{T}}{S}^{-1}\\ \widehat{\mathit{\text{x}}}(t+\Delta t|t+\Delta t)=\mathit{\text{F}}\widehat{\mathit{\text{x}}}(t|t)+\mathit{\text{K}}(z(t+\Delta t)-h(\mathit{\text{F}}\widehat{\mathit{\text{x}}}(t|t)))\\ \mathit{\text{P}}(t+\Delta t|t+\Delta t)=(\mathit{\text{I}}-\mathit{\text{K}}\mathit{\text{H}})\mathit{\text{P}}(t+\Delta t|t),\end{array}$$

where

$$\begin{array}{l}{{\mathit{\text{H}}}^{\mathrm{T}}\triangleq {\left(\frac{\partial h}{\partial \mathit{\text{x}}}\right)}^{\text{T}}|}_{\widehat{\mathit{\text{x}}}(t+\Delta t|t)=\mathit{\text{F}}\widehat{\mathit{\text{x}}}(t|t)}\\ =\left[\begin{array}{c}1\\ sin{\widehat{\theta }}_1(t+\Delta t|t)\\ ⋮\\ sin{\widehat{\theta }}_m(t+\Delta t|t)\\ 0\\ {\widehat{r}}_1(t+\Delta t|t)cos{\widehat{\theta }}_1(t+\Delta t|t)\\ ⋮\\ {\widehat{r}}_m(t+\Delta t|t)cos{\widehat{\theta }}_m(t+\Delta t|t)\end{array}\right],\end{array}$$

and P(·) ≜ E [x̂(·)x̂(·)^T] denotes the state estimate covariance, whose initialization is described later in this section. Note that the time dependencies for F, K, S, and H have been dropped for notational convenience. The EKF as presented here is a slight variant on that first introduced by Parker and Anderson (1990).

To initialize this filter, we first assume that y(t) has constant fundamental frequency yielding N noisy measurements over the interval t ∈ [0, NΔt]. Observation of Figure 3 indicates that the dominant frequency peak is the fundamental frequency of the signal (i.e. heart rate). We apply a fast Fourier transform (FFT) to the data sequence with a Hamming window to obtain the power spectrum. The maximum frequency peak within a reasonable human heart rate range (0.5 to 2.5 Hz) is used to initialize the estimate of ω̂₀ ≜ ω(t = NΔt).

Assuming ω̂₀ to be correct, the problem can be rewritten as a linear estimation problem to obtain the harmonic amplitudes and coefficients. Equation (4) is equivalently reparametrized as

$$y(t)=c_0+\sum _{i=1}^m[a_{i}sin(i{\widehat{\omega }}_{0}t)+b_{i}cos(i{\widehat{\omega }}_{0}t)].$$ (6)

Collecting the measurements z(t), 0 ≤ t ≤ NΔt we have z̃ = Ax̂₀ + ν, where z̃ = [z(0), z(Δt),…, z(NΔt)]^T, x̂₀ = [c₀, a₁,…, a_m, b₁,…, b_m]^T, ν is a vector of measurement noise, and

$${\mathit{\text{A}}}^{\mathrm{T}}=\left[\begin{array}{cccc}1& 1& \cdots & 1\\ sin({\widehat{\omega }}_{0}0)& sin({\widehat{\omega }}_0\Delta t)& \cdots & sin({\widehat{\omega }}_{0}N\Delta t)\\ ⋮& ⋮& & ⋮\\ sin(m{\widehat{\omega }}_{0}0)& sin(m{\widehat{\omega }}_0\Delta t)& \cdots & sin(m{\widehat{\omega }}_{0}N\Delta t)\\ cos({\widehat{\omega }}_{0}0)& cos({\widehat{\omega }}_0\Delta t)& \cdots & cos({\widehat{\omega }}_{0}N\Delta t)\\ ⋮& ⋮& & ⋮\\ cos(m{\widehat{\omega }}_{0}0)& cos(m{\widehat{\omega }}_0\Delta t)& \cdots & cos(m{\widehat{\omega }}_{0}N\Delta t)\end{array}\right],$$

to which the least squares estimate is obtained as ${\widehat{\stackrel{\sim }{x}}}_0={({\mathit{\text{A}}}^{\mathrm{T}}\mathit{\text{A}})}^{-1}{\mathit{\text{A}}}^{\mathrm{T}}\stackrel{\sim }{\mathit{\text{z}}}$. x̂(T|T) is then initialized with the values ĉ(T) = ĉ₀, ω̂(T) = ω̂₀, ${\widehat{r}}_i(T)={({\widehat{a}}_i^2+{\widehat{b}}_i^2)}^{-1/2}$, and θ̂_i(T) = arctan(b̂_i, â_i). The state estimate covariance is set to $\mathit{\text{P}}(T|T)=\mathit{\text{diag}}[{\sigma }_R^2/N,{\sigma }_1^2,{\sigma }_1^2/2^2,\dots ,{\sigma }_1^2/m^2,{\sigma }_{\omega }^2,0.02{\text{rad}}^2,\dots ,0.02{\text{rad}}^2]$. The relationship between the amplitude uncertainties is chosen to reflect the decreasing harmonic strength seen in Figure 3, while the phase uncertainties follow those used in (Parker and Anderson 1990). Parameters ${\mathit{\sigma }}_1^2$ and ${\sigma }_{\omega }^2$ are determined through experimentation. Last we assume that the process noise covariance Q is diagonal with all values set to 10⁻⁴ except for q_ω, the entry corresponding to ω(t).

4.2. Simulation Studies

Three simulation studies were conducted to evaluate the capabilities of the EKF, AR filter, and fading AR filter to the primary sources of random error in the system: measurement noise and heart rate variability. For illustrative purposes, the filters were also compared with the WFLC estimator (Riviere et al. 1998) and a simpler method of using the previous cardiac cycle trajectory for the prediction of the next. A more sophisticated version of the latter method, called the last cycle here, was used successfully in a beating heart tracking system (Bebek and Cavusoglu 2007).

In the first simulation, we subjected the predictors to varying levels of measurement noise on a fixed-rate trajectory (60 bpm). The mitral annulus trajectory of Figure 2 was reinterpolated to 28 Hz and corrupted by additive zero-mean Gaussian noise with standard deviation 0.3 ≤ σ_R ≤ 3 mm. Each predictor was then given 30 sec of data to initialize and performance was judged for the following 10 sec on 1-sample ahead predictions.

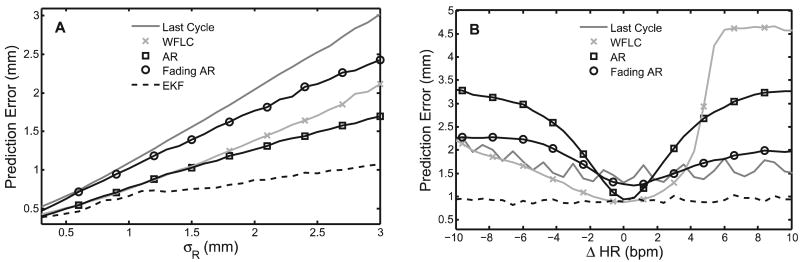
The RMSEs for each predictor averaged across 100 Monte Carlo trials are shown in Figure 9A. The EKF, WFLC, AR, and fading AR filtering methods clearly give higher-accuracy predictions than the inherent uncertainty of the measurements, with the EKF doing the best. As expected, the last cycle method had error statistics equal to σ_R since it attempts no smoothing. It should be noted that the fading AR filter was tuned with f = 0.985 in order to achieve errors that are approximately equal to σ_R. This setting represents the lowest reasonable value for the fading AR filter since a lower value would give performance below the last cycle method. The EKF was run with m = 8 harmonics, N = 280 initialization points (10 seconds), ${\mathit{\sigma }}_1^2=2{\text{mm}}^2$, ${\sigma }_{\omega }^2=0.11{(\text{rad}/\text{s})}^2$ (roughly twice the frequency resolution of the FFT), and q_ω = 10⁻³ (rad/s)². The WFLC was initialized in the same manner as the EKF, run with m = 8 harmonics, and experimentally set with its adaptive gain parameters μ₀ = 7 × 10⁻⁶ and μ₁ = 0.03 for best performance in this and subsequent simulations.

Fig. 9.

RMS prediction error results for parametric simulation studies. A, Error for varying measurement noise; B, error for step heart rate changes.

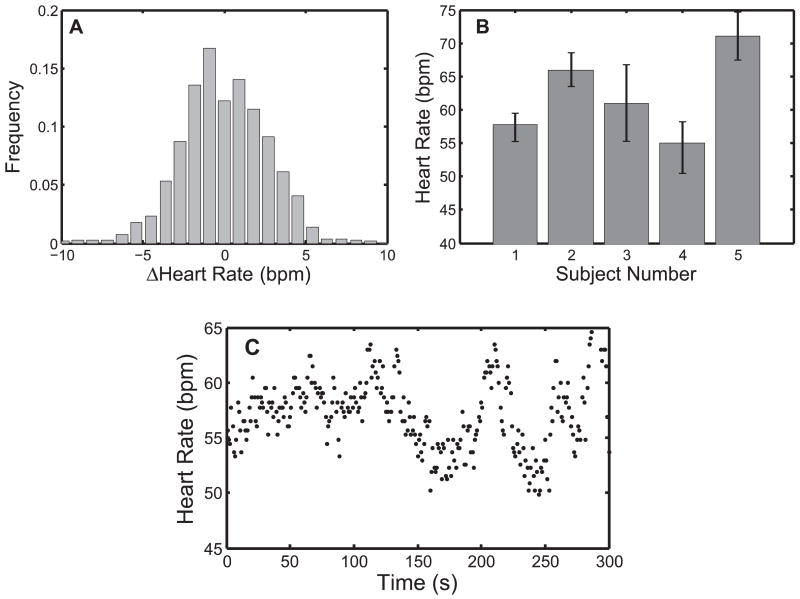
In a second parametric simulation study, we gauged the tolerance of each predictor to a sudden change in heart rate. A trajectory was assembled by piecing together 30 seconds of heart motion at 60 bpm and 10 seconds of motion at (60 + ΔHR) bpm. The second portion of the trajectory was generated by compression/dilation of the target trajectory in Figure 2 to obtain the desired heart rate. Like before, the composite trajectory was reinterpolated to 28 Hz and corrupted with σ_R = 1.30 mm noise; the measured uncertainty of the 3DUS annulus estimates (Novotny 2007). The last 10 seconds were used to evaluate performance. A reasonable range of −10 bpm ≤ ΔHR ≤ 10 bpm was determined from clinical RR data (Figure 10), which is discussed later.

Fig. 10.

Heart rate statistics on five human subjects. A, Distribution of beat-to-beat variation; B, subject-specific mean ± one standard deviation; C, heart rate data for subject 1.

Figure 9B shows the mean RMSEs for each predictor across 100 Monte Carlo trials. The EKF provided better predictions than the other four methods. It was also the only method that yielded sub-σ_R error for the majority of heart rate changes. The WFLC had similar accuracies to the EKF at small ΔHR but showed slow convergence to the new heart rate for ΔHR > 4 bpm. As expected, the accuracy of the AR filter also approached that of the EKF for small ΔHR and quickly degraded as ΔHR increased. Exponential weighting of the measurements allowed the filter to adjust to changes in the trajectory, as demonstrated by the fading AR filter's superior performance over the AR filter for large ΔHR. However, this adaptability decreased accuracy when the trajectory did not change significantly. Finally, the last cycle method showed performance comparable to the fading AR filter. For this simulation all filter parameters were chosen to be the same as in the previous simulation, with the exception of q_ω = 5 × 10⁻³ (rad/s)² and ${\sigma }_{\omega }^2=1$ (rad/s)² for the EKF.

Finally, to investigate the performance of each predictor to the more realistic case of a continuously changing heart rate, we modulated the period of the annulus trajectory with clinically obtained cardiac cycle records. Annotated ECG records for five human subjects were selected from the MIT–BIH Normal Sinus Rhythm Database (Goldberger et al. 2000) and composite mitral valve trajectories were generated in a manner similar to the previous simulation study. Noise-corrupted measurements were generated as before, with σ_R = 1.30 mm. Summary statistics for each subject are presented in Figure 10B and an example of the beat-to-beat heart rate for subject number 1 is shown in Figure 10C.

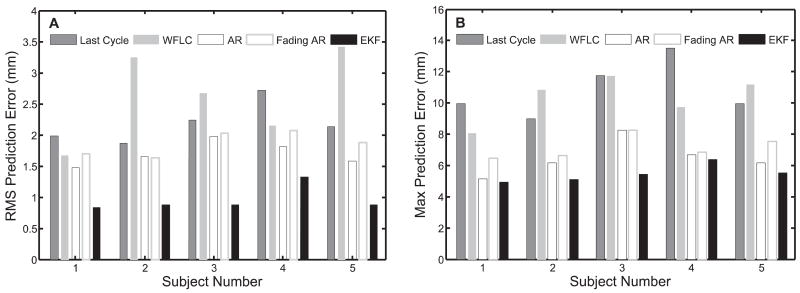
Results from this study indicate that the EKF is more suited to tracking and prediction in this application than the other four methods because it adjusts to rapid changes in heart rate through explicit modeling of quasiperiodicity (Figure 11). Interestingly, the AR filter showed moderately better performance than the fading AR filter. The reason for this is that the AR filter locked on to an “average” trajectory for each subject while the fading AR filter continuously readjusted to more recent noisy data. Ultimately, deviations from the “average” motion were less than the measurement noise. The last cycle method performed worse for similar reasons: persistent variations in heart rate and measurement noise degraded the accuracy of the previous cycle as a predictor for the next. The slow convergence of the WFLC to changing heart rates caused it to have severely degraded performance.

Fig. 11.

Comparison of prediction error results on clinical data using last cycle, WFLC, AR filter, fading AR filter, and EKF: A, RMSE; B, maximum absolute error.

5. Performance Evaluation in a Surgical Task

In order to quantify the amount of assistance that motion compensation provides to operators working on a moving target, we conducted two studies of user performance with the MCI in an in vitro setting. These studies additionally provide insight on how sensitive performance is to potential shortcomings of a 3DUS-guided system. Specifically, user study 1 determined the extent to which user performance is dependent on time delay and random positional error. These error types are of interest because both positional precision errors and computational delays develop while generating 3DUS tracking data in realtime. User study 2 investigated user performance with EKF delay compensation on targets with both fixed and variable heart rates. Subjects performed a drawing task on a moving target using the MCI under different tracking conditions. A total of 18 test subjects (14 male and 4 female, aged 22 to 36; 8 subjects for user study 1 and 10 subjects for user study 2) voluntarily participated following informed consent under a protocol approved by the University Institutional Review Board.

5.1. Experimental Setup

The tests were run on a setup which emulates the intended surgical environment. To simulate the moving mitral valve, a target platform was mounted on a cam-driven device that replicates the 1D motion of the mitral annulus centroid as measured from the 3DUS tracking data. During trials, a paper target was affixed to this platform to record the subject's drawing. A 0.5 cm hard foam rubber pad between the target paper and target platform provided a small measure of compliance. In combination with the pen used in the trials, the pad had a stiffness of 4.5 N mm⁻¹. For the purposes of this experiment, the cam was used to simulate a heart rate of 60 bpm. Opposite the target platform, the MCI was mounted in a gimbal allowing both angular motion and translation towards and away from the target (Figure 12). A rod was mounted on the MCI with a ballpoint pen affixed to one end and a force sensor incorporated along its length. The force sensor had a stiffness of 10 N mm⁻¹. In place of the 3DUS-based tracking and controls algorithms that would be used in surgery, target position was directly measured at 1 kHz by a contact arm with a potentiometer attached to the target platform. This sensing method provided the robust tracking data necessary to evaluate the efficacy of MCI mitral valve tracking and the performance of predictive filtering algorithms.

Fig. 12.

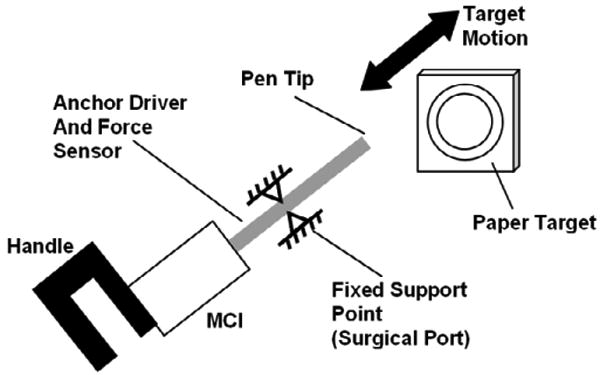
User trial setup. The bold arrow indicates the cyclical motion of the simulated valve target. The tool shaft has free rotational and sliding motion at the fixed support point.

5.2. User Task

Subjects were instructed to draw a circle on the moving target platform. The circle must be drawn between two concentric target circles with 2.29 and 2.92 cm diameters. Subjects started at the top of the circle and proceeded in the clockwise direction. If the pen bounced off the target surface or outside the target circles, the subject was instructed to continue drawing from the clockwise-most mark they made between the target circles. Subjects could only draw around the circle once. They could not go back to draw in gaps they originally missed. To prevent subjects from spending an inordinate amount of time on the task, a 25-second time limit was set. All subjects finished every trial before the time expired.

Both dexterity and force metrics were used to evaluate subject performance. In all trials, the quality of each circle drawn was characterized by digitally scanning the target and computing the drawn line's “angular surround” value. This value indicates what percentage of 360 discrete 1° arc segments the user's line covered between the two concentric target circles. This metric reflects positioning accuracy both in the plane of the target and in tracking the motion of the target perpendicular to this plane. If the user-drawn line strayed from the concentric target circles, it did not contribute to the angular surround metric and resulted in a lower score. Similarly, if the user and MCI were unable to track the motion of the target, the pen tended to bounce off of the target surface, producing widely spaced marks and a low angular surround score.

The axial force applied by the subject to the target was also recorded for 4 of the 8 test subjects in user study 1 and 9 of the 10 subjects in user study 2. In all 18 cases, subjects were informed of both evaluation metrics. They were instructed that their foremost objective was to draw continuous circles conforming to the angular surround metric and only secondly to use the minimum amount of force necessary.

This task was selected to emulate the motion requirements of placing a surgical anchor. In order to apply the surgical anchors developed for this procedure, the tip of the anchor driver, consisting of 14 gauge hypodermic tubing, must be accurately located and pressed against the target surface with a force of at least 1.5 N (Wagner et al. 2006). This contact must be maintained for several seconds as the surgeon inserts the anchor, tests whether it is deployed properly, and then releases the anchor. This process requires a combination of accuracy and prolonged contact with the surface. At the same time, forces must be minimized so as not to cause damage to the valve.

5.3. User Study 1: Tracking with Time Delay and Positional Error

Subjects of this study completed the task under eight different tracking conditions. In the “solid” condition, the motion of the MCI was rigidly locked in order to simulate a traditional, solid endoscopic tool. For the “baseline” MCI tracking condition, the current position of the target (RMSE = 0.015 mm) was sent to the MCI as a position command. This baseline condition resulted in a 14 ms delay. The remaining six tracking conditions were divided into two groups of three conditions corresponding to differing levels of the considered error.

Random positional error was simulated by the superposition of a time-varying error value with the cam position command used in the baseline tracking state. A new positional error was calculated at 8 Hz. These errors were uniformly distributed random values ([−1, 1]), multiplied by an amplitude factor of 0.35, 0.70, or 1.05 mm.

Delay error was implemented by recording the cam tracking position and holding it for a specified period before sending this position to the MCI as a motion command. For this set of trials, the three levels of added delay used were 25, 35, and 45 ms. Including the MCI lag time of 14 ms, the effective delay settings were 39, 49, and 59 ms. This range of times was chosen as representative of the imaging and transmission delays associated with real-time 3DUS-guided procedures (Novotny et al. 2007).

5.4. User Study 2: Delay-compensated Tracking with Heart Rate Variation and Measurement Noise

To test the EKF under conditions similar to those seen in 3DUS-guided procedures, the 1 kHz measurements of target position were downsampled to 28 Hz and corrupted by additive Gaussian noise ∼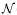(0, 1.30² mm) (Novotny 2007). The target was commanded to beat at 60 bpm or with a variable rate that had additive Gaussian beat-to-beat fluctuations $\sim \mathcal{N}(0,{\sigma }_{\mathit{\text{HR}}}^2)$. Finally, a time delay of 39, 59, or 89 ms was injected into the measurements to simulate the delays encountered with 3DUS. Note that the 89 ms delay exceeds the delays used in user study 1 to also account for the additional computational delays from instrument and target segmentation in 3DUS (Novotny 2007).

Overall, the subjects of this study performed the task under 10 tracking conditions, all with varying amounts of time delay. Three tracking conditions evaluated user performance with EKF delay compensation against 39, 59, and 89 ms time-delayed, noise-corrupted measurements on a 60 bpm target. For comparison, three tracking conditions were conducted on the same set of delays but without delay compensation and without measurement noise.

The remaining four tracking conditions evaluated user performance with EKF delay compensation on a variable heart rate target. Measurements were delayed by 89 ms and noise-corrupted. The four levels of beat-to-beat variation were chosen as σ_HR = {1.0, 2.0, 3.0, 4.0} bpm. These values span those observed in the clinical RR data from Section 4.2. An illustrative example of this tracking condition with σ_HR = 4.0 bpm and the subsequent behavior of the EKF and the MCI is shown in Figure 13.

Fig. 13.

Variable heart rate tracking condition (σ_HR = 4.0). A, Noise-corrupted, time-delayed measurements and the resulting EKF predictions; B, MCI position and the true position of the target.

5.5. Testing Protocol

Each subject test consisted of a practice period followed by the trials corresponding to the tracking conditions of their study. Practice was intended to familiarize the test subject with the MCI and the evaluation task in order to bring subjects to a uniform level of ability and to limit learning effects during trials. Practice was divided into three one-minute segments during which the subject was free to experiment with using the MCI to draw on a target paper. During the first minute of training, the target was stationary and the tool was set in the solid condition. The second minute of training involved a moving target and a solid tool. In the third and final minute, the target was moving and the MCI was in the baseline tracking condition. Following the completion of training, each test subject ran through the trials corresponding to the tracking conditions of their study. The order in which these conditions were administered was varied between trials using a balanced Latin square to minimize the effects of between-trial carry-over and learning on collected data.

The means of collected angular surround error metric were compared for statistically significant differences using the SPSS statistical analysis software package (Version 14.0, SPSS Inc., Chicago, IL, USA). These comparisons were made using t-tests and analysis of variance (ANOVA) with a least significant difference (LSD) post hoc test. In all cases, significance corresponds to p < 0.05.

5.6. User Study 1 Results

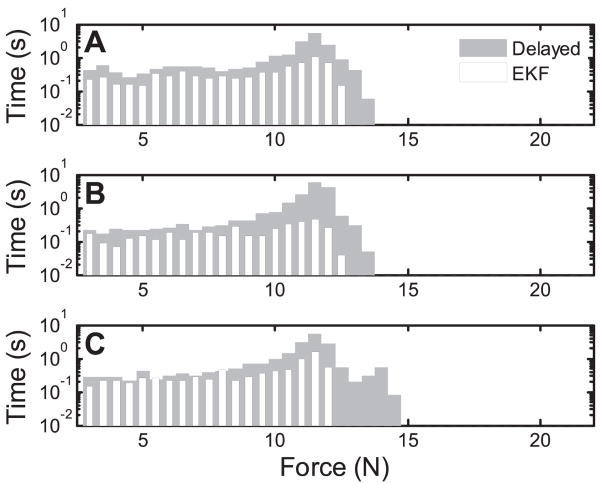
The results of this study indicate that the MCI can provide significant assistance while operating on a moving target. Figure 14 shows typical target results. Mean angular surround metric scores (Figure 15) for the baseline tracking condition (81.9 ± 4.5% (mean ± standard error)) were over 50% greater than for the solid condition (53.8 ± 5.0%), with clear statistical significance (t(14) = 0.1987, p = 0.0009). Similarly, axial force data indicates that subjects applied less than 50% as much force and spent less time at elevated forces under the baseline MCI tracking condition. Aggregating the data from all four subjects (Figure 16), the 90th percentile for force samples using the solid tool (17.5 N) is roughly double the 90th percentile for the baseline tracking condition (8.5 N).

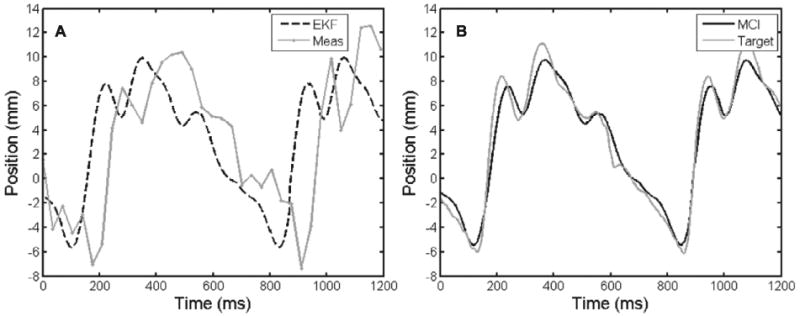
Fig. 14.

Targets with median angular surround scores under solid (A), baseline (B), and 59 ms time-delayed (C) tracking conditions. The baseline circle is the most continuous and round. While the solid target has more continuous lines than the time-delayed target, it also has heavy dots and dimpling indicative of high forces.

Fig. 15.

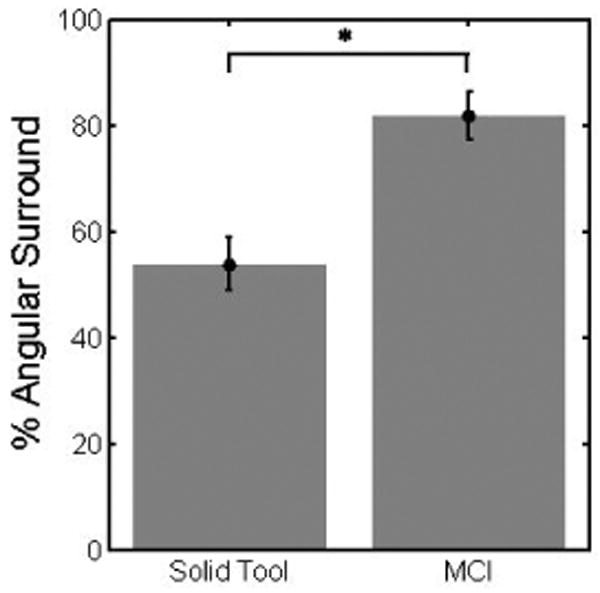
Performance under baseline MCI and solid tool tracking conditions. Error bars indicate standard error. “*” marks statistical significance.

Fig. 16.

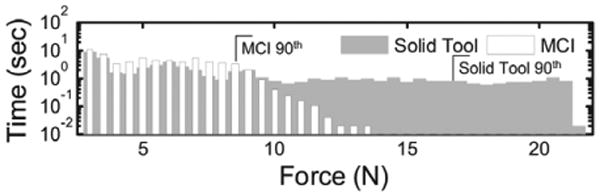
Histogram of applied force samples under baseline MCI and solid tool tracking conditions. Smaller forces are consistently applied under the baseline condition. 90th percentiles are marked. The zero force bin is not shown.

A comparison of mean angular surround metric scores related to the amount of delay error (Figure 17) demonstrates decreases in performance ranging from 67% to 33% with increasing delay (f (3, 28) = 16.005, p < 0.001). Statistically significant differences were indicated between the baseline condition and tracking with delays of 39 ms (61.2 ± 1.5%), 49 ms (56.0 ± 3.7%), and 59 ms (48.8 ± 3.8%). A significant difference also exists between the means of the 39 and 59 ms tracking conditions (p = 0.02). Trend analysis indicates that the data is well fit by a linear model (p < 0.001).

Fig. 17.

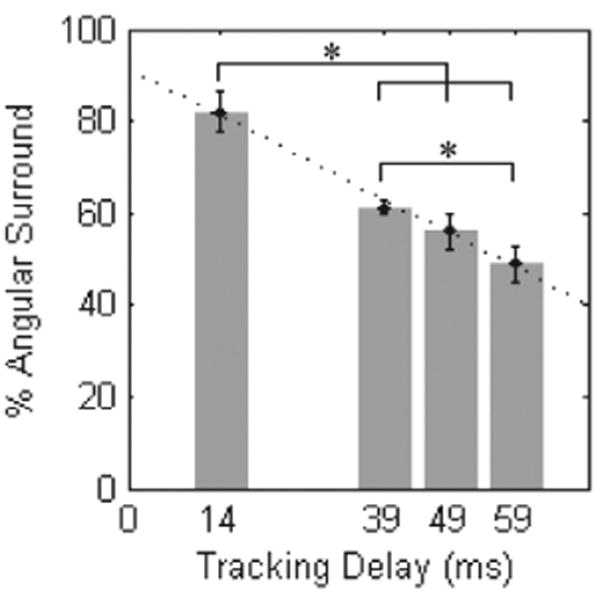
Performance under delay tracking conditions. Error bars indicate standard error. Asterisks indicate statistical significance. The dotted line shows the fitted linear model (R² = 0.9937).

An analysis of mean angular surround metric scores related to positional error did not demonstrate significant differences under ANOVA analysis (f (3, 28) = 0.638, p = 0.597). As seen in Figure 18, the mean score under the baseline condition differed very little from those with error amplitude factors of 0.35 mm (81.7±3.3%), 0.70 mm (78.0±5.5%), and 1.05 mm (74.2 ± 4.6%).

Fig. 18.

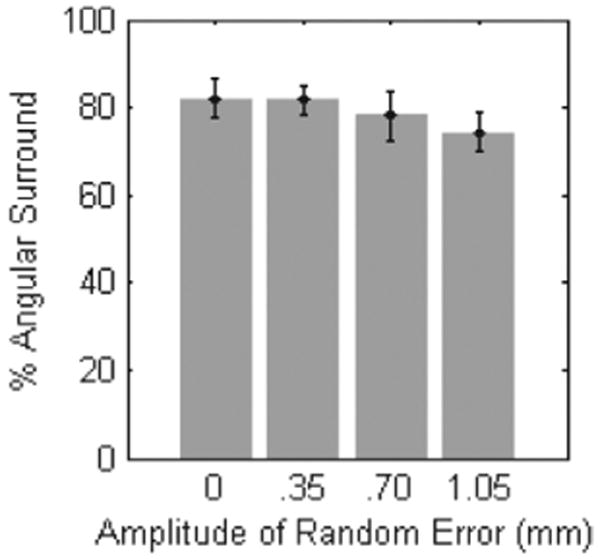
Performance under positional error tracking conditions. Error bars indicate standard error.

5.7. User Study 2 Results

Results from this study demonstrate that the EKF is an effective approach for compensating time delay. Figure 19 shows typical target results. Mean angular surround scores for EKF delay-compensated tracking (Figure 20) were similar to the baseline tracking condition from user study 1 for all three conditions of 39 ms (83.1 ± 3.7%), 59 ms (85.2 ± 2.6%), and 89 ms (84.4 ± 3.8%). Likewise, delay-compensated tracking showed performance increases over delayed tracking ranging from 13% to 24%. The mean angular scores for delayed tracking were 70.4 ± 4.8%, 61.1 ± 4.6%, and 61.0 ± 5.2% for 39, 59, and 89 ms delays, respectively. Statistically significant differences at p < 0.05 were observed between the mean scores of each delay-compensated tracking condition to each delayed tracking condition. Delay-compensated tracking also yielded smaller axial forces than those observed for delayed tracking (Figure 21).

Fig. 19.

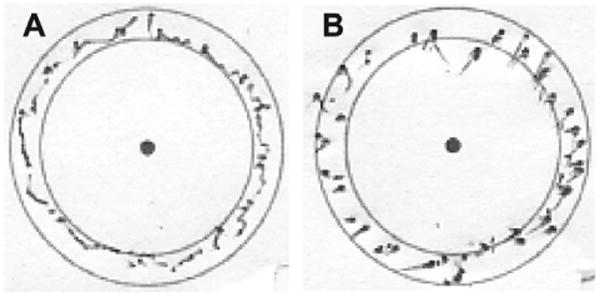
Targets with median angular surround scores under 89 ms EKF delay-compensated (A) and time-delayed (B) tracking conditions. The delay-compensated example is more continuous and round than the time-delayed example. The latter is fragmented and has heavy dots and dimpling that are indicative of high forces.

Fig. 20.

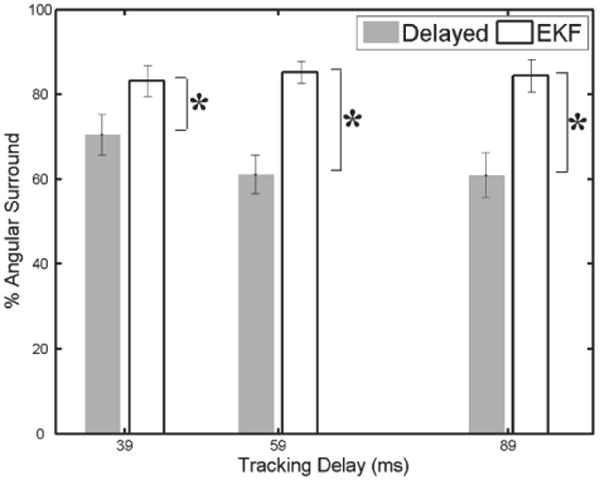
Performance with EKF delay compensation and without. Error bars indicate standard error. Asterisks indicate statistical significance.

Fig. 21.

Force application with and without delay compensation for delays of (A) 39 ms, (B) 59 ms, and (C) 89 ms. Smaller forces are consistently applied under the delay-compensated tracking conditions. The zero force bin is not shown.

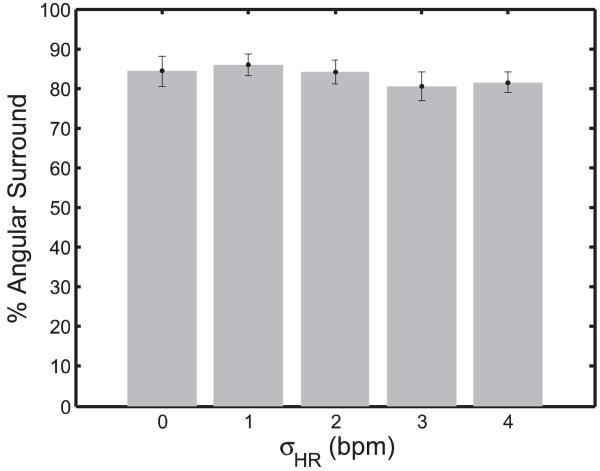
An analysis of mean angular surround metric scores related to heart rate variability did not demonstrate significant differences under ANOVA analysis (f (3, 36) = 0.705, p = 0.555). As seen in Figure 22, the performance against a fixed-rate target was comparable to that against a variable rate target with σ_HR equal to 1.0 bpm (85.9 ± 2.6%), 2.0 bpm (84.1 ± 2.9%), 3.0 bpm (80.5 ± 3.6%), and 4.0 bpm (81.5 ± 2.5%).

Fig. 22.

Performance under variable heart rate tracking conditions. Error bars indicate standard error.

6. System Accuracy Under 3D Ultrasound Guidance

Water tank experiments were conducted to measure the motion synchronization accuracy of the system under 3DUS guidance. To do these, a real-time 3DUS target segmentation algorithm was first incorporated into the system to provide position measurements to the EKF. The target was set to be an X-shaped fiducial that can be easily mounted to an annuloplasty ring (Figure 23B). This fiducial was specifically chosen because detecting two intersecting lines is suited for an existing real-time 3DUS segmentation algorithm based on the modified Radon transform (Novotny 2007). This algorithm is known to provide target position measurements with 1.30 mm RMS accuracy under in vitro conditions. Because higher noise may be present in vivo, we also tested this system in two other noise conditions in which large Gaussian terms ∼ (0, σ), σ = {2.0, 3.0} mm were added to the segmented target positions. This yielded three noise conditions with overall RMS accuracies of σ_R = {1.30, 3.30,4.30} mm. We anticipate in vivo noise levels to be less than 3.5 mm RMS.

Fig. 23.

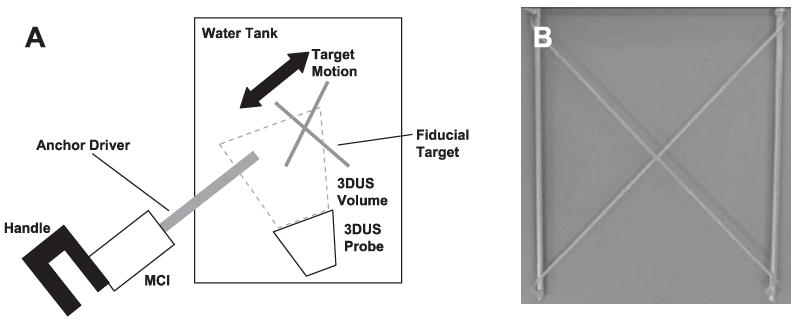
(A) Setup for motion synchronization experiments and (B) X-shaped fiducial target.

6.1. Experimental Setup

The target and instrument were imaged by a real-time 3DUS probe in a water tank at 28 Hz (Figure 23A). Data was streamed from the ultrasound machine (SONOS 7500, Philips Medical, Andover, MA) to a computer over an ethernet connection. The stream was captured by the computer and passed to a graphics processing unit (8800GTS, nVidia Corp, Santa Clara, CA) where the volumes were automatically segmented using the modified Radon transform segmentation algorithm (Novotny 2007) to obtain target position measurements. The measurements were corrupted with additive Gaussian noise (depending on the noise condition), then passed to a third thread for EKF processing. This returned predicted target positions 82 ms in the future (68 ms from imaging and segmentation, 14 ms from instrument lag time) and were sent to the 1 kHz PID control loop for the robot.

Five motion synchronization trials were conducted per noise condition. The target simulated mitral valve motion at 60 bpm with the cam-driven mechanism described in Section 5.1. MCI position and true target position were measured at 1 kHz with potentiometers and stored for offline processing. Target measurements and EKF predictions were acquired at the 3DUS sampling rate (28 Hz) and stored as well. Accuracy evaluation was performed on the 20 s of tracking data following 20 s of EKF initialization.

6.2. Results

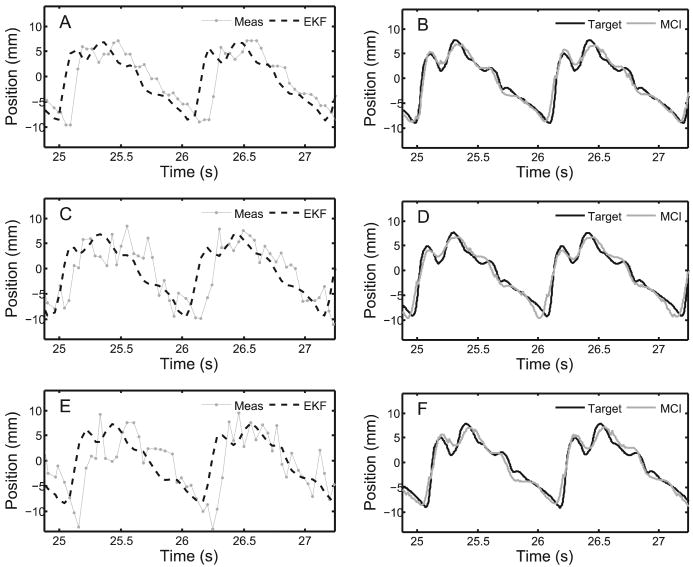
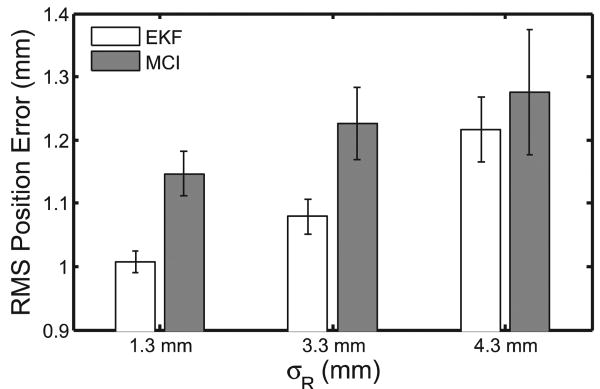
Results from this experiment demonstrate that the motion compensation system is robust to the noise levels present in 3DUS imaging. Typical data and results for each noise condition are shown in Figure 24 and overall performance is summarized in Figure 25. Mean RMS accuracies for EKF predictions were 1.01 ± 0.02, 1.08 ± 0.03, and 1.22 ± 0.05 mm for σ_R = {1.30,3.30,4.30} mm (respectively) and showed statistically significant reductions in measurement error (p < 0.0001 for each case). Mean MCI synchronization errors were 1.15 ± 0.04, 1.23 ± 0.06, and 1.28 ± 0.10 mm RMS for the three noise conditions. The mean RMSE added to the system from the MCI following the prescribed EKF trajectory was 0.14±0.01 mm and this difference was statistically significant (p = 0.002). The RMS noise accuracy for the X-tracking algorithm observed across all 15 trials was 1.30 ± 0.01 mm, in agreement with previous reports (Novotny 2007).

Fig. 24.

Examples of data, filtering, and motion tracking results. Left column shows measurements from 3DUS target segmentation and EKF predicted target trajectories for each noise condition: (A) σ_R = 1.30 mm; (C) σ_R = 3.30 mm; and (E) σ_R = 4.30 mm. Corresponding MCI and true target trajectories for each noise condition are shown in the right column: (B) σ_R = 1.30 mm; (D) σ_R = 3.30 mm; (F) σ_R = 4.30 mm.

Fig. 25.

EKF prediction performance and MCI tracking performance over three increasing noise conditions. Error bars indicate standard error.

7. Discussion

User trials demonstrate that the motion compensation system described here is an effective aid for surgical tasks on beating mitral valve targets. Motion synchronization allowed users to operate with both increased dexterity and reduced forces. In user study 1, the angular surround scores indicative of dexterity increased by approximately 50% between the solid tool and baseline tracking conditions while the 90th percentile for force decreased by a similar ratio. These performance gains were maintained when increasing levels of positional error were inserted into the system, but disappeared when uncompensated time delays were added to the tracking data.

The strong dependence of user performance on delay emphasizes that precise timing is essential for successful motion compensation. Left uncompensated, tracking delays produced serious errors during the rapid recoil of the target associated with the relaxation of the left ventricle. During this motion the valve moves towards the operator, nearly covering its entire 18 mm range of motion. Owing to the delay, the MCI continued to servo towards the oncoming target and abruptly collided with it. Qualitatively, while subjects did not always notice added positional error, they universally correctly identified and expressed dismay over tracking delay.

The introduction of a predictive EKF into the system effectively removed the performance decrease associated with tracking delays. The angular surround scores for delay-compensated tracking conditions exceeded their respective delayed tracking conditions by 13% to 24%, depending on the degree of delay. The forces applied in the delay-compensated conditions also decreased relative to the delayed conditions, although to a lesser extent than seen between baseline tracking and the solid tool. The delay-compensated scores of user study 2 marginally exceeded the baseline scores of user study 1 by an amount that is consistent with the removal of the MCI's 14 ms lag time (as predicted by the linear model from user study 1). However, caution must be taken when making a direct comparison of the angular surround scores between user studies 1 and 2 because of differing amounts of in-trial training (8 trials in user study 1 and 10 trials in user study 2). It is reasonable to conclude that EKF delay compensation restored the MCI tracking performance to at least baseline tracking conditions in cases of delay. Moreover, the performance increases observed for delay-compensated tracking showed no degradation across the range of time delays expected for 3DUS-guided procedures.

Surprisingly, the levels of random positional error explored in the user studies had a negligible effect on the benefits of MCI tracking. No statistically significant differences were found between user performance under all three positional error conditions and the baseline condition. This result suggests that if the timing with the valve's sudden recoil is maintained, the value of the MCI's tracking is robust in the face of positional errors as high as ±1 mm. This may be attributed, in part, to compliance in the system: in the MCI's mechanism and in the foam pad on the target platform, which introduce compliance similar in nature to that in the heart. An in vivo characterization of MCI performance is necessary to determine whether compliance acts in the same way to assist operation on the mitral valve annulus.

Heart rate variations in the target motion also provided no significant degradation in user performance over the clinically obtained beat-to-beat statistics (Figure 10). This is not surprising given that the EKF estimates did not degrade on these levels of heart rate variation. In some respects, tracking a variable rate target was another approach to injecting positional error into the system since the filter remained in phase with the target (see, for instance, Figure 13). We anticipate that extremely large beat-to-beat variations will cause the EKF to break synchronization with the target as the linearization of the measurement function, h(x(t)), becomes inappropriate. Should more aggressive heart rate variations be encountered in future in vivo experiments, there are several potential routes for improvement. First, heart rate variability could be reduced through drug treatment and/or electrical pacing of the heart. Second, following Bebek and Cavusoglu (2007), ECG information could be used to obtain direct measurements of heart rate. This could reduce the effect of the non-linearity in h(x(t)) since, as mentioned before, perfect knowledge of ω(t) turns this into a linear estimation problem (6). Note that the EKF, a non-linear filtering approach, would still be useful with these measurements because they are sampled at discrete intervals but ω(t) is continuous.

The efficacy of this motion compensation system is based on the assumption that the motion which must be tracked is modeled well by a 1D approximation. Previous research on augmenting surgical procedures with robotic tracking have focused on coronary artery bypass grafting, requiring a 3D model of surface motion (Nakamura et al. 2001; Ortmaier et al. 2005; Ginhoux et al. 2006; Bebek and Cavusoglu 2007). The characterization of the mitral valve annulus motion above shows that the fast motion of the mitral valve is primarily along one axis; however, we also observe approximately 2 mm of off-axis motion (Figure 2). Our preliminary tests suggest that the passive compliance of the mitral valve annulus and the surgeon's hand will assist with these minor off-axis deviations. In addition, in vivo conditions will present slow out-of-axis motions owing to the respiration of the subject. Fortunately, surgeons already overcome this in current heart procedures, either by manually compensating for the slow motion or momentarily stopping the controlled ventilation to the patient.

In this work, particular emphasis has been placed on predictive filtering to mitigate the dominant sources of tracking error in the system: 3DUS delay and noise. Using this approach with the MCI in a 3DUS-guided servoing task, we achieved synchronization accuracies of less than 1.3 mm RMS in the presence of large measurement noise (1.3–4.3 mm RMS) and 82 ms of system delay. This is a significant improvement over the approximately 4.6 mm RMSEs that would be incurred in a time-delayed but otherwise noiseless tracking system. Although errors in the current system are low, there is potential for further lowering error through a more sophisticated controller. Repetitive control methods are well suited for quasiperiodic servoing tasks (Hara et al. 1988; Chew and Tomizuka 1990; Kempf etal. 1993; Horowitz 1993) and model predictive control has shown promising results in external beating heart tracking (Ginhoux et al. 2006; Bebek and Cavusoglu 2007). These techniques may reduce the 0.14 mm tracking error that is attributable to the PID controller used in the current system.