Abstract
Neural representations of even temporally unstructured stimuli can show complex temporal dynamics. In many systems, neuronal population codes show “progressive differentiation,” whereby population responses to different stimuli grow further apart during a stimulus presentation. Here we analyzed the response of auditory cortical populations in rats to extended tones. At onset (up to 300 ms), tone responses involved strong excitation of a large number of neurons; during sustained responses (after 500 ms) overall firing rate decreased, but most cells still showed a statistically significant difference in firing rate. Population vector trajectories evoked by different tone frequencies expanded rapidly along an initially similar trajectory in the first tens of ms after tone onset, later diverging to smaller amplitude fixed points corresponding to sustained responses. The angular difference between onset and sustained responses to the same tone was greater than between different tones in the same stimulus epoch. No clear orthogonalization of responses was found with time, and predictability of the stimulus from population activity also decreased during this period compared to onset. The question of whether population activity grew more or less sparse with time depended on the precise mathematical sense given to this term. We conclude that auditory cortical population responses to tones differ from those reported in many other systems, with progressive differentiation not seen for sustained stimuli. Sustained acoustic stimuli are typically not behaviorally salient: we hypothesize that the dynamics we observe may instead allow an animal to maintain a representation of such sounds, at low energetic cost.
Introduction
Spike trains of neocortical neurons have an intricate temporal structure. In sensory areas, even presentation of a temporally unstructured stimulus such as a static visual image or pure tone is likely to induce a complex temporal pattern of spiking. The structure of these patterns varies with both the stimulus, and between simultaneously recorded neurons, indicating complex spatiotemporal patterns in neuronal populations (Hoffman et al., 2007; Luczak et al., 2007; Ji & Wilson, 2008; Luczak et al., 2009). In recent years it has become possible to record from large enough numbers of neurons to study this structure experimentally. The analysis of the resulting data, however, is a complex problem, with no single approach that completely characterizes the structure of population spike trains. Progress in this field depends not just on the development of new technical approaches, but the development of mathematical language in which to precisely clarify the meaning of biological questions.
A useful concept to study neuronal population activity is the firing rate vector (Laurent, 2002; Stopfer et al., 2003), a representation f of the mean rate of a population of N cells as a point in an N-dimensional space. Considering the dependence of this vector on time, one obtains a trajectory f(t) that characterizes the dynamics of the population rate – that is, a description of how it evolves during stimulus presentation. Though this approach cannot capture variability and correlations in activity on individual trials, it provides important information, and allows the use of geometrical concepts that have proved invaluable in other sciences. Similarity measures between vectors, such as Euclidean distance or angle, also allow the comparison of the state of the population at different time/stimulus combinations.
The simplest geometrical possibility one might expect for trajectories during presentations of static stimuli is linear scaling. Neurons of many sensory systems, including primary receptors, adapt to static stimuli so that stimulus onsets cause large responses that then progressively diminish thereafter (Adrian and Zotterman, 1926; Fettiplace and Ricci, 2003). Provided that the neurons of a population adapt at approximately similar rates, the resulting rate vector should linearly shrink toward the origin. Such as scheme would have a natural computational interpretation. In many neural network models, normalization mechanisms ensure that the set of downstream cells activated by a pattern is determined by the orientation, rather than the length the rate vector (Grossberg, 1976; Kohonen, 1989; Parkinson & Parpia, 1998); linear scaling would therefore allow stimulus identity to be read out in the same way at all times into the stimulus, while perhaps allowing for lower stimulus salience due to decreasing magnitude as time progresses. This simple picture, however, appears to be violated in a number of sensory systems in which rate vector trajectories show not just scaling, but rotation during the stimulus period (Friedrich and Laurent, 2001; Hegde and Van Essen, 2004; Hegde and Van Essen, 2006; Mazor and Laurent, 2005; Menz and Freeman, 2003; Menz and Freeman, 2004; Stopfer et al., 2003).
An example of a biological question that has been addressed with rate vector methods is whether neural representations progressively differentiate: i.e., whether during the course of a stimulus presentation, population responses to different stimuli grow progressively further apart. In this scenario, the initial activity triggered by stimulus presentation carries coarse information about the stimulus, with progressively finer details emerging later, affording animals a more detailed representation of stimuli as time progresses. Progressive differentiation has been reported in many neural systems (Sugase et al., 1999; Friedrich & Laurent, 2001; Hegde & Van Essen, 2004). Is this a general feature of sensory processing by neuronal populations? Or are there other systems that do not exhibit this behavior? A second, related question concerns sparsening – the possibility that neuronal representation involves progressively fewer cells with time into a sensory stimulus. There are multiple definitions of sparseness (Willmore & Tolhurst, 2001; Perez-Orive et al., 2002), and progress in this regard requires understanding of which measures give which results.
The auditory cortical response to tones provides an excellent opportunity to study the neuronal representation of temporally sustained stimuli. Sustained auditory stimuli are generally not perceptually salient, and information about sustained background sounds rarely influences animal behavior. This raises two related questions: are sustained acoustic stimuli represented in auditory cortex throughout their entire length? And if so, how does the nature of their encoding change with time? For the first question, the very existence of sustained responses is controversial. Many studies reported only transient responses at stimulus onset and offset in anesthetized animals (Phillips, 1985; deCharms & Merzenich, 1996; Heil, 1997; DeWeese et al., 2003), while others (Vaadia et al., 1982; Sally & Kelly, 1988; Volkov & Galazjuk, 1991; Bieser & Muller-Preuss, 1996; Recanzone, 2000; Lu et al., 2001; Wang et al., 2005) found sustained responses under certain conditions.
We addressed these questions by studying population responses to extended tone stimuli in auditory cortex under urethane anesthesia. We found that most cells have statistically significant responses even 1000 ms after stimulus onset, although during the sustained period firing rates were typically smaller than in the early response. At the rate vector level, stimulus onset started with large amplitude deflection and rotation. By ~300ms after tone onset, rate vectors had asymptotically tended to fixed points of smaller amplitudes. Progressive differentiation from onset to sustained period was not present by most measures, mainly because the smaller population vectors during sustained response produced a low signal-to-noise ratio. This corresponded to lower predictability of the stimulus from population activity on a single-trial basis. While the question of whether population activity grew more or less sparse with time depended on the precise mathematical sense given to this term, all analyses were consistent with a picture in which the majority of neurons fire at close to baseline rate during the sustained period, with a minority firing at substantially elevated rates for each stimulus.
Materials and Methods
Surgery and recording
Sprague-Dawley rats (300–450 g) were anesthetized with urethane (1.5 g/kg) and placed in a stereotaxic apparatus. A 2–4 mm hole was drilled in the skull above the auditory cortex, and the dura removed. The skull cavity was filled with a mixture of wax and paraffin to decrease brain pulsation and provide lateral support for the recording probes. For recording, the head was held in a custom naso-orbital restraint and a silicon microelectrode (Neuronexus Tech, Ann Arbor MI) was lowered into the brain perpendicular to the cortical surface, to a depth of 1–1.5 mm. Electrodes were estimated to be in deep layers by field potential reversal (Kandel & Buzsaki, 1997), most likely layer V due to electrode depth and the presence of broadly tuned units of high background rate (Sakata and Harris, SFN Abstract #389.14, 2007). Probes consisted of eight shanks (200-μm shank separation), and each shank had four recording sites (160 μm2 each site; 1–3 MΩ impedance, tetrode configuration). The location of the recording sites was estimated to be primary auditory cortex (A1/AAF) by stereotaxic coordinates, vascular structure (Doron et al., 2002; Rutkowski et al., 2003; Sally and Kelly, 1988), tonotopic variation of frequency tuning across recording shanks, and the presence of cells with V-shaped tuning curves. Extracellular signals were band-pass filtered (1 Hz-8 kHz) and amplified (1,000 times) using a 64-channel amplifier (Sensorium, Charlotte, VT). The wide-band signal was digitized continuously at 20 kHz with an analog-to-digital converter card (UEI, Walpole, MA) inside a standard PC. Units were isolated by a semiautomatic algorithm (Harris et al., 2000), followed by manual adjustment (http://klusters.sourceforge.net). Multiunit activity, clusters with low separation quality (isolation distance <20; Harris et al., 2001; Schmitzer-Torbert et al., 2005) were excluded from analysis. All experiments were carried out in accordance with protocols approved by the Rutgers University Animal Care and Use Committee.
Acoustic stimulation
All experiments were conducted in a single-walled sound attenuating chamber (IAC, Bronx NY), internally coated with Sonex acoustic foam (Acoustical solutions Richmond, VA). Sounds were generated by a RP2 signal processor, attenuated by a PA5 attenuator, and delivered free field by an ED1-ES1 speaker system (Tucker-Davis Technologies, Alachua FL). The stimulus battery consisted of 18 pure tones logarithmically spaced from 3–43 kHz. To compensate for the transfer function of the acoustic chamber, tone amplitudes were calibrated prior to the experiment using a condenser microphone placed next the animal’s head (7017, ACO Pacific, Belmont CA) and a MA3 microphone amplifier (Tucker-Davis). Stimuli were 1 s long, interleaved by 1 s silence, at 70 dB SPL (4 datasets), or 500 ms long interleaved by 500 ms silence at 30, 40, 50, 60, and 70 dB SPL (7 datasets); in the present manuscript, only responses to 70 dB tones were analyzed. Tones were presented repeatedly (~200 repetitions of each frequency, for experiments with 1s tones and ~100 for 500ms tones) in random order; in a subset of experiments, the order of tones was fixed between repetitions (see supplementary figure S2).
Data analysis
Data analyses were performed in MATLAB (Mathworks, Natick MA). Early (onset), late (sustained), and baseline periods were defined as 0–200ms, 500–1000ms (800–1000 ms, when the epoch needed to be of equal duration for statistical analysis), and -200-0 ms relative to tone presentation; offset period was defined as 0–200ms after tone offset. Population vector trajectories fs(t) were computed for each stimulus s (i.e. each tone frequency) giving the mean rate of all cells at time t after tone onset, by averaging firing rates across all ~200 repetitions in 5ms bins, and smoothing by convolution with a Hamming window (50ms width).
The similarity of population vectors was computed either using Euclidean distance ||f1−f2||, or their angle . When ||f1||||f2|| =0, α was set to π/2. Prior to angle comparison the baseline firing rate was subtracted for each cell.
Coding sparseness was assessed by multiple measures. Lifetime (cell-wise) sparseness was computed for each cell as , where n is number of stimuli, and f is the cell’s firing rate vector across frequencies. Population sparseness was computed for each stimulus using the same formula, but now with n the number of cells, and f the firing rate vector across cells for that stimulus. Lifetime and population skewness and kurtosis were calculated similarly, according to the formulas , and , where μ and σ are the mean and standard deviation of f.
For Principal Component Analysis, the population firing rate vectors fs(t) for each combination of stimulus s and time t were collected, and projections were computed from the top two eigenvectors of the covariance matrix of these vectors (variances were not normalized before applying PCA). For discriminant analysis, vectors were combined for the late period only (500–1000ms), and projections were computed from the top two eigenvectors of (where Σw and Σb are the within-stimulus and between-stimulus covariance matrices, respectively), to maximize the separation of the responses to different stimuli.
To evaluate the accuracy with which single-trial population responses could predict the presented stimulus, we used one of two metrics based on cross-validation (Kjaer et al., 1994). For the first metric, based on information theory, we estimated for each stimulus response an a posteriori probability distribution for the presented stimuli as follows. For a given response f, a measure of the distance of this response to all other responses fi in the data set was computed, which we denote as d(f, fi). Two distance measures were used, Euclidean distance and vector angle, as described above. Based on these distances, the probability that the response f observed on any trial was generated by stimulus s was estimated as , where the sum in the numerator runs over the responses to all other repetitions of the same stimulus s, and the sum in the denominator runs over all stimuli, and y is a regularization parameter. We note that this is equivalent to a zeroth order local likelihood estimator (Loader, 1999). Stimulus predictability was estimated as , providing a lower-bound estimate of mutual information. The regularization parameter y was varied over a range of values, and that giving the maximal information estimate chosen. For the second “winner-take-all” method, trials were repeatedly divided to training (90%) and test (10%) sets, and test set trials were classified by their Eucidean distance/vectorangle from the group centroids of the training set. The process was repeated until all test/training set combinations were exhausted.
Results
Sustained firing to tone stimuli
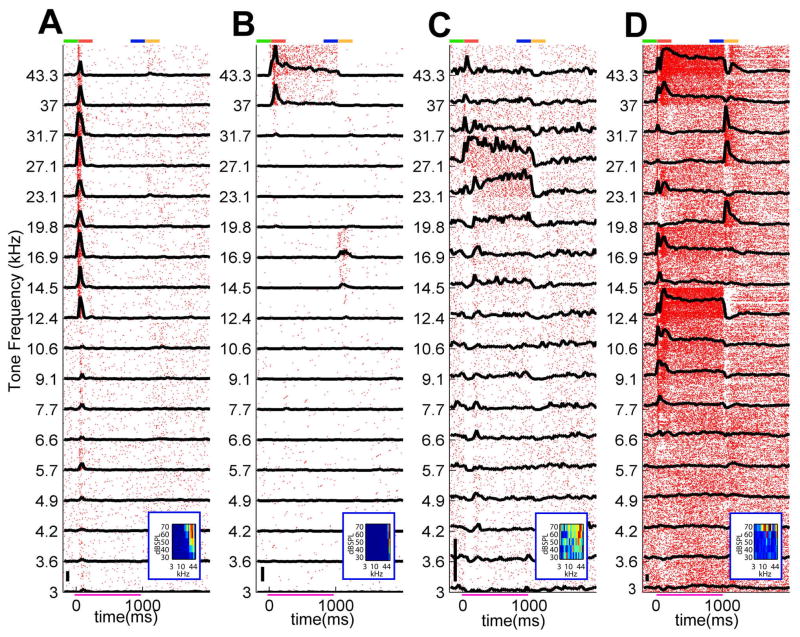
We recorded a total of 698 cells in primary auditory cortex of 5 rats under urethane anesthesia, while playing tone stimuli of 18 frequencies logarithmically spaced between 3 and 43.2 kHz at 70 dB SPL (see Supplementary Fig. 1 for an illustration of the spike-sorting procedure). We started our analysis at the single cell level. Examples of spike rasters and computed peristimulus time histograms (PSTHs) are shown in Figure 1 for four representative cells. Visual inspection of spike rasters (Fig. 1) revealed a wide diversity of stimulus tuning and response dynamics across the cell population. As expected, neurons typically showed the greatest increases in rate shortly after stimulus onset, but visible elevations or depressions of firing rate could often be seen throughout the stimulus period.
Figure 1.
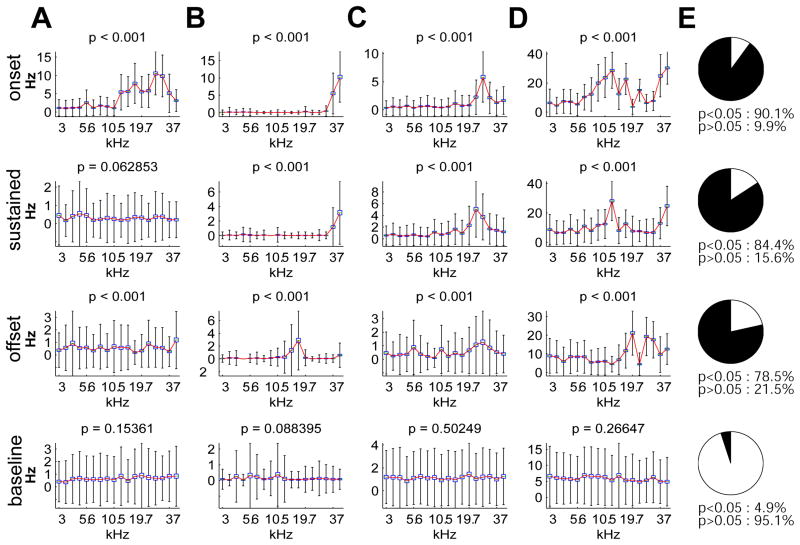
To statistically analyze these results, we first divided the stimulus period into three epochs of equal duration corresponding to the onset (0–200 ms after tone onset), sustained response (800–1000 ms after tone onset), and offset (0–200 ms after tone offset). For each epoch, the firing rate distribution of single trials was computed for each stimulus (Fig. 2, box-and-whisker plots), and the presence of sensory tuning was assessed by testing the null hypothesis that firing rate was independent of stimulus frequency (Kruskal-Wallis nonparametric ANOVA; parametric ANOVA also gave similar results). Most cells showed significant tuning in each time bin. In particular, a surprisingly large number of cells (84.4%) showed a significant effect of tone frequency on rate during the sustained period (p<0.05), compared to 90.1% in the onset period and 78.5% at offset (Fig. 2). Visual inspection of firing rate curves as a function of frequency (Fig. 2A–D) revealed that the differences in rate between frequencies corresponding to significant differences could be very subtle, especially during the sustained period. In our experiments, each tone was repeated a large number of times (>100), enabling the detection of small but significant differences in firing rate. To confirm that this significance did indeed reflect an effect of the stimulus rather than a statistical artifact, we performed a control analysis on the baseline periods (−200–0 ms) immediately before stimulus presentation (Fig 2, bottom). As expected, the fraction of cells significantly tuned in this epoch (4.9%) was close to the test’s expected false positive rate of 0.05. We therefore conclude that a majority of cells show some degree of tuning to tones throughout the stimulus, but that this tuning may be very weak during the sustained period, requiring averaging over many stimulus repetitions to be detected.
Figure 2.
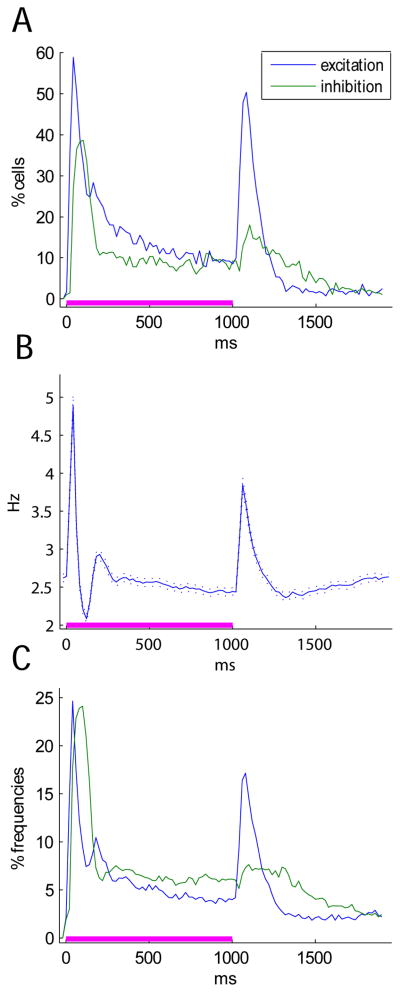
Neurons can encode information both by firing rate elevation or suppression. To characterize how the balance of elevation and suppression changes during the stimulus, we performed a different analysis. For each cell, firing rates were computed in 20 ms bins, and compared against a 20 ms baseline period preceding stimulus onset (Wilcoxon’s rank-sum test), revealing whether the cell responded significantly. Since multiple comparisons were made, the significance level was adjusted accordingly (Bonferroni correction). Figure 3A shows the percentage of cells showing significant excitation/suppression, as a function of time into the stimulus presentation. Excitatory tuning peaks shortly after tone onset, followed quickly by a second partially overlapping period of suppression; this pattern of elevation followed by suppression was mirrored in a plot of the mean rate as a function of time averaged over all stimulus frequencies (Fig. 3B). Note that the smaller fraction of tuned neurons than detected in Figure 2 reflects decreased statistical power due to the smaller time bins (20ms vs. 200ms) and use of the Bonferroni method. The decrease in overall firing rate during the sustained period was also accompanied by an increase in tuning selectivity; Figure 3C shows that a smaller percentage of stimulus frequencies elicit significant excitation or inhibition during the sustained response, compared to the onset period. Note that tuning selectivity as defined here is not the same as tuning sharpness of an ideal V-shaped tuning curve, but simply the percentage of stimuli the cell responds to significantly.
Figure 3.
Dynamics of population representations
We next asked how the responses of single neurons combine to form population representations. To address this, we collected each cell’s peri-stimulus time histogram (PSTH) in response to each stimulus, into a rate vector fs(t), giving the mean firing rate of each cell at a time t into the presentation of stimulus s. Data from the 4 experiments presenting 1s tones were pooled to form a “virtual population” (Harris, 2005) of 282 cells. For each stimulus, we therefore obtain a trajectory through a 282-dimensional space over the course of the stimulus.
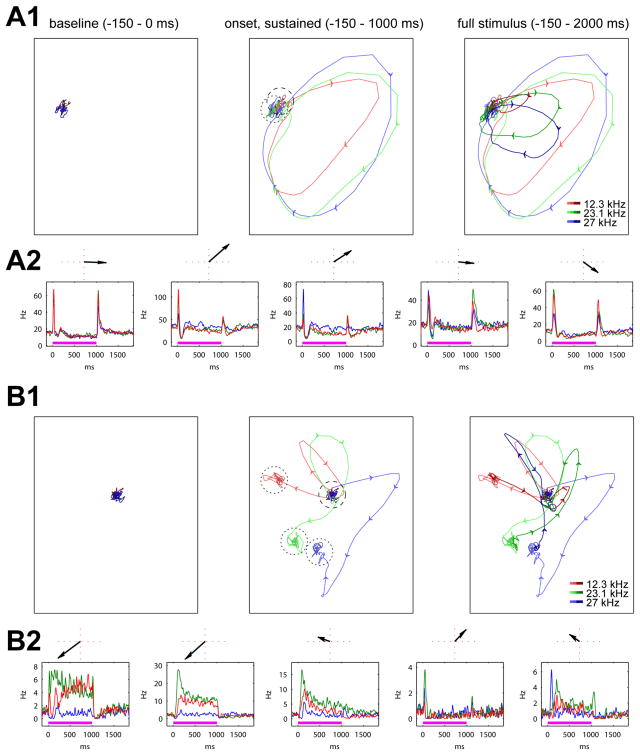
To gain intuition into the character of these trajectories, we started with a visualization analysis. Visualization of high-dimensional data can be achieved by multiple methods, typically involving projection of the data onto a two-dimensional space. We first applied principal component analysis (PCA; see Materials and Methods), which projects the trajectories onto the dimensions accounting for the maximum fraction of total variance (Fig. 4A1). In this projection, the most clearly visible feature was the onset response, which showed a similar circular trajectory that was largely independent of tone frequency. Sustained responses were barely distinguishable from baseline firing in this projection, and offset responses again showed circular profiles, broadly similar between tone frequencies, but different to those seen at onset. Cells contributing most to this projection had prominent onset and offset responses, but barely any sustained responses (Fig 4A2),
Figure 4.
To visualize sustained activity, we therefore adopted a different method, multiple discriminant analysis, which selects a projection that optimizes the separation of a chosen feature (in our case, sustained firing rates; Fig. 4B1; see methods). In this projection, the peak no longer dominated, and sustained responses were clearly distinguishable from baseline and from each other. However, even though this projection was chosen to maximize the differentiation of sustained responses between stimuli, the onset responses are of approximately equal magnitude to sustained responses. These data therefore indicate that at the population level activity is dominated by onset responses, and that information about tone frequency is also present in the sustained period, but visible only in specially chosen projections.
Time course of population vector rotation
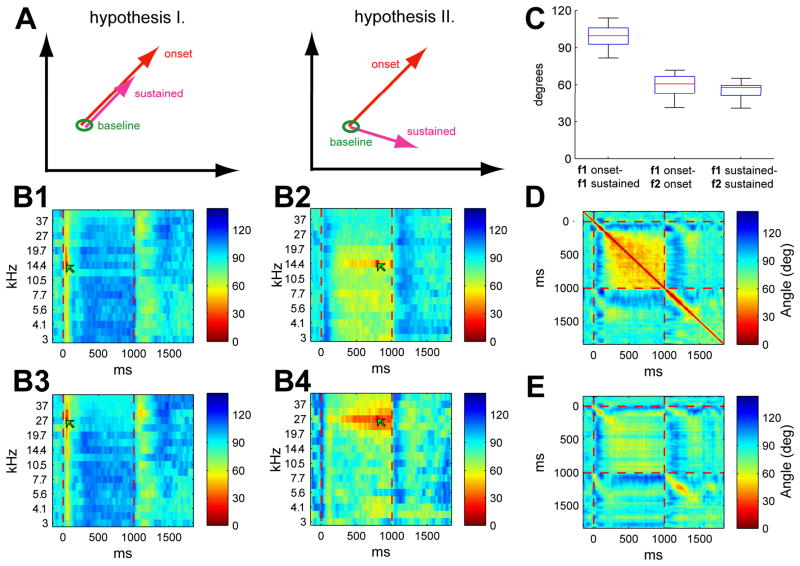
The visualization analysis suggested that presentation of tone stimuli caused rate vectors to rotate for an initial period after onset, leading to fixed points during the sustained period. These fixed points differ from the onset trajectories of the same stimulus, and are also distinct between different stimuli. We note that rotation is not a priori the only way for rate vectors to evolve during sustained stimuli. For example, if the dynamics of tone responses were dominated by simple firing rate adaptation, and if different cells adapted with a similar time course, one would expect the vectors to scale down linearly throughout the tone time course, but not rotate (Fig. 5A). To statistically investigate the rotation of population vectors, we performed an analysis of the angles between rate vectors. For a particular reference vector, observed in response to a stimulus s0 and post-stimulus time t0, the angle between the reference vector fs0(t0) and all other vectors fs(t) was computed, after subtraction of baseline firing rate vector f̄:
Figure 5.
Figure 5B shows four examples of this analysis. It can be seen in these examples that responses to different frequencies, but at the same time (e.g. onset vs. onset) are closer in angle than responses to the same frequency at different times. To confirm that these examples were indeed representative of the general case, we computed the angles between responses to the same tone at different times (f1 onset vs. f1 sustained) and between responses to different tones at the same time (f1 onset vs. f2 onset; f1 sustained vs. f2 sustained). The angles between responses to the same tone at different times were significantly greater, confirming that rate vector rotation makes a greater contribution to angular differences than differences between tone frequency (Fig. 5C).
To investigate the time course over which the rate vector rotation occurs, Figure 5D shows the angle between the population vectors evoked by a 14.4 kHz tone stimulus for each pair of times. A thin diagonal stripe is visible after onset, leading to a square patch spanning 300ms-1s; this indicates that the population vector begins rotating immediately after stimulus onset, and continues to do so for ~300ms, before converging to a steady state response. Similar dynamics are seen after tone offset. Figure 5E shows the angles between population vectors evoked by 14.4kHz and 31.6kHz tones; while the angles here are typically greater, a small spot is seen at onset, reflecting the angular similarity of onset vectors induced by different tones. These analyses therefore confirm that, in keeping with the visual picture presented in Fig. 4, the transition between onset and sustained responses consists of a nonlinear population vector rotation, rather than linear scaling, leading to a fixed point a few hundred milliseconds after stimulus onset. Furthermore the angular difference between responses to the same tone at different times exceeds the difference between different tones at the same time.
Do rate vectors progressively differentiate?
In some neural systems, the time evolution of population representations has been reported to progressively differentiate neural responses, meaning that while similar stimuli evoke similar rate vectors at stimulus onset, their responses diverge with time thereafter (Friedrich & Laurent, 2001; Menz & Freeman, 2003; Hegde & Van Essen, 2004; 2006). Because the tuning selectivity of individual neurons increases into the sustained period, we asked whether auditory cortical tone representations might also show progressive differentiation. The similarity between rate vectors can be assessed using multiple measures. Here we consider two: the angle between vectors (c.f. Fig. 5A), and also the Euclidean distance between them.
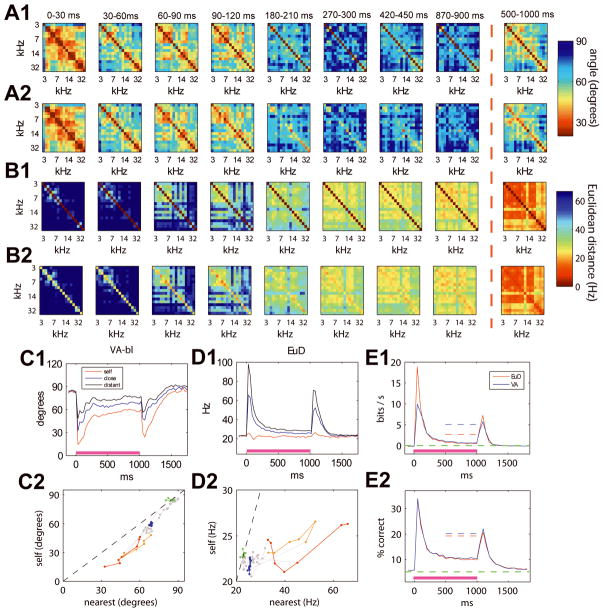
Figure 6A presents the results of an analysis measuring vector similarity through angles. We divided the stimulus into fixed time bins (0–30ms, 30–60ms, etc), and computed for each time bin the similarity between the population vectors evoked by each stimulus pair (e.g. 3 kHz vs. 7 kHz tone). The evolution of response similarity as measured by the angle between population vectors is shown in Fig. 6A1. Population vectors at onset (0–30ms) are nonorthogonal (angle < 90 degrees), even for widely spaced tone frequencies. As time goes by, the angle between vectors for even similar tones tends to 90 degrees, apparently indicating that these vectors do orthogonalize; these results bear a striking resemblance to the results of (Friedrich & Laurent, 2001) in the fish olfactory system.
Figure 6.
Nevertheless, caution is required in interpreting this result. In high dimensional spaces, random vectors are orthogonal with high probability (Scott, 1992); we must therefore verify that the apparent differentiation seen in Fig. 6A1 is not simply due to the effects of random noise superimposed on vectors of small length. To investigate this question, we applied a “cross-validation” approach: each of the N repetitions of each stimulus was randomly assigned to one of two sets, which were used to generate two independent estimates of the rate vector trajectories fs(t). We then repeated the analysis of Figure 6A1 for these two vectors (Fig. 6A2). For the first few time bins, the results appear similar to those of Fig. 6A1. For later time bins, while the off-diagonal elements (corresponding to the angles between vectors for different frequencies) are similar to those seen in Fig. 6A1, the diagonal stripe, which shows the similarity of the population vectors estimated for a single time and frequency from the two halves of the data set (similarity with itself), also fades with time, indicating that the rate vector responses to a single stimulus, estimated during the sustained period in 30ms time bins, are barely more similar across halves of the data set than responses to different stimuli. When computing sustained rate vectors using a larger time bin (500–1000ms), the diagonal line reappears, confirming that reliable responses to tones are present in the sustained period, but require averaging over longer data epochs. Note, however, that the appearance of this plot is visually similar to the 30–60ms bin, indicating that progressive differentiation, as measured by vector angle, is weak at best.
Figure 6C1 shows the average angle between population responses from two halves of the dataset, comparing the stimulus with itself (“self angle,” red line), with the stimulus of the nearest tone frequency (“nearest angle,” blue line), and stimuli of distant frequencies (black line). Progressive differentiation would require the angle between non-identical stimuli to decrease compared to identical stimuli, which is not the case except perhaps for the first time bin. Similarly, by plotting self angle against nearest angle (Fig 6C2), we should see differentiation as a horizontal line; however this plot is only close to horizontal between the 0–30ms and 30–60ms bins, meaning that any progressive differentiation is restricted to this early period. If similarities between vectors are measured using Euclidean distance, the results are even more striking. As Figs. 6B and 6D1-2 indicate, rate vectors for separate tones move closer together, not further apart, with time into the stimulus. We conclude that, although some progressive differentiation as measured by vector angle may occur over the first 60ms of tone presentation, progressive differentiation does not occur over the sustained period as assessed by vector angle, and the opposite (“progressive compression”) occurs as measured by Euclidean distance.
To assess the relevance of these results to encoding of information on single trials, we performed a stimulus reconstruction analysis. The tone period was divided into successive 50ms time bins. From the population response in each time bin on each trial, we predicted the posterior probability that each possible stimulus would have generated it, using a local smoothing method based on the similarity of this response to exemplars from the rest of the data set (Loader, 1999). The accuracy of this prediction was measured by log2-likelihood, giving a lower-bound estimate of the mutual information of the stimulus with population activity (Kjaer et al., 1994; Harris et al., 2003; Itskov et al., 2008). Stimulus prediction was based on two measures of response similarity, vector angle and Euclidean distance. With both methods, stimulus predictability shows a constant decrease throughout the tone presentation, confirming that activity at all points in the sustained period contains less information than at onset (Fig. 6E1). Even using an extended bin (500–1000ms), predictability is still smaller than in the 0–30ms bin. We then used a second approach (“winner-take-all” prediction), in which the population vector on each trial was used to compute the most likely stimulus based on Euclidean distance/angle from the centroid of each stimulus’ responses on the training set. This method gave similar results (Fig. 6E2). We thus conclude that representation of the stimulus persists into the sustained period, but in a weakened form.
Do rate vectors sparsen with time?
A “sparse code” is typically defined as a neural representation where information is carried by the activity of a small number of neurons. Although this concept sounds simple, multiple mathematical measures exist for quantifying sparseness (Willmore & Tolhurst, 2001), suggesting that the character of a neural code cannot be summarized by a single parameter. As shown above, the fraction of auditory cortical cells showing significant excitation decreased during tone presentation, along with the number of stimuli evoking excitation in these cells. We therefore set out to investigate how multiple sparseness measures change between onset and sustained responses.
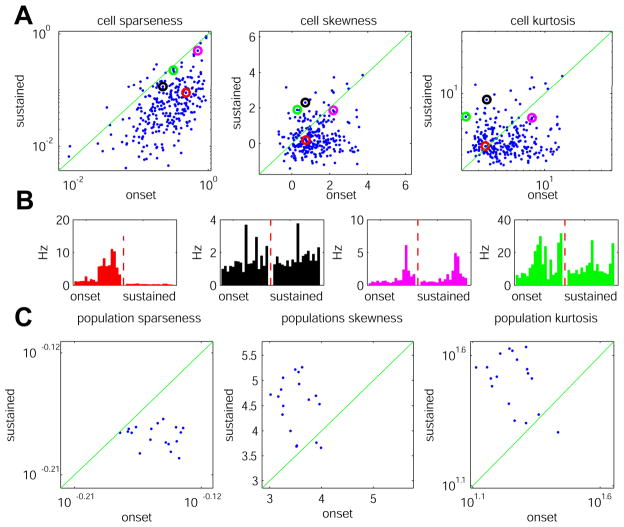
Sparseness measures are divided into two types: those that assess the tuning of single cells across multiple stimuli, and those that assess the distribution of activity in neuronal populations to individual stimuli. We started with the former. Three measures were used: “lifetime sparseness” (essentially the coefficient of variation, transformed to lie between 0 and 1), and the skewness and kurtosis of the distribution of firing rates evoked by all stimuli (see Methods). The three measures yielded different results, with most neurons showing larger lifetime sparseness at onset than in the sustained period, but many of the same neurons showing larger values of skewness and kurtosis in the sustained period (Fig. 7). This apparent paradox is caused by the cells’ non-zero background firing rate. Lifetime sparseness measures the difference in firing rates between stimuli, relative to the cell’s mean rate. Even for cells with more selective tuning during the sustained period (such as the black and green cells in Fig. 7B), variance is greater at onset, while the mean rate remains essentially the same in the two periods; therefore lifetime sparseness decreases, while kurtosis (which does not depend on mean rate), increases.
Figure 7.
A similar picture emerges from consideration of population measures, which are computed from the histogram of firing rates evoked in the population by a single stimulus. Population sparseness again decreases during sustained periods (also due to the non-zero baseline firing rates), but population skewness and kurtosis show an almost uniform increase in the sustained period, indicating that activity in the sustained period is characterized by a smaller number of neurons firing at above mean rate. Although the multiple measures of code sparseness thus yield different numerical results on our data, all these analyses are consistent with a simple picture: during stimulus onset, information is carried by a large number of neurons, which respond strongly to multiple stimuli; during the sustained period, information is carried by a smaller number of neurons firing with more selective tuning, with the majority of neurons weakly tuned and firing close to baseline rate.
Discussion
We have examined the responses of neural populations in auditory cortex to tone stimuli using rate vector methods. We found that rate vectors evolve during the first few hundred milliseconds of tone presentation, from a robust onset response to a more subtle sustained response. Most neurons showed a statistically significant effect of tone frequency on firing rate throughout the tone presentation. The nature of the code, however, markedly changed between stimulus onset and the late (sustained) period. Population rate vectors rotated during the initial ~300 ms of stimulus presentation, with the angular difference between onset and sustained responses to a single tone exceeding the angles between responses to different tones during a single stimulus epoch. Despite more selective tuning of individual neurons, population responses to different stimuli did not progressively differentiate, instead producing a code in which the information carried by selectively tuned neurons is counterbalanced by noise from the larger population of neurons firing close to baseline rate.
For many questions, the answers depended on the precise mathematical definitions given to biological terms. For example, while the use of Euclidean distance and vector angle gave similar answers to the question of progressive differentiation, performing the analysis without cross-validation resulted in a misleadingly strong apparent effect. For the question of sparsening, measures based on coefficient of variation gave different answers to skewness and kurtosis. Despite these differences, our results were all consistent with a single coding strategy, in which the majority of neurons fire at close to non-zero baseline rate during the sustained period, with a minority firing at substantially elevated rates for each stimulus. It is likely that a single term such as “sparseness” cannot fully capture the range of strategies a neural population may use to encode information. As population coding is studied in more systems, use of multiple quantitative measures may more fully characterize differences between potential coding strategies, as well as providing new terminology to describe these strategies.
We were surprised by the large fraction of neurons showing statistically significant frequency tuning during the late response period. Many of these neurons showed only small differences in firing rate with frequency. As statistical analysis of small effects is highly sensitive to assumptions about the data, we took care to ensure this result was not a false positive. First, the use of a non-parametric test (Kruskal-Wallis, rather than ANOVA) ensured that significance would not be erroneously detected due to non-Gaussianity of the spike count data. Second, an analysis of the baseline periods immediately preceding tone stimuli, where frequency tuning is impossible, yielded a false-positive rate close to that expected with a 0.05 significance level. We therefore concluded that the large number of significantly tuned cells indeed reflected detection of small effects by a powerful statistical test; the statistical power of this analysis is high due to the large number of repetitions of each tone (>100). We note also that the 84% fraction of tuned cells found is likely an underestimate, and that analysis of even more repetitions might find that virtually every cell in auditory cortex has a small degree of frequency tuning in the late period.
The finding that auditory cortical neurons show complex temporal dynamics, including sustained firing, during tone presentation, is consistent with reports of previous single-cell recordings in awake, ketamine-, halothane- or barbiturate-anesthetized subjects (Sally & Kelly, 1988; Volkov & Galazyuk, 1992; Wang et al., 2005; Moshitch et al., 2006), but contrasts with other reports using barbiturates or ketamine-xylazine (deCharms & Merzenich, 1996; DeWeese et al., 2003), which have suggested reliable spiking at onset without rate changes during the sustained period. While a full analysis of the comparative effects of multiple anesthetics on sustained responses is beyond the scope of the current study, our results suggest that absence of auditory cortical sustained responses is not a consequence of anesthesia per se, but rather of particular anesthetic/stimulus conditions.
Dynamic evolution of neural codes during presentation of temporally unstructured stimuli has been reported in many sensory systems, in evolutionarily remote species (Sugase et al., 1999; Friedrich & Laurent, 2001; Menz & Freeman, 2003; Stopfer et al., 2003; Mazor & Laurent, 2005; Brincat & Connor, 2006). Why should such dynamics be such a common feature of neural coding? Although the systems shown to exhibit this behavior differ in many ways, they are all recurrent neural networks. In models of recurrent networks, dynamical evolution of population activity is common, and indeed can only be suppressed by fine tuning of synaptic weights (Brody et al., 2003). Dynamical evolution of population codes may thus be an almost inevitable consequence of information processing by recurrent networks.
What benefit could such representational dynamics provide an organism? Although population vector rotation is a very common feature of neural codes, the endpoint of this dynamics varies between systems. In some sensory systems, population responses progressively differentiate with time, so that perceptually similar stimuli that evoke similar onset responses exhibit divergent sustained responses (Sugase et al., 1999; Friedrich & Laurent, 2001; Hegde & Van Essen, 2004), thus producing finer stimulus discrimination with time. In our results this appears to be the case when the dataset is not cross-validated; with cross-validation, however, progressive differentiation in the sustained period is unclear or absent. While Friedrich & Laurent did not perform a cross-validated analysis of progressive differentiation, other analyses from their study suggest that the differences between their results and ours do indeed reflect differences in population coding of the two sensory systems, rather than different analysis techniques. For example, while we found that stimulus discriminability decreased with time, they found it increased (with cross-validation); while we found most cells’ firing rates decayed close to baseline during the sustained period, they found more sustained high rate responses.
Our results therefore suggest that population coding dynamics in auditory cortex differs from that in many other systems studied to date. Instead of progressive differentiation, we observed a re-coding of information from an onset response requiring rapid firing of a large number of neurons, to a sustained response in which most neurons continue to fire around baseline rate. This may relate to the fact that continuous acoustic stimuli are typically not perceptually or behaviorally salient. The progressive re-coding we observe may instead allow an animal to maintain a representation of ongoing sounds, at low energetic cost.
Acknowledgments
This study was supported by NIH grants MH073245 and RO1DC009947. K.D.H. is an Alfred P. Sloan fellow.
References
- Bieser A, Muller-Preuss P. Auditory responsive cortex in the squirrel monkey: neural responses to amplitude-modulated sounds. Exp Brain Res. 1996;108:273–284. doi: 10.1007/BF00228100. [DOI] [PubMed] [Google Scholar]
- Brincat SL, Connor CE. Dynamic shape synthesis in posterior inferotemporal cortex. Neuron. 2006;49:17–24. doi: 10.1016/j.neuron.2005.11.026. [DOI] [PubMed] [Google Scholar]
- Brody CD, Romo R, Kepecs A. Basic mechanisms for graded persistent activity: discrete attractors, continuous attractors, and dynamic representations. Curr Opin Neurobiol. 2003;13:204–211. doi: 10.1016/s0959-4388(03)00050-3. [DOI] [PubMed] [Google Scholar]
- deCharms RC, Merzenich MM. Primary cortical representation of sounds by the coordination of action-potential timing. Nature. 1996;381:610–613. doi: 10.1038/381610a0. [DOI] [PubMed] [Google Scholar]
- DeWeese MR, Wehr M, Zador AM. Binary spiking in auditory cortex. J Neurosci. 2003;23:7940–7949. doi: 10.1523/JNEUROSCI.23-21-07940.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedrich RW, Laurent G. Dynamic optimization of odor representations by slow temporal patterning of mitral cell activity. Science. 2001;291:889–894. doi: 10.1126/science.291.5505.889. [DOI] [PubMed] [Google Scholar]
- Grossberg S. On the development of feature detectors in the visual cortex with applications to learning and reaction-diffusion systems. Biol Cybern. 1976;21:145–159. doi: 10.1007/BF00337422. [DOI] [PubMed] [Google Scholar]
- Harris KD. Neural signatures of cell assembly organization. Nat Rev Neurosci. 2005;6:399–407. doi: 10.1038/nrn1669. [DOI] [PubMed] [Google Scholar]
- Harris KD, Csicsvari J, Hirase H, Dragoi G, Buzsaki G. Organization of cell assemblies in the hippocampus. Nature. 2003;424:552–556. doi: 10.1038/nature01834. [DOI] [PubMed] [Google Scholar]
- Harris KD, Henze DA, Csicsvari J, Hirase H, Buzsaki G. Accuracy of tetrode spike separation as determined by simultaneous intracellular and extracellular measurements. J Neurophysiol. 2000;84:401–414. doi: 10.1152/jn.2000.84.1.401. [DOI] [PubMed] [Google Scholar]
- Hegde J, Van Essen DC. Temporal dynamics of shape analysis in macaque visual area V2. J Neurophysiol. 2004;92:3030–3042. doi: 10.1152/jn.00822.2003. [DOI] [PubMed] [Google Scholar]
- Hegde J, Van Essen DC. Temporal dynamics of 2D and 3D shape representation in macaque visual area V4. Vis Neurosci. 2006;23:749–763. doi: 10.1017/S0952523806230074. [DOI] [PubMed] [Google Scholar]
- Heil P. Auditory cortical onset responses revisited. II. Response strength. J Neurophysiol. 1997;77:2642–2660. doi: 10.1152/jn.1997.77.5.2642. [DOI] [PubMed] [Google Scholar]
- Hoffman KL, Battaglia FP, Harris K, MacLean JN, Marshall L, Mehta MR. The upshot of up states in the neocortex: from slow oscillations to memory formation. J Neurosci. 2007;27:11838–11841. doi: 10.1523/JNEUROSCI.3501-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Itskov V, Curto C, Harris KD. Valuations for spike train prediction. Neural Comput. 2008;20:644–667. doi: 10.1162/neco.2007.3179. [DOI] [PubMed] [Google Scholar]
- Ji D, Wilson MA. Firing rate dynamics in the hippocampus induced by trajectory learning. J Neurosci. 2008;28:4679–4689. doi: 10.1523/JNEUROSCI.4597-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kandel A, Buzsaki G. Cellular-synaptic generation of sleep spindles, spike-and-wave discharges, and evoked thalamocortical responses in the neocortex of the rat. J Neurosci. 1997;17:6783–6797. doi: 10.1523/JNEUROSCI.17-17-06783.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kjaer TW, Hertz JA, Richmond BJ. Decoding cortical neuronal signals: network models, information estimation and spatial tuning. J Comput Neurosci. 1994;1:109–139. doi: 10.1007/BF00962721. [DOI] [PubMed] [Google Scholar]
- Kohonen T. Self-organization and associative memory. Springer; 1989. [Google Scholar]
- Laurent G. Olfactory network dynamics and the coding of multidimensional signals. Nat Rev Neurosci. 2002;3:884–895. doi: 10.1038/nrn964. [DOI] [PubMed] [Google Scholar]
- Loader C. Local regression and likelihood. Springer-Verlag; New York: 1999. [Google Scholar]
- Lu T, Liang L, Wang X. Temporal and rate representations of time-varying signals in the auditory cortex of awake primates. Nat Neurosci. 2001;4:1131–1138. doi: 10.1038/nn737. [DOI] [PubMed] [Google Scholar]
- Luczak A, Bartho P, Harris KD. Spontaneous events outline the realm of possible sensory responses in neocortical populations. Neuron. 2009;62:413–425. doi: 10.1016/j.neuron.2009.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luczak A, Bartho P, Marguet SL, Buzsaki G, Harris KD. Sequential structure of neocortical spontaneous activity in vivo. Proc Natl Acad Sci USA. 2007;104:347–352. doi: 10.1073/pnas.0605643104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazor O, Laurent G. Transient dynamics versus fixed points in odor representations by locust antennal lobe projection neurons. Neuron. 2005;48:661–673. doi: 10.1016/j.neuron.2005.09.032. [DOI] [PubMed] [Google Scholar]
- Menz MD, Freeman RD. Stereoscopic depth processing in the visual cortex: a coarse-to-fine mechanism. Nat Neurosci. 2003;6:59–65. doi: 10.1038/nn986. [DOI] [PubMed] [Google Scholar]
- Moshitch D, Las L, Ulanovsky N, Bar-Yosef O, Nelken I. Responses of neurons in primary auditory cortex (A1) to pure tones in the halothane-anesthetized cat. J Neurophysiol. 2006;95:3756–3769. doi: 10.1152/jn.00822.2005. [DOI] [PubMed] [Google Scholar]
- Parkinson AM, Parpia DY. Intensity encoding in unsupervised neural nets. Neural Netw. 1998;11:723–730. doi: 10.1016/s0893-6080(98)00002-1. [DOI] [PubMed] [Google Scholar]
- Perez-Orive J, Mazor O, Turner GC, Cassenaer S, Wilson RI, Laurent G. Oscillations and sparsening of odor representations in the mushroom body. Science. 2002;297:359–365. doi: 10.1126/science.1070502. [DOI] [PubMed] [Google Scholar]
- Phillips DP. Temporal response features of cat auditory cortex neurons contributing to sensitivity to tones delivered in the presence of continuous noise. Hear Res. 1985;19:253–268. doi: 10.1016/0378-5955(85)90145-5. [DOI] [PubMed] [Google Scholar]
- Recanzone GH. Response profiles of auditory cortical neurons to tones and noise in behaving macaque monkeys. Hear Res. 2000;150:104–118. doi: 10.1016/s0378-5955(00)00194-5. [DOI] [PubMed] [Google Scholar]
- Sally SL, Kelly JB. Organization of auditory cortex in the albino rat: sound frequency. J Neurophysiol. 1988;59:1627–1638. doi: 10.1152/jn.1988.59.5.1627. [DOI] [PubMed] [Google Scholar]
- Scott D. Multivariate Density Estimation: Theory, Practice, and Visualization (Wiley Series in Probability and Statistics) Wiley-Interscience; 1992. [Google Scholar]
- Stopfer M, Jayaraman V, Laurent G. Intensity versus identity coding in an olfactory system. Neuron. 2003;39:991–1004. doi: 10.1016/j.neuron.2003.08.011. [DOI] [PubMed] [Google Scholar]
- Sugase Y, Yamane S, Ueno S, Kawano K. Global and fine information coded by single neurons in the temporal visual cortex. Nature. 1999;400:869–873. doi: 10.1038/23703. [DOI] [PubMed] [Google Scholar]
- Vaadia E, Gottlieb Y, Abeles M. Single-unit activity related to sensorimotor association in auditory cortex of a monkey. J Neurophysiol. 1982;48:1201–1213. doi: 10.1152/jn.1982.48.5.1201. [DOI] [PubMed] [Google Scholar]
- Volkov IO, Galazjuk AV. Formation of spike response to sound tones in cat auditory cortex neurons: interaction of excitatory and inhibitory effects. Neuroscience. 1991;43:307–321. doi: 10.1016/0306-4522(91)90295-y. [DOI] [PubMed] [Google Scholar]
- Volkov IO, Galazyuk AV. Peculiarities of inhibition in cat auditory cortex neurons evoked by tonal stimuli of various durations. Exp Brain Res. 1992;91:115–120. doi: 10.1007/BF00230019. [DOI] [PubMed] [Google Scholar]
- Wang X, Lu T, Snider RK, Liang L. Sustained firing in auditory cortex evoked by preferred stimuli. Nature. 2005;435:341–346. doi: 10.1038/nature03565. [DOI] [PubMed] [Google Scholar]
- Willmore B, Tolhurst DJ. Characterizing the sparseness of neural codes. Network. 2001;12:255–270. [PubMed] [Google Scholar]