INFERIOR OLIVE OSCILLATION AS THE TEMPORAL BASIS FOR MOTRICITY AND OSCILLATORY RESET AS THE BASIS FOR MOTOR ERROR CORRECTION

Abstract

The cerebellum can be viewed as supporting two distinct aspects of motor execution related to a) motor coordination and the sequence that imparts such movement temporal coherence and b) the reorganization of ongoing movement when a motor execution error occurs. The former has been referred to as “motor time binding” as it requires that the large numbers of motoneurons involved be precisely activated from a temporal perspective. By contrast, motor error correction requires the abrupt reorganization of ongoing motor sequences, on occasion sufficiently important to rescue the animal or person from potentially lethal situations. The olivo-cerebellar system plays an important role in both categories of motor control. In particular, the morphology and electrophysiology of inferior olivary neurons have been selected by evolution to execute a rather unique oscillatory pacemaking function, one required for temporal sequencing and a unique oscillatory phase resetting dynamic for error correction. Thus, inferior olivary (IO) neurons are electrically coupled through gap junctions, generating synchronous subthreshold oscillations of their membrane potential at a frequency of 1–10 Hz and are capable of fast and reliable phase resetting. Here I propose to address the role of the olivocerebellar system in the context of motor timing and reset.

The climbing fiber system, shown morphologically as originating from the inferior olive nucleus (Szentagothai and Rajkovits, 1959), is one of the two major afferent pathways to the cerebellar cortex (Cajal, 1888). Climbing fibers innervate Purkinje cells (PC) directly in the cerebellar cortex generating the largest synaptic junction in the vertebrate CNS. Indeed, activation of a climbing fiber is followed by an all or none burst of spikes in all of its postsynaptic PCs (Eccles et al., 1966). On average, each inferior olive (IO) neuron generates 10 or so climbing fibers (Armstrong and Schild, 1970) that distribute rostrocaudally over many folia over the cerebellar cortex. In addition to contacting PCs, climbing fibers also produce collateral branches that terminate in all cerebellar nuclei (Palay and Chan-Palay, 1974).

IO neurons fire spontaneously at 1–10 Hz and can exhibit rhythmic oscillatory activity near 10 Hz (Crill, 1970; Llinas and Yarom, 1981a,b). Likewise, the resulting complex spikes in the PCs are also rhythmic and have an average frequency of 10 Hz (Bell and Kawasaki, 1972). The fact that IO neurons are electrically coupled and tend to fire in groups (Llinas, 1974; Sotelo et al., 1974) led to the proposal that climbing fibers may perform a timing function in motor coordination (Llinas et al., 1975). Furthermore, simultaneous electrode recordings from multiple PCs have shown that complex spikes occur synchronously in a group of PCs (Bower and Woolston, 1983; Llinas and Sasaki, 1989; Lang et al., 1996; De Zeeuw et al., 1998; Fukuda et al., 2001a). Such synchronous activation of multiple PCs by the IO nucleus suggests that clusters of IO neurons have the ability to fire rhythmically and in unison. This spatial organization would be the actual product of dynamic plasticity established during development (Nicholson and Freeman, 2003). These synchronous IO oscillations have been proposed to be important in determining the timing and spatial organization of motor sequence during motor coordination (Llinas, 1988; Lampl and Yarom, 1997; Welsh and Llinas, 1997). According to that hypothesis, IO activity functions as a motor timing signal by generating synchronous and rhythmic activation of cerebellar nuclear and descending vestibular nuclear neurons. The timing of these nuclei is controlled additionally by the synchronized inhibitory barrage originated by the climbing fiber activation of PCs. Evidence in support of this motor timing proposal includes the synchronous firing of a population of PCs in an anesthetized and awake animal (Llinas and Sasaki, 1989; Lang et al., 1999; Fukuda et al., 2001b); recordings of rhythmic inhibitory potential in the deep cerebellar nuclei (Llinas and Muhlethaler, 1988); and temporal correlation between the firing of the olivocerebellar system and the execution of movements (Welsh et al., 1995). At a more global level, the inferior olive has been shown to have a deep and significant role in the maintenance of the dynamic properties of the cerebellar control of motricity by regulating the firing properties of the Purkinje. Thus, in the absence of the climbing fiber input PC fire constantly, indicating a dysregulation of their intrinsic electrical properties (Strata and Montarolo, 1982).

THE ISSUES OF TIMING AND ERROR CORRECTION

The functioning of the olivocerebellar system has been viewed as (A) addressing the time coherence of muscle activation required to generate the massively parallel event known as motor coordinated, and (B) as a system that responds to errors in motor execution.

Timing signal via temporal coherence clustering in the inferior olive

Concerning motor coordination and timing several general issues are evident in the electrophysiology of the olivocerebellar system. (i) The system generates a timing signal that is inscribed in the intrinsic electrical properties of single neurons and (ii) the organization of the nucleus via electrical coupling allows for synchronous multicellular temporal coherence that generates a close to simultaneous neuronal cluster activation. (iii) Due to the remarkable property of conduction isochronicity the timing signal does not disperse, against distance, as it is conducted along the pathways carrying it to the final integration sites at cerebellar nuclear level.

Single cell electrophysiology

The ability of the olivocerebellar system to generate synchronous rhythmic activity has been attributed to the intrinsic oscillatory properties of the IO neurons (Llinas and Yarom, 1981a,b; Benardo and Foster, 1986; Bal and McCormick, 1997) and their electrotonic coupling (Llinas, 1974; Sotelo et al., 1974; Llinas and Yarom, 1981b; Lampl and Yarom, 1997; Makarenko and Llinas, 1998; Yarom and Cohen, 2002). In particular, several types of voltage-dependent calcium and potassium conductances, in addition to those involved in action potential generation, enable IO cells to oscillate and fire rhythmically at 1–10 Hz. These conductances include a high-threshold Ca²⁺ conductance, a somatic low-threshold Ca²⁺ conductance, a Ca²⁺-activated K⁺ conductance, and a hyperpolarization-activated cationic conductance (Llinas and Yarom, 1981a,b, 1986; Bal and McCormick, 1997).

Concerning the electrical coupling, as in other CNS structures (Bennett, 2000), gap junctions constitute the main communication pathway between the IO neurons (Sotelo et al., 1974; De Zeeuw et al., 1996). Such electrotonic coupling has been assumed to play a crucial role in synchronizing IO oscillations and in generating groups of concurrently oscillating neurons (Llinas and Yarom, 1986), and was assumed to be controllable by return glomerular inhibition (Llinas et al., 1975). IO afferents were, in fact found to modulate the efficiency of electrotonic coupling, via inhibition at the glomerulus. The pathway turned out to be supported by a set of cerebellar nuclear GABAergic neurons (Sotelo et al., 1986; De Zeeuw et al., 1989; Fredette and Mugnaini, 1991; De Zeeuw et al., 1996; Medina et al., 2002) that additionally represent almost 50% of the total neuronal population in such nuclei, giving some measure of the importance of this feedback inhibitory pathway. Indeed, it was determined experimentally that such input can control the degree and distribution of synchronous oscillatory activity in the IO nucleus (Leznik et al., 2002) and the cerebellar cortex (Lang et al., 1996; Lang, 2001, 2002). Moreover, dynamic groups of IO neurons oscillating in phase can synchronously activate a population of PCs and thereby control patterns of synchronous activity in the cerebellum during motor coordination (Welsh et al., 1995).

Although synchronized IO oscillations are a neuronal ensemble event, they have been studied primarily on a single-cell level and no information has been available about their spatial profiles. Thus, an attempt was made to address this issue by utilizing a voltage-sensitive dye optical imaging technique (Leznik et al., 2002; Leznik and Llinas, 2005). This technique is presently the methodology of choice in studying the geometrical distribution of activity in a large neuronal ensemble (see, for instance, Ebner and Chen, 1995). We have shown that ensemble oscillations in the IO emanate from clusters of synchronized activity, where each cluster is a localized functional event composed of hundreds of cells. Given the distribution of complex spike activity in the cerebellum cortex, we have proposed that these clusters are very likely to be responsible for the synchronized activation of the PC observed in previous in vivo multielectrode experiments (Lang et al., 1996). Furthermore, when comparing our experimental results with those obtained by computational modeling of IO neuronal ensembles endowed with oscillatory electrical properties and electrotonic coupling (Makarenko and Llinas, 1998; Velarde et al., 2002), we could show that neuronal oscillatory clustering is a direct consequence of the combined electrotonic/intrinsic properties of coupled IO neurons (Leznik et al., 2002).

Inferior olive cluster activity: visualization using voltage dependent dye imaging and intracellular recordings

While electrical recording of IO neurons in vitro had indicated the possibility that electrically coupled IO cells could actually cluster into synchronized ensemble neuronal groupings, no direct demonstration for such dissipative structures has been presented. In searching for such dissipative structures, voltage-sensitive dye imaging of oscillatory theoretical activity was attempted and successfully implemented in rodent IO slices (Leznik et al., 2002).

Voltage-sensitive dye imaging of oscillatory activity was implemented successfully in rodent IO slices (Leznik et al., 2002). Thus, following IO electrical stimuli, which served to reset the phase of subthreshold oscillation and to entrain a large proportion of neurons to in-phase oscillations imaging of the spatiotemporal profiles of ensemble IO oscillations was unambiguously observed. Indeed, synchronization of oscillatory activity over the IO network increased the amplitude of the optical signal to a level that could be detected easily with our imaging setup. Such oscillatory reset was also observed with intracellular recordings from IO neurons (Fig. 1). The optically recorded oscillatory clusters have a dynamic spatial organization, and their amplitude depends on the oscillation phase such that they embraced the largest area during the upward phase of the oscillations. Each cluster consisted of a core region and the adjoining area. The core region demonstrated a close to constant size, but the extent of the adjoining area was found to be phase-dependent.

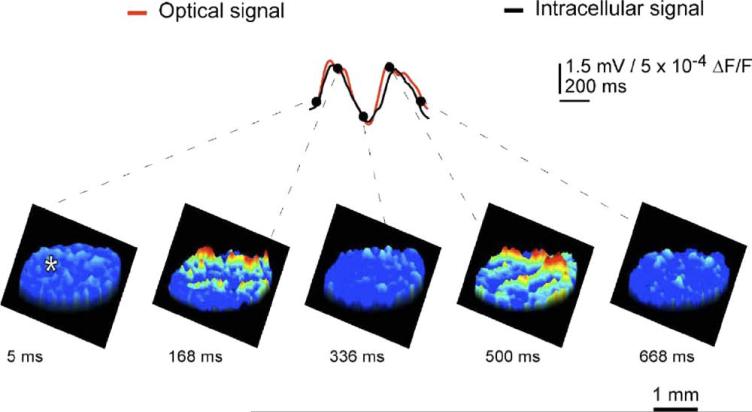
Fig. 1.

IO. Spontaneous oscillatory electrical activity was acquired simultaneously using optical voltage imaging and intracellular recording. The beginning of oscillatory sequence was defined as 0 ms. The upper panel superimposed the optical signal in red and intracellular voltage recording (asterisk) in black demonstrate temporal waveform coherence. The lower panels illustrate the spatial distribution of voltage imaging at five different time points indicated by dots in the upper panel from two successive oscillation cycles averaged three times over the oscillatory sequence. Note that ensemble oscillations emanated from several fluorescent clusters of coherent activity, and that the spatial and temporal structure of the IO cluster activity is discernable directly from cluster distribution and size. Time voltage and spatial distribution are as indicated by the calibration bars (modified from; Leznik and Llinas, 2005).

We calculated the core area and maximum area (i.e. the core region plus the adjoining area at its utmost extent) for several representative clusters in each experiment. The mean core area and the mean maximum area of a cluster occupied an area of several hundred μm². IO clusters are three-dimensional structures and measurement calculation of their volume suggests that they are composed of hundreds of cells. Thus, our optical data indicate that at the network level, the IO nucleus is organized in functionally coupled activity clusters. Each cluster is composed of several hundreds of cells, which may act in unison to activate groups of thousands of cerebellar PC simultaneously in agreement with multiple electrode recordings observed previously.

In conclusion, the dimensions of clusters are probably determined by the IO electrical coupling coefficient, and thus by the magnitude and distribution of the return inhibition from the cerebellar nuclear feedback, which has been demonstrated in previous in vivo experiments (Ruigrok and Voogd, 1995; Lang et al., 1996) and supported with mathematical modeling (Leznik et al., 2002; Velarde et al., 2002).

The climbing fiber conduction isochronicity

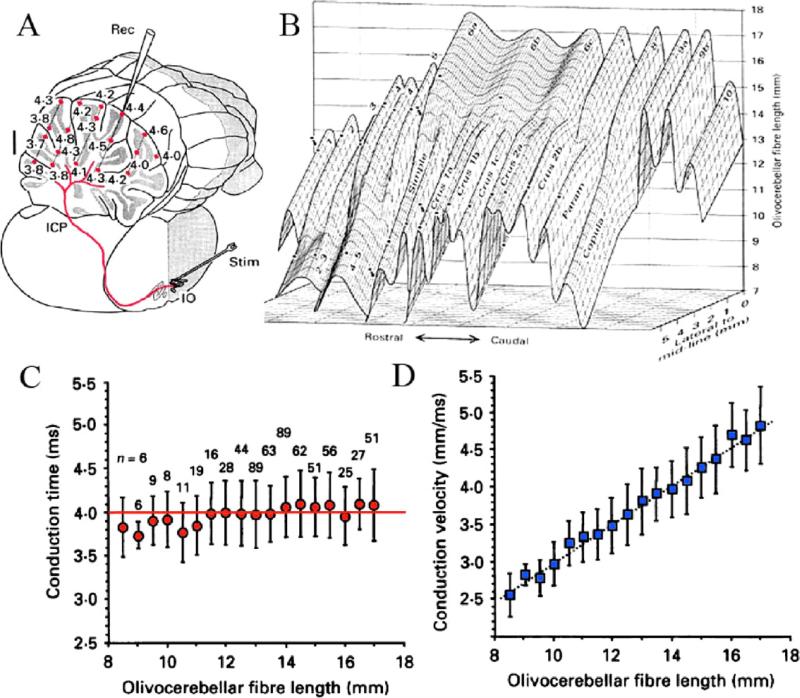
From another perspective, while the temporal distribution of activity is well demonstrated at the olivary level, one may wonder about the time dispersion produced by the olivocerebellar pathway given the different distances between the olive and their target PC. I came to the realization that if isochronicity is to be present, then the conduction time between the inferior olive and its target Purkinje cell should be close to uniform, independent from the distance such a signal had to travel. This issue is particularly significant given that the folding nature of such a cortex can increase the path length to the PC by more than 50%; furthermore, the correction of the conduction velocity required ensuring that synchronicity was related linearly to distance. Having tested this hypothesis with my colleagues Sugihara and Lang (Sugihara et al., 1993), it was very gratifying to find that the time dispersion for a nearly 4 ms conduction time was ±500 μs to any regions of the cerebellar mantle, regardless of the distance between the olive and the cerebellar cortex at the bottom or top of the deep cerebellar folia or at any point in between (Fig. 2). The results were based on complex spike latency from 660 different PC from 12 rats.

Fig. 2.

Olivo-cerebellar conduction time constancy throughout the extent of the cerebellar cortex. (A) Diagram of the path for a single climbing fiber (red). Microelectrode recorded PC complex spike latency at different depths (red dots) is shown in ms following IO electrical stimulation. (B) Tridimensional representation of CF length. The X and Z coordinates indicate, respectively, rostrocaudal/mediolateral CF localization in the different folia (indicated) and the Y-coordinate the CF length. (C) Conduction time is plotted against CF length (4 ms [variance±500 μs]). (D) Conduction velocity related linearly to length (modified from Sugihara et al., 1993).

Since that time, the isochrony was confirmed in further experiments with other cerebellar systems (Ariel, 2005; Brown and Ariel, 2009). A similar finding concerning conduction isochronicity has also been observed in the thalamocortical system and has been interpreted, as in the case of the olivo-cerebellar system, as a mechanism for temporal coherence. In this case, such timing has been related to the temporal coherence associated with cognitive binding (Engel et al., 1997; Salami et al., 2003; Chomiak et al., 2008; Vicente et al., 2008).

Therefore, the results indicated that the cerebellar cortex, while being deeply folded anatomically behaves, functionally, as an isochronous sphere as far as the olivocerebellar system is concerned. Further, such isochronicity is actually related to the onset time and duration required for proper motor execution (Welsh et al., 1995).

Error sensing

Finally, the issue of error sensing, which previously occupied a great deal of interest in cerebellar physiology, has been treated in detail in excellent reviews concerning inferior olive function (Simpson et al., 1996). My personal view is that the error sensing signal, in which climbing fiber responses are often observed—while being a very important functional phenotype—is not the central cerebellar function some authors claim.

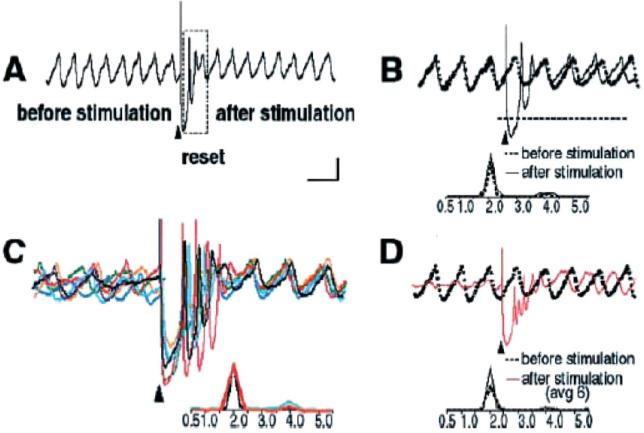
From my perspective, the high probability of complex spike activation in relation to unexpected error signals correlates well with such events simply because it is easier to detect, as climbing fiber activation is massive when a large reset of the oscillatory phase occurs (Makarenko and Llinas, 1998; Leznik et al., 2002; Chorev et al., 2007, Khosrovani et al. 2007; see also Van der Giessen et al., 2008, for the connexin 36 role in this reset) and when requiring a massive temporal reorganization of motor pattern activity. In agreement with previous intracellular results (Llinas and Yarom, 1986), an extracellular stimulation given at the dorsal border of the IO nucleus generated a full action potential followed by a membrane hyperpolarization in nearby neurons. These results also demonstrate that if the cell was oscillating at the time of the stimulus, its oscillations are stopped momentarily, but resumed with a different phase shortly after the stimulation. Moreover, in later experiments, it was also determined that such extracellular stimulation may reset the phase without affecting the amplitude or frequency of the subthreshold oscillation (Leznik et al., 2002), and that for most cells recorded, this phase reset could be observed repeatedly with subsequent stimuli. However, the most surprising property discovered was the fact that the oscillation phase shift was remarkably constant (Fig. 1C(im) and D) and independent from the original phase moment at which the stimulus was delivered. This property is of central importance in defining IO function, as it gives a clear time constraint to the functional states generated by the neuronal ensemble. This electrophysiological property is illustrated in Fig. 3.

Fig. 3.

Intracellular in vitro recording of spontaneous subthreshold oscillations and its phase reset by an electrical extracellular stimulus. (A) Following an extracellular stimulation (marked with an arrowhead), the oscillations disappeared for 750 ms (boxed area) and then resumed. The membrane potential was at –60 mV. (B) On the right, intracellular recordings of spontaneous (dashed black line) and stimulus-evoked (solid black line) oscillations from the same cell are superimposed. Their corresponding power spectra are shown below. Note that extracellular stimulation only modified the phase of spontaneous oscillations without affecting their amplitude and frequency. On the left (C), six individual intracellular traces of stimulus-evoked oscillations from the same cell are superimposed. Each trace is shown in a different color. Their corresponding power spectra are displayed below. Note that in each trace, the stimulation-induced shift in the cell's oscillatory rhythm is remarkably similar. Oscillations are seen clearly (D) after the stimulus-induced reset but can barely be detected before the stimulation. Scale bar=1 mV 1 s (Modified from Leznik et al., 2002).

The reset property of the IO circuit can thus be considered as the main component in the large correction that must be generated when a movement error is generated. This is best illustrated by the fast recovery that we all experience when tripping during locomotion and the fact that we do not fall, while robots do, under similar circumstances. The issue of error correction has been studied elegantly under conditions where random stimuli require temporal resting in cases in which robust activation of cerebellar system is encountered (Schweighofer et al., 2004); however, this issue must be addressed further as other views are also clearly present (Horn et al., 2004). The image one has is that of a very large population of PC-activated that then mediated a rapid inhibition of the inhibitory effect of the nucleo-olivary, thus resulting in increased coupling at the olivary level. This event will produce a large and coherent activation of IO neurons; thus, an increased probability of complex spike Purkinje activation ensues. In short, then, error correction is one mode, but not the main mode of inferior olive function.

From a motor control perspective, a previous study (Makarenko and Llinas, 1998) demonstrated that IO neurons have robust but sensitive dynamics of subthreshold oscillations with respect to interaction among themselves (“long-term” stimulation by electrotonic coupling) and external stimulus (“short-term” stimulation by synaptic input). From that study, it was determined that the dynamics exhibit weakly chaotic properties allowing almost regular periodic oscillations, and they are at the same time nonlinearly sensitive to initial conditions, which results in the fast renewal of the system's memory (at 4 ms). Indeed, the phase plane portrait of the oscillation demonstrates radial trajectory divergence (stretching and folding) with little azimuthal divergence, as a result of the channel's kinetics responsible for the membrane potential oscillation. These experimental findings were supported by a formal model of IO neurons’ subthreshold oscillations using a Rössler-type nonlinear system (Makarenko and Llinas, 1998).

In a more recent study using a nonlinear dynamical system Kazantsev et al. (2003) modeled the SPR effect, originally observed experimentally in IO neurons (Llinas and Yarom, 1986; Lang et al., 1999). The results of the study presented demonstrated an excellent fit to the experimental data.

Moreover, this network dynamic has true non-trivial attributes concerning the type of global motor control function implemented by the olivo-cerebellar network. Since its response is independent of the IO oscillatory phase when the stimulus arrives, the system demonstrates extraordinary flexibility in organizing a given motor intention and in modifying its activity online according to sensory feedback. The system does not need an operational memory. This makes it very reliable and prevents “computational overloads” that appear when memorizing the states. In fact, the speed of the operation (of the order of an oscillation period) is limited only by the oscillatory frequency, thus it can operate many times faster than the actuators it controls.

The motor control property of the IO oscillator can be very clearly demonstrated in artificial control systems. Indeed, the oscillatory network embodies a phase controller that can set and maintain a required phase by delivering to the oscillator an appropriate stimulus pulse. If a system is developed where the oscillatory phase is associated with any given physical parameter (e.g. position, velocity, angle, or temperature) such phase controller can maintain a pre-specified posture or motor sequence. In contrast with standard control systems, the controlling principle deals with a “motor recovery response” (Pikovsky et al., 2001). Within limits, a walking animal may stumble without falling, in which case it recovers its walking rhythm promptly irrespective of when an obstacle is encountered during the stride. Such synchronization of a large oscillator array requires only a synchronous reset stimulus. A fundamental aspect concerns the possibility of phase encoding when the map has both periodic orbits and chaotic attractors. In this case, the phase resets associated with these orbits are naturally transformed into neuron spiking. In turn, neurons fire spike trains with inter-spike intervals that are correlated directly with the orbits. Finally, the phase reset effect can be viewed as an effective tool to represent and/or store information in the form of oscillatory clusters. In contrast to Hopfield gradient networks (Hopfield, 1982), cluster reorganization can be extremely fast as the oscillator frequency may be moved up to the limits of the constituent materials. This is compared with Kuramoto-like oscillatory systems (Kuramoto, 2003), where a complex coupling matrix can work directly with information converted to the stimulus template. In fact, a recent paper (Bandyopadhyay et al., 2009) describes an actual biologically inspired underwater vehicle using olivo-cerebellar dynamics as a motor control system, which demonstrates that an analog IO-based circuit allows better control per unit time than a numerically controlled system.

CONCLUSIONS AND IMPLICATIONS

Three main issues have been addressed in this short paper concerning the functional organization of the olivo-cerebellar system. (a) The olivocerebellar system seems to be related centrally to the control of motor timing, and the rather exceptional neuronal and network properties it supports make this quite a unique control system, where timing seems to be a central theme. (b) The combination of strong and rather stereotyped intrinsic electrical properties, and of electrical coupling among the neuronal elements allows the synchronous activation of clusters of neurons, and via feedback inhibition, the dynamic variance of the membership to such coupled clusters. And finally, the very fundamental property of the phase resetting of a group of neurons, such that the resulting phase is coherent and independent from the phase at which the stimulus was given makes this event truly spectacular. These three elements give the inferior olive a very powerful set of network properties allowing not only the temporal control of many variables simultaneously, as occurs during motor control, but also the possibility of rapid correction in the presence of unexpected events that require rapid global motor correction. (c) Finally, nature has evolved a mechanism by which this very elaborate cluster dynamic generating system can transmit the timing sequences into a folded cortical geometry, without differential conduction time aberrations, and terminate its path by generating the most powerful synapse in the CNS. As if this were not sufficient, the neurons it activates are the largest in the brain and receive just one such climbing fiber efferent, and its output is inhibitory onto its target elements (Ito and Yoshida, 1966)! And so, nature has devised one of its most conserved neuronal systems (cf (Llinas, 1969)) to the control motricity by inhibition, a very fitting attribute as it is by selection, via inhibition, that most elaborate neuronal patterns are generated in the CNS.

Abbreviation

PC

Purkinje cells