Modeling and Estimating Recall Processing Capacity: Sensitivity and Diagnostic Utility in Application to Mild Cognitive Impairment

Abstract

We investigate the potential for using latency-based measures of retrieval processing capacity to assess changes in perfomance specific to individuals with mild cognitive impairment (MCI), a reliable precursor state to Alzheimer's Disease. Use of these capacity measures is motivated in part by exploration of the effects of atrophy on a computational model of a basic hippocampal circuit. We use this model to suggest that capacity may be a more sensitive indicator of undelying atrophy than speed of processing, and test this hypothesis by adapting a standard behavioral measure of memory (the free and cued selective reminding test, FCSRT) to allow for the collection of cued recall latencies. Participants were drawn from five groups: college-aged, middle-aged, healthy elderly, those with a diagnosis of MCI, and a sample of MCI control participants. The measure of capacity is shown to offer increased classificatory sensitivity relative to the standard behavioral measures, and is also shown to be the behavioral measure that correlated most strongly with hippocampal volume.

Since the time of Ebbinghaus (1885), the study of memory has been guided by numerous conceptualizations and metaphors for what memory is and does (see, e.g., Kandel, Schwartz & Jessell, 2000; Neath & Suprenant, 2003; Roediger, 1980; Spear, 1978). Although there are numerous differences among these views, a common thread is that a comprehensive understanding of memory functioning requires consideration of four aspects of memory functioning: encoding, consolidation, retention, and expression (retrieval). Within that consensus view, however, there does exist a critical dichotomy. Specifically, aspects of encoding, consolidation, retention, and expression have typically been considered either in terms of the information involved or in terms of the processes that operate on that information (see, e.g., Kolers & Roediger, 1984; Massaro, 1998; O'Toole, Wenger & Townsend, 2001; Roediger, Gallo & Geraci, 2002; Wenger, 1999). Typically, the conceptual distinction has been expressed in the choice of the dependent variable, with questions regarding information relying on frequencies of various types of outcomes, and questions regarding processing relying on reaction times (RTs).

This same dichotomy has also characterized much of the research on life-span changes in memory, with respect to both changes associated with normal development and aging, and changes associated with impairments or disease states (see in particular Cerella & Hale, 1994; Kail & Salthouse, 1994; Petersen, Smith, Ivnik, Tangalos, Schaid, Thibodeau, Kokmen, Waring & Kurland, 1995; Petersen, Smith, Kokmen, Ivnik & Tangalos, 1992; Petersen, 2007; Petersen & Negash, 2008). A central purpose of the work described here was to use a novel (in this context) measure of memory performance to provide a link between the focus on memory information and the focus on memory processes. That link is provided by adding a theoretically-motivated measure of a fundamental characteristic of processing—specifically, a measure of processing capacity—to a memory task that has been shown to be very sensitive in characterizing and detecting changes associated with mild cognitive impairment (MCI). MCI is a diagnostic category that has been shown to reliably distinguish the mild deficits associated with normal aging from the more profound deficits associated with Alzheimer's disease (AD, e.g., Petersen, 2007; Petersen & Negash, 2008; Petersen, Smith, Kokmen, Ivnik & Tangalos, 1992; Petersen, Smith, Waring, Ivnik, Tangalos & Komken, 1999). MCI status has also been shown to be predictive of a transition to AD (e.g., Dickerson, Sperling, Hyman, Albert & Blacker, 2007; Morris, Storandt, Miller, McKeel, Price, Rubin & Berg, 2001).

We begin with a general consideration of the distinction between processing speed and processing capacity, as this distinction will be crucial to understanding the potential issues for maximizing the sensitivity of behavioral changes associated with early neural pathology. We then use a computational model of hippocampal connectivity and integrity to investigate the extent to which the various behavioral measures of processing speed and capacity may be differentially sensitive to the types of degeneration and atrophy that have been shown to be characteristic of MCI and AD. Finally, we describe an experimental investigation of the utility of combining measures of processing speed and capacity with standard measures of recall. To our knowledge, the experimental work represents the first and only use of reaction times with frequencies of cued and free recall in application to this clinical issue.

Processing Speed And Capacity in Memory

Studies concerned with the characteristics of memory processing have often focused on the speed or rate with which memory tasks can be performed. This reflects a long history (dating at least to work in the nineteenth century, such as that of Donders, Wundt, and Jastrow Boring, 1957; Jastrow, 1890; Townsend & Ashby, 1983) of relying on response latencies as a source of evidence for the temporal and logical relationships among mental processes (see Luce, 1986; Townsend & Ashby, 1983; Townsend & Wenger, 2004a, for historical reviews). With respect to changes across the life span, suggestions that response latencies may be critical to understanding both normal aging and disease states also have a reasonably long history (e.g., Birren, 1974; Salthouse, 1985; Welford, 1958).

Reviews of the literature (see in particular Cerella & Hale, 1994; Kail, 1991; Kail & Salthouse, 1994) have outlined a general pattern relating overall response time to age: an inverted-U shaped function (see, e.g., Kail & Salthouse, 1994, Figure 1, p. 200). That is, processing speeds increase from early childhood through adolescence, peaking in young adulthood, remaining stable through very early middle age, before beginning an uninterrupted decline. The tasks that have been used to provide evidence for this pattern of changes include a wide range of tests of perceptual, mnemonic, and cognitive abilities, such as simple and choice RT, same-different and categorization judgments, short-term memory scanning, recognition, and recall (see, e.g., Cerella & Hale, 1994, Table 1, p. 130).

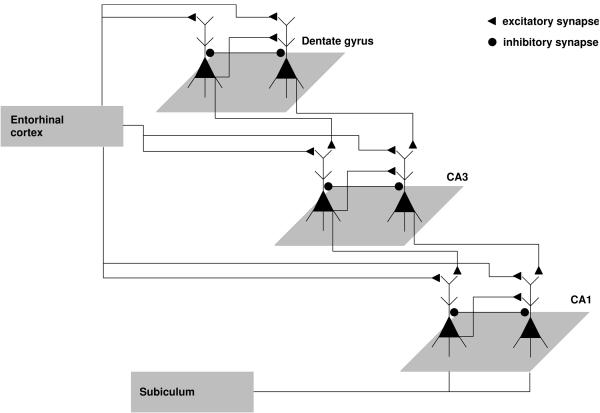
Figure 1.

Schematic representation of the architecture of the computational model of the hippocampal circuit.

Table 1.

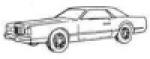
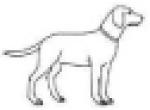
Stimuli used in the FCSRT task. Images are from Snodgrass & Vanderwart (1980), and are not to scale.

		Cues				Cues
Item		Category	Instance	Item		Category	Instance
	book	reading material	chapter		mountain	earth formation	climb
	car	vehicle	dashboard		dog	domestic animal	pet
	shirt	clothing	collar		bed	furniture	sheets
	pot	kitchen tool	copper		heart	part of body	artery
	church	type of building	chapel		ring	type of jewelry	pearl
	ball	type of toy	soccer		window	part of building	shutter
	gun	weapon	trigger		cherry	fruit	strawberry
	piano	keyboard instrument	organ		stove	major appliance	range
	shoe	footwear	lace		bread	type of food	butter
	eye	part of the face	sight		cow	farm animal	herd
	trumpet	brass instrument	trombone		knife	eating utensil	fork
	fly	insect	spider		pencil	writing implement	lead

Kail, Salthouse, and colleagues (e.g., Kail & Salthouse, 1994; Salthouse, 1985, 2000, 2001) have argued that differences in processing speed can be interpreted in terms of global differences in mental capacity (e.g., as a general cognitive resource) or in terms of general executive control functions. There have been numerous criticisms of this and related conceptualizations of capacity (e.g., Fisher & Glaser, 1996; Kantowitz & Knight, 1976; Light & Burke, 1988; Schweickert & Boggs, 1984), most focusing on the extent to which the typically-used measures of response speed—particularly mean or median RT—can be interpreted in terms of processing capacity.

There are a number of conceptual problems associated with using mean or median RT as a measure of processing capacity. Two are of particular relevance for the present effort. The first concerns the manner in which capacity differences are revealed. As discussed in detail elsewhere (see in particular Townsend & Ashby, 1978, 1983; Wenger & Gibson, 2004; Wenger & Townsend, 2000, 2006), capacity is best understood in terms of the response of a system (e.g., memory) to variations in workload. In the work presented here, workload is operationalized as the number of retrieval cues presented on each trial of a cued recall task. A system that shows degraded performance with increases in workload is characterized as possessing a capacity limitation. A system that shows no changes in performance with increases in workload is characterized as possessing unlimited capacity (at least across a specified range of workload manipulations, see Fisher, 1984). Finally, a system that shows performance improvements with increases in workload is characterized as possessing unlimited capacity. A central characteristic of much of the work that has been used to support age-related differences in capacity is that manipulations of workload are not consistently employed, nor are contrasts made with respect to the effects of variations in workload. Consequently, differences in processing speed cannot be unambiguously interpreted in terms of differences in capacity.

The second conceptual problem concerns the information that is provided by, for example, the mean RT. By definition, the mean gives the expectation for task completion time (overall speed). In this sense, it is at best only coarsely reflective of the notion of processing capacity (see the detailed exposition in Townsend & Ashby, 1978). In contrast, the work reported here uses a measure on the entire RT distribution, one originally suggested by Townsend and Ashby in a critical and comprehensive consideration of the theoretical and statistical characterization of processing capacity (Townsend & Ashby, 1978, 1983). Specifically we make use of the hazard function of the RT distribution,

$$\begin{array}{cc}\hfill h\left(t\right)& =\underset{\Delta t\to 0}{\lim }\frac{P(t\le T\le t+\Delta t\mid T\ge t)}{\Delta t}\hfill \\ \hfill & =\frac{f\left(t\right)}{S\left(t\right)},\hfill \end{array}$$

where f(t) is the probability density function (pdf) and S(t) is the survivor function of the RT distribution. This measure is one that is commonly applied in areas as diverse as reliability engineering (e.g., Cooper & McGillem, 1999) and epidemiology (e.g., Collett, 1994), where it is also known as the intensity function (see also Townsend & Ashby, 1978), as the variation in the hazard function characterizes the intensity with which (for example) a disease state is progressing. The integrated form of the hazard function has been of central importance in characterizing capacity in work focused on strong empirical tests of process characteristics of a variety of cognitive processes. For example, Townsend and Nozawa (1995), Wenger and Townsend (2001), and Ingvalson and Wenger (2005) used these functions to characterize individual observers' performance in detection and identification tasks involving manipulations of target redundancy. Wenger and Gibson (2006) used a similar approach to measure effects in selective attention. (e.g., Ingvalson & Wenger, 2005; Townsend & Nozawa, 1995; Wenger & Gibson, 2004; Wenger & Townsend, 2006)

Focusing the Question: A Model of Hippocampal Atrophy

At this point, we have established a general case for why and how capacity at a system level can be characterized, and how that characterization can allow for a principled distinction to be made between processing capacity and overall speed. We now turn to consideration of how one of the more prominent changes associated with MCI and AD can provide a concrete motivation for using these measures. Accumulating data suggests that measures of atrophy across a restricted set of brain regions is highly predictive of the conversion from MCI to AD (e.g., Fleisher et al., 2008; Jack et al., 1999; Vemuri et al., 2008; Whitwell et al., 2007, 2008a,b). Of particular interest for present purposes is hippocampal atrophy, given the critical role that hippocampal circuits play in a range of memory tasks (see, e.g., Davachi & Wagner, 2002; O'Reilly & Rudy, 2001, among others).

We created a computational representation of a basic hippocampal circuit,¹ shown in schematic form in Figure 1, in order to contrast measures of capacity with measures of overall speed, given varying levels of structural integrity. The model architecture was based on the established intrinsic connectivity of the hippocampus (see Shepherd, 2004). We assumed the output of the entorhinal cortex as the input to model, and assessed the output of the model at the level of the subiculum. The major pathway in the circuit was from entorhinal cortex to dentate gyrus, then to CA3, CA1, and the subiculum. In addition, CA3 and CA1 also took input directly from the entorhinal cortex.

Each of the three regions in the circuit was modeled as a network of discrete-time integrate-and-fire neurons (Amit & Brunel, 1995, 1997a,b; Dayan & Abbott, 2001). The sub-threshold dynamics of the membrane potential V for each cell i in any given region evolved over time (t) according to

$$V_i(t+\mathit{dt}=\left(1-\frac{\mathit{dt}}{{\tau }_{\alpha }}\right)V_i\left(t\right)\frac{\mathit{dt}}{{\tau }_{\alpha }}\left[I_i^{\mathrm{rec}}\left(t\right)+I_i^{\mathrm{ext}}\left(t\right)\right]$$ (1)

with τ_α being the membrane time constant, $I_i^{\mathrm{rec}}$ being the recurrent (within-region) input, and $I_i^{\mathrm{ext}}$ being the external input. The state of the recurrent input to each cell i at each point in time is modeled as a combination of excitatory (E) and inhibitory (I) inputs from all other cells j ≠ i, in that region,

$$I_i^{\mathrm{rec}}\left(t\right)=\frac{\mathit{dt}}{{\tau }_{\alpha }}\left\{\underset{j\in E}{\Sigma }{\rho }_j\left(t\right)J_{\mathit{ij}}{S}_j(t-{\delta }_{\mathit{ij}})-\underset{j\in I}{\Sigma }{\rho }_j\left(t\right)J_{\mathit{ij}}{S}_j(t-{\delta }_{\mathit{ij}})\right\}$$ (2)

Here, ρ_j(t) is a reliability variable, set to 1 with probability r and 0 otherwise (see also Tsodyks & Sejnowski, 1995); J_ij is the relative efficiency of the synapse between cells j and i (0 for cells that are not connected); δji is the time required to transmit a signal from cell j to cell i and S_j indicates if a pre-synaptic spike has (= 1) or has not (= 0) occurred in cell j during the interval from t − δ_ji to t.

Each cell in each region was assumed to posses a threshold value for the membrane potential V_i(t), such that if V_i(t) ≥ γ at time t, V (t + dt) was forced to an upper limit V_max (simulating a spike), and then returned to a lower limit V_min. Each cell was assumed to have a resting value, V₀, which was also used as the default value for each cell at the beginning of each simulated trial. The sub-threshold dynamics of cells in CA1 were also governed by a waiting time function

$$w\left(t\right)=\lambda \left\{1-\exp \left[-\frac{s\left(t\right)}{\beta }\right]\right\}$$ (3)

where w(t) is the minimum number of time steps (dt) that needed to elapse before the cell could spike, λ is an upper asymptote, β determines the slope of the function, and s(t) is the cumulative number of spikes generated by the cell by time t. This allowed for the type of spike-rate adaptation observed for cells in CA1 (Shepherd, 2004). The spiking behavior of CA3 neurons was modified such that successive spikes diminished the magnitudes of V_max and V_min linearly as a function of the total number of spikes generated up to time t,

$$V_{\max }(t+\mathit{dt})=V_{\max }\left(t\right)\{1-[s\left(t\right)\times p]\},$$ (4)

in order to mimic the known behavior of CA3 cells (Shepherd, 2004).

Specific values for each of the simulation parameters were fixed according to published data (see, e.g., Amit & Brunel, 1995, 1997a,b; Shepherd, 2004, and see Appendix A for the simulation methods). The number of cells in each region, and the relative number of excitatory and inhibitory connections within and between regions were also set according to published biological and simulation data.

The critical dependent variable in the simulations was the time required to reach a criterion number of action potentials at the output end of the circuit (see Gold & Shadlen, 2007; Smith & Ratcliff, 2004, for reviews of similar approaches). We then assumed that observable response times (RTs) were proportional to the time to criterion for the circuit. Our critical independent variables were those manipulated in order to simulate the effects of varying processing load on a circuit at differential levels of integrity (atrophy). We simulated processing load by varying the criterion number of action potentials (this corresponding to an assumption of limited capacity for the circuit). We simulated atrophy by reducing the total number of cells in each region.

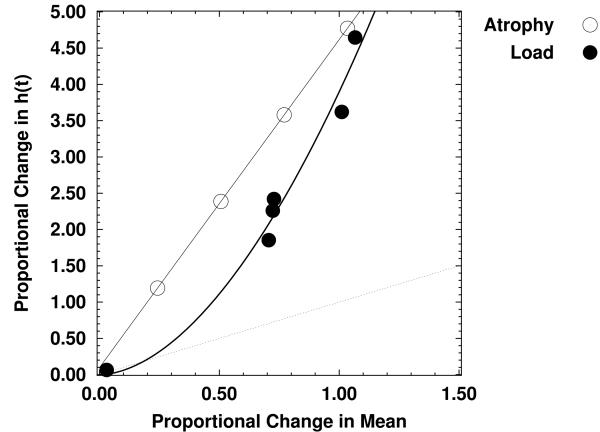
Figure 2 plots the outcomes of all of the simulations of the model circuit, showing the relationship between the relative increase in mean RT and the relative change in the proportional hazards estimates. The open symbols show the effects on these two measures of increasing atrophy at the lowest level of processing load, and the filled symbols show the effects of load at each level of atrophy. The dashed diagonal line indicates equality of proportional change at the levels of the hazard function and the mean. The data clearly show that proportional change in the estimated hazard functions is always greater than proportional change in the mean, with this being true both for changes in load and changes in circuit integrity. These results suggest that the hazard function analyses may be superior to analyses of mean RTs in detecting changes due to deterioration of a critical portion of the overall set of circuits responsible for memory performance.

Figure 2.

Effects of increasing atrophy and load (at each level of atrophy) on proportional change in the mean and the hazard function, for the computational model of the hippocampal circuit.

Connecting Theory and Data

Following from the results of the simulation, and from earlier work on similar issues in other domains (e.g., Townsend & Ashby, 1978; Wenger & Gibson, 2004; Wenger & Townsend, 2006), our hypotheses regarding capacity take the form of orderings on hazard functions for individual observers in two or more conditions, defined in terms of some manipulation of workload. For example, imagine that we have the hypothesis that individuals in the early stages of Alzheimer's disease show a pronounced limitation in their capacity to process memory information, with variation in the number of retrieval cues (one vs. two) being used as the manipulation of workload. We can state this hypothesis at the level of the hazard function as

$$h_2\left(t\right)<h_1\left(t\right)$$

for all t > 0, where the subscripts indicate the number of retrieval cues presented. Note that this hypothesis, by extension, implies that

$$\frac{h_2\left(t\right)}{h_1\left(t\right)}<1$$

with the corresponding null hypothesis being

$$H_0:\frac{h_2\left(t\right)}{h_1\left(t\right)}\ge 1$$

for all t > 0.

The advantages of this measure of capacity, relative to mean RT, are both conceptual and statistical. As discussed earlier the hazard function characterization maps onto the notion of processing capacity in a way that is much more direct than the mapping allowed by, for example, the mean RT (Townsend & Ashby, 1978; Townsend & Nozawa, 1995). There is also an inferential (statistical) advantage associated with having information from the entire RT distribution, rather than a point-estimate of central tendency (see particular Townsend, 1990; Townsend & Ashby, 1978). Specifically, Townsend (1990) has demonstrated that an ordering on hazard functions always implies an ordering on means, whereas an ordering on means does not of necessity imply an ordering on hazard functions. Finally, and pragmatically, framing hypotheses regarding capacity at the level of the hazard functions allows one to make use of a robust and very general semi-parametric regression model known as the Cox proportional hazards model (e.g., Allison, 1984, 1995; Collett, 1994; Cox, 1972; Therneau & Grambsch, 2000).

The standard Cox proportional hazards model is based on the assumption that the hazard function for an observer in any experimental condition i can be written as

$$h_i\left(t\right)={\lambda }_0\left(t\right)\exp [{\beta }_1{x}_{i1}+\dots +{\beta }_k{x}_{\mathit{ik}}]$$ (5)

where x_i1, x_i2, … x_ik are a set of k independent variables or covariates (with corresponding weights β_i1, β_i2, … β_ik), and λ₀(t) is an underlying but unspecified baseline hazard. Consequently, it is not necessary to make any assumptions about the parametric form of the baseline hazard (thus getting past many of the technical concerns discussed by Luce, 1986; Van Zandt, 2000, 2002, in estimating the form of individual hazard functions). For this reason, proportional hazards models are sometimes referred to as “semi-parametric” (see, e.g., Allison, 1995; Collett, 1994; Therneau & Grambsch, 2000). All that is required of this baseline hazard is that it not be negative.

If it can be assumed that the hazard functions for the observer in any two experimental conditions i and j are proportional for all values of t, then the model for the effects of the independent variables and covariates can be simplified as follows:

$$\frac{h_i\left(t\right)}{h_j\left(t\right)}=\frac{{\lambda }_0\left(t\right)\exp [{\beta }_1{x}_{i1}+\dots +{\beta }_k{x}_{\mathit{ik}}]}{{\lambda }_0\left(t\right)\exp [{\beta }_1{x}_{j1}+\dots +{\beta }_k{x}_{\mathit{jk}}]}$$ (6)

$$=\exp [{\beta }_i(x_{i1}-x_{j1})+\dots +{\beta }_k(x_{\mathit{ik}}-x_{\mathit{jk}})]$$ (7)

Further, taking the log of this relationship results in a linear model whose parameters can be estimated using well-understood statistical methods (e.g., maximum likelihood).

The robustness of this statistical model in the face of the known challenges associated with analyzing RT distributions (e.g., Luce, 1986; Van Zandt, 2000, 2002) was initially explored in a set of simulation studies (reported in detail in Wenger et al., 2006). That work involved generating data that possessed a known proportionality relationship at the level of the hazard function, across a set of distributional forms commonly associated with RT data, given varying levels of sample size, and examining the ability of the proportional hazards model to both detect reliable orderings and recover the true magnitude of the proportionality relationship. The Weibull (1951) distribution was used as the basis for these simulations, given its ability to be parameterized so as to produce distributional shapes that are commonly used to model and analyze RT distributions (as in, e.g., Logan, 1992; Spieler & Balota, 1997; Spieler et al., 2000). In addition, these simulations were performed so as to produce two types of data: one from contexts in which enough observations are taken to allow distributional analyses at the level of the individual observer (e.g., as in Townsend & Nozawa, 1995; Wenger & Townsend, 2001), and one from contexts in which distributional analyses consider data from multiple observers (as is generally the case in studies of memory across the life span). This second context allowed us to further examine extensions to the proportional hazards model (in particular Allison, 1995, 1996; Klein, 1992; McGilchrist, 1993; Therneau & Grambsch, 2000) that take into account the unobserved heterogeneity due to multiple observations on multiple observers.

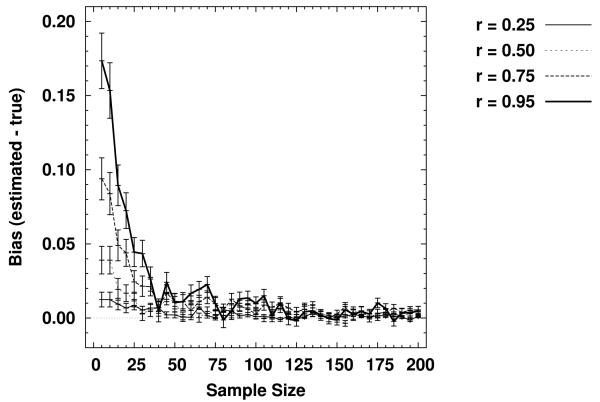
However, these initial simulations did not address a question that is of critical interest in any clinical application. Specifically, it may be the case that it is possible to obtain only a limited number of observations on any single individual. Consequently, we performed an additional set of numeric simulations to investigate the effects of varying sample size on the ability of the proportional hazards model to recover known levels of proportionality on the hazard functions. We generated data at four levels of proportionality or ordering (representing a range of experimental effect sizes), for sample sizes between five and 200 observations; details of the numeric simulations are presented in Appendix B. The results are plotted in Figure 3. Here it can be seen that there is a liberal bias in the estimated proportionality that is amplified at small sample sizes and with small effect sizes. In addition, the bias drops off rapidly and approaches asymptotic levels for all effect sizes when the sample sizes exceed 30 observations. The presence of a consistent liberal bias implies that any deleterious effects of load will be underestimated, meaning that estimates of capacity drawn from inferred orderings will of necessity be conservative.

Figure 3.

Bias in estimates of proportionality at the level of the hazard function, as a function of sample size, for four levels of known proportionality (r).

Experiment: Applying the Measures to Memory Performance

Our approach to investigating the potential for this latency-based measure of capacity involved a modification of a well-established experimental paradigm that has demonstrated significant utility in both basic and applied research, the free and cued selective reminding test (FCSRT, Bushke, 1984; Grober & Bushke, 1987). Before describing the specific modification to the FCSRT used in the present study, it is worth considering the nature of that paradigm and the advantages it provides in the study of memory deficits.

Studies of the information involved in encoding, consolidation, retention, and expression often focus on the relative frequency of specific types of observable events, such as items correctly recalled or recognized. However, when such measures are used in the study of changes in memory performance as a function of age and/or impairment, interpretation of these measures can be complicated by a number of potentially confounding factors. In particular, as discussed by Grober and Bushke (1987), any observed deficiencies in performance may be due to at least two contributing effects: “apparent” memory deficits, or performance decrements that are revealed in a test of memory but that are attributable to difficulties with processes outside of those associated with successful encoding, consolidation, retention, and retrieval (e.g., perceptual or motoric processes); and “genuine” memory deficits, or performance decrements that can be isolated to some aspect of encoding, consolidation, retention, and expression.

In order to distinguish between apparent and genuine deficits, it is necessary to show that a decrement in performance is observable in conditions which are optimal on all possible dimensions of processing (Bushke, 1984; Petersen et al., 1992, 1995, 1999). The necessity of these conditions is indicated by documented age-related differences in abilities related to encoding and immediate memory (e.g., Eysenck & Eysenck, 1979; Salthouse & Babcock, 1991; Waugh & Barr, 1982), in the extent to which both general (e.g., Larrabee, Youngjohn, Sudilovsky & Crook, 1993) and specific information (e.g., episodic features) are retained over time (e.g., Johnson, Leonardis, Hashtroudi & Ferguson, 1995), and in the relative effectiveness of various types of cuing conditions (e.g., Craik, 1994; Faust, Balota & Spieler, 2001; Micco & Masson, 1992; Smith, 1977).

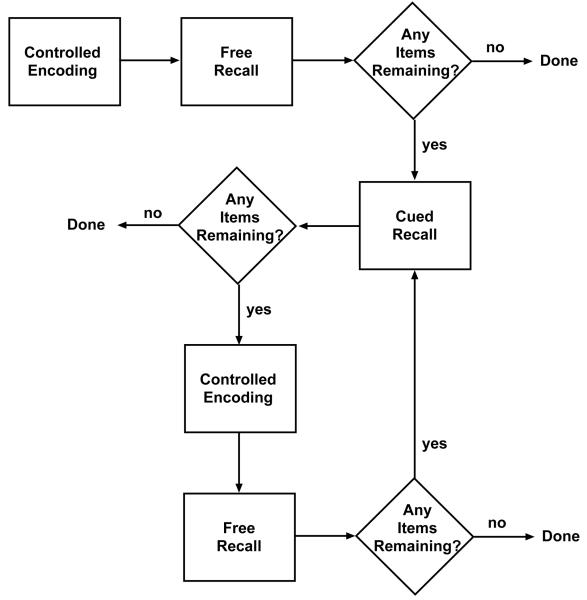
The FCSRT was developed by Bushke and colleagues (Bushke, 1984; Grober & Bushke, 1987) in order to provide the conditions that would allow for discriminating between apparent and genuine deficits in memory performance. Figure 4 presents a flow-chart summary of the task. Initial encoding (learning) in this task is controlled by requiring semantic processing of each of the to-be-remembered (TBR) items, for example, by requiring participants to search for and verbally identify a picture of a particular object (e.g., “sweater”) among a set of pictures in response to a categorical cue (e.g., “item of clothing”). Following presentation of the entire set of TBR items, participants freely recall as many items as possible during a fixed period (e.g., 2-3 min). After the free recall period, retrieval cues (e.g., the category labels that were used to guide initial encoding) are provided for words that were not recalled. The total number of items that are retrieved using both free and cued recall provides a minimum estimate of the number of items available for retrieval. Following this, an additional set of encoding trials and free and (if necessary) cued recalls for the remaining set of items is performed. At the outset of each of these iterations, the orienting cues for items not recalled either freely or with cues on the preceding iteration are provided, with participants re-performing the search for and identification of these items, a process that acts as a form of selective reminding (Bushke, 1973).

Figure 4.

Flow-chart representation of the free and cued selective reminding task (FCSRT).

Since the introduction of the FCSRT, its sensitivity and effectiveness in detecting age- and pathology-related changes in memory performance have been documented in a number of studies (e.g., Grober et al., 1988; Grober & Kawas, 1997; Grober et al., 1998, 2000; Petersen et al., 1995; Tuokko & Crockett, 1989; Tuokko et al., 1991). The test is easy to administer, provides a high degree of diagnostic accuracy with respect to memory impairment (e.g., Grober & Bushke, 1987; Grober et al., 1988; Grober & Kawas, 1997; Grober et al., 2000; Petersen et al., 1999), and (due to the iterative nature of the procedure) allows for a reasonable number of samples to be obtained from each participant. While it is possible to obtain measures of response latency on the cued trials, latency data have not (to our knowledge, prior to the present study) been systematically collected and/or reported in the literature. Given the known sensitivity of latency measures for revealing important aspects of cognitive functioning that are often not detectable with frequency data (see, e.g., Luce, 1986; Townsend & Ashby, 1983; Van Zandt, 2002, for general reviews), and given the potential of the latency-based capacity measures to be sensitive to the effects of hippocampal atrophy, we augmented the FCSRT by collecting RTs to the retrieval cues in the cued portion of the paradigm.

Method

Participants

Five groups of participants were recruited, three groups from the area in and around South Bend, Indiana, and two groups in and around Rochester, Minnesota. The first group (to be referred to as the CA group) included 103 healthy undergraduate students from the University of Notre Dame; data from three of these individuals were discarded prior to analysis for reasons unrelated to performance (e.g., equipment malfunctions, etc., with the most common being difficulties with the lapel microphone). The second group included 107 healthy middle-aged (25-65 years of age, to be referred to as the MA group) individuals from the South Bend community; data from three of these individuals were discarded prior to analyses. The third group included 104 healthy elderly individuals (over the age of 65, to be referred to as the HE-SB group) from the South Bend community; data from seven of these individuals were discarded prior to analyses. The fourth and fifth groups were recruited from a registry of individuals participating in the Mayo Clinic Study of Aging (see Roberts et al., 2008, for methodological and demographic details of this effort). Each of these two groups included 50 individuals. Individuals in one of these two groups had been previously assigned a diagnosis of MCI (to be referred to as the MCI group), and individuals in the other were age-matched controls (no diagnosis of MCI, to be referred to as the MCI-C group); data from two individuals in the MCI-C group was discarded prior to analyses. All participants reported fluency with spoken and written English, and all received financial compensation for their participation.

Materials

The items used in the memory task were 24 line-drawings from the Snodgrass and Vanderwart (1980) norms (see Table 1). For each of these drawings, a category label and a highly-associated instance were selected from the McEvoy and Nelson (1982) category and instance norms. The images were drawn in black on white squares, 6.4 cm on each side, so that at an unconstrained viewing distance of approximately 70 cm, the squares subtended approximately 5.2° of visual angle. Stimulus presentation and data recording were done using either a desktop (for the CA, MA, and HE-SB participants) or laptop (for the MCI-C and MCI participants) computer. Screen resolutions in both cases were set to 800 × 600 pixels, at a refresh rate of 17 ms. Manual responses were collected and timed using the computer keyboards, and verbal responses were timed using a lapel microphone attached to the computers; timing of responses in all cases was accurate to ±1 ms (Forster & Forster, 2003).

Design

The overall design was cross-sectional, with the groups (CA, MA, HE-SB, MCI-C, MCI) defined by age and MCI status. With the exception of the FCSRT, none of the experimental tasks—visual threshold estimation, naming time, FCSRT—involved any other between-subjects manipulation. In the case of the FCSRT, the independent variables were number of cues in the cued recall portion (one or two, manipulated within-subjects), and the specific type of cue used on the single-cue trials (category label or instance, manipulated between-subjects). Half of all subjects in each group were randomly assigned to each of the single-cue-type conditions.

Procedure

Testing sessions for the CA, MA, and HE-SB participants took place in a quiet, dimly-lit room in the first author's laboratory on the campus of the University of Notre Dame. Testing sessions for the MCI-C and MCI participants took place in the Alzheimer's Disease Research Center, Mayo Clinic College of Medicine, in Rochester, MN. Sessions lasted between 45 and 90 min, with variations in duration due to longer sessions for the older participants.

Background data

Each session began with participants completing a background questionnaire consisting of a total of 21 questions, covering basic demographic and health information, along with quality-of-life items from the Health and Retirement Survey (Gustman, Mitchell & Steinmeier, 1995). Items were presented sequentially in a fixed order in plain text on the computer screen, and participants were given the option of either reading and entering their responses on their own, or having the items read to them with responses entered by the experimenter.

Visual identification thresholds

Following this, participants′ visual identification thresholds (as a function of exposure duration) were estimated using the method of constant stimuli. This was done in order to provide measures that could help distinguish latency-based effects specific to memory processing from general age-related slowing. The range and specific values for the set of seven exposure durations varied for each of the groups, with the specific values selected on the basis of pilot testing. The exposure durations for the CA and MA participants ranged from 17 to 119 ms in 17 ms steps. The exposure durations for the HE-SB and MCI-C participants ranged from 34 to 238 ms in 34 ms steps,. The exposure durations for the MCI participants ranged from 68 to 476 ms in 68 ms steps. A total of 20 trials were presented at each level of exposure duration, and order of presentation was determined randomly for each participant.

Trials began with a fixation stimulus, presented centrally for between 510 and 1020 ms, with the specific duration determined by a uniform distribution over this interval (rounded to the closest multiple of 17 ms). This was followed by the presentation of either the target ([ + ]) or non-target ([ - ]) stimulus for the appropriate exposure duration. Participants signaled their perception of the target stimulus by pressing either the “z” or “/” key on the computer keyboard, using the index finger of their dominant hand, and the non-target stimulus using the middle finger of their dominant hand. Feedback (the word “Correct” or the word “Incorrect,” presented centrally) was provided on each trial.

Naming time

Participants then performed a simple naming-time task. This task, like the visual identification threshold task, was included in order to help differentiate latency-based effects specific to memory processing from generalized age-related slowing. A set of 20 three- or four-letter words was chosen from the labels for items in the Snodgrass and Vanderwart (1980). These words were chosen on the basis of pilot testing to be minimally confusable with the set of items used in the FCSRT. Each word was presented once only, and the order of presentation was determined randomly for each participant.

Trials began with a fixation screen presented centrally for between 510 and 1020 ms, with the specific duration determined by a uniform distribution over this interval (rounded to the closest multiple of 17 ms). This was followed by the presentation of one of the words, in upper-case letters, with the word remaining visible until the participant responded. Participants responded verbally, speaking at a normal (conversational) volume, triggering the software voice key. The experimenter logged each trial as correct, incorrect, or artifact (cough, etc.). No feedback was provided.

FCSRT

The final task was the FCSRT. The encoding portion of this task required participants to find a target image located in a display involving three randomly selected non-target images on the basis of both a category cue and a related instance cue. The cues were presented in sentence form at the top of each display of four images, and took the form “Find the category label that is related to instance.” The location of the target image was determined randomly on each encoding trial. Participants responded by pointing to the target item, and the display remained available until the participant responded. Each encoding trial was initiated and terminated by the experimenter.

Once the entire list of target items had been presented, participants were asked to recall, verbally, as many of the encoded items as possible, with no requirement for serial recall. The experimenter logged the items correctly recalled, then initiated the cued recall trials. Each cued recall trial began with the presentation of either one or two cues at the top of the screen. On the double-cue trials, the instance and category cues were separated by eight spaces and a pair of upright brackets centered in those eight spaces. The specific location of each of the cues was determined randomly on each trial, and the number of single- and double-cue trials was set to be approximately equal for each participant on the basis of the number of words available for cued recall following the first free recall. The cue(s) were available until the participant responded. Participants responded verbally, triggering a software voice key. The RT for the trial was the time from the onset of the retrieval cue(s) to the onset of the participant's vocal response. Following each response, the experimenter logged the response as being correct, incorrect, or an artifact (cough, etc.). Each of the items that had not been recalled in the free recall trials was cued once, with order determined randomly. If items remained not-recalled following the cued recall trials, those items were used in another set of encoding, free recall, and cued recall trials. This sequence was repeated either until all of the items were recalled, or a total of six replications of the sequence were completed.

Results

Unless otherwise indicated, all analyses used an α of 0.05. We begin with a summary of the basic characteristics of individuals in each group (including visual identification thresholds and mean naming times), then consider the frequency- and latency-based measures of memory performance, including (for a subset of the participants) a consideration of the relationship between these measures and measures of hippocampal integrity.

Participant characteristics

Table 2 presents a summary of a relevant subset of the information reported on the background questionnaire. At least 93% of all participants in each group reported being native speakers of English and, overall, the percentage of total age during which participants reported speaking English was at least 97% for all groups. In addition to the results reported here and in the sections following, we performed analyses in which we excluded (a) participants reporting head injury, (b) participants reporting depression, and (c) all females. The qualitative results did not differ in any way from those obtained using all of the participants' data. In addition, we estimated pairwise correlations among a subset of the demographic and individual difference variables (age, years of eduction, years of spoken English, visual identification threshold) and a subset of the critical dependent measures (cumulative free recall, cumulative cued recall, total change in recall, mean RT on cued recall, and the individual estimate of capacity) within each group. None of these correlations reached criterion for statistical reliability.

Table 2.

Participant characteristics, as reported on the background questionnaire. Note: for the education variable, it was assumed that all participants in the CA group would graduate.

	CA	MA	HE-SB	MCI-C	MCI
N	100	104	97	48	50
Age: mean	20.3	46.5	72.7	77.3	79.3
Sex: % female	56	63	64	50	37
Race: % reporting white	90	82	100	100	98
Education: mean years	14.0	16.2	14.3	13.4	13.6
Education: % with bachelors or advanced degree	100	62	32	36	29
English: % native speakers	97	97	97	93	98
English: (mean yrs spoken / mean age) × 100	99	97	99	97	98
Employment: % reporting retired	0	5	66	86	87
Head injury: % reporting ever experiencing	13	9	0	4	0
Depression: % reporting ever experiencing	6	16	14	0	0

Visual identification thresholds

Thresholds for each individual were estimated by fitting a two-parameter Weibull cdf

$$F\left(t\right)=1-\exp \left[-{\left(\frac{t}{\beta }\right)}^{\alpha }\right]$$ (8)

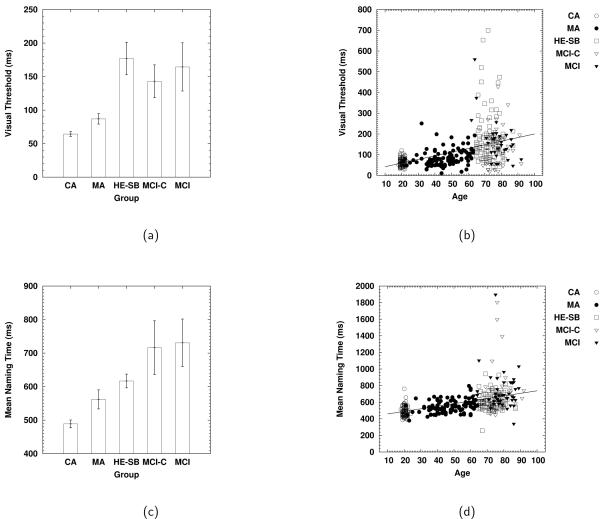
to identification accuracy as a function of exposure duration (t), then finding the value of t for which the parameterized function was equal to 0.79. Figure 5(a) and (b) present the group means and individual estimates as a function of age for the entire sample. Individual estimates were analyzed using a one-way analysis of variance (ANOVA), with age as the single factor. This analysis revealed a reliable effect due to group status, F(4, 397) = 34.70, MSE = 5994, with the temporal thresholds for the CA (64 ms) and MA (87 ms) participants being reliably shorter than those for the HE-SB (177 ms), MCI-C (143 ms), and MCI (165 ms) participants, and there being no reliable differences (based on Tukey post-hoc tests) between the CA and MA participants, or among the HE-SB, MCI-C, and MCI participants.

Figure 5.

Group means (a) and individual estimates (b) of visual identification threshold. Group means (c) and individual means (d) for naming times. Error bars indicate the width of the 95% confidence intervals.

Naming times

Panels (c) and (d) of Figure 5 present the group means and individual means on the naming as a function of age for the entire sample. Individual means were analyzed using a one-way ANOVA, with group as the single factor. This analysis revealed a main effect for group, F(4, 397) = 29.77, MSE = 208008, with naming latencies being reliably shortest for the CA participants (489 ms), followed by the MA (562 ms) and HE-SB (617 ms) participants, with mean latencies for the MCI-C (716 ms) and MCI (731 ms) being the longest, with there being no reliable differences within each grouping (MA vs. HE-SB, and MCI-C vs. MCI).

FCSRT: Free and cued recall

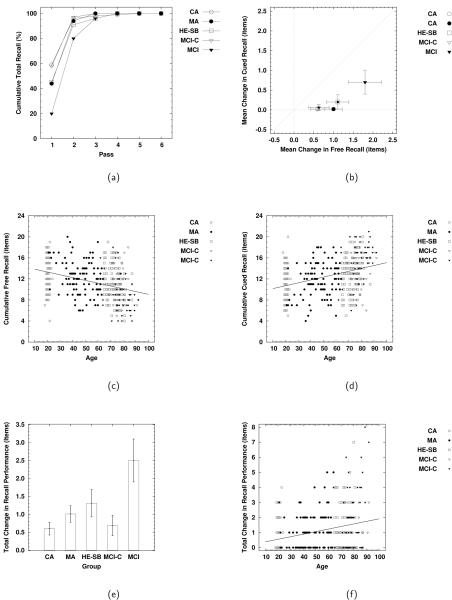
Participants in all five groups completed recall by, at the latest, the fourth pass through the procedure (see panel (a) of Figure 6), with the majority of the improvement occurring between the first and second pass. Consequently, we analyzed all of the data from the FCSRT with respect to differences between initial and asymptotic levels of performance.

Figure 6.

(a) Cumulative total recall by pass for each of the five groups; (b) mean change (final - initial) in free and cued recall for each of the five groups; (c) final free recall for all participants as a function of age; (d) final cued recall for all participants as a function of age; (e) mean total change in recall for each of the five groups; (f) total change in recall for all participants as a function of age. Error bars indicate 95% confidence intervals.

The data for change in cumulative free recall (initial to asymptotic) were analyzed using a 5 (group: CA, MA, HE-SB, MCI-C, MCI) × 2 (single-cue condition: category, instance) ANOVA, collapsing across total number of cues. The only effect to reach the criterion level for reliability was the main effect of group F(4, 389) = 10.85, MSE = 13.96: participants in the MCI group on average increased cumulative free recall by an amount (1.8 items) that was reliably greater than that for individuals in the CA (0.6 items), MA (1.0 items), HE-SB (1.1 items) or MCI-C (0.6 items) groups, with there being no reliable differences among these latter four groups. Post-hoc examination of the group means showed all of the increases in cumulative free recall to be reliably different from 0.0, all ts > 4.74, all ps < .001.

A similar result was obtained in the analysis of the data for change in cumulative cued recall (collapsing across number of cues), which were analyzed using a 5 (group: CA, MA, HE-SB, MCI-C, MCI) × 2 (single-cue condition: category, instance) ANOVA. As with the cumulative free recall data, the only effect to reach criterion for reliability was the main effect for group, F(4, 389) = 14.19, MSE = 0.35. Participants in the MCI group increased their cumulative cued recall by 0.7 items (on average), reliably more than was the case for participants in the CA (0.1 items), MA (0.2 items), HE-SB (0.2 items), or MCI-C (0.2) items, with there being no reliable differences among the latter four groups. In addition, only the increase for the MCI participants was reliably different from 0, t = 4.78, p < .001, all other ts < 1.77, all other ps > .09.

Unsurprisingly, then, the analysis of the data for change in cumulative total (free plus cued) recall revealed the same basic result. These data were analyzed using a 5 (group: CA, MA, HE-SB, MCI-C, MCI) × 2 (single-cue condition: category, instance) ANOVA. As in the preceding analyses, only the main effect of group reached the criterion level for reliability, F (4, 389) = 16.36, MSE = 20.52, with the overall increase for participants in the MCI group (2.5 items) being reliably greater than was the case for participants in the CA (0.7 items), MA (1.2 items), HE-SB (1.3 items), or MCI-C (0.8 items) groups, with there being no reliable differences among the latter four groups, and with all five of the means being reliably greater than 0. Our data are, then, at this level of analysis, consistent with established findings in the literature with respect to differences in performance on the FCSRT—particularly deficits on the initial pass with associated increases on subsequent passes—being reliable indicators of MCI (e.g. Grober et al., 2000; Kelley & Petersen, 2007; Petersen, 2007; Petersen & Negash, 2008).

FCSRT: Cued recall, mean RT

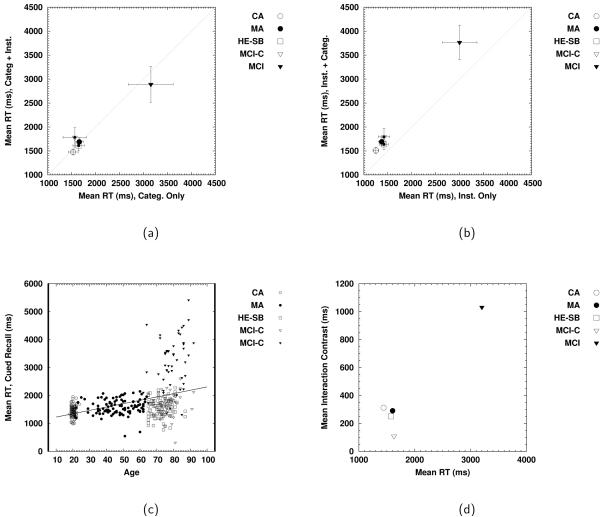
Systematic effects at the level of overall speed of processing were examined by way of mean RTs on the cued recall trials. Prior to analyses, all RTs less than 200 ms were deleted, as were all RTs associated with incorrect responses. Median RTs were calculated for each participant at each level of cuing (one vs. two), and the data (means of those medians) were then analyzed using a 5 (group: CA, MA, HE-SB, MCI-C, MCI) × 2 (single-cue condition: category, instance) × 2 (number of cues: one vs. two) ANOVA, with group and single-cue condition being between-subjects variables, and number of cues being a within-subjects factor. The data are summarized in the three panels of Figure 7.

Figure 7.

(a) Mean RTs for single- and double-cue cued recall trials, given that the single cue was a category cue; (b) mean RTs for single- and double-cue cued recall trials, given that the single cue was an instance cue; (c) mean RTs overall per participant as a function of age; (d) interaction contrast (see Equation 9) for the interaction of single-cue condition and number of cues for each group, relative to the overall mean RT for that group.

The analyses of these data are summarized in Table 3. Critically, the three-way interaction of group, single-cue condition, and number of cues was reliable. To understand the form of this interaction, we calculated the following interaction contrast (Maxwell & Delaney, 2004) for the interaction of single-cue condition and number of cues, separately for each group:

$$\mathit{IC}=({\stackrel{‒}{RT}}_{C1}-{\stackrel{‒}{RT}}_{C2})-({\stackrel{‒}{RT}}_{I1}-{\stackrel{‒}{RT}}_{I2})$$ (9)

The subscripts indicate the type of cue used on the single-cue trials (category, C, or instance, I) and the number of cues present on the trial (one or two). Thus, ${\stackrel{‒}{RT}}_{C1}$ and ${\stackrel{‒}{RT}}_{C2}$ are the mean RTs for single- and double-cue trials for those individuals who were presented with category cues on the single-cue trials. The values of the interaction contrast are plotted in panel (d) of Figure 7. The first difference on the right-hand side of Equation 9 $({\stackrel{‒}{RT}}_{C1}-{\stackrel{‒}{RT}}_{C2})$ was generally small and negative, reflecting little in the way of cost of adding an instance cue to a category cue (see panel (a) of Figure 7). The exception was the MCI group, which showed a reliable benefit of adding an instance cue to the category cue. The second difference on the right-hand side of Equation 9 $({\stackrel{‒}{RT}}_{I1}-{\stackrel{‒}{RT}}_{I2})$ was generally negative, but larger in magnitude than the first difference (see panel (b) of Figure 7), indicating an overall cost of adding a category cue to an instance cue. In contrast, the difference for the MCI group was quite large. Taken together the interaction contrast indexes the extent to which the cost of adding a category cue to an instance cue exceeded either the cost or the benefit adding an instance cue to a category. As can be seen in panel (d) of Figure 7, this cost was largest for the MCI group.²

Table 3.

Mean RT for cued recall trials, summary of the ANOVA.

Factor	df	F	MSE
Group (G)	4	185.47 ‡	324786
Single-cue condition (SC)	1	0.05	324786
Number of cues (NC)	1	60.00 ‡	104847
G × SC	4	3.90 †	324786
G × NC	4	2.91 *	104847
SC × NC	1	66.91 ‡	104847
G × SC × NC	4	8.47 ‡	104847

Note:

^*p < .05

^†p < .01

^‡p < .001.

FCSRT: Effect of load on capacity

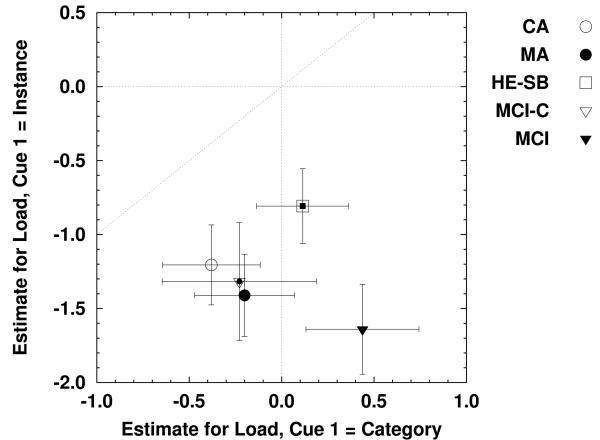
To estimate the effects of varying the number of cues (workload) on cued recall RT, we fit the proportional hazards model to the correct RTs for each observer for each combination of group status and single-cue condition separately, with number of cues as the predictor.³ The results of these analyses are presented in Table 4 and Figure 8. Consistent with the analyses of the mean RTs, adding a category cue to an instance cue produced a reliable reduction in capacity for participants in all five groups. However, only the MCI group showed a reliable effect of adding an instance cue to a category cue, in this case producing a reliable increase in capacity. Thus, at this level of analysis, participants in the MCI condition appear to be much more sensitive to the effect of varying processing load, showing both negative and positive effects for increasing the number of cues.

Table 4.

Estimated parameters for the effect of varying the number of retrieval cues on capacity (proportional hazards), for each combination of group type and single-cue condition.

Group	Single-cue Condition	βˆ	SE	χ2	% Change
CA	Category	−0.380	0.264	2.08	−32
	Instance	−1.205	0.270	19.90 ‡	−70
MA	Category	−0.201	0.271	0.55	−18
	Instance	−1.411	0.278	25.78 ‡	−76
HE-SB	Category	0.114	0.249	0.21	12
	Instance	−0.807	0.253	10.20 †	−55
MCI-C	Category	−0.229	0.418	0.30	−20
	Instance	−1.317	0.398	10.93 ‡	−73
MCI	Category	0.437	0.206	4.04 *	55
	Instance	−1.681	0.305	14.96 ‡	−81

Note:

^*p < .05

^†p < .01

^‡p < .001.

Figure 8.

Effects of increasing cues on capacity, as estimated using the proportional hazards model, for each combination of group and single-cue condition. Error bars are 95% confidence intervals on the parameter estimates.

Relative diagnostic utility

The analyses of the mean RTs and the capacity estimates suggest that the latency information may be of equal if not more importance in distinguishing the MCI group from the others. Specifically, it was the case that the RT data revealed an effect of cuing that was not evidenced in the free and cued recall frequency data. Consequently, we sought to evaluate the relative diagnostic utility of the latency measures by using discriminant function analysis (DFA, e.g. Rao, 1973). DFA uses one or more predictor (independent) variables to estimate a function that is used to assign each observation to one or more categories (values of the dependent variable). The specific goal of this analysis was to determine how well the capacity measures would do, relative to the acknowledged ability of the free and cued recall measures, in correctly classifying participants as to their MCI status.

We considered the data only for the HE-SB, MCI-C, and MCI groups for this analysis.⁴ We evaluated the relative ability of models formed by five different combinations of three predictor variables to correctly categorize individuals as to their MCI status. The three predictor variables were each observer's (a) total change in free recall (initial to asymptotic), (b) mean RT on the cued recall trials (collapsing across cue type and number), and (c) absolute value of the change in capacity as a function of adding a second cue. Preliminary analyses indicated that the overall mean RT produced model fits that were statistically no different from those obtained using means specific to cue number and type. The absolute (versus signed) value of the estimate capacity change was used given the differential effect of the two types of cues.

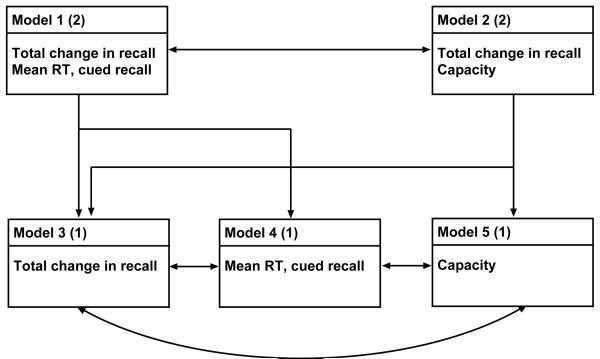
These three predictor variables were used to parameterize five different DFA models, with the relationships among the models illustrated schematically in Figure 9. The models were fit to the data assuming a linear form for the discriminant function, and the quality of the fit of each obtained model was assessed in two ways, first with respect to a general set of measures of model performance, and second using a set of measures of diagnostic sensitivity and utility. Both methods of assessment used the predicted set of categorization frequencies and probabilities as their basis.

Figure 9.

Relations among five models for predicting MCI status on the basis of three predictor variables. Numbers in parentheses indicate the number of predictor variables in each model, with those variables listed in the lower portion of each box. Single-headed arrows indicate relationships among models differing in the nunmber of predictor variables, double-headed arrows indicate relationships involving the same number of predictor variables

The quality of each model's fit to the data was first quantified by calculating the log likelihood

$$\ln \left(L\right)=\underset{i=0}{\overset{1}{\Sigma }}\underset{j=0}{\overset{1}{\Sigma }}{f}_{\mathit{ij}}\ln \left[P(R_i\mid S_j)\right]$$ (10)

where f_ij was the observed frequency of individuals with known MCI status j being assigned status i (i, j = 0, 1), and P (R_i|S_j) was the overall probability of the model assigning MCI status i to an individual with MCI status j. The log likelihood was used to compare the relative performance of the five models, following a strategy outlined by Thomas (2001). Models that differed in terms of the total number of predictor variables were compared using

$${\chi }^2=-2\ln \left(\frac{L_r}{L_g}\right)=2[\ln \left(L_g\right)-\ln \left(L_r\right)]$$ (11)

where L_r is the log likelihood for the model with the smaller number of predictor variables (the restricted model) and L_g is the log likelihood for the model with the larger number of predictor variables (the general model). The degrees of freedom for the comparison is given by the difference in the number of predictor variables for the two models under consideration. Models that had the same number of predictor variables were compared using the Akaike Information Criterion

$$\mathrm{AIC}=-2\ln \left(L\right)+2\nu$$ (12)

(Akaike, 1983; Ashby & Lee, 1991), where ν is the total number of predictor variables for the model under consideration. The model with the smallest value of the AIC was selected as providing the best account of the data. Table 5 summarizes this analysis. Among the single-variable models, the one based on the capacity measure provided the superior account of the data, while between the two two-variable models, the one that combined the capacity measure with total change in recall provided the best account of the data. Finally, the model that combined the capacity and total recall measures provided a statistically superior account of the data, relative to the models that relied on either of these two measures alone.

Table 5.

Evaluation (top section) and comparison (bottom section) of the five models for MCI status, based on the discriminant function analyses.

Model	ln(L)	ν	AIC
1	−37.864	2	79.728
2	−34.587	2	53.174
3	−54.775	1	111.550
4	−57.964	1	117.928
5	−44.499	1	90.998
Restricted Model	General Model	df	χ 2
3	1	1	33.822‡
3	2	1	60.376‡
4	1	1	40.200‡
5	2	1	39.824‡

We also contrasted the performance of the five sets of predictor variables using a set of measures reflecting diagnostic (or choice) accuracy, sensitivity, and bias (see Table 6). For the purposes of these comparisons, we coded the rate of correct and incorrect categorizations for each predictor as follows. A “hit” was defined as correctly classifying an individual with a diagnosis of MCI, with a “miss” being the associated error. A “correct rejection” was defined as correctly classifying an individual who did not have a diagnosis of MCI, and a “false alarm” was the associated error.

Table 6.

Measures of diagnostic accuracy, sensitivity, and bias based on the frequencies of hits (H), misses (M), correct rejections (CR), and false alarms (FA), obtained from the discriminant function analyses. Note: z(HR), z(FR) = inverse normal transformation of the hit and false alarm rates.

Measure	Form
Diagnostic sensitivity (hit rate, HR)	$\frac{H}{H+M}$
Diagnostic specificity	$\frac{\mathit{CR}}{\mathit{FA}+\mathit{CR}}=1-\mathit{FR}$
Positive predictive value	$\frac{H}{H+\mathit{FA}}$
Negative predictive value	$\frac{\mathit{CR}}{\mathit{CR}+M}$
2AFC d′ (sensitivity)	$\frac{1}{\sqrt{2}}[z\left(\mathit{HR}\right)-z\left(\mathit{FR}\right)]$
2AFC c (bias)	$\frac{1}{2\sqrt{2}}[z\left(\mathit{HR}\right)+z\left(\mathit{FR}\right)]$

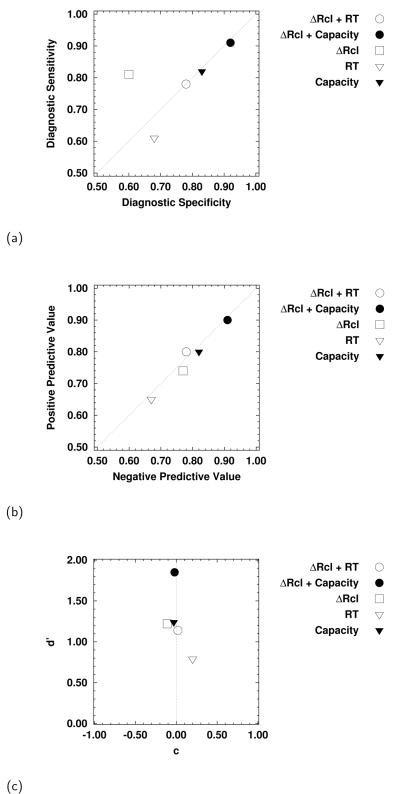
The results of the DFA are summarized in panels (a)-(c) of Figure 10, and show that, generally, the capacity measure when used either alone or in combination with total change in recall, performed well with minimal bias. With respect to diagnostic sensitivity and specificity (Figure 10(a)), the capacity measure alone performed as well as the total change in recall in terms of sensitivity (true positive), and outperformed total change in recall in terms of specificity (true negative). The best performance on both measures was obtained when the capacity and recall measures were combined. This same pattern held for the relationship between the measures of positive and negative predictive value (Figure 10(b)). Finally, the superior categorization performance of the model that combined change in total recall with capacity can be seen in the values of d′ and c ((Figure 10(c)): this model gives the highest value for the sensitivity parameter with minimal levels of bias.

Figure 10.

Measures of diagnostic sensitivity, accuracy, and bias, based on the outcomes of the discriminant function analyses. Note: ΔRcl = total change in recall, RT = mean cued recall RT.

Capacity estimates and hippocampal volumes

Structural MRI scans, obtained within one month of the behavioral testing, were available for total of 36 individuals in the MCI-C (17) and MCI (19) groups. Of these, data for two individuals (both in the MCI-C group) were excluded, as their behavioral data was incomplete (see the “Participants” section above). For the remaining 34, we obtained estimates of total hippocampal volume in order to determine the potential relationship of each of our dependent measures with a measure of hippocampal atrophy.

Hippocampal volumes were estimated using voxel-based morphology methods, as part of a larger ongoing research effort; parameters for image acquisition and analysis are provided in reports pertinent to that work (e.g., Whitwell et al., 2008b), with a brief summary reported here. In order to quantify total hippocampal volume, the borders of the left and right hippocampi were traced sequentially from posterior to anterior. In-plane hippocampal anatomic boundaries were defined to include the CA1 through CA4 sectors of the hippocampus proper, the dentate gyrus, and subiculum. The posterior boundary was determined by the oblique coronal anatomic section on which the crura of the fornices were identified in full profile. The inferior boundary of the hippocampus was determined by the gray-white interface formed by the subiculum and underlying parahippocampal gyrus.

Simple linear correlations were calculated between total hippocampal volume, each participant's age, and each of the predictor variables considered in the DFA. The results are summarized in Table 7. Here it can be seen that the only correlations to be reliably different from 0 were those for total change in recall and for the capacity estimate, and then only in the case of the individuals in the MCI group. In addition, the magnitude of the correlation between capacity and hippocampal volume was reliably greater than the correlation between total recall and hippocampal volume (Z = 2.12, p < .05). The correlation between change in recall and hippocampal volume is consistent with the findings, here and in a range of other studies, suggesting that changes in FCSRT performance can reliably distinguish individuals with a diagnosis of MCI from those without. And the correlation between the capacity measure and hippocampal volume, particularly given the lack of a reliable correlation for the mean RT measures, suggests the potential importance of considering the effects of atrophy in terms of capacity rather than speed of processing.

Table 7.

Correlations between individual predictors and total hippocampal volume, for MCI-C and MCI participants in each of the two single-cue conditions.

	MCI-C		MCI
Measure	Category	Instance	Category	Instance
Age	.052	−0.427	−0.008	−0.050
Total change in recall	−.411	−0.020	−0.759*	0.636*
Mean RT, cued recall	.034	−0.042	−0.267	−0.181
Capacity	.194	0.062	0.845†	0.775*

Discussion

The motivation for the present investigation was the question of whether a measure of processing capacity (Townsend & Ashby, 1978) could offer advantages in distinguishing individuals with a diagnosis of MCI from those without. We considered this question in the context of known findings regarding hippocampal atrophy, and used a computational model of the hippocampal circuit to demonstrate that measures of capacity showed more change with degeneration than did measures of speed of processing.

In order to test the ability of measures of capacity to identify individuals with a diagnosis of MCI, we modified a behavioral task that has repeatedly demonstrated its utility in distinguishing memory impairment from normal age-related changes in memory, the FCSRT. Specifically, we collected RTs on cued recall trials, using a voice key to allow for verbal responses. In addition, we also collected visual identification thresholds (as a function of exposure duration) and mean naming times, in order to provide a set of covariates that could help us distinguish deficits in recall from more general slowing of processing.

At the level of free and cued recall, we replicated standard findings in the literature. Participants in the MCI group showed a deficit in recall on the initial pass of the task, and consequently showed the largest change from initial to final levels of recall. The analysis of mean RTs in the cued recall task also showed differences specific to participants in the MCI group, with the impact of increasing recall cues from one to two being most pronounced (in terms of both facilitation and inhibition) for participants in the MCI group. Importantly, this effect of cuing was not observed in the recall frequency data, suggesting that the latency data may be relatively more sensitive in refining the characterization of specific deficits in MCI.

The effects of adding recall cues (increasing load in cued recall) with respect to processing capacity was assessed by estimating proportional changes in the hazard function of the RT data for each participant. These analyses documented that the manipulation of load had reliable positive and negative impacts on processing capacity, selective to participants in the MCI group. Having demonstrated that the capacity measures can be used in this context, and that they are selectively sensitive to differences in performance, we then compared the capacity measures to a set of alternative predictors of MCI status, and demonstrated the general superiority of the capacity measures, in terms of sensitivity, specificity, and minimal selection bias. Finally, we also showed that the capacity measures alone showed a reliable relationship to total hippocampal volume, with this being specific to the individuals diagnosed with MCI.

We find these outcomes to be very promising, though admittedly preliminary. The approach taken in the present study was easily implemented on a lap-top computer, and as a consequence could be taken into the community. The capacity estimates were done at the level of the individual participant, with that participant providing their own baseline data. This allows the effect of load to be distinguished from age-related slowing. This also allows the potential for positively-biased estimates of proportionality due to small sample size to be in some sense “canceled out” at the level of the individual. Finally, the diagnostic sensitivity and specificity of the capacity estimates, and the reliable relationship between the capacity measures and hippocampal volume, relative to the effects at the level of mean RT, are consistent with the hypothesis drawn from the computational simulations, that hippocampal atrophy is expressed most strongly in behavior in terms of processing capacity (“bandwidth,” or information processed per unit time) rather than in terms of overall speed of processing.

Much, of course, can be done to follow-up on these preliminary findings. The numerical simulations reported in the introduction suggest the need to create experimental and diagnostic situations in which larger sample sizes can be obtained. This can easily be done by increasing list length. The sample size (for the MCI-C and MCI) groups were small for this initial investigation, and the results should be replicated with much larger groups. The differential effects of cuing condition need to be systematically investigated, with particular stress on cuing conditions that differentially require episodic information (e.g., Davachi & Wagner, 2002; Davachi, Mitchell & Wagner, 2003). Finally, it seems important to validate the relationship between changes in hippocampal volume and changes in processing capacity in a longitudinal design.

Characterizing processing capacity in a disciplined, theoretically-motivated manner, has been repeatedly suggested as being foundational to understanding the foundational characteristics of human information processing (Townsend & Ashby, 1978, 1983; Townsend & Nozawa, 1995; Townsend & Wenger, 2004a,b). We hope to have demonstrated here the critical role that characterizing capacity can have in one specific application, and as a consequence demonstrated how foundational theory in human information processing can naturally inform applied research.

Appendix A: Simulation Methods, Model of the Hippocampal Circuit

The model circuit represented in Figure 1 was parameterized using published values in the literature (specifically Shepherd, 2004), including those used in previous simulations of similar architectures (specifically Amit & Brunel, 1995, 1997a,b). Thus, the only free parameters were the total number of cells in each of the regions (dentate gyrus, CA3, and CA1) and the criterion number of spikes at the output end of the circuit needed to infer completion of processing. Table 8 lists all of the parameters and their values. Each trial of the simulation involved a 200 ms presentation of input, followed by 200 ms of no input. Equations 1 and 2 describe the (discrete-time) sub-threshold dynamics for each neuron in each region, and Equations 3 and 4 describe spike-dependent modifications for CA3 and CA1 neurons, respectively.

Table 8.

Parameters, their roles, and values in the numeric simulations of the hippocampal circuit.

Parameter	Role	Values
dt	simulation time step	1 ms
t +	time, input on	200 ms
t −	time, input off	100 ms
NE	total excitatory cells, each region	3,000
NI	total inhibitory cells, each region	$\frac{1}{5}\times N_E$
N 0̸	total cells receiving no input	$\frac{1}{6}\times (N_E+N_I)$
a	proportion of cells in each region deleted, atrophy	0.10 to 0.50 by 0.10
NS	max synapses from any cell i to any other cell j	35
τ α	membrane time constant	5 ms
V 0	resting value, membrane potential	5 mV
Vmax	maximum value, membrane potential (spike)	25 mV
Vmin	minimum value, membrane potential	1 mV
γ	spiking threshold	20 mV
λ	asymptotic inter-spike (waiting) time	100 ms
β	slope, spike-rate adaptation function	200
Jij, i, j ∈ E	mean synaptic efficiency, excit./excit. connections	0.20
Jij, i ∈ E, j ∈ I	mean synaptic efficiency, inhib./excit. connections	0.30
Jij, i ∈ I, j ∈ E	mean synaptic efficiency, excit./inhib. connections	0.60
Jij, i, j ∈ I	mean synaptic efficiency, inhib./inhib. connections	1.00
σ(J)	standard deviation, synaptic efficiency (all cases)	0.10
s	sparseness parameter, synaptic efficiencies	0.25
δ i,j	transmission delay between cells	1 ms within a given region 1 ms between EC and DG 2 ms between EC and CA3, CA1
$I_i^{\mathrm{ext}}$	mean external input	20
$\sigma \left(I_i^{\mathrm{ext}}\right)$	standard deviation, external input	$\frac{1}{4}\times I_i^{\mathrm{ext}}$
γL, γH	criterion number of output spikes, low and high load	1000, 2000
NR	number of replications at each level	5,000

Each trial in each replication, at each level of load and each level of atrophy, began by first setting the values of the synaptic efficiency matrix J using independent samples from normal distributions with means J_ij and standard deviations σ(j). Sparseness was introduced in each matrix by setting all values less than s to 0. External inputs (from entorhinal cortex to each of the other regions) were randomly set on each trial using independent samples from normal distributions with mean $I_i^{\mathrm{ext}}$ and standard deviation $\sigma \left(I_i^{\mathrm{ext}}\right)$. The input was stepped from 0 to the specific value of $I_i^{\mathrm{ext}}$ for each cell i at the beginning of each trial, and remained on for t₊ ms, with the trial continuing for another t₋ ms. Cumulative counts of total spikes at the output end of the circuit (subiculum) were recorded at each value of t, and the time required to reach the criteria γ_L and γ_H were recorded.

Appendix B: Numeric Methods, Effects of Sample Size and Effect Size on Proportional Hazards Estimates

In order to assess the level of bias in estimates of proportionality obtained using the Cox proportional hazards model, we simulated samples RT measurements that varied in size and in the magnitude true proportional relationship (r) between the underlying hazard functions

$$r=\frac{h_1\left(t\right)}{h_2\left(t\right)}$$

We assumed a two-parameter Weibull distribution in all cases, with cumulative distribution function

$$F\left(t\right)=1-\exp \left[-{\left(\frac{t}{\beta }\right)}^{\alpha }\right]$$

and hazard function

$$h\left(t\right)=\frac{\alpha }{\beta }{\left(\frac{t}{\beta }\right)}^{\alpha -1}$$

(Blumenfeld, 2001), where α and β are shape and scale parameters, respectively. For each level of proportionality

$$r=\frac{h_1\left(t\right)}{h_0\left(t\right)}$$

where h₀(t) was parameterized as the reference distribution, and h₁(t) was parameterized to give the desired value of r, we generated n observations, and repeated this N times. The simulated data were then submitted to the Cox proportional hazards analysis to obtain an estimate of the proportionality r̂. Bias of the estimate was calculated as r̂ − r for each replication, and the bias estimates were averaged over replications. Table 9 lists all simulation parameters and their values.

Table 9.

Parameters, their roles, and values in the numeric simulations used to assess the bias in estimates of proportionality, as a function of sample size and effect (true level of proportionality).

Parameter	Role	Values
α	Shape parameter, Weibull distribution	1.90
β	Location parameter, Weibull distribution	600
r	Proportionality, two samples	0.25 to 1.00 by 0.05
n	Sample size	5 to 200 by 5
N	Replications at each level	10,000