Estimating classification images with generalized linear and additive models

Abstract

Conventional approaches to modeling classification image data can be described in terms of a standard linear model (LM). We show how the problem can be characterized as a Generalized Linear Model (GLM) with a Bernoulli distribution. We demonstrate via simulation that this approach is more accurate in estimating the underlying template in the absence of internal noise. With increasing internal noise, however, the advantage of the GLM over the LM decreases and GLM is no more accurate than LM. We then introduce the Generalized Additive Model (GAM), an extension of GLM that can be used to estimate smooth classification images adaptively. We show that this approach is more robust to the presence of internal noise and, finally, we demonstrate that GAM is readily adapted to estimation of higher-order (nonlinear) classification images and to testing their significance.

1. Introduction

Since its introduction to the vision community (Ahumada, 1996), the classification image paradigm has proven useful in investigating sensory encoding and perceptual strategies in a wide range of visual problems (Abbey & Eckstein, 2002; Ahumada, 2002; Bouet & Knoblauch, 2004; Neri et al, 1999; Neri & Heeger, 2002; Gold, Murray, Bennett & Sekuler, 2000; Hansen & Gegenfurtner, 2005; Kontsevich & Tyler, 2004; Levi & Klein, 2002; Mangini & Biederman, 2004; Thomas & Knoblauch, 2005). Among the reasons for its rapid adoption are its simplicity in execution and analysis and the ready interpretability of results.

In a typical experiment, observers classify signals presented against a background of added noise. Over a large number of trials, the observer will make some erroneous classifications, and the noise present in trials that were classified correctly or incorrectly is analyzed to reveal the features of the stimulus on which the observer’s perceptual decisions were based. The technique has been formally characterized in terms of reverse correlation (Ahumada, 2002).

The model on which the paradigm is based is as follows. Let s(x) denote a signal along a physical continuum x. The physical continuum can be unidimensional (e.g. time) or multidimensional (e.g., locations in an image) and we sample the signal at locations x_j, j = 1,···,p. The resulting samples s(x_j), j = 1,···,p form a vector of length p that we denote s (j), j = 1,···,p for convenience.

The stimulus presented to the observer is composed of the signal with added noise,

$$\mathbf{S}=\mathbf{s}+\mathbf{\epsilon },$$ (1)

where ε is a p-dimensional vector of identically-distributed random variables drawn from a distribution with mean 0 and a p×p covariance matrix C. The noise values ε are typically drawn from a Gaussian or uniform distribution and are typically independent so that the covariance matrix C = σ²I is diagonal with diagonal entries equal to the variance σ² of the noise.

We assume that detection is mediated through a linear mechanism with a weighting function (or template¹) 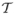(x) defined on the physical continuum x. The sampled values of the template 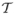(x_j), j = 1,···,p form a vector denoted T(j), j = 1,···,p The output, D, of the linear mechanism is determined by the inner product between the template vector and the stimulus vector,

$$D=\mathbf{T}•\mathbf{S}$$ (2)

The observer bases his response on the value of the random variable D, the decision variable. In the simple case in which there are only two possible signals, a and b, the observer’s decision rule on a given trial might be to choose a if

$$D>c$$ (3)

for some fixed criterion c, and otherwise choose b. In effect, the inner product of the template with the stimulus reduces the decision problem to one dimension. If the noise is independent, identically-distributed Gaussian, the decision rule that results in the highest expected proportion of correct responses is of the form of Eq. 3 as shown in Duda, Hart & Stork (2000, Chap. 2).

The possible outcomes in this simple binary case are often described using the terminology of Yes/No signal detection experiments. One of the responses “Yes” is put in correspondence with the signal a, the response “No”, with the signal b (Green and Swets, 1966; Macmillan & Creelman, 2005). There are only four possible types of response referred to as Hit (H), when the signal is a and the response is a, False Alarm (FA), when the signal is b and the response is a, Miss (M), when the signal is a and the response is b and Correct Rejection (CR), when the signal is b and the response is b. The decision rule in Equation 3 leads to a method of estimating the classification image by averaging the trial-by-trial noise profiles for each type of response Ī^H,Ī^M,Ī^FA,Ī^CR where the p-vector Ī^H is the average of the noise profiles, ε, presented on Hit trials, the p-vector Ī^FA, the average for False Alarm trials, etc (Ahumada, 2002). We then combine these mean images to form two classification images for stimulus present Î_p = Ī^H − Ī^M and for stimulus absent, Î_a = Ī^FA − Ī^CR and then add these two images to get an estimated classification image based on all of the data,

$$\widehat{\mathbf{I}}={\widehat{\mathbf{I}}}_p+{\widehat{\mathbf{I}}}_a$$ (4)

If the linear model of the classification process presented above is valid then Î_p and Î_a should have the same expectation (that is, differences between them are due only to random variation). However, as we shall see below, it is useful to analyze the images Î_p, Î_a separately before combining them (Ahumada, 2002; Solomon, 2002a, 2002b; Thomas & Knoblauch, 2005).

The estimated classification image Î is often smoothed to emphasize low frequency information at the expense of high frequency information, although typically no criterion for the amount and kind of smoothing employed is given (but see Chauvin, Worsley, Schyns, Arguin & Gosselin, 2005). The resulting p-vector Î is interpreted as an estimate of the linear template responsible for the observed classification performance.

The estimation method in Equation 4 is the least-squares solution of a linear model (LM) of the observer’s behavior on each trial of the classification image experiment. The stimulus S presented on each trial is a p-vector. If the experiment consists of n trials, we obtain the terms of Equation 4 from the solution to the equation

$$\mathbf{E}=\mathbf{X}\mathbf{\beta }$$ (5)

where E is a np vector² of concatenated noise vectors ε_i=[ε_i1, ···, ε_ip]′, i = 1, ···,n. presented on successive trials, X is an np×4p incidence matrix indicating which of four outcomes (H, FA, etc) occurred on the trial and β is a 4p vector that represents the elements of the 4 components of Equation 4. The matrix X is a block matrix consisting of n×4 submatrices with one row of submatrices for each trial, each of which is either a p×p zero matrix 0_p×p or a p×p identity matrix I_p×p. An example of such a block matrix X is

$$\left(\begin{array}{c}{\epsilon }_{11}\\ ⋮\\ {\epsilon }_{1p}\\ {\epsilon }_{21}\\ ⋮\\ {\epsilon }_{np}\end{array}\right)=\left(\begin{array}{cccc}{\mathbf{0}}_{p\times p}& {\mathbf{0}}_{p\times p}& {\mathbf{I}}_{p\times p}& {\mathbf{0}}_{p\times p}\\ {\mathbf{0}}_{p\times p}& {\mathbf{I}}_{p\times p}& {\mathbf{0}}_{p\times p}& {\mathbf{0}}_{p\times p}\\ {\mathbf{0}}_{p\times p}& {\mathbf{0}}_{p\times p}& {\mathbf{I}}_{p\times p}& {\mathbf{0}}_{p\times p}\\ {\mathbf{I}}_{p\times p}& {\mathbf{0}}_{p\times p}& {\mathbf{0}}_{p\times p}& {\mathbf{0}}_{p\times p}\\ & \cdots & & \\ {\mathbf{0}}_{p\times p}& {\mathbf{0}}_{p\times p}& {\mathbf{I}}_{p\times p}& {\mathbf{0}}_{p\times p}\end{array}\right)\left(\begin{array}{c}{\beta }_1^H\\ ⋮\\ {\beta }_p^H\\ {\beta }_1^{FA}\\ ⋮\\ {\beta }_p^{CR}\end{array}\right),$$ (6)

There is only one identity matrix in each block matrix row and it is placed so that its first column is either at column 1, p + 1, 2p + 1 or 3p + 1 of X depending on whether the trial is a Hit, False Alarm, Miss or Correct Rejection, respectively. In Equation 6, for example, the first trial resulted in a Miss and the identity matrix I_p×p is the third submatrix beginning in column 2p + 1 of X. The least-squares solution of Equation 5 is a 4p-vector β̂. The solution can be divided into four vectors ${\mathbf{\beta }}^H={\left[{\beta }_1^H,\cdots ,{\beta }_p^H\right]}^{\prime },{\mathbf{\beta }}^{FA}={\left[{\beta }_1^{FA},\cdots ,{\beta }_p^{FA}\right]}^{\prime },{\mathbf{\beta }}^M={\left[{\beta }_1^M,\cdots ,{\beta }_p^M\right]}^{\prime },{\mathbf{\beta }}^{CR}={\left[{\beta }_1^{CR},\cdots ,{\beta }_p^{CR}\right]}^{\prime }$ and the least-squares solutions of Equation 5 for these four vectors are the corresponding mean vectors Ī^H, Ī^M,Ī^FA,Ī^CR in Equation 4. The classification image estimate Î is therefore readily computed from the solution to Equation 5.

Equation 6 can be solved with standard linear modeling methods. We used the function 1m in the programming environment of R (R Development Core Team, 2008). See Appendix A.1.

It is interesting to note that this formulation is “inverted” with respect to the typical conception of the linear model. The responses are distributed across the model matrix X on the right hand side of Equation 5 where one traditionally finds the explanatory variables (regressors), and the noise samples, a fixed part of the stimulus, are on the left hand side, where one typically finds the response. The stochastic component is the random placement of submatrices in the matrix X according to observer’s responses. The Generalized Linear Model (GLM) and the Generalized Additive Model (GAM) presented later in this article are set up in a more traditional manner, with the response on the left and the stimulus, explanatory variables on the right.

Alternative procedures have been proposed for estimating classification images (for a review, see Victor, 2005). Several studies have used noise composed of random amplitudes of fixed Fourier components (Ahumada & Lovell, 1971; Levi & Klein, 2002; Mangini & Biederman, 2004). In other studies, observers rated the detectability of a signal on a multi-point scale (rather than just giving a binary response) with the classification image estimated by linear regression of ratings on the component energies (Levi & Klein, 2002) or by combining only the noise profiles from extreme classifications on the scale (Mangini & Biederman, 2004).

Subspace methods

The articles, Levi & Klein (2002) and Mangini & Biederman (2004), provide examples of subspace methods in which the noise samples and the estimated classification image were constrained to be expressed as a weighted sum of basis p-vectors,

$$\mathbf{I}=\sum _{i=1}^m{\alpha }_i{\mathbf{B}}_i$$ (7)

The basis vectors are selected by the experimenter and in the two articles just cited the experimenters chose Fourier components (sine and cosine basis functions) so that the resulting classification images are constrained to be “low-pass”. These methods potentially yield more accurate classification images with fewer trials. When Fourier components are chosen as a fixed basis, the resulting classification images are effectively “smoothed.”

Using the subspace method to smooth data in this way is similar in spirit to appyling Generalized Additive Models (Hastie & Tibshirani, 1990; Wood, 2006) discussed in detail below. However, as we describe below, GAM is an adaptive method that can be used to adjust the degree of smoothing to improve the fit according to a model fitting criterion.

Solomon (2002a, 2002b) obtained classification images by setting up the problem as the maximization of a binomial likelihood. Using the inner product form from Equation 2, the likelihood can be written as

$$L(\mathbf{T},\sigma )=\prod _{i=1}^n\mathrm{\Phi }{\left(\frac{\mathbf{T}•{\mathbf{\epsilon }}_i}{\sigma }\right)}^{R_i}{\left(1-\mathrm{\Phi }\left(\frac{\mathbf{T}•{\mathbf{\epsilon }}_i}{\sigma }\right)\right)}^{1-R_i},$$ (8)

where L is the likelihood defined as a function of, T, the template coefficients, σ, a scale factor, ε_i is the added noise profile on the i^th trial, Φ the cumulative Gaussian function with mean 0 and variance 1 and R_i an indicator variable taking on the values 1 or 0 if the response on the i^th trial is that the signal is a or b, respectively. The model is identifiable with p parameters if one constraint is placed on the vector 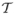, such as that its length ||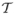|| = 1. The argument of Φ is the decision variable from Equation 8 but scaled by σ and with this parameterization is in the same units as the signal detection parameter d′ (Green & Swets, 1966; Macmillan & Creelman, 2005).

The negative logarithm of likelihood (Equation 8) can be minimized with optimization procedures that are standard in modern computational programming environments. Solomon also substituted a smooth parametric function of many fewer parameters for 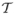and chose the parameters to optimize the likelihood. For example, his signals were spatial Gabor functions. Constraining 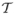to be of this form, the optimization procedure estimates the parameters of the best fitting Gabor function. The two models are nested and can be compared with a likelihood ratio test. While this approach leads to a more parsimonious description of the data, the choice of a parametric form could distort the structure of the estimated template.

The first objective of this paper is to show how the model of Equation 7 can be implemented as a Generalized Linear Model (GLM) (McCullagh & Nelder, 1989; Venables & Ripley, 2002). Several classic signal detection models have been reformulated in terms of GLM (for example, DeCarlo, 1998; Macmillan & Creelman, 2005). The observer decision model for difference scaling has also recently been implemented as a GLM (for example, Charrier Maloney, Cherifi & Knoblauch, 2007; Knoblauch & Maloney, 2008). Abbey & Eckstein (2002) mentioned GLM approach as an alternative for modeling classification images and also investigated GLM (Abbey & Eckstein, 2001; Abbey et al, 2002). Victor (2005) has also discussed some of the approaches and issues considered here as have Mineault & Pack (2008).

One advantage of GLM is that it naturally relates the expected probabilities of response to the decision space through a link function in a way that is a simple generalization of a psychometric function.

We will show that GLM yields classification image estimates that are closer to the template with fewer numbers of trials than required by the LM but that the addition of internal noise reduces and eventually eliminates the advantage of GLM over LM. We will then describe how an optimally smoothed model that is more robust to internal noise can be obtained using a Generalized Additive Model or GAM (Hastie & Tibshirani, 1990; Wood, 2006). Finally, we will show how to extend this framework to estimate and test higher-order (nonlinear) classification images (Neri and Heeger, 2002; Neri, 2004).

2. Generalized Linear Model: Theory

The GLM is an extension of the LM in which a linear predictor is related to the expected value of the response through a link function, η

$$\eta (\text{E}[\mathbf{Y}])=\mathbf{X}\beta ,$$ (9)

where the distribution of the elements of Y is a member of the exponential family (not to be confused with the exponential distribution) which consists of distributions whose probability density functions can be written in the form

$$f(y;\theta )=exp\left[a(y)b(\theta )+c(\theta )+d(y)\right],$$ (10)

for some specific choice of functions a, b, c and d (McCullagh & Nelder, 1989).

The exponential family contains many commonly used distributions such as the Gaussian, the Poisson, the gamma and the binomial and, as a consequence, GLM can potentially be applied to model experiments whose outcomes are random variables with these distributions and more.

However, in this article, we focus on the case where the random variable Y is a Bernoulli (or binary) random variable, a random variable with two possible outcomes 1, and 0, that takes on the value 1 with a fixed probability θ ∈ (0,1) and is otherwise 0. The Bernoulli distribution for observing y ∈ {0,1} is,

$$f(y,\theta )={\theta }^y{(1-\theta )}^{1-y},$$ (11)

We can recast Equation 11 in the form of Equation 9 as

$$f(y;\theta )=exp\left[ylog\left(\frac{\theta }{1-\theta }\right)+log(1-\theta )\right],$$ (12)

where a(y) = y, b(θ) = log(θ/(1 − θ)), c(θ) = nlog(1 − θ), d(y) = 0, demonstating that the Bernoulli is a member of the exponential family. Note that θ is the expected value E[Y] of the response variable, Y.

To specify the GLM model we need to select a link function η (•). We can choose the function b(θ) = log(θ/(1 − θ)) and the resulting GLM is then equivalent to logistic regression (McCullagh & Nelder, 1989). We can, however, select any alternative link function that maps the interval (0,1) onto the range (−∞, +∞). One common choice of link function is the inverse of the cumulatve distribution function of the Gaussian function, denoted Φ⁻¹ (•) leading to the probit model (Finney, 1971).

Using GLM permits the data to be appreciated on two levels. First, the individual responses of the observer are modeled directly in the fitting process. We can rewrite Equation 9 as

$$\text{E}[\mathbf{Y}]={\eta }^{-1}(\mathbf{X}\beta ),$$ (13)

which in the Bernoulli case becomes,

$$P[\mathbf{Y}=1]={\eta }^{-1}(\mathbf{X}\beta )$$ (14)

and the GLM model is seen to be a natural generalization of the psychometric function to the case in which a single intensity variable is replaced by a weighted linear combination Xβ of intensity variables. The inverse of the link function is the psychometric function.

Second, through the link function, the responses are related to a linear model. Within this formalism, the scale of the linear predictor corresponds to the decision space of the observer with σ =1. Thus, we can conceptualize Equation 14 as the linear predictor with the stimulus as the covariates and the template as the coefficients to estimate. The term Xβ can be used to model experimental designs with multiple conditions that are structured as analysis of variance designs or multiple regression designs. We pursue this point in the example below.

The GLM is readily adaptible to experiments where the observers response is not binary but is a numerical rating or a continuous adjustment (DeCarlo, 1998). The GLM with different choices of distributions allows considerable freedom in modeling the observer’s behavior. With different choices of linking functions the model is easily generalized to the multinomial logisitic model so that classification images can be computatable in experiments making use of multiple response categories.

2.1. An example

To demonstrate how the notions advanced in the last section are exploited to estimate a classification image, we consider an example. Thomas & Knoblauch (2005) reported results from a Yes/No experiment in which the observers’ task was to detect a temporal luminance modulation perturbed by uniform random luminance noise. On each trial, the luminance of a circularly symmetric region following a two-dimensional Gaussian spatial profile (σ_s = 2.5 deg) was modulated over a 640 ms interval on a calibrated monitor. The modulation consisted of 32 sequential samples, each of 20 ms duration. On a given trial, the samples were either set to random luminance values chosen from a uniform distribution centered on the mean luminance of the screen or to random luminance values added to a temporal luminance modulation following a Gabor function. The temporal luminance modulation was described by

$$\mathit{Lum}(t_i)=e^{-\frac{1}{2}{\left(\frac{t_i-\mu }{{\sigma }_t}\right)}^2}sin\frac{\pi t_i}{{\sigma }_t}$$ (15)

where t_i is the time of the i^th sample, i =1,32, μ = 320 ms and σ_t = 160 ms. Three different carrier frequencies were tested in the article, but here, we consider only data collected from one observer at the highest carrier frequency used, 3.125 Hz.

The sampled signal is shown in Figure 1a and an example of the signal with uniform noise added in Figure 1b. The observer’s task was to judge whether the signal was present on each trial. The signal strength and the amplitude of the noise modulation were chosen in pilot experiments so that the observer’s performance approximated d′ = 1.

Figure 1.

a. The sampled temporal signal from the experiment of Thomas & Knoblauch (2005). b. An example of the sampled temporal signal with independent, identically-distributed uniform noise added.

The observer performed 16 sessions of 224 trials each, yielding 3584 trials. The data set is organized as 114688 rows and 4 columns, a sample of whose rows are

	resp	time	Time	N
1	H	1	0.02	−0.196	Start trial 1
2	H	2	0.04	−0.197
		.
		.
		.
32	H	32	0.64	−0.189	End Trial 1
33	H	1	0.02	0.039	Start trial 2
34	H	2	0.04	0.131
		.
		.

where the lines are numbered, and we have rounded the numbers here to 3 significant digits for display. Each trial is distributed across a block of 32 rows. The meaning of the column names is

• resp a 4 level factor indicating the category of the response, H, FA, M, CR,

• time a 32 level factor indicating the time points of each sample of the stimulus,

• Time a numeric value indicating the time in seconds of the sample with respect to the beginning of the trial,

• N a numeric value indicating the relative luminance modulation of the noise component of the stimulus at the indicated time sample.

All calculations in this article were performed with the open source software R (R Core Development Team, 2008) and the code used appears in the Appendices. The data set is available in an Rdata file from the corresponding author.

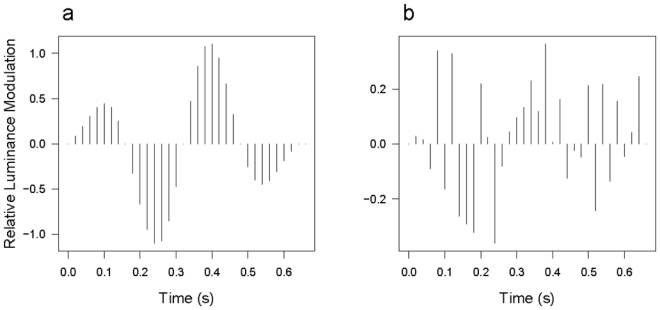
Using the linear model formulation, Equation 5 which gives exactly the same results as Equation 4 we obtain the classification image shown in Figure 2a plotted with circles connected by line segments. The results have been scaled by least squares to fit the actual signal Equation 14, shown as a red dashed curve.

Figure 2.

a. The circles indicate the estimated classification image obtained with LM as a function of the time in seconds. The red dashed curve is the signal and corresponds to the ideal template. b. The circles indicate the estimated classification image obtained with GLM plotted as a function of time in seconds. The red dashed curve is identical to that in Figure 1a. c. The two estimated classification images Î_p, Î_a based on signal present trials and signal absent trials, respectively. Î_p is plotted with unfilled circles, Î_a, with filled. The red dashed curve is identical to that in Figure 1a. d. the overall classification image Î = Î_p + Î_a. The red dashed curve is identical to that in Figure 1a.

To estimate the classification image using the GLM, it is convenient to reorganize the data. First, the four-level factor resp is recoded as two factors that we name Stim, a two level factor with labels 0 and 1 indicating whether or not the signal was present and Resp, a two level factor with the same labels indicating whether or not the observer classified the trial as containing the signal. Second, we reshape the column N into 32 columns, each indicating a time sample. We show the first 8 columns of a sample of rows of the modified data set below with line numbers

	Res	Stim	t1	t2	t3	t4	t5	t6	...
1	1	1	−0.196	−0.197	−0.038	−0.114	−0.136	0.204	…	Trial 1
2	1	1	0.039	0.131	0.233	−0.053	−0.133	0.295	…	Trial 2
			.
			.
			.
32	0	0	−0.249	0.219	−0.073	0.257	−0.142	−0.235	…	Trial 32
33	1	0	0.022	−0.109	0.076	−0.013	0.044	−0.249	…	Trial 33
34	1	1	0.254	−0.193	−0.197	0.162	0.285	−0.264	…	Trial 34
			.
			.

In this new format, each row corresponds to one trial of the experiment. The time points, t1, …, t32,³ enter the model now as independent covariates, taking on the instantaneous values of the noise on each trial.

We fit these data set using GLM in two different ways. First, we combine all of the data from all trials to estimate a single classification image. The model can be represented as

$$\eta (E[Y])=\mathbf{S}+{\beta }_1{\mathbf{t}}_1+{\beta }_2{\mathbf{t}}_2+\dots +{\beta }_{32}{\mathbf{t}}_{32}$$ (16)

where S denotes Stim, a two level factor indicating the presence or absence of the signal, the t₁, …, t₃₂ are the noise samples (vectors) at each time point acting in the model as covariates and the coefficients β₁, … β₃₂ provide the estimated classification image. The R code is given in Appendix A.2 and the resulting classification image is shown in Figure 2b. Comparing the fits in Figs 2a and b reveals that the two methods, LM and GLM, yield very similar results. Both methods lead to an estimated classification image that reveals the same pattern of systematic differences from the signal. We note that the main effect of the term S (see Appendix A.2) provides an estimate of d′ (DeCarlo, 1998).

However, Thomas & Knoblauch (2005, p. 2260) have already demonstrated that the simple linear model of the decision process is violated for these data. As mentioned in the discussion leading to Equation 4, we can use LM to compute distinct classification images Î_p, Î_a separately for trials on which the signal is present, and trials on which it is absent, respectively. We can easily do this with GLM as well. In doing so, we test whether there is an interaction between the presence/absence of the signal and the estimated classification images Î_p, Î_a. If there is none, we can combine the two classification images Î_p, Î_a according to Equation 4. The model can be represented as

$$\eta (E[Y])=\mathbf{S}+\mathbf{S}\times \left[{\beta }_1^s{\mathbf{t}}_{\mathbf{1}}+{\beta }_2^s{\mathbf{t}}_{\mathbf{2}}+\dots +{\beta }_{32}^s{\mathbf{t}}_{\mathbf{32}}\right]$$ (17)

where × denotes component-wise multiplication of vectors and the estimated value of the ${\beta }_i^s$ now depend on whether the signal is present (s = p) or absent (s = a). The estimated values ${\widehat{\beta }}_i^p$, i = 1, …, 32 and ${\widehat{\beta }}_i^a$, i = 1, …, 32 correspond to the two estimated classification images Î_p and Î_a, respectively.

The R code for this fit is given in Appendix A.2 and the results indicate a significant effect of signal absent/present with the estimated classification image. A summary of the nested hypothesis test is shown as an “analysis of deviance table” in Table 1. Analysis of deviance is a convenient way to summarize multiple nested hpyothesis tests within the GLM framework and, as the name suggests, an analysis of deviance table can be interpreted much as an analysis of variance table but with difference of deviance (twice the negative log likelihood) replacing ratios of variances.

Table 1. Analysis of deviance table for the Thomas & Knoblauch (2005) data.

The table summarizes a nested hypothesis test comparing a model in which a single classification image is estimated on signal present and absent trials (model 1) to a model in which separate images are estimated for each type of trial (model 2). The difference in deviance (twice the negative log likelihood) is large, allowing us to reject the hypothesis that the two estimated classification images are the same (p < .0001).

	Residual df	Residual deviance	df	deviance	P [> χ2]
1	3550	4213.0
2	3518	3977.2	32	235.8	<0.00001

In other words, we confirm the conclusion of Thomas & Knoblauch (2005): the two separate images are plotted in Figure 2c with unfilled circles (Î_p) and filled circles (Î_a), respectively. For comparison, we plot Î = Î_p + Î_a in Figure 2d. It can be seen that it differs little from the fit that did not include an interaction (Figure 2b).

2.2. Comparison of LM and GLM: Simulated Observer

2.2.1. Noiseless Observer

We simulated an observer performing an experiment similar to that described above except that the signal was a Gaussian modulation described by

$$g(t_i)=e^{-\frac{1}{2}{\left(\frac{t_i-\mu }{{\sigma }_t}\right)}^2},i=1,32$$ (18)

with the parameters set to the same values as in Thomas & Knoblauch (2005), but with additive Gaussian noise instead of uniform. Gaussian noise was used in all simulations in this article for convenience. However, we have repeated this first simulation with uniform noise equated in variance to that of the Gaussian and reached the same conclusions.

The simulated observer used the signal as the template. In the experiment, each trial consisted of a 32 element vector. On half of the trials, the signal was added to random values drawn from 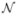(0,1) and on the other half, no signal was added in. Simulations were run with 5 different numbers of trials: 100, 500, 1000, 5000 and 10000, each simulation repeated 100 times. For each trial, the inner product between the stimulus and the template was computed. If the result was greater than 0, the response to the trial was classified as “Present”, if not “Absent”. The signal amplitude was set so that d′ ≈ 1. For each simulation, the classification image was estimated using both LM and GLM. The estimated classification images were then scaled to the template and the residual variance was calculated as a measure of goodness of fit.

The simulation results are summarized in Figure 3. Each point is the median variance obtained for the 100 replications. The black circles were obtained with LM and the white with GLM. The grey zones surrounding each set of results correspond to the 2.5% and 97.5% percentile points in the density estimates of the results. The residual variance between the template and signal decreases faster using GLM than LM. By 10000 trials, the difference is nearly 2 orders of magnitude in variance (corresponding to one order of magnitude in standard deviation). Put another way, the precision of the estimate analyzed by GLM using only 1000 trials is about the same as that using LM with 10000 trials.

Figure 3.

The residual variance for the estimated classification images of the simulated observer is plotted as a function of the number of experimental trials. The black circles are the median of 100 repetitions of the experiment analyzed using LM, and the white, by GLM. The grey regions around each curve mark 95% confidence intervals of the values about the median.

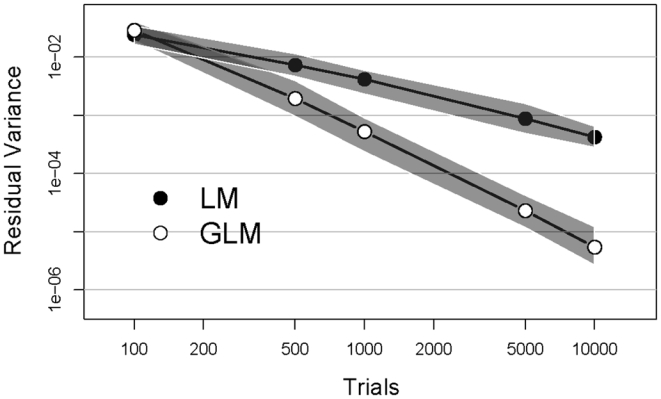
In Figure 4a, we present examples of single classification images estimated during the simulations. The first row illustrates how the estimated template converges as we increase the number of trials from 100 to 10000, fitting with the LM. The second row shows a series of estimates for different samples sizes, but fitting with the GLM. It is evident that the GLM converges more rapidly and this is what we expect given the results in Figure 3. Figure 4b shows the residuals of the fits in Figure 4a. The third row in each of Figs. 4a,b shows comparable examples but for GAM. We discuss the results in these rows after we introduce GAM in a later section of the article. We include these results now only to facilitate later comparison.

Figure 4.

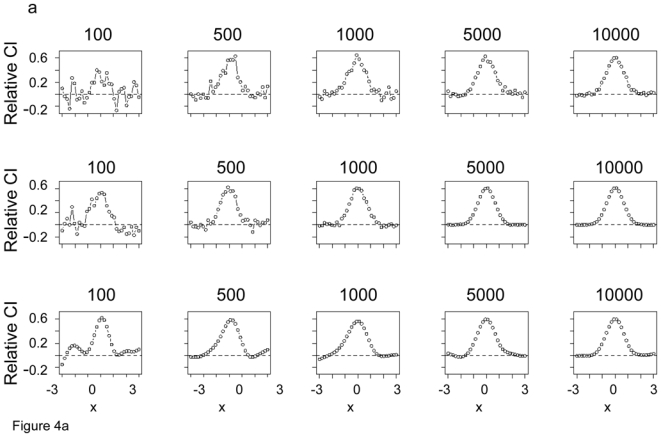
a. Examples of estimates of the classification image (unnormalized) obtained with LM (first row), GLM (second row), and GAM (third row) as a function of number of trials, 100, 500, 1000, 5000, 1000. The results for the third row will be discussed later, after presentation of GAM, but are included here to facilitate comparison across all three models. b. The residuals from the template after normalization corresponding to each plot in Figure 4a.

2.2.2. Noisy Observer

The results in the previous section suggest that classification image estimation using GLM is more efficient than LM for an observer with no internal sources of noise to perturb the classification judgments. However, in any experiment, the observer’s uncertainty in judgment is affected not only by the experimenter’s choice of noise perturbation added to the stimulus, but also by endogenous noise processes that we refer to collectively as internal noise.

We simulated internal noise by adding random Gaussian values to each element of the template before it was multiplied by the stimulus to generate the decision variable. The level of internal noise was varied by adjusting the standard deviation of the Gaussian values. The experiments were simulated for 8 levels of internal noise: 0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1 and 2. Other than the introduction of template noise on each trial, the simulation conditions were the same as in the previous section. We only ran tests for experiments of 500 and 5000 trials. We note that we did not force d′ to equal 1 in these experiments and that with increasing internal noise, the observer’s d′ decreased.

The results of the simulations are shown in Figs 5a and b in which the residual variance is plotted as a function of the standard deviation of the internal noise. Each point is the median value of the 100 replications of the experiment and the grey zones indicate the range within which 95% of the observations fell. The white points correspond to the analyses using GLM and the black with LM. The results indicate that while the GLM analysis is superior for the noiseless observer, this advantage disappears as the level of internal additive noise increases. For both numbers of trials, the curves converge at similar internal noise levels, near σ = 0.05. While internal noise reduces the advantage of the maximum likelihood fit, the result is never worse than that obtained using LM.

Figure 5.

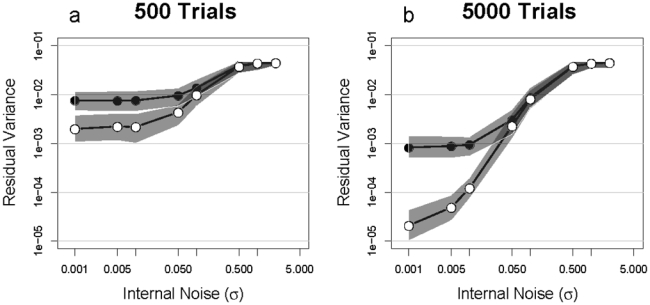
Residual variance between estimated classification image and the template is plotted as a function of the standard deviation of the Gaussian noise added to the template. Each point is the median of 100 repetitions and the grey regions correspond to 95% confidence intervals. The black points correspond to fits with LM and the white, with GLM. a. Each run is 500 trials. b. Each run is 5000 trials.

To summarize, we found that GLM fits are never worse than those for LM although with large magnitude of internal noise the two methods are comparable in performance. We would still recommend that researchers use GLM rather than LM for three reasons: (1) GLM corresponds to the typical underlying model that the experimenter has in mind and it is the maximum likelihood estimate for classification images with this model, (2) we find that GLM fits are never worse than corresponding LM fits, and (3) the computational costs of GLM fits using modern packages are not unreasonable. The second point is particularly important if the experimenter has not measured the magnitude of internal noise for a particular psychophysical task.

3. Generalized Additive Model: Theory

A criticism of both LM and GLM methods is that the elements of the stimulus, pixels, time samples, etc., are treated independently and discretely, as factor levels with LM and as covariates with GLM. The noise at one element is uncorrelated with that at nearby elements. Taken over all of the stimuli in the experiment, this is true within the limits of the random number generator used. This should not be the case, however, for the subset of noise samples that the observer classifies similarly. The LM and GLM approaches do not take into account the dependencies introduced into the noise profiles by the observer’s choices. One method of dealing with this would be to allow the possibility of interactions between the covariates with the GLM, but doing so would introduce more parameters to fit and not lead to parsimonious models.

In practice, classification images are often smoothed by some form of low-pass filtering (Ahumada, 1996). Implicitly, this procedure recognizes dependencies in the data and explicitly introduces them. The sampling rate of the noise is often finer than the resolution of the judgment made by the observer, so the classification image will tend to be uncorrelated on a fine scale. The smoothing will bring out the large scale dependencies. Pooling nearby samples will also increase the sensitivity of statistical tests at detecting the modulation in the image. The major criticism of such ad hoc smoothing is that the degree of smoothing used is arbitrary. Methods to determine how much smoothing is appropriate or optimal have not typically been applied (but see Chauvin et al (2005), an exception).

Generalized Additive Models (Hastie & Tibshirani, 1990; Wood, 2006) provide an appealing method for estimating a smooth classification image. They are extensions of the GLM, so the models developed above apply. The difference is that smooth terms that are functions of the stimulus dimensions can be included in the model. Thus, the linear predictor is a function of the continuous stimulus dimension(s). The specification of the GAM model to fit to our example data set would be as follows,

$$\eta (\text{E}[\mathbf{Y}])=f_0(t){\mathbf{X}}_P+f_1(t){\mathbf{X}}_A,$$ (19)

where f_i are smooth functions of the continuous covariate, t, which here is time, and X_P and X_A are the instantaneous noise values, also taken as covariates, for Present and Absent trials, respectively, extracted from the main effects model matrix. The intercept term can be absorbed directly into the smooth terms. The smooth functions, f, are approximated by the sum of known basis functions

$$f(t)=\sum _{i=1}^q{\beta }_i{b}_i(t)$$ (20)

where b_i are basis functions evaluated at the covariate values for unknown values of the parameters, β_i. Thus, they can be added as columns to the model matrix and fitted as linear covariates. In most circumstances spline curves are used as bases, but alternatives are possible, such as Fourier terms similar to those used by Levi & Klein (2002) and by Mangini & Biederman (2004). More basis terms are chosen than is generally necessary, and smoothness is controlled by adding a penalty for undersmoothing during the process of maximizing the likelihood. The penalty is usually implemented as a proportion, λ, of the integrated square of the second derivative of f. Larger contributions of this term result in less smooth models. Because the function is expressed as a linear combination of basis elements, the penalty term can be written as a quadratic form in β.

$$\int {\mid f^{″}(t)\mid }^{2}dt={\beta }^T\mathbf{S}\beta ,$$ (21)

where S is a known matrix obtained from the basis functions, b_i(t). The model is fit then by minimizing the expression

$$\mathrm{\Delta }(\beta )+\sum _{i=1}^m{\lambda }_i{\beta }^T{\mathbf{S}}_i\beta ,$$ (22)

with respect to β, where Δ is the negative of twice the logarithm of the likelihood, termed the deviance, and m is the number of smooth terms in the model.

In the case of additive models in which the scale (variance) is unknown, the contribution of the penalty can be regulated by the technique of cross validation, in which λ is chosen to minimize the prediction error to a subset of the data left out of the fit, taken across all or a large number of subsets of the data (Wood, 2006). In the case of the binomial family for which the scale parameter is known, the degree of smoothing is chosen to minimize a statistic called the Un-Biased Risk Estimator (UBRE, Wood, 2006, pp. 172–173) which is defined as

$${\mathcal{V}}_u(\lambda )=\frac{1}{n}\mathrm{\Delta }(\widehat{\beta })-{\sigma }^2+\frac{2}{n}\text{tr}(\mathbf{A}){\sigma }^2,$$ (23)

where σ² is the known binomial variance, A is the influence or hat matrix and tr is the trace function. The trace of the influence matrix corresponds to the effective number of parameters estimated in the fit. The reduction of deviance obtained by increasing the number of parameters is offset by adding back in a function of the number of parameters, reminiscent of Akaike’s Information Criterion (AIC; Akaike, 1973). In fact, this criterion is effectively a linear transformation of AIC (Wood, 2006, p. 178). Like AIC, this measure favors a model that maximizes the predictability of future rather than the actual data and, thus, serves to reduce the tendency to overfit the data with too many parameters. The literature on model selection is growing rapidly and AIC is only one choice of criterion of many. For a review see Burnham & Anderson (2003) and also Myung, Navarro & Pitt (2006) and other articles in the same special issue.

3.1. An example, continued

To obtain a GAM estimate of the classification image for the Gabor detection experiment, the data set can be organized as it was initially for the LM fit, as described in Section 2.1. Instead of using the factor time, the real time in the variable Time is used as a covariate of the smooth terms. Each smooth term is multiplied by either the noise in the trial or 0 depending on whether the signal was present or not. We used the gam function in the R package mgcv (Wood, 2006). The code fragment to fit the model is shown in Appendix A.3. The function allows several different possible choices of basis functions. We chose thin plate regression splines with shrinkage (Wood, 2006, Sections 4.1.5–4.1.6). The term “shrinkage” implies that smooth terms which do not contribute significantly to the fit can be dropped from the model. An alternative fit using a cubic spline basis produces similar results to those reported here. Spline fits can show biases at the boundaries of the data. Such effects are possibly visible in Figure 5 but small. A detailed discussion of considerations that serve to guide the choice of basis functions can be found in Wood (2006, Section 4.1).

The estimated classification image is shown in Fig 6 as the solid curve. Since the estimate is a continuous function of time, we could define it at as many points as we like, although here we have simply connected the 32 estimates at the sampled time points by linear segments. The white disks are the GLM classification estimates from Figure 2b and the red dashed curve indicates the ideal template. In fact, the fitted curve from the GAM is based on only about 11 parameters, one-third less than the number required to specify the LM and GLM models. Interestingly, the GAM estimate is closer to the ideal template than the GLM one over most of the trial duration and follows it more closely. These observations suggest that the GLM and LM are “overfitting” the data and that a model with many fewer parameters could be adequate. This question and others are addressed by repeating the simulations above using a GAM to fit the simulated data.

Figure 6.

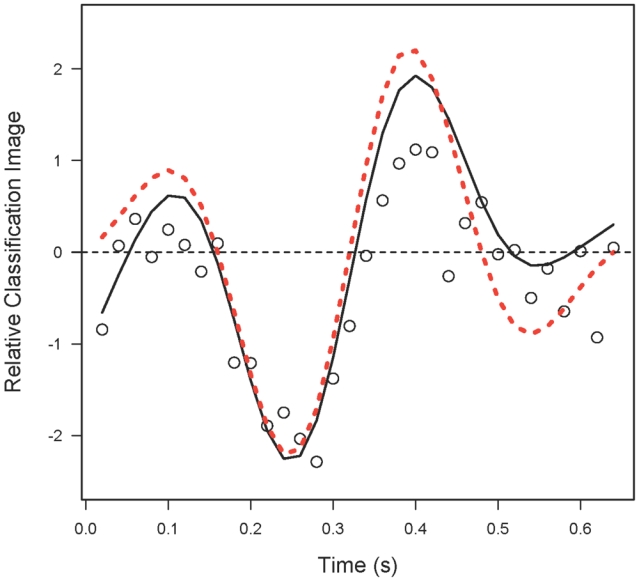
The solid black line indicates the classification image as a function of time, estimated using a GAM. The red dashed curve is the ideal template as in Figure 2a,b. The white circles correspond to the GLM classification image replotted from Figure 2d.

3.2. Comparison of GAM with LM and GLM: Simulated observer

3.2.1. Noiseless observer

We used the same simulated, noiseless observer performing the detection of a Gaussian signal, described above. Experiments of 100, 500, 1000, 5000 and 10000 trials were each repeated 100 times. For each experiment, a classification image was estimated using a GAM. As before, we recorded the residual variance between the estimated classification image and the ideal template. The median values are shown in Figure 7 as blue circles connected by blue line segments. The 95% range of values around the medians is shown as the grey envelope. The previous results obtained by LM and GLM are replotted as black and white circles, respectively.

Figure 7.

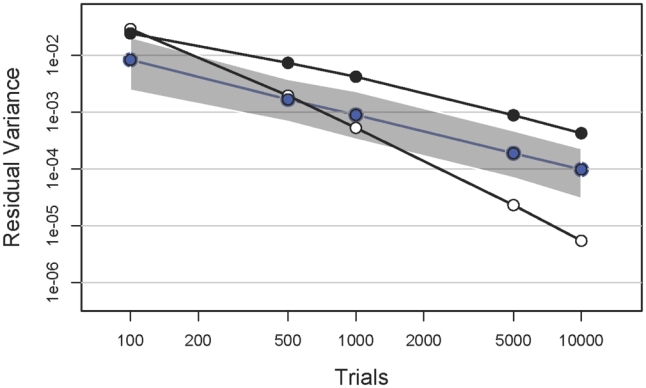
The residual variance between the classification image and the template is plotted as a function of the number of trials. The blue points and line segments correspond to the median values of 100 experiments from the GAM fits and the grey regions are the 95% confidence interval. The black and white points correspond to the LM and GLM models, respectively, and are replotted from Figure 3

The residual variance of the GAM fits decreases in parallel to the LM fits in the double-logarithmic coordinate system. For the smallest experiment, the GAM estimate is less variable than the other two. As the number of trials is increased the GLM fit equals and then surpasses the GAM estimate in closeness to the template.

This outcome is likely the result of a bias in GAM introduced by our choice of the ideal template. While the GAM basis we chose can provide very close approximations to the ideal template, these approximations are not perfect. With enough data, GLM will eventually converge to the ideal template but GAM in this case cannot. The difference between the ideal template and the approximation through GAM is very slight and the apparent advantage of GLM with large numbers of trials is also very slight, as can be seen in Figure 4a (third row) where we present estimated classification images for different numbers of trials and in Figure 4b (third row) where we present the residuals from the fits. While the residuals for GAM with 10000 trials are larger than those for GLM (second row) with 10000 trials, both are negligible. Overall, the GAM fit remains on average about 4 times less variable than that provided by LM.

3.2.2. Noisy observer

We evaluated the influence of 8 levels of noise added to the template on each trial on the GAM fits for experiments of 500 and 5000 trials. Each experiment was, again, repeated 100 times. The median residual variances (blue points and line segments) are plotted in Figs. 8a and b with the 95% envelopes (grey regions). For comparison, the LM and GLM values from Figs. 5a and b are replotted, as black and white circles, respectively. At 500 trials, where the noiseless observer estimates are similar using either GLM or GAM, the two methods yield similar results for the low noise conditions. The average GAM fit, however, yields a slightly lower average squared residual systematically for all but the highest noise condition.

Figure 8.

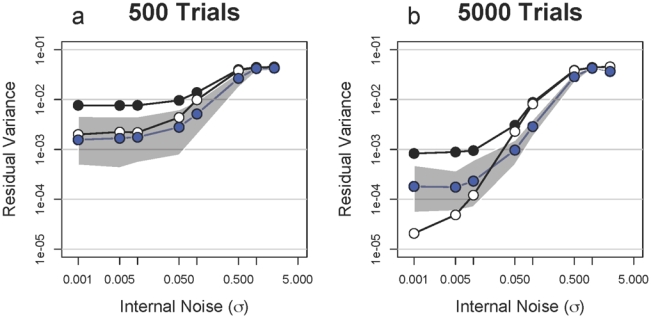
Residual variance between estimated classification image and the template is plotted as a function of the standard deviation of the Gaussian noise added to the template. Each point is the median of 100 repetitions and the grey regions correspond to the 95% envelope. The blue points and curves indicate the results obtained with the GAM model. The black points indicate fitting with LM and the white with GLM replotted from Figure 5a. a. Each run is 500 trials. b. Each run is 5000 trials.

For a 5000 trial experiment, the GLM performs better at the lowest noise level, but the GAM results do not increase as fast as those obtained using the GLM. Thus, for intermediate noise levels the GAM fit is more robust and yields an estimate closer to the ideal template. This outcome is consistent with the results of Figure 6, a 3584 trial experiment, in which the GAM estimate is more similar to the signal than the GLM estimate.

3.2.3. Higher order classification images

As mentioned above, Thomas & Knoblauch (2005) found that these data violated the linear template model implicit in Equation 4 in that the classification images for stimulus present and absent trials differed significantly. Their results could be explained by assuming that the observer based his judgments on frequency information independently of the phase of the stimulus. Thomas & Knoblauch (2005) verified this explanation by computing the classification images in the Fourier rather than the temporal domain.

An alternative method of investigating nonlinearities in the decision processes of the observer was proposed by Neri and Heeger (2002; See also Neri, 2004). They calculated second order classification images by squaring the noise before fitting. Higher order classification images could be calculated in this way by using higher powers.

Higher order classification images can be easily incorporated into the GLM and GAM approaches by including powers of the noise distribution in the linear predictor and estimating their coefficients. For example, the specification of a GAM model with a quadratic component of the classification image would include additional smooth components to weight the square of the noise.

$$\eta (E[\mathbf{Y}])=f_0(t){\mathbf{X}}_P+f_1(t){\mathbf{X}}_A+f_2(t){\mathbf{X}}_P^2+f_3(t){\mathbf{X}}_A^2.$$ (24)

where the exponents denote squaring the elements of the appropriate column of the model matrix. Successive higher order components would require adding successively higher order powers of the noise to the linear predictor. We note that we are only looking at the diagonal of the second-order kernel, and therefore the lower plots in the results to be presented below (Figure 9) are one-dimensional rather than two-dimensional. See Neri (2004) for discussion of the full second-order kernel.

Figure 9.

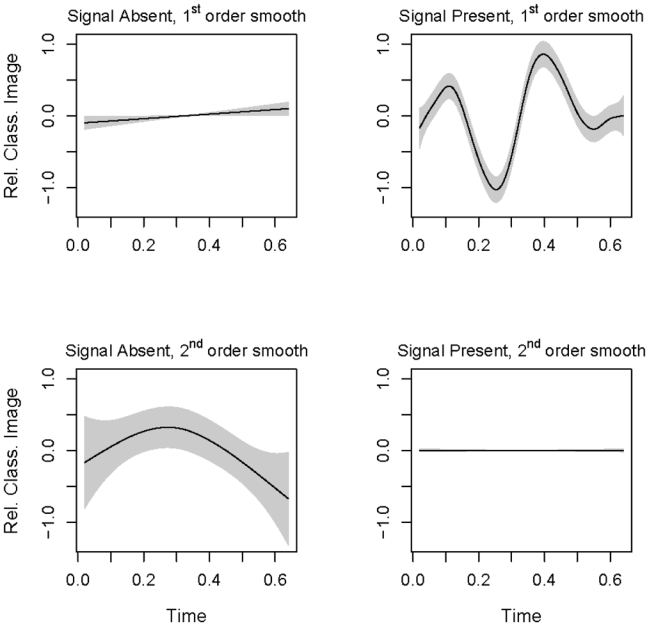
The smooth functions estimated for each of the terms of Eq (24) fit to the Gabor data set. The top two graphs are the terms for the linear component and the bottom two for the quadratic component. The left two graphs are fit to the stimulus absent data and the right two to stimulus present. The grey envelopes correspond to ± 2 standard errors for each curve.

We fit quadratic and cubic classification images to the Gabor data set with a GAM. The successive models are nested so that we can compare them with a likelihood ratio test. The results are displayed in Table 2 which indicates that the addition of a squared term led to a significantly better fit than a linear model (p = 0.02). However, an additional cubic component did not improve the fit significantly (p = 0.09). Similarly, of the three models, the UBRE score is lowest for the quadratic model.

Table 2. Analysis of deviance table for the Thomas & Knoblauch (2005) data.

We compare fits of GAM models with 1) only first order contributions, 2) additional quadratic contributions and 3) additional cubic contributions.

	Residual Df	Resid. Dev	Df	Deviance	P [> χ2]
1	114677	158295
2	114675	158287	2.07	8	0.02
3	114671	158279	3.96	8	0.09

The four estimated component classification images are displayed in Figure 9. The top two images correspond to the linear first-order classification images and reproduce what Thomas & Knoblauch (2005) reported.

The stimulus absent component (left) is not significantly modulated while the component for stimulus present (right) follows closely the signal as in Figure 6. The bottom two images show the second-order classification images for stimulus absent (left) and present (right). Here, the pattern is reversed, so that the stimulus present image is unmodulated while the stimulus absent image displays a peak near the center of the trial. This suggests that the observer exploited primarily the middle of the stimulus in classifying a trial and, perhaps, judged the signal present if he detected either a dark-light or a light-dark transition, i.e., independent of temporal order. This is a different interpretation than that put forward by Thomas & Knoblauch (2005), who suggested that the observer extracted frequency information independent of phase.

The 2nd order stimulus present image is flat suggesting that this component can be explained by the linear model. However, the observer could not know whether the signal was present or not on a trial, and it is improbable that he could thusly modify his strategy. The explanation of the authors is likely, that when “the signal is present, any noise component similar in temporal frequency and phase will increase the effective contrast of the signal…” and thereby bias the observer toward responding “present”. Thus, the linearity implied by this behavior is only apparent.

We could in principle estimate higher order classification images with GLM just as we did with GAM. The resulting model is straightforward and we include code specifying it in the Appendix. The results are similar (not shown) but, without the extra smoothing provided by GAM, harder to interpret.

4. Discussion

The Generalized Linear Model with a Bernoulli family provides a natural framework for obtaining maximum likelihood estimates of classification images. The model incorporates a relation between the expected probability of the observer’s response and a decision variable through a link function, here implemented as an inverse cumulative Gaussian. The decision variable is obtained from a weighted linear combination of the stimuli, the noise samples in a trial in the current application. The weighting coefficients correspond to the estimated classification image. The inverse link function plays the role of the psychometric function relating the decision variable to probabilities of response and, thereby placing the model within the framework of signal detection theory.

In the absence of observer noise, we have shown that GLM estimates are more efficient than estimates obtained using LM in that the estimated template is closer to the true template for a given number of trials. In the range of trials used in typical classification image experiments, the residual variance between the GLM estimated template and the true template can be more than an order of magnitude less than that obtained using LM. Solomon (2002a) previously has reported that maximum likelihood estimation is more efficient at estimating classification images than the linear model in Equation 4. Since the GLM is fit by maximizing likelihood, our results replicate his. However, we found that this advantage is quickly lost when appreciable internal noise is present and the GLM does no better than the LM. The evident conclusion is, however, that the GLM does no worse than the LM when appreciable internal noise is present and may do better if internal noise is low. On balance, the experimenter is better off using the GLM.

Generalized Additive Models offer several advantages over LM and GLM approaches. First, they provide a principled method for estimating the template that typically requires fewer parameters to describe the template than pixel-based LM and GLM methods. Parametric models also provide fits requiring only a few parameters, but such models may not always be capable of revealing some details of a template as can be done with the nonparametric smooth terms of the GAM. For example, the fixed shape of a Gabor function used as a model of the observer’s template in Figure 6 would overestimate the weight given to the beginning and especially at the end of the trial compared to the GAM and GLM fits.

An alternative smoothing criterion is obtained from Gaussian Random Field Theory to determine the cluster size of correlated pixels in an image (Chauvin et a, 2005). This is a statistical test applied after the image has been estimated, for example by a linear or generalized linear model. GAMs incorporate the smoothing step directly in the fitting procedure with the degree of smoothing determined by a model fitting criterion.

The simulations reveal that the GAM outperforms both the LM and GLM models for small numbers of trials in the case of an observer with a noiseless template. With a noisy template, GAMs are more robust, in that they generate closer estimates to the template than LM and GLM methods for a considerable range of noise levels for a small number of trials. For a large number of trials, their performance falls off more slowly than the GLM method, so that they outperform it over an intermediate range of noise levels.

These results help to explain why techniques using noise composed of random Fourier components also perform well with modest numbers of trials (Levi & Klein, 2002; Mangini & Biederman, 2004). The Fourier components form a basis for a smooth subspace. To the extent that the underlying classification image is, in fact, smooth, then some combination of these components, if enough are included, will form a good estimate of the classification image. It is only a question of getting the relative contributions of the components correct and not of averaging out uncorrelated variation at the level of the noise samples (for example, pixels in an image). For example, suppose that we want to estimate the distribution of a sample. However, instead of looking directly at its histogram, we estimate it by the best fit Gaussian. If the underlying distribution is, in fact, Gaussian, then our smooth estimate may well be closer to the true distribution then the actual histogram of the sample.

GAMs also permit estimating a model in a low dimensional (i.e., smooth) subspace, but they do not exclude the possibility of fitting a more complex structure, if the data require it. The search for a model takes place in a large subspace but components with high variation are penalized by a proportion of the square of the second derivative if they increase prediction error. Thus, we do not need to decide in advance what information the observer is likely to use in performing the task. We estimate it using GAM. In the fit displayed in Figure 6, 25 parameters were allocated to each smooth term, i.e., a 50-dimensional parameter subspace (see Appendix A3), but only a total of 11 were retained in the final result.

Machine learning methods (Ripley, 1996; Bishop, 2007) can also be used to estimate classification images. GAM is an example of such a method and the machine learning field is rapidly developing newer methods. Wichmann et al (2005), for example, evaluated a method with an initial linear stage followed by a non-linearity, analogous to GLM. Kienzle, Wichmann, Schölkopf & Franz (2007) propose a non-linear extension of the method. A fundamental problem in statistical estimation is to make use of known constraints on a solution without biasing (or dictating) the resulting estimates. Machine learning methods provide principled ways to do just that and thereby enhance what we can learn from a fixed amount of experimental data.

In summary, we have shown that Generalized Linear and Additive Models provide useful approaches to modeling classification image data. In the presence of low internal noise, the GLM procedure is the most efficient and yields the most accurate estimate. The GAM approach, however, is more robust in the presence of internal noise and, in addition, generates an optimally smoothed estimate of the classification image. To our knowledge, we are the first to point out the benefits of using GAM to smooth images in a principled way and the first to evaluate the use of GAM for classification image estimation.

A separate issue that we do not address is testing the validity of the template estimated by any of these methods. One interesting and recent approach is that of Wichmann et al (2005) who compared predicted versus actual data obtained in a second experiment using a novel experimental paradigm.

Finally, the generalized linear and additive models allow the estimation of higher order classification images by incorporating additional terms into the linear predictor, and these higher order terms can be evaluated with respect to the significance of their contribution to the decision strategy of the observer while performing the task.

Appendix

All of the computations in this article were performed using the open source software R (R Development Core Team, 2008). We also generated all of the graphs with R. In this appendix, we provide the code fragments that we used to fit the models described in the main article.

The data set used in the code fragments below is contained in an object named Gabor that was described in the article. In each code fragment, the “>” is the R prompt and the “+” indicates a continuation from the previous line.

A.1. Fitting with LM

Linear models in R are fit with the function lm whose first argument is a formula object and whose second object is a data frame. The data frame is in basic terms a matrix whose rows correspond to trials and whose columns correspond to variables coding the response and the stimuli including the external noise. We have seen data frames printed out as matrices in the main text. A data frame in R can also store information about the variables including the names we wish to be used in plotting results and in referring to them in code.

A formula object contains two terms separated by a tilde ~ that can be read as “is modeled by”. The left hand side corresponds to the response to be modeled which here is the instantaneous noise values in the column named N in the data frame. The right hand side of the formula gives the explanatory variables, time and resp. The first is a 32 level factor indicating the time samples of the stimulus; the second is a 4 level factor indicating the response classifications of the observer. The slash indicates that a separate linear model will be estimated for each time sample and the −1 signifies that the global intercept should be removed from the model. Thus, a mean for each of the 4 response classifications at each of the 32 time samples will be estimated. As all explanatory variables are factors in this model, it corresponds to an analysis of variance.

We also include the data frame as the second argument. The terms in the formula will then be interpreted as the named columns of the data frame.

The results are stored in the model object Gabor.lm.

> Gabor.lm <- lm (N ~ time/resp - 1, Gabor)

> ClsLM <- crossprod (matrix (coef (Gabor.lm),

+ nrow = 4, byrow = TRUE), c (0, 1, −1, −1))

To extract the classification image, we have composed several operations into a single line. Starting from the inside, we extract the 128 coefficients from the model object with the function coef. This vector is then coerced into a 4 row matrix. Finally, this matrix is multiplied by a 4 element vector that weights and combines the coefficients to yield the 32 element classification image plotted in Figure 2a as white circles.

A.2. Fitting with GLM

Prior to fitting the GLM model the data frame is reorganized so as to facilitate the modified specification of the model and stored in a new data frame named Gabor.wide.

> Resp <- factor (unclass (Gabor$resp) < 3,

+ labels = 0:1) [seq (1, nrow (Gabor), 32) ]

> Stim <- factor (unclass (Gabor$resp) %% 2,

+ labels = 0:1) [seq (1, nrow (Gabor), 32) ]

> Gabor.wide <- data.frame (matrix (Gabor$N, ncol = 32,

+ byrow = TRUE))

> names (Gabor.wide) <- paste (“t”, 1:32, sep = “”)

> Gabor.wide <- cbind (Resp, Stim, Gabor.wide)

Initially, the column resp is recoded as 2 two-level factors, Resp and Stim. The first codes the responses of the observer as 0 and 1 for absent and present, respectively; the second codes the absence and presence of the signal, similarly. Then, the 32 instantaneous noise values for each trial are distributed across 32 columns of a data frame, so that each may be treated as an independent covariate in the formula object. For later identification, these are given names t1, t2, …, t32. Finally, the vectors Resp and Stim are attached as the first two columns of the data frame.

Fitting the GLM model works in a similar fashion to the LM model except that we use the function glm and family and link functions must be specified:

> Gabor.glm <- glm (Resp ~ . - 1,

+ family = binomial (link = “probit”),

+ data = Gabor.wide)

> ClsImGLM <- coef (Gabor.glm) [- (1:2) ]

The column Resp is the response. The dot is a convenient shorthand for a model in which each column of the data frame except for Resp enters as a covariate additively as in Equation 16, which saves writing out the 33 terms. Finally, the global intercept is excluded. The model yields 34 coefficients in all. The first two correspond to main effects of the two levels of Stim that we ignore here. The next 32 specify the coefficients for each time sample. The negative indices indicate a sequence in which these coefficients are excluded from the vector.

To specify a model in which the coefficients depend on the level of the factor Stim, the form of the model from the LM example is used.

> Gabor2.glm <- glm (Resp ~ Stim/. - 1,

+ family = binomial (link = “probit”),

+ data = Gabor.wide)

Again, the dot is a convenience to indicate all columns but the Resp. Terms of the form Stim/Stim are silently removed. As before, the global intercept is excluded. As with the LM model, the slash indicates that a coefficient is estimated for each level of Stim. The model yields 66 coefficients in all. The first two correspond to main effects of the two levels of Stim ignored here. The next 64 specify the coefficients for each time sample, alternating between the estimates for the two levels of Stim. The set of coefficients for each level of Stim correspond to the component images on the right hand side of Equation 4, here for stimulus absent and present, respectively.

The two models are nested and can be compared using a likelihood ratio test with the function anova.

> anova (Gabor.glm, Gabor2.glm, test = “Chisq”)

which generated the results of Table 1.

To estimate higher order classification images using GLM, the easiest strategy is to add additional columns to the data frame corresponding to powers of the noise samples. The following code fragment demonstrates how to accomplish this for a second order image.

> sqt <- Gabor.wide [, - (1:2)]^2

> colnames (sqt) <- paste (“tt”, 1:32, sep = “”)

> Gabor.wide <- cbind (Gabor.wide, sqt)

The first line squares all of the noise values except those in the first two columns, Resp and Stim. The second line assigns names to distinguish these columns from those used for the first order components. The third line joins these columns to the data frame. With this organization of the data frame the call to glm is the same as for the previous model.

> Gabor3.glm <- glm (Resp ~ Stim/. - 1,

+ family = binomial (link = “probit”),

+ data = Gabor.wide)

This model yields 130 coefficients. The first 66 are organized the same as those for the previous model. The next 64 correspond to those of the second order images. The process of adding columns with higher powers of the noise can be continued to estimate higher order classification images.

A.3. Fitting with GAM

To fit the GAM model, the original organization of the data frame is appropriate except that the column resp must be decoded into responses and signal status as in fitting the GLM. Additionally, to obtain separate estimates for signal present and absent conditions, the noise profiles for each trial must be separated into separate columns as a function of signal status. This is performed with the model.matrix function, that takes a one-sided formula and a data frame and outputs a model matrix specified by the formula. Here the formula specifies a two-column matrix indicating the interaction of the signal status with the noise profile with the column corresponding to the intercept removed. For convenience, we store each column of this matrix in a separate variable in the data frame.

> Gabor$Stim <- factor (with (Gabor, unclass (resp) %% 2))

> Gabor$Resp <- factor (with (Gabor, unclass (resp) < 3),

+ labels = c (“0”, “1”))

> Imat <- model.matrix (~Stim:N - 1, data = Gabor)

> Gabor$by0 <- Imat [, 1]

> Gabor$by1 <- Imat [, 2]

> Gabor.gam <- gam (Resp ~

+ s (Time, bs = “ts”, by = by0, k = 25) +

+ s (Time, bs = “ts”, by = by1, k = 25),

+ family = binomial (“probit”), data = Gabor)

The functions s in the GAM model specify the smooth terms and the argument bs the type of spline basis, here thin plate regression splines with shrinkage. The by argument is used to specify a term by which to multiply the smooth term, generating a “variable coefficient model” (Hastie & Tibshirani, 1990; Wood, 2006). Multiplying the smooth term by the noise profile on each trial corresponds to the inner product rule of (2). The arguments k specify the maximum number of parameters to allocate to each smooth term in fitting the model. Generally, specifying more than would be necessary helps in finding the model requiring fewer parameters, giving the best fit to the data. We could specify k up to 32 per smooth term, in this example, the length of the covariate Time, but the results were unchanged and the smaller value resulted in a faster execution time of the code. To extend this model to include the nonlinear terms discussed in the text, we simply add additional smooth terms to the model formula that contain powers of the by argument. For example, to include the second order terms, we fit the model

> Gabor.gam2 <- gam (Resp ~

+ s (Time, bs = “ts”, by = by0, k = 25) +

+ s (Time, bs = “ts”, by = by1, k = 25) +

+ s (Time, bs = “ts”, by = by0^2, k = 25) +

+ s (Time, bs = “ts”, by = by1^2, k = 25),

+ family = binomial (“probit”), data = Gabor)

Additional higher order terms are fit by including successive powers of the by argument, but at the cost of significant increases in processing time and memory requirements for fitting the model. The likelihood ratio test between a set of nested models is obtained using the anova function, that outputs a table in the typical form of an analysis of variance, although in the case of the binomial models here, it is deviance that is evaluated. For example,

> anova (Gabor.gam, Gabor.gam2, Gabor.gam3, test = “Chisq”)

which outputs the table in the text, including the fit with 3rd order terms. The χ² test is appropriate here because the dispersion in a binomial model is not estimated. Extracting the predicted smooth curve is accomplished with the aid of the predict method for objects of class gam as illustrated in the following code fragment.

> nd <- data.frame (Time = unique (Gabor$Time),

+ N = rep (1, 32),

+ by0 = rep (0, 32),

+ by1 = rep (1, 32) )

> s1 <- predict (Gabor.gam, newdata = nd)

A new data frame, nd, is required that has all the same variables used in the fit with gam, but only containing values for which predictions are desired. By default, the predictions are on the scale of the linear predictor, but a type argument can be used to specify that the predictions be on the response scale that, in this case, corresponds to the probability of responding “Present”.