Calculating Asymptotic Significance Levels of the Constrained Likelihood Ratio Test with Application to Multivariate Genetic Linkage Analysis

Abstract

The asymptotic distribution of the multivariate variance component linkage analysis likelihood ratio test has provoked some contradictory accounts in the literature. In this paper we confirm that some previous results are not correct by deriving the asymptotic distribution in one special case. It is shown that this special case is a good approximation to the distribution in many situations. We also introduce a new approach to simulating from the asymptotic distribution of the likelihood ratio test statistic in constrained testing problems. It is shown that this method is very efficient for small p-values, and is applicable even when the constraints are not convex. The method is related to a multivariate integration problem. We illustrate how the approach can be applied to multivariate linkage analysis in a simulation study. Some more philosophical issues relating to one-sided tests in variance components linkage analysis are discussed.

1. Introduction

There are numerous statistical applications for which one-sided tests may be justified. Indeed, any quick search of the literature on one-sided tests or constrained tests will reveal applications in clinical studies, pharmacokinetics, genetic epidemiology and many other fields. This paper is motivated by a variance component testing problem that occurs in multivariate linkage analysis. In most one-sided situations we have a very simple hypothesis to test, such as H₀ : μ = 0 vs H_a : μ > 0. Here, something like the one-sided t-test is sufficient. However, sometimes the one-sided hypothesis is more complex, such as can be expressed as special cases of H₀ : θ ∈ Ω₁ vs H_a : θ ∈ Ω₂. The statistics available for this kind of test (Silvapulle and Sen 2005) do not necessarily follow simple asymptotic distributions. Perhaps the most obvious choice of statistic is the constrained maximum likelihood ratio test (CLRT) statistic discussed below. Numerous authors, such as Self and Liang (1987), have shown that in some cases this statistic asymptotically follows a mixture of chi-squared distributions, while in other cases the distribution is more complex. In this paper we discuss some results for constrained hypothesis testing that are relevant to multivariate linkage analysis.

In section 2 we briefly review some of the literature on the CLRT. In section 3 we suggest a simple and efficient approach to calculating the asymptotic significance levels of the CLRT even when the null distribution cannot be described as a mixture of chi-squared distributions. We demonstrate that our method has a strong computational advantage over another known method when small p-values are involved. We then show that the asymptotic distribution may be reduced to a hyperspherical integration problem. In section 4, we demonstrate our method for the multivariate variance component linkage analysis problem (Amos, de Andrade et al. 2001). This model has a particularly complex asymptotic distribution. The general consensus seems to be that “this issue warrants further detailed attention” (Marlow, Fisher et al. 2003), and, “there is an urgent need to characterize the asymptotic distribution associated with these multivariate tests” (Evans, Zhu et al. 2004). In a recent paper, Han and Chang (2008) have challenged the correctness of several relevant results in the literature. They also suggest a fairly simple way of simulating from the asymptotic null distribution. In this paper we confirm some of the findings of Han and Chang by showing that, under certain restrictive assumptions, analytical results are available. When these assumptions are not met, we show that much faster simulation methods are available. In section 5 we discuss some philosophical points concerning constrained testing in the variance component linkage setting, and review our results.

2. Asymptotics under Nonstandard Conditions

By definition, a cone C with its vertex at θ₀ is a set such that, at, if x ∈ C, then a (x – θ₀) + θ₀ ∈ C for all a ≥ 0. We say that a cone C (Ω, θ₀)approximates a set Ω at θ₀ if: $\underset{C\left(\Omega ,{\mathbf{\theta }}_0\right)}{\text{inf}}\Vert x-y\Vert =o\left(\Vert y-{\mathbf{\theta }}_0\Vert \right)$ ∀y ∈ Ω and $\underset{\Omega }{\text{inf}}\Vert x-y\Vert =o\left(\Vert x-{\mathbf{\theta }}_0\Vert \right)$ ∀x ∈ C (Ω,θ₀). A function f (z) is said to be o(z) if $\underset{z\to 0}{\text{lim}}f\left(z\right)/z=0$. The above definition of approximating cones was introduced by Chernoff (1954). Geyer (1994) has discussed its relation to other approximating cones. The primary intuition behind the approximating cone is that, near θ₀, there is a similar shape for both C (Ω,θ₀) and Ω. We know from the (typical) consistency of the maximum likelihood estimate that, with a large enough sample size, estimates of a parameter θ will be very close to the true value θ₀. At this point we may substitute C (Ω,θ₀) for the parameter space Ω. The beauty of a cone is that no matter how close we zoom in on the vertex, it looks the same. One fact that falls easily out of the definition of an approximating cone is that all cones approximate themselves. Furthermore, it is quite obvious that the space of positive semidefinite matrices is a cone with vertex at the zero matrix (if M is positive semidefinite, then so is aM for all a ≥ 0). Indeed, the parameter spaces that are relevant to the present work are already cones and they do not need to be approximated.

Chernoff (1954) produced one of the original works on this subject. Perhaps the most well known work in this area was by Self and Liang (1987). It has been shown (Geyer 1994) that the regularity conditions used by Self and Liang are not sufficient to guarantee all the results given, but the results still hold with corrected regularity conditions. There have been numerous reformulations of the basic results presented below under relaxed regularity conditions (Geyer 1994; Vu and Zhou 1997; Delmas and Foulley 2007). The results have been extended to include the non-identically distributed case (Vu and Zhou 1997; Delmas and Foulley 2007). A thorough review of the literature on constrained testing is given by Silvapulle and Sen (2005).

When some of the parameters lie on the boundary of the parameter space, the asymptotic distribution of the CLRT quickly becomes complicated. We first reproduce the main result from Self and Liang (1987) and Chernoff (1954). However, we assume the regularity conditions used in Theorem 4.4 of Geyer (1994). Let θ be a vector with p elements containing all model parameters, and let θ₀ be the actual parameters for the generating distribution of y. Let l (θ;y) be the log-likelihood for the data. Let us define the Fisher information as $\mathbf{\text{f}}(\mathbf{\theta })=-E\left[\frac{{\partial }^2}{\partial {\mathbf{\theta }}^2}l\left(\theta ;y\right)\right]$. Suppose we are performing a hypothesis test such that under the null hypothesis θ ∈ Ω₀, and under the alternative hypothesis θ ∈ Ω₁. The CLRT statistic is defined as:

$$\lambda =2\left[\underset{\theta \in {\Omega }_1}{\text{sup}}l\left(\theta ;y\right)-\underset{\theta \in {\Omega }_0}{\text{sup}}l\left(\theta ;y\right)\right].$$

We have the following well-known result:

Theorem 1: Let Z be a multivariate normal (MVN) random variable with mean θ₀ and variance f^–1 (θ₀). Let Ω ₀ and Ω ₁ be sets with non-empty approximating cones C (Ω₁, θ₀) and C (Ω₀, θ₀). Then, under certain regularity conditions, the asymptotic null distribution of the CLRT is the same as the distribution of the likelihood ratio test of θ ∈ C (Ω₀, θ₀) versus the alternative θ ∈ C (Ω₁, θ₀) based on a single realization of Z.

To restate Theorem 1, the asymptotic distribution of the CLRT statistic is equivalent to the distribution of a function of a multivariate random variable (Z):

$$g(\mathbf{\text{Z}})=\underset{\theta \in C_{{\Omega }_0}}{\text{inf}}{(\mathbf{\text{Z}}-\mathbf{\theta })}^T\mathbf{\text{f}}({\mathbf{\theta }}_0)(\mathbf{\text{Z}}-\mathbf{\theta })-\underset{\theta \in C_{{\Omega }_1}}{\text{inf}}{(\mathbf{\text{Z}}-\mathbf{\theta })}^T\mathbf{\text{f}}({\mathbf{\theta }}_0)(\mathbf{\text{Z}}-\mathbf{\theta }).$$ (1)

This can be simplified somewhat. Let f^1/2 be a matrix such that f^1/2f^1/2 = f and let Z̃ be a MVN random variable with mean 0 and variance the identity matrix. Theorem 1 then implies that the asymptotic distribution of the CLRT statistic is the same as that of:

$$\tilde{g}(\widetilde{\mathbf{\text{Z}}})=\underset{\theta \in \tilde{C}({\Omega }_0,{\mathbf{\theta }}_0)}{\text{inf}}{\Vert \widetilde{\mathbf{\text{Z}}}-\mathbf{\theta }\Vert }^2-\underset{\theta \in \tilde{C}({\Omega }_1,{\mathbf{\theta }}_0)}{\text{inf}}{\Vert \widetilde{\mathbf{\text{Z}}}-\mathbf{\theta }\Vert }^2,$$ (2)

where C̃ (Ω_i, θ₀) = {f^1/2 (θ – θ₀) | θ ∈ C (Ω_i, θ₀)}. Note that C̃ (Ω_i, θ₀) is a cone with vertex at the origin. Also note that g (•) and g̃ (•) are related by the simple identity g̃(V) = g (f^−1/2V + θ₀).

In many cases the asymptotic distribution turns out to be a mixture of chi-squared distributions. It is fairly easy to understand this nice behavior when g(Z) involves projections onto a set of flat surfaces in C (Ω_i, θ₀). In fact, it can be shown that when testing a hypothesis of the form H₀ : θ = θ₀ vs H₀ : θ ∈ Ω₁, where C (Ω₁, θ₀) is a piecewise smooth convex cone, the asymptotic distribution under the null hypothesis will always be a mixture of chi-squared distributions (Takemura and Kuriki 1997). However, deriving the mixing proportions is often a difficult task. Furthermore, many realistic situations violate these conditions. For example, in variance component linkage analysis it is desirable to use a nonconvex space as the alternative hypothesis. This space is illustrated in Figure 1.b. Also, the existence of nuisance parameters may cause the hypothesis to be of a different form. In this paper we suggest that a direct derivation or estimation of mixing proportions is not necessary. To calculate statistical significance it is easy to implement efficient algorithms that do not assume the asymptotic distribution is a mixture of chi-squared random variables.

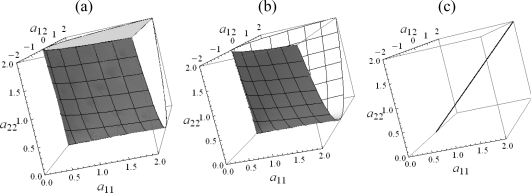
Figure 1:

Geometric view of the alternative hypothesis in the bivariate case. (a) Constraint 1: Ω_a = {A | A ≥ 0}, (b) Constraint 2: Ω_a = {φφ^T | φ ∈ ℝ^t}, (c) Constraint 3: ${\Omega }_d=\left\{\left(1_t{1}_t^T\right)a|a>0\right\}$.

3. Calculating Statistical Significance

Method 1: Simple Simulation

As discussed earlier, the asymptotic distribution may be represented as a function (g̃(Z̃)) of standard normal variables. Suppose that f is the distribution function of Z̃, and S is a likelihood ratio statistic. Then the p-value for S is:

$$P\left(\tilde{g}(\widetilde{\mathbf{\text{Z}}})>S\right)=\underset{g(\mathbf{\text{z}})>S}{\int }f(\mathbf{\text{z}})d\mathbf{\text{z}}.$$ (3)

The simplest possible approach to finding the asymptotic p-value would be to sample from Z̃ and find the fraction of samples for which g̃(Z̃) > S. Various authors have suggested this (Silvapulle and Sen 2005, pp. 78–81). In multivariate linkage analysis this has been suggested by Han and Chang (2008). With very small p-values, often necessary to allow for multiple comparisons, accurate estimates require a large number of simulation samples.

Other simulation methods have been suggested that calculate mixing proportions (Silvapulle and Sen 2005 p 78–81). However, such methods are not applicable when the distribution is not a mixture of chi-squared distributions.

Method 2: Direction and Length Decomposition

We now suggest a more computationally efficient method. We can decompose the MVN distribution into two pieces: a directional p-vector V = Z̃ / ‖Z̃‖ and a scalar ‖Z̃‖. Thus Z̃ = ‖Z̃‖ V. V can be visualized as a point on the unit hypersphere, while ‖Z̃‖ is the Euclidian length of Z̃. It can be shown that ${\Vert \widetilde{\mathbf{\text{Z}}}\Vert }^2\sim {\chi }_d^2$, where d is the number of elements in θ and V has a uniform distribution on the surface of a unit hypersphere.

The function g̃(z) has some very interesting properties, including being continuous. Let C̃_i = C̃ (Ω_i, θ₀). The one property that we wish to exploit follows (in line 3 below) from the definition of a cone:

$$\begin{array}{ccc}\tilde{g}(a\mathbf{\text{z}})& =& \underset{\theta \in {\tilde{C}}_0}{\text{inf}}{\Vert a\mathbf{\text{z}}-\mathbf{\theta }\Vert }^2-\underset{\theta \in {\tilde{C}}_1}{\text{inf}}{\Vert a\mathbf{\text{z}}-\mathbf{\theta }\Vert }^2\hfill \\ & =& a^2\underset{\theta \in {\tilde{C}}_0}{\text{inf}}{\Vert \mathbf{\text{z}}-\mathbf{\theta }/a\Vert }^2-a^2\underset{\theta \in {\tilde{C}}_1}{\text{inf}}{\Vert \mathbf{\text{z}}-\mathbf{\theta }/a\Vert }^2\hfill \\ & =& a^2\underset{\theta \in {\tilde{C}}_0}{\text{inf}}{\Vert \mathbf{\text{z}}-\mathbf{\theta }\Vert }^2-a^2\underset{\theta \in {\tilde{C}}_1}{\text{inf}}{\Vert \mathbf{\text{z}}-\mathbf{\theta }\Vert }^2\hfill \\ & =& a^2\tilde{g}(\mathbf{\text{z}}).\hfill \end{array}$$ (4)

Let F_d be the cumulative distribution function of ${\chi }_d^2$. Also, define F_d (S / 0) = 1 for S > 0 and F_d (0 / 0) = 0. Using this notation, we can express the p-value as:

$$\begin{array}{ccc}P\left(\tilde{g}(\widetilde{\mathbf{\text{Z}}})\ge S\right)& =& P\left(\tilde{g}(\Vert \widetilde{\mathbf{\text{Z}}}\Vert \mathbf{\text{V}})\ge S\right)\hfill \\ & =& P\left({\Vert \widetilde{\mathbf{\text{Z}}}\Vert }^2\tilde{g}(\mathbf{\text{V}})\ge S\right)\hfill \\ & =& E_{g(\mathbf{\text{V}})}P\left({\Vert \widetilde{\mathbf{\text{Z}}}\Vert }^2\tilde{g}(\mathbf{\text{V}})\ge S|\tilde{g}(\mathbf{\text{V}})\right)\hfill \\ & =& E_{g(\mathbf{\text{V}})}\left[1-F_d\left(S/\tilde{g}(\mathbf{\text{V}})\right)\right].\hfill \end{array}$$ (5)

The following simulation can be performed to calculate the p-value:

1. Simulate a d-vector from a multivariate normal distribution with mean 0, then divide it by its norm to obtain a sample from V.

2. Calculate g̃(V) = g (f^1/2V + θ₀). Note: this will usually be the most computationally demanding step.

3. Repeat steps 1 and 2 n times.

4. Find the estimated p-value:

   $${\widehat{p}}_n=1-\frac{1}{n}\sum _i{F}_d\left(S/\tilde{g}({\mathbf{\text{V}}}_i)\right).$$ (6)

Implementing the simulation in this way can involve significant computational gains. Let us denote 1 – F_d (S) as p_U for the unconstrained p-value and let p denote the actual p-value. We point out the following inequality which is shown in Appendix A:

$$Var\left({\widehat{p}}_n\right)\le \frac{\left(p_U-p\right)p}{n}.$$ (7)

As a crude estimate of what we gain in efficiency, we looked at the ratio of the variances achieved by using Method 2 (designated p̂_n) versus that using Method 1 (designated p̃_n) :

$$Var\left({\widehat{p}}_n\right)/Var\left({\tilde{p}}_n\right)\le \frac{p_U-p}{1-p}.$$ (8)

Now note that (p_U (S) – p(S))/(1 – p(S)) → 0 as S → ∞. In other words, for very small p-values (and large S), Var (p̂_n) is a tiny fraction of Var (p̃_n). This improvement is purchased at virtually no increased computational expenditure.

Consider the special case of testing H₀ : θ = θ₀ versus H_a : θ ∈ Ω₁ where Ω is sufficiently regular to define the non-trivial cone C̃ (Ω₁, θ₀). In this case we may improve upon (8) somewhat. We show in Appendix A that:

$$Var\left({\widehat{p}}_n\right)/Var\left({\tilde{p}}_n\right)\le 1-\frac{F_d\left[F_1^{-1}\left(1-2p\right)\right]}{1-p}.$$ (9)

Equation (9) shows again that for very small p-values Var (p̂_n) is a tiny fraction of Var (p̃_n). These equations, however, show only worst case scenarios and in actual practice the benefits of Method 2 may be even greater. In section 4 we show an empirical evaluation of the relative variance of the two estimators in several situations.

One potential way to speed up the simulation is this: for each new V_i we can use – V_i as another observation. This leads to a negative correlation among the observations, thus reducing the variance. Another modification of the basic procedure is to implement a stopping rule to determine how many simulations to perform. In general, very large p-values do not need to be estimated accurately.

Method 3: Numerical Integration Approach

It is possible to avoid completely the use of Monte Carlo simulation. V can be represented in a hyperspherical coordinate system (Blumenson 1960). This involves a transformation from a series of d-1 angles to the d elements of V. So:

$$\mathbf{\text{V}}=\left(\begin{array}{l}\hfill v_1\hfill \\ \hfill v_2\hfill \\ \hfill v_3\hfill \\ ⋮\\ v_{p-1}\\ v_p\end{array}\right)=\left(\begin{array}{c}\text{cos}\left({\phi }_1\right)\\ \text{sin}\left({\phi }_1\right)\text{cos}\left({\phi }_2\right)\\ \text{sin}\left({\phi }_1\right)\text{sin}\left({\phi }_2\right)\text{cos}\left({\phi }_3\right)\\ ⋮\\ \text{sin}\left({\phi }_1\right)\text{sin}\left({\phi }_2\right)\dots \text{sin}\left({\phi }_{p-2}\right)\text{cos}\left({\phi }_{p-1}\right)\\ \text{sin}\left({\phi }_1\right)\text{sin}\left({\phi }_2\right)\dots \text{sin}\left({\phi }_{p-2}\right)\text{sin}\left({\phi }_{p-1}\right)\end{array}\right),$$ (10)

where φ_p–1 goes from 0 to 2π, and φ₁ through φ_p–2 go from 0 to π. The Jacobian for this transformation is: J = sin^p–2 (φ₁) sin^p–3 (φ₂)...sin (φ_p–2). Using this transformation it is possible to evaluate the integral numerically:

$$\begin{array}{ccc}P(\tilde{g}(\widetilde{\mathbf{\text{Z}}})>S)& =& E_{g(\mathbf{\text{V}})}\left[1-F_d\left(\frac{S}{\tilde{g}(\mathbf{\text{V}})}\right)\right]\hfill \\ & =& \frac{1}{S_p}{\int }_{\phi }\left[1-F_d\left(\frac{S}{\tilde{g}(\mathbf{\text{V}})}\right)\right]Jd\mathit{\phi }\hfill \end{array}.$$ (11)

Here S_d = 2π^d/2 / Γ (d / 2) is the surface area of a d dimensional hypersphere of radius 1. We use the integral representation in our proof of theorem 2 below.

Nuisance Parameters

Suppose that we divide the parameter space into q parameters to be tested and d-q nuisance parameters: θ^T = [ψ^T λ^T]. Similarly, we partition the Fisher information matrix as:

$$\mathbf{\text{f}}(\mathbf{\theta })=\left(\begin{array}{cc}{\mathbf{\text{f}}}_{\psi \psi }& {\mathbf{\text{f}}}_{\psi \lambda }^T\\ {\mathbf{\text{f}}}_{\psi \lambda }& {\mathbf{\text{f}}}_{\lambda \lambda }\end{array}\right).$$ (12)

We wish to test a hypothesis of the form H₀ : θ ∈ Ω₀ = {θ : ψ = b and λ ∈ Ω_*} versus H_a : θ ∈ Ω₁ = {θ : ψ ∈ Ω_a and λ ∈ Ω_*}. We define Ω_b = {θ : ψ = b} for notational convenience. In other words, we allow for the nuisance parameters to have constraints imposed upon them. This may be reasonable, for example, in the variance component setting. The first problem with having a large number of nuisance parameters is that the function g (Z) involves optimizing two quadratic forms each with d² terms. Lemma 1, below, states two conditions under which we may reduce these quadratic forms to have only q² terms. Let $\mathbf{\text{M}}\left({\mathbf{\theta }}_0\right)={\mathbf{\text{f}}}_{\psi \psi }-{\mathbf{\text{f}}}_{\psi \lambda }{\mathbf{\text{f}}}_{\lambda \lambda }^{-1}{\mathbf{\text{f}}}_{\psi \lambda }^T$ be the Schur complement of the block f_λλ of f, and $h\left(\mathbf{\text{Y}}\right)=\underset{\psi \in C\left({\Omega }_b,\mathbf{\text{b}}\right)}{\text{inf}}{\left(\mathbf{\text{Y}}-\psi \right)}^T\mathbf{\text{M}}\left(\mathbf{\text{Y}}-\psi \right)-\underset{\psi \in C\left({\Omega }_a,\mathbf{\text{b}}\right)}{\text{inf}}{\left(\mathbf{\text{Y}}-\psi \right)}^T\mathbf{\text{M}}\left(\mathbf{\text{Y}}-\psi \right)$. Also, define $\tilde{h}\left(\widetilde{\mathbf{\text{Y}}}\right)=\underset{\psi \in \tilde{C}\left({\Omega }_b,\mathbf{\text{b}}\right)}{\text{inf}}{\Vert \widetilde{\mathbf{\text{Y}}}-\psi \Vert }^2-\underset{\psi \in \tilde{C}\left({\Omega }_a,\mathbf{\text{b}}\right)}{\text{inf}}{\Vert \widetilde{\mathbf{\text{Y}}}-\psi \Vert }^2$.

Lemma 1: If either (a) f_ψλ (θ₀) = 0 or (b) C (Ω_*, θ₀) = ℝ^d–q, then P_Y[h (Y) ≥ S] = P_Z[g (Z) ≥ S], where Y and Z are MVN variables with means b and θ₀ and variances M and f, respectively.

Proof of Lemma 1 is given in Appendix A. Note that only one of the two conditions must be met for the results to follow. One situation where condition (a) is met is in the normal variance component setting where the fixed effects are being tested. In this situation, the part of the Fisher information corresponding to the covariances between the estimators of the main effects and the variance components is usually 0 and, as a result, enforcing constraints on variance components has no effect on the asymptotic distribution of the test. Note that if condition (a) is met, then we may set M = f_ψψ. Condition (b) requires that any constraints on the nuisance parameters disappear asymptotically. Condition (b) is satisfied when λ is an interior point of Ω_*.

A second problem with nuisance parameters is that using Theorem 1 and Lemma 1 requires us to know the actual parameter values (θ₀). One natural approach would be replace θ₀ and f in g (Z;f (θ₀); C (Ω₀, θ₀), C (Ω₁, θ₀)) with some consistent estimate (θ̂, f̂). Unfortunately, this will not always work because g (Z;f;C (Ω₀, θ₀), C (Ω₁, θ₀)) is not a continuous function of θ₀. The approximating cone C (Ω, θ₀) may behave badly as a function of θ₀. As a simple example, consider the space Ω = {θ|θ ≥ 0}. If θ₀ > 0, then C (Ω, θ₀) = ℝ; but if θ₀ = 0, then C (Ω, θ₀) = {θ|θ ≥ 0. This problem has been discussed from a different point of view by Wolak (1991). Under the null hypothesis discussed above, ψ is specified and does not need to be estimated, while λ must be estimated. However, C (Ω_b, b) and C (Ω_a, b) are not functions of λ and hence the bad behavior of the approximating cone may be avoided when the conditions for Lemma 1 hold. Let f̂_n be an estimate of f(θ₀), ${\hat{M}}_n={\widehat{\mathbf{\text{f}}}}_{\psi \psi n}-{\widehat{\mathbf{\text{f}}}}_{\psi \lambda n}{\widehat{\mathbf{\text{f}}}}_{\lambda \lambda n}^{-1}{\widehat{\mathbf{\text{f}}}}_{\psi \lambda n}^T$, $S_{jn}=\left\{{\hat{M}}_n^{1/2}\left(\mathbf{\theta }-\mathbf{\text{b}}\right)|\mathbf{\theta }\in C\left({\Omega }_j,\mathbf{\text{b}}\right)\right\}$ and ${\tilde{h}}_n\left(\widetilde{\mathbf{\text{Y}}}\right)=\underset{\psi \in S_{bn}}{\text{inf}}{\Vert \widetilde{\mathbf{\text{Y}}}-\psi \Vert }^2-\underset{\psi \in S_{an}}{\text{inf}}{\Vert \widetilde{\mathbf{\text{Y}}}-\psi \Vert }^2$. Also, suppose that LR_n is an observed test statistic.

Theorem 2: Suppose that ${\widehat{\mathbf{\text{f}}}}_n\stackrel{P}{{\displaystyle \to }}\mathbf{\text{f}}\left({\mathbf{\theta }}_0\right)$ under H₀. If (a) f_ψλ (θ₀) = 0 or (b) C (Ω_*, θ₀) = ℝ^d–q, then for all 0 ≤ α < 1 – P(g̃ (Z̃) = 0)

$$P\left\{P_{\widetilde{\mathbf{\text{Y}}}}\left[{\tilde{h}}_n\left(\widetilde{\mathbf{\text{Y}}}\right)\ge L{R}_n|{\widehat{\mathbf{\text{f}}}}_n,L{R}_n\right]\le \alpha \right\}\to \alpha$$ (13)

where the elements of Ỹ are distributed as independent standard normal random variables.

A sketch of the proof for Theorem 2 is deferred to Appendix A. Hence simulating from h̃_n (Ỹ) is equivalent asymptotically to simulating from g̃ (Z̃). This approach has been criticized by some (Silvapulle and Sen 2005, p. 153) because the asymptotic distribution may be quite sensitive to the nuisance parameters. However, as we show below, there are at least some situations where the asymptotic distribution is relatively insensitive to the actual values of the nuisance parameters.

4. Multivariate Variance Component Linkage Analysis

Some Model Properties

First, we present the basic model for multivariate variance component linkage analysis (Amos, de Andrade et al. 2001). Let there be t traits (variates), n_k individuals in the k^th pedigree, and K pedigrees. Let y_ki be a t × 1 vector of trait values for individual i in pedigree k, and let $y_k={\left[y_{k1}^T y_{k2}^T \cdots y_{k{n}_k}^T\right]}^T$. The commonly used genetic model for quantitative traits assumes that y_ki is formed by adding together a set of independent random effects. For example, there may be a random environmental (including measurement error) effect and a random polygenic effect (i.e. the cumulative effect of alleles in many genes acting together additively). Because family members share on average a certain proportion of their alleles there will be some correlation between the random polygenic effects of family members. In linkage analysis, we are interested in testing whether a particular locus in the genome is linked to the traits of interest, and so we also have a random effect for a single gene of interest. Using genetic marker data we may calculate the proportion of alleles shared identical by descent (IBD) (Haseman and Elston 1972) for each pair of relatives at a particular genomic location. While there are many variations and additional random effects suggested in the literature, we will consider only these three random effects: linked locus, polygenic and environmental. First we define the following:

• Π_k specifies the proportion of alleles shared identical by descent for each pair of relatives at a particular genomic location.

• Φ_k is a matrix of kinship coefficients.

• I_k is an n_k × n_k identity matrix.

• A represents the covariance matrix for the additive component of variance.

• P represents a polygenic covariance matrix and

• E represents an environmental (including measurement error) covariance matrix.

Note that A, P and E are each t × t covariance matrices containing parameters, while Π_k, Φ_k and I_k are n_k × n_k matrices containing observed properties of the pedigree. In the multivariate variance component model, it is assumed that, given the number of alleles shared identical by descent for the pairs of members in each pedigree, y_k follows a MVN distribution with covariance matrix

$${\mathbf{\text{C}}}_k={\mathbf{\Pi }}_k\otimes \mathbf{\text{A}}+{\mathbf{\Phi }}_k\otimes \mathbf{\text{P}}+{\mathbf{\text{I}}}_k\otimes \mathbf{\text{E}},$$ (14)

where ⊗ represents the Kronecker product.

In general, we wish to test for linkage using the model above. This is a hypothesis test of the form H₀ : A = 0 vs H_a : A ∈ Ω_a. For example, in the univariate case (t = 1) we have H₀ : a = 0 vs H_a : a > 0 because we expect variances to be positive. However, in the multivariate case there are several options for Ω_a. As we point out in the discussion, each of these options is valid if decided upon a priori. First, we may set Ω_a = {A | A ≥ 0} where A ≥ 0 means that A is positive semi-definite. We will refer to this as constraint 1. Constraint 1 may be justified by the fact that covariance matrices must be positive semidefinite by definition. Second, we may y choose Ω_a = {φφ^T | φ ∈ ℝ^t} which we will refer to as constraint 2 (Todorov, Vogler et al. 1998; Amos, de Andrade et al. 2001; Marlow, Fisher et al. 2003). This is equivalent to constraining all the cross-trait correlations to be ±1. Constraint 2 may be justified when the polymorphisms at a given genomic location responsible for the trait are effectively diallelic. Third, we may have ${\Omega }_a=\left\{a\left(1_t{1}_t^T\right)|a>0\right\}$, where 1_t is a column t-vector of ones (Evans, Zhu et al. 2004). This kind of constraint may be reasonable for repeated measures if we believe the gene will have the same effect on all measurements. Each of these constraints is illustrated in Figure 1. Wang (2003) and Amos et al. (2001) present some other possible constraints. A number of similar tests of variance components have been presented in contexts other than linkage analysis (Stram and Lee 1994; Stram and Lee 1995).

Under the third constraint, the asymptotic distribution is a ½:½ mixture of ${\chi }_0^2$ and ${\chi }_1^2$, where ${\chi }_0^2$ represents a point mass at 0 (Evans, Zhu et al. 2004). To our knowledge, the literature does not directly address the asymptotic null distribution under constraint 1. However, constraint 2 has prompted some confusion and even contradiction within the literature. As mentioned earlier, Han and Chang (2008) have challenged several claims in the literature regarding constraint 2.

Although pedigrees come in various structures and sizes, it is still possible to force the variance component models discussed in the introduction into an independent identically distributed context. We assume that there is an infinite population of non-overlapping pedigree structures from which we randomly sample. Although the whole human population can be considered as a single pedigree, in practice the way pedigrees are sampled can ensure that they are nonoverlapping overlapping (Ginsburg, Elston et al. 2006). Thus, the probability P (Π_k, Φ_k, n_k) is not a function of the variance component parameters, and the likelihood function is of the form ∏_k P (y_k | Π_k, Φ_k, n_k) P (Π_k, Φ_k, n_k). In the likelihood ratio, the factor P (Π_k, Φ_k, n_k) will cancel out. We have not proven in this work that the multivariate variance component model meets the regularity requirement for Theorems 1 and 2. However, our simulation results show the usefulness of our approach. In fact, the regularity requirements given by Geyer (1994) require global optima. The likelihood that needs to be optimized for our model is not convex, and it would be difficult to prove that the global maximum was truly achieved. Instead, we depend on the heuristic approach of using multiple starting points.

We have chosen below to enforce the constraint that P and E are positive definite under both the null and alternative hypotheses. However, we assume that the true parameters P and E do not lie on the boundary of the parameter space, and hence these constraints disappear asymptotically. Thus conditions (a) and (b) in Theorem 2 are both satisfied.

We are now ready to define a set of conditions:

• (C1) P and E do not lie on the boundary of the parameter space.

• (C2) Given the pedigree structure, the data generating process actually follows a MVN distribution with Var (y_k) = C_k = Φ_k ⊗ P + I ⊗ E and E (y_ki) = μ.

• (C3) The random variables Π and Φ may only take on a finite number of possible values.

Next we define the following space:

$$\begin{array}{l}\Gamma \left(\epsilon ,\eta \right)=\{\mathbf{\theta }|{\lambda }_{\text{min}}\left(\mathbf{\Pi }\otimes \mathbf{\text{A}}+\mathbf{\Phi }\otimes \mathbf{\text{P}}+\mathbf{\text{I}}\otimes \mathbf{\text{E}}\right)\ge \epsilon for all \mathbf{\Pi },\mathbf{\Phi }\\ and \Vert \mathbf{\theta }\Vert \le \eta \}\end{array}$$ (15)

Lemma 2: If (C1) through (C3) are met, then for constraints 1 and 2 Theorem 1 and 2 may be applied to the variance component likelihood ratio test for linkage. Here the likelihood ratio test is defined for arbitrarily large η and for ɛ > 0 arbitrarily close to 0, and the test statistic is

$$\lambda =2\left[\underset{\theta \in {\Omega }_1\cap \Gamma \left(\epsilon ,\eta \right)}{\text{sup}}l\left(\theta ;y\right)-\underset{\theta \in {\Omega }_1\cap \Gamma \left(\epsilon ,\eta \right)}{\text{sup}}l\left(\theta ;y\right)\right].$$

We have not rigorously proven Lemma 2, but a very brief discussion of how these conditions may be related to the regularity conditions given by Geyer may be found in Appendix B. In fact, the regularity requirements given by Geyer (1994) require global optima. The likelihood function for our model is not convex, and it would be difficult to prove that the global maximum was truly achieved. Instead, we depend on the heuristic approach of using multiple starting points. Our simulation results show the usefulness of our approach.

It is convenient to reparametrize the covariance structure to be Σ_k = (Π_k – Φ_k) ⊗ A + Φ_k ⊗ P^* + I_k ⊗ E, where P^* = P – A. Let ${\mathbf{\text{B}}}_{ij}=e_i{e}_j^T+e_j{e}_i^{T}If\left[j\ne i\right]$, where e_i is the unit vector of length t in the i^th direction, and let If [•] be the indicator function, In this case we can easily derive that, conditional on Π_k and the pedigree structure, the Fisher information for A and the cross parameter information between A and P* and that between A and E are respectively:

$$\begin{array}{l} {\widehat{\mathbf{\text{f}}}}_{a_{i_1{i}_2}{a}_{j_1{j}_2}}=\frac{1}{K}\sum _{k}tr\left[{\mathbf{\text{C}}}_k^{-1}\left(\left({\mathbf{\Pi }}_k-{\mathbf{\Phi }}_k\right)\otimes {\mathbf{\text{B}}}_{i_1{i}_2}\right){\mathbf{\text{C}}}_k^{-1}\left(\left({\mathbf{\Pi }}_k-{\mathbf{\Phi }}_k\right)\otimes {\mathbf{\text{B}}}_{j_1{j}_2}\right)\right] \\ {\widehat{\mathbf{\text{f}}}}_{p_{i_1{i}_2}{a}_{j_1{j}_2}}=\frac{1}{K}\sum _{k}tr\left[{\mathbf{\text{C}}}_k^{-1}\left({\mathbf{\Phi }}_k\otimes {\mathbf{\text{B}}}_{i_1{i}_2}\right){\mathbf{\text{C}}}_k^{-1}\left(\left({\mathbf{\Pi }}_k-{\mathbf{\Phi }}_k\right)\otimes {\mathbf{\text{B}}}_{j_1{j}_2}\right)\right]\\ {\widehat{\mathbf{\text{f}}}}_{e_{i_1{i}_2}{a}_{j_1{j}_2}} =\frac{1}{K}\sum _{k}tr\left[{\mathbf{\text{C}}}_k^{-1}\left({\mathbf{\text{I}}}_k\otimes {\mathbf{\text{B}}}_{i_1{i}_2}\right){\mathbf{\text{C}}}_k^{-1}\left(\left({\mathbf{\Pi }}_k-{\mathbf{\Phi }}_k\right)\otimes {\mathbf{\text{B}}}_{j_1{j}_2}\right)\right].\end{array}$$ (16)

However, E [Π_k] – Φ_k = 0 and therefore f̂_pi1i2aj1j2 and f̂_ei1i2aj1j2 will converge in probability to 0.

The above formulas show the Fisher information conditional on Π_k and pedigree structure, but f̂_ai1i2aj1j2 will converge in probability to some value f_ai1i2aj1j2 that is dependent on the pedigree structures in the population. It may also be of interest to know some typical values for f_ai1i2aj1j2. Assume we have a population of families containing only a father, mother and two siblings each with a fully informative marker. For this population, letting $\mathbf{\Delta }=e_3{e}_4^T+e_4{e}_3^T$, where e_i is the unit vector in the i^th direction of length 4, the Fisher information is:

$${\mathbf{\text{f}}}_{a_{i_1{i}_2}{a}_{j_1{j}_2}}=\frac{1}{8}tr\left[{\mathbf{\text{C}}}^{-1}\left(\Delta \otimes {\mathbf{\text{B}}}_{i_1{i}_2}\right){\mathbf{\text{C}}}^{-1}\left(\Delta \otimes {\mathbf{\text{B}}}_{j_1{j}_2}\right)\right]$$ (17)

Alternative Hypothesis Constraint 1

Constraint 2, as pictured in Figure 1, requires that A be positive semi-definite. Such a constraint is defensible because variances must be positive. To our knowledge there is no work suggesting an asymptotic distribution for the multivariate linkage model under this constraint. In Theorem 3 we show that in one special case the asymptotic distribution is available. We first define one more condition: (C4) P = γE for some positive scalar γ.

Theorem 3: If (C1) through (C4) are met, then for an arbitrary number of traits the null asymptotic cumulative distribution function (CDF) of the multivariate linkage analysis CLRT statistic under constraint 1 is a mixture of chi-squared random variables with mixing proportions derivable by the recursion given in Kuriki (1993).

Theorem 3 follows immediately from Lemma 2 and Lemmas 3 and 5 in Appendix B and the work of Kuriki (1993). In Table 1 we give some of the mixing proportions derivable from the recursive formulas in Kuriki (1993).

Table 1:

Mixing Proportions for Constraint 1

DF	t=1	t=2	t=3
0	2−1	$2^{-1}-\left(2{\sqrt{2}}^{-1}\right)$	$2^{-2}-\left(\pi {\sqrt{2}}^{-1}\right)$
1	2−1	${\left(2\sqrt{2}\right)}^{-1}$	$2^{-2}-\left(\sqrt{2}-1\right)$
2	0	${\left(2\sqrt{2}\right)}^{-1}$	${\left(\pi \sqrt{2}\right)}^{-1}$
3	0	$2^{-1}-{\left(2\sqrt{2}\right)}^{-1}$	$1-1/\sqrt{2}$
4	0	0	${\left(\pi \sqrt{2}\right)}^{-1}$
5	0	0	$2^{-2}\left(\sqrt{2}-1\right)$
6	0	0	$2^{-2}{\left(\pi \sqrt{2}\right)}^{-1}$

Of course, it is not reasonable to assume that P = γE, and so we might expect the asymptotic distribution derived in Theorem 3 to be of only theoretical interest. However, we may still use the methods suggested in section 3 if P ≠ γE. Our approach requires us to replace the nuisance parameters P and E with consistent estimates. As mentioned earlier, if the distribution is strongly dependent on P and E, then this approach may be subject to some criticism for finite samples. We briefly investigate this in Figure 2. We recalculated the asymptotic CDF under different possible values for r, where

$$P=\left[\begin{array}{cc}1& r\\ r& 1\end{array}\right]\text{ and }E=\left[\begin{array}{cc}1& -r\\ -r& 1\end{array}\right].$$ (18)

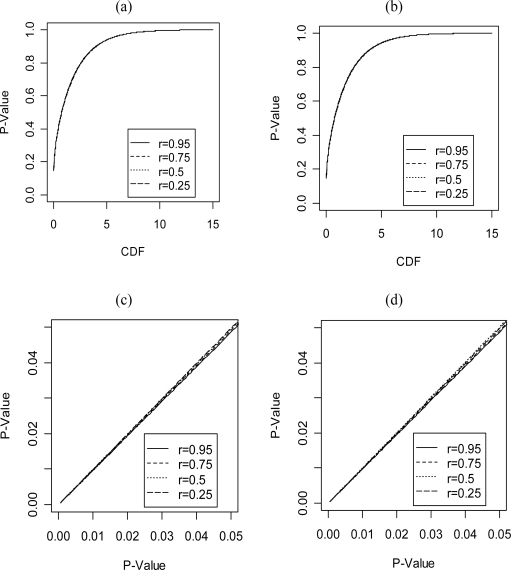
Figure 2:

Comparison of the asymptotic distribution of the CLRT statistic for a population of pedigrees containing only a father, mother and two sibs when P and E are parameterized as in equation (18). The CDFs were calculated based on Method 2 in section 3. (a) CDF under constraint 1. (b) CDF under constraint 2. (c) This comparison is for constraint 1. The x-axis represents a p-value from the analytical formula derived in Theorem 3; The y-axis represents the p-value calculated as in (a). (d) This comparison is for constraint 2. The x-axis represents a p-value from the distribution derived in Theorem 4; The y-axis represents the p-value calculated as in (b).

The results in Figure 2 were obtained from 200,000 simulation samples using Method 2 in section 3. We implemented this method in MATLAB and used the cutting-plane algorithm suggested by Shaw and Geyer (1997) for the optimization. As can be seen, in the cases investigated, the asymptotic distribution using different values for P and E appear to be nearly indistinguishable. While these results seem to indicate that Theorem 3 has some practical value, we have no guarantee that P and E will have such a small effect on the asymptotic distribution for other pedigree structures, numbers of traits or population parameter values. Therefore, we can only recommend using Theorem 3 as a first pass approximation.

Alternative Hypothesis Constraint 2

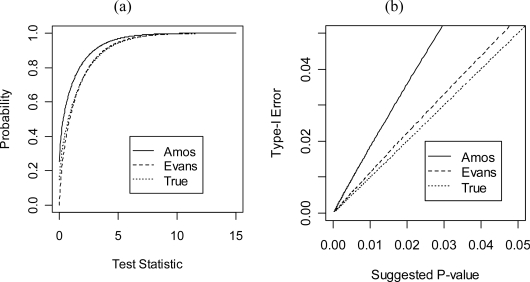
Constraint 2, as pictured in Figure 1, requires that A be of the form φφ^T (Todorov, Vogler et al. 1998; Amos, de Andrade et al. 2001; Marlow, Fisher et al. 2003). This is equivalent to constraining all the cross-trait correlations to be ±1. In the bivariate case, Evans (2002) seems to have claimed that the asymptotic distribution is $\frac{1}{2}{\chi }_1^2+\frac{1}{2}{\chi }_2^2$ while Amos et al. (2001) have claimed that the asymptotic distribution is $\frac{1}{4}{\chi }_0^2+\frac{1}{2}{\chi }_1^2+\frac{1}{4}{\chi }_2^2$. In fact, both of these claims are incorrect, although the distribution suggested by Evans closely approximates the true asymptotic distribution in the tails for some values of θ₀. Theorem 4 gives the asymptotic distribution in one special case, and Figure 3 displays a graphical comparison of the two previous suggestions and the true distribution in this special case.

Figure 3:

Comparison of some suggested distributions to the true asymptotic distribution. (a) Plot of the CDF function. (b) The x-axis of this plot represents a p-value from one of the suggested distributions; the y-axis represents the p-value that would have been calculated using the distribution in Theorem 4.

Theorem 4: If (C1) through (C3) are met, then the null asymptotic CDF of the bivariate (t = 2) linkage analysis statistic under constraint 2 is: $F\left(z\right)=\left(\Phi \left(\sqrt{2\text{z}}\right)-e^{-z/2} \Phi \left(\sqrt{\text{z}}\right)/\sqrt{2}\right)If\left[z>0\right]$.

Here Φ (x) represents the CDF of the standard normal distribution and If [.] is the indicator function. Proof of Theorem 4 is discussed in Appendix B. Note that the asymptotic distribution in Theorem 4 does not appear to be a mixture of chi-squared random variables. This is precisely what we would expect, because the alternative hypothesis is not convex. Figure 3 shows that using the distribution suggested by Amos et al. (2001) may be asymptotically quite liberal in terms of type 1 error, as may be expected from the simulation results given by Amos et al. (2001). This also confirms the work of Han and Chang (2008).

As with constraint 1, we investigated the sensitivity of the asymptotic distribution to the values of P and E. Figure 2 shows that the models investigated have nearly identical asymptotic distributions. Hence P and E have very little effect, as we may have suspected from the simulation work of Amos et al. (2001).

Empirical Evaluation of Method 2 versus Method 1

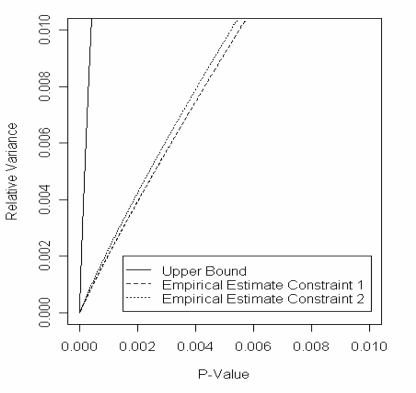
In equation (9) we gave an upper bound for the relative variances of estimation Methods 1 and 2. We now give an empirical evaluation of the relative variances. Consider the situation that P = E = I₂. We may use the formulas derived in Appendix B to easily find the Fisher information in this case. We simulated 100,000 samples of V as in Method 2, and in each case we evaluated 1 – F_d (S/g̃(V)) at a large number of possible values for S. At each of those values for S we estimated the associated p-value and its variance for Methods 1 and 2. Figure 4 shows the results. As may be seen, the relative variance is much better than the upper bound, and for small p-values Method 2 is much better than Method 1.

Figure 4:

Empirical evaluation of the benefit of Method 2. The y-axis is the relative variance (Var (p̂_n) / Var (p̃_n)). The x-axis is the estimated p-value. The upper bound is as derived in (9). The lines for constraints 1 and 2 are based on 100,000 simulations using Method 2.

Simulation Study of Convergence

To see how large a sample is needed for the statistic to approach the asymptotic distribution under the null hypothesis, we performed a small simulation study. Pedigrees with 2 parents and 2 siblings were simulated. A fully informative marker was assumed. The data were simulated to follow the actual variance component model. All simulations were performed using a program written in MATLAB release 2007b. For likelihood maximization, A, P and E were constrained to be positive semi-definite using the Cholesky method (Marlow, Fisher et al. 2003).

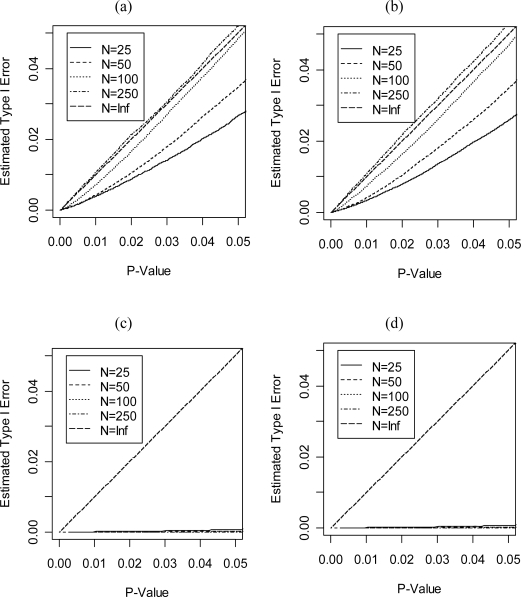
For our first set of simulations, we assumed d that E = I₂ and P was either I₂ or 0. We let the sample sizes be 25, 50, 100 and 250 pedigrees. We simulated 200,000 replicates for each situation. Note that when P = 0, the assumptions used in this paper are violated because the nuisance parameters are not allowed to be on the boundary of the parameter space. Figure 5 shows the empirical type 1 error rates when Theorems 3 and 4 are used to calculate statistical significance. As can be seen, when P = I₂ the asymptotic distribution nicely approximates the empirical distribution with only around 100 pedigrees. However, when P = 0 the type I error rate is unreasonably conservative. We give some additional comments on this problem in the discussion.

Figure 5:

Empirical Type I error for different samples sizes assuming the statistic follows the distribution given in Theorems 3 and 4 for: (a) Constraint 1 and P = E = I₂, (b) Constraint 2 and P = E = I₂, (c) Constraint 1 and E = I₂, P = 0 and (d) Constraint 2 and E = I₂, P = 0.

In a second set of simulations we parameterized P and E as in equation (18). for differing values of r. We then calculated the p-values using Method 2 in section 3. As stopping rule, for each simulation we tested whether the p-value was statistically different from 0.001 at an alpha level of 0.01. To our knowledge, the simulation algorithm failed to yield a p-value only once, probably due to a failed optimization. Missing values were ignored. For each parameter setup we used 50,000 simulated replicates. Table 2 shows the results. As can be seen, when r comes close to 1, the statistic approaches its asymptotic distribution more slowly. Again we see that using the asymptotic method described in this paper leads to conservative results when the nuisance parameters are near the boundary. We give some additional comments on this problem in the discussion.

Table 2.

Type I error rates for various genetic models parameterized as in equation (18) when α = 0.001. A value of 1 represents the theoretically correct Type 1 error. Each cell is estimated from 50,000 simulated replicates.

		Type I Error
Constraint	Sample Size	r = 0	r = 0.25	r = 0.5	r = 0.75	r = 0.95
1	50	0.32	0.36	0.20	0.20	0.36
	100	0.38	0.36	0.40	0.32	0.20
	250	0.82	0.84	0.50	0.28	0.44
	1000	1.18	1.06	1.18	0.50	0.40
2	50	0.18	0.24	0.44	0.58	0.48
	100	0.52	0.30	0.46	0.24	0.10
	250	0.90	0.66	0.64	0.50	0.44
	1000	1.02	1.06	0.84	0.50	0.50

5. Discussion

There are two possible motivations for a one-sided test. First, we may only be interested in the results of the study if the deviation from the null hypothesis is in a specific direction. In this case we really have a compound null hypothesis such as H₀ : μ ≥ 0 vs H_a : μ > 0 Second, we may be convinced that the parameter could fall on only one side of the null hypothesis. It is this second reason that justifies the use of a one-sided test in the variance component setting. We test H₀ : a = 0 against H_a : a > 0 because we have a strong a priori commitment to the notion that a, as a variance, must be positive. In the univariate tests mentioned above, the one-sided p-value will be half the two-sided p-value if the parameter estimate is positive. Hence, one-sided tests cannot be performed after peeking at the data. We must justify the one-sided constraint by substantive knowledge, and not because it produces a lower p-value. Looking at the estimated covariance matrix before choosing a test is not an acceptable statistical procedure. In terms of type I error, any alternative hypothesis is defensible when decided upon a priori, although it may result in lower power. It is this last point that we wish to emphasize in the rather confusing set of possible alternative hypotheses.

We must make one additional cautionary note about one-sided tests in linkage analysis. While each of the constraints suggested above seems intuitively reasonable, we cannot say that A must always be positive semi-definite. It is only the total variance that is mathematically constrained to be positive semi-definite, and not the individual components of variance. Some bizarre scenarios are remotely possible. For example, suppose that there is a gene for contrarianism (i.e., family members intentionally seek to differentiate themselves). In such a situation, many behavioral traits would have a negative familial correlation induced by the locus for contrarianism. We would not be able to detect the linkage due to such behavioral traits using a one-sided test. There are also examples where environmental factors such as competition could result in negative familial correlations (Verbeke and Molenberghs 2003), but in such cases the one-sided test of linkage may still be valid. We also point out that estimation and testing are distinct issues. Within the context of estimation it may not be advisable to restrict variances to be positive because the accumulation of such results across studies may result in upwardly biased estimates (Lynch and Walsh 1998 pp. 563–564).

In this paper we have shown that it is possible to evaluate asymptotic significance levels using fairly simple methods, even in the absence of analytical results. While others (Silvapulle and Sen 2005, pp. 78–81) have discussed similar methods, our results are unique in that they are both efficient and applicable even to non-convex spaces. Our method may be easily transformed into a numerical integration problem. We have also shown that replacing the information matrix with a consistent estimate is sometimes reasonable. With regard to variance component linkage analysis, we have shown that analytical formulas for the distribution function may be derived that can be used to obtain a first pass approximation to the statistical significance. However, we recommend that Method 2 above should generally be used and not the analytical formulas.

In this paper we have investigated a multivariate variance component likelihood ratio test that enforces constraints on the nuisance parameters. We do not recommend that this statistic be routinely used in practice for two reasons. First, when nuisance parameters are too near the boundary convergence to the asymptotic distribution may be very slow. A similar observation has been made in the univariate case (Shugart, O'Connell et al. 2002). However, in all cases simulated, the statistic was conservative. The most natural approach to deal with this problem is to stop enforcing constraints on the nuisance parameters. This may lead to increased computational difficulties, but it would improve the performance of the methods we have suggested. Second, tests of variance components that make use of the normal likelihood are not necessarily robust to the multivariate normal assumption. This is a well known problem in the univariate case (Allison, Neale et al. 1999). Our simulations assumed that the multivariate normal variance component model was actually correct. In reality, we expect a mixture distribution and many other sources of non-normality. Fortunately, there are many ways to make the variance component framework robust to the normality assumption (Chen, Broman et al. 2005). In future work we plan to address both these concerns by developing a robust score test that does not enforce constraints on the nuisance parameters. The asymptotic approach developed in this paper may also be used with these robust score tests.

Appendix A

Explanation of Equation (7):

Notice first that:

$$\underset{\theta \in \tilde{C}({\Omega }_1,{\mathbf{\theta }}_0)}{\text{inf}}{\Vert \mathbf{\text{V}}-\mathbf{\theta }\Vert }^2\ge 0$$ (19)

because distance measures are greater than 0. Also:

$$\underset{\theta \in \tilde{C}({\Omega }_0,{\mathbf{\theta }}_0)}{\text{inf}}{\Vert \mathbf{\text{V}}-\mathbf{\theta }\Vert }^2\le {\Vert \mathbf{\text{V}}-0\Vert }^2=1,$$ (20)

because 0 ∈ C̃ (Ω₀, θ₀). Putting (19) and (20) together we obtain:

$$\begin{array}{l}\tilde{g}({\mathbf{\text{V}}}_i)=\underset{\theta \in \tilde{C}({\Omega }_0,{\mathbf{\theta }}_0)}{\text{inf}}{\Vert \mathbf{\text{V}}-\mathbf{\theta }\Vert }^2-\underset{\theta \in \tilde{C}({\Omega }_1,{\mathbf{\theta }}_0)}{\text{inf}}{\Vert \mathbf{\text{V}}-\mathbf{\theta }\Vert }^2\\ \le 1.\end{array}$$ (21)

Furthermore, it is clear that $\underset{\theta \in \tilde{C}\left({\Omega }_1,{\mathbf{\theta }}_0\right)}{\text{inf}}{\Vert \mathbf{\text{V}}-\mathbf{\theta }\Vert }^2\le \underset{\theta \in \tilde{C}\left({\Omega }_0,{\mathbf{\theta }}_0\right)}{\text{inf}}{\Vert \mathbf{\text{V}}-\mathbf{\theta }\Vert }^2$, under the very general assumption that C̃ (Ω₀, θ₀) ⊂ C̃ (Ω₁, θ₀). As a result,

$$0\le \tilde{g}({\mathbf{\text{V}}}_i)\le 1.$$ (22)

Now notice that 1 – F_d (S/x) is an increasing function because it is a decreasing function composed with a decreasing function. Note also that 1 – F_d (S/0) = 0 by definition and 1 – F_d (S/1) = 1 – F_d (S). Therefore, from (22) and the fact that 1 – F_d (S/x) is increasing in x:

$$0\le 1-F_d\left(S/\tilde{g}({\mathbf{\text{V}}}_i)\right)\le 1-F_d\left(S\right).$$ (23)

We note that the variance of each simulated distribution is at its maximum when all its probability is concentrated at either end of the limits described above. That is, its variance is as large as possible when it is distributed as a point mass at 0 and a point mass at p_U. We let ζ be the amount of probability concentrated at p_U. Then E [p̂_n] = p = ζ p_U. So ζ = p / p_U, and

$$Var\left({\hat{p}}_n\right)\le \frac{\left(1-\zeta \right){\left(p-0\right)}^2+\zeta {\left(p-p_U\right)}^2}{n}=\frac{\left(p_U-p\right)p}{n}.$$ (24)

Explanation of Equation (9):

Consider the cone C̃ (Ω₁, θ₀) that has vertex at 0. Because it is nontrivial, there exists some non-zero vector e ∈ C̃ (Ω₁, θ₀). We define the cone Ω₂ = {ae | a > 0}. Define ${\tilde{g}}^{*}\left(\mathbf{\text{V}}\right)={\Vert \mathbf{\theta }\Vert }^2-\underset{\theta \in {\Omega }_2}{\text{inf}}{\Vert \mathbf{\text{V}}-\mathbf{\theta }\Vert }^2$. Clearly Ω₂ ⊆ C̃ (Ω₁, θ₀) and therefore $\underset{\theta \in {\Omega }_2}{\text{inf}}{\Vert \mathbf{\text{V}}-\mathbf{\theta }\Vert }^2\ge \underset{\theta \in \tilde{C}\left({\Omega }_1,{\mathbf{\theta }}_0\right)}{\text{inf}}{\Vert \mathbf{\text{V}}-\mathbf{\theta }\Vert }^2$. Thus

$${\tilde{g}}^{*}(\mathbf{\text{V}})={\Vert \mathbf{\theta }\Vert }^2-\underset{\theta \in {\Omega }_2}{\text{inf}}{\Vert \mathbf{\text{V}}-\mathbf{\theta }\Vert }^2\le {\Vert \mathbf{\theta }\Vert }^2-\underset{\theta \in \tilde{C}({\Omega }_1,{\mathbf{\theta }}_0)}{\text{inf}}{\Vert \mathbf{\text{V}}-\mathbf{\theta }\Vert }^2=\tilde{g}(\mathbf{\text{V}}).$$ (25)

But, because 1 – F_d (S/x) is increasing in x, 1 – F_d (S/g̃^*(V) ≤ – 1 F_d (S/g̃(V)). Thus

$$E_{\text{v}}\left[1-F_d\left({S/\tilde{g}}^{*}(\mathbf{\text{V}})\right)\right]\le E_{\text{v}}\left[1-F_d\left(S/\tilde{g}(\mathbf{\text{V}})\right)\right]=p.$$ (26)

However, the test statistic for H₀ : θ = 0 versus H_a : θ ∈ Ω₂ is asymptotically distributed as $\frac{1}{2}{\chi }_0^2+\frac{1}{2}{\chi }_1^2$, and therefore $E_v\left[1-F_d\left({S/\tilde{g}}^{*}\left(\mathbf{\text{V}}\right)\right)\right]=\frac{1}{2}\left(1-F_1\left(S\right)\right)$. Combining this with (26) we get that $\frac{1}{2}\left(1-F_1\left(S\right)\right)\le p$ and thus $S\ge F_1^{-1}\left(1-2p\right)$ We then have

$$p_U=1-F_d\left(S\right)\le 1-F_d\left(F_1^{-1}\left(1-2p\right)\right).$$ (27)

Equation (9) then follows by combining (27) with (8).

(28)

Proof of Lemma 1:

Define $Q_2(\mathbf{\theta })={\left({\mathbf{\text{Z}}}_2-\lambda +{\mathbf{\text{f}}}_{\lambda \lambda }^{-1}{\mathbf{\text{f}}}_{\psi \lambda }^T\left({\mathbf{\text{Z}}}_1-\psi \right)\right)}^T{\mathbf{\text{f}}}_{\lambda \lambda }\left({\mathbf{\text{Z}}}_2-\lambda +{\mathbf{\text{f}}}_{\lambda \lambda }^{-1}{\mathbf{\text{f}}}_{\psi \lambda }^T\left({\mathbf{\text{Z}}}_1-\psi \right)\right)$ and let Q₁ (ψ) = (Z₁ – ψ)^T M (Z₁ – ψ), where ${\mathbf{\text{Z}}}^T={\left[{\mathbf{\text{Z}}}_1^T {\mathbf{\text{Z}}}_2^T\right]}^T$. It is easily verified that (Z – θ)^T f (Z – θ) = Q₁ (ψ) + Q₂ (θ). Thus we see that

$$\underset{\mathbf{\psi }\in C_i,\lambda \in C_{*}}{\text{inf}}{\left(\mathbf{\text{Z}}-\mathbf{\theta }\right)}^T\mathbf{\text{f}}\left(\mathbf{\text{Z}}-\mathbf{\theta }\right)=\underset{\mathbf{\psi }\in C_i}{\text{inf}}\left[Q_1(\mathbf{\psi })+\underset{\lambda \in C_{*}}{\text{inf}}{Q}_2(\mathbf{\theta })\right],$$ (29)

where C_i = C (Ω_i, θ₀). Under condition (a), Q₂ (θ) is only a function of λ, so $\underset{\psi \in C_i,\lambda \in C_{*}}{\text{inf}}{\left(\mathbf{\text{Z}}-\mathbf{\theta }\right)}^T\mathbf{\text{f}}\left(\mathbf{\text{Z}}-\mathbf{\theta }\right)=\underset{\psi \in C_i}{\text{inf}}{Q}_1\left(\psi \right)+\underset{\lambda \in C_{*}}{\text{inf}}{Q}_2(\mathbf{\theta })$. Under condition (b) $\underset{\psi \in C_i,\lambda \in C_{*}}{\text{inf}}{\left(\mathbf{\text{Z}}-\mathbf{\theta }\right)}^T\mathbf{\text{f}}\left(\mathbf{\text{Z}}-\mathbf{\theta }\right)=\underset{\psi \in C_i}{\text{inf}}{Q}_1\left(\psi \right)$. Thus under either condition (a) or (b) h (Z₁) = g(Z). It is a well known property of the Schur complement (M) of the block f_ΨΨ of f that M⁻¹ is the first block entry of f̂⁻¹. Thus the distribution of the first q entries of f^−1/2Z̃ + θ₀, where Z̃ is a vector of independent standard normal random variables, is identical in distribution to that of M^−1/2Ỹ + b where Ỹ is a vector of independent standard normal random variables. Therefore

$$\begin{array}{ccc}{P}_{\mathbf{\text{Y}}}\left[h\left(\mathbf{\text{Y}}\right)\ge S\right]& =& P_{\widetilde{\mathbf{\text{Y}}}}\left[h\left({\mathbf{\text{M}}}^{-1/2}\widetilde{\mathbf{\text{Y}}}+\mathbf{\text{b}}\right)\ge S\right]\hfill \\ & =& P_{\widetilde{\mathbf{\text{Z}}}}\left[g\left({\mathbf{\text{f}}}^{-1/2}\widetilde{\mathbf{\text{Z}}}+{\mathbf{\theta }}_0\right)\ge S\right].\hfill \\ & =& P_{\mathbf{\text{Z}}}\left[g\left(\mathbf{\text{Z}}\right)\ge S\right].\hfill \end{array}$$ (30)

Proof of Theorem 2:

First we prove that ${\tilde{h}}_n\left(\widetilde{\mathbf{\text{Y}}}\right)=h\left({\hat{M}}_n^{-1/2}\widetilde{\mathbf{\text{Y}}}+\mathbf{\text{b}}\right)$ is a continuous function of f̂_n. Note that M̂_n is a continuous function of f̂_n because the matrix inverse is a continuous mapping (Lange 2004, p. 31). Also, suppose ${\hat{M}}_n^{1/2}$ is the Cholesky decomposition, which is also a continuous mapping of M̂_n (Schatzman and Taylor 2002, p. 295). It can be easily shown that $\underset{\psi \in \Omega }{\text{inf}}{\Vert x-A\Psi \Vert }^2$ is a continuous function of x and A. So

$$h\left({\widehat{\mathbf{\text{M}}}}_n^{-1/2}\widetilde{\mathbf{\text{Y}}}+\mathbf{\text{b}}\right)=\underset{\mathbf{\Psi }\in C_b}{\text{inf}}{\Vert \widetilde{\mathbf{\text{Y}}}-{\widehat{\mathbf{\text{M}}}}_n^{1/2}\left(\mathbf{\Psi }-\mathbf{\text{b}}\right)\Vert }^2-\underset{\mathbf{\Psi }\in C_a}{\text{inf}}{\Vert \widetilde{\mathbf{\text{Y}}}-{\widehat{\mathbf{\text{M}}}}_n^{1/2}\left(\mathbf{\Psi }-\mathbf{\text{b}}\right)\Vert }^2$$ (31)

is a continuous function of f̂_n.

Let β (B, l) = P_Ỹ [h̃_n (Ỹ) ≥ LR_n|f̂_n = B, LR_n = l]. By inspection of equation (11), we have β (B, l) = ∫_φ[1-F_p (l/h M(B)^−1/2Ỹ + b))] Jdφ/S_p. Let (B_i, l_i) → (B, l) be a convergent sequence with l > 0 and B > 0. Note that 0 ≤ F_p (x) ≤ 1, so, by the dominated convergence theorem, β (B_i, l_i) → β (B, l) and β is thus continuous for l > 0 and B > 0. A discontinuity at l = 0 occurs because by our definition F_p (S / 0) = 1 for S > 0 and F_p (0 / 0) = 0. To fix this discontinuity define:

$$\gamma \left(\mathbf{\text{B}},l\right)=\{\begin{array}{cc}{P}_{\widetilde{\mathbf{\text{Y}}}}\left[{\tilde{h}}_n\left(\widetilde{\mathbf{\text{Y}}}\right)>0|{\widehat{\mathbf{\text{f}}}}_n=\mathbf{\text{B}},L{R}_n=l\right]& l\le 0\\ \beta \left(\mathbf{\text{B}},l\right)& l>0\end{array}.$$ (32)

But γ (B, l) is fairly clearly a continuous function for B > 0 and l ∈ ℝ. Also $L{R}_n\stackrel{L}{\to }\tilde{h}\left(\widetilde{\mathbf{\text{Y}}}\right)$ and ${\widehat{\mathbf{\text{f}}}}_n\stackrel{P}{\to }\mathbf{\text{f}}\left({\mathbf{\theta }}_0\right)$. From Slutsky’s Theorem, $\gamma \left({\widehat{\mathbf{\text{f}}}}_n,\hspace{0.17em}L{R}_n\right)\stackrel{L}{\to }\gamma \left(\mathbf{\text{f}}\left({\mathbf{\text{θ}}}_0\right),\hspace{0.17em}\tilde{h}(\widetilde{\mathbf{\text{Y}}})\right)$. Theorem 2 follows from the definition of convergence in distribution.

Appendix B

Discussion of Lemma 2:

For sufficiently large η and sufficiently small ε the true parameter will be an interior point of Γ(ε, η) and hence this constraint will asymptotically disappear. For i ∈ {0,1}, Ω_i ∩ Γ (ε, η) is a compact space with bounded derivatives for the likelihood up to the 3^rd derivative. As mentioned earlier, our problem fits into the independent identically distributed framework if we consider pedigree structure and IBD values to be random. Geyer (1994) gives four regularity conditions (excluding the Chernoff regularity of the cone, which is clearly satisfied in our case) for establishing theorem 1. See Theorem 4.4 and the remark at the end of section 4 in Geyer (1994). The first regularity condition is the existence of a local quadratic approximation of the likelihood. This appears to be obviously satisfied in our case. The second condition is termed stochastic equicontinuity. This condition is more difficult to verify, but it appears that an application of the Equicontinuity Lemma on p. 150 of Pollard (1984) could be used. The third regularity condition is the existence of a central limit theorem for the first derivative, and this again seems to be fairly obviously satisfied. The final condition is the use of a consistent root-K minimizer. Consistency may be established for example by Theorem 17 of Ferguson (1996), and the root-K minimizer is guaranteed by how we have defined the likelihood ratio.

Let vecA_t×t = [a₁₁ … a_1t a₂₁ … a_tt] and vechA_t×t = [a₁₁ … a_1t a₂₂ … a_tt] as defined for example in (Henderson and Searle 1979). There exists matrices G and H such that vecA = GvechA and vechA = HvecA, again defined for example in Henderson and Searle (1979).

Lemma 3: If A = 0 and P = γE for some positive scalar γ, then M = κ [G^T (E⁻¹ ⊗ E⁻¹)G], where M is the Schur complement of the block f_ΨΨ of f and κ is some constant dependent upon the population.

Proof of Lemma 3:

Let τ represent a random pedigree structure sampled from a population. The covariance structure for a given τ is C_τ = Φ_τ ⊗ P + I_τ ⊗ E = (γΦ_τ + I_τ) ⊗ E. Let Δ_τ = Π_τ – Φ_τ and ${\mathbf{\text{B}}}_{ij}=e_i{e}_J^T+e_j{e}_i^{T}If\left[j\ne i\right]$, where e_i is the unit vector of length t in the i^th direction. Then:

$$\begin{array}{ccc}{\mathbf{\text{f}}}_{a_{i_1{i}_2}{a}_{j_1{j}_2}}& =& E_{\tau }{E}_{{\Pi }_{\tau }}tr\left[{\mathbf{\text{C}}}_{\tau }^{-1}\left({\mathbf{\Delta }}_{\tau }\otimes {\mathbf{\text{B}}}_{i_1{i}_2}\right){\mathbf{\text{C}}}_{\tau }^{-1}\left({\mathbf{\Delta }}_{\tau }\otimes {\mathbf{\text{B}}}_{j_1{j}_2}\right)\right]\hfill \\ & =& E_{\tau }{E}_{{\Pi }_{\tau }}tr\left[{\left(\gamma {\mathbf{\Phi }}_{\tau }+{\mathbf{\text{I}}}_{\tau }\right)}^{-1}{\mathbf{\Delta }}_{\tau }{\left(\gamma {\mathbf{\Phi }}_{\tau }+{\mathbf{\text{I}}}_{\tau }\right)}^{-1}{\mathbf{\Delta }}_{\tau }\otimes {\mathbf{\text{E}}}^{-1}{\mathbf{\text{B}}}_{i_1{i}_2}{\mathbf{\text{E}}}^{-1}{\mathbf{\text{B}}}_{j_1{j}_2}\right]\hfill \\ & =& tr\left[{\mathbf{\text{E}}}^{-1}{\mathbf{\text{B}}}_{i_1{i}_2}{\mathbf{\text{E}}}^{-1}{\mathbf{\text{B}}}_{j_1{j}_2}\right]\kappa \hfill \\ & =& \kappa {\left(vec{\mathbf{\text{B}}}_{i_1{i}_2}\right)}^T\left({\mathbf{\text{E}}}^{-1}\otimes {\mathbf{\text{E}}}^{-1}\right)vec{\mathbf{\text{B}}}_{i_1{i}_2},\hfill \end{array}$$ (33)

where κ = E_τE_Πτ tr [(γΦ_τ + I_τ)]⁻¹Δ_τ (γΦ_τ + I_τ)⁻¹Δ_τ]. Line 4 above follows from line 9 of Henderson and Searle (1979). Applying the same algebraic steps and using the fact that E_ΠτΔ_τ = 0, we obtain f_ai1i2pj1j2 = 0 and f_ai1i2ej1j2 = 0. Note that G = [vecB₁₁ … vecB_1t vecB₂₂ … vecB_tt]. Lemma 3 follows immediately.

Lemma 4: If M can be factored as [G^T (T⁻¹ ⊗ T⁻¹) G] and P and E are not on the boundary of the parameter space, then the asymptotic null distribution of the variance component CLRT statistic (λ) for H₀ : A = 0 vs. H_a : A ≥ 0 is equivalent to the distribution of ${\lambda }^{*}=\sum _{i=1}^i{\left[\text{max}\left(b_i,0\right)\right]}^2$ Here b_i represents the eigenvalues of a symmetric random matrix Z̃_t×t, and the elements Z̃ are independent with distribution N (0,1) on the diagonals and N (0, ½) on the off diagonals.

Proof of Lemma 4:

Let X and θ be t × t symmetric matrices with Z = vechX distributed as a MVN random variable with mean 0 and variance M⁻¹. Then

$$\begin{array}{ccc}vech{\left(\mathbf{\text{X}}-\mathbf{\theta }\right)}^T \mathbf{\text{M}}vech\left(\mathbf{\text{X}}-\mathbf{\theta }\right)& =& vec{\left(\mathbf{\text{X}}-\mathbf{\theta }\right)}^T\left({\mathbf{\text{T}}}^{-1}\otimes {\mathbf{\text{T}}}^{-1}\right)vec(\mathbf{\text{X}}-\mathbf{\theta })\hfill \\ & =& vec{\left(\mathbf{\text{X}}-\mathbf{\theta }\right)}^{T}vec\left[{\mathbf{\text{T}}}^{-1}\left(\mathbf{\text{X}}-\mathbf{\theta }\right){\mathbf{\text{T}}}^{-1}\right]\hfill \\ & =& tr\left[{\left({\mathbf{\text{T}}}^{-1/2}\mathbf{\text{X}}{\mathbf{\text{T}}}^{-1/2}-{\mathbf{\text{T}}}^{-1/2}\mathbf{\theta }{\mathbf{\text{T}}}^{-1/2}\right)}^2\right].\hfill \end{array}$$ (34)

Let X̃ = T^−1/2XT^−1/2. Note that M⁻¹ = H(T ⊗ T)H^T. This may be easily verified using line (24) and (20) of Henderson and Searle (1979). Note also that vechX̃ = H (T^−1/2 ⊗ T^−1/2) GvechX. Hence vechX̃ is distributed as MVN with mean 0 and variance

$$\begin{array}{ccc}\text{var}\left(vech\widetilde{\mathbf{\text{X}}}\right)& =& \mathbf{\text{H}}\left({\mathbf{\text{T}}}^{-1/2}\otimes {\mathbf{\text{T}}}^{-1/2}\right)\mathbf{\text{GH}}\left(\mathbf{\text{T}}\otimes \mathbf{\text{T}}\right){\mathbf{\text{H}}}^T{\mathbf{\text{G}}}^T\left({\mathbf{\text{T}}}^{-1/2}\otimes {\mathbf{\text{T}}}^{-1/2}\right){\mathbf{\text{H}}}^T\hfill \\ & =& \mathbf{\text{H}}{\mathbf{\text{H}}}^T\end{array}$$ (35)

But HH^T is a diagonal matrix with 1 corresponding to the diagonal elements of X̃ and ½ for the off diagonal elements. S̃ = {θ̃:θ̃ = T^−1/2θ_T^−1/2 for some θ ≥ 0}= {θ̃:θ̃ ≥ 0}. From Theorem 1 and 2, λ has the same asymptotic distribution as:

$$\begin{array}{ccc}g\left(\mathbf{\text{Z}}\right)& =& vech{\left(\mathbf{\text{X}}\right)}^T\mathbf{\text{M}}veck\left(\mathbf{\text{X}}\right)-\underset{\theta \ge 0}{\text{inf}}vech{\left(\mathbf{\text{X}}-\mathbf{\theta }\right)}^T\mathbf{\text{M}}vech\left(\mathbf{\text{X}}-\mathbf{\theta }\right)\\ & =& tr\left[{\tilde{X}}^2\right]-\underset{\theta \in S}{\text{inf}}tr\left[{\left(\tilde{X}-\tilde{\theta }\right)}^2\right].\end{array}$$ (36)

Lemma 4 then follows from Theorem 8 in Chapter 2 of Dimedenco (2005).

Note that Lemmas 3 and 4 show the asymptotic distribution to be identical to the traditional multivariate variance component model in one special case.

Lemma 5: If M can be factored as [G^T (T⁻¹ ⊗ T⁻¹)G], where T > 0, then the asymptotic null distribution of the CLRT statistic (λ) for a variance component linkage model, testing H₀ : A = 0 vs. H_a : A ≥ 0, is equivalent to the distribution of: λ^* = [max (b₁, 0)]². Here b₁ ≥ … ≥ b_t represent the eigenvalues of a symmetric random matrix X̃_t×t, and the elements Z̃ are independent with distribution N (0,1) on the diagonals and N (0, ½) on the off-diagonals.

Proof of Lemma 5:

Define S̃ = {T^−1/2φφ^TT^−1/2 | φ ∈ ℝ^t} = {φφ^T | φ ∈ ℝ^t}. Following the same steps as in Lemma 3, we have:

$$\begin{array}{ccc}\tilde{g}\left(\tilde{X}\right)& =& tr{\tilde{X}}^2-\underset{\theta \in S}{\text{inf}}tr\left[{\left(\tilde{X}-\tilde{\theta }\right)}^2\right]=\underset{\phi \in {ℝ}^t}{\text{sup}}\left(tr\left(\tilde{X}\phi {\phi }^T\right)-tr\left[\phi {\phi }^T\phi {\phi }^T\right]\right)\\ & =& \underset{\phi \in {ℝ}^t}{\text{sup}}\left({\phi }^T\tilde{X}\phi -{\left({\phi }^T\phi \right)}^2\right)=\underset{\Vert \mathbf{\text{V}}\Vert =1}{\text{sup}}\underset{r}{\text{sup}}\left(r^2{\mathbf{\text{V}}}^2\tilde{X}V-r^4{\Vert \mathbf{\text{V}}\Vert }^4\right)\\ & =& \underset{\Vert \mathbf{\text{V}}\Vert =1}{\text{sup}}{\left(\frac{{\mathbf{\text{V}}}^T\tilde{X}V}{{\mathbf{\text{V}}}^T\mathbf{\text{V}}}I\left[{\mathbf{\text{V}}}^T\tilde{X}V>0\right]\right)}^2.\end{array}$$

Lemma 5 follows from this.

Sketch of Proof for Theorem 4:

By using Lemmas 3 and 5 we may conclude that the asymptotic distribution is a function of the maximum eigenvalue of a random matrix. The eigenvalue distribution has been given in numerous places, such as Amemiya, Anderson et al. (1990). The distribution function for t = 2 is: $\left(b_1-b_2\right)\text{exp}[-\frac{1}{2}\left(b_1^2+b_2^2\right)]/2\sqrt{\pi }$. It is a fairly straightforward application of calculus to derive the distribution in Theorem 4 using a symbolic computational system such as Mathematica.