Extensions of Sparse Canonical Correlation Analysis with Applications to Genomic Data

Abstract

In recent work, several authors have introduced methods for sparse canonical correlation analysis (sparse CCA). Suppose that two sets of measurements are available on the same set of observations. Sparse CCA is a method for identifying sparse linear combinations of the two sets of variables that are highly correlated with each other. It has been shown to be useful in the analysis of high-dimensional genomic data, when two sets of assays are available on the same set of samples. In this paper, we propose two extensions to the sparse CCA methodology. (1) Sparse CCA is an unsupervised method; that is, it does not make use of outcome measurements that may be available for each observation (e.g., survival time or cancer subtype). We propose an extension to sparse CCA, which we call sparse supervised CCA, which results in the identification of linear combinations of the two sets of variables that are correlated with each other and associated with the outcome. (2) It is becoming increasingly common for researchers to collect data on more than two assays on the same set of samples; for instance, SNP, gene expression, and DNA copy number measurements may all be available. We develop sparse multiple CCA in order to extend the sparse CCA methodology to the case of more than two data sets. We demonstrate these new methods on simulated data and on a recently published and publicly available diffuse large B-cell lymphoma data set.

1. Introduction

Canonical correlation analysis (CCA), due to Hotelling (1936), is a classical method for determining the relationship between two sets of variables. Given two data sets X₁ and X₂ of dimensions n × p₁ and n × p₂ on the same set of n observations, CCA seeks linear combinations of the variables in X₁ and the variables in X₂ that are maximally correlated with each other. That is, w₁ ∈ $\mathbb{\text{R}}$^p₁ and w₂ ∈ $\mathbb{\text{R}}$^p₂ maximize the CCA criterion, given by

$${\text{maximize}}_{{\text{w}}_1,{\text{w}}_2}{\text{w}}_1^T{\text{X}}_1^T{\text{X}}_2{\text{w}}_2 \text{subject} \text{to} {\text{w}}_1^T{\text{X}}_1^T{\text{X}}_1{\text{w}}_1={\text{w}}_2^T{\text{X}}_2^T{\text{X}}_2{\text{w}}_2=1,$$ (1)

where we assume that the columns of X₁ and X₂ have been standardized to have mean zero and standard deviation one. In this paper, we will refer to w₁ and w₂ as the canonical vectors (or weights), and we will refer to X₁w₁ and X₂w₂ as the canonical variables.

In recent years, CCA has gained popularity as a method for the analysis of genomic data. It has become common for researchers to perform multiple assays on the same set of patient samples; for instance, DNA copy number (or comparative genomic hybridization, CGH), gene expression, and single nucleotide polymorphism (SNP) data might all be available. Examples of studies involving two or more genomic assays on the same set of samples include Hyman et al. (2002), Pollack et al. (2002), Morley et al. (2004), Stranger et al. (2005), and Stranger et al. (2007). In the case of, say, DNA copy number and gene expression measurements on a single set of patient samples, one might wish to perform CCA in order to identify genes whose expression is correlated with regions of genomic gain or loss. However, genomic data is characterized by the fact that the number of features generally greatly exceeds the number of observations; for this reason, CCA cannot be applied directly.

To circumvent this problem, Parkhomenko et al. (2007), Waaijenborg et al. (2008), Parkhomenko et al. (2009), Le Cao et al. (2009), and Witten et al. (2009) have proposed methods for penalized CCA. In this paper, we will restrict ourselves to the criterion proposed in Witten et al. (2009), which takes the form

$$\begin{array}{l}{\text{maximize}}_{{\text{w}}_1,\hspace{0.17em}{\text{w}}_2}{\text{w}}_1^T{\text{X}}_1^T{\text{X}}_2{\text{w}}_2\\ \text{subject} \text{to} \parallel {\text{w}}_1{\parallel }^2\le 1,\parallel {\text{w}}_2{\parallel }^2\le 1,P_1({\text{w}}_1)\le c_1,P_2({\text{w}}_2)\le c_2\end{array}$$ (2)

where P₁ and P₂ are convex penalty functions. Since P₁ and P₂ are generally chosen to yield w₁ and w₂ sparse, we call this the sparse CCA criterion. This criterion follows from applying penalties to w₁ and w₂ and also from assuming that the covariance matrix of the features is diagonal; that is, we replace ${\text{w}}_1^T{\text{X}}_1^T{\text{X}}_1{\text{w}}_1$ and ${\text{w}}_2^T{\text{X}}_2^T{\text{X}}_2{\text{w}}_2$ in the CCA criterion with ${\text{w}}_1^T{\text{w}}_1$ and ${\text{w}}_2^T{\text{w}}_2$. The sparse CCA criterion results in w₁ and w₂ unique, even when p₁, p₂ ≫ n, for appropriate choices of P₁ and P₂.

It has been shown that sparse CCA can be used to identify genes that have expression that is correlated with regions of DNA copy number change (Waaijenborg et al. 2008, Witten et al. 2009), to identify genes that have expression that is correlated with SNPs (Parkhomenko et al. 2009), and to identify sets of genes on two different microarray platforms that have correlated expression (Le Cao et al. 2009). However, some questions remain:

1. Sometimes, in addition to data matrices X₁ ∈ $\mathbb{\text{R}}$^n×p₁ and X₂ ∈ $\mathbb{\text{R}}$^n×p₂, a vector of outcome measurements in $\mathbb{\text{R}}$ⁿ is also available. For instance, a survival time might be known for each patient. CCA and sparse CCA are unsupervised methods; that is, they do not make use of an outcome. However, if outcome measurements are available, then one might seek sets of variables in the two data sets that are correlated with each other and associated with the outcome.

2. More than two sets of variables on the same set of observations might be available. For instance, it is becoming increasingly common for researchers to collect gene expression, SNP, and DNA copy number measurements on the same set of patient samples. In this case, an extension of sparse CCA to the case of more than two data sets is required.

In this paper, we develop extensions to sparse CCA that address these situations and others.

The rest of this paper is organized as follows. Section 2 contains methods for sparse CCA when the data consist of matrices X₁ and X₂. In Section 2.1, we present details of the sparse CCA method from Witten et al. (2009), and in Section 2.2, we explain the connections between that method and those of Waaijenborg et al. (2008), Le Cao et al. (2009), and Parkhomenko et al. (2009). The remainder of Section 2 contains some extensions of sparse CCA for two sets of features on a single set of observations. Section 3 contains an explanation of sparse multiple CCA, an extension of sparse CCA to the case of K data sets X₁, ..., X_K with features on a single set of samples. In Section 4, we present sparse supervised CCA, a method for performing sparse CCA when the data consist of matrices X₁, X₂, and y, a vector containing an outcome measurement for each sample. Section 5 contains the discussion. Throughout the paper, methods are applied to the diffuse large B-cell lymphoma (DLBCL) data set of Lenz et al. (2008), which consists of 17350 gene expression measurements and 386165 DNA copy number measurements for 203 patients. For each patient, two clinical outcomes are available: a possibly censored survival time, as well as the subtype of DLBCL to which that patient’s disease belongs.

2. Sparse CCA

2.1. The sparse CCA method

The sparse CCA criterion was given in Equation (2) for general penalty functions P₁ and P₂. We will be interested in two specific forms of these penalty functions:

• P₁ is an L₁ (or lasso) penalty; that is, P₁(w₁) = ||w₁||₁. This penalty will result in w₁ sparse for c₁ chosen appropriately. We assume that $1\le c_1\le \sqrt{p_1}$.

• P₁ is a fused lasso penalty (see e.g. Tibshirani et al. 2005), of the form P₁(w₁) = ∑_j |w_1j | + ∑_j |w_1j – w_1(j–1)|. This penalty will result in w₁ sparse and smooth, and is intended for cases in which the features in X₁ have a natural ordering along which smoothness is expected.

In order to indicate the form of the penalties P₁ and P₂ in use, we will refer to the method as sparse CCA(P₁, P₂). That is, if both penalties are L₁, then we will call this sparse CCA(L₁, L₁), and if P₁ is an L₁ penalty and P₂ a fused lasso penalty, then we will call it sparse CCA(L₁, FL) (where “FL” indicates fused lasso). Note that when P₁ and P₂ are L₁ or fused lasso penalties, the resulting canonical vectors are unique, even when p₁, p₂ ≫ n. Witten et al. (2009) propose the use of sparse CCA(L₁, FL) in the case where X₁ corresponds to gene expression measurements and X₂ corresponds to copy number measurements (ordered by position along the chromosomes); this is related to the proposal of Tibshirani & Wang (2008) for estimating copy number for a single CGH sample.

Now, consider the criterion (2) with P₁ and P₂ convex penalty functions. With w₁ fixed, the criterion is convex in w₂, and with w₂ fixed, it is convex in w₁. The objective function of this biconvex criterion increases in each step of a simple iterative algorithm.

Algorithm for sparse CCA:

1. Initialize w₂ to have L₂ norm 1.

2. Iterate the following two steps until convergence:

   1. w₁ ← arg max_w1 ${\text{w}}_1^T{\text{X}}_1^T{\text{X}}_2{\text{w}}_2$ subject to ||w₁||² ≤ 1, P₁(w₁) ≤ c₁.
   2. w₂ ← arg max_w2 ${\text{w}}_1^T{\text{X}}_1^T{\text{X}}_2{\text{w}}_2$ subject to ||w₂||² ≤ 1, P₂(w₂) ≤ c₂.

If P₁ is an L₁ penalty, then the update has the form

$${\text{w}}_1\leftarrow \frac{S({\text{X}}_1^T{\text{X}}_2{\text{w}}_2,{\Delta }_1)}{\parallel S({\text{X}}_1^T{\text{X}}_2{\text{w}}_2,{\Delta }_1){\parallel }_2},$$ (3)

where Δ₁ = 0 if this results in ||w₁||₁ ≤ c₁; otherwise, Δ₁ > 0 is chosen so that ||w₁||₁ = c₁. Here, S(·) denotes the soft-thresholding operator; that is, S(a, c) = sgn(a)(|a| – c)₊. Soft-thresholding arises in the update due to the L₁ penalty and the assumption that the covariance matrices are independent. Δ₁ can be chosen by a binary search. If P₁ is instead a fused lasso penalty, then a slightly modified version of the sparse CCA criterion yields the update step

$${\text{w}}_1\leftarrow {\text{argmin}}_{{\text{w}}_1}\{\frac{1}{2}\parallel {\text{X}}_1^T{\text{X}}_2{\text{w}}_2-{\text{w}}_1{\parallel }^2+{\lambda }_1\sum _j\left|w_{1j}\right|+{\lambda }_2\sum _j|w_{1j}-w_{1(j-1)}|\},$$ (4)

which can be computed using software implementing fused lasso regression. w₂ can be updated analogously.

Methods for selecting tuning parameter values and assessing significance of the resulting canonical vectors are presented in Appendix A. The above algorithm is easily extended to obtain multiple canonical vectors, as described in Witten et al. (2009) and summarized in Appendix B. However, to simplify interpretation of the examples presented in this paper, we will only consider the first canonical vectors w₁ and w₂, as given in the criterion (2).

2.2. Connections with other sparse CCA proposals

This paper extends the sparse CCA proposal of Witten et al. (2009). As mentioned earlier, the Witten et al. (2009) method is closely related to a number of other methods for sparse CCA. We briefly review those methods here.

Waaijenborg et al. (2008) first recast classical CCA as an iterative regression procedure; then an elastic net penalty is applied in order to obtain penalized canonical vectors. An approximation of the iterative elastic net procedure results in an algorithm that is similar to that of Witten et al. (2009) in the case of L₁ penalties on w₁ and w₂. However, Waaijenborg et al. (2008) do not appear to be exactly optimizing a criterion.

Parkhomenko et al. (2009) develop an iterative algorithm for estimating the singular vectors of ${\text{X}}_1^T{\text{X}}_2$. At each step, they regularize the estimates of the singular vectors by soft-thresholding. Though they do not explicity state a criterion, it appears that they are approximately optimizing a criterion that is related to (2) with L₁ penalties. However, they use the Lagrange form, rather than the bound form, of the constraints on w₁ and w₂. Their algorithm is closely related to that of Witten et al. (2009), though extra normalization steps are required due to computational problems with the Lagrange form of the constraints. The algorithm of Le Cao et al. (2009) is also closely related to those of Parkhomenko et al. (2009) and Witten et al. (2009), though again Le Cao et al. (2009) use the Lagrange form, rather than the bound form, of the penalties.

Hence, the Waaijenborg et al. (2008), Parkhomenko et al. (2009), Le Cao et al. (2009) and Witten et al. (2009) methods are all closely related; we pursue the criterion (2) in this paper.

2.3. Sparse CCA with nonnegative weights

The sparse CCA method will result in canonical vectors w₁ and w₂ that are sparse, if the penalties P₁ and P₂ are chosen appropriately. However, the nonzero elements of w₁ and w₂ may be of different signs. In some cases, one might seek a sparse weighted average of the features in X₁ that is correlated with a sparse weighted average of the features in X₂. Then one will want to additionally restrict the elements of w₁ and w₂ to be nonnegative (or nonpositive). If we require the elements of w₁ and w₂ to be nonnegative, the sparse CCA criterion becomes

$$\begin{array}{ll}{\text{maximize}}_{{\text{w}}_1,{\text{w}}_2}& {\text{w}}_1^T{\text{X}}_1^T{\text{X}}_2{\text{w}}_2 \text{subject} \text{to} \parallel {\text{w}}_1{\parallel }^2\le 1,\parallel {\text{w}}_2{\parallel }^2\le 1,\\ & w_{1j}\ge 0,w_{2j}\ge 0,P_1({\text{w}}_1)\le c_1,P_2({\text{w}}_2)\le c_2,\end{array}$$ (5)

and the resulting algorithm is as follows:

Algorithm for sparse CCA with nonnegative weights:

1. Initialize w₂ to have L₂ norm 1.

2. Iterate the following two steps until convergence:

   1. w₁ ← arg max_w1 ${\text{w}}_1^T{\text{X}}_1^T{\text{X}}_2{\text{w}}_2$ subject to ||w₁||² ≤ 1, w_1j ≥ 0, P₁(w₁) ≤ c₁.
   2. w₂ ← arg max_w2 ${\text{w}}_1^T{\text{X}}_1^T{\text{X}}_2{\text{w}}_2$ subject to ||w₂||² ≤ 1, w_2j ≥ 0, P₂(w₂) ≤ c₂.

Consider the criterion (5) with w₁ fixed; we can write the optimization problem for w₂ with ${\text{X}}_2^T{\text{X}}_1{\text{w}}_1=\text{a}$ as

$${\text{minimize}}_{{\text{w}}_2}-{\text{a}}^T{\text{w}}_2 \text{subject} \text{to} \parallel {\text{w}}_2{\parallel }^2\le 1,w_{2j}\ge 0,P_2({\text{w}}_2)\le c_2.$$ (6)

Assume that P₂ is an L₁ penalty. It is obvious that if a_j ≤ 0, then w_2j = 0. For j such that a_j > 0, w_2j can be found by solving the optimization problem

$${\text{minimize}}_{w_{2j}:a_j>0}-\sum _{j:a_j>0}{a}_j{w}_{2j} \text{subject} \text{to} \sum _{j:a_j>0}{w}_{2j}^2\le 1,\sum _{j:a_j>0}\left|w_{2j}\right|\le c_2.$$ (7)

This can be solved using the following update for w₂:

$${\text{w}}_2\leftarrow \frac{S({({\text{X}}_2^T{\text{X}}_1{\text{w}}_1)}_{+}{,\Delta }_2)}{\parallel S({({\text{X}}_2^T{\text{X}}_1{\text{w}}_1)}_{+},{\Delta }_2){\parallel }_2},$$ (8)

where Δ₂ = 0 if this results in ||w₂||₁ ≤ c₂; otherwise, Δ₂ > 0 is chosen so that ||w₂||₁ = c₂. An analogous update step can be derived for w₁ if P₁ is an L₁ penalty.

2.4. Application of sparse CCA to the DLBCL data

We demonstrate the sparse CCA method on the lymphoma data set of Lenz et al. (2008), which consists of gene expression and array CGH measurements on 203 patients with DLBCL. The data set is publicly available at http://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE11318. There are 17350 gene expression measurements and 386165 copy number measurements. (In the raw data set, more gene expression measurements are available. However, we limited the analysis to genes for which we knew the chromosomal location, and we averaged expression measurements for genes for which multiple measurements were available.) For computational reasons, sets of adjacent CGH spots on each chromosome were averaged before all analyses were performed. In previous research, gene expression profiling has been used to define three subtypes of DLBCL, called germinal center B-cell-like (GCB), activated B-cell-like (ABC), and primary mediastinal B-cell lymphoma (PMBL) (Alizadeh et al. 2000, Rosenwald et al. 2002). For each of the 203 observations, survival time and DLBCL subtype are known.

For chromosome i, we performed sparse CCA(L₁, FL) using X₁ equal to expression data of genes on all chromosomes and X₂ equal to DNA copy number data on chromosome i. Tuning parameter values were chosen by permutations; details are given in Appendix A. P-values obtained using the method in Appendix A, as well as the chromosomes on which the genes corresponding to nonzero w₁ weights are located, can be found in Table 1. Canonical vectors found on almost all chromosomes were significant, and for the most part, cis interactions were found. Cis interactions are those for which the regions of DNA copy number change and the sets of genes with correlated expression are located on the same chromosome. The presence of cis interactions is not surprising because copy number gain on a given chromosome could naturally result in increased expression of the genes that were gained.

Table 1:

Column 1: The number indicates the chromosome to which the CGH data corresponds. Sparse CCA was performed using all gene expression measurements, and CGH data from chromosome i only. Column 2: In almost every case, the canonical vectors found were highly significant. P-values were obtained using the permutation approach given in Appendix A. Column 3: For the most part, CGH measurements on chromosome i were found to be correlated with the expression of sets of genes on chromosome i. That is, the canonical vectors found for the expression data had non-zero elements only for genes on chromosome i. Columns 4 and 5: P-values are reported for the Cox proportional hazards and multinomial logistic regression models that use the canonical variables to predict survival and cancer subtype.

Chr.	P-Value	Chr. of Genes w/Nonzero Weights	P-Value w/Surv.	P-Value w/Subtype
1	0	1 1 1	0.346978	0.020115
2	0	2 2	0.139221	0.000336
3	0	3 3 3	0.000395	0
4	0	4 4	0.473788	0.127702
5	0	5 5 5 5 5	0.607717	0.015423
6	0	6 6 6	0.421753	6e-05
7	0	7 7	0.530759	0
8	0	8 8	0.698352	0.000375
9	0	9 9 9 9 9 9 9 9	0.435872	0
10	0	10 10 10 10 10	0.123747	7e-06
11	0	11 11 11	0.344889	0.000265
12	0	12 12	0.436956	0.000557
14	0.02	1 14	0.006953	0
15	0	15 15 15 15 15 15 15 15	0.000552	3.5e-05
16	0	16 16	0.298069	0.029809
17	0	17 17 17 17 17 17 17	0.047078	0.775681
18	0	18 18	0.00619	5e-06
19	0	19 19 10	0.046235	0
20	0	20 20 20 2 3 20 20 20	0.922793	0.004198
21	0	21 21	0.309212	0.012914
22	0.06	22 1 1	0.441799	0.000272

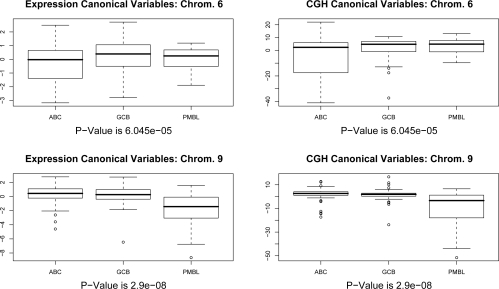
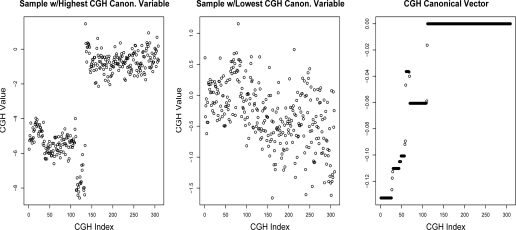
We used the CGH and expression canonical variables as features in a multivariate Cox proportional hazards model to predict survival. Note that X₁w₁ and X₂w₂ are vectors in $\mathbb{\text{R}}$ⁿ. We also used the canonical variables as features in a multinomial logistic regression to predict cancer subtype. The resulting p-values are shown in Table 1. The Cox proportional hazards models predicting survival from the canonical variables were not significant on most chromosomes. However, on many chromosomes, the canonical variables were highly predictive of DLBCL subtype. Boxplots showing the canonical variables as a function of DLBCL subtype are displayed in Figure 1 for chromosomes 6 and 9. For chromosome 9, Figure 2 shows w₂, the canonical vector corresponding to copy number, as well as the raw copy number for the samples with largest and smallest (absolute) value in the canonical variable for the CGH data. It is not surprising that there are many significant p-values for the prediction of cancer subtype in Table 1, since the subtypes are defined using gene expression, and it was found in Lenz et al. (2008) that the subtypes are characterized by regions of copy number change.

Figure 1:

Sparse CCA was performed using CGH data on a single chromosome and all gene expression measurements. For chromosomes 6 and 9, the gene expression and CGH canonical variables, stratified by cancer subtype, are shown. It is clear that the values of the canonical variables differ by subtype. Pvalues reported are replicated from Table 1; they reflect the extent to which the canonical variables predict cancer subtype in a multinomial logistic regression model.

Figure 2:

Sparse CCA was performed using CGH data on chromosome 9, and all gene expression measurements. The samples with the highest and lowest absolute values in the CGH canonical variable are shown, along with the canonical vector corresponding to the CGH data. As expected, the sample with the highest CGH canonical variable is highly correlated with the CGH canonical vector, and the sample with the lowest CGH canonical variable shows little correlation. The sample with highest CGH canonical variable is of subtype PMBL, and the sample with lowest canonical variable is of subtype ABC. The CGH data on chromosome 9 consists of 309 features, of which 111 have non-zero weights in the right-hand panel.

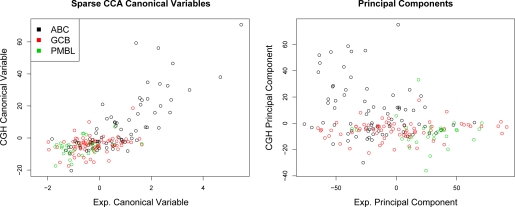
We can also compare the sparse CCA canonical variables obtained on the DLBCL data to the first principal components that arise if principal components analysis (PCA) is performed separately on the expression data and on the copy number data. PCA and sparse CCA were performed using all of the gene expression data, and the CGH data on chromosome 3; Figure 3 shows the resulting canonical variables and principal components. Sparse CCA results in CGH and expression canonical variables that are highly correlated with each other, due to the form of the sparse CCA criterion. PCA results in principal components that are far less correlated with each other, and, as a result, may yield better separation between the three subtypes. But PCA does not allow for an integrated interpretation of the expression and CGH data together.

Figure 3:

Sparse CCA and PCA were performed using CGH data on chromosome 3, and all gene expression measurements. The resulting canonical variables and principal components are shown. The CGH and expression canonical variables are highly correlated with each other. Both sparse CCA and PCA result in some separation between the three DLBCL subtypes, although PCA results in better separation because the first principal components of the CGH and expression data are less correlated with each other.

In this section, we assessed the association between the canonical variables found using sparse CCA and the clinical outcomes in order to determine if the results of sparse CCA have biological significance. However, in general, if a clinical outcome of interest is available, then the sparse sCCA approach of Section 4 may be appropriate.

2.5. Connection with nearest shrunken centroids

Consider now a new setting in which we have n observations on p features, and each observation belongs to one of two classes. Let X₁ denote the n × p matrix of observations by features, and let X₂ be a binary n × 1 matrix indicating class membership of each observation of X₁. In this section, we will show that sparse CCA applied to X₁ and X₂ yields a canonical vector w₁ that is closely related to the nearest shrunken centroids solution (NSC, Tibshirani et al. 2002, Tibshirani et al. 2003).

Assume that each column of X₁ has been standardized to have mean zero and pooled within-class standard deviation equal to one. NSC is a high-dimensional classification method that involves defining “shrunken” class centroids based on only a subset of the features; each test set observation is then classified to the nearest shrunken centroid. We first explain the NSC method, applied to data X₁. For 1 ≤ k ≤ 2, we define vectors d_k, d′_k, X̄′_1k ∈ $\mathbb{\text{R}}$^p as follows:

$${\text{d}}_k=\frac{{\overline{\text{X}}}_{1k}}{m_k}, {\text{d}}_k^{\prime }=S({\text{d}}_k,\delta ), {\overline{\text{X}}}_{1k}^{\prime }=m_k{\text{d}}_k^{\prime }.$$ (9)

Here, X̄_1k is the mean vector of the features in X₁ over the observations in class k, and $m_k=\sqrt{\frac{1}{n_k}-\frac{1}{n}}$ where n_k is the number of observations in class k. X̄′_1k is the shrunken centroid for class k obtained using tuning parameter δ ≥ 0. As in Section 2.1, S is the soft-thresholding operator.

Now, consider the effect of applying sparse CCA with L₁ penalties to data X₁ and X₂. Rescale X₂ so that the class 1 values are $\frac{1}{n_1}$ and the class 2 values are $-\frac{1}{n_2}$. The sparse CCA criterion is

$$\begin{array}{l}{\text{maximize}}_{{\text{w}}_1,{\text{w}}_2}{\text{w}}_1^T{\text{X}}_1^T{\text{X}}_2{\text{w}}_2\\ \text{subject} \text{to} \parallel {\text{w}}_1{\parallel }^2\le 1,\parallel {\text{w}}_2{\parallel }^2\le 1,\parallel {\text{w}}_1{\parallel }_1\le c_1,\parallel {\text{w}}_2{\parallel }_1\le c_2.\end{array}$$ (10)

Since w₂ ∈ $\mathbb{\text{R}}$¹, the constraints on its value result in w₂ = 1. The criterion reduces to

$${\text{maximize}}_{{\text{w}}_1}{\text{w}}_1^T{\text{X}}_1^T{\text{X}}_2 \text{subject} \text{to} \parallel {\text{w}}_1{\parallel }^2\le 1,\parallel {\text{w}}_1{\parallel }_1\le c_1,$$ (11)

which can be rewritten as

$${\text{maximize}}_{{\text{w}}_1}{({\overline{\text{X}}}_{11}-{\overline{\text{X}}}_{12})}^T{\text{w}}_1 \text{subject} \text{to} \parallel {\text{w}}_1{\parallel }^2\le 1,\parallel {\text{w}}_1{\parallel }_1\le c_1.$$ (12)

The solution to (12) is

$${\text{w}}_1=\frac{S({\overline{\text{X}}}_{11}-{\overline{\text{X}}}_{12},\Delta )}{\parallel S({\overline{\text{X}}}_{11}-{\overline{\text{X}}}_{12},\Delta ){\parallel }_2}=\frac{S((1+\frac{n_1}{n_2}){\overline{\text{X}}}_{11},\Delta )}{\parallel S((1+\frac{n_1}{n_2}){\overline{\text{X}}}_{11},\Delta ){\parallel }^2}$$ (13)

where Δ = 0 if that results in ||w₁||₁ ≤ c₁; otherwise, Δ > 0 is chosen so that ||w₁||₁ = c₁. So sparse CCA yields a canonical vector that is proportional to the shrunken centroid X̄′₁₁ when the tuning parameters for NSC and sparse CCA are chosen appropriately.

3. Sparse multiple CCA

3.1. The sparse multiple CCA method

CCA and sparse CCA can be used to perform an integrative analysis of two data sets with features on a single set of samples. But what if more than two such data sets are available? A number of approaches for generalizing CCA to more than two data sets have been proposed in the literature, and some of these extensions are summarized in Gifi (1990). We will focus on one of these proposals for multiple-set CCA.

Let the K data sets be denoted X₁, ..., X_K; data set k contains p_k variables, and each variable has mean zero and standard deviation one as in previous sections. Then, the single-factor multiple-set CCA criterion involves finding w₁, ..., w_K that maximize

$$\sum _{i<j}{\text{w}}_i^T{\text{X}}_i^T{\text{X}}_j{\text{w}}_j \text{subject} \text{to} {\text{w}}_k^T{\text{X}}_k^T{\text{X}}_k{\text{w}}_k=1 \forall k,$$ (14)

where w_k ∈ $\mathbb{\text{R}}$^p_k. It is easy to see that when K = 2, then multiple-set CCA simplifies to ordinary CCA. We can develop a method for sparse multiple CCA by imposing sparsity constraints on this natural formulation for multiple-set CCA. In the spirit of our criterion for sparse CCA with two sets of variables (2), we assume that the features are independent within each data set: that is, ${\text{X}}_k^T{\text{X}}_k=\text{I}$ for each k. Then, our criterion for sparse multiple CCA (sparse mCCA) is as follows:

$${\text{maximize}}_{{\text{w}}_1,\dots ,{\text{w}}_K}\sum _{i<j}{\text{w}}_i^T{\text{X}}_i^T{\text{X}}_j{\text{w}}_j \text{subject} \text{to} \parallel {\text{w}}_i{\parallel }^2\le 1,P_i({\text{w}}_i)\le c_i{\forall }_i,$$ (15)

where P_i are convex penalty functions. Then, w_i is the canonical vector associated with X_i. If P_i is an L₁ or fused lasso penalty and c_i is chosen appropriately, then w_i will be sparse.

It is not hard to see that just as (2) is biconvex in w₁ and w₂, (15) is multiconvex in w₁, ..., w_K. That is, with w_j held fixed for all j ≠ i, (15) is convex in w_i. This suggests an iterative algorithm that increases the objective function of (15) at each iteration.

Algorithm for sparse mCCA:

1. For each i, fix an initial value of w_i ∈ $\mathbb{\text{R}}$^p_k.

2. Repeat until convergence: For each i, let

   $${\text{w}}_i\leftarrow {\text{argmax}}_{{\text{w}}_i}{\text{w}}_i^T{\text{X}}_i^T(\sum _{j\ne i}{\text{X}}_j{\text{w}}_j) \text{subject} \text{to} \parallel {\text{w}}_i{\parallel }^2\le 1,P_i({\text{w}}_i)\le c_i.$$ (16)

For instance, if P_i is an L₁ penalty, then the update takes the form

$${\text{w}}_i\leftarrow \frac{S({\text{X}}_i^T({\sum }_{j\ne i}{\text{X}}_j{\text{w}}_j),{\Delta }_i)}{\parallel S({\text{X}}_i^T({\sum }_{j\ne i}{\text{X}}_j{\text{w}}_j),{\Delta }_i){\parallel }_2},$$ (17)

where Δ_i = 0 if this results in ||w_i||₁ ≤ c_i; otherwise, Δ_i > 0 is chosen such that ||w_i||₁ = c_i.

We demonstrate the performance of sparse mCCA on a simple simulated example. Data were generated according to the model

$${\text{X}}_i=\text{u}{\text{w}}_i^T+{\epsilon }_i,1\le i\le 3$$ (18)

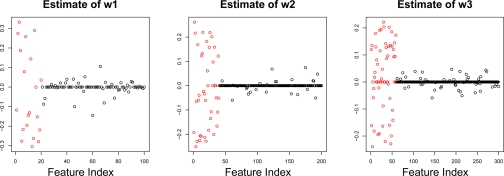
where u ∈ $\mathbb{\text{R}}$⁵⁰, w₁ ∈ $\mathbb{\text{R}}$¹⁰⁰, w₂ ∈ $\mathbb{\text{R}}$²⁰⁰, w₃ ∈ $\mathbb{\text{R}}$³⁰⁰. Only the first 20, 40, and 60 elements of w₁, w₂, and w₃ were nonzero, respectively. Sparse mCCA was run on this data, and the resulting estimates of w₁, w₂, and w₃ are shown in Figure 4.

Figure 4:

Three data sets X₁, X₂, and X₃ are generated under a simple model, and sparse mCCA is performed. The resulting estimates of w₁, w₂, and w₃ are fairly accurate at distinguishing between the elements of w_i that are truly nonzero (red) and those that are not (black). From left to right, the three canonical vectors shown have 57, 67, and 92 nonzero elements.

A permutation algorithm for selecting tuning parameter values and assessing significance of sparse mCCA can be found in Appendix A. In addition, an algorithm for obtaining multiple sparse mCCA factors is given in Appendix B.

3.2. Application of sparse mCCA to DLBCL copy number data

If CGH measurements are available on a set of patient samples, then one may wonder whether copy number changes in genomic regions on separate chromosomes are correlated. For instance, certain genomic regions may tend to be coamplified or codeleted.

To answer this question for a single pair of chromosomes, we can perform sparse CCA(FL, FL) with two data sets, X₁ and X₂, where X₁ contains the CGH measurements on the first chromosome of interest and X₂ contains the CGH measurements on the second chromosome of interest. If copy number change on the first chromosome is independent of copy number change on the second chromosome, then we expect the corresponding p-value obtained using the method of Appendix A not to be small. A small p-value indicates that copy number changes on the two chromosomes are more correlated with each other than one would expect due to chance. However, in general, there are ( $\begin{array}{c}24\\ 2\end{array}$) pairs of chromosomes that can be tested for correlated patterns of amplification and deletion; this leads to a multiple testing problem and excessive computation. Instead, we take a different approach, using sparse mCCA. We apply sparse mCCA to data sets X₁, ..., X₂₄, where X_i contains the CGH measurements on chromosome i. A fused lasso penalty is used on each data set. The goal is to identify correlated regions of gain and loss across the entire genome.

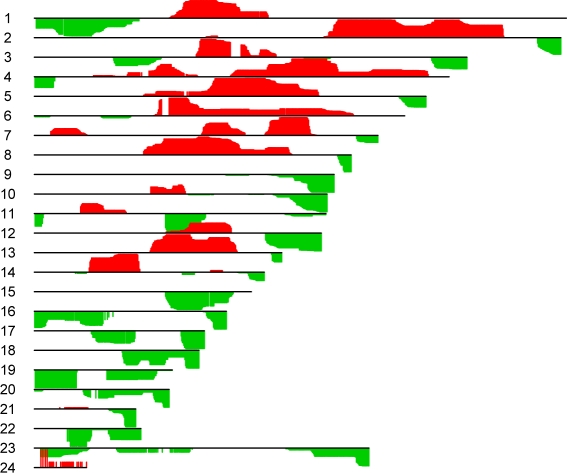
This method is applied to the DLBCL data set mentioned previously. We first denoise the samples by applying the fused lasso to each sample individually, as in Tibshirani & Wang (2008). We then perform sparse mCCA on the resulting smoothed CGH data. The canonical vectors that result are shown in Figure 5. From the figure, one can conclude that complex patterns of gain and loss tend to co-occur. It is unlikely that a single sample would display the entire pattern found; however, samples with large values in the canonical variables most likely contain some of the patterns shown in the figure.

Figure 5:

Sparse mCCA was performed on the DLBCL copy number data, treating each chromosome as a separate “data set”, in order to identify genomic regions that are coamplified and/or codeleted. The canonical vectors w₁, ..., w₂₄ are shown. Positive values of the canonical vectors are shown in red, and negative values are in green.

4. Sparse supervised CCA

In Section 2.4, we determined that on the lymphoma data, many of the canonical variables obtained using sparse CCA are highly associated with tumor subtype (and for some chromosomes, the canonical variables are also associated with survival time). Though an outcome was available, we took an unsupervised approach in performing sparse CCA. In this section, we will develop a framework to directly make use of an outcome in sparse CCA. Our method for sparse supervised CCA (sparse sCCA) is closely related to the supervised principal components analysis (supervised PCA) method of Bair & Tibshirani (2004) and Bair et al. (2006), and so we begin with an overview of that method.

4.1. Supervised PCA

Principal components regression (PCR; see e.g. Massy 1965) is a method for predicting an outcome y ∈ $\mathbb{\text{R}}$ⁿ from a data matrix X ∈ $\mathbb{\text{R}}$^n×p. Assume that the columns of X have been standardized. Then, PCR involves regressing y onto the first few columns of XV, where X = UDV^T is the singular value decomposition of X. Since V is estimated in an unsupervised manner, it is not guaranteed that the first few columns of XV will predict y well, even if some of the features in X are correlated with y.

Bair & Tibshirani (2004) and Bair et al. (2006) propose the use of supervised PCA, which is a semisupervised approach. Their method can be described simply:

1. On training data, the features that are most associated with the outcome y are identified.

2. PCR is performed using only the features identified in the previous step.

Theoretical results regarding the performance of this method under a latent variable model are presented in Bair et al. (2006).

4.2. The sparse supervised CCA method

Suppose that a quantitative outcome is available; that is, we have y ∈ $\mathbb{\text{R}}$ⁿ in addition to X₁ and X₂. Then we might seek linear combinations of the variables in X₁ and X₂ that are highly correlated with each other and associated with the outcome.

We define the criterion for supervised CCA as follows:

$$\begin{array}{ll}{\text{maximize}}_{{\text{w}}_1,{\text{w}}_2}& {\text{w}}_1^T{\text{X}}_1^T{\text{X}}_2{\text{w}}_2 \text{subject} \text{to} \parallel {\text{w}}_1{\parallel }^2\le 1,\parallel {\text{w}}_2{\parallel }^2\le 1,\\ & w_{1j}=0\forall j\notin Q_1,w_{2j}=0\forall j\notin Q_2\end{array}$$ (19)

where Q₁ is the set of features in X₁ that are most correlated with y, and Q₂ is the set of features in X₂ that are most correlated with y. The number of features in Q₁ and Q₂, or alternatively the correlation threshold for features to enter Q₁ and Q₂, can be treated as a tuning parameter or can simply be fixed. If X₁ = X₂, then the criterion (19) simplifies to supervised PCA; that is, w₁ and w₂ are equal to each other and to the first principal component of the subset of the data containing only the features that are most associated with the outcome.

sCCA can be easily extended to give sparse sCCA,

$$\begin{array}{ll}{\text{maximize}}_{{\text{w}}_1,{\text{w}}_2}& {\text{w}}_1^T{\text{X}}_1^T{\text{X}}_2{\text{w}}_2 \text{subject} \text{to} \parallel {\text{w}}_1{\parallel }^2\le 1,\parallel {\text{w}}_2{\parallel }^2\le 1,P_1({\text{w}}_1)\le c_1,\\ & P_2({\text{w}}_2)\le c_2,w_{1j}=0\forall j\notin Q_1,w_{2j}=0\forall j\notin Q_2,\end{array}$$ (20)

where as usual, P₁ and P₂ are convex penalty functions.

We have discussed the possibility of y being a quantitative outcome (e.g. tumor diameter), but other options exist as well. For instance, y could be a time to event (e.g. a possibly censored survival time) or a class label (for instance, DLBCL subtype). Our definition of sparse sCCA must be generalized in order to accommodate other outcome types. If y is a survival time, then for each feature, we can compute the score statistic (or Cox score) for the univariate Cox proportional hazards model that uses that feature to predict the outcome. Only features with sufficiently high (absolute) Cox scores will be in the sets Q₁ and Q₂. In the case of a multiple class outcome, only features with a sufficiently high F-statistic for a one-way ANOVA will be in Q₁ and Q₂. Other outcome types could be incorporated in an analogous way. The algorithm for sparse sCCA can be written as follows:

Algorithm for sparse sCCA:

1. Let X͂₁ and X͂₂ denote the submatrices of X₁ and X₂ consisting of the features in Q₁ and Q₂. Q₁ and Q₂ are calculated as follows:

   1. In the case of an L₁ penalty on w_i, Q_i is the set of indices of the features in X_i that have highest univariate association with the outcome.
   2. In the case of a fused lasso penalty on w_i, the vector of univariate associations between the features in X_i and the outcome is smoothed using the fused lasso. The resulting smoothed vector is thresholded to obtain the desired number of nonzero cofficients. Q_i contains the indices of the coefficients that are nonzero after thresholding.

2. Perform sparse CCA using data X͂₁ and X͂₂.

Note that the fused lasso case is treated specially because one wishes for the features included in X͂_i to be contiguous, so that smoothness in the resulting w_i weights will translate to smoothness in the weights of the original variable set. Algorithms for tuning parameter selection and assessment of significance, as well as a method for obtaining multiple canonical vectors, are given in the Appendix.

We explore the performance of sparse sCCA with a quantitative outcome on a toy example. Data are generated according to the model

$${\text{X}}_1=\text{u}{\text{w}}_1^T+{\epsilon }_1, {\text{X}}_2=\text{u}{\text{w}}_2^T+{\epsilon }_2, \text{y}=\text{u},$$ (21)

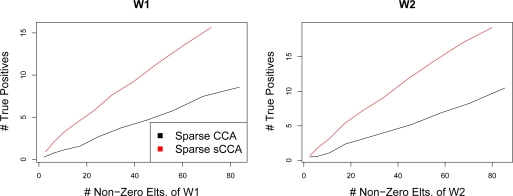
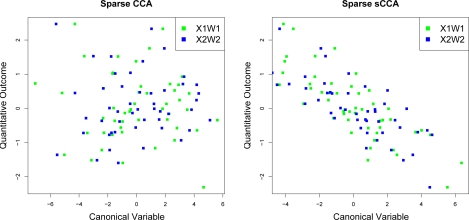
with u ∈ $\mathbb{\text{R}}$⁵⁰, w₁ ∈ $\mathbb{\text{R}}$⁵⁰⁰, w₂ ∈ $\mathbb{\text{R}}$¹⁰⁰⁰, ɛ₁ ∈ $\mathbb{\text{R}}$^50×500, ɛ₂ ∈ $\mathbb{\text{R}}$^50×1000. 50 elements of w₁ and 100 elements of w₂ are non-zero. The first canonical vectors of sparse CCA and sparse sCCA (using L₁ penalties) were computed for a range of values of c₁ and c₂. In Figure 6, the resulting number of true positives (features that are nonzero in w₁ and w₂ and also in the estimated canonical vectors) are shown on the y-axis, as a function of the number of nonzero elements of the canonical vectors. It is clear that greater numbers of true positives are obtained when the outcome is used. In Figure 7, the canonical variables obtained using sparse CCA and sparse sCCA are plotted against the outcome. The canonical variables obtained using sparse sCCA are correlated with the outcome, and those obtained using sparse CCA are not. Note that under the model (21), in the absence of noise, the canonical variables are proportional to u; therefore, sparse sCCA more accurately uncovers the true canonical variables.

Figure 6:

Sparse CCA and sparse sCCA were performed on a toy example, for a range of values of the tuning parameters in the sparse CCA criterion. The number of true positives in w₁ and w₂ is shown as a function of the number of nonzero elements in the estimates of the canonical vectors.

Figure 7:

Sparse CCA and sparse sCCA were performed on a toy example. The canonical variables obtained using sparse sCCA are highly correlated with the outcome; those obtained using sparse CCA are not.

In theory, one could choose Q₁ and Q₂ in Step 1 of the sparse sCCA algorithm to contain fewer than n features; then, ordinary CCA could be performed instead of sparse CCA in Step 2. However, we recommend using a less stringent cutoff for Q₁ and Q₂ in Step 1, and instead performing further feature selection in Step 2 via sparse CCA.

4.3. Connection with sparse mCCA

Given X₁, X₂, and a two-class outcome y, one could perform sparse mCCA by treating y as a third data set. This would yield a different but related method for performing sparse sCCA in the case of a two-class outcome.

Note that the outcome y is a matrix in $\mathbb{\text{R}}$^n×1. We code the two classes (of n₁ and n₂ observations, respectively) as $\frac{\lambda }{n_1}$ and $-\frac{\lambda }{n_2}$. Assume that the columns of X₁ and X₂ have mean zero and pooled within-class standard deviation equal to one. Consider the sparse mCCA criterion with L₁ penalties, applied to data sets X₁, X₂, and y:

$$\begin{array}{ll}{\text{maximize}}_{{\text{w}}_1,{\text{w}}_2,{\text{w}}_3}& {\text{w}}_1^T{\text{X}}_1^T{\text{X}}_2{\text{w}}_2+{\text{w}}_1^T{\text{X}}_1^T\text{y}{\text{w}}_3+{\text{w}}_2^T{\text{X}}_2^T\text{y}{\text{w}}_3\\ & \text{subject} \text{to} \parallel {\text{w}}_i{\parallel }^2\le 1,\parallel {\text{w}}_i{\parallel }_1\le c_i\forall i.\end{array}$$ (22)

Note that since w₃ ∈ $\mathbb{\text{R}}$¹, it follows that w₃ = 1. So we can re-write the criterion (22) as

$$\begin{array}{l}{\text{maximize}}_{{\text{w}}_1,{\text{w}}_2}{\text{w}}_1^T{\text{X}}_1^T{\text{X}}_2{\text{w}}_2+{\text{w}}_1^T{\text{X}}_1^T\text{y}+{\text{w}}_2^T{\text{X}}_2^T\text{y}\\ \text{subject} \text{to} \parallel {\text{w}}_1{\parallel }^2\le 1,\parallel {\text{w}}_2{\parallel }^2\le 1,\parallel {\text{w}}_1{\parallel }_1\le c_1,\parallel {\text{w}}_2{\parallel }_1\le c_2.\end{array}$$ (23)

Now, this criterion is biconvex and leads naturally to an iterative algorithm. However, this is not the approach that we take with our sparse sCCA method. Instead, notice that

$${\text{w}}_1^T{\text{X}}_1^T\text{y}=\lambda {({\overline{\text{X}}}_{11}-{\overline{\text{X}}}_{12})}^T{\text{w}}_1=\lambda \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}{\text{t}}_1^T{\text{w}}_1,$$ (24)

where X̄_1k ∈ $\mathbb{\text{R}}$^p is the mean vector of the observations in X₁ that belong to class k, and where t₁ ∈ $\mathbb{\text{R}}$^p is the vector of two-sample t-statistics testing whether the classes defined by y have equal means within each feature of X₁. Similarly, ${\text{w}}_2^T{\text{X}}_2^T\text{y}=\lambda \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}{\text{t}}_2^T{\text{w}}_2$ for t₂ defined analogously. So we can rewrite (23) as

$$\begin{array}{l}{\text{maximize}}_{{\text{w}}_1,{\text{w}}_2}{\text{w}}_1^T{\text{X}}_1^T{\text{X}}_2{\text{w}}_2+\lambda \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}({\text{t}}_1^T{\text{w}}_1+{\text{t}}_2^T{\text{w}}_2)\\ \text{subject} \text{to} \parallel {\text{w}}_1{\parallel }^2\le 1,\parallel {\text{w}}_2{\parallel }^2\le 1,\parallel {\text{w}}_1{\parallel }_1\le c_1,\parallel {\text{w}}_2{\parallel }_1\le c_2.\end{array}$$ (25)

As λ increases, the elements of w₁ and w₂ that correspond to large |t₁| and |t₂| values increase in absolute value relative to those that correspond to smaller |t₁| and |t₂| values.

Rather than adopting the criterion (25) for sparse sCCA, our sparse sCCA criterion results from assigning nonzero weights only to the elements of w₁ and w₂ corresponding to large |t₁| and |t₂|. We prefer our proposed sparse sCCA algorithm because it is simple, generalizes to the supervised PCA method when X₁ = X₂, and extends easily to non-binary outcomes.

4.4. Application of sparse sCCA to DLBCL data

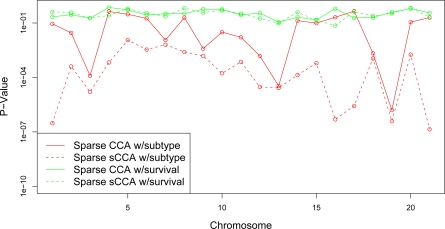
We evaluate the performance of sparse sCCA on the DLBCL data set, in terms of the association of the resulting canonical variables with the survival and subtype outcomes. We repeatedly split the observations into training and test sets (75% / 25%). Let ( ${\text{X}}_1^{\mathit{\text{train}}}$, ${\text{X}}_2^{\mathit{\text{train}}}$, y^train) denote the training data, and let ( ${\text{X}}_1^{\mathit{\text{test}}}$, ${\text{X}}_2^{\mathit{\text{test}}}$, y^test) denote the test data. (y can denote either the survival time or the cancer subtype.) We perform sparse sCCA analysis on the training data. As in Section 2.4, for each chromosome, sparse sCCA is run using CGH measurements on that chromosome, and all available gene expression measurements. An L₁ penalty is applied to the expression data, and a fused lasso penalty is applied to the CGH data. Let ${\text{w}}_1^{\mathit{\text{train}}}$, ${\text{w}}_2^{\mathit{\text{train}}}$ denote the canonical vectors obtained. We then use ${\text{X}}_1^{\mathit{\text{test}}}{\text{w}}_1^{\mathit{\text{train}}}$ and ${\text{X}}_2^{\mathit{\text{test}}}{\text{w}}_2^{\mathit{\text{train}}}$ as features in a Cox proportional hazards model or a multinomial logistic regression model to predict y^test. The resulting p-values are shown in Figure 8 for both the survival and subtype outcomes; these are compared to the results obtained if the analysis is repeated using unsupervised sparse CCA on the training data. On the whole, for the subtype outcome, the p-values obtained using sparse sCCA are much smaller than those obtained using sparse CCA. The canonical variables obtained using sparse CCA and sparse sCCA with the survival outcome are not significantly associated with survival. In this example, sparse CCA was performed so that 20% of the features in X₁ and X₂ were contained in Q₁ and Q₂ in the sparse sCCA algorithm.

Figure 8:

On a training set, sparse CCA and sparse sCCA were performed using CGH measurements on a single chromosome, and all available gene expression measurements. The resulting test set canonical variables were used to predict survival time and DLBCL subtype. Median p-values (over training set / test set splits) are shown.

5. Discussion

As it becomes more commonplace for biomedical researchers to perform multiple assays on the same set of patient samples, methods for the integrative analysis of two or more high-dimensional data sets will become increasingly important. The sparse CCA methods previously proposed in the literature (Parkhomenko et al. 2007, Waaijenborg et al. 2008, Parkhomenko et al. 2009, Le Cao et al. 2009, Witten et al. 2009) provide an attractive framework for performing an integrative analysis of two data sets. In this paper, we have developed extensions to sparse CCA that can be used to apply the method to the case of more than two data sets, and to incorporate an outcome into the analysis.

The methods proposed in this paper will be available on CRAN as part of the PMA (Penalized Multivariate Analysis) package.

APPENDIX.

A Tuning parameter selection and calculation of p-values

We first present a permutation-based algorithm for selection of tuning parameters and calculation of p-values for sparse CCA. Note that a number of methods have been proposed in the literature for selecting tuning parameters for sparse CCA (see e.g. Waaijenborg et al. 2008, Parkhomenko et al. 2009, Witten et al. 2009). The method proposed here has the advantage over the proposals of Waaijenborg et al. (2008) and Parkhomenko et al. (2009) that it does not require splitting a possibly small set of samples into a training set and a test set. Witten et al. (2009) present a method for tuning parameter selection for their penalized matrix decomposition; however, it does not extend in a straightforward way to the sparse CCA case.

Algorithm to select tuning parameters and determine significance for sparse CCA:

1. For each tuning parameter value (generally this will be a two-dimensional vector) T_j being considered:

   1. Compute w₁ and w₂, the canonical vectors using data X₁ and X₂ and tuning parameter T_j. Compute d_j = Cor(X₁w₁, X₂w₂).
   2. For i ∈ 1, ..., N, where N is some large number of permutations:

      1. Permute the rows of X₁ to obtain the matrix ${\text{X}}_1^i$, and compute canonical vectors ${\text{w}}_1^i$ and ${\text{w}}_2^i$ using data ${\text{X}}_1^i$ and X₂ and tuning parameter T_j.
      2. Compute $d_j^i=\text{Cor}({\text{X}}_1^i{\text{w}}_1^i,{\text{X}}_2{\text{w}}_2^i)$.
   3. Calculate the p-value $p_j=\frac{1}{N}{\sum }_{i=1}^N{1}_{d_j^i\ge d_j}$.

2. Choose the tuning parameter T_j corresponding to the smallest p_j. Alternatively, one can choose the tuning parameter T_j for which $(d_j-\frac{1}{N}{\sum }_i{d}_j^i)/\text{sd}(d_j^i)$ is largest, where sd ( $d_j^i$) indicates the standard deviation of $d_j^1,\dots ,d_j^N$. The resulting p-value is p_j.

Since multiple tuning parameters T_j are considered in the above algorithm, a strict cut-off for the p-value p_j should be used in order to avoid problems associated with multiple testing.

Given the above algorithm, the analogous method for selecting tuning parameters and determining significance for sparse sCCA is straightforward. For simplicity, we assume that the threshold for features to enter Q₁ and Q₂ in the sparse sCCA algorithm is fixed (not a tuning parameter).

Algorithm to select tuning parameters and determine significance for sparse sCCA:

1. For each tuning parameter (generally this will be a two-dimensional vector) T_j being considered:

   1. Compute w₁ and w₂, the supervised canonical vectors using data X₁, X₂, and y and tuning parameter T_j. Compute d_j = Cor(X₁w₁,X₂w₂).
   2. For i ∈ 1, ..., N, where N is some large number of permutations:

      1. Permute the rows of X₁ and X₂ separately to obtain the matrices ${\mathbf{\text{X}}}_1^i$ and ${\mathbf{\text{X}}}_2^i$, and compute supervised canonical vectors ${\mathbf{\text{w}}}_1^i$ and ${\mathbf{\text{w}}}_2^i$ using data ${\mathbf{\text{X}}}_1^i$, ${\mathbf{\text{X}}}_2^i$, y, and tuning parameter T_j.
      2. Compute $d_j^i=\text{Cor} ({\mathbf{\text{X}}}_1^i{\mathbf{\text{w}}}_1^i,{\mathbf{\text{X}}}_2^i{\mathbf{\text{w}}}_2^i)$.
   3. Calculate the p-value $p_j=\frac{1}{N}{\sum }_{i=1}^N{1}_{d_j^i\ge d_j}$.

2. Choose the tuning parameter T_j corresponding to the smallest p_j. Alternatively, one can choose the tuning parameter T_j for which $(d_j-\frac{1}{N}{\sum }_i{d}_j^i)/\text{sd}(d_j^i)$ is largest, where sd ( $d_j^i$) indicates the standard deviation of $d_j^1,\dots ,d_j^N$. The resulting p-value is p_j.

Note that in the permutation step, we permute the rows of X₁ and X₂ without permuting y; this means that under the permutation null distribution, y is not correlated with the columns of X₁ and X₂.

We can similarly use the following permutation-based algorithm to assess the significance of the canonical vectors obtained using sparse mCCA:

Algorithm to select tuning parameters and determine significance for sparse mCCA:

1. For each tuning parameter (generally this will be a K-dimensional vector) T_j being considered:

   1. Compute w₁, ..., w_K, the canonical vectors using data X₁, ..., X_K and tuning parameter T_j. Compute d_j = ∑_s<t Cor (X_sw_s, X_tw_t).
   2. For i ∈ 1, ..., N, where N is some large number of permutations:

      1. Permute the rows of X₁, ..., X_K separately to obtain the matrices ${\mathbf{\text{X}}}_1^i,\dots ,{\mathbf{\text{X}}}_K^i$, and compute canonical vectors ${\mathbf{\text{w}}}_1^i,\dots ,{\mathbf{\text{w}}}_K^i$ using data ${\mathbf{\text{X}}}_1^i,\dots ,{\mathbf{\text{X}}}_K^i$ and tuning parameter T_j.
      2. Compute $d_j^i={\sum }_{s<t}\text{Cor} ({\mathbf{\text{X}}}_s^i{\mathbf{\text{w}}}_s^i,{\mathbf{\text{X}}}_t^i{\mathbf{\text{w}}}_t^i)$.
   3. Calculate the p-value $p_j=\frac{1}{N}{\sum }_{i=1}^N{1}_{d_j^i\ge d_j}$.

2. Choose the tuning parameter T_j corresponding to the smallest p_j. Alternatively, one can choose the tuning parameter T_j for which $(d_j-\frac{1}{N}{\sum }_i{d}_j^i)/\text{sd}(d_j^i)$ is largest, where sd ( $d_j^i$) indicates the standard deviation of $d_j^1,\dots ,d_j^N$. The resulting p-value is p_j.

B Extension of methods to obtain multiple canonical vectors

We first review the method of Witten et al. (2009) for obtaining multiple sparse CCA canonical vectors. Note that the sparse CCA algorithm uses the cross-product matrix $\mathbf{\text{Y}}={\mathbf{\text{X}}}_1^T{\mathbf{\text{X}}}_2$ and does not require knowledge of X₁ and X₂ individually.

Algorithm for obtaining J sparse CCA factors:

1. Let ${\mathbf{\text{Y}}}^1\leftarrow {\mathbf{\text{X}}}_1^T{\mathbf{\text{X}}}_2$.

2. For j ∈ 1, ..., J:

   1. Compute ${\mathbf{\text{w}}}_1^j$ and ${\mathbf{\text{w}}}_2^j$ by applying the single-factor sparse CCA algorithm to data Y^j.
   2. ${\mathbf{\text{Y}}}^{j+1}\leftarrow {\mathbf{\text{Y}}}^j-({\mathbf{\text{w}}}_1^{j^T}{\mathbf{\text{Y}}}^j{\mathbf{\text{w}}}_2^j){\mathbf{\text{w}}}_1^j{\mathbf{\text{w}}}_2^{j^T}$.

3. ${\mathbf{\text{w}}}_1^j$ and ${\mathbf{\text{w}}}_2^j$ are the j^th canonical vectors.

To obtain J sparse sCCA factors, submatrices X͂₁ and X͂₂ are formed from the features most associated with the outcome; the algorithm for obtaining J sparse CCA factors is then applied to this new data.

To obtain J sparse mCCA factors, note that the sparse mCCA algorithm requires knowledge only of the ( $\begin{array}{c}K\\ 2\end{array}$) cross-product matrices of the form ${\mathbf{\text{X}}}_s^T{\mathbf{\text{X}}}_t$ with s < t, rather than the raw data X_s and X_t.

Algorithm for obtaining J sparse mCCA factors:

1. For each 1 ≤ s < t ≤ K, let ${\mathbf{\text{Y}}}_{st}^1\leftarrow {\mathbf{\text{X}}}_s^T{\mathbf{\text{X}}}_t$.

2. For j ∈ 1, ..., J:

   1. Compute ${\mathbf{\text{w}}}_1^j,\dots ,{\mathbf{\text{w}}}_K^j$ by applying the single-factor sparse mCCA algorithm to data ${\mathbf{\text{Y}}}_{st}^j$ for 1 ≤ s < t ≤ K.
   2. ${\mathbf{\text{Y}}}_{st}^{j+1}\leftarrow {\mathbf{\text{Y}}}_{st}^j-({\mathbf{\text{w}}}_s^{j^T}{\mathbf{\text{Y}}}_{st}^j{\mathbf{\text{w}}}_t^j){\mathbf{\text{w}}}_s^j{\mathbf{\text{w}}}_t^{j^T}$.

3. ${\mathbf{\text{w}}}_1^j,\dots ,{\mathbf{\text{w}}}_K^j$ are the j^th canonical vectors.