A Bayesian Analysis Strategy for Cross-Study Translation of Gene Expression Biomarkers

Abstract

We describe a strategy for the analysis of experimentally derived gene expression signatures and their translation to human observational data. Sparse multivariate regression models are used to identify expression signature gene sets representing downstream biological pathway events following interventions in designed experiments. When translated into in vivo human observational data, analysis using sparse latent factor models can yield multiple quantitative factors characterizing expression patterns that are often more complex than in the controlled, in vitro setting. The estimation of common patterns in expression that reflect all aspects of covariation evident in vivo offers an enhanced, modular view of the complexity of biological associations of signature genes. This can identify substructure in the biological process under experimental investigation and improved biomarkers of clinical outcomes. We illustrate the approach in a detailed study from an oncogene intervention experiment where in vivo factor profiling of an in vitro signature generates biological insights related to underlying pathway activities and chromosomal structure, and leads to refinements of cancer recurrence risk stratification across several cancer studies.

1. Introduction

The routine use of gene expression microarrays in experimental studies on cultured human cells and cancer cells lines has escalated the ability to generate data on changes in genome-wide expression levels of genes under widely varying conditions. In vitro intervention experiments are increasingly coupled with studies to evaluate patterns of expression of resulting sets of genes within in vivo contexts, such as human cancer data sets. The interest lies in linking the biological pathways responding to in vitro interventions to real-world biological variation and outcomes [e.g. 1, 5, 12, 17, 18]. A set of apparently differentially expressed genes together with numerical summaries of the activation of those genes is commonly referred to as a signature of the intervention. The translation of experimentally derived signatures to observational data can help to establish links between the measured signature and observed phenotypes such as disease status, drug responses, mutations, survival profiles, etc. [e.g. 1, 17]. However, effecting this translation raises challenging questions of calibration of data between contexts, and of potentially major differences in the complexity of biological activity between cells in culture and living organisms. The highly controlled settings of designed experiments often result in narrow characterization of biological activity that is unlikely to fully represent the various sources of variability present in vivo. We have found utility in applying sparse regression and latent factor models in an overall strategy to address this core problem faced in many translational biomedical studies.

We focus here on cancer genomics, where gene expression biomarkers arising from experimental comparisons, whether in vitro laboratory studies or controlled animal models, hold promise as biomarkers of oncogenic states in human populations. Sparse multivariate regression models are useful in the identification of signatures in controlled experiments. Flexible evaluation of the complexity of patterns of association underlying signature genes when translated to observational contexts can then be carried out using non-Gaussian sparse latent factor models [2]. This allows for evaluation of the potentially increased structure evident in transcriptionally activated signature genes in the in vivo context, as well as more extensive evaluations using additional genes not identified in the in vitro signature but apparently linked into the broader biological network of intersecting pathways playing roles in vivo. The latter concept can be effectively addressed using iterative, evolutionary refinement of latent factor models to successively explore and expand the analysis around an initial signature gene set. Our detailed application involves translational analysis of the signature of over-expression of the Myc oncogene, with data arising from an earlier in vitro study of the effects of interventions to over-express several oncogenes in cultured cells [1, 13]. This example illustrates the methodological strategy, and highlights the potential for in vivo factor profiling of in vitro signatures to both improve the prognostic value of such signatures as biomarkers of clinical outcomes and generate biological insights in a cancer genomics context.

2. Example: Markers of Myc Overexpression

Our example study concerns the expression profiling of biological activities related to the Myc gene, and we use this context here to convey the methodology using sparse statistical modeling for the integration of in vitro and in vivo data and translational analysis. Myc is a transcription factor known to be involved in numerous biological pathways including cell proliferation, cell growth, apoptosis, cellular differentiation and stem cell renewal; it is also a well-known oncogene involved in many types of human cancers [6, 20, 23]. Improved understanding of the roles of Myc and its numerous influences in cancer will rely in part on improved understanding of the Myc pathway – its transcriptional target genes and the many genes involved in interacting biological function downstream of Myc.

Studies of molecular pathways in cancer, as in other areas, increasingly focus on experiments to define microarray-based expression signatures of activation or deregulation of selected genes via targeted interventions on those genes. In [1], Myc was one of 9 oncogenes investigated in such experiments on cultured human mammary epithelial cells. In each single experiment, higher than normal levels of one oncogene were induced; following a period of cell growth gene expression profiles were generated on Affymetrix microarrays. Each intervention was replicated several times, and several control samples with no intervention were also generated; see [1] and [15] for further details and some summary analyses.

For our purposes here, this study design is a nice example of a one-way layout with replication and a multivariate response, for which sparse multivariate regression analysis is appropriate (section 3). Further, given the importance of Myc in breast cancer (among other cancers), we are naturally interested in studying the translation of Myc pathway signatures into human breast data, and have available a number of relevant expression data sets from breast cancer to develop the translational analysis.

3. Sparse Regression Modeling

3.1. General Framework

In an experimental context such as above, let x_g,i be the measured expression level (on a traditional log₂ scale) of gene g = 1, . . ., p on sample i = 1, . . ., n, assumedly independent across the n samples. The multivariate regression model for the p × 1 vector x_i = (x_1,i, . . ., x_p,i)′ is

$$\begin{array}{cc}{x}_i=\mu +B{h}_i+v_i& i=1:n,\end{array}$$ (1)

where μ is the p–vector of baseline expression levels μ_g, h_i is the r × 1 vector of known covariates, B is the p × r matrix of regression coefficients with elements β_g,j and ν_i is the p–vector of gene-specific noise terms ν_g,i with individual normal error variances ψ_g. Note that by fitting the entire vector x_i jointly, rather than an independent analysis for each, we are able to learn about the underlying distribution of the β_g,j. In the case of sparse regression, this allows us to fit the probability that any particular β_g,j = 0 based on the overall rate of zero coefficients.

The two key types of covariates most relevant here are dummy variables reflecting the experimental design (section 3.2) and observed values of expression variables that are often useful to adjust for experimental artifacts (section 3.3).

3.2. Regression with Design Factors

In a context such as the oncogene experiment example of section 2, each h_i contains dummy variables indicating design factors. One example in the study in [27] concerns a cross-classified design with multiple interactions of interest, while the oncogene experiment is a simple one-way layout. In the oncogene example, take j = 1, . . ., 9 to indicate the 9 oncogene design factors, with Myc being j = 1. Then, β_g,1 is the average change in expression of gene g due to Myc over-expression, and h_i,1 = 1 for samples i that received the Myc over-expression intervention, with h_i,1 = 0 otherwise.

3.3. Covariates for Normalization and Artifact Control

Gene expression data often shows evidence of both marked and subtle study or data collection effects (such as time of data collection, chip batch, small effects of variations in experimental conditions, etc). If the microarray used has built-in control gene sequences, such as in the case of Affymetrix housekeeping gene sets or spiked-in genes on custom arrays, the resulting expression readouts of such probe sequences can often be useful to assess variation that can then be attributed, primarily, to experimental artifacts. For example, [15] and [2] use several principal components from the expression data on multiple housekeeping and spiked-in genes as covariates for this purpose, and give some examples of their utility. This fits into the general model of equation (1) where h_i now contains values of these assay artifact correction covariates, and the corresponding β_g,j represent the impact of these control terms on expression of each gene.

3.4. Sparsity Priors

In experiments such as the oncogene example, the vast majority of genes are not expected to show changes in expression at all as a response to any particular intervention. Any subset that does show significant changes will represent a signature gene set for that intervention, but the biological expectation is that such subsets will represent only a small part of the tens of thousands of genes in the data. This is reflected in standard Bayesian variable selection priors, or sparsity priors [15] that explicitly allow many zero values among the β_g,j. In particular, the analysis adopts priors under which:

• Each β_g,j may be zero, controlled by some uncertain base-rate of non-zero values that is related to the design factor or covariate j, and the posterior analysis estimates that base-rate to assess the overall sparsity of effects on covariate j.

• Non-zero β_g,j values come from a prior N(0,τ_j) that is also specific to covariate j, and with an inverse-gamma prior on τ_j that governs the likely scale of actual effects on expression of gene g.

• Posterior analysis produces inferences on sparsity and gene-specific effect via, among other things, posterior estimates of the sparsity probabilities

  $${\pi }_{g,j}^{*}=\text{Pr}({\beta }_{g,j}\ne 0|X)$$ (2)

  where X = (x₁, . . ., x_n) is the observed data. Importantly, analysis automatically induces shrinkage effects that shrink each ${\pi }_{g,j}^{*}$ towards the estimated underlying base-rate for covariate j, thus naturally and automatically adjusting for the multiple tests that are implicitly being made.

• Posterior analysis produces inferences on non-zero coefficients in terms of summaries of p(β_g,j|X, β_g,j ≠ 0) for each g, j, including posterior means ${\beta }_{g,j}^{*}=E({\beta }_{g,j}|X,{\beta }_{g,j}\ne 0)$.

• Posterior analysis produces inferences on other model parameters including the residual variances ψ_g = V (ν_g,i).

Full mathematical details are given in [15] and also [2].

The probabilities ${\pi }_{g,j}^{*}$ are simply central to investigating the implications of an analysis. In the oncogene intervention experiment example, identifying genes g for which ${\pi }_{g,1}^{*}$ is large (if any) focuses on candidates for Myc signature genes – genes that are apparently significantly changed in expression as a result of Myc over-expression. Choosing a threshold on these probabilities allows us to select a smaller group of signature genes for translational analysis. The ${\beta }_{g,j}^{*}$ then allow study of the relative impact of the covariate on expression changes gene by gene within any selected signature set.

3.5. Signature Scores

A signature score is a single numerical summary of the gene expression response of a set of signature genes in an experimental context such as above. In the oncogene experiment, each intervention oncogene generates a signature gene set – some selected subset of genes showing significant expression changes – and an average of the expression values on that set provides a simple overall measure of the level of activation of the underlying pathway. Thus, for example, we can estimate Myc signature scores on each of a set of breast cancer samples. The dominant principal component of signature gene sets (earlier referred to as a metagene) has been widely used, as have simple equally weighted averages. [e.g. 5, 12, 17, 33]. This direct projection of signature scores has been fundamental to studies of pathway deregulation in vivo and also emerging drug response studies [e.g. 1].

Our over-riding goal in this paper is to promote a broader view of the statistical complexity of this enterprise of signature translation from in vitro to in vivo contexts, and the importance of a refined statistical strategy. As part of this, projected signature scores are needed for comparison with the results of the refined statistical approach. The specific choice of weighting of genes to define a score is a minor consideration; we use a definition arising from the sparse regression model used to analyze the experimental data.

In the model of equation (1) applied to the one-way layout of the oncogene experiment, consider an hypothetical further sample x_* and ask about the level of Myc pathway activation that sample seems to reflect. A comparison of whether x_* appears to be a Myc upregulated sample compared to a normal, control sample would involve comparison of corresponding covariate vectors h_* with h_*,1 = 1 compared to h_*,1 = 0, and for which h_*,j = 0 for the other design factors j ≠ 1. Probabilistic assessment involves the likelihood ratio p(x_*|h_* = (1, 0, . . .)′)/p(x_*|h_* = 0) which turns out to be an increasing function of ${\sum }_{g=1}^p{\beta }_{g,1}{x}_{g,*}/{\psi }_g$, a natural weighted average of expression across genes. This leads to the general definition of signature score for each design factor j as

$$s_j^{*}=\sum _{g=1}^p{\pi }_{g,j}^{*}{\beta }_{g,j}^{*}{x}_{g,*}/{\psi }_g^{*}$$ (3)

using posterior mean estimates of parameters, i.e., $E({\beta }_{g,j}|X)={\pi }_{g,j}^{*}{\beta }_{g,j}^{*}$ and ${\psi }_g^{*}=E({\psi }_g|X)$. In practice, it is typical that many of the sparsity probabilities ${\pi }_{g,j}^{*}$ are, for any design factor j, very small, so that restricting the sum in equation (3) to only a smaller, selected signature gene set for which probabilities exceed some high threshold will suffice. Note also that, in models with other covariates that are not part of the intervention – such as the experimental assay artifact terms discussed above – the above definition will be applied to adjusted data that replaces x_g,* in equation (3) with corrected values obtained by subtracting the regression on those covariates with corresponding ${\beta }_{g,j}^{*}$ coefficients.

4. Nonparametric Latent Factor Models

4.1. General Framework

Latent factor models [14, 32], either alone or as components of more elaborate latent factor regression models [2, 15] have found use in representing multiple, interacting patterns of association among genes in observational expression data sets in a number of studies. In considering the expression patterns in an observational setting, sparse latent factor models can: (a) represent all significant aspects of covariation in the data, (b) identify interconnections between subsets of genes through estimated gene-factor relationships, with opportunity to relate these statistical relationships to underlying biological pathways, and (c) identify genes that are simply not expressed, or not apparent, in vivo, among other things. These models provide a means to address the core question of interest in this paper: increasing the understanding of concordance, or lack of concordance, of an experimentally defined expression biomarker with expression patterns realized in vivo.

Consider an observational expression data set such as expression profiles on a series of human breast tumors. A general latent factor regression model [2] extends equation (1) to

$$x_i=\mu +B{h}_i+A{\lambda }_i+v_i$$ (4)

where the k × 1 vector λ_i = (λ_1,i, . . ., λ_k,i)′ represents the realized values of k latent factors, and A is the p × k factor loadings matrix A = {α_g,j}.

Sparse factor models arise when A has many zero elements, and this is developed using the same Bayesian variable selection priors as for the sparse regression model in section 3.4. That is, each column of the factor loading matrix A has its own base-rate of non-zero entries, that base-rate being estimated in the analysis to generate an overall assessment of sparsity of loadings on that factor. The analysis then delivers posterior distributions that include summaries ${\pi }_{g,j}^{*},{\alpha }_{g,j}^{*}=E({\alpha }_{g,j}|X)$, now related to the regression on latent factor j rather than the known covariates as earlier. Model fitting using Markov chain Monte Carlo (MCMC) methods are nowadays standard; see [2] and the software implementation in [30]. Note also that the model of equation (4) allows the incorporation of known covariates, and the use of assay artifact control covariates, as in section 3.3, is often particularly relevant when analyzing observational data sets.

4.2. Non-Gaussian Factors

The potential for, and expectation of, non-Gaussian structure evident in observational gene expression data underlies the use of nonparametric Bayesian models for the distributions generating latent factors λ_i. This uses the standard Dirichlet process model [8, 34] that is exible and will adapt to arbitrary non-Gaussian structure. The specific class of models used is such that, for any set of m samples Λ_m = (λ₁, . . ., λ_m) from the latent factor distribution, we predict a new factor vector λ = λ_m+1 via the theoretically implied conditional distribution

$$(\lambda |{\Lambda }_m) \sim (1-a_m)N(\lambda |0,I_k)+a_m\sum _{i=1}^m{\delta }_{{\lambda }_i}(\lambda ),$$ (5)

where δ_e(·) is the Dirac delta function representing a point mass at e and a_m = 1/(α + m) and where α > 0 is the precision parameter of the underlying Dirichlet process. Model fitting is effectively standard using MCMC methods, now including learning about the uncertain Λ_1:n and α; see [2] and [30].

A key interest is predicting factor structure on new samples. Suppose a specified model of the form of equation (4) has been fitted to the sample of n observations. Equation (5) at m = n defines the prior for the factor vector on the new sample. Then, on observing the data vector x = x_n+1 on that sample we can deduce the implied conditional distribution for λ as follows. Let ○ represent all model parameters including Λ_n. Further, define z = x – μ – Bh_i, and d = DA′Ψ⁻¹z with D⁻¹ = I + A′ where Ψ = diag(ψ₁, . . ., ψ_p). Then

$$(\lambda |x,○) \sim c_{0}N(\lambda |d,D)+\sum _{i=1}^n{c}_i{\delta }_{{\lambda }_i}(\lambda )$$ (6)

where c₀ ∝ α N (z|0, AA′ + Ψ) and, for i = 1, . . ., n, c_i ∝ α N (z|Aλ_i, Ψ) subject to c₀, . . ., c_n having unit sum. Given full posterior samples of the model parameters – now including Λ_1:n and α – based on the observed data X, we can evaluate the terms defining this predictive distribution for the new λ. Approximations based on fixing parameters at estimated posterior means yield point estimates such as the directly projected vector

$${\lambda }^{*}=c_0^{*}{d}^{*}+\sum _{i=1}^n{c}_i^{*}{\lambda }_i^{*}$$ (7)

in an obvious notation.

5. Signature Factor Profiling Strategy

The strategy is as follows. For a single experimental pathway under investigation, assume an in vitro study has generated data analyzed via sparse regression modeling. This is not strictly required, as one may start with any coherent set of probes, such as a pathway list from online databases. Suppose design factor j to be the intervention of interest. Translate to an in vivo data set for analysis using sparse factor model profiling of the signature gene set as follows.

• In the experimental context, select some subset of significant genes by thresholding the ${\pi }_{g,j}^{*}$ above a cutoff. The point here is not to focus on specific genes, but a larger subset of differentially expressed genes that coordinately reflect the pathway response and will define an initial gene set for in vivo analysis. Suppose this selects q genes (in some of our examples, q runs between several tens and several hundreds).

• Fit a sparse latent factor model to these q genes using the observational data; this allows evaluation of relevant values of the number of factors k, among other things, with larger values of k reflecting higher levels of heterogeneity of the patterns of expression evident among the genes in vivo. Thus a single, one-dimensional signature of coordinate up/down expression of these genes in the controlled experimental context becomes refined to a k–dimensional estimated set of what might be referred to as in vivo subpathway signatures.

• Using theory from [2] as implemented in the BFRM software [30], iteratively refine the analysis and expand the gene set. At each refinement step, this first projects and approximately evaluates values of the gene-factor association probabilities ${\pi }_{g,j}^{*}$ for all genes g not in the current model, for each of the current factors j = 1, . . ., k. Large values of these probabilities identifies (any) genes whose expression variation across samples seems to relate to the currently estimated factors; that is, genes that seem to tie-in to the current subpathway structure evident from the current factor analysis. With a view to exploring the likely increased biological complexity of the in vivo setting, we can now add in some of the most highly scoring genes, and rerun the factor analysis. Having added in some more genes, this may well lead to an increased number of factors at the next model analysis step, with additional factors needed to reflect additional patterns of covariation in the expanded gene set.

Our biological focus is reflected in this stochastic search strategy: we are initially concerned with the expression signature of intervention on a single biological pathway, typically from an experiment on a single cell type under highly controlled and hence potentially artificial circumstances. Involvement of multiple other, intersecting biological processes will generally be evident in the observational data set. Thus (i) we will be able to identify other genes that show related expression patterns; and (ii) as we include these genes in the analysis, we are either including genes that are part of the initial pathway, but not expressed in the cell line in which the signature was defined, or including genes in intersecting pathways. This leads to the need for additional latent factors to reflect the newly observed patterns. The evolutionary model refinement process is repeated, stopping after a select number of steps or using thresholds to control the numbers of genes added, the number of factors fitted, or on the inclusion probabilities ${\pi }_{g,j}^{*}$ at each stage [2]. By restricting the termination requirements, we can control how closely the final list of factors remains to the initial set of probes, or how rich it can in principle become by exploring the biological “neighborhood” of the original in vitro response.

6. Myc Signature Profiling in Breast Cancer

6.1. Data and Signature Identification

The oncogene expression data set of [1] was analyzed using sparse regression analysis as described above; the data uses Affymetrix u133 microarrays and generated data on p = 22215 gene probesets across n = 118 samples; full details of prior specifications and MCMC analysis, including input and output text files from the analysis using the BFRM software, are recorded in the supplementary web-based material.

Our interest here is in translational analysis of the Myc signature in tissue samples excised from breast cancer patients in the normal course of therapy. One of the known etiologies for the over-expression of Myc in breast cancer is duplication of the Myc gene. For this reason, we chose to study variation in expression of the genes in this signature in a breast cancer data set from [4] which also has comparative genomic hybridization (CGH) data; the latter data allows us to examine relationships between gene copy number variation (CNV) and estimated factors, in addition to relationships between factors and various clinical phenotypes. Because the data from [4] was generated on u133a Affymetrix chips, we restrict our analysis to the probes on this chip. From among these, we identify those gene probes g for which ${\pi }_{g,1}^{*}>0.95$ and ${\pi }_{g,j}^{*}<0.25$ for all j = 2, . . ., 9. This identifies a signature gene set of q = 190 genes, each apparently strongly associated with the in vitro Myc pathway response while apparently not responding to interventions on any of the other 8 oncogenes.

6.2. Evolutionary Sparse Factor Analysis in Breast Data

The analysis evolved through a series of iterations, at each stage bringing in at most 20 additional genes most highly related to the “current” latent factors, and then exploring whether or not to add additional latent factors and re-fit the model. As with the analysis of in vitro data, details of prior specification and additional details of the evolutionary MCMC analysis, including input and output text files from the analysis using the BFRM software, are recorded in the supplementary web-based material. Thresholding the ${\pi }_{g,j}^{*}$ probabilities at 0.75 was used for both new gene inclusion and new factor inclusion; an additional factor was added to the model only when at least 15 genes showed ${\pi }_{g,j}^{*}>0.75$. The evolutionary analysis was run in the context of allowing expansion to no more than 700 genes and 20 factors. This led to a final model with 700 genes and k = 12 factors Based on this model on genes most proximally related to the Myc pathway, we can then also assess the relationships of all remaining thousands of genes with the estimated factors via the estimated ${\pi }_{g,j}^{*}$ values for all genes not included in the 700 model genes. In what follows, when then draw on this full set of probabilities over all p = 22215 genes in investigating those genes apparently related to one or more of the 12 fitted factors. These probabilities are key to exploring aspects of the fitted factor analysis and its relationships to underlying biological pathways. We refer to posterior means ${\lambda }_{j,i}^{*}$ as, simply, factor j or, the value of factor j, on sample i. Referring to the full vector of factors on sample i implicitly denotes the approximate posterior mean ${\lambda }_i^{*}$. In discussing genes related to a specific factor, we refer to genes being involved in the factor, associated with the factor and/or significantly loaded on the factor, based on ${\pi }_{g,j}^{*}>0.99$.

6.3. Factors Related to Breast Cancer Survival

Gene expression biomarkers of risk and progression are increasingly evident in clinical cancer research. To explore the possibility that some of the 12 Myc factors may have prognostic value in connection with malignancy reflected in survival outcomes, we used the 12 estimated factors as candidate covariates in Weibull survival regression models as used in early survival studies in cancer genomics [7, 26]. This used Bayesian regression model search and averaging [25] to explore the space of subset regression models, via the shotgun stochastic search approach [10]. Among other things, this produces estimated relative probabilities over all models as well as individual and pairwise inclusion probabilities for the 12 factors.

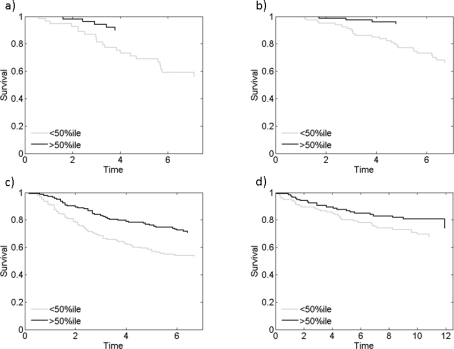
Figure 1(a) shows the stratification of the survival data into two groups, plotting the empirical survival curve for women deemed low versus high risk based on the fitted model. Specifically, we identified the median survival time in the overall, model averaged predictive survival function from the mixture over Weibull regression models; the data set was then split at this value, and the resulting Kaplan-Meier survival curves drawn for illustration. Since this is from the model fitted to this data set, we need to explore the robustness and broader validity in prediction of additional test data. We did this using three separate and, in terms of the populations sampled and clinical characteristics, heterogeneous data sets: those from [17], [22] and [31]. For each patient in each of these samples, estimated factors were predicted using equation (7), and these covariate values then used split each data set into two using precisely the same predictive median survival time from the training data analysis; results are in Figures 1(b-d). We see that the predictor consistently stratifies patients into high and low risk groups based solely on these subfactors of the Myc signature.

Figure 1:

A model averaged Weibull survival model built on the Myc factors 5 and 10 is able to differentiate high and low risk breast cancer patients. (a) shows performance on the training data set from Chen et al. (2006) (b-d) show predictive performance on three separate validation data sets from Pawitan et al. (2005), Wang et al. (2005) and Miller et al. (2005) respectively.

The Weibull regression model with the highest posterior probability involves only factors 5 and 10 (λ₅ and λ₁₀); all of the top 20 models, ordered by posterior probability, contain these two factors. Each of these factors involves ${\pi }_{g,j}^{*}>0.99$ for a large number of genes – over 1000 probes from the full set of 22215. We use the GATHER [3] biological annotation analysis in exploring such gene lists by factor; this provides an automated method for searching for associations between a given list of genes and subsets of genes from a number of databases including Gene Ontology, Medline Keywords, Medical Subject Headings, KEGG Pathways, Protein Binding, miRNA targets, Transfac and Chromosomal locations. This analysis indicates that genes in factor 5 show very high association with both protein biosynthesis and cellular metabolism functions (Gene Ontology database). This is supported by additional associations with ribosomal proteins (Medical Subject Headings database) and this factor contains 45 of the approximately 120 genes listed in the Entrez Gene (protein binding, [16]) database as interacting with the protein paxillin that is known to exhibit transcriptional over-expression in some breast cancers [29].

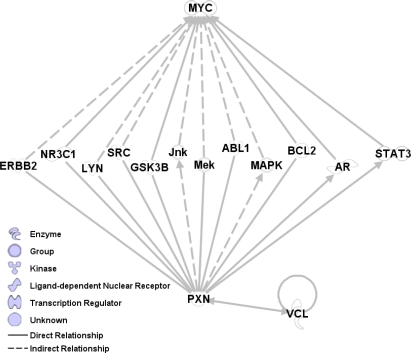
Gene ontology is a collection of functional and structural units from cellular biology, along with lists of genes associated with them and relationships between them. Examining the gene ontology of genes in factor 10, we find relationships with G-protein coupled receptor protein signalling as well as cellular metabolism. Additionally, using GATHER to compare this factor to the gene lists in the Entrez Gene database, shows association with Vinculin which is a binding partner of the Paxillin protein already noted in association with factor 5. There are many known low-order biochemical interactions between Paxillin, Vinculin, and Myc, as shown in Figure 2. Thus, we suggest that these factors represent aspects of the interaction between Myc and the protein Paxillin, along with its binding partners and genes downstream.

Figure 2:

Myc factor 5 is highly related to Paxillin (PXN) while factor 10 is related to Vinculin (VCL). Paxillin and Vinculin are known to be binding partners, and Paxillin is known to be related to Myc through a number of intermediaries. This pathway graph represents known, biochemical interactions between genes and is generated from the Ingenuity pathway analysis system.

6.4. Factors Related to Breast Cancer Subtypes

Breast cancer is an extremely heterogeneous disease, with many cancers being resistant to any one of the many existing chemotherapies due to either a lack or excess of activation of the corresponding target pathways. To date, one main focus in breast cancer genomics has been on increasing understanding about classes of cancers – breast cancer subtypes – that are related to substantial molecular differences involving key hormonal pathways. A now traditional view is that of five broad, intersecting types referred to as Basal, Luminal A, Luminal B, ERBB2, and Normal-Like [24], with typing related to levels of activation of estrogen receptor (ER) and epidermal growth factor (especially Erb-b2) pathways. This broad classification is very high-level, in that any one tumor may generate molecular data that is compatible with more than one of these five subtypes; the classification is a really an aggregated view of underlying continuous variation in activation levels of multiple, interacting pathways. Since Myc plays multiple roles in processes of cell growth and proliferation pathways that ER and Erb-b2 also influence, it is natural to expect some relationship between Myc factors and these subtypes; indeed, Figure 3 shows two of the 12 Myc factors which clearly relate to subtypes defined in this data set by Perou et al. Factor 7 shows a strong association with the basal subtype of breast tumor. One feature of this tumor subtype is the over-expression of the nestin gene [21], which is believed to be directly regulated by Myc [28]. This factor then appears to represent the activity of the Myc-Nestin pathway, downstream of Myc, as evident in gene expression. A further relationship is with factor 6 that has a strong association with the Lumina B subtype as well as a strong correlation with CNV in the tail of the long arm of chromosome 8; in fact, this is precisely the chromosomal region the Myc gene is located. There have been no previous associations between Myc duplication and the luminal B subtype, and this combination of links in both expression (related to gene function) and chromosomal location seem to point to a significant role for Myc in relation to this subtype. We explore this further in the next sections.

Figure 3:

Scatter plot of Myc factors 6 and 7 in the breast cancer data set used for the sparse factor analysis. Tumors are coded by subtype: Luminal B type as o, Basal type as + and all others as points. These two factors separate Luminal B and Basal type tumors from all others.

6.5. Factors Related to Gene Copy Number

This breast cancer expression data set [4] has accompanying data on competitive hybridization (CGH) levels that measure gene CNV across the genome. Measurement of CNV compares measured orescence levels of gene sequences in normal (control) versus tumor tissues on microarrays, using a technological process similar to that measuring mRNA expression. CGH measurements are on a continuous scale representing levels of apparent abundance of gene sequences across all chromosomes. We can therefore investigate whether CNV bears any relationship to expression patterns represented by the Myc factor profile.

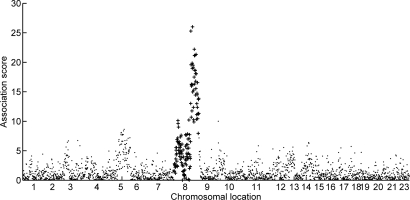
Figure 4 shows strong association between factor 6, as implicated above, and CNV at CGH clone “RP11-125O21”. This clone is located on chromosome 8 in band 22 of the long arm (position 8q22). Figure 5 provides a visual display of measures of association between levels of expression of factor 6 and copy number across the genome. CNV across all of the tail of the long arm of chromosome 8 demonstrate clearly interesting association with the factor. Additionally, examining the collection of genes in this factor using GATHER, we find that a disproportionate number are from regions 8q22 and 8q24 (BF 47 and 30 respectively). One well-known feature of many breast cancers is the presence of increased copies Myc; indeed, this is a key reason that the Myc oncogene was a target of study in [1] as well as here. That Myc is itself located in the 24th band of the long arm of chromosome 8 strong supports the view that the identified factor 6 is reflecting pathway activation linked to Myc and now potentially also driven by upregulation through chromosomal amplification, and certainly warrants further detailed investigation. One statistical next-step is to further explore factor 6 by additional analysis of the genes on which it highly loads, as we now discuss.

Figure 4:

Scatterplot of Myc factor 6 and the CGH data identified by clone “RP11-125O21” in region 8q22 of the genome.

Figure 5:

Association score of Myc factor 6 with CHG levels at 2149 locations across the entire genome, computed in the breast tumor data analysis. The horizontal axis labels indicate chromosomes (22 is present but unlabeled), with each label placed at approximately the middle of the set of clones within that chromosome. The association score is simply a summary measure of concordance between the estimated factor 6 and the pointwise CGH levels; this is computed as – log(p) where p is the p-value of the Pearson test of correlation of factor 6 and CNV. Clones from chromosome 8 are drawn with + to highlight the relationship between the tail of this chromosome and Myc factor 6.

6.6. Factor Refinement

Figure 5 indicates an apparently wide range over which associations with chromosome 8 and factor 6 – that we can now refer to as the Myc duplication expression biomarker – appear to be significant. There are 1011 probes in this factor (at ${\pi }_{g,6}^{*}>0.99$), corresponding to 877 named genes (some genes are represented via multiple distinct probe sequences on the microarray). This large number of genes raises challenges from the perspective of assigning relevance in terms of the activities of biological pathways. One refinement of the overall strategy for evolutionary factor analysis as a tool in exploring substructure in gene expression is to focus in on selected subsets of genes and develop further factor analysis at a more focused level. This was done here to narrow the focus to these 1011 probes and model them separately. Specifically, we extracted the data on just these p = 1101 probes and for analysis using a sparse factor model but now restricted to just these probes, i.e., precluding inclusion of additional probes through evolutionary search.

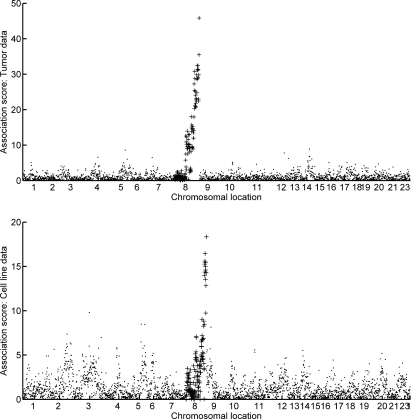
This analysis indicates relevance of 12 subfactors of the Myc duplication biomarker. Among these, two subfactors (those numbered 4 and 12) appear to relate to duplications of two distinct regions of chromosome 8. The upper frame of Figure 6 illustrates the relationship of subfactor 12 to the genome-wide CHG data and also to a shorter sequence in the tail of chromosome 8; the strength of relationship to CHG patterns in a small clonal region of the chromosome is even more apparent in the first frame of Figure 7. Refining the focus to the tail region of chromosome 8, we see that both subfactors 4 and 12 are specific to two different regions of the chromosome; see Figure 8.

Figure 6:

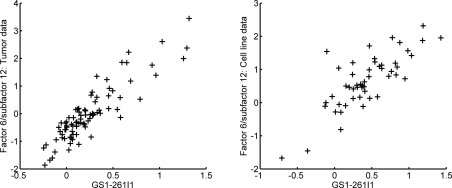
Genome-wide association scores of Myc factor 6/subfactor 12 with CHG levels, in a format and with definitions as in Figure 5. The upper frame is from the analysis of the breast tumor data set, and the lower frame the associations after direct prediction of the subfactor 12 levels in the breast cell line data set. Chromosome 8 values are indicated by +. The plots indicate strong association of this expression biomarker of downstream Myc pathway activation with CNV at the tail of the long arm of chromosome 8.

Figure 7:

Scatterplots of the association measures from Figure 6 for those genome locations within the last CGH clone on chromosome 8 (this is also the clone with the strongest correlation to Myc factor 6/subfactor 12 in both data sets).

Figure 8:

Association scores of subfactors 4 (+) and 12 (o) of the Myc factor 6 with CNV data across chromosome 8. The graphs are for the tumor data analysis (left frame) and using predicted factors in the breast cancer cell line data set (right frame). Subfactor 4 (+) has a higher association with 8q22 relative to subfactor 12 (o), whereas the latter shows a stronger association with 8q24. Elucidation of the genes involved in each of these two factors corroborates this association.

To explore the broader validity of this apparent relationship between Myc expression subfactors and chromosomal structure, we studied a separate data set consisting of a collections of breast cancer cell lines [19]. This data set contains both gene expression and CGH data generated on each of 51 individual breast cancer cell lines. We can map the subfactor structure to this data set precisely as described in equation (7). The lower frame of Figure 6 and the second frame of Figure 7 show the remarkable concordance of the results of this with those in the primary breast cancer data; that is, subfactor 12 is predictive of duplication of the same Myc-related chromosomal region. This is particularly remarkable since, in cancer genomics more widely, it is quite common to find major differences in expression patterns between cell lines and tumor tissue samples; tissue samples have substantially higher levels of biological noise (such as due to heterogeneity of cell types and inclusion of normal tissue) as well as technical noise (such as due to noise induced through sample handling in tumor resection and subsequent pathological analysis), which sometimes leads to difficulty translating between factors generated from the two types of data.

Finally, it is of interest to tie-back to the exploration of expression patterns across breast cancer subtypes now with these refined subfactors of the key Myc duplication factor. In direct exploratory data analysis and in more formal binary regression models drawing on the subfactors as candidate predictors of the Luminal subtype, it is clear that two of the subfactors – number 8 and the subfactor 12 already identified in connection with CGH – are markers of Luminal Type B breast cancer. We have already seen that factor 12 is specific to CNV at location 8q24. Examining the collection of genes that are most highly loaded on factor 8 and using the Entrez Gene database, we find a high degree of association with genes that are known to be binding partners of PLK1 gene. This relates to a previous study [9] that defined an expression signature which distinguishes luminal breast cancers with poor prognosis based on a collection of sixteen kinases, one of which is PLK1. Using Ingenuity to examine the two sets of genes shows a high degree of inter-relatedness as well as a high degree of relatedness with Myc; see Figure 9.

Figure 9:

An Ingenuity pathway analysis containing about half of the genes in subfactor 8 of Myc factor 6. Also included are 15 of the 16 kinase genes in the set underlying the expression signature of Finetti et al (2008) that is linked to poor prognosis in patients with Luminal type breast cancer (drawn with pentagons) and 6 genes added by Ingenuity by a pathway search (drawn with triangles). Finally, Myc itself is shown as a square in the center with incoming and outgoing edges as solid lines. The high density of known biochemical relationships between the genes in subfactor 8 and the kinases in the Finetti et al signature suggest that this signature and Myc factor 6/subfactor 8 are measuring the activity of the same pathway.

7. Additional Comments

While there are many studies focused on either tissue samples from cancer patients, or on in vitro studies of cancer cell lines, it is generally difficult to translate results between the two types of experiments. Often, the patterns of expression observed in vitro are simply not present in in vivo samples. This is due to the heterogeneity of tissue samples, and arises from many technical and biological factors. This loss of fidelity makes direct translation between the two difficult. We have described a technique, using sparse latent factors, for translating a signature built in a controlled, in vitro study that allows for the discovery and elucidation of closely related pathways in tissue samples.

The factor modules resulting from our analysis contain subsets of genes with common expression patterns and generally common biological activities. These expression patterns are quantified, leading to estimates of the activities of each of the samples for the relevant biological pathways. The analysis may be thought of as a dimension reduction technique, in that the resulting factor scores are usable as explanatory variables in any arbitrary model. We have demonstrated their use and robustness with a survival model, and have examined correlations with known phenotypic variables, but their use is general.

In our example, we used sparse latent factor models for the exploration of the Myc signature in breast cancer. The analysis has led to a number of observations regarding the activity of Myc and closely related pathways in breast cancer, many of which are already corroborated in the literature. Additionally, the analysis has generated the hypothesis that Luminal B tumors may be characterized by Myc duplication together with PLK1 upregulation. This can be directly tested in cell lines or xenographs by specifically upregulating these genes and testing for conversion to the Luminal B subtype.

Our approach provides a general technique for the generation of pathway signatures that are related both to known biology (Myc and its subpathways in our case) and clinical phenotypes (such as disease free survival). While we have focused on the Myc pathway for this paper, the procedure is generally applicable and we expect to be of broad interest to researchers in gene expression genomics in cancer and other applied contexts.

Supplementary Materials

Further details of model and prior specifications, and of controls and samples sizes for MCMC analyses of sparse regression and factor models in the application study here, are available at the web site at http://ftp.stat.duke.edu/WorkingPapers/08-30.html. This includes all the text files used for data and model specification for the sparse regression and factor analyses reported, using the BFRM software, and all corresponding text files of analysis summaries. That sites also includes links to the freely available software for model implementation.