Abstract
Case-control genome-wide association (GWA) studies have facilitated the identification of susceptibility loci for many complex diseases; however, these studies are often not adequately powered to detect gene-environment (GxE) and gene-gene (GxG) interactions. Case-only studies are more efficient than case-control studies for detecting interactions and require no data on control subjects. In this paper, we discuss the concept and utility of the case-only genome-wide interaction (COGWI) study, in which common genetic variants, measured genome-wide, are screened for association with environmental exposures or genetic variants of interest. An observed G-E (or G-G) association, as measured by the case-only odds ratio, suggests interaction, but only if the interacting factors are unassociated in the population from which the cases were drawn. The case-only odds ratio is equivalent to the interaction risk ratio. In addition to risk-related interactions, we discuss how the COGWI design can be used to efficiently detect GxG, GxE, and pharmacogenetic interactions related to disease outcomes in the context of observational clinical studies or randomized clinical trials. Such studies can be conducted using only data on individuals experiencing an outcome of interest or individuals not experiencing the outcome of interest. Sharing data among GWA and COGWI studies of disease risk and outcome can further enhance efficiency. Sample size requirements for COGWI studies, as compared to case-control GWA studies, are provided. In the current era of genome-wide analyses, the COGWI design is an efficient and straightforward method for detecting GxG, GxE and pharmacogenetic interactions related to disease risk, prognosis, and treatment response.
Keywords: Case-only study, genome-wide association, pharmacogenetics, efficiency
INTRODUCTION
Case-control genome-wide association (GWA) studies have facilitated the identification of susceptibility loci for many complex diseases [McCarthy, et al., 2008]; however, these studies are often not adequately powered to detect gene-environment (GxE) and gene-gene (GxG) interactions. The case-only study has been proposed as an efficient design for the detection of GxE [Khoury and Flanders, 1996; Piegorsch, et al., 1994] and GxG interactions [Yang, et al., 1999] in human disease. To conduct a case-only study, researchers must collect relevant data on genotype (G) and environmental exposure (E) for diseased individuals only; data on control subjects is not required. An observed association between a G and an E in a sample of diseased individuals suggests that G and E interact to influence disease risk, but this conclusion relies on a key assumption: G and E must be uncorrelated in the population from which the cases arose (the “source population”). The case-only design is an attractive alternative to the case-control design for detecting statistical interactions because case-only studies require far fewer total study participants [Yang, et al., 1997] and avoid difficulties associated with appropriate control group selection [Khoury and Flanders, 1996]. However, the utility of the case-only study is limited by its inability to assess additive interactions and genotype-phenotype associations (i.e. “main effects”).
In this paper, we discuss the concept and utility of the case-only genome-wide interaction (COGWI) study for detecting interactions related to disease risk, prognosis, and treatment outcomes. We begin by providing an overview of approaches for detecting GxE and GxG interactions. We then discuss the details of detecting risk-related interactions in COGWI studies of diseased individuals only and then extend these ideas to the detection of prognosis-related interactions using data from only cases who experience an outcome of interest. Similarly, we introduce the novel utility of COGWI studies in assessing gene-drug interactions (i.e., pharmacogenetics) in the context of randomized clinical trials (RCTs) or other therapeutic/chemoprevention studies, by only genotyping participants experiencing the study outcome. Finally, we briefly discuss genome-wide analysis issues and sample size requirements, as well as the strengths and limitations of the COGWI study design.
DETECTING GENE-ENVIRONMENT AND GENE-GENE INTERACTIONS
Several motivations for identifying GxE interactions in complex disease have been previously described [Hunter, 2005], many of which also pertain to GxG interactions. For example, knowledge of interactions may be useful for generating better attributable risks for genetic and environmental risk factors, estimating risks by subgroups, understanding disease mechanisms, identifying specific molecular risk factors in complex mixtures, designing preventative and therapeutic strategies, and offering advice on personalized disease prevention and treatment [Hunter, 2005]. Furthermore, interacting factors may have weak marginal associations with disease, making the detection of interactions crucial for the identification of both genetic and environmental determinants of disease [Ottman, 1996].
Study Designs for detecting interactions
The most common design used to detect interactions is the case-control study, in which interaction can be tested using data from a simple 2×4 table [Botto and Khoury, 2001] if the outcome and the interaction factors are dichotomous. Case-control studies may be feasible for detecting interacting factors that are common, but will be underpowered to detect interactions as the frequencies of the interacting factors decrease [Hwang, et al., 1994], suggesting a need for more efficient study designs [Goldstein, et al., 1997]. Power and efficiency can be enhanced in case-control studies by employing two-stage design strategies that oversample cases and controls with rare exposures (or genotypes) or countermatch controls to cases based on environmental exposures or genotypes (or surrogates thereof) [Andrieu and Goldstein, 1998]. Interaction estimates from case-control studies are subject to well-known problems, such as selection bias, recall bias (misclassification of exposure), population stratification, and control selection issues. In addition, prospective measures of biomarkers of interest (for assessing temporality between biomarkers and disease) are generally not available.
Interactions can also be tested in the context of cohort studies (or nested case-control studies), where the likelihood of selection bias, survival bias, and recall bias can be reduced or eliminated, and the prospective collection of biomarker data (i.e. temporality) is feasible. Traditional cohort studies will typically not be practical for detecting interactions related to relatively rare phenotypes on the genome-wide scale because the number of cohort members whose genotype and environmental data will be needed is too large and thus cost prohibitive. Furthermore, the collection of additional phenotype measures (such as fresh-frozen tumor samples for cancer patients) will be difficult to obtain for individuals in a large cohort study, compared to case-control studies conducted at a small number of institutions [Hunter, 2005].
There are several statistical methods for testing interactions, and the presence or absence of statistical interaction depends on the scale chosen to measure association. In case-control studies with dichotomous genetic and environmental factors, deviation from multiplicative or additive models of interaction can be tested [Botto and Khoury, 2001]. These models are based on the case-control odds ratio (OR), which estimates odds, rate, or risk ratios, depending on the method of control selection [Schmidt and Schaid, 1999]. The multiplicative model has the advantage of being easily testable in the context of a logistic regression, which can generate ORs adjusted for potential confounders, while it has been argued that the additive model is more relevant to addressing public health issues [Rothman, et al., 2008]. In cohort studies, additive or multiplicative interaction can be tested, using RRs, ORs, or rate ratios. As the number of genotypes and exposures categories increases, models of interaction become more complicated; however, modeling interactions is an active area of research (reviewed in [Kraft and Hunter, 2005]).
Family-based association tests, which measure departures from Mendelian transmission from parents to affected children, can be extended to assess GxE interactions, and such extensions have been made to well-known family based association methods (essentially by stratifying based on the exposure status of affected offspring) such as the family-based association test (FBAT) [Lake and Laird, 2004], the log-linear approach [Umbach and Weinberg, 2000], and transmission disequilibrium test (TDT) [Khoury and Flanders, 1996]. Interactions can also be tested using a family-based case-control study using related controls (e.g., discordant sib-pairs) [Andrieu, et al., 2005; Andrieu and Goldstein, 1996], or a combination of related and unrelated controls [Andrieu and Goldstein, 2004; Goldstein, et al., 2006], in a similar manner as in a case-control study.
Detecting interactions using a case-only (or outcome-only) design
In case-only studies, an interaction that influences disease risk can be detected as an association between the interacting factors in a sample of diseased individuals. An observed positive association suggests synergistic interaction, while an inverse association suggests antagonistic interaction [Ottman, 1996]. Detecting a true interaction in a case-only study is dependent upon a key assumption: the interacting factors must be uncorrelated in the population from which the cases arose (the “source population”). Such correlations will be rare, but may arise in situations where G(s) influences uptake, dependence, or avoidance of E(s) or due to G-G linkage disequilibrium (LD). Violation of this assumption will lead to a distorted interaction estimate [Albert, et al., 2001]; however, if the source of this non-independence can be measured, it is possible to control for non-independence and estimate valid measures of interaction [Gatto, et al., 2004].
The interaction parameter in case-only studies (i.e., the case-only OR) estimates departure from multiplicative risk ratios (RRs) derived from a cohort study of the source population, when the interacting factors are independent in the source population [Gatto, et al., 2004] (Figure I). The genetic variant(s) of interest can be modeled as a dichotomous variable (i.e. dominant or recessive mode of inheritance) as in Figure I, or as three genotypes, which can be modeled as a log-additive mode of inheritance in the interaction model (i.e. in the presence of the interacting exposure, the presence of two interacting alleles increases risk twice as much as the presence of one interacting allele). The case-only design can also be used to detect prognostic interactions, using only data on diseased individuals experiencing an outcome of interest. In this case, the interaction estimate (i.e., the case-only OR for disease outcome) is equivalent to the interaction RR, but only if the interacting factors are uncorrelated in the source population of diseased individuals (i.e. case-only OR for risk = 1.0) (Figure I).
Figure I. An overview of the case-only study design for detecting GxE interactions related to disease risk and disease outcome.
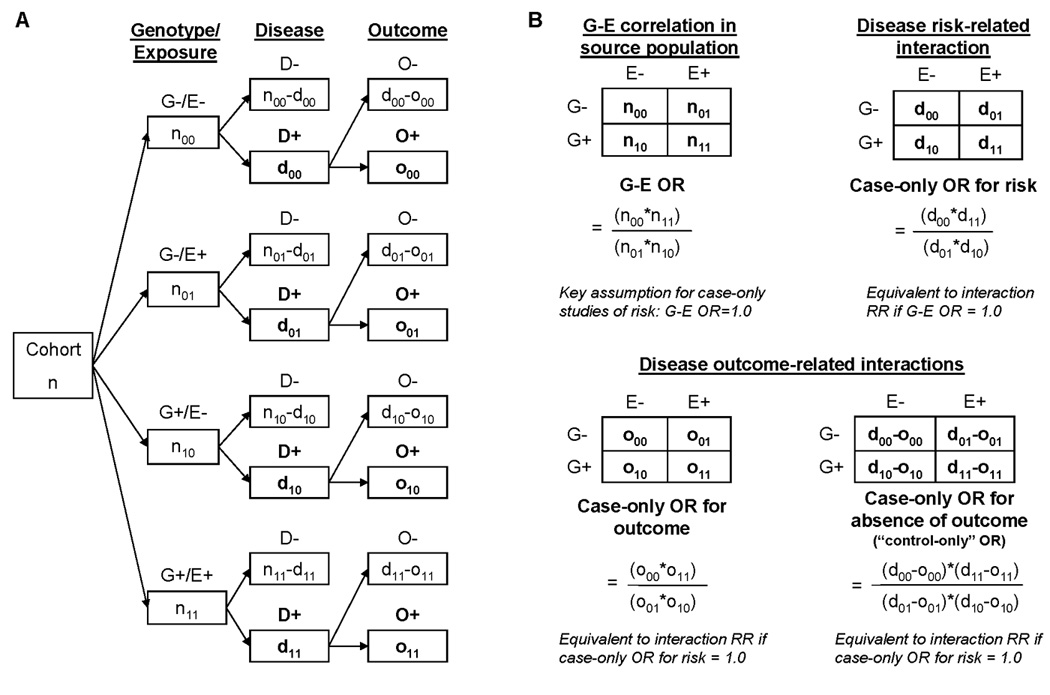
(A) A hypothetical cohort of individuals is drawn from a population of interest and classified according to presence or absence of G and E. Individuals are then classified according to disease and disease outcome status. Actual data is collected on individuals in categories shown in bold, for case-only studies of risk (D+) and outcome (O+). (B) The key association measures for case-only studies are dependent upon assumptions related to G-E associations in the source population.
CASE-ONLY GENOME-WIDE INTERACTION STUDY OF DISEASE RISK
Researchers conducting GWA studies have successfully identified genetic variants that influence a wide array of diseases [McCarthy, et al., 2008]; however, the extent to which these associations differ by disease characteristics and are modified by other environmental or genetic factors still needs to be described. Additional research is also needed to identify interacting factors that have weak or no marginal effects on disease risk, as these factors will only be detectable in the context of studies designed and powered to detect interactions [Ottman, 1996]. Employing dense genotyping technologies in studies of interaction may facilitate rapid discovery, similar to that of early GWA studies.
Study design and analysis
A COGWI study of disease risk could include cases from an existing case-control GWA study (Figure II). Simply discarding the controls from such a study would increase power to detect interaction [Piegorsch, et al., 1994]; however, depending on the size of the GWA study, additional cases would likely be needed to achieve adequate power [Smith and Day, 1984]. Diseases that are tracked in population-based registries are ideal for COGWI studies, as these registries provide an excellent resource for unbiased recruitment of cases [Botto and Khoury, 2004].
Figure II. Overview of data requirements, analysis opportunities, and strategies for efficient multi-study design related to case-only genome-wide interaction studies of disease risk and outcome.
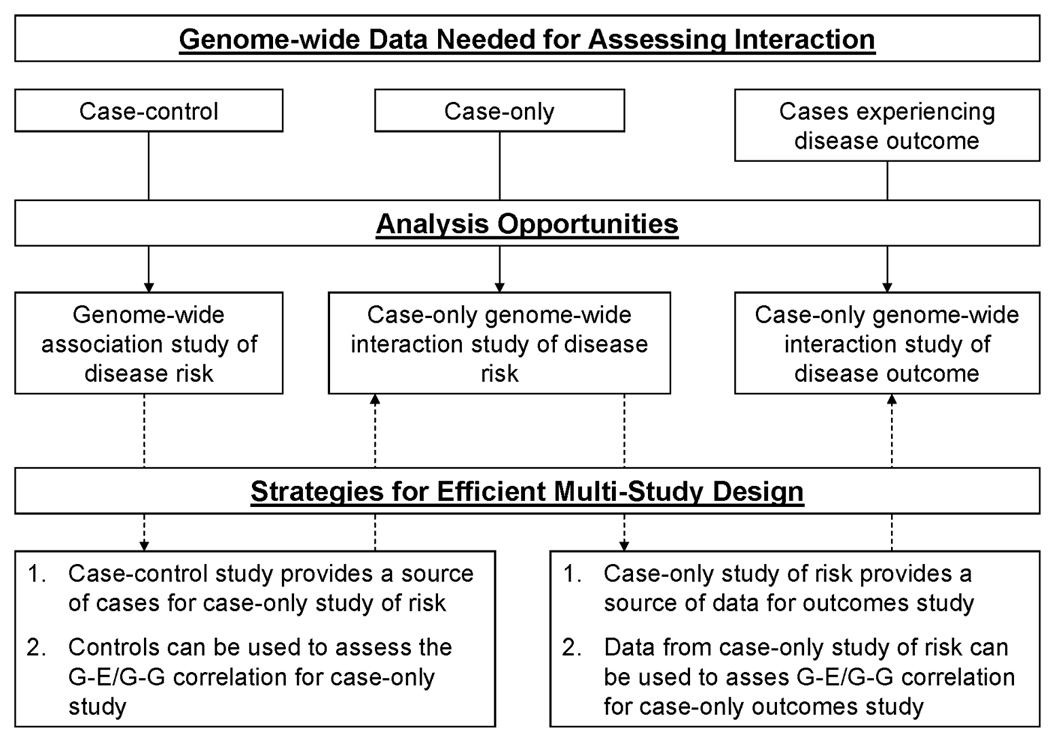
A general analysis plan for COGWI studies of GxE interaction would be to choose an environmental exposure of interest, perhaps an established risk factor for a disease, and screen for genetic variants that modify the magnitude of the risk factor’s association with disease, in a genome-wide fashion. In other words, in the case-only setting, one would simply screen all genetic variants for an association with an exposure of interest.
Detecting GxG interactions in the case-control GWA setting, without any prior hypotheses regarding candidate interacting loci, is a computationally intensive task that is further complicated by issues of multiple testing and statistical modeling [Evans, et al., 2006; Marchini, et al., 2005]. Similarly, exploratory COGWI studies of all possible 2-way G-G interactions would involve approximately k2/2 tests of interaction (ignoring LD), where k is the number of genotyped markers. Modeling would be somewhat simpler in COGWI studies, because of the inability to detect marginal associations with disease. In order to mitigate the multiple testing problem, preliminary GxG COGWI studies can be conducted that screen the genome for variants that interact with a candidate polymorphism in an identical fashion to the GxE scans described above.
The COGWI study and the case-only assumption
Detecting interactions in a COGWI study relies on the assumption that the interacting factors are uncorrelated in the source population. With respect to GxE interactions, the vast majority of variants included on a genome-wide panel will be independent of any environmental exposure in the population of interest. There may be exceptions, but they will be the overwhelming minority. The group of promising variants identified in a COGWI screen may be enriched for variants that show a G-E correlation in the source population. Therefore, it would be ideal to independently assess the G-E correlation for these promising variants in a smaller group of samples randomly selected from the source population to insure G-E independence.
Correlations between health behaviors and knowledge of genetic susceptibility (and the resulting G-E correlation) will not be of significant concern in COGWI studies. Assuming the marginal risks conferred by variants implicated in GxE interactions are modest, any variant being tested for interaction will weakly associate with family history. Thus, confounding by family history is less of a concern in COGWI studies than in GxE studies of more penetrant mutations (i.e., those with strong main effects), which strongly associate with family history and are more likely to result in G-E correlations.
With respect to GxG interactions, any given single nucleotide polymorphism (SNP) is expected to be uncorrelated with the vast majority of other SNPs in the genome, making the case-only design an attractive option for investigating GxG interactions. The primary exception is SNPs that are in close proximity to one another and correlated due to LD. However, commercial genome-wide panels (e.g., Illumina platforms) are designed to efficiently capture the majority of variation in the human genome with a minimal number of tagging SNPs (tagSNPs). As a result, LD between neighboring SNPs is minimized, without losing a great deal of information. Nevertheless, associations between SNPs residing in the same chromosomal region should be interpreted with caution, using knowledge of population-specific patterns of LD [Ardlie, et al., 2002]. Ideally, associations between promising SNPs pairs identified in GxG studies should be tested in the source population, to ensure the validity of the case-only interaction estimate.
Additional applications of the COGWI study
In addition to genome-wide GxE screens, similar screens could be conducted to identify genetic factors that correlate with clinical, pathological, or molecular characteristics of interest, perhaps those with prognostic or etiologic significance [Begg and Zhang, 1994; Botto and Khoury, 2004]. Variants identified would be hypothesized to put carriers of specific alleles at higher risk for developing disease associated with specific clinical, pathological, or molecular characteristics. These types of analyses would not be dependent on any assumptions regarding the source population.
It is possible to use genetic information as a surrogate for endogenous biological exposures. GWA studies have successfully identified numerous protein quantitative trait loci (pQTLs) for many clinically relevant serum and plasma proteins [Melzer, et al., 2008]. For endogenous exposures of interest for which measures are not available, it may be appropriate to use genetic determinants of that exposure to screen for GxG interactions, as a surrogate screen for GxE interactions. The surrogate GxG estimate is less susceptible to confounding and reverse causality than the GxE estimate because G can be viewed as an instrument variable that is independent of disease outcome conditional on E [Lawlor, et al., 2008]. In other words, because the relationship between E and disease risk may be confounded (within strata of G), a GxG interaction provides evidence that GxE interact (in a causal manner) to influence disease risk (i.e. “Mendelian randomization”), although this method will be less powerful than studies incorporating information on the endogenous exposure.
CASE-ONLY GENOME-WIDE INTERACTION STUDY OF DISEASE OUTCOME
The COGWI study design is equally applicable to the detection of interactions that influence outcome (i.e., prognosis) among diseased individuals. In a COGWI study of disease outcome, study participants are selected based upon the presence (or absence) of an outcome of interest (e.g., mortality, disease recurrence, outcomes defined by biomarkers or intermediate endpoints). As in a COGWI study of disease risk, individuals with the outcome of interest are genotyped using a dense panel of genetic markers, and these markers are screened for associations with exposures or genetic variants of interest. A G-E (or G-G) association suggests that G and E (or G and G) interact to influence the outcome under study, assuming the two factors are independent in the source population of all cases.
Relatively little research has focused on the impact of GxE or GxG interactions on disease outcomes, and there is a need for new approaches to model the contributions of interactions in outcomes research [Ambrosone, et al., 2006]. Any prognostic information (including information related to GxG or GxE interactions) is of obvious value to physicians and patients making decisions about appropriate treatments. The diagnosis represents a time point at which individuals often become motivated to learn about modifiable prognostic factors and make lifestyle changes to enhance the their quality of life and survival [Demark-Wahnefried, et al., 2005], changes that could be related to diet, physical activity, weight loss, or nutritional supplements. COGWI studies can facilitate the identification of genetic and/or environmental factors that influence disease outcomes.
Study design and analysis
The most common design for studying disease outcome (and prognostic interactions) is the longitudinal cohort study, which requires tracking many diseased individuals over time. Such a study may not be practical for detecting interactions, especially in genome-wide studies, which require very large sample sizes. A COGWI study of outcome would be conducted retrospectively, making a study of interactions more practical, in terms of sample size and costs. Participants experiencing the outcome of interest could be selected from existing studies of disease risk or prognosis, assuming the data of interest could be extracted from these studies (Figure II). Similar to case-only studies of risk, COGWI studies of prognosis are ideal for conditions tracked in population registries, should events of interest be tracked as well.
Choice of outcome is a critical feature of COGWI studies of prognosis, as many diseases have a wide range of outcomes which can be measured in multiple ways. The outcome and criteria for participation need to be clearly defined and clinically relevant [Laupacis, et al., 1994; Mak and Kum, 2005]. The outcome could be based on a dichotomous clinical event (e.g., second primary cancer, recurrence, metastasis, or intermediate endpoint), vital status, or a threshold of a continuous measure of health status (i.e. sampling individuals from the tails of phenotypic distributions). Researchers may want to focus on outcomes which appear to have some genetic basis, although the evidence supporting such a hypothesis may be limited. The time period between diagnosis and enrollment needs to be sufficiently long to fully capture the outcome of interest and the selected participants should represent the full spectrum of the disease of interest to avoid selection bias [Laupacis, et al., 1994; Mak and Kum, 2005]. For outcomes that are inevitable, such as mortality, well defined restrictions (such as “disease-specific mortality” or “death within 5-years”) will be needed to accurately define the relevant outcome of interest. These definitions should be based on sound biological, clinical, and/or epidemiological reasoning.
Exposures of interest in interaction studies of outcome may be substantially different than those considered in interaction studies of risk. For instance, clinical, molecular, or pathological features of disease, including molecular phenotypes, could interact with genetic variants to influence prognosis, whereas these features can not interact with genetic variants to influence disease risk. In addition, the biological mechanisms (and the exposures related to these mechanisms) underlying disease etiology may be distinct from those underlying disease progression and survival. Known prognostic factors without a significant role in disease etiology may be of primary interest in interaction studies of outcome.
COGWI study of the absence of outcome (“control-only” study)
When the outcome of interest is common, an interaction related to outcome will induce a G-E association in the group experiencing the outcome (case-only OR = (o00*o11)/(o01*o10)) and the group not experiencing the outcome (case-only OR=((d00-o00)*(d11-o11))/((d01-o01)*(d10-o10))), assuming there is no G-E association in the source population of diseased individuals (Figure I). If the interaction is synergistic (i.e., case-only OR>1) then the association between G and E in those without the outcome of interest will be negative (case-only OR<1), and vice versa. Thus, depending on the frequency of the outcome and strength of the anticipated interactions, there may be two groups of samples appropriate for screening for interactions related to outcomes using case-only methods: individuals experiencing the outcome and individuals not experiencing the outcome.
Assuming a constant case-only OR (i.e. interaction RR) for outcome, as the frequency of the outcome increases, power to detect an interaction in cases not experiencing the outcome increases (i.e. the case-only OR for absence of outcome moves further from the null). For example, if the outcome of interest has a low absolute risk (<25%), a case-only study of individuals experiencing the outcome will generally be more powerful for detecting interactions than a study of those not experiencing the outcome, although the lower risks will result in few available cases. For outcomes with relatively high absolute risks (>75%), a case-only study of the absence of outcome will be more powerful than a case-only study of the outcome, although the higher risks will result in fewer individuals not experiencing the outcome (unpublished calculations not shown here). Such studies would be especially applicable to outcomes such as mortality, where DNA may not be available for deceased subjects. Details of the utility and epidemiologic properties of these two approaches will be explored further in a subsequent paper.
CASE-ONLY GENOME-WIDE INTERACTION STUDIES OF DRUG RESPONSE
In addition to the study of prognostic and risk-related interactions, the COGWI study design can be used to identify genetic variants that predict response to treatment. In a sample of individuals who have experienced an outcome of interest, an association between a genetic variant and a specific treatment suggests a gene-drug interaction is influencing the outcome, provided the genetic variant is uncorrelated with treatment in source population. For COGWI studies of therapeutic treatments, case groups should be selected based on outcomes similar to that of COGWI studies of prognosis or based on adverse side effects of interest. For COGWI chemoprevention studies, case group selection should be similar to that of COGWI studies of disease risk.
The ideal setting in which to test for gene-drug interactions is in a randomized clinical trial (RCT). Individuals with an outcome of interest could be selected for inclusions in a COGWI study of pharmacogenetic interactions, where treatment assignment is the exposure of interest. In this scenario, the key assumption of the case-only analysis is valid by design, because treatment is randomly assigned. In other words, there will be no systematic correlation between treatment assignment and any potential effect modifier (genetic or otherwise) in the “source population” (i.e. all RCT participants at risk for the outcome of interest).
Studying gene-drug interactions in well-designed observational studies of treatment or drug response is also possible, and the implementation of the COGWI study design is similar to that of studies of prognosis, although interacting variants would be interpreted as “predictive” rather than interacting “prognostic” variants. Predictive variants influence a patient’s response to a specific treatment (e.g. efficacy and toxicity), while prognostic variants influence a patient’s overall outcome independent of treatment [Vallbohmer and Lenz, 2006]. In some instances, genetic variants may be related to both prognosis and drug response [Fagerholm, et al., 2008]. A prognostic variant that is associated with clinical, pathological, or molecular characteristics of prognostic significance may also be associated with treatment assignment, leading to a violation of the key assumption of case-only interaction analyses: a G-E association in the source population of cases.
The application of the COGWI study design to RCTs is particularly attractive because there is existing data and stored samples for many large therapeutic and chemopreventative RCTs. The main effects of these treatments are well described, as a result of the primary RCT analyses. Exploring pharmacogenetic interactions is the next logical step towards understanding the effects of these treatments and may facilitate the discovery of treatment effects specific to subgroups defined by genetic variants.
Special applications to clinical trials: Phase I, Phase II, and 2×2 factorial Phase III trials
There are certain types of gene-treatment interactions that cannot be detected using a COGWI study. For example, if a genetic variant interacts with a treatment to increase risk of drug toxicity, only individuals taking the drug will experience that toxicity, and there will be no variability in treatment (or treatment assignment in an RCT) among individuals who experienced toxicity. Toxicity (i.e. drug safety) is usually assessed in Phase I and Phase II clinical trials, where all subjects are given treatment. In scenarios where only the treated group is of interest, a GWA analysis limited to individuals receiving treatment could potentially identify the interacting variant (as demonstrated in [Link, et al., 2008]). For a COGWI analysis to be feasible, the outcome of interest must occur in both treated and non-treated individuals (such as myocardial infarction). However, a COGWI study of individuals experiencing a drug-specific toxicity could be used to detect GxG or GxE interactions related to toxicity, without taking treatment into account.
The COGWI design can also be applied to RCTs employing a 2×2 factorial design, an efficient design for evaluating the effects of two treatments simultaneously assuming the treatments do not interact. Individuals are randomized to either one of two treatments, both treatments, or placebo. Similarly, data on individuals from all four study arms who experience some outcome of interest could be used to detect pharmacogenetic interactions related to either treatment, provided that the two treatments do not interact to influence the outcome of interest. In other words, the efficiency of the 2×2 factorial design in assessing main effects of treatment on outcomes can be preserved in a COGWI study of pharmacogenetic interactions. In the case were the two treatments interact, analyses models stratified on or adjusted for one treatment, could be employed to account for this interaction when screening for pharmacogenetic interactions related to the other treatment.
ANALYSIS STRATEGIES FOR COGWI DATA
Genome-wide studies typically involve a large number of tests (300,000–1,000,000), requiring investigators to use higher levels of significance (p~10−7) to guard against false positives (which in turn requires larger sample sizes). The number of expected false positives in a COGWI screen using a single exposure/treatment or a single candidate genetic variant will be identical to that of GWA study using the same panel of markers, assuming one p-value for interaction is generated per variant. As more environmental exposures, treatments, genetic variants, or clinical/prognostic factors are tested for interaction or heterogeneity, the total number of expected false positives will increase.
Pooling data among several studies is often a requirement to achieve the samples sizes required to conduct a GWA study, and the same will be true for COGWI studies. When working with multi-site data, researchers also need to ensure that the key assumption of case-only analysis is valid for each study site. In order to reduce genotyping costs (with little power loss), researchers often employ staged designs, conducting genome-wide genotyping on only a subset of participants and in a second stage, typing only markers showing evidence of interaction in the first stage. In COGWI studies, existing genome-wide data could be used for stage one, while a smaller subset of candidate markers could be genotyped inexpensively in additional cases. Analyzing data from both stages jointly has been shown to enhance power to detect associations in GWA studies [Skol, et al., 2007], a strategy that will also enhance the power of COGWI studies.
In GWA analyses, several computational techniques can be employed to increase the probability that a true association is detected. Knowledge of LD patterns can be used to impute genotypes for all variants whose correlations with other SNPs are known [Marchini, et al., 2007]. Alternatively, SNPs can be weighted according to how many other SNPs they tag (under the hypothesis that a tagSNP tagging many SNPs is more likely to be associated with disease than a tagSNP tagging few SNPs) [Carlson, 2006], or according to prior knowledge related to the functional consequences of the nucleotide change [Roeder, et al., 2007]. Confounding due to ancestry (which may of increased importance in multi-site analyses) can be addressed using several methods that account for population structure using the available genome-wide data, including principal components analysis [Price, et al., 2006] and model-based clustering methods [Pritchard, et al., 2000].
STRENGTHS AND LIMITATIONS OF THE COGWI APPROACH
The COGWI study is an efficient method for detecting GxE, GxG, and pharmacogentic interactions [Yang, et al., 1997], as case-only studies produce more precise estimates of interaction (i.e., smaller standard errors) than case-control studies [Piegorsch, et al., 1994] and other family-based methods, thus requiring smaller sample sizes [Kazma, et al., 2007]. This is a significant benefit considering the cost of genome-wide genotyping and the large samples sizes needed when searching for modest effects using many statistical tests.
Sample size requirements for whole-genome screening for interactions with a candidate exposure of interest using COGWI and case-control GWA studies are compared in Figure III. These estimates are based on 80% power, a type 1 error rate of 10−7, a synergistic model of interaction with no main effects, and a one to one case to control ratio. Sample size estimates vary by gene variant frequency, exposure frequency, and magnitude of risk due to interaction. Estimates were generated using the Quanto program [Gauderman, 2002; Gauderman and Morrison, 2006]. For all parameter combinations, the sample size requirement for COGWI studies is consistently lower than those for case-control GWA studies, often 2- to 3-fold lower. For common interacting exposures (prevalence ≥0.5), relatively uncommon interacting variants (frequency ≤0.3) require larger samples sizes than do more common variants, especially for stronger interactions (Figure III).
Figure III. Sample size estimates for detecting GxE interactions in COGWI and case-control GWA studies.
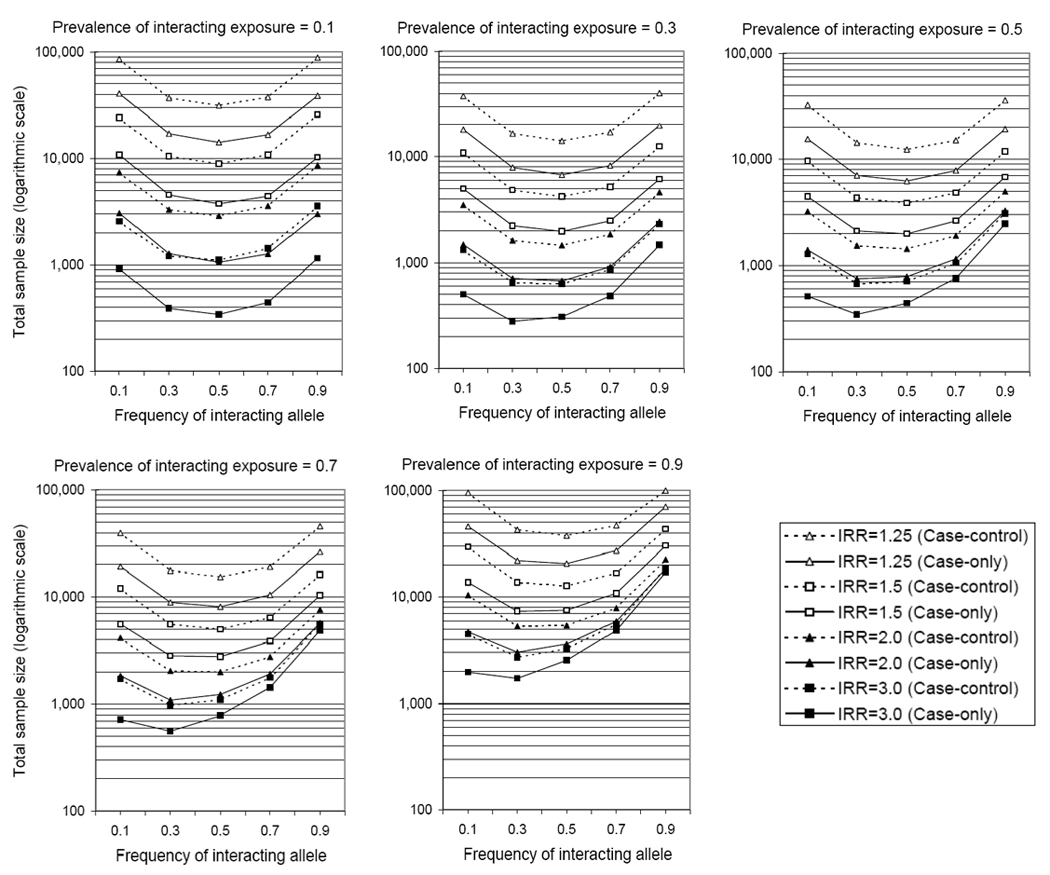
Estimates are based on 80% power, a significance threshold of p<10−7, a synergistic model of interactions with no main effects, a log-additive mode of inheritance (in the presence of E), and a one to one case-control ratio. IRR is the interaction relative risk per allele copy in the presence of E (Homozygous RR=IRR2). Individuals lacking E or having 0 copies of G were assigned an IRR of 1.00.
In COGWI studies of disease risk that utilize data from an existing case-control GWA studies, available data on controls can be used to assess G-E or G-G independence for promising interactions identified in the COGWI analysis (Figure II) [Schmidt and Schaid, 1999], as G-E or G-G correlations in the source population will lead to distorted interaction estimates [Albert, et al., 2001]. However, this method may be problematic in some instances, as the association observed in controls may not accurately reflect the association between interacting factors in the source population [Gatto, et al., 2004]. The association in controls will tend to underestimate the association in the source population as baseline risk of disease and the magnitude of the interaction increase [Gatto, et al., 2004]. Ideally, one would measure this association in a random sample from the source population.
An interaction estimate from a case-only study is equivalent to an interaction estimate based on RRs, as derived from a prospective cohort study, while an interaction estimate from a case-control study is typically based on ORs, which tend to overestimate the true RR [Schmidt and Schaid, 1999]. However, case-only studies are limited to assessing a multiplicative model of interaction; interactions based on additive models, which may be more relevant to addressing public health issues, cannot be assessed [Rothman, et al., 2008]. Similar to the case-control study, the case-only study is susceptible to selection bias, recall bias (if data is collected retrospectively), and population stratification [Wang and Lee, 2008]. Potential confounding related to both G and E should be considered, although any G-E association that is heavily attenuated by confounder adjustment suggests that a confounder may be participating in the interaction, rather than the genetic or environmental factor with which the confounder is associated.
In COGWI studies of disease outcome, risk-related interactions will result in G-E (or G-G) associations in the source population of diseased individuals. For these pairs of interacting factors, the key case-only assumption will be violated, and the results will not be valid, unless this correlation is taken into account. Similarly, this assumption would be violated if a genetic variant increased risk for a disease subtype associated with the outcome under study (i.e., the variant would be associated with the subtype in the source population). Although these scenarios will undoubtedly be very rare considering the number of variants being tested, G-E (or G-G) associations observed in COGWI studies may be enriched for such variants, again suggesting that interacting factors should be tested for independence in a random sample of individuals from the source population. If study participants are drawn from an existing sample of cases from the source population (e.g. a case-only study; see Figure I and Figure II), this study can serve as a convenient source of data to test the key assumption or quantify the association.
In COGWI studies where death is the outcome of interest, DNA samples may be unavailable; although, this limitation could potentially be addressed by conducting a case-only study of the absence of an outcome, if death is a common outcome. In addition, COGWI studies cannot incorporate quantitative information regarding the outcome of interest (unless a threshold is used as a cutpoint), including time-to-event information, which is often utilized in longitudinal analyses of prognosis. Furthermore, if the outcome of interest is uncommon, it may not be feasible to recruit the number of participants needed for a well-powered study, considering the large sample size requirements (see Figure III).
CONCLUSION
The COGWI design is an efficient method for detecting GxE and GxG interactions related to disease risk, prognosis, or drug response, requiring data on far fewer study subjects than other study designs [Yang, et al., 1997]. In addition, no controls are needed, eliminating concerns related to bias created by inadequate control selection [Khoury and Flanders, 1996]. Sharing data across GWA and COGWI studies of disease risk and outcome can further enhance efficiency. COGWI studies are limited by their reliance on the assumption of independence of interacting factors in the source population and their inability to test “main effects”. COGWI analyses should initially focus on screening for genes that interact with established or suspected risk factors (genetic or environmental), prognostic factors, and treatments, a straightforward strategy for detecting risk- and outcome-related GxE, GxG and pharmacogenetic interactions on a genome-wide scale.
ACKNOWLEDGEMENTS
This work was supported in part by grants from National Cancer Institute grants UO1 CA122171, RO1 CA107431, RO1 CA102484 and P30 CA014599, and National Institute of Environmental Health Sciences grant P42 ES10349.
REFERENCES
- Albert PS, Ratnasinghe D, Tangrea J, Wacholder S. Limitations of the case-only design for identifying gene-environment interactions. Am J Epidemiol. 2001;154(8):687–693. doi: 10.1093/aje/154.8.687. [DOI] [PubMed] [Google Scholar]
- Ambrosone CB, Rebbeck TR, Morgan GJ, Albain KS, Calle EE, Evans WE, Hayes DF, Kushi LH, McLeod HL, Rowland JH, Ulrich CM. New developments in the epidemiology of cancer prognosis: traditional and molecular predictors of treatment response and survival. Cancer Epidemiol Biomarkers Prev. 2006;15(11):2042–2046. doi: 10.1158/1055-9965.EPI-06-0827. [DOI] [PubMed] [Google Scholar]
- Andrieu N, Dondon MG, Goldstein AM. Increased power to detect gene-environment interaction using siblings controls. Ann Epidemiol. 2005;15(9):705–711. doi: 10.1016/j.annepidem.2005.01.002. [DOI] [PubMed] [Google Scholar]
- Andrieu N, Goldstein AM. Use of relatives of cases as controls to identify risk factors when an interaction between environmental and genetic factors exists. Int J Epidemiol. 1996;25(3):649–657. doi: 10.1093/ije/25.3.649. [DOI] [PubMed] [Google Scholar]
- Andrieu N, Goldstein AM. Epidemiologic and genetic approaches in the study of gene-environment interaction: an overview of available methods. Epidemiol Rev. 1998;20(2):137–147. doi: 10.1093/oxfordjournals.epirev.a017976. [DOI] [PubMed] [Google Scholar]
- Andrieu N, Goldstein AM. The case-combined-control design was efficient in detecting gene-environment interactions. J Clin Epidemiol. 2004;57(7):662–671. doi: 10.1016/j.jclinepi.2003.11.014. [DOI] [PubMed] [Google Scholar]
- Ardlie KG, Kruglyak L, Seielstad M. Patterns of linkage disequilibrium in the human genome. Nat Rev Genet. 2002;3(4):299–309. doi: 10.1038/nrg777. [DOI] [PubMed] [Google Scholar]
- Begg CB, Zhang ZF. Statistical analysis of molecular epidemiology studies employing case-series. Cancer Epidemiol Biomarkers Prev. 1994;3(2):173–175. [PubMed] [Google Scholar]
- Botto LD, Khoury MJ. Commentary: facing the challenge of gene-environment interaction: the two-by-four table and beyond. Am J Epidemiol. 2001;153(10):1016–1020. doi: 10.1093/aje/153.10.1016. [DOI] [PubMed] [Google Scholar]
- Botto LD, Khoury MJ. Facing the challenge of complex genotypes and gene-environment interaction: the basic epidemiologic units in case-control and case-only designs. In: Khoury MJ, Little J, Burke W, editors. Human Genome Epidemiology: a scientific foundation for using genetic information to improve health and prevent disease. New York: Oxford University Press; 2004. pp. 111–126. [Google Scholar]
- Carlson CS. Agnosticism and equity in genome-wide association studies. Nat Genet. 2006;38(6):605–606. doi: 10.1038/ng0606-605. [DOI] [PubMed] [Google Scholar]
- Demark-Wahnefried W, Aziz NM, Rowland JH, Pinto BM. Riding the crest of the teachable moment: promoting long-term health after the diagnosis of cancer. J Clin Oncol. 2005;23(24):5814–5830. doi: 10.1200/JCO.2005.01.230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans DM, Marchini J, Morris AP, Cardon LR. Two-stage two-locus models in genome-wide association. PLoS Genet. 2006;2(9):e157. doi: 10.1371/journal.pgen.0020157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fagerholm R, Hofstetter B, Tommiska J, Aaltonen K, Vrtel R, Syrjakoski K, Kallioniemi A, Kilpivaara O, Mannermaa A, Kosma VM, Uusitupa M, Eskelinen M, Kataja V, Aittomaki K, von Smitten K, Heikkila P, Lukas J, Holli K, Bartkova J, Blomqvist C, Bartek J, Nevanlinna H. NAD(P)H:quinone oxidoreductase 1 NQO1*2 genotype (P187S) is a strong prognostic and predictive factor in breast cancer. Nat Genet. 2008;40(7):844–853. doi: 10.1038/ng.155. [DOI] [PubMed] [Google Scholar]
- Gatto NM, Campbell UB, Rundle AG, Ahsan H. Further development of the case-only design for assessing gene-environment interaction: evaluation of and adjustment for bias. Int J Epidemiol. 2004;33(5):1014–1024. doi: 10.1093/ije/dyh306. [DOI] [PubMed] [Google Scholar]
- Gauderman WJ. Sample size requirements for association studies of gene-gene interaction. Am J Epidemiol. 2002;155(5):478–484. doi: 10.1093/aje/155.5.478. [DOI] [PubMed] [Google Scholar]
- Gauderman WJ, Morrison JM. QUANTO 1.1: A computer program for power and sample size calculations for genetic-epidemiology studies. 2006 http://hydra.usc.edu/gxe.
- Goldstein AM, Dondon MG, Andrieu N. Unconditional analyses can increase efficiency in assessing gene-environment interaction of the case-combined-control design. Int J Epidemiol. 2006;35(4):1067–1073. doi: 10.1093/ije/dyl048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldstein AM, Falk RT, Korczak JF, Lubin JH. Detecting gene-environment interactions using a case-control design. Genet Epidemiol. 1997;14(6):1085–1089. doi: 10.1002/(SICI)1098-2272(1997)14:6<1085::AID-GEPI87>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- Hunter DJ. Gene-environment interactions in human diseases. Nat Rev Genet. 2005;6(4):287–298. doi: 10.1038/nrg1578. [DOI] [PubMed] [Google Scholar]
- Hwang SJ, Beaty TH, Liang KY, Coresh J, Khoury MJ. Minimum sample size estimation to detect gene-environment interaction in case-control designs. Am J Epidemiol. 1994;140(11):1029–1037. doi: 10.1093/oxfordjournals.aje.a117193. [DOI] [PubMed] [Google Scholar]
- Kazma R, Dizier MH, Guilloud-Bataille M, Bonaiti-Pellie C, Genin E. Power comparison of different methods to detect genetic effects and gene-environment interactions. BMC Proc. 2007;1 Suppl 1:S74. doi: 10.1186/1753-6561-1-s1-s74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khoury MJ, Flanders WD. Nontraditional epidemiologic approaches in the analysis of gene-environment interaction: case-control studies with no controls! Am J Epidemiol. 1996;144(3):207–213. doi: 10.1093/oxfordjournals.aje.a008915. [DOI] [PubMed] [Google Scholar]
- Kraft P, Hunter D. Integrating epidemiology and genetic association: the challenge of gene-environment interaction. Philos Trans R Soc Lond B Biol Sci. 2005;360(1460):1609–1616. doi: 10.1098/rstb.2005.1692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lake SL, Laird NM. Tests of gene-environment interaction for case-parent triads with general environmental exposures. Ann Hum Genet. 2004;68(Pt 1):55–64. doi: 10.1046/j.1529-8817.2003.00073.x. [DOI] [PubMed] [Google Scholar]
- Laupacis A, Wells G, Richardson WS, Tugwell P. Users' guides to the medical literature. V. How to use an article about prognosis. Evidence-Based Medicine Working Group. JAMA. 1994;272(3):234–237. doi: 10.1001/jama.272.3.234. [DOI] [PubMed] [Google Scholar]
- Lawlor DA, Harbord RM, Sterne JA, Timpson N, Davey Smith G. Mendelian randomization: using genes as instruments for making causal inferences in epidemiology. Stat Med. 2008;27(8):1133–1163. doi: 10.1002/sim.3034. [DOI] [PubMed] [Google Scholar]
- Link E, Parish S, Armitage J, Bowman L, Heath S, Matsuda F, Gut I, Lathrop M, Collins R. SLCO1B1 variants and statin-induced myopathy--a genomewide study. N Engl J Med. 2008;359(8):789–799. doi: 10.1056/NEJMoa0801936. [DOI] [PubMed] [Google Scholar]
- Mak K, Kum CK. How to appraise a prognostic study. World J Surg. 2005;29(5):567–569. doi: 10.1007/s00268-005-7914-x. [DOI] [PubMed] [Google Scholar]
- Marchini J, Donnelly P, Cardon LR. Genome-wide strategies for detecting multiple loci that influence complex diseases. Nat Genet. 2005;37(4):413–417. doi: 10.1038/ng1537. [DOI] [PubMed] [Google Scholar]
- Marchini J, Howie B, Myers S, McVean G, Donnelly P. A new multipoint method for genome-wide association studies by imputation of genotypes. Nat Genet. 2007;39(7):906–913. doi: 10.1038/ng2088. [DOI] [PubMed] [Google Scholar]
- McCarthy MI, Abecasis GR, Cardon LR, Goldstein DB, Little J, Ioannidis JP, Hirschhorn JN. Genome-wide association studies for complex traits: consensus, uncertainty and challenges. Nat Rev Genet. 2008;9(5):356–369. doi: 10.1038/nrg2344. [DOI] [PubMed] [Google Scholar]
- Melzer D, Perry JR, Hernandez D, Corsi AM, Stevens K, Rafferty I, Lauretani F, Murray A, Gibbs JR, Paolisso G, Rafiq S, Simon-Sanchez J, Lango H, Scholz S, Weedon MN, Arepalli S, Rice N, Washecka N, Hurst A, Britton A, Henley W, van de Leemput J, Li R, Newman AB, Tranah G, Harris T, Panicker V, Dayan C, Bennett A, McCarthy MI, Ruokonen A, Jarvelin MR, Guralnik J, Bandinelli S, Frayling TM, Singleton A, Ferrucci L. A genome-wide association study identifies protein quantitative trait loci (pQTLs) PLoS Genet. 2008;4(5) doi: 10.1371/journal.pgen.1000072. pe1000072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ottman R. Gene-environment interaction: definitions and study designs. Prev Med. 1996;25(6):764–770. doi: 10.1006/pmed.1996.0117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piegorsch WW, Weinberg CR, Taylor JA. Non-hierarchical logistic models and case-only designs for assessing susceptibility in population-based case-control studies. Stat Med. 1994;13(2):153–162. doi: 10.1002/sim.4780130206. [DOI] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38(8):904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155(2):945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roeder K, Devlin B, Wasserman L. Improving power in genome-wide association studies: weights tip the scale. Genet Epidemiol. 2007;31(7):741–747. doi: 10.1002/gepi.20237. [DOI] [PubMed] [Google Scholar]
- Rothman KJ, Greenland S, Lash TL. Modern Epidemiology. Philadelphia: Lippincott Williams & Wilkins; 2008. [Google Scholar]
- Schmidt S, Schaid DJ. Potential misinterpretation of the case-only study to assess gene-environment interaction. Am J Epidemiol. 1999;150(8):878–885. doi: 10.1093/oxfordjournals.aje.a010093. [DOI] [PubMed] [Google Scholar]
- Skol AD, Scott LJ, Abecasis GR, Boehnke M. Optimal designs for two-stage genome-wide association studies. Genet Epidemiol. 2007;31(7):776–788. doi: 10.1002/gepi.20240. [DOI] [PubMed] [Google Scholar]
- Smith PG, Day NE. The design of case-control studies: the influence of confounding and interaction effects. Int J Epidemiol. 1984;13(3):356–365. doi: 10.1093/ije/13.3.356. [DOI] [PubMed] [Google Scholar]
- Umbach DM, Weinberg CR. The use of case-parent triads to study joint effects of genotype and exposure. Am J Hum Genet. 2000;66(1):251–261. doi: 10.1086/302707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vallbohmer D, Lenz HJ. Predictive and prognostic molecular markers in outcome of esophageal cancer. Dis Esophagus. 2006;19(6):425–432. doi: 10.1111/j.1442-2050.2006.00622.x. [DOI] [PubMed] [Google Scholar]
- Wang LY, Lee WC. Population stratification bias in the case-only study for gene-environment interactions. Am J Epidemiol. 2008;168(2):197–201. doi: 10.1093/aje/kwn130. [DOI] [PubMed] [Google Scholar]
- Yang Q, Khoury MJ, Flanders WD. Sample size requirements in case-only designs to detect gene-environment interaction. Am J Epidemiol. 1997;146(9):713–720. doi: 10.1093/oxfordjournals.aje.a009346. [DOI] [PubMed] [Google Scholar]
- Yang Q, Khoury MJ, Sun F, Flanders WD. Case-only design to measure gene-gene interaction. Epidemiology. 1999;10(2):167–170. [PubMed] [Google Scholar]


