The learning curve for surgical margins after open radical prostatectomy: implications for the use of margin status as an oncologic endpoint

Abstract

Purpose

Surgical margin status is commonly used as an endpoint for surgical learning. In this study, we examine the learning curve for surgical margins and investigate whether surgical margins are good marker for oncologic outcome.

Materials and Methods

The study cohort included 7765 prostate cancer patients who were treated with radical prostatectomy by one of 72 surgeons at four major U.S. academic medical centers. We calculated the learning curve for surgical margins and a concordance probability between the surgeon's rates of positive surgical margins and 5-year biochemical recurrence.

Results

A positive surgical margin was identified in 2059 patients (27%). On multivariable analysis, surgeon experience was strongly associated with surgical margin status (p=0.017). The probability of a positive surgical margin was 40% for a surgeon with 10 prior cases, and decreased to 25% for a surgeon with 250 prior cases (absolute difference 15%, 95% CI 11% to 18%). Learning curves differed dramatically between surgeons. For pairs of surgeons, the surgeon with the superior positive surgical margin rate also had the better biochemical recurrence rate only 58% of the time.

Conclusions

We have demonstrated a learning curve for surgical margins after open radical prostatectomy. The poor concordance between a surgeon's margin and recurrence rates suggests that, while margins clearly matter, and efforts should be made to reduce positive margin rates, surgical margin status is not a strong surrogate for cancer control. These results have implications for the use of margin rates to evaluate changes in surgical technique and as feedback for surgeons.

Introduction

We have previously reported the surgical learning curve for open radical prostatectomy in terms of biochemical recurrence. In our primary analysis, we reported that a typical patient had a 17.9% risk of recurrence by five years if treated by an inexperienced surgeon with 10 prior cases, compared to a 10.7% risk if treated by a more experienced surgeon with 250 prior cases¹. We recently reported similar results for an independent data set of patients undergoing laparoscopic radical prostatectomy².

Our data on the learning curve is naturally informative about how surgeons learn and improve technique. In this respect, use of biochemical recurrence is a somewhat problematic endpoint for learning because it is not available for many years after a surgeon completes a radical prostatectomy. Many papers discussing technique in radical prostatectomy therefore use surgical margins as an endpoint. Indeed, in the landmark paper describing the nerve-sparing operation pioneered by Walsh, the authors reported good erectile outcomes and low surgical margin rates³. Since that time it has been common to use surgical margins as an endpoint to draw conclusions, such as that a certain structure can be spared or new approach taken without compromising “cancer control”^4-5.

Our radical prostatectomy data set includes both recurrence and margin endpoints. In this study, we compare and contrast the learning curves for biochemical recurrence and surgical margins to determine whether surgical margins are good marker for oncologic outcome.

Methods

Our study cohort has been described previously¹. In brief, a total of 7765 prostate cancer patients underwent open radical retropubic prostatectomy between 1987 and 2003 from one of 72 surgeons at one of four academic institutions. All information was obtained with appropriate institutional review board waivers.

To evaluate the association between surgeon experience and surgical margin status, we fitted a multivariable logistic regression model, with surgeon experience was entered in the model using restricted cubic splines with knots at the quartiles. Differences in case mix were adjusted for by including in the model preoperative PSA level, pathologic Gleason grade (categorized as ≤ 6, 7, and ≥ 8), extraprostatic extension, seminal vesicle invasion, and lymph node involvement. To adjust for the possibility of stage migration, we included as a covariate the year during which the surgery was performed. As observations from patients treated by the same surgeon form non-independent “clusters”, the sandwich estimator of variance was used in the regression models to provide a robust estimator of variance; this was done by specifying cluster in Stata statistical software (version 10; StataCorp LP, College Station, TX). To produce a learning curve, we used the mean value for covariates to estimate the probability of a positive surgical margin predicted by the model for each level of surgical experience. Confidence intervals for the difference between selected points on the curve were obtained by bootstrapping. All P values are two-sided.

To explore the relationship between positive surgical margins and recurrence, we calculated the concordance probability between the surgeons' rates of positive surgical margins and 5-year biochemical recurrence, which was defined as the proportion of pairwise comparisons between surgeons where the surgeon with the lower adjusted positive surgical margin rate also had a lower adjusted 5-year probability of recurrence. Because predicted probabilities close to each other are clinically equivalent, we performed a sensitivity analysis allowing for an error rate of 1% between estimates. In other words, for any two surgeons i and j, the pairwise comparison c_ij equals 1 if (a) both the recurrence rate and margin rate for surgeon i were at least 1% higher than the respective rates for surgeon j; (b) both rates were at least 1% lower; (c) both the recurrence rates and margin rates for surgeon i and j were within 1% of each other; all other comparisons were given a value of 0. The concordance probability allowing for the error rate of 1% was then calculated by summing c_ij, and dividing by the total number of pairwise comparisons. The probability of a positive surgical margin for each surgeon was computed from a logistic regression model with the same covariates as specified above, excluding surgeon experience, and entering surgeon as a fixed effect. The 5-year probability of recurrence for each surgeon was computed from a parametric survival time model using the same predictors as those used for prediction of a positive surgical margin; we assumed a log-logistic survival distribution, which was found to be appropriate in previous analyses of these data¹. Percentile based confidence intervals for the concordance probability were obtained by bootstrapping with 2000 replications.

We performed two additional analyses to determine whether our findings were robust to the statistical methods used. First, we used a two-stage model: we calculated the adjusted probability of a positive surgical margin for each surgeon and then entered this probability as a predictor into a multivariable survival model for biochemical recurrence. Second, we calculated the Spearman's rank correlation between a surgeon's adjusted rates of potency and continence.

Results

Patient characteristics by surgeon experience are given descriptively in Table 1. A positive surgical margin was identified in 2059 patients (27%), and was less frequent in patients treated by more experienced surgeons. A positive surgical margin was identified in 42% (582/1402) of patients treated by a surgeon with fewer than 50 prior cases. Although this rate was lower in the subgroup of patients treated after 1995 (after which stage migration appeared to be largely complete in this cohort¹), it was still higher than the rate among patients treated by a surgeon with at least 1000 prior cases: 36% (241/668) for < 50 versus 11% (125/1152) for ≥ 1000 prior cases.

Table 1.

Patient and tumor characteristics by surgeon experience^*. Note that this is the same table as that presented in our previous manuscript examining the learning curve for biochemical recurrence, as the same data set was used for both analyses.

	Surgeon experience (no. of cases before the incident case)					P†
	< 50	50–99	100–249	250–999	≥1000
Number of patients	1402	696	1575	2940	1152
Patient or tumor characteristic
Median preoperative PSA level, ng/mL (IQR)	7.3 (5.1–12.1)	6.8 (4.9–9.9)	7.3 (5.2–12.0)	6.6 (4.8–9.4)	6.0 (4.7–8.0)	.002
Median age at surgery, yr (IQR)	63 (58–67)	62 (57– 66)	61 (56–66)	61 (56–66)	59 (54–64)	<.001
Gleason grade, no. (%)						.6
≤5	95 (7)	31 (4)	146 (9)	133 (5)	25 (2)
6	547 (39)	286 (41)	556 (35)	1117 (38)	529 (46)
7	669 (48)	341 (49)	748 (47)	1489 (51)	553 (48)
8	75 (5)	27 (4)	86 (5)	133 (5)	26 (2)
≥9	16 (1)	11 (2)	39 (2)	68 (2)	19 (2)
Extraprostatic extension	419 (30)	196 (28)	491 (31)	893 (30)	262 (23)	.004
Seminal vesicle invasion	164 (12)	64 (9)	166 (11)	249 (8)	52 (5)	<.001
Lymph node involvement	56 (4)	28 (4)	53 (3)	118 (4)	36 (3)	.5
Non-organ confined cancer‡	458 (33)	216 (31)	536 (34)	940 (32)	273 (24)	<.001
Number of operations performed by time period (%)						<.001
1987–1990	202 (14)	32 (5)	152 (10)	51 (2)	0 (0)§
1991–1995	532 (38)	179 (26)	646 (41)	864 (29)	0 (0)§
1996–2000	504 (36)	293 (42)	441 (28)	1294 (44)	485 (42)
2001–2003	164 (12)	192 (28)	336 (21)	731 (25)	667 (58)
Unadjusted outcomes
Positive surgical margin, no. (%)	582 (42)	235 (34)	493 (31)	624 (21)	125 (11)
Five-year probability of recurrence, % (95% CI)	27 (24 to 30)	23 (19 to 27)	19 (17 to 22)	16 (14 to 17)	8 (6 to 10)

^*PSA = prostate-specific antigen; IQR = interquartile range; CI = confidence interval.

^†P values (two-sided) were determined by regression models in which the number of prior cases was entered as a continuous variable, with adjustment for clustering by surgeon.

^‡Non-organ confined cancer = extraprostatic extension, seminal vesicle invasion, or lymph node involvement.

^§The two surgeons who treated 1000 or more patients treated their 1000^th cases in 1996 and 2001, respectively. Hence, no patient who received surgery before 1996 was operated on by a surgeon who, at the time, had 1000 or more prior cases.

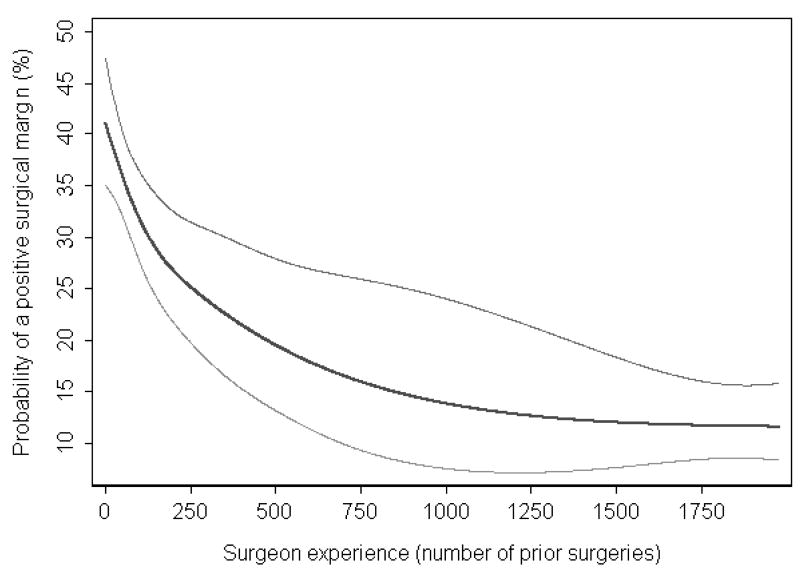
On multivariable analysis controlling for tumor characteristics and year of surgery, surgeon experience was strongly associated with surgical margin status (p=0.017). The learning curve for positive surgical margins is given in Figure 1. With increasing experience, the probability of a positive surgical margin decreases: the probability of a positive surgical margin was 40.1% for a surgeon with 10 prior cases, and decreased to 25.2% for a surgeon with 250 prior cases (absolute difference 14.9%, 95% CI 11.3% to 18.2%, Table 2).

Figure 1. The surgical learning curve for a positive surgical margin.

Predicted probability (black curve) and 95% confidence intervals (gray curves) of a positive surgical margin are plotted against increasing surgical experience. Probabilities are for a patient with typical cancer severity (mean prostate-specific antigen level, pathologic stage, and grade) treated in 1997 (approximately equal numbers of patients were treated before and after 1997).

Table 2.

Adjusted probability of positive surgical margin for a surgeon with 10 vs 250 prior cases

	Adjusted P value for surgeon experience†	Adjusted probability of positive surgical margin, %		Difference in 250 vs 10 prior cases (95% Confidence Interval)
		10 prior cases	250 prior cases	Absolute difference, %	Relative difference
Main analyses
Overall	0.017	40.1	25.2	14.9 (11.3, 18.2)	1.59 (1.43, 1.76)
Organ confined	<0.001	33.8	18.6	15.2 (11.2, 19.6)	1.82 (1.56, 2.14)
Non-organ confined	0.008	55.3	43.1	12.2 (6.1, 18.7)	1.28 (1.13, 1.46)

^*Probabilities are for a patient with typical cancer severity (mean prostate-specific antigen level, pathologic stage and grade) treated in 1997 (approximately equal numbers of patients were treated before and after 1997). PSA = prostate-specific antigen.

^†Test for the association between experience and outcome in the multivariable model (two-sided p value)

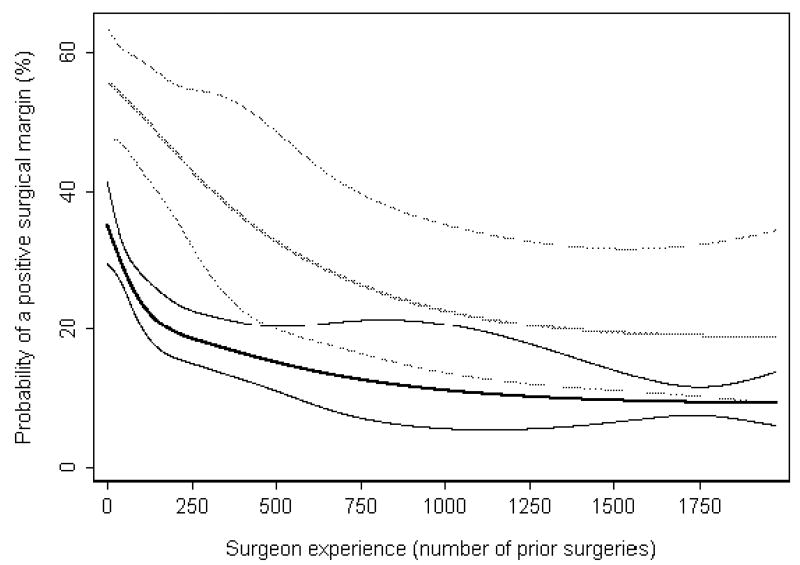
Figure 2 shows the learning curves for positive surgical margins stratified by pathologic stage (extraprostatic extension, seminal vesical invasion, or lymph node involvement vs. organ-confined disease). The significant association between surgeon experience and surgical margin status remained within each group (both p<0.01). The shapes of the learning curves are fairly similar: in both groups, there is a decrease in positive surgical margins until approximately 500 prior cases, at which point both curves level off. The absolute risk reduction associated with 250 versus 10 prior cases was 15.2% (95% CI 11.2% to 19.6%) for organ confined and 12.2% (95% CI 6.1% to 18.7%) for non-organ confined disease.

Figure 2. The surgical learning curve for a positive surgical margin, stratified by presence of organ-confined disease.

Predicted probability and 95% confidence intervals (organ confined: black curves; non-organ confined: gray curves) of a positive surgical margin are plotted against increasing surgical experience. Probabilities are for a patient with typical cancer severity (mean prostate-specific antigen level, pathologic stage, and grade) within each group, treated in 1997 (approximately equal numbers of patients were treated before and after 1997).

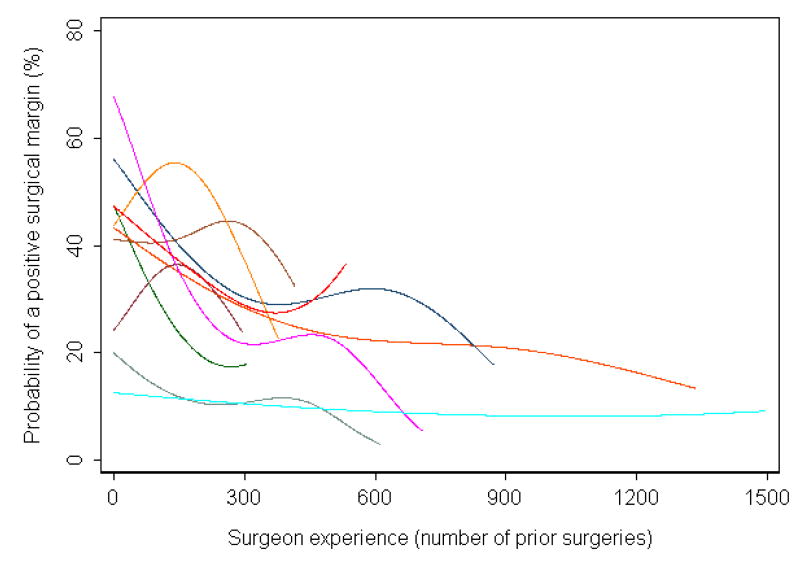
The learning curves of individual surgeons who performed at least 250 cases are shown in Figure 3. It is clear that, not only do margin rates vary dramatically between surgeons for a given level of surgical experience, but that the shape of the learning curve also varies: two surgeons have low positive margin rates throughout their entire careers, while others start with high rates that decrease dramatically. One surgeon appears to have results that get worse and then improve. On closer examination of this surgeon's data, we found that the rate of positive surgical margins stayed the same approximately constant over time, but that patients in the middle of the series had substantially lower risk disease.

Figure 3. Learning curve for positive surgical margins, separately by surgeon, for those who performed at least 250 cases.

If one assumes that the propensity to call a particular surgical specimen as margin positive might vary by pathologist, it may be that observations from patients treated at the same institution, and whose specimens are thus examined by the same group of pathologists, are not independent. We explored various models that controlled for this clustering effect, including GEE models correcting for institution, and multi-level models correcting for both surgeon and institution. The institution effect was small in all cases and the association between surgeon experience and positive surgical margins remained statistically significant (p<0.05).

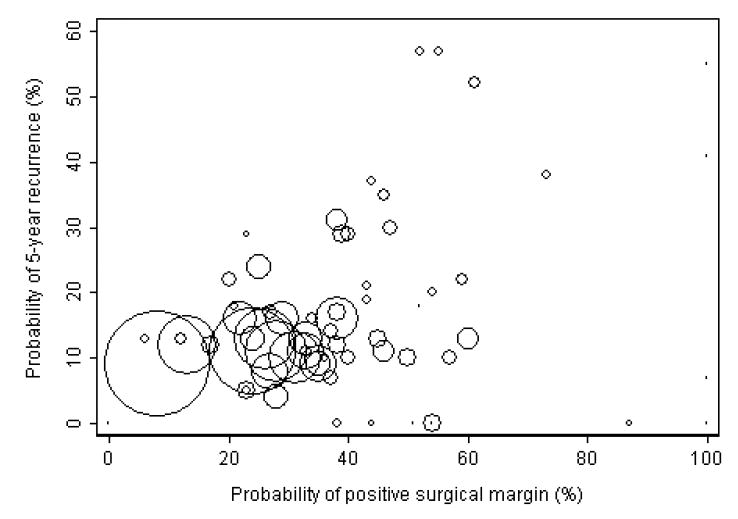
A scatter plot of the adjusted probability of 5-year biochemical recurrence by the adjusted probability of positive surgical margins for each surgeon is given in Figure 4. The concordance probability between the surgeons' rates of positive surgical margins and 5-year biochemical recurrence is given in Table 3. The surgeon with the superior positive surgical margin rate also had the better 5-year biochemical recurrence rate only 58% of the time, not much better than a coin flip. Sensitivity analyses (table 3) failed to improve this result. No analyses suggested that a surgeon's margin results were a useful surrogate for cancer control. These results were confirmed by additional analyses. On multivariable analysis, the surgeons' rate of positive surgical margins was significantly associated with subsequent biochemical recurrence (p<0.001), however, the effect size was very small (coefficient of 0.2 for each 10% increase in rate of positive surgical margin, compared to a coefficient of 1.2 for presence of extracapsular extension). Similarly, the correlation between the surgeons' rates of positive surgical margins and 5-year biochemical recurrence was statistically significant, but small (Spearman rank correlation 0.29; 95% confidence interval 0.06 to 0.49, p=0.015, Table 3).

Figure 4. Scatter plot of adjusted probability of 5-year biochemical recurrence versus adjusted probability of positive surgical margins.

Each circle represents a single surgeon, and the size of the circle is proportional to the number of patients treated by that surgeon.

Table 3.

Concordance probability and Spearman rank correlation between the rates of positive surgical margins and 5-year biochemical recurrence. 95% confidence intervals are given in parentheses.

		Number of surgeons	Number of patients	Concordance Probability (%)		Spearman rank correlation
				0% error	1% error
(1)	Main analyses	72	7765	58 (50, 62)	55 (49, 61)	0.29 (0.06, 0.49)
(2)	Patients treated after 1995	60	5107	53 (44, 57)	52 (42, 56)	0.19 (-0.07, 0.42)
(3)	(2) and surgeons with ≥ 40 total cases	38	4931	46 (34, 55)	45 (32, 53)	0.01 (-0.31, 0.33)
(4)	(3) and patients with organ confined disease	38	3637	49 (35, 55)	47 (33, 53)	0.12 (-0.20, 0.43)

Discussion

We have demonstrated a learning curve for surgical margins after open radical prostatectomy. A patient treated by an experienced surgeon (250 procedures), compared to a patient treated by an inexperienced surgeon with 10 prior procedures, has an absolute risk reduction of a positive margin of 15%, and a relative risk reduction close to 40%.

There are various lines of evidence to suggest that, although improvements in margin status associated with experience are correlated with those for biochemical recurrence, there is no strong causal association between the two. Firstly, as we have previously reported, the learning curve for recurrence is not importantly affected by adjustment for margins: for example, the absolute risk reduction for 250 versus 10 prior surgeries is was 5.3% after adjustment for margin status, and 7.2% without adjustment. Second, margin status plateaus at about 10% for organ-confined cancer. In contrast, recurrence rates in organ-confined disease continue to improve with increasing experience, with recurrence rates approaching 1% for the most experienced surgeons.

Furthermore, we saw very poor concordance between a surgeon's margin and recurrence rates in this group of academic surgeons. It seems natural to assume that a surgeon with lower positive margin rates than a colleague would also have lower rates of biochemical recurrence. Our data, however, suggest that the two are virtually independent.

This suggests that margin rates and recurrence improve with experience by independent mechanisms. There is a clear and obvious explanation for such a difference: learning for surgical margins, but not biochemical recurrence, involves feedback. Traditional learning theory gives a feedback a central role: in the case of a straightforward task, such as learning to shoot a basketball free throw, individuals learn by directly observing success and failure; for more complex tasks, such as learning to talk, repeated feedback from adults about errors allows children to learn the rules of grammar. In either case, the individual is able to link particular actions to success, others to failure, and thereby improve success rates over time. This is certainly plausible in the case of surgical margins, as the surgeon is told of the patient's margin status relatively soon after surgery, when the memory of the procedure is still fresh, and so may be able to relate a positive margin a particular aspect of the procedure. In contrast, biochemical recurrences occur many years later, at which time the surgeon is unlikely to remember any specifics about the patient's surgery. Improvements in biochemical recurrence rates therefore must occur by some general process of improved surgical technique.

Our findings have several implications. First, it becomes questionable whether margin rates can be used to evaluate changes in surgical technique. The common claim is that a new technique can improve functional outcomes without compromising oncologic control is generally based on equivalent surgical margin rates. Yet if margin rates do not have a strong concordance with biochemical recurrence, it is quite possible for a technique to have similar margin rates but lead to poorer (or conceivably superior) recurrence outcomes. Our findings also have implications for the use of margin rates as feedback for surgeons. It has been suggested that, in an effort to improve outcomes, surgeons might be given data as to their margin rates in comparison to their peers, perhaps adjusted for case mix. Yet if differences in margin rates between surgeons have only a marginal association with differences in recurrence rates, it is questionable whether such feedback would ultimately improve cancer outcomes. Indeed, it is possible that such a system might create an incentive for surgeons to treat low risk cases - many of whom would suffer no ill-effects of their cancer in the absence of treatment - at the expense of patients with high risk cancer, who stand to gain the most from surgery. It is also possible that surgeons told that they have above average margin rates would tend towards a wider excision, with consequent effects on functional outcomes.

The failure of margins to provide an acceptable surrogate for surgical performance seems counter-intuitive. The aim of cancer surgery is, after all, to remove cancer, and a positive margin suggests that cancer has been left in the body. Yet it is clear that some margins are likely artifactual; note, for example, in some series, apical margins had no apparent association with recurrence⁶. It is also apparent that the recurrence can occur even if tumor cells are not detected at the edges of the pathologic specimen: in this series, there was a 5% recurrence probability by 5 years for patients with negative margins and organ confined disease. Conversely, a positive margin is far from an inevitable harbinger of recurrence: patients with organ-confined disease but positive margins had greater than a 75% probability of being free of recurrence at 5 years.

Our findings may be taken as contradicting previous work on the importance of surgical margins, including our own prior studies^7-8. This contradiction is more apparent than real. Like previous authors, we did find an overall association between positive surgical margins and biochemical recurrence (hazard ratio of 2.1, p<0.0005, after adjustment for pathologic stage, grade and PSA) and, more specifically, a statistically significant association between a surgeon's margin and recurrence rates. What we are reporting is not that the association is absent, but that it is weak. This is in keeping with prior research. For example, in a recent postoperative nomogram⁷, a positive surgical margin has one-quarter of the effect of primary Gleason grade, one-third the effect of seminal vesicle invasion and one-half the effect of extraprostatic extension.

Conclusions

The existence of a surgical learning curve for positive surgical margins reconfirms the importance of surgeon experience for optimizing outcomes after radical prostatectomy. Surgical margins clearly matter, and efforts should be made to reduce margin rates; nonetheless, it appears questionable whether positive margin rates can be used to evaluate changes in surgical technique or as feedback for surgeons as to outcome.