Sensitivity Enhancement of Separated Local Field Experiments: Application to Membrane Proteins

Abstract

Separated local field (SLF) experiments have been used for almost three decades to obtain structural information in solid-state NMR. These experiments resolve chemical shift anisotropy (CSA) from dipole-dipole interactions (dipolar couplings, DC) in isolated spin systems. Both CSA and DC data can be converted into orientational constraints to elucidate the secondary structure and topology of membrane proteins in oriented lipid bilayers. Here, we propose a new suite of sensitivity enhanced SLF pulse sequences to measure CSA and DC for aligned membrane proteins and liquid crystalline molecules that will decrease the time needed for data acquisition. We demonstrate the efficacy of these new sensitivity enhanced experiments using both a single crystal of N-acetyl leucine and a single pass membrane protein sarcolipin reconstituted in aligned lipid bicelles. These results lay the groundwork for the routine application of these methods for studying the structure and topology of membrane proteins.

INTRODUCTION

Dipole-dipole couplings (DC) and chemical shift anisotropy (CSA) are of central importance to structure determination of membrane proteins by solid-state NMR (ssNMR) spectroscopy ^1-3. These parameters are directly measured using separated local field (SLF) experiments that resolve CSA of spin S and DC between spins I and S in two dimensions ^{2, 4, 5}. If the CSA tensor of spin S and the distance between spins I and S are known, then the observables are easily converted into orientational-dependent restraints for structure determination ^6-12.

SLF experiments have been widely used by chemists and biophysicists to characterize the structures of liquid crystals as well as macromolecules such as membrane proteins in mechanically and magnetically aligned lipid bilayers ^13-24.

Since the introduction of the SLF experiment⁴, several variants have emerged ^25-28, of which, PISEMA (Polarization Inversion Spin Exchange at the Magic Angle) has been the most widely used ^{25, 29, 30}. Significant advantages of the PISEMA experiment are the large scaling factor (0.82) for dipolar evolution and the narrow spectral lines in the dipolar coupling dimension, which has enabled the spectroscopic analysis of several ¹⁵N labeled membrane proteins reconstituted in oriented lipid membranes ². Although quite robust, the PISEMA experiment has several disadvantages that have limited its application to structural biology. First, the values of the DC strongly depend on the proton frequency offset during FSLG (Frequency Switched Lee-Goldburg) decoupling ³¹ in the t₁ evolution. Second, small dipolar couplings are often obscured by intense zero frequency peaks in the dipolar dimension. Third, the PISEMA experiment, similar to all SLF experiments observed on the rare spin S, is relatively insensitive, which has limited the routine application of this approach to ~12 membrane protein structures ².

To overcome the problems of frequency offset and zero frequency peaks, several pulse sequences have been proposed (broadband-PISEMA, SAMPI4, and HIMSELF) ^25-28. These experiments differ primarily in the pulse schemes used during the t₁ evolution period, when I-S spin exchange occurs (heteronuclear DC evolution). Depending on the sample conditions (bicelles versus mechanically aligned bilayers) and DC values, these SLF experiments offer valuable alternatives to the PISEMA experiment.

Recently, we proposed a new experiment called sensitivity-enhanced PISEMA (SE-PISEMA), which increases the sensitivity up to 40% ³². Unlike the original PISEMA pulse sequence, which records only the cosine modulated dipolar coherences, the SE-PISEMA scheme detects both sine and cosine dipolar modulated coherences. Addition and subtraction of these components enhance the signals with a direct dependence on the DC value, which is optimized by changing τ in the constant dipolar evolution period (see Figure 1).

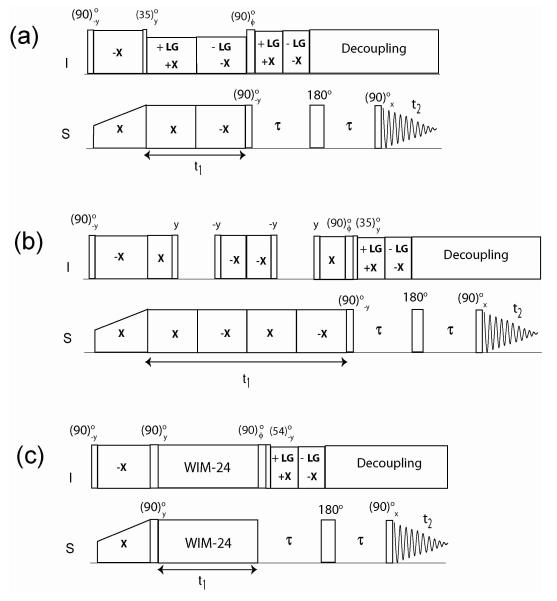
Figure 1.

Pulse sequences for SE-PISEMA (A), SE-SAMPI4 (B) and SE-HIMSELF (C). Phase ϕ is cycled between y and −y to achieve sensitivity enhancement.

In this work, we report a generalized theory for SLF experiments and devise new sensitivity enhanced SAMPI4 and HIMSELF experiments (SE-SAMPI4 and SE-HIMSELF). These experiments will extend the application of SLF pulse sequences on systems with small dipolar couplings by increasing the signals up to 40%. We demonstrate the efficacy of these pulse sequences for a single crystal of ¹⁵N N-acetyl leucine (NAL) and for the membrane protein sarcolipin (SLN) aligned in 1,2-dihexanoyl-sn-glycero-3-phosphocholine/1,2-dimyristoyl-sn-glycero-3-phosphocholine (DHPC/DMPC) bicelles.

THEORY AND METHODS

The theory of PISEMA, SAMPI4 and HIMSELF has been thoroughly discussed in the literature ^{25-28, 33, 34}. Here, we report the relevant spin operators that give rise to the dipolar oscillations, describing the resulting density matrices and deriving the corresponding SE observables.

Each of the SLF sequences (Figure 1) starts with a (90)^o_−y pulse applied on I spins followed by Hartmann-Hahn cross polarization ³⁵ on I and S spins with phases −x and x, respectively. In each of these sequences the effective Hamiltonian during the t₁ evolution period is given by,

$$H_{\mathit{SLF}}\left(t_1\right)=s_{\mathit{SLF}}\cdot {\omega }_{\mathit{IS}}(I_x{S}_x+I_y{S}_y)$$ (1)

where s_SLF =0.82 for PISEMA, s_SLF =1.09 for SAMPI4, and s_SLF=0.66 for HIMSELF; ω_IS = 2π D_IS, where D_IS is heteronuclear DC between I and S. All of the relevant transformations are reported in the Supporting Information. The final density matrix for the SLF experiments is given by:

$${\rho }_{\mathit{SLF}}=S_x.\cos \left(s_{\mathit{SLF}}{\omega }_{\mathit{IS}}{t}_1\right).e^{i{\omega }_s{t}_2}$$ (2)

From equation 2, it is clear that during t₂ acquisition only the cosine dipolar coherence is detected, while the sine term is encoded in the undetectable two-spin operator (see Supporting Information). In SE-SLF experiments, 90^o pulses are applied on I and/or S spins after t₁ evolution, so that the S_x operator is converted into S_z and one operator of the multiple quantum coherences associated with sine dipolar coherence is converted into an antiphase operator 2I_zS_y. For both the PISEMA and SAMPI4 experiments, a (90)^S_−y pulse converts S_x into S_z, whereas for the HIMSELF experiment the S spin operator associated with cosine term is already along the z direction (see Supporting Information). Therefore, for the latter experiment no flip angle pulse is required on the S spins. The multiple quantum term 2I_xS_y is converted into 2I_zS_y by applying a (90)^o_y pulse on the I spin. The resulting density matrices are:

$$\begin{array}{cc}\hfill & {\rho }_{\mathit{SE}-\mathit{PISEMA}}(t_1-{\left(90\right)}_y^I-{\left(90\right)}_{-y}^S)=(I_x-S_z)\cos \left(s_{\mathit{PISEMA}}{\omega }_{\mathit{IS}}{t}_1\right)-(2I_y{S}_x+2I_Z{S}_y)\sin \left(s_{\mathit{PISEMA}}{\omega }_{\mathit{IS}}{t}_1\right)\hfill \\ \hfill & {\rho }_{\mathit{SE}-\mathrm{SAMPI}4}(t_1-{\left(90\right)}_y^I-{\left(90\right)}_{-y}^S)=(I_x-S_z)\cos \left(s_{\mathrm{SAMPI}4}{\omega }_{\mathit{IS}}{t}_1\right)-(2I_y{S}_x+2I_Z{S}_y)\sin \left(s_{\mathrm{SAMPI}4}{\omega }_{\mathit{IS}}{t}_1\right)\hfill \\ \hfill & {\rho }_{\mathit{SE}-\text{HIMSELF}}(t_1-{\left(90\right)}_y^I)=(I_x-S_z)\cos \left(s_{\mathit{SE}-\text{HIMSELF}}{\omega }_{\mathit{IS}}{t}_1\right)-(2I_y{S}_x+2I_Z{S}_y)\sin \left(s_{\mathit{SE}-\text{HIMSELF}}{\omega }_{\mathit{IS}}{t}_1\right)\hfill \end{array}$$ (3)

The spin operators of eq 3 are with respect to the sigly-tilted rotating frames defined in eq 5S. After the evolution period, FSLG spin lock is applied on I spins which gives the scaled heteronuclear dipolar coupling Hamiltonian H_IS(τ) in the singly-tilted rotating frame defined by the operator U_τ.

$$\begin{array}{cc}\hfill & H_{\mathit{IS}}\left(\tau \right)=\cos {\theta }_m.2I_z{S}_z\hfill \\ \hfill & U_{\tau }=e^{-i{\theta }_m{I}_y}.1\hfill \end{array}$$ (4)

To match the rotating frames of eq 5S to those of U_τ in eq 4, suitable transformation pulses are applied prior to the τ period. The tilted rotating frames of eq 5S can be related to U_τ:

$$\begin{array}{cc}\hfill & U_{\mathit{PISEMA}}^{\prime }=U_{\tau }\hfill \\ \hfill & U_{\mathrm{SAMPI}4}^{\prime }=e^{-i\left(\right(\pi ∕2)-{\theta }_m)I_y}.U_{\tau }\hfill \\ \hfill & U_{\text{HIMSELF}}^1=e^{i{\theta }_m{I}_y}.U_{\tau }\hfill \end{array}$$ (5)

From eq 5, it is apparent that U’PISEMA = U_τ and for the SE-PISEMA experiment no transformation pulse is required, whereas (35.3)^o_y and (54.7)^o_−y transformation pulses are needed for both SE-SAMPI4 and SE-HIMSELF, respectively. The resulting density matrices at τ = 0 with the spin operators represented in a tilted rotating frame U_τ, are:

$$\begin{array}{cc}\hfill & {\rho }_{\mathit{SE}-\mathit{PISEMA}}(t_1-{\left(90\right)}_y^I-{\left(90\right)}_{-y}^S)=(I_x-S_z)\cos \left(s_{\mathit{PISEMA}}{\omega }_{\mathit{IS}}{t}_1\right)-(2I_y{S}_x+2I_Z{S}_y)\sin \left(s_{\mathit{PISEMA}}{\omega }_{\mathit{IS}}{t}_1\right)\hfill \\ \hfill & {\rho }_{\mathit{SE}-\mathrm{SAMPI}4}(t_1-{\left(90\right)}_y^I-{\left(90\right)}_{-y}^S-{\left(35\right)}_y^o)=(I_x-S_z)\cos \left(s_{\mathrm{SAMPI}4}{\omega }_{\mathit{IS}}{t}_1\right)-(2I_y{S}_x+2I_Z{S}_y)\sin \left(s_{\mathrm{SAMPI}4}{\omega }_{\mathit{IS}}{t}_1\right)\hfill \\ \hfill & {\rho }_{\mathit{SE}-\text{HIMSELF}}(t_1-{\left(90\right)}_y^I-{\left(54.7\right)}_{-y}^o)=(I_x-S_z)\cos \left(s_{\text{HIMSELF}}{\omega }_{\mathit{IS}}{t}_1\right)-(2I_y{S}_x+2I_Z{S}_y)\sin \left(s_{\text{HIMSELF}}{\omega }_{\mathit{IS}}{t}_1\right)\hfill \end{array}$$ (6)

Since the spin operators are of the same form and are defined in the same tilted rotating frame U_τ, eq 6 can be reformulated into a master equation valid for all of the SLF experiments:

$${\rho }_{\mathit{SE}-\mathit{SLF}}(\tau =0)=(I_x-S_z)\cos \left(s_{\mathit{SLF}}{\omega }_{\mathit{IS}}{t}_1\right)-(2I_y{S}_x+2I_Z{S}_y)\sin \left(s_{\mathit{SLF}}{\omega }_{\mathit{IS}}{t}_1\right)$$ (7)

where subscript SLF indicates any SLF experiment (PISEMA, SAMPI4, or HIMSELF).

During the τ period, the antiphase S spin operator 2I_zS_y evolves under scaled heteronuclear DC Hamiltonian H_IS(τ). The chemical shift evolution of the S spin during the first τ period is refocused by a 180^o pulse followed by another τ period under the effect of the heteronuclear DC. The evolution of 2I_zS_y operator during the 2τ period is given by:

$$2I_z{S}_y\to 2I_z{S}_y\cos \left(\cos {\theta }_m{\omega }_{\mathit{IS}}\tau \right)-S_x\sin \left(\cos {\theta }_m{\omega }_{\mathit{IS}}\tau \right)$$ (8)

The other spin operators I_x and 2I_yS_x are evolved into unobservable two-spin operators and are neglected. Combining eqs 7 and 8 and considering only the S spin operators, the density matrix at the end of the 2τ period is given by:

$${\rho }_{\mathit{SE}-\mathit{SLF}}\left(2\tau \right)=-S_z\cos \left(s_{\mathit{SLF}}{\omega }_{\mathit{IS}}{t}_1\right)+S_x\sin \left(s_{\mathit{SLF}}{\omega }_{\mathit{IS}}{t}_1\right).\sin \left(\cos {\theta }_m{\omega }_{\mathit{IS}}\tau \right)$$ (9)

A final (90)^o_x pulse on S spin followed detection of S under I spin decoupling gives the density matrix ρ₁:

$${\rho }_1=\left[S_y\cos \left(s_{\mathit{SLF}}{\omega }_{\mathit{IS}}{t}_1\right)+S_x\sin \left(s_{\mathit{SLF}}{\omega }_{\mathit{IS}}{t}_1\right).\sin \left(\cos {\theta }_m{\omega }_{\mathit{IS}}\tau \right)\right]e^{i{\omega }_s{t}_2}$$ (10)

In the subsequent scan, the phase of the 90^o pulse on I spin after t₁ is set to −y. This inverts the sign of the antiphase term 2I_zS_y, which gives the final density matrix ρ₂.

$${\rho }_2=\lfloor S_y\cos \left(s_{\mathit{SLF}}{\omega }_{\mathit{IS}}{t}_1\right)-S_x\sin \left(s_{\mathit{SLF}}{\omega }_{\mathit{IS}}{t}_1\right).\sin \left(\cos {\theta }_m{\omega }_{\mathit{IS}}\tau \right)\rfloor e^{i{\omega }_s{t}_2}$$ (11)

ρ₁ and ρ₂ are stored in separate files, with addition and subtraction of ρ₂ from ρ₁ giving the cosine and sine dipolar coherences, ρ_c and ρ_s, respectively.

$$\begin{array}{cc}\hfill & {\rho }_c={\rho }_1+{\rho }_2=\left[2S_y\cos \left(s_{\mathit{SLF}}{\omega }_{\mathit{IS}}{t}_1\right)\right]e^{i{\omega }_s{t}_2}\hfill \\ \hfill & {\rho }_s={\rho }_1-{\rho }_2=\sin \left(\cos {\theta }_m{\omega }_{\mathit{IS}}\tau \right)\left[2S_x\sin \left(s_{\mathit{SLF}}{\omega }_{\mathit{IS}}{t}_1\right)\right]e^{i{\omega }_s{t}_2}\hfill \end{array}$$ (12)

The terms ρ_c and ρ_s can also be obtained by phase cycling the last 90^o pulse on the ¹⁵N channel ³². Note that ρ_c and ρ_s have a relative 90^o phase shift in both t₁ and t₂ dimensions. Thus, after Fourier transformation a 90^o zero-order phase correction is applied on ρ_c and ρ_s to obtain absorptive peak shapes. The resultant SE-SLF spectrum is obtained by adding ρ_c and ρ_s.

$${\rho }_{\mathit{SE}-\mathit{SLF}}={\rho }_c({\omega }_1,{\omega }_2)+{\rho }_s({\omega }_1,{\omega }_2)$$ (13)

Note that the zero order phase correction can also be applied prior to Fourier Transform. From eqs 10-12, it is clear that one can detect and uncouple the cosine and sine dipolar coherences by using a two-step phase cycle. The final density matrix for the SLF experiments (PISEMA, SAMPI4, and HIMSELF, see eq 2) with two scans for each increment is given by

$${\rho }_{\mathit{SLF}}(t_1,t_2)=2S_x\cos \left({\omega }_{\mathit{IS}}{t}_1\right)e^{i{\omega }_s{t}_2}$$ (14)

The dipolar peaks in each doublet have the same sign for ρ_c, whereas they have opposite sign for ρ_s. Addition of these two data sets gives a two-dimensional spectrum, in which the intensity of one component of each dipolar doublet is increased by the factor [1 + sin(cos θ_mω_ISτ)] with respect to the corresponding peak in the classical SLF experiment performed with two scans. The RMS noise of ρ_c and ρ_s is identical to that of ρ_slf (see eq 14). Similar to the SE scheme in liquid-state NMR, the addition or subtraction of two datasets (ρ_c and ρ_s, whose RMS noises are uncorrelated) causes the noise level to increase by $\sqrt{2}$³⁶. Therefore, the signal to noise for the SE-SLF experiment (S/N_SE-SLF) is related to that of the SLF experiment (S/N_SLF) by the following equation:

$${\left(\frac{S}{N}\right)}_{\mathit{SE}-\mathit{SLF}}=\frac{1+\sin \left(\cos {\theta }_m{\omega }_{\mathit{IS}}\tau \right)}{\sqrt{2}}{\left(\frac{S}{N}\right)}_{\mathit{SLF}}$$ (15)

SLN expression, purification and solid-state NMR sample preparation

[U-¹⁵N] labeled SLN was expressed in E. coli bacteria and purified as reported previously ³⁷. Bicelles were formed drying 37.2 mg of DMPC and 7.6 mg of DHPC in chloroform into separate glass vials under a stream of N₂ gas (DMPC/DHPC molar ratio of 3.2/1.). The lipids were placed in a vacuum desiccator overnight to ensure complete removal of the chloroform. An aqueous solution of DHPC was obtained by adding 50 μL of NMR buffer (120 mM NaCl, 20 mM phosphate, 0.02% NaN₃, pH 6) to the dry DHPC lipid followed by extensive vortexing and a brief bath sonication (~1 min). The DHPC solution was added to 1 mg of [U-¹⁵N] labeled sarcolipin powder, and vortexed until a clear solution was obtained. Large vesicles of DMPC were prepared by adding 100 μL of NMR buffer to the dry DMPC lipids followed by three freeze/thaw cycles (liquid N₂/45 °C) until a white suspension was obtained. The DHPC/SLN solution was added to the DMPC vesicles and the mixture was extensively vortexed. Bicelles were formed after 3-5 freeze/thaw cycles, which resulted in a non-viscous solution between 0 and 15 °C, and a viscous and clear solution above 30 °C. The final volume was adjusted to 160 μL by addition of NMR buffer, giving a final lipid concentration of 28% (w/v). Bicelles were transferred to a flat-bottom glass tube (New Era Enterprises) and tightly sealed with a polytetrafluoroethylene cap.

NMR Spectroscopy

All of the NMR experiments were performed with a Varian VNMRS spectrometer operating at ¹H frequency of 700 MHz equipped with a low-E bicelle probe built by the RF program at the National High Magnetic Field Laboratory (NHMFL) in Florida ³⁸. A cross polarization time of 2 ms applied at ¹H and ¹⁵N RF field strength of ~50 kHz were used for all of the pulse sequences. SPINAL64 decoupling ³⁹ was used during acquisition with 50 kHz ¹H RF field strength. The t₁ decoupling on the proton channel⁴⁰ was achieved by phase-modulated Lee-Goldberg (PMLG) ^{41, 42}. For SE-SLF experiments, the effective ¹H field during the τ period was 80 kHz, corresponding to τ = 100 μs (or 75 μs for flipped bicelles), which gives a maximum enhancement for DC values of 4.2 kHz (or 6 kHz). For PISEMA and SE-PISEMA the effective field on ¹H and ¹⁵N during t₁ was 50 kHz. For SAMPI4, HIMSELF and in the corresponding SE versions, the ¹H and ¹⁵N RF field strengths during t₁ were 62.5 kHz. The dwell times for t₁ evolution in PISEMA, SAMPI4 and HIMSELF were 40 μs, 60 μs, and 96 μs, respectively. A recycle delay of 5 s was used between each scan. The spectra for the ¹⁵N N-acetyl leucine (NAL) sample were acquired with 16 scans, and 128, 100 and 64 t₁ increments for PISEMA, SAMPI4, and HIMSELF. The spectra for [U-¹⁵N] SLN sample in unflipped bicelles were acquired with 1024 scans and 30, 25, and 20 t₁ increments for PISEMA, SAMPI4, and HIMSELF, respectively. The spectra in flipped bicelles were acquired with 2800 scans and 20 t₁ increments for PISEMA. All SE-SLF experiments were acquired with identical increments in the t₁ dimension. Importantly, due to the number of scans used for [U-¹⁵N] SLN sample, all SE-SLF and SLF experiments were acquired in an interleaved mode to ensure accurate measurement of the sensitivity enhancement.

RESULTS

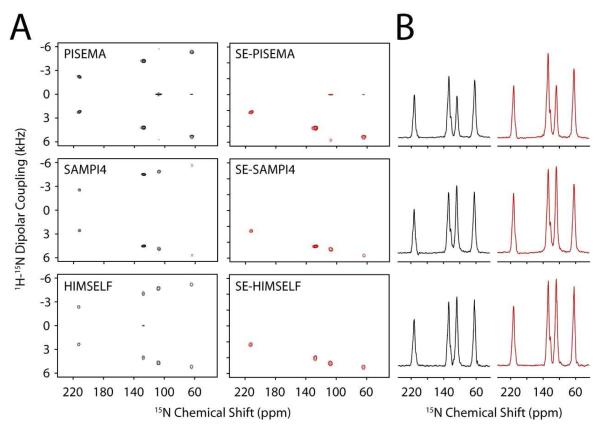
Figure 2A shows the spectra obtained for SE-SLF and SLF experiments using the NAL single crystal. The dipolar dimension spectral widths have been scaled to compensate for the theoretical scaling factors (eq 1). Also, since the RMS noise of SE-SLF data is $\sqrt{2}$ times larger than the SLF data, the SE-SLF spectra were divided by $\sqrt{2}$ to match the noise level ³⁶. Thus in Figure 2, a comparison of the height of the peaks between SE-SLF and SLF spectra is a direct measurement of the sensitivity enhancement. Figure 2B shows the summation of 1D cross-sections between 2 and 7 kHz from the dipolar coupling dimension. The tabulated signal to noise (S/N) enhancement values obtained from these cross-sections are shown in Table 1 and compared to the theoretical S/N enhancements calculated from eq 15. Note: the theoretical DC values for the NAL crystal are calculated from the HIMSELF spectra. Consistent with our previously published values for the SE-PISEMA experiment ³², the enhancements observed for SE-SAMPI4 and SE-HIMSELF agree well with theoretical values. With τ = 100 μs, the maximum enhancement factor of $\sqrt{2}$ will be achieved for DC values equal to 4.2 kHz, which is in agreement with the resonance at 127 ppm. The slight deviation of experimental (S/N) enhancement from the theoretical values could be due to transverse relaxation of antiphase magnetization during the 2τ period or effect of proton frequency offset during FSLG of the τ period. In fact, the theoretical calculations reported in the Theory and Methods section are carried out for an isolated I-S spin system and assumes on-resonance pulses for I and S spins. These factors affect only the sine term ρ_s of eq 12, since the cosine term is aligned along the z-direction in the 2τ period. In fact, the two resonances showing the largest discrepancies with theoretical values (64 and 108 ppm), had the largest amount of zero-frequency and broadening in the DC dimension of the PISEMA experiment, consistent with the ¹H_N chemical shift of these peaks positioned off-resonance from the proton carrier frequency. This is a known drawback of using FSLG (or PMLG) that is not seen in the SAMPI4 or HIMSELF spectra within Figure 2A ^{25-28, 33}.

Figure 2.

(A) 2D spectra of SLF (left) and SE-SLF (right) ¹⁵N N-acetyl leucine single crystal. (B) The sum of the corresponding dipolar cross sections between 2 and 7 kHz for SLF (left) and SE-SLF (right) spectra. The data is zero filled to 4096 in F₁ and 4096 in F₂. A cosine-shifted sine-bell window function is applied in the F₁ dimension with 100 Hz exponential line-broadening, and 100 Hz exponential line-broadening is applied in the F₂ dimension followed by baseline correction. The dipolar dimension is suitably scaled to compensate the theoretical scaling factors. All the SE-SLF experiments were performed with τ = 100 μs

TABLE I.

	Experimental			Theoretical
15N Chemical Shift (ppm)	SE-PISEMA	SE-SAMPI4	SE-HIMSELF
212	1.22	1.35	1.28	1.24
128	1.38	1.38	1.32	1.41
108	1.27	1.28	1.25	1.41
64	1.20	1.13	1.18	1.38

To demonstrate the effectiveness of these experiments for membrane proteins, we performed each of the SE-SLF experiments with the membrane protein sarcolipin (SLN), an endogenous inhibitor of the sarcoplasmic Ca²⁺-ATPase. SLN has been extensively studied by solution and solid-state NMR in DPC micelles and mechanically oriented DOPC/DOPE lipid bilayers ^43-46, as well as in DOPC using molecular dynamics simulations ⁴⁷. SLN is comprised of three structural domains: two unstructured termini and a stable helix that can be divided into two regions, one hydrophobic and the second hydrophilic. SLN crosses the DOPC lipid bilayer at an angle of ~20°, as estimated from several PISEMA experiments in mechanically aligned lipid bilayers on glass plates ^43-46. For this work, we have reconstituted SLN into magnetically aligned lipid bicelle preparations using DMPC and DHPC in a molar ratio of 3.2/1 (q = 3.2). The orientation of the bicelle sample preparations are checked using ³¹P NMR experiments as previously reported ⁴⁸, and found to be optimally aligned at a temperature of 40 °C. The linewidths of the ¹⁵N CSA in bicelles are substantially sharper than in the corresponding spectra obtained with mechanically aligned bilayers (3-5 ppm vs. 10-15 ppm), reflecting a substantial reduction in mosaic spread of the bicelle samples. In this work, we refer to unflipped bicelles as those with the bilayer normal perpendicular to the direction of the static magnetic field and the flipped bicelles (addition of 9 mM Yb³⁺ ions) as those where the normal of the bilayer is parallel to the direction of the magnetic field. Due to the motion of the bicelle in the unflipped case, the anisotropic parts of the chemical shift and dipolar coupling are scaled by a factor of $-\frac{1}{2}$ ⁴⁹. All SE-SLF and SLF experiments were performed with the unflipped bicelle sample and only the SE-PISEMA and PISEMA experiments were acquired with the flipped bicelle sample.

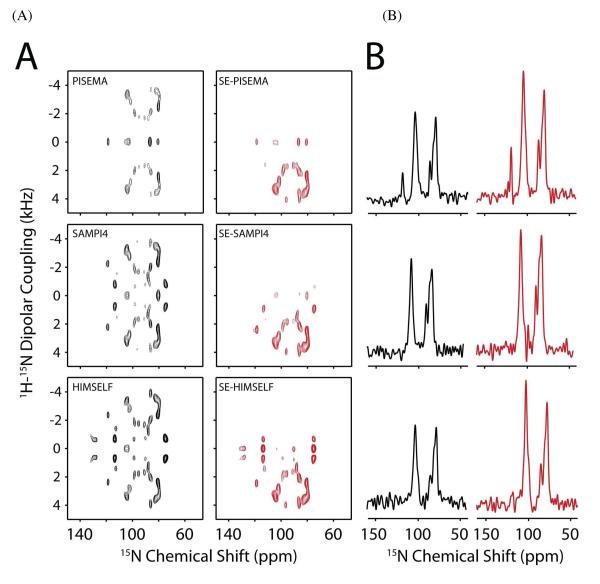
Figure 3A shows the 2D spectra obtained for the SE-SLF and SLF experiments using [U-¹⁵N] SLN reconstituted in unflipped bicelles. Due to the relatively long acquisition times (2-3 days), the SE-SLF and SLF experiments were acquired in interleaved mode, removing possible experimental differences between the datasets such as probe detuning, and ensuring accurate determination of the sensitivity enhancement. The SE-SLF data in Figure 3 have been scaled by $\sqrt{2}$ to match the noise level to the corresponding SLF spectra. Figure 3B shows the 1D cross-section from Figure 3A at 3.5 kHz dipolar coupling. From Figure 3, it is clear that the SE-SLF spectra give a larger S/N value than the SLF experiments. We quantified the signal enhancement by measuring the integrated intensity of the PISA wheel pattern between 70 and 130 ppm of the ¹⁵N CSA and 2 and 5 kHz of the DC dimension. The signal enhancement measured for SE-PISEMA, SE-SAMPI4, and SE-HIMSELF experiments with respect to the corresponding SLF spectra is 30, 30 and 32%, respectively. The enhancement factors are smaller than the maximum achievable value of 41% due to the fact that not all of the dipolar couplings observed in Figure 3 can be maximized with one value of τ. To further visualize the signal enhancement, we extracted 1D traces from the 2D spectra at 3.5 kHz DC and show these in Figure 3B (SLF-black, SE-SLF-red). These enhancements are consistent with those determined from the 2D integrated intensities.

Figure 3.

(A) SLF (left) and SE-SLF (right) spectra on [U-¹⁵N] SLN oriented in unflipped bicelles. (B). 1D cross-section of panel A at 3.5 kHz DC. The data is zero-filled to 2048 and 1024 in the F₂ and F₁ dimensions, respectively. A sine-bell window function is applied in F₁ dimension and baseline correction is applied in the F₂ dimension. All the SE experiments were performed with τ duration of 100 μs.

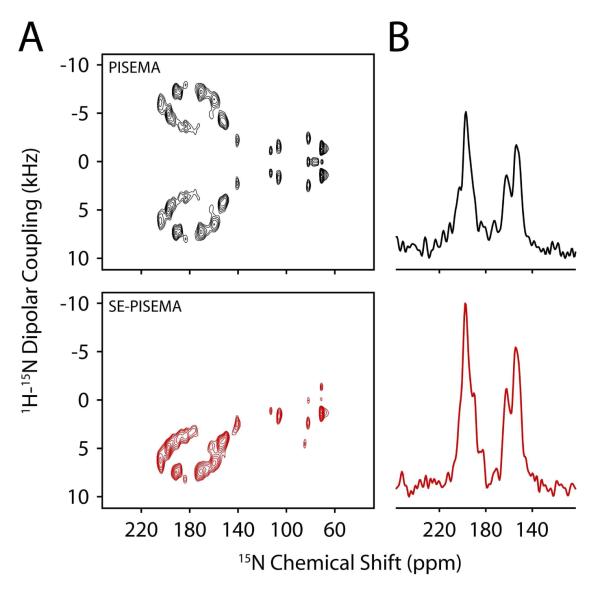
Finally, to ensure we could obtain signal enhancements for the flipped bicelles, we added YbCl₃ (9 mM) to the [U-¹⁵N] SLN sample and acquired PISEMA and SE-PISEMA experiments in an interleaved mode as described before (Figure 4). As expected, the change in orientation of the bicelles with a membrane plane perpendicular to the direction of the static field led to a more dispersed helical wheel, allowing for a significant gain in spectral resolution. The comparison between PISEMA and SE-PISEMA show an average gain of ~20% in the signal-to-noise ratio with the sensitivity enhancement scheme. This enhancement is slightly lower than expected. This likely results from faster relaxation of antiphase magnetization (2I_zS_y) during τ, due to the change in orientation of the protein with respect to the magnetic field and/or paramagnetic broadening from the YbCl₃ ⁵⁰.

Figure 4.

(A) PISEMA (top) and SE-PISEMA (bottom) spectra of [U-¹⁵N] SLN in flipped bicelles. (B). 1D cross-section of panel A at 4.8 kHz DC. Each spectrum is recorded with 20 t₁ increments and 2800 scans per increment. The τ value is set to 75 μs. The dipolar dimension is suitably scaled to compensate the theoretical scaling factors. The data is zero-filled to 8192 × 4096. A sine-bell window function is applied in F₁ dimension and baseline correction is applied in F₂ dimension.

DISCUSSION

The use of anisotropic parameters in NMR structure determination of biomolecules has become fundamental in calculating accurate and precise structures. The foundation for this idea began when Pake revealed DC was angular and distance dependent ⁵¹, and has reached everyday usage with residual dipolar couplings (RDCs) and residual chemical shift anisotropy (RCSA) for the structure refinement of biomacromolecules by solution NMR ^52-54. In principle, the observables from SLF experiments (DC, CSA) on static NMR samples of membrane proteins aligned in lipid membranes are used in a similar method as those for RDCs and RCSA. The primary difference is that the alignment tensor is fixed in the case of solid-state NMR, which corresponds to the bilayer normal, allowing for determination of protein topology. Although there have been attempts to determine membrane protein topology by magic-angle-spinning (MAS) experiments ⁵⁵, the major advantage of using oriented solid-state NMR is the accurate determination of topology ^{2, 56}. Unfortunately, the application of these methodologies has been limited to a few selected cases ², mainly due to experimental difficulties in preparing oriented samples. It is our experience that the narrowest spectral resolution is achieved by dilute membrane protein samples with 100/1 or 200/1 lipid/protein molar ratios ^{24, 43, 45, 57, 58}. Coupled with the fact that most oriented experiments observe on ¹⁵N, these samples are quite insensitive when compared with solution NMR or MAS. Another drawback is that the classical sample preparations (mechanically aligned samples) require the use of glass plates to support the lipid bilayers, which further reduces the volume available in the RF coil for isotopically labeled samples (~60-70% of coil volume is occupied with glass).

The introduction of bicelles as an alternative membrane mimic represented a major advancement in the application of oriented solid-state NMR techniques ^{48, 49, 59, 60}. While the preparation of membrane proteins on mechanically aligned lipid bilayer samples are robust and continue to be applied for the determination of the topology of membrane-bound proteins and peptides, the low sensitivity of these sample preparations has prevented widespread use. In addition, the introduction of probe technology that reduced the heating in the probe due to the electric field (low-E) has dramatically improved sample stability ^{38, 61}. Taken with these implementations, our new suite of sensitivity enhanced experiments (Figure 1) lays the groundwork for the expansion of oriented solid-state NMR methodology for membrane proteins by drastically reducing the acquisition time for NMR experiments. For the same S/N, the SLF experiment (PISEMA, HIMSELF, and SAMPI4) would require a 70% longer acquisition time than the corresponding SE-SLF experiment due to the 30% sensitivity enhancement scheme (Figure 3). For instance, the spectra shown in Figure 3 required an acquisition time of 57 hr compared with 34 hr for the SE-SLF experiment. The combination of sensitivity enhanced methods, low-E probes, observation on more sensitive nuclei such as ¹³C, and optimized bicelle sample preparations will result in robust, site-specific assignments on uniformly labeled proteins without the need of extensive selective labeling samples to assign the SLF spectra.

CONCLUSIONS

We present a new suite of SLF pulse sequences with improved sensitivity. These sequences have been shown to be effective on a model compound and applied on a membrane protein. With the single crystal, the enhancements in S/N ratio are in close agreement to the theoretical values. For the membrane protein SLN aligned in unflipped bicelles, the increase in S/N is ~30%. These new experiments will substantially decrease the time needed for data acquisition, which will result in more efficient determination of structures and topologies for this important class of proteins as well as liquid crystals.