The Molecular Basis of Frictional Loads in the In Vitro Motility Assay with Applications to the Study of the Loaded Mechanochemistry of Molecular Motors

Abstract

Molecular motors convert chemical energy into mechanical movement, generating forces necessary to accomplish an array of cellular functions. Since molecular motors generate force, they typically work under loaded conditions where the motor mechanochemistry is altered by the presence of a load. Several biophysical techniques have been developed to study the loaded behavior and force generating capabilities of molecular motors yet most of these techniques require specialized equipment. The frictional loading assay is a modification to the in vitro motility assay that can be performed on a standard epifluorescence microscope, permitting the high-throughput measurement of the loaded mechanochemistry of molecular motors. Here, we describe a model for the molecular basis of the frictional loading assay by modeling the load as a series of either elastic or viscoelastic elements. The model, which calculates the frictional loads imposed by different binding proteins, permits the measurement of isotonic kinetics, force-velocity relationships, and power curves in the motility assay. We show computationally and experimentally that the frictional load imposed by alpha-actinin, the most widely employed actin binding protein in frictional loading experiments, behaves as a viscoelastic rather than purely elastic load. As a test of the model, we examined the frictional loading behavior of rabbit skeletal muscle myosin under normal and fatigue-like conditions using alpha-actinin as a load. We found that, consistent with fiber studies, fatigue-like conditions cause reductions in myosin isometric force, unloaded sliding velocity, maximal power output, and shift the load at which peak power output occurs.

Introduction

The myosin family of molecular motors is a diverse superfamily of actin binding proteins (ABP) that convert the energy from ATP hydrolysis into motion and force in order to accomplish an array of cellular functions (for review, see (O'Connell et al. 2007; Sellers 2000)). The in vitro motility assay is a useful tool for studying the molecular basis of myosin-based movement under a variety of well controlled experimental conditions (Rock et al. 2000; Tyska and Warshaw 2002). This technique permits the study of myosin mechanics while at the same time, retaining many of the features of solution biochemistry. In the in vitro motility assay, myosin is bound to a cover glass surface and a solution containing fluorescently labeled actin filaments is applied to the myosin surface in the presence of ATP, allowing for the measurement of actin filament movement via fluorescence microscopy (Kron and Spudich 1986). The typical motility assay measures the sliding velocity of myosin in the absence of an exogenously added load, providing important information on the actomyosin contractile mechanism. Under physiological conditions, however, myosins typically operate against a load, making it desirable to study myosin force generation in the presence of a mechanical load.

Several different biophysical modifications to the in vitro motility assay have been applied to study the force generation of myosin motors, including microneedles (Kishino and Yanagida 1988), centrifuges (Oiwa et al. 1990), magnetic fields (Holohan and Marston 2005), and optical traps (Block et al. 1990; Finer et al. 1994; Rief et al. 2000). These methods have been employed to study a vast array of molecular motors beyond myosin (for review, see (Neuman and Nagy 2008)). These methods are sensitive to absolute changes in myosin force and provide reproducible results. However, they have the drawback that they are experimentally time intensive and require extensive and costly equipment engineering.

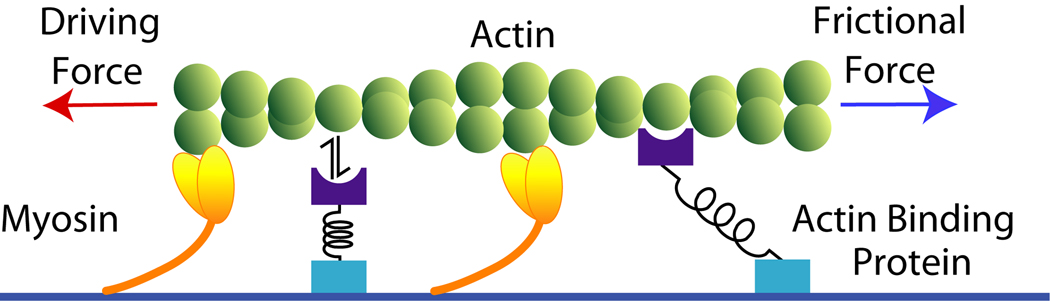
Frictional loading assays are modified versions of the standard in vitro motility assay that provide a high-throughput method for measuring relative changes in myosin isometric force using a standard epifluorescence microscope (Bing et al. 2000; Haeberle 1994; Haeberle and Hemric 1995; Warshaw et al. 1990). In a frictional loading motility assay, the bed of myosin provides a driving force that propels actin filament translocation. A frictional load is introduced into the flow cell by adding actin binding proteins to the flow cell surface. These actin binding proteins transiently bind to actin, providing a frictional load that opposes the propelling force of the bed of myosin (Fig. 1). Typically, the amount of actin binding protein needed to stop filament motility is reported as a measure of myosin isometric force (Bing et al. 2000; Haeberle 1994; Janson et al. 1992). Several actin binding proteins have been employed in frictional loading assays, including alpha-actinin (Bing et al. 2000; Greenberg et al. 2009b; Janson et al. 1992), N-ethylmaleimide modified myosin (Haeberle 1994; Haeberle et al. 1992), pPDM myosin (Warshaw et al. 1990), and filamin (Janson et al. 1992). Each of these actin-binding proteins have different kinetic and mechanical properties, yet they all appear to be able to exert a frictional load that opposes the propelling force of the bed of myosins.

Figure 1. Illustration of the interactions between actin binding proteins (ABP) and actin in the in vitro motility assay.

Fluorescently labeled actin filaments are translocated over a bed of myosin molecules in the presence of ATP. Myosin molecules apply a driving force to the actin filament, initiating filament motility. When ABPs are added to the flow cell surface, the ABPs transiently bind to actin, providing a frictional force that opposes the driving force of the bed of myosins. The ABP will bind to actin during which time, the compliance in the ABP is stretched until the ABP is either kinetically or mechanically detached from actin.

Frictional loading assays have been exceptionally useful in the study of muscle myosin II, a low duty ratio, non-processive motor (for review see (Tyska and Warshaw 2002)). Muscle myosin typically operates in specialized muscle cells containing large, macromolecular structures that regulate and activate the actomyosin contractile apparatus. Studies of the force generating ability of the actomyosin complex in muscle fibers are complicated by the fact that it is difficult to directly assign changes in force to alterations in the actomyosin complex. Thus, frictional loading assays are particularly useful in the study of disease, where broad cellular based changes such as myofibrillar disarray in hypertrophic cardiomyopathy (for review, see (Morita et al. 2005)), complicate the interpretation of observed changes in force. Furthermore, myosin II is a non-processive motor and, whereas the unloaded sliding velocity of a bed of myosins is primarily detachment limited (Huxley 1957), the loaded velocities will depend on both attachment and detachment kinetics. Furthermore, probing the attachment kinetics of myosin under load is extremely difficult using the three bead optical trap assay (Steffen et al. 2001).

Although frictional loading assays have been widely employed to measure the relative changes in myosin force production, the mechanism of the frictional load exerted by an actin binding protein on an actin filament is poorly understood. Frictional loading experiments give relative measurements of changes in myosin force generation yet not absolute values (as could be obtained using optical traps or microneedles). Furthermore, there is no consensus within the field as to the best method for analyzing frictional loading experiments. While some investigators have examined the fraction of filaments moving as a function of added actin binding protein (Bing et al. 2000; Janson et al. 1992), others have investigated the velocity dependence of actin filament sliding as a function of added actin binding protein (Bing et al. 2000; Greenberg et al. 2009b; Janson et al. 1992). These measurements are further complicated by the differing criteria between labs in determining whether an actin filament is considered moving or simply an artifact of the in vitro motility assay (surface in homogeneities etc.).

Here, we propose a molecular model for the mechanism of the frictional load imposed by actin binding proteins on actin filament motility by modeling the interaction of actin binding proteins with actin as a series of either elastic or viscoelastic elements (depending on the mechanical and kinetic properties of the actin binding protein), similar to other models of protein friction (Howard 2001; Janson and Taylor 1994; Palmer et al. 2007; Schoenberg 1985; Tawada and Sekimoto 1991a; Tawada and Sekimoto 1991b). This model differs from previous models of the frictional load exerted by actin binding proteins on actin (Janson and Taylor 1994; Tawada and Sekimoto 1991a; Tawada and Sekimoto 1991b) in that it considers mechanical detachment of the actin – actin binding protein linkages once the bond rupture force is exceeded. The model describes the underlying basis for the frictional load exerted by the actin binding proteins. Also, the model, by introducing the calculation of the frictional forces due to actin binding protein – actin interactions, permits the measurement of force-velocity and power curves in the in vitro motility assay. Furthermore, the model sets the foundation for isotonic studies of myosin motility in the in vitro motility assay.

Using the model, we show computationally and experimentally that the frictional load imposed by alpha-actinin, the most widely employed frictional loading actin binding protein, is viscoelastic (i.e. velocity dependent) rather than purely elastic (i.e. velocity independent), making determination of the index of retardation (i.e., the velocity at which filament movement stops) unfeasible. As a test of the model, we examined the frictional loading behavior of rabbit skeletal muscle myosin under normal and fatigue-like (Cooke 2007) conditions using alpha-actinin to provide a load. We found that, consistent with fiber studies (for review, see (Cooke 2007)), fatigue-like conditions cause a reduction in both myosin force and velocity. Furthermore, consistent with fiber studies (Jones et al. 2006), fatigue causes a reduction in both peak power output and the force at which peak power output occurs.

Materials and Methods

Protein Preparation

Rabbit skeletal myosin was isolated from rabbit fast skeletal muscle taken from freshly sacrificed New Zealand White rabbits as previously described (Greenberg et al. 2009a). Briefly, muscle was minced and extracted on ice for 20 minutes in 1.5 l/500g of ice cold Guba Straub solution (0.1 M potassium monophosphate, 0.05 M potassium diphosphate, and 0.3 M potassium chloride, pH 6.5). The mince was then centrifuged at 11,000 × g for 30 minutes at 4 °C and the resulting supernatant was poured through glass wool and then precipitated with 14 volumes of cold 1mM EDTA. The precipitate was collected by serial centrifugation at 7,000 × g for 10 minutes with a final spin at 11,000 × g. The resulting pellet was then resuspended in 20 mM MOPS, pH 7, 1 mM DTT, and KCl to a final concentration of 0.5 M. The myosin was then ultracentrifuged at 200,000 × g for 1.5 hours at 4 °C to remove any myosin aggregates. Following ultracentrifugation, the supernatant was precipitated on ice with 14 volumes of cold distilled water. The precipitated myosin was then collected by centrifugation at 6,500 × g for 10 minutes and then mixed into glycerol and stored at −20°C until use.

Actin was prepared from chicken pectoralis muscle acetone powder using the method of Straub (Straub 1942) with the modification of Drabikowski et al. (Drabikowski and Gergely 1964). The actin was suspended in actin buffer (25 mM KCl, 1 mM EGTA, 10 mM DTT, 25 mM imidazole, 4 mM MgCl₂). TRITC phalloidin labeled actin was prepared by incubating a 1:1 molar ratio of TRI TC phalloidin and actin in actin buffer overnight at 4 °C.

Alpha-Actinin Frictional Loading Assays

The in vitro motility assays were performed as previously described with some subtle modifications (Greenberg et al. 2009b; Szczesna-Cordary et al. 2007). Approximately 200 µg of myosin in glycerol was suspended in 1 ml of 10 mM DTT in water and allowed to precipitate for one hour on ice. This step ensured the removal of glycerol and, if present, any oxidized myosin molecules unable to form thick filaments. The myosin was then centrifuged at 16,000 × g for 30 minutes at 4 °C. The pellet was then resuspended in 200 µl of myosin buffer (300 mM KCl, 25 mM imidazole, 1 mM EGTA, 4 mM MgCl₂, 10 mM DTT). Any damaged myosin heads that were unable to bind to and release from actin were removed by a “dead-head” spindown in which the myosin, 1 mM ATP, and 1.1 µM actin were centrifuged in an Airfuge for 30 min at 100,000 × g. The myosin concentration after centrifugation was determined using a Bradford assay (Bio-rad Labs. Hercules, CA), and the myosin diluted 100 µg/ml in myosin buffer.

Flow cells were constructed by forming a channel between nitrocellulose coated coverslips and a standard glass slide using double stick tape (100 µm width 3 M Corp., St. Paul, MN). Myosin was adsorbed to the coverslip surface by incubating 30 µl of 100 µg/ml myosin with the appropriate concentration of alpha-actinin (Cytoskeleton Inc., Denver, CO) for 1 minute. Any remaining surface lacking myosin was blocked by adding 30 µl of 0.5 mg/ml bovine serum albumin (BSA) suspended in myosin buffer followed by a 60 µl wash with actin buffer (25 mM KCl, 25 mM imidazole, 1 mM EGTA, 4 mM MgCl₂, 10 mM DTT). As a further measure to minimize the effects of damaged myosin heads, 30 µl of 1 µM unlabeled actin (myosin : unlabeled actin molar ratios were approximately 40:1) in actin buffer was vortexed and added to the flow cell. After incubating for two minutes, the flow cell was washed with 60 µl of actin buffer containing 1 mM ATP and then 120 µl of actin buffer in the absence of ATP. 30 µl of 5 nM TRITC labeled actin was then added to the flow cell and allowed to incubate for 1 minute. Motility was initiated by the addition of motility buffer to the flow cell.

Motility Buffers

Fatigue and non-fatigue conditions were simulated by generating motility buffers using Bathe, a program that balances ionic conditions using binding constants determined by Godt et al. (Godt and Lindley 1982). All buffers contained 0.5% methyl cellulose, 2 mM dextrose, 160 units glucose oxidase, 2 µM catalase, and were run at pCa 9. The normal (non-fatigue) (5 mM ATP, 0.02 mM ADP, 2 mM Pi, pH 7) and the fatigue-like buffers (1 mM ATP, 0.3 mM ADP, 30 mM Pi, pH 6.2) were balanced using Bathe (Godt and Lindley 1982). Fatigue-like conditions were chosen based on the work by several groups (Cady et al. 1989; Cooke 2007; Dawson et al. 1978; Fitts 1994; Fitts 2008; Karatzaferi et al. 2008; Myburgh and Cooke 1997; Pate et al. 1995; Wilson et al. 1988).

Microscopy

Rhodamine labeled actin filaments were observed on a Nikon Eclipse TE2000-U microscope (Nikon (Melville, NY)) with standard epifluoresence illumination. All experiments were performed at 30 °C using a Bioptechs objective heater (Bioptechs Inc., Butler, PA). Images of actin filament sliding were captured to a Scion frame grabber (Model AG-5) using Scion Image (Scion Corp. (Frederick, MD)). 5 to 10 images were captured at an appropriate frame rate (1 to 7 seconds per frame) depending on the speed of the actin filament sliding. Only motile filaments were measured. The filament velocity was determined using the freeware Retrac motility software (http://mc11.mcri.ac.uk/Retrac). Fifteen to thirty moving filaments were analyzed from at least two different areas of the flow cell to ensure that there were no surface artifacts.

Statistics

Filament motility was recorded in several areas of the flow cell. For each actin filament, the average velocity was measured over 5 to 10 frames. Then, for each flow cell, the velocities of 15 to 30 actin filaments were averaged together. Each point shown in the data plots represents the average velocity of these 15 to 30 actin filaments with error bars given by the standard error of the mean actin filament sliding velocity. Data was taken from at least two different myosin preparations. Appropriate models were fit to the data using a non-linear least-squares algorithm (SigmaPlot, Systat Software Inc., San Jose, CA). A two-tailed t-test was used to examine the significance of the differences between velocities as determined from the errors in the fits of the data to the model curve. The p values were calculated from the Student’s t-test distribution.

Curve Fitting

Equation A7 was fit to the the raw data of sliding velocity versus alpha-actinin concentration in the presence and absence of fatigue-like conditions with 2 fitting parameters: the driving force of the bed of myosins, F_d, and the maximal unloaded shortening velocity, V_max. Force-velocity curves were generated by transforming the frictional loading data according to equation A2 to obtain the frictional force exerted by the loaded actin filaments on the bed of myosin. The Hill equation describing the force-velocity relationship was then fit to these data (Hill 1938):

$$V=\frac{b^{*}(F_o-F)}{F+a}$$ (1)

where F_o is the isometric force, F is the force of the frictional load, and a and b are constants. These data could then be converted to power, P, since P = F*V. The Hill equation describing power output was then fit to these data (Hill 1938):

$$P=b^{*}{F}^{*}(\frac{F_o+a}{F+a}-1)$$ (2)

Results

Model for the molecular interactions involved in frictional loading assays

In motility assays, actin filament motion is dominated by the mechanics of low Reynolds number (Purcell 1977). As such, inertial forces are negligible and all motions are over damped (Howard 2001). In order to move at a constant velocity, a constant force must be applied to the actin filament since the actin filament stops almost instantaneously when the actin filament is no longer being actively propelled (Purcell 1977).

In the frictional loading motility assay, myosin generates the net driving force (the force of the driving crossbridges minus the contributions of the dragging and weakly bound crossbridges), F_d, that propels an actin filament at a velocity, V_max, in the absence of an exogenously added load. Addition of actin binding proteins (ABP) to the motility assay surface introduces an exogenous frictional load on the actin filament that opposes the driving force of the myosin heads, F_fric (Fig. 1). The resulting velocity is determined by the balance of forces:

$$V=V_{\text{max}}\frac{(F_d-F_{\mathit{\text{fric}}})}{F_d}$$ (3)

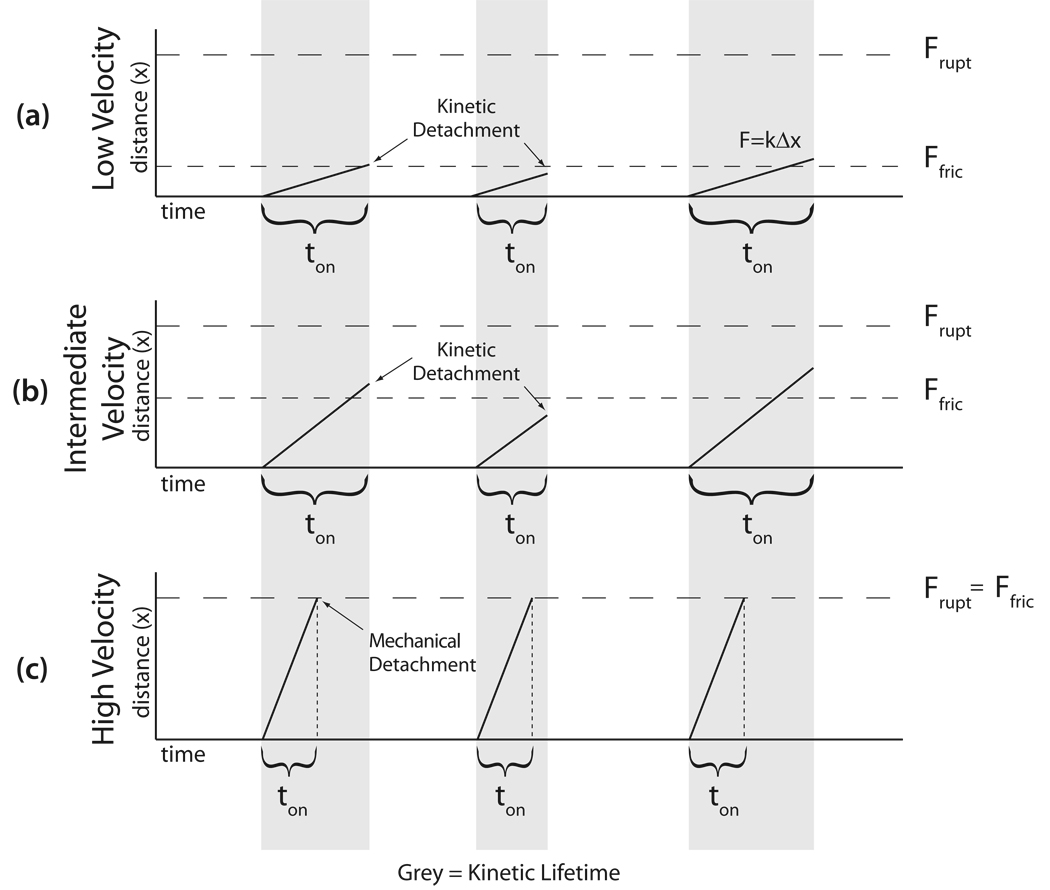
The frictional load exerted by the ABPs can be modeled as a series of either elastic or viscoelastic elements depending on the mechanical and kinetic properties of the ABP and the actin-ABP bond (Fig. 2). All ABPs have at least some spring-like elastic properties, stemming from the elasticity of stretching the ABP itself, the actin-ABP bonds, the actin filament, and the ABP-surface linkage. For simplicity, we will refer to the system elasticity as the elasticity of the ABP. Once an ABP binds to the actin filament, the ABP is stretched by the force of the myosin bed pulling the actin filament. Since the actin-ABP interaction occurs as an equilibrium process, there is an inherent kinetic lifetime of the bond and strain will accumulate on the ABP as long as it remains attached to actin. The strain on the ABP will increase until the ABP detaches from the actin filament either mechanically or kinetically. If the strain developed during the lifetime of the attached state is less than the actin-ABP bond rupture force, the spring-like strain on the ABP will be dissipated once the ABP kinetically detaches from the actin (Fig. 2a). The amount of strain developed on the bond will be determined by the mechanical properties of the ABP, the duration of the attached state, and the velocity of the actin filament. Thus, for a faster moving actin filament, there will be a greater strain developed in the ABP during the attached state since the compliant elements of the system will be extended over a longer distance during the inherent bond kinetic lifetime (Compare figures 2a and b). Therefore, there will be a velocity dependence to the frictional load experienced by the myosin and the ABP will behave as a viscoelastic damping element.

Figure 2. Qualitative description of the model for a single molecule interaction between actin and an ABP.

The ABP will transiently bind to actin with an inherent kinetic lifetime, t_on. During this time, the ABP, possessing an elastic spring constant, k, will be stretched a distance, Δx, and the ABP will exert a force, F_fric, that opposes the bed of myosin. During the course of this kinetic lifetime, a slower moving actin filament (A) will be stretched a smaller distance than a filament moving at an intermediate velocity (B) and thus experience a lower frictional force. In this case, where the kinetic lifetime of the actin-ABP bond determines the attachment time, there is a velocity dependence to the frictional load and the ABP behaves as a viscoelastic damping element. On the other hand, at higher velocities (C), if the strain developed in the ABP exceeds the rupture force, F_rupt, then the bond will detach once the rupture force threshold is exceeded, regardless of the inherent kinetic lifetime of the bond. In this case, the load is velocity independent and the ABP behaves as a purely elastic damping element.

On the other hand, if the amount of time required to exceed the rupture force of the actin-ABP bond is shorter than the inherent kinetic lifetime (i.e. the time required for non-mechanical detachment) of the bond, the ABP will mechanically detach from the actin filament once a sufficient load to the rupture the bond is reached. The attachment time in this case is then set by the amount of time necessary for sufficient strain to accumulate on the ABP to rupture the bond mechanically rather than the inherent kinetic lifetime of the bond (Figure 2c). In this case, since all bonds will stretch until rupture occurs, the developed force will equal the rupture force, regardless of the velocity of the actin filament. Since the frictional load exerted by the ABP will be velocity independent, the ABP will behave as a purely elastic damping element. The elastic model of frictional loading is thus the limiting case of the viscoelastic model in which the strain accumulated on the ABP during the kinetic lifetime of the actin-ABP bond exceeds the actin-ABP rupture force.

In the appendix, we develop a mathematical formalism to describe the frictional load exerted by ABPs in an in vitro motility assay by both elastic and viscoelastic damping elements. We show that in the case of a viscoelastic load, the velocity (V) dependence of actin filament sliding as a function of ABP added ([α]) is given by:

$$V=\frac{{V_{\text{max}}}^{*}{F}_d}{F_d+\frac{{V_{\text{max}}}^{*}{\kappa }^{*}{\zeta }^{*}{L}^{*}{r}^{*}{k_A}^{*}{\chi }^{*}{[\alpha ]}^{5/2}}{{k_D}^{*}({k_A}^{*}{\chi }^{*}{[\alpha ]}^{3/2}+k_D)}}$$ (A7)

where V_max is the maximal sliding velocity, F_d is the driving force of the bed of myosins, κ is the system compliance associated with the ABP and the ABP linkages, L is the length of a typical actin filament, r is the reach of an ABP to bind to an actin filament, k_A is the second order rate constant for ABP attachment to actin, k_D is the ABP detachment rate, and ζ and χ are constants that define the surface geometry of ABPs on the surface. Based on equation A7, the velocity will never completely reach zero rather, it will asymptotically approach zero as the concentration of ABP is increased. The viscoelastic model holds as long as the force developed on a single ABP during the kinetic lifetime (given by: $F_{\alpha }=\frac{F_{\mathit{\text{fric}}}}{{\rho }^{*}{L}^{*}{r}^{*}{f}_{\alpha }}=\frac{{\kappa }^{*}V}{{k_D}^{*}{\rho }^{*}{L}^{*}{r}^{*}{f}_{\alpha }}$ where ρ is the surface density of ABP and f_a is the ABP duty cycle) is less that the rupture force. Once the force developed during the attachment time exceeds the rupture force, the load begins to behave as a purely elastic damping element and alpha-actinin dependence of the velocity is given by:

$$V={V_{\text{max}}}^{*}\frac{(F_d-{F_{\mathit{\text{rupt}}}}^{*}{\zeta }^{*}{L}^{*}{r}^{*}\frac{{k_A}^{*}{\chi }^{*}{[\alpha ]}^{5/2}}{{k_A}^{*}{\chi }^{*}{[\alpha ]}^{3/2}+k_D})}{F_d}$$ (A9)

where F_rupt is the rupture force. In this case, there will be a defined stop to motility once the numerator equals zero.

Alpha-actinin frictional loading experiments: a viscoelastic frictional load

One of the most frequently used ABPs for frictional loading experiments is alpha-actinin ((Bing et al. 2000; Greenberg et al. 2009b; Janson et al. 1992; Malmqvist et al. 2004; Okada et al. 2008; Pant et al. 2009; VanBuren et al. 2002)). Typically, the index of retardation (the amount of alpha-actinin necessary to stop actin filament sliding velocity) is reported (Bing et al. 2000). However, careful analysis of frictional loading data shows that even though the velocity is constantly decreasing with increasing amounts of ABP, it is not possible to completely stop actin filament motility, even at extremely high surface concentrations of alpha-actinin, consistent with a viscoelastic load (Fig. 3, 4) rather than an elastic load. Furthermore, the kinetic and mechanical properties of the alpha-actinin - actin bond suggest that detachment of the bond will occur before the strain on the ABP exceeds the rupture force (see discussion).

Figure 3. Frictional loading assay of skeletal myosin under normal and fatigue-like conditions.

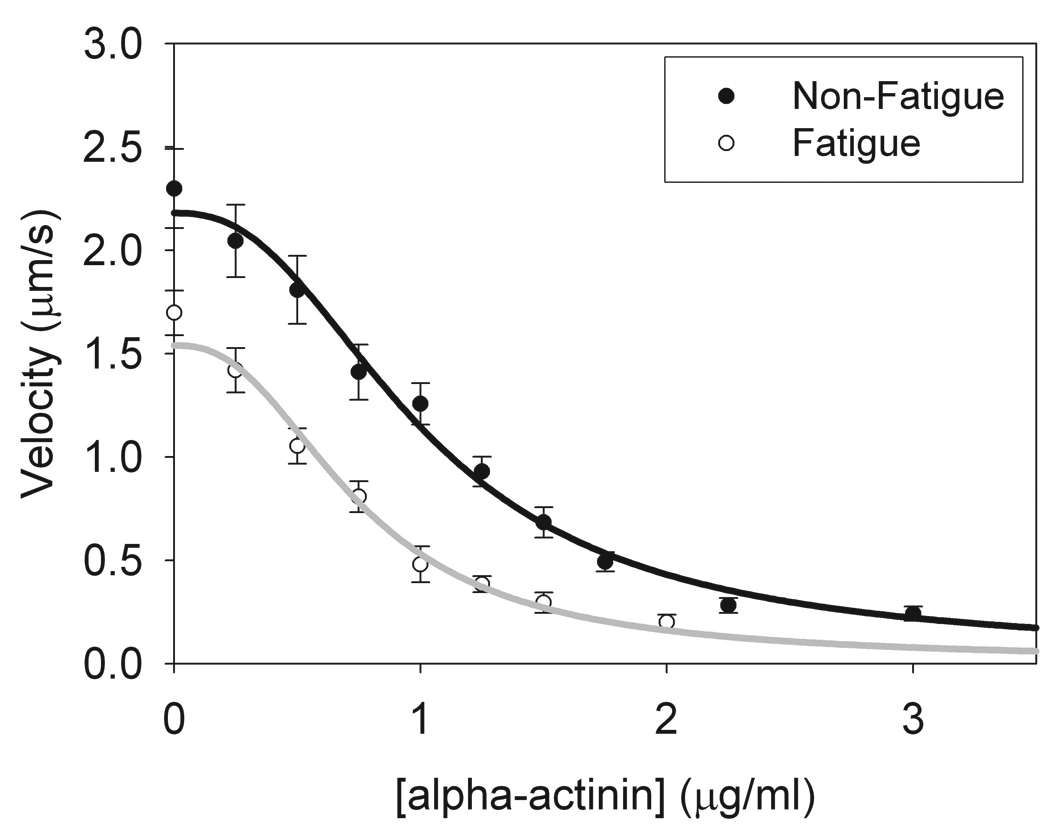
Frictional loading data was collected using alpha-actinin as a frictional load in the presence of either normal (5 mM ATP, 0.02 mM ADP, 2 mM Pi, pH 7.0) or fatigue-like (3 mM ATP, 0.3 mM ADP, 30 mM Pi, pH 6.2) motility buffers. Data were fitted to equation A7 with the fitting parameters of the myosin driving force, F_d, and maximal unloaded sliding velocities, V_max. Consistent with fiber studies, fatigue caused reductions in unloaded sliding velocity (V_max(normal) = 2.18 ± 0.05 µm/s, V_max(fatigue) = 1.68 ± 0.05 µm/s; p<0.001) and isometric force (F_d(normal) = 590 ± 40 pN, F_d(fatigue) = 180 ± 20 pN; p<0.001).

Figure 4. Force-velocity curves fit to the Hill equation for skeletal muscle myosin under both normal and fatigue-like conditions.

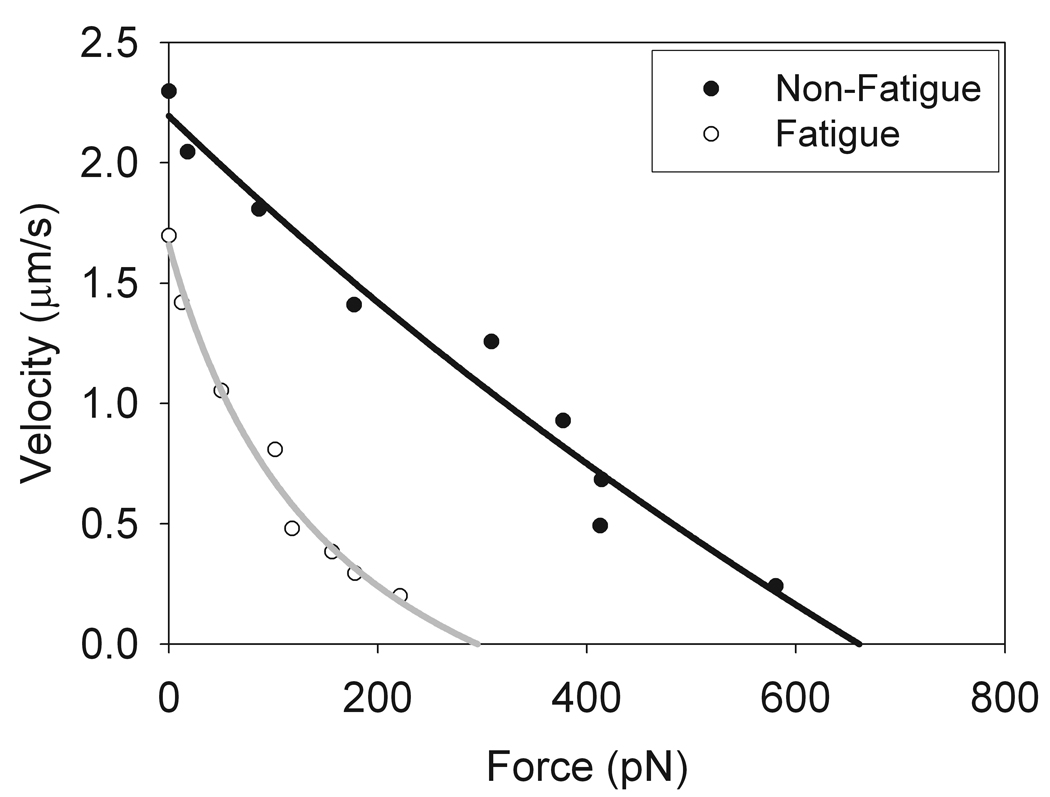
Using the data from figure 3, alpha-actinin concentrations added to the flow cell were converted to forces using equation A2. From this data, force velocity curves were generated and the data were fit to the Hill equation (Eq. 1) [Hill, 1938[. The plots of the data confirm the results seen in figure 3 which showed a reduction in unloaded sliding velocity and isometric force with fatigue.

The mechanical and kinetic properties of alpha-actinin have been extensively characterized, allowing frictional loading data measuring the relationship between alpha-actinin and velocity to be fit with known biochemical quantities (see the appendix for details). Using these parameters, one can fit the data of velocity versus concentration of alpha-actinin to determine the net driving force of the myosin, F_d, and the maximal unloaded actin sliding velocity in the absence of an exogenously added load, V_max. As a test of the ability of the model to determine changes in force and unloaded sliding velocity, we examined muscle myosin under fatigue-like conditions where one would expect to see changes in both force and velocity, based on muscle fiber studies (Cooke 2007).

Effects of fatigue conditions on force

During exertion, muscle fiber and whole organism studies have shown that fatigue-like conditions directly impact the actomyosin contractile apparatus, causing reductions in myosin isometric force, maximal unloaded sliding velocity, power output, and the load at which maximal power output is produced (For review see (Cooke 2007)). Therefore, investigating the direct molecular effect of fatigue-like conditions on myosin unloaded shortening velocity and isometric force using an alpha-actinin frictional loading assay serves as good test case for the viscoelastic model. Frictional loading of rabbit skeletal myosin was measured in the presence of either non-fatigue buffer (5 mM ATP, 0.02 mM ADP, 2 mM Pi, pH 7) or fatigue-like buffer (3 mM ATP, 0.3 mM ADP, 30 mM Pi, pH 6.2) at 30°C (Standard fatigue-like conditions defined in (Cooke 2007)). The data were fit to the viscoelastic model (Eq. A7) using the biochemical and mechanical constants described in the appendix. As can be seen, the data are well fit by the model (Fig. 3). Furthermore, fatigue-like conditions cause reductions in both the unloaded sliding velocity and isometric force of myosin, consistent with previous reports in muscle fibers. The unloaded sliding velocity was reduced from 2.18 ± 0.05 µm/s to 1.68 ± 0.05 µm/s (p<0.001) in the presence of fatigue-like conditions and the driving force of the bed of myosin was reduced from 590 ± 40 pN to 180 ± 20 pN with fatigue (p<0.001).

Force-velocity relationships can also be constructed from the alpha-actinin frictional loading data using the framework of the viscoelastic model. The frictional force imposed by alpha-actinin binding to actin can be calculated using equation A2. Using this mathematical transformation we calculated the absolute force imposed by the bed of ABPs on thin filament sliding, taking into account the velocity dependence of the load. Force-velocity curves examining the effect of fatigue-like conditions on myosin motility are shown in figure 4. The data was then fit to the Hill force-velocity relationship (Eq. 1). As can be seen from the data, the data is well fit and yields the expected force-velocity relationship (Hill 1938). This implies that the model of alpha-actinin as a viscoelastic load is reasonable since the transformation of the data from relative to absolute forces yields the expected force-velocity relationships, with fatigue-like conditions causing reductions in both myosin velocity and isometric force. Furthermore, consistent with fiber studies (Jones et al. 2006), the curvature of the force-velocity relationship for myosin under fatigue-like conditions is greater than that for myosin under non-fatigue conditions.

The force-velocity relationship of myosin in the motility assay also defines the power producing capability of myosin since power is the product of force and velocity. The power output of a muscle is a critical indicator of muscle function since muscles typically work under conditions where both force and velocity are generated from the energy of ATP hydrolysis. The data from the force-velocity curve we transformed to power-force curves by taking the product of force and velocity. The data were fit to the Hill relationship describing the power-force (Eq. 2) relationship (Fig. 5). As can be seen from the data, transformation of the velocity - alpha-actinin data to power results in curves that are well described by the Hill power-force relationship (Hill 1938). Furthermore, consistent with fiber studies (Jones et al. 2006), the data shows that fatigue-like conditions cause reductions in both the peak power of the myosin and the force at which peak power occurs.

Figure 5. Power curves fit to the Hill equation for skeletal muscle myosin under both normal and fatigue-like conditions.

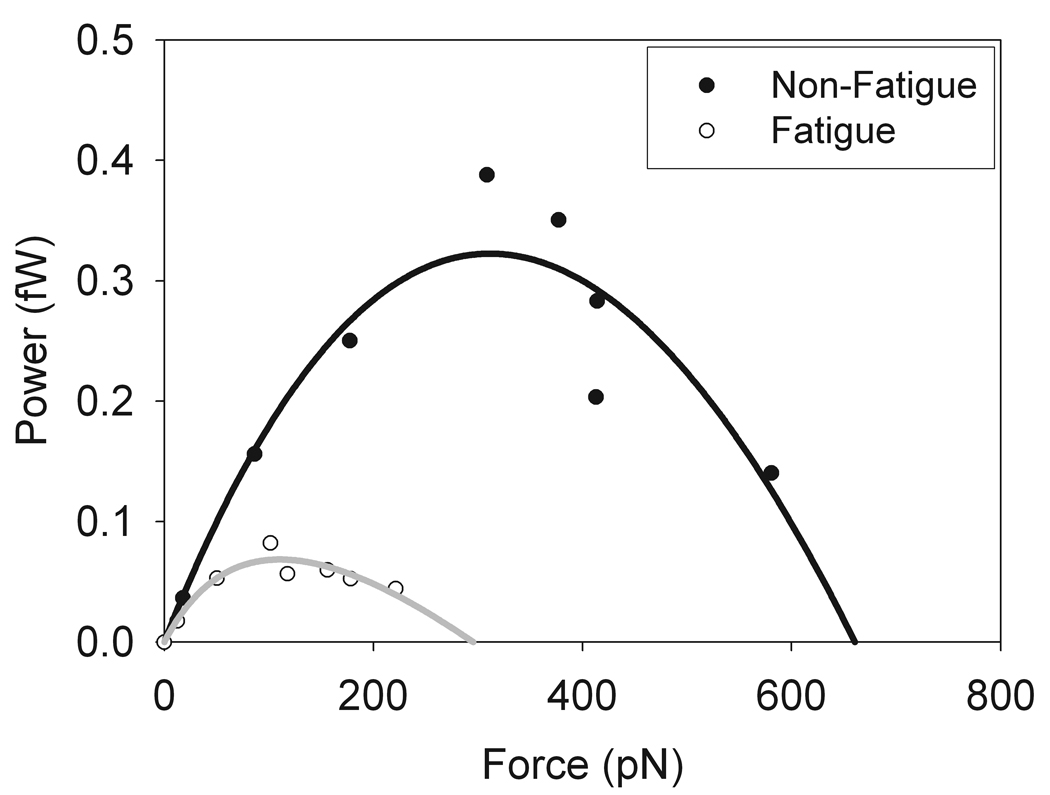
Data from figure 4 were converted to power by multiplying the force by the velocity and then plotting power versus force. These data were then fit to the Hill equation for power (Eq. 2) [Hill, 1938]. As can be seen from the data, consistent with fiber studies [Jones et al., 2006], fatigue caused both a reduction in peak power output as well as a shift in the load at which peak power occurs.

Discussion

Alpha-actinin imposes a viscoelastic frictional load

We have developed here a model to describe the frictional load exerted by ABPs opposing actomyosin motility in the in vitro motility assay. The frictional load exerted by a bed of ABPs can be described as a series of viscoelastic or elastic damping elements, depending on the mechanical and kinetic properties of the ABP and the actin-ABP interactions.

The most widely employed frictional load in motility assays is alpha-actinin (Bing et al. 2000; Greenberg et al. 2009b; Janson et al. 1992; Malmqvist et al. 2004; Okada et al. 2008; Pant et al. 2009; VanBuren et al. 2002)). In frictional loading experiments using alpha-actinin, we have shown that the velocity decreases with the addition of alpha-actinin and approaches zero asymptotically over a wide range of alpha-actinin concentrations. The slower moving actin filaments in the asymptotic plateau region were not historically considered in the determination of myosin isometric force generating capability (Bing et al. 2000; Greenberg et al. 2009b), where the amount of ABP required to completely prevent filament motility was used as an indicator of myosin force generation. These filaments were either omitted by a velocity threshold (Greenberg et al. 2009b; Janson et al. 1992) or automated binning of tracking data (Bing et al. 1998) since it was assumed that such filaments represent artifacts rather than a real population of moving filaments. We propose that these filaments, rather than being artifacts of the motility assay surface or the analysis method, represent the viscoelastic nature of the actin - alpha-actinin molecular interaction. In fact, careful analysis of the frictional loading data (Figure 3) shows that the point at which velocity became relatively insensitive to increasing amounts of ABP occurs at different concentrations of alpha-actinin for myosin under normal and fatigue-like conditions. Since the concentration of added myosin is the same for both of these conditions, this suggests that the asymptotic plateau behavior is not due to saturation of the cover glass surface by alpha-actinin or inhomogeneties in the flow cell surface but rather due to the viscoelastic nature of the frictional load.

Our assertion that the load exerted by alpha-actinin is a viscoelastic load is also supported by the following calculation. Based on our model, we can calculate the average force borne by a single alpha-actinin molecule during sliding as: $F_{\alpha }=\frac{{\kappa }^{*}V}{{k_D}^{*}{\rho }^{*}{L}^{*}{r}^{*}{f}_{\alpha }}$ since viscoelastic elements in parallel are additive. For a typical 3.1 µm long actin filament traveling at 1 µm/s (V) incubated over a bed of alpha-actinin (with an initial loading concentration of 1 µg/ml ([α])), the average viscoelastic load on the actin filament per alpha-actinin molecule is 0.12 pN, well below the rupture force of 18 pN (Miyata et al. 1996) reported for randomly oriented alpha-actinin molecules on a nitrocellulose surface. The rupture force measured by Miyata et al. most accurately measures the rupture force in our assay since the nature of the attachment of alpha-actinin to the surface directly effects the measurement of the rupture force (Ferrer et al. 2008). Since the viscoelastic force is less than the rupture rate, it is not surprising that the viscoelastic regime gives a reasonable physical description of the data. It is possible however, that there could be deviations from viscoelasticity in alpha-actinin frictional loading experiments at extremely low concentrations of alpha-actinin and in experiments with myosins with high sliding velocities.

The direct molecular effects of fatigue-like conditions

It has been shown that muscle, under fatigue-like conditions shows several changes in contractility including decreases in maximal sliding velocity, isometric force, power output, and a shift in the load at which maximal power output is achieved (See (Cooke 2007) for review). The physiological basis of fatigue induced changes in contractility stem from many different factors, including changes in neuronal activity, excitation-contraction coupling, and actomyosin contraction (for review, see (Cooke 2007; Fitts 1994)). It has previously been shown using muscle fibers that the direct changes in the actomyosin contractile complex are a result of alterations in the levels of metabolites, oxidative damage, and an increase in myosin regulatory light chain phosphorylation.

As a test case of the frictional loading model, we examined the direct molecular effects of fatigue-like changes in metabolites and acidosis on myosin contractility in the frictional loading assay by measuring the alpha-actinin dependence of sliding velocity. Studying fatigue-based changes in the in vitro motility assay has the distinct advantage over skinned fiber studies in that all of the observed changes in contractility can be assigned to the direct effect of fatigue on the actomyosin contractile apparatus rather than broader cellular based changes such as myofilament disarray at physiological temperatures (Myburgh and Cooke 1997).

The alpha-actinin - velocity relationships for myosin under normal and fatigue-like conditions appear to be well described by the viscoelastic model of frictional loading (Fig. 3). Furthermore, the data show clear reductions in unloaded velocity and isometric force in the presence of excess metabolic end products, consistent with muscle fibers subjected to similar conditions (Cady et al. 1989; Cooke 2007; Dawson et al. 1978; Fitts 1994; Fitts 2008; Karatzaferi et al. 2008; Myburgh and Cooke 1997; Pate et al. 1995; Wilson et al. 1988) Since the degree of depression in contractility depends on the extent of fatigue, it is difficult to make a direct comparison of our in vitro motility results with fiber studies. However, the three-fold reduction in isometric force seen here in the frictional loading assay is consistent with other reports using muscle fibers (Thompson et al. 1992).

Using the data collected for the alpha-actinin dependence of velocity, force-velocity and power curves can be assembled. The force-velocity and power-force relationships were well fit by the empirically derived equations of Hill from studies of muscle fibers (Eq. 1 and Eq. 2) (Hill 1938), further validating the model of alpha-actinin as a viscoelastic load. Furthermore, the reductions in velocity and force along with the increased curvature of the force-velocity relationship observed under fatigue-like conditions is consistent with previous measurements in muscle fibers (Jones et al. 2006). Similarly, consistent with fiber studies, the data show that fatigue-like conditions cause reductions in both the peak power of the myosin and the load at which peak power occurs. The shift in peak power suggests that under physiologically relevant loads, a fatigued muscle would show a further reduction in power output, further reducing the work capacity of the muscle. It is intriguing to note that this methodology would allow for the force-velocity and power relationships of non-muscle and unconventional myosins to be determined. Taken together, these data, in addition to verifying the observed depressions in myosin contractility observed in studies of muscle fibers, demonstrate that fatigue-like accumulations of metabolites can cause a direct depression of contractility in the actomyosin complex in the absence of other cellular structures.

Determination of when the viscoelastic or elastic regime apply and the extension to isotonic studies in the in vitro motility assay

The frictional loading model described here provides the molecular basis for the load imposed by actin binding proteins in the in vitro motility assay. The frictional load depends on whether one is working in the elastic or viscoelastic regime. The frictional force in the viscoelastic regime is given by multiplying equation A2 by the sliding velocity. When this value approaches the rupture force, there will be a transition from the viscoelastic regime to the elastic regime. This transition will depend on the stiffness of the ABP, the detachment kinetics of the ABP from actin, the ABP duty cycle, and the actin filament sliding velocity. Although not developed here, the transition from the viscoelastic to the elastic regime could be modeled using a Boltzman distribution where the probability of rupture is related to the change in free energy for the rupture transition (Tinoco and Bustamante 2002).

With the careful choice of ABP, the frictional loading behavior of the imposed load could be controlled. Such control could come from choosing ABPs with different mechanical properties and affinities for actin or by adjusting experimental conditions that would alter the kinetics of the myosin propelling the actin filament (nucleotides, temperature, etc.). Based on the long kinetic lifetime of the NEM myosin - actin bond (Pemrick and Weber 1976), one would expect the frictional load exerted by NEM myosin to behave more closely to an elastic damping element where the force would be independent of velocity over a large range of sliding velocities.

The role of myosin as a force generating motor in muscle contraction and cellular transport as well as its role in modulating tension in the cell necessitates that myosin work under mechanically loaded conditions. Furthermore, the kinetics of myosin motors have been shown to be strain dependent and this strain dependence has been shown to be critical for the functioning of the myosin motor under physiological conditions (Fenn 1923; Hill 1938; Laakso et al. 2008; Veigel et al. 2002). As such, it is desirable to study myosin kinetics and mechanochemistry under isotonic conditions in the in vitro motility assay. Isotonic conditions in the in vitro motility assay could be achieved through control over whether the frictional load behaves elastically or viscoelastically. In the viscoelastic regime, the load imposed on the actin filament will depend on both the actin filament sliding velocity and the amount of ABP on the surface. Thus, in an isotonic experiment, where some kinetic parameter that affects myosin velocity (i.e. [ATP] or [ADP]) is altered, the velocity dependence of the imposed load in the viscoelastic regime would make these experiments extremely challenging. However, in the elastic regime, the imposed load is independent of velocity and thus the imposed load is determined by only the amount of ABP added to the motility assay surface and not by external factors that would also alter myosin kinetics, permiting isotonic studies of motor proteins using the in vitro motility assay.

Conclusions

We have presented here a model that describes the molecular basis for the myosin-based frictional loading assay, which describes the behavior of alpha-actinin frictional loading experiments. It should be noted that the model is general and thus could be extended to other molecular motors with different substrates and binding proteins without modification. The ability of the model to detect reductions in velocity and isometric force under conditions where isometric force and force were expected to decrease indicates that the model provides a robust assessment of changes in isometric force. Finally, the model can be extended to examine force-velocity relationships, power outputs, and isotonic kinetic, extending the ability of the motility assay to examine the contractile properties of the actomyosin interaction under more physiologically relevant conditions.

Appendix

In an effort to characterize the myosin driven movement of actin filaments over a range of alpha-actinin concentrations and to relate the load-dependent behavior of the myosin to myosin force producing capability, we have developed a model for ABP frictional loading. Consistent with theoretical (Tawada and Sekimoto 1991a; Tawada and Sekimoto 1991b) and experimental considerations (Uyeda et al. 1990), we have made the simplifying assumption that solvent viscosity is negligible compared to the load imposed by actin binding proteins. Also, we have assumed that all actin binding proteins will bind to actin until either they are kinetically or mechanically detached from actin. Furthermore, we have made the simplifying assumption that the lifetime of the actin-ABP bond is independent of strain. While these assumptions simplify the model, the model could be altered to accommodate effects due to solvent viscosity and strain dependent detachment kinetics without loss of generality.

Viscoelastic Model

If the inherent kinetics of the actin-ABP bond lifetime rather than the time needed to reach rupture force determines the actin-ABP attachment time, then the frictional load behaves as a viscoelastic load and the relative amount of strain absorbed by the ABP before kinetic detachment occurs will depend on the velocity of the actin filament, analogous to the friction experienced by a body moving through a fluid. In this case, the average frictional load exerted by a single ABP molecule is proportional to velocity and is given by F_fric = γ*V where γ is the frictional coefficient and V is the sliding velocity. The frictional coefficient is given by

$$\gamma ={\kappa }^{*}{t}_{\mathit{\text{on}}}=\frac{\kappa }{k_D}$$ (A1)

where κ is the elastic stiffness constant, t_on is the amount of time that ABP spends attached to actin (which is the reciprocal of the detachment rate, k_D), and f_α is the fraction of the ABP lifetime spent attached to actin (i.e. the duty cycle).

For an ensemble of ABP molecules:

$$F_{\mathit{\text{fric}}}={\gamma }^{*}{V}^{*}{\rho }^{*}{L}^{*}{r}^{*}{f}_{\alpha }$$ (A2)

where r is the distance over which an ABP can reach and attach to actin, ρ is the surface density of ABP, and L is the average length of an actin filament. Substituting this expression into equation 3 and solving for V we find that:

$$V=\frac{{V_{\text{max}}}^{*}{F}_d}{F_d+{\gamma }^{*}{\rho }^{*}{r}^{*}{L}^{*}{f_{\alpha }}^{*}{V}_{\text{max}}}$$ (A3)

The surface concentration of ABP, in units of molecules per area, is given by:

$$\rho =\frac{{\lambda }^{*}{[\alpha ]}^{*}{\nu }^{*}{N}_A}{A}\equiv {\zeta }^{*}[\alpha ]$$ (A4)

where λ is the fraction of ABP that bound to the surface, v is the volume of ABP added, [α] is the molar concentration of ABP added, N_A is Avogadro’s number, and A is the surface area of the flow cell. Furthermore, we can define the effective molarity of ABP on the surface is given by:

$${[\alpha ]}_{\mathit{\text{eff}}}=\frac{{\rho }^{3/2*}{10}^{-3}}{N_A}=\frac{{\zeta }^{3/2*}{[\alpha ]}^{3/2*}{10}^{-3}}{N_A}\equiv {\chi }^{*}{[\alpha ]}^{3/2}$$ (A5)

where the factor 10⁻³ is necessary to convert meters³ to liters. Using this definition, we can calculate the ABP – actin bond duty cycle as:

$$f_{\alpha }=\frac{t_{\mathit{\text{on}}}}{t_{\mathit{\text{on}}}+t_{\mathit{\text{off}}}}=\frac{\frac{1}{k_D}}{\frac{1}{{k_A}^{*}{[\alpha ]}_{\mathit{\text{eff}}}}+\frac{1}{k_D}}=\frac{{k_A}^{*}{[\alpha ]}_{\mathit{\text{eff}}}}{{k_A}^{*}{[\alpha ]}_{\mathit{\text{eff}}}+k_D}=\frac{{k_A}^{*}{\chi }^{*}{[\alpha ]}^{3/2}}{{k_A}^{*}{\chi }^{*}{[\alpha ]}^{3/2}+k_D}$$ (A6)

where k_A is the second order attachment rate constant. Finally, we can substitute equations A4–A6 into equation A3 and we find that:

$$V=\frac{{V_{\text{max}}}^{*}{F}_d}{F_d+\frac{{V_{\text{max}}}^{*}{\kappa }^{*}{\zeta }^{*}{L}^{*}{r}^{*}{k_A}^{*}{\chi }^{*}{[\alpha ]}^{5/2}}{{k_D}^{*}({k_A}^{*}{\chi }^{*}{[\alpha ]}^{3/2}+k_D)}}$$ (A7)

Thus, if ABP acts as a viscoelastic element rather than an elastic element, the velocity of actin sliding as a function of ABP added approaches zero asymptotically at higher ABP concentrations and it will not be possible to report an alpha-actinin concentration where motility stops.

Elastic Model

The limiting case of the viscoelastic model is the elastic model. If a strain greater than the rupture force is able to develop during the amount of time that the ABP is kinetically attached to the actin, then the ABP will act as a purely elastic element and the driving force due to the myosin will stretch the ABP molecule until the stored elastic energy exceeds the rupture force of the ABP – actin bond and the ABP molecule is forcibly detached from the actin filament. This is an analogous case to macroscopic friction in which the imposed frictional load is independent of velocity. The only velocity dependence that would exist would be due to changes in the strength of the actin – ABP bond due to loading rate. The effect due to loading rate stems from the fact that some proteins will “harden” when stretched in a non-equilibrium process (Tinoco and Bustamante 2002).

In the pure elastic case, the frictional load imposed by the bed of ABP molecules would be given by:

$$F_{\mathit{\text{fric}}}={F_{\mathit{\text{rupt}}}}^{*}{\rho }^{*}{r}^{*}{L}^{*}{f}_{\alpha }$$ (A8)

where F_rupt is the rupture force of the ABP, Substituting equations A4–A6 and A8 into equation 3, we arrive at the expression for the frictional load imposed by a purely elastic element:

$$V={V_{\text{max}}}^{*}\frac{(F_d-{F_{\mathit{\text{rupt}}}}^{*}{\zeta }^{*}{L}^{*}{r}^{*}\frac{{k_A}^{*}{\chi }^{*}{[\alpha ]}^{5/2}}{{k_A}^{*}{\chi }^{*}{[\alpha ]}^{3/2}+k_D})}{F_d}$$ (A9)

In this case, eventually enough ABP could be added such that the frictional force due to the bed of ABP would equal the propelling force due to the bed of myosin, and motility stops.

Higher Order Corrections to the Model

In this model, we have made several simplifying assumptions that collectively add some error to our estimates of the values predicted by the model. The estimates in the simplified model provide a first order approximation of the molecular interactions in a frictional loading assay. These simplifying assumptions can be changed in order to give a more realistic picture of the interactions between ABPs and actin however, these higher order corrections require further characterization of physical constants via other experiments. As such, all of the analysis in this report has used the simplified model.

Our model includes the simplifying assumption that the rupture force is insensitive to rupture rate. However, the loading rate of the ABP can change the rupture force of a bond. The relationship between loading rate and rupture force is given by the equation:

$$F_{\mathit{\text{rupt}}}=\frac{{k_B}^{*}T}{x_{\beta }}*\text{ln}(\frac{x_{\beta }}{{k_D^o}^{*}{k_B}^{*}T})+\frac{{k_B}^{*}T}{x_{\beta }}*\text{ln}(r_f)$$ (A10)

where F_rupt is the rupture force, k_D^o is the detachment rate in the absence of a load, x_β is a characteristic length for the bond, and r_f is the loading rate (Evans and Ritchie 1997). Measurement of the rupture force over a large range of loading rates is necessary to characterize the molecular behavior of the actin-ABP interaction since in some APBs, rupture has been shown to occur at different characteristic lengths for different loading rates (Evans 2001; Evans and Ritchie 1997; Guo and Guilford 2006; Merkel et al. 1999; Tees et al. 2001). The importance of this measurement can be seen by fitting equation A11 to the data of Ferrer et al. (Ferrer et al. 2008) for actin – alpha actinin rupture forces in which at least two regimes for rupture can be seen, consistent with the observations of Miyata et al. (Miyata et al. 1996). It should be noted that the data of Ferrer et al., 2008 is not sufficient for a statistically reliable estimation of the parameters required to make these corrections to the model. A greater characterization of the rupture behavior, such as was done by Guo et al. (Guo and Guilford 2006) is required in order to apply this higher order correction to frictional loading assays.

In our model, we have made the simplifying assumption that the kinetic lifetimes of the actin-ABP bonds are independent of load. While this is true as a first order approximation, a more complete approximation of the load dependence of the kinetic lifetimes can be obtained using the Bell equation (Bell 1978):

$$k_D(F)={k_D^o}^{*}\mathit{\text{Exp}}(\frac{F^{*}{x}_{\beta }}{{k_B}^{*}T})$$ (A11)

where k_D(F) is the load dependent detachment rate and F is the load on the ABP. The characteristic bond length, x_β can be measured by recording the rupture force of the bond as a function of loading rate (reviewed in (Evans 2001)). However, as has been stated earlier, a better characterization of this characteristic length is needed in order to apply this correction.

Lastly, our model describes the viscoelastic and the elastic regimes of frictional loading yet it does not describe the transition between the two regimes. The transition between these regimes could be modeled using a Boltzman distribution (Tinoco and Bustamante 2002). This modification to the model would more realistically describe the transition yet it would not significantly change our model under situations where the load on the ABP is much higher or lower than the rupture force.

Model parameters for alpha-actinin experiments

The mechanical and kinetic properties of alpha-actinin have been well characterized, allowing the relationship between velocity and added alpha-actinin to be fit with known quantities. It should be noted, however, that differences between the conditions of the motility assay and conditions where these quantities were determined will probably introduce some error. The second-order attachment rate constant for the alpha-actinin - actin interaction is 4*10⁶ M⁻¹ s⁻¹ (Kuhlman et al. 1994) and the detachment rate constant is 9.6 s⁻¹ (Goldmann and Isenberg 1993; Kuhlman et al. 1994). Ferrer et al. showed that the rupture force and thus mechanics of the actin – ABP interaction depends on both the alpha-actinin molecule orientation and the properties of the coverslip surface (Ferrer et al. 2008). The rupture force measured for randomly oriented alpha-actinin molecules over a nitrocellulose surface (Miyata et al. 1996) (which is similar to the experimental geometry used in alpha-actinin frictional loading experiments) was measured to be around 18 pN. Since the stiffness measurement of the alpha-actinin molecule depends on both the surface-linkage method and the orientation of the ABP (Ferrer et al. 2008), we estimated the stiffness of a randomly oriented alpha-actinin molecule using the stiffness of randomly oriented myosin adhered to a nitrocellulose surface based on the fact that the rupture forces of randomly oriented alpha-actinin and myosin molecules bound to actin over a nitrocellulose surface are similar (Miyata et al. 1996; Nishizaka et al. 1995). The value for the stiffness of a myosin crossbridge has been reported to be between 0.7 (Veigel et al. 1998) and 1.7 pN/nm (Lewalle et al. 2008) when measured at the single molecule level using an optical trap. The fraction of alpha-actinin binding to a nitrocellulose surface under similar buffer conditions to those employed here was measured to be approximately 6 percent (λ) (Miyata et al. 1996). Assuming that a typical actin filament is 5 nm (Holmes et al. 1990; Kabsch et al. 1990) and 3.1 µm long (L) (Szczesna-Cordary et al. 2007), that an alpha-actinin molecule has a length of 40 nm (Imamura et al. 1988; Meyer and Aebi 1990), and that an actin filament in a motility assay is 10 nm above the flow cell surface, then alpha-actinin molecules can reach a single actin filament with a reach of 82 nm (r). Using these parameters, one can fit the data of velocity versus concentration of alpha-actinin to determine the net driving force of the myosin F_d and the maximal sliding velocity in the absence of an exogenously added load, V_max.

The model presented above provides a molecular description of the frictional loading assay for motor proteins. The validity of the model is supported by the agreement with the relation ship between velocity and the amount of actin binding protein added to a standard in vitro motility assay as well as the agreement of the in vitro motility results under fatigue-like conditions with the experimental results from fiber studies. Finally, the theoretical relationship presented in this model provides a means to understand the physical parameters that define the interaction between single actin filaments and actin binding proteins as well as the calculation of force-velocity curves and power output using the in vitro motility assay.