Abstract
Contrary to the traditional view that shapes and their hierarchical level (local or global) are a priori integrated in perception, recent evidence suggests that the identity of a shape and its level are encoded independently, implying the need for shape-level binding to account for normal perception (Hübner, & Volberg, 2005). What is the binding mechanism in this case? Using hierarchically arranged letter shapes we support a proposal that the left hemisphere (LH) has a preference for binding shapes to the local level while the right hemisphere (RH) has a preference for binding shapes to the global level. More importantly, binding is modulated by attentional selection of higher or lower spatial frequencies (SFs). We demonstrate that attentional selection in a preceding stimulus of higher SFs facilitated binding by the LH at the local level and attentional selection of lower SFs facilitated binding by the RH at the global level.
One question that has been pervasive across cognitive, computational, neuropsychological and neurophysiological studies is how local elements in a visual scene (e.g., branches, leaves, trunk) are integrated to produce global percepts (e.g., tree). From Gestalt psychology to more recent studies of functional hemispheric differences, a central question has been how local parts are integrated into global wholes. Within this context, one aspect that has been largely ignored is how the level of processing (local or global) is perceptually integrated with the shapes in the display. This aspect may have remained dormant because an implicit assumption in much of the literature on hierarchical perception has been that the hierarchical level is not processed separately from the identity of the perceived shape at that level (e.g., Navon, 1977; Lamb & Yund, 1996; Robertson, 1996). In other words, when the tree is defined as the global level, its representation as being global is assumed to be intrinsic to the perceptual process. In this “traditional view” shape and level are bound throughout visual processing, although one level may be processed before another (Navon, 1977).
The traditional view may appear reasonable when considering the displays used to study hierarchical perception. These often consist of a series of smaller (local) shapes spatially arranged to form a larger (global) shape (“Navon” displays; Figure 1). Intuitively, the local and global levels seem unambiguous. However, when considering hierarchically structured objects in the natural environment, the traditional view seems wanting since the same element might be a local percept in one instance (e.g., local tree in a global forest) and a global percept in a different instance (e.g., global tree composed of local branches), depending on the focus of attention. In line with this challenge, Hübner and Volberg (2005) proposed a hierarchical “integration theory” in which visual information at different levels is initially represented independently of level and only later bound to form an integrated representation at a particular level. They adopted the framework of feature integration theory (FIT), which posits attentional selection of a spatial location as the medium by which individual representation of surface features (e.g., color, shape and orientation) are bound into a coherent whole (Treisman & Gelade 1980; Treisman, 1999). Evidence for FIT lies in the fact that deficits in spatial attention after brain injury lead to incorrect feature combinations in perception known as “illusory conjunctions” (e.g., mistakenly reporting a red X when presented with a blue X and a red T; Robertson el al., 1997). Illusory conjunctions also occur in normal perception when attention is diverted and the stimuli are briefly presented (Treisman & Schmidt, 1982).
Figure 1.
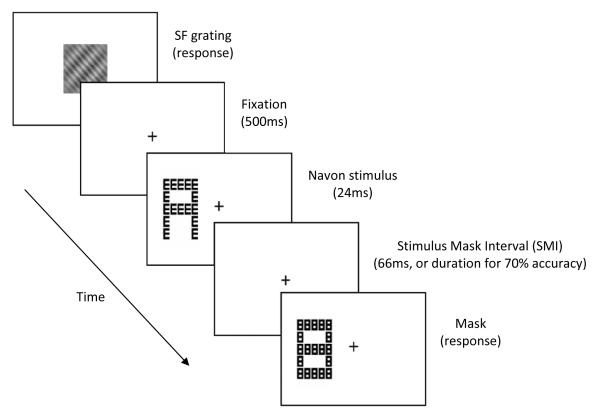
Example trial from the primary experiment. First, a compound SF grating appeared until response and participants reported the orientation (left or right) of the LSF or HSF component in separate blocks of trials. Next, a Navon stimulus flashed for 24ms to the left or right of fixation (randomly) and was replaced by a mask. Participants reported the identity of the global or local letter in separate blocks of trials by selecting among 4 alternatives. The stimulus-mask interval (SMI) started at 66ms and was gradually decreased when participants performed better than 70% accuracy in a given block. In the control experiment, there was no prime task; a trial began with the 300ms fixation cross.
Addressing the question of binding shape and level (local/global), Hübner and Volberg (2005) interrupted processing of Navon displays by masking them after randomly flashing them in the left visual field (LVF) or right visual field (RVF), and asking participants to identify the letter at a directed level. Under these conditions, the rationale was that if shape and level are initially represented separately, then an interruption in processing should lead to instances in which binding fails, and illusory conjunctions of shape and level result (i.e., the letter at the unattended level should be seen as the letter at the attended level). Indeed, Hübner & Volberg (2005) found a high incidence of shape-level conjunction errors that exceeded chance and could not be explained by guessing.
In addition, by presenting the displays in the LVF or RVF, Hübner and Volberg (2005) examined whether a visual field asymmetry in conjunction errors occurred consistent with evidence for functional hemispheric differences in hierarchical processing (e.g., Delis, Robertson & Effron, 1986; Martin, 1979; Martinez et al., 1997; Robertson & Delis, 1986; Robertson, Lamb & Knight, 1988; Robertson, Lamb, M. R., & Zaidel, E., 1993; Weissman & Woldorff, 2005). Although some studies have not found this difference (Heinze et al., 1998; Fink et al., 1997; Polster & Rapcsak, 1994), a meta-analysis showed that overall there was strong evidence for a left hemisphere (LH) bias in local processing and a right hemisphere (RH) bias in global processing (Van Kleeck, 1989). This meta-analysis also showed that the hemispheric differences were more pronounced when the stimuli were incongruent (i.e., letter identity differed at the local and global levels), which would produce more illusory conjunctions in line with the integration theory. Hübner and Volberg (2005) found that participants made significantly more conjunction errors to local targets (i.e., when asked to report local letters they reported global ones) when the stimulus was presented in the LVF (projected to the RH), and they made significantly more conjunction errors to global targets (i.e., when asked to report global letters they reported local ones) when the stimulus was presented in the RVF (projected to the LH).
These results provide evidence that shape and level are represented separately during some early visual processing stage, followed by a binding stage, and that the rate of binding errors depends on the visual field in which the hierarchical displays are presented. However, the mechanism underlying shape-level binding is unknown. In FIT (Treisman & Gelade, 1980), features must be co-located (through spatial attention) to be properly bound. In contrast, the integration theory formulated by Hübner and Volberg (2005) does not offer a binding mechanism.
The goal of the present study was to examine whether the medium of hierarchical binding is attentional selection of task-relevant spatial frequencies (SFs). This hypothesis is based on previous data suggesting that SFs cue the level of representation (Robertson, 1996) and that the relevant SFs in a stimulus can drive hemispheric differences in performance (Ivry & Robertson, 1998). Evidence that the LH is biased in selecting relatively higher spatial frequencies (HSFs) while the RH is biased in selecting relatively lower spatial frequencies (LSFs) has been demonstrated for discrimination of sinusoidal gratings (Christman, Kitterle & Hellige, 1991; Flevaris et al, 2009; Kitterle, Christman & Hellige, 1990) as well as processing letters, faces, scenes and objects (Iidaka et al., 2004; Jonsson & Hellige, 1986; Keenan, Whitman & Pepe, 1989; Parker, Lishman & Hughes, 1996; Peyrin et al., 2005). Studies have also demonstrated that global perception relies more on the selection of relatively LSFs in the stimulus, whereas local perception relies more on the selection of relatively HSFs (Han et al., 2003; Hughes, Fendrich & Reuter-Lorenz, 1990; Hughes, Nozawa & Kitterle, 1996; Jian & Han, 2005; Robertson, 1996; Shulman et al., 1986; Shulman & Wilson, 1987; Yoshida et al., 2007). Perhaps most importantly, SF processing is flexible and contingent both on bottom-up factors such as image information as well as on top-down factors such as attention and task constraints (Peyrin et al., 2006; Sowden & Schyns, 2006).
Given this evidence, our hypothesis is that SF is the medium for hierarchical binding, such that attentional selection of relatively HSFs facilitates shape-level binding by the LH, and attentional selection of relatively LSFs facilitates binding by the RH. To test this hypothesis, we used a priming paradigm designed to examine how directing attention to SF (relatively high or relatively low) modulates shape-level conjunction errors in a hierarchical display. On each trial participants first discriminated the orientation of either the lower or higher SFs in a centrally presented compound grating (e.g., Olzak, 1986). A Navon display then flashed in the LVF or RVF and was masked. Participants indicated which of four possible letters appeared at the local or global level. Importantly, they were informed that each display would be constructed of two different letters, so if they only identified the letter at the unattended level, they should guess from the remaining three alternatives. Errors in which participants inadvertently reported the letter at the unattended level were considered to be shape-level “conjunction errors” and errors in which participants reported one of the two letters that were not presented at any level were considered to be “feature errors.”
If letters and levels are bound a priori (i.e., the traditional view), then there should be an even distribution of errors across conjunction and all possible feature errors (i.e., with 3 possible erroneous responses, conjunction errors should not exceed ⅓ of the total errors). First, we replicated Hübner and Volberg’s (2005) findings, showing that participants made many more than ⅓ conjunction errors, and that conjunction errors to local targets were greater when the stimulus was projected to the RH than to the LH, and conjunction errors to global targets were greater when they were projected to the LH than to the RH. More importantly, the attended SF in the prime task modulated the hemispheric asymmetry of conjunction errors such that attentional selection of HSFs reduced the hemispheric asymmetry in conjunction errors to local targets and attentional selection of LSFs reduced the hemispheric asymmetry in conjunction errors to global targets.
Method
Participants
Twenty-four undergraduates from the University of California, Berkeley participated in the experiment for course credit. Sixteen (twelve women) were tested in the primary experiment and eight (five women) in a subsidiary control experiment (see below). All were right handed and had normal or corrected-to-normal vision. All gave informed consent as approved by the committee for the protection of human subjects at the University of California, Berkeley.
Stimuli
The compound gratings were generated in Matlab™ (Mathworks, Natick, MA) with a sinusoid function for each SF. At 100% contrast, each compound grating subtended 6.6° of visual angle and was composed of a 3.6cycle/degree grating (the relatively HSF component) and a 1.2cycle/degree grating (the relatively LSF component). One SF component was oriented at +45° (tilted to the right) and the other was oriented at −45° (tilted to the left).
The Navon displays were black on a white background, and were made using Adobe Photoshop ™. Seen from a distance of 57cm, each local letter subtended .9° of visual angle and was spatially arranged on a 5×5 grid to form a global letter that was 4.5° wide by 6° high. The letters used were squared A, E, H, and S in all their local and global combinations with the exception of congruent combinations (e.g., a global A composed of local As), resulting in twelve distinct Navon displays. A mask was composed of local figure 8s arranged on the same grid to form a global figure 8, which overlapped with all possible letter combinations.
Procedure
The stimuli were shown on a 17 inch color monitor with a vertical refresh rate of 60Hz at a resolution of 1024×768 pixels. Trial timing was controlled by Presentation™ (Neurobehavioral Systems, Albany, CA) and is depicted in Figure 1.
On each trial, a compound SF grating (prime) first appeared until response. In separate blocks of trials, participants reported the orientation of either the “thin bars” (HSFs) or “thick bars” (LSFs) quickly but accurately without moving their eyes over the grating. The grating was then replaced by a central, 300ms fixation cross, followed by a Navon display that flashed for 24ms with its medial edge 1° to the left or right of fixation and 3.25° from the midline. Visual field of presentation was randomized within each block. The mask then appeared in the same location as the Navon display and remained on the screen until response. In separate blocks of trials, participants were asked to indicate the identity of the local or global letter. The stimulus-mask interval (SMI) was initially 66ms (i.e., the mask appeared 66ms after the offset of the Navon stimulus) and was gradually decreased to maintain ~ 70% accuracy. The SMI was adjusted separately for local and global blocks. That is, if participants started in a local block condition, the SMI was adjusted accordingly for blocks in that condition and was reset to 66ms when they started the global block condition.
Importantly, participants were instructed to guess if they did not see the target letter. They were told that each Navon display would be composed of two different letters among the letters A, E, H and S, and if they did not see the letter at the target level, but did see the letter at the other, non-target level, not to report this letter but to guess from the remaining three alternatives. There were four blocks of 48 trials for each of the four prime (HSF versus LSF)/probe (local versus global) conditions, performed in sequential order while the order of conditions was counterbalanced across participants. We used this blocked design rather than cuing participants to a specific level on a trial by trial basis to lessen confusion about the dual task.
Eight participants used their left hand for the prime task and their right hand for the probe task, and vice versa for the other eight. For the prime task, participants used the index and middle finger of the response hand; the left finger was used to indicate a “left” orientation of the target SF and the right finger was used to indicate a “right” orientation. For the probe task, tabs indicating “A”, “E”, “H” and “S” were placed over keys on the keyboard and participants pressed the corresponding button to make their response.
Prior to the main experiment, a control experiment was run (testing eight different participants from the same population) in order to assure that we could replicate Hübner and Volberg’s (2005) findings when blocking attended level (local/global) and using our stimuli. In the control experiment the same design was used as in the primary experiment except that there was no prime, resulting in only two blocked conditions, local and global. The control experiment was successful and will be presented at the end of the results section.
Results
Main Experiment
Participants had no trouble performing the priming task, as average accuracy in reporting the orientation of the target SF was 98%. We were therefore confident that attention was directed to the relevant SF in each block.
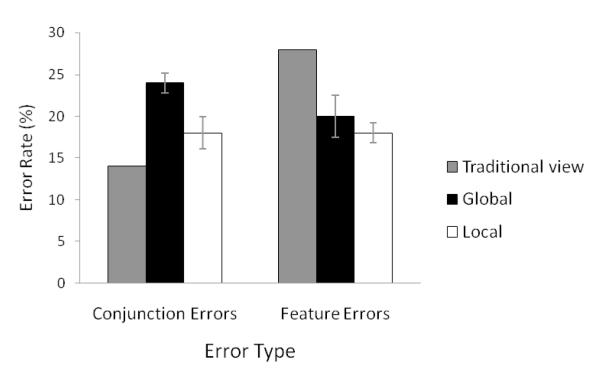
We first established the separation of letter identity and hierarchical level as predicted by integration theory, by comparing the observed distribution of errors with that predicted by the traditional view (Figure 2). The mean error rate across all conditions was 42%. Conjunction errors occurred in 21% of error trials, and feature errors occurred in the other 21%. As in Hübner and Volberg (2005), the distribution of errors was significantly different from that predicted by the traditional view, indicated statistically by the Model (traditional versus observed) × Error type (feature versus conjunction) interaction [F(1,15)=56.2, MSe=13.0, p< .0001; p_rep=1.0; partial η2=.79]. Follow-up t-tests (using Bonferroni correction) indicated that the rate of conjunction errors was significantly greater than that predicted by the traditional view [t(15)=7.5, p< .0001; p_rep=1.0; d=2.5] and the rate of feature errors was significantly less than that predicted by the traditional view [t(15) 7.5, p< .0001; p_rep=1.0; d=1.0]. An analysis comparing the observed pattern of errors with the pattern predicted by the traditional view for local and global blocks separately mirrored the overall analysis. For local blocks, the significant Model × Error type interaction [F(1,15)=130.9, MSe=5.2, p< .0001; p_rep=1.0; partial η2=.89] revealed significantly more conjunction errors (18%) than predicted by traditional view (13%; t(15) 6.7, p< .0001; p_rep=1.0; d=.93) and significantly less feature errors (18%) than predicted by traditional view (26%; t(15) 6.7, p< .0001; p_rep=1.0; d=1.0; both significant using Bonferroni correction). Likewise, for global blocks, the Model × Error type interaction [F(1,15)=52.0, MSe=26.2, p< .0001; p_rep=1.0; partial η2=.78] revealed significantly more conjunction errors (24%) than predicted by the standard view (16%; t(15)=7.2, p< .0001; p_rep=1.0; d=2.2) and significantly less feature errors (20%) than predicted by the standard view (29%, t(15)=7.2, p< .0001; p_rep=1.0; d=1.1; both significant using Bonferroni correction). These results replicate those found by Hübner and Volberg (2005), showing that when participants made an error, they were more likely to report the letter at the unattended level as being the target letter rather than a letter that was not present.
Figure 2.
The percentage of conjunction and feature errors for global and local trials, compared with those predicted by the traditional view. Error bars reflect standard errors of the mean.
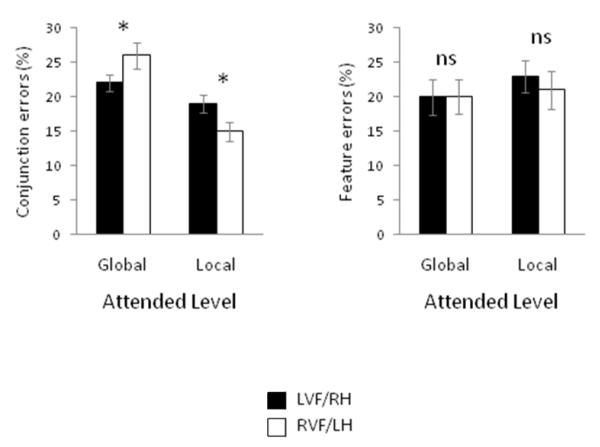
To examine our primary prediction that attentional selection of SFs would modulate the shape-level binding depending on the visual field of presentation, we conducted a 2×2×2 ANOVA of the conjunction errors, with attended SF in the prime (HSF versus LSF), attended target Level (local versus global), and Hemisphere (left versus right) as factors. This analysis revealed a Level × Hemisphere interaction [F(1,15)=9.3, MSe=52.8, p=.008; p_rep=.98; partial η2=.38], which is depicted in Figure 3. There were significantly more conjunction errors to local targets projected to the RH (19%) than to the LH (15%; t(15)=2.5, p=.03; p_rep=.95; d=.73) and significantly more conjunction errors to global targets projected to the LH (26%) than to the RH (22 %; t(15)=2.4, p=.03; p_rep=.95; d=.65; both significant using Bonferroni correction). There was no Level × Hemisphere interaction for feature errors, F> 1, and no other effects in the feature error analyses were close to significant levels.
Figure 3.
The Level × Hemisphere interaction for conjunction errors (significant) and feature errors (not significant). Errors bars reflect standard errors of the mean. LVF/RH: Navon display presented in the left visual field/ projected to the right hemisphere; RVF/LH: Navon display presented in the right visual field/ projected to the left hemisphere.
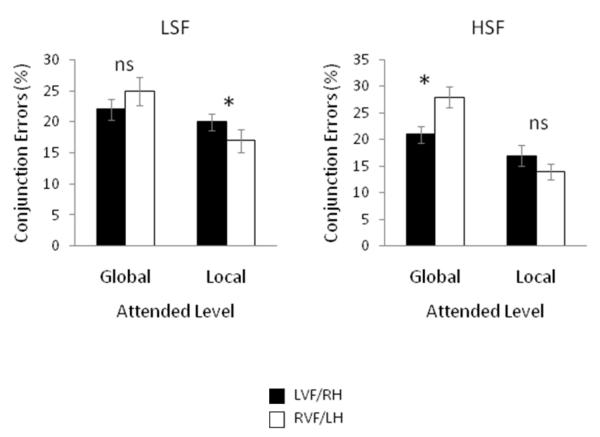
Importantly, the analysis of the conjunction errors also revealed a SF × Level × Hemisphere second-order interaction [F(1,15)=8.2, MSe=5.6, p=.01; p_rep=.97; partial η2=.35]. To examine this interaction, we conducted Level (local versus global) × Hemisphere (left versus right) ANOVAs for the LSF and HSF conditions separately, and these data are shown in Figure 4. For the LSF condition, there was a significant Level × Hemisphere interaction [F(1,15)=5.1, MSe=24.4, p=.04; p_rep=.93; partial η2=.25]. As predicted, follow-up t-tests showed that following LSF selection, there were significantly more conjunction errors for local targets projected to the RH (20%) than the LH (17%; t(15)=2.8, p=.01; p_rep=.97; d=.44; significant using Bonferroni correction), whereas there was no significant hemispheric difference global targets following LSF primes [t(15)=1.3, p=.22; p_rep=.81; d=.30]. The Level × Hemisphere ANOVA for the HSF condition also revealed a significant Level × Hemisphere interaction [F(1,15),=12.0, MSe=34.9, p=.004; p_rep=.99; partial η2=.44]. As predicted, follow-up t-tests showed the opposite pattern than what was found for LSF primes. That is, following HSF primes, there were significantly more conjunction errors to global targets projected to the LH (28%) than to the RH (21%, t(15)=3.2 , p=.006; p_rep=.98; d=.96; significant using Bonferroni correction), whereas there was no statistically significant difference between the hemispheres for local targets following HSF primes [t(15)=1.8, p=.09; p_rep=.89; d=.46].
Figure 4.
The Level × Hemisphere interaction for conjunction errors modulated by the spatial frequency attended in the prime. Following attention to low spatial frequencies (LSFs), there was an increased rate of conjunction errors to local targets presented in the left visual field (LVF)/right hemisphere (RH) and no reliable hemispheric difference in conjunction errors for global targets. Conversely, following attention to high spatial frequencies (HSFs), there was an increased rate of conjunction errors to global targets presented in the right visual field (RVF)/left hemisphere (LH) and no reliable hemispheric difference for local targets. Error bars reflect standard errors of the mean.
Control experiment
The results from the control experiment were similar to the results found for probes in the primary experiment collapsed over SF. The average overall error rate was 19%, with feature errors occurring in 17% of trials and conjunction errors occurring in 20% of trials. Participants made significantly more conjunction errors (20%) than predicted by the traditional view (12%), indicated by a significant Model (traditional versus observed) × Error type (feature versus conjunction) interaction [F(1,15)=46.6, MSe=10.7, p< .0001; p_rep=1.0; partial η2=.87]. Akin to the primary experiment, the rate of conjunction errors was significantly greater than that predicted by the traditional view [t(15)=6.8, p<.0001; p_rep=1.0; d=2.8], and the rate of feature errors was significantly less than that predicted by the traditional view [t(15)=6.8, p< .0001; p_rep=1.0; d=1.8; both significant using Bonferroni correction].
The attended Level (local versus global) × Hemisphere (left versus right) ANOVA was also consistent with the results from the primary experiment, revealing a Level × Hemisphere interaction [F(1,7)=18.7, MSe=14.5, p=.003; p_rep=.99; partial η2=.73]. There were significantly more conjunction errors to local targets projected to the RH (18%) than to the LH (13%; t(7)=2.7, p=.03; p_rep=.95; d=1.0) and significantly more conjunction errors to global targets projected to the LH (28%) than to the RH (22%; t(7)=4.3, p=.004; p_rep=.99; d=1.1; both significant using Bonferroni correction). There was no level × hemisphere interaction for feature errors, F> 1, and no other effects in the feature error analyses approached significant levels.
Discussion
The results of this study demonstrate that the selected SF in a previously presented stimulus facilitates shape-level binding in hierarchical displays. We replicated the disproportionately large incidence of conjunction errors relative to feature errors and the modulation of these errors across the two hemispheres (Hübner & Volberg, 2005). Most importantly, attentional selection of SF modulated shape-level binding in a manner consistent with hierarchical integration theory and the functional hemispheric literature. Attentional selection of relatively LSFs reduced the hemispheric asymmetry for global conjunction errors and facilitated binding by the RH of letters to global level. Conversely, selection of relatively HSFs reduced the hemispheric asymmetry for local conjunction errors and facilitated binding by the LH of letters to local level. This SF modulation occurred despite any habituation effects that may have occurred from presenting the same SF gratings throughout the experiment (albeit in different orientations).
Although, by their nature HSF stripes are smaller than LSF stripes, a recent study provided evidence that relative SF, rather than attentional window size, is the critical factor (Flevaris et al., submitted). In that study compound gratings similar to those used here were presented as target stimuli, preceded by hierarchical Navon letters as primes. Attention to the global level in the prime improved discrimination of the LSFs in the compound grating whereas attention directed to the local level improved discrimination of the HSFs. This pattern was observed despite differences in the retinal location of the hierarchical displays and the grating. Most importantly, these effects were determined by the relationship between the two SFs in the grating rather than by the absolute SF: Discrimination of a 1.8cycles/degree grating was facilitated by local attention when it was paired with a 0.9cycles/degree grating (lower SF) in the compound, but was facilitated by global attention when it was paired with a 5.3cycles/degree grating (higher SF). These findings strongly suggest that the current results cannot be attributed to the size of the attentional window.
The results from the current study are consistent with the Double Filtering by Frequency (DFF) theory of hemispheric specialization posited by Ivry and Robertson (1998, 2000) but with a new twist. According to DFF theory, the two cerebral hemispheres differ in how they amplify relative SF information in the stimulus. Attention first selects the task-relevant SF range, and the SFs in this range are projected to both cerebral hemispheres. The RH selectively emphasizes the relatively LSFs within that range, and the LH selectively emphasizes the relatively HSFs. The current data together with Hübner and Volberg’s (2005) initial findings suggest that the asymmetry in selective tuning to SFs provides the basic features that segregate local and global levels, but when attention is overtaxed and biased toward one SF than another, the shapes are more likely to be perceptually bound incorrectly to the wrong level (as reflected by illusory shape-level conjunctions). An important tenet of DFF theory is that both hemispheres have access to the initial task-relevant selection of the SF spectrum, making the asymmetrical SF filtering between the hemispheres a higher level mechanism. That we did not find an interaction between SF and hemisphere is consistent with this idea. That is, attention to relatively HSFs or LSFs did not generally facilitate processing by the LH or RH, respectively. Rather, attention to SF modulated specific, task-relevant processing in each hemisphere - namely, the binding of letter identity to hierarchical level.
Although SFs are involved in parsing information into global and local levels (Robertson, 1996), studies have shown that other features of a stimulus can also be valuable in parsing levels under conditions when SF differences are degraded (Lamb, Yund, and Pond, 1999). Whether image properties such as size can also facilitate binding of identity and hierarchical level and whether binding varies as a function of the SF differences present in the display are interesting avenues for future research. Moreover, given that attention to spatial location plays a key role in binding surface properties into integrated object percepts (Treisman & Gelade, 1980), it will also be important to determine how spatial attention interacts with the mechanisms underlying the binding of individual objects to the relative scale at which they exist in the visual environment. The results from the current study open the door for these explorations by showing attentional selection of SF information plays a key role in binding elements of hierarchical displays to the level of the display at which they occur.
Acknowledgments
This study was supported by a NIMH grant to LR and SB (RO1 MH 64458). We thank Lara Krisst and Sasa Redzepovic for help with running participants.
References
- Christman S, Kitterle FL, Hellige J. Hemispheric asymmetry in the processing of absolute versus relative spatial frequency. Brain and Cognition. 1991;16(1):62–73. doi: 10.1016/0278-2626(91)90085-m. [DOI] [PubMed] [Google Scholar]
- Delis DC, Robertson LC, Efron R. Hemispheric specialization of memory for visual hierarchical stimuli. Neuropsychologia. 1986;24(2):205–214. doi: 10.1016/0028-3932(86)90053-9. [DOI] [PubMed] [Google Scholar]
- Fink GR, Halligan PW, Marshall JC, Frith CD, Frackowiak RS, Dolan RJ. Neural mechanisms involved in the processing of global and local aspects of hierarchically organized visual stimuli. Brain. 1997;120(Pt 10):1779–1791. doi: 10.1093/brain/120.10.1779. [DOI] [PubMed] [Google Scholar]
- Flevaris AV, Bentin S, Robertson LC. Attention to hierarchical level influences attentional selection of spatial scale; Poster presented at Vision Sciences Society; Naples, Florida. May, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flevaris AV, Bentin S, Robertson LC. Attention to hierarchical level influences attentional selection of spatial scale. Manuscript submitted for publication. [DOI] [PMC free article] [PubMed]
- Han S, Yund EW, Woods DL. An ERP study of the global precedence effect: the role of spatial frequency. Clinical Neurophysiology. 2003;114(10):1850–1865. doi: 10.1016/s1388-2457(03)00196-2. [DOI] [PubMed] [Google Scholar]
- Heinze HJ, Hinrichs H, Scholz M, Burchert W, Mangun GR. Neural mechanisms of global and local processing: A combined PET and ERP study. Journal of Cognitive Neuroscience. 1998;10(4):485–498. doi: 10.1162/089892998562898. [DOI] [PubMed] [Google Scholar]
- Hübner R, Volberg G. The integration of object levels and their content: a theory of global/local processing and related hemispheric differences. Journal of Experimental Psychology: Human Perception and Performance. 2005;31(3):520–41. doi: 10.1037/0096-1523.31.3.520. [DOI] [PubMed] [Google Scholar]
- Hughes HC, Fendrich R, Reuter-Lorenz PA. Global versus local processing in the absence of low spatial frequencies. Journal of Cognitive Neuroscience. 1990;2(3):272–282. doi: 10.1162/jocn.1990.2.3.272. [DOI] [PubMed] [Google Scholar]
- Hughes HC, Nozawa G, Kitterle F. Global precedence, spatial frequency channels, and the statistics of natural images. Journal of Cognitive Neuroscience. 1996;8(3):197–230. doi: 10.1162/jocn.1996.8.3.197. [DOI] [PubMed] [Google Scholar]
- Iidaka T, Yamashita K, Yonekura Y. Spatial frequency of visual image modulates neural responses in the temporo-occipital lobe. An investigation with event-related fMRI. Cognitive Brain Research. 2004;18(2):196–204. doi: 10.1016/j.cogbrainres.2003.10.005. [DOI] [PubMed] [Google Scholar]
- Ivry RB, Robertson LC. The two sides of perception. The MIT Press; Cambridge, MA, USA: 1998. [Google Scholar]
- Jian Y, Han S. Neural mechanisms of global/local processing of bilateral visual inputs: an ERP study. Clinical Neurophysiology. 2004;116(6):1444–1454. doi: 10.1016/j.clinph.2005.02.014. [DOI] [PubMed] [Google Scholar]
- Jonsson JE, Hellige JB. Lateralized effects of blurring: a test of the visual spatial frequency model of cerebral hemisphere asymmetry. Neuropsychologia. 1986;24(3):351–362. doi: 10.1016/0028-3932(86)90020-5. [DOI] [PubMed] [Google Scholar]
- Keenan PA, Whitman RD, Pepe J. Hemispheric asymmetry in the processing of high and low spatial frequencies: a facial recognition task. Brain Cognition. 1989;11(2):229–237. doi: 10.1016/0278-2626(89)90019-5. [DOI] [PubMed] [Google Scholar]
- Kitterle FL, Christman S, Hellige JB. Hemispheric differences are found in the identification, but not the detection, of low versus high spatial frequencies. Perception & Psychophysics. 1990;48(4):297–306. doi: 10.3758/bf03206680. [DOI] [PubMed] [Google Scholar]
- Lamb MR, Yund EW, Pond HM. Is attentional selection to different levels of hierarchical structure based on spatial frequency? Journal of Experimental Psychology: General. 1999;128(1):88–94. doi: 10.1037//0096-3445.128.1.88. [DOI] [PubMed] [Google Scholar]
- Martin M. Hemispheric specialization for local and global processing. Neuropsychologia. 1979;17(1):33–40. doi: 10.1016/0028-3932(79)90019-8. [DOI] [PubMed] [Google Scholar]
- Martinez A, Moses P, Frank L, Buxton R, Wong E, Stiles J. Hemispheric asymmetries in global and local processing: Evidence from fMRI. Neuroreport. 1997;8(7):1685–1689. doi: 10.1097/00001756-199705060-00025. [DOI] [PubMed] [Google Scholar]
- Navon D. Forest before trees: the precedence of global features in visual perception. Cognitive Psychology. 1977;9:353–383. [Google Scholar]
- Olzak LA. Widely separated spatial frequencies: Mechanism interactions. Vision Research. 1986;27(7):1143–1153. doi: 10.1016/0042-6989(86)90048-9. [DOI] [PubMed] [Google Scholar]
- Parker DM, Lishman JR, Hughes J. Role of coarse and dine spatial information in face and object processing. Journal of Experimental Psychology: Human Perception and Performance. 1996;22(6):1448–1466. doi: 10.1037//0096-1523.22.6.1448. [DOI] [PubMed] [Google Scholar]
- Peyrin C, Mermillod M, Chokron S, Marendaz C. Effect of temporal constraints on hemispheric asymmetries during spatial frequency processing. Brain and Cognition. 2006;62(3):214–220. doi: 10.1016/j.bandc.2006.05.005. [DOI] [PubMed] [Google Scholar]
- Peyrin C, Schwartz S, Seghier M, Michel C, Landis T, Vuilleumier P. Hemispheric specialization of human inferior temporal cortex during coarse-to-fine and fine-to-coarse analysis of natural visual scenes. Neuroimage. 2005;28(2):464–473. doi: 10.1016/j.neuroimage.2005.06.006. [DOI] [PubMed] [Google Scholar]
- Polster MR, Rapcsak SZ. Hierarchical stimuli and hemispheric specialization: two case studies. Cortex. 1994;30(3):487–97. doi: 10.1016/s0010-9452(13)80344-9. [DOI] [PubMed] [Google Scholar]
- Robertson L, Treisman A, Friedman-Hill S, Grabowecky M. The interaction of spatial and object pathways: Evidence from Balint’s Syndrome. Journal of Cognitive Neuroscience. 1997;9(3):295–317. doi: 10.1162/jocn.1997.9.3.295. [DOI] [PubMed] [Google Scholar]
- Robertson LC. Attentional persistence for features of hierarchical patterns. Journal of Experimental Psychology: General. 1996;125(3):227–249. doi: 10.1037//0096-3445.125.3.227. [DOI] [PubMed] [Google Scholar]
- Robertson LC, Delis DC. ‘Part-whole’ processing in unilateral brain-damaged patients: Dysfunction of hierarchical organization. Neuropsychologia. 1986;24(3):363–370. doi: 10.1016/0028-3932(86)90021-7. [DOI] [PubMed] [Google Scholar]
- Robertson LC, Ivry R. Hemispheric asymmetries: Attention to visual and auditory primitives. Current Directions in Psychological Science. 2000;9(2):59–63. [Google Scholar]
- Robertson LC, Lamb MR, Knight RT. Effects of lesions of temporal-parietal junction on perceptual and attentional processing in humans. Journal of Neuroscience. 1988;8(10):3757–3769. doi: 10.1523/JNEUROSCI.08-10-03757.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertson LC, Lamb MR, Zaidel E. Interhemispheric relations in processing hierarchical patterns: Evidence from normal and commissurotomized subjects. Neuropsychology. 1993;7(3):325–342. [Google Scholar]
- Shulman GL, Sullivan MA, Gish K, Sakoda WJ. The role of spatial-frequency channels in the perception of local and global structure. Perception. 1986;15(3):259–273. doi: 10.1068/p150259. [DOI] [PubMed] [Google Scholar]
- Shulman GL, Wilson J. SF and selective attention to local and global information. Perception. 1987;16(1):89–101. doi: 10.1068/p160089. [DOI] [PubMed] [Google Scholar]
- Sowden PT, Schyns PG. Channel surfing in the visual brain. Trends in Cognitive Sciences. 2006;10(12):538–545. doi: 10.1016/j.tics.2006.10.007. [DOI] [PubMed] [Google Scholar]
- Treisman A. Solutions to the binding problem: progress through controversy and convergence. Neuron. 1999;24(1):105–110. doi: 10.1016/s0896-6273(00)80826-0. [DOI] [PubMed] [Google Scholar]
- Treisman AM, Gelade G. A feature-integration theory of attention. Cognitive Psychology. 1980;12:97–136. doi: 10.1016/0010-0285(80)90005-5. [DOI] [PubMed] [Google Scholar]
- Treisman A, Schmidt H. Illusory conjunctions in the perception of objects. Cognitive Psychology. 1982;14:107–141. doi: 10.1016/0010-0285(82)90006-8. [DOI] [PubMed] [Google Scholar]
- Weissman DH, Woldorff MG. Hemispheric asymmetries for different components of global/local attention occur in distinct temporo-parietal loci. Cerebral Cortex. 2005;15(6):870–876. doi: 10.1093/cercor/bhh187. [DOI] [PubMed] [Google Scholar]
- Van Kleeck MH. Hemispheric differences in global versus local processing of hierarchical visual stimuli by normal subjects: New data and a meta-analysis of previous studies. Neuropsychologia. 1989;27:1165–1178. doi: 10.1016/0028-3932(89)90099-7. [DOI] [PubMed] [Google Scholar]
- Yoshida T, Yoshino A, Takahashi Y, Nomura S. Comparison of hemispheric asymmetry in global and local information processing and interference in divided and selective attention using spatial frequency filters. Experimental Brain Research. 2007;181(3):519–529. doi: 10.1007/s00221-007-0948-6. [DOI] [PubMed] [Google Scholar]