Matching in an Undisturbed Natural Human Environment

Abstract

Data from the Oregon Youth Study, consisting of the verbal behavior of 210 adolescent boys determined to be at risk for delinquency (targets) and 210 of their friends (peers), were analyzed for their conformance to the complete family of matching theory equations in light of recent findings from the basic science, and using recently developed analytic techniques. Equations of the classic and modern theories of matching were fitted as ensembles to rates and time allocations of the boys' rule-break and normative talk obtained from conversations between pairs of boys. The verbal behavior of each boy in a conversation was presumed to be reinforced by positive social responses from the other boy. Consistent with recent findings from the basic science, the boys' verbal behavior was accurately described by the modern but not the classic theory of matching. These findings also add support to the assertion that basic principles and processes that are known to govern behavior in laboratory experiments also govern human social behavior in undisturbed natural environments.

The application of basic behavior-analytic principles to socially relevant human behavior has most often taken the form of therapeutic intervention, where basic principles are used to engineer human social environments to produce desired outcomes (e.g., O'Leary & O'Leary, 1977). Far less common are purely observational studies in natural environments, where the question under investigation is whether basic principles discovered in the laboratory also govern behavior in unengineered natural environments. Applied research has shown that many basic behavior-analytic principles can be used to change clinically significant human behavior in social environments. Although such findings are obviously of practical value, it does not necessarily follow from them that the basic principles are also operating in the absence of specific interventions. From a basic science perspective this is an important issue. Specifically, do the variables and processes that govern behavior in laboratory environments also govern naturally occurring behavior in undisturbed environments? It might seem that the second of Newton's well known rules of scientific reasoning would be sufficient to answer this question in the affirmative:

To the same natural effects we must, as far as possible, assign the same causes. As to respiration in a man, and in a beast; the descent of stones in Europe and in America; the light of our culinary fire and of the sun… (Newton, 1999/1726).

This rule is usually interpreted to mean that, in the absence of contrary evidence, like phenomena must have like causes. Hence, just as the light of our culinary fire and of the sun must have the same causes and must operate in the same way, so too must adaptive behavior in the laboratory and in the natural environment. This rule will be sufficient for many students of human behavior, as it certainly was for Skinner, judging from books like Science and Human Behavior. But the caveat in the rule is the condition, “in the absence of contrary evidence.” Many philosophers and psychologists would no doubt argue that behavior in natural environments, especially human behavior in natural social environments, may be just the sort of phenomenon where contrary evidence, such as intentional choice, could be found. This makes it necessary to demonstrate specifically that the basic principles govern behavior in both engineered environments and undisturbed natural environments.

Philosopher of science, Terry L. Smith, discussed this issue in the context of the analogy between operant conditioning and evolution by natural selection (McDowell, 1991, 2004: Skinner, 1981; Staddon & Simmelhag, 1971). Smith (1983) pointed out that selective animal breeding, that is, artificial or engineered selection, was known to be useful in producing desired animal phenotypes long before it was suggested that the same process might occur naturally and be responsible for phenotypic differences among species. Given the known results of selective animal breeding, one might think again that Newton's second rule of scientific reasoning would occasion widespread support for the idea of natural selection, but this did not happen. Evidently, the caveat in the rule also was salient in the case of natural selection. The diversity of species may be just the sort of phenomenon where contrary evidence, such as independent acts of creation, could be found. It was not until Darwin's extensive documentation in On the Origin of Species that the idea of natural selection began to be taken seriously. Smith (1983) noted that

Darwin discussed animal breeding in Chapter One of a fifteen chapter book [On the Origin of Species]—as a way of motivating the plausibility of his claim that natural selection plays a central role in the origin of species. The next fourteen chapters, however, contained the main argument, which was designed to show that natural contingencies play the same role as the artificial contingencies practiced by breeders (p. 151, italics in the original).

Behavior analysts are still mostly at work on their Chapter One. There is no doubt that it is an extensive and valuable Chapter One, however, and that it is an important source for the remaining chapters, the main argument.

A large number and wide variety of basic behavior-analytic phenomena, principles, and theories can be studied in unengineered natural environments. Among the most challenging of these are the mathematical accounts that began appearing in the basic science literature around 1960, and that have become increasingly prevalent. Probably the most successful mathematical account in basic behavior analysis is matching theory, although there are many others, such as contingency discriminability theory (Davison & Jenkins, 1985), behavioral momentum theory (Nevin, 1992), stay-switch theory (MacDonall, 2000), and hyperbolic discounting theory (Mazur, 1997), to name a few. Matching theory consists of a family of equations, some with absolute response rates as dependent variables, and some with relative response rates, that is, proportions or ratios of response rates, as dependent variables. A few studies have evaluated absolute response rate forms of matching theory in natural unengineered environments (e.g., Fernandez & McDowell, 1995; Martens & Houk, 1989; McDowell, 1981, 1982), and a few have evaluated relative response rate forms of matching theory in such environments (e.g., Borrero & Vollmer, 2002; Houston, 1986; Oliver, Hall, & Nixon, 1999; Snyder & Patterson, 1995; Symons, Hoch, Dahl, & McComas, 2003). Behavior consistent with the matching theory equations was reported in all of these studies. Reed, Critchfield and Martens (2006) and Vollmer and Bourret (2000) found that the behavior of athletes in sporting events was also consistent with a relative response rate equation of matching theory. Although athletic competitions take place in unengineered environments, they entail the additional constraints of game rules, which complicate the interpretation of findings from these competitions.

In the research presented in this article, the verbal behavior of 210 adolescent boys who were determined to be at risk for delinquent behavior (targets) and 210 of their friends (peers) was studied. Pairs of boys engaged in conversations and the verbal behavior of each target boy and each peer boy was recorded and categorized as either “rule-break” or “normative”. Positive social responses from each boy to the other were also recorded. These data were then analyzed for their conformance to the complete family of matching theory equations in light of recent findings from the basic science, and using recently developed analytic techniques. Previous researchers have reported that human verbal behavior supported by social consequences in engineered environments was well described by matching theory (Borrero et al., 2007; Conger & Killeen, 1974; Pierce, Epling, & Greer, 1981). The principal purpose of the present article is to add to and extend the literature on the governance by matching theory of naturally occurring human behavior, which in this case happens to be verbal behavior. A second purpose is to introduce applied researchers to modern theoretical developments, and to new analytic procedures from the basic science that are relevant to applications of matching theory. And a final purpose is to add to the basic-science literature that compares the classic version of matching theory with a modern version of the theory.

Classic and Modern Matching Theory

The classic theory of matching consists of three equations, namely,

1

2

and

3

where the Bs in all equations represent response rates, the rs represent reinforcement rates, and the numerical subscripts refer to each of two response alternatives. Equation 1 is the original matching equation (Herrnstein, 1961) expressed in ratio form, and states that organisms allocate their behavior to each of two response alternatives in the same proportion or, equivalently, in the same ratio, as reinforcement is distributed across those alternatives. Equations 2 and 3 express the absolute response rate on each of the two concurrently available alternatives as a function of the rates of reinforcement obtained from both alternatives. These single-alternative forms were derived from Equation 1 by Herrnstein (1970), who assumed that there is an ever present rate of background behavior, B_e, supported by a rate of background reinforcement, r_e, in a two-alternative environment, and that the sum of the rates of responding on the two alternatives and on the background alternative, B₁ + B₂ + B_e, is constant with respect to changes in reinforcement properties. This sum is represented by the parameter, k, in Equations 2 and 3 (McDowell, 1986). This constant-k assumption is necessary in order to obtain Equations 2 and 3 from Equation 1. Note that when there is no second source of arranged reinforcement (r₂  =  0), Equation 2 reduces to the familiar Herrnstein hyperbola (Herrnstein, 1970) for single-alternative responding. Similarly, when there is no first source of arranged reinforcement (r₁  =  0), then Equation 3 also reduces to the familiar Herrnstein hyperbola. Equations 1–3 and the derivation of Equations 2 and 3 are discussed in detail by McDowell (1986). Equations 1–3 can also be expressed in time allocation forms, where the dependent variables are T₁ and T₂, the amount of time spent engaging in each alternative. Note finally that Equations 1–3 contain two parameters, k and r_e.

All translational applications of matching theory either have entailed Equation 1, sometimes expressed in an equivalent proportional form, and sometimes expressed in a power function form (as in Equation 4 below), or they have entailed a single-alternative equation like Equations 2 and 3, with one source of reinforcement contingent on the behavior of interest, as just described. No translational applications of matching theory have examined Equations 2 and 3 in the context of a concurrent schedule and, interestingly, very few basic-science applications have done so. Yet the strongest test of matching theory on data from concurrent schedules entails considering all three equations, one that describes the ratio of response rates, and two that describe the absolute rates of responding in the two components (McDowell, 1986). This is a strong test of the theory because it engages the theory's constant-k assumption, and also because it constrains the data more severely than does considering Equation 1 alone. Note that no additional experimentation or data collection is necessary to consider all three equations, as compared to considering just Equation 1. Whatever data are collected to test Equation 1 are simply further constrained by applying Equations 2 and 3 as well.

A key vulnerability of classic matching theory is its constant-k assumption (Herrnstein, 1974; McDowell, 1986). As noted earlier, this assumption is required in order to derive Equations 2 and 3 from Equation 1. But as early as 1984 experimental evidence began to appear that suggested the assumption did not hold (McDowell & Wood, 1984). In the past 20 years or so, a considerable amount of evidence has accumulated indicating that the assumption is in fact false (McDowell, 2005, but cf. McLean, 2006). But if the constant-k assumption is false, then Equations 2 and 3 cannot be derived legitimately from Equation 1, and this means that the so-called quantitative law of effect (Herrnstein, 1970), which is a form of Equations 2 and 3, as explained earlier, does not follow from Equation 1. It has been known for some time that Equation 1 fails to describe much of the data from two-alternative experiments (Baum, 1974, 1979; Wearden & Burgess, 1982). Based in part on the extensive literature showing the limited applicability of Equation 1, and on the experimental evidence against the constant-k assumption, McDowell (2005) concluded that all three equations of classic matching theory were false, or at best applied only in limited circumstances.

The sole survivor of the disconfirmatory evidence is the power-function version of Equation 1, which was discussed by Staddon (1968) and Baum and Rachlin (1969), and was formalized and studied extensively by Baum (1974, 1979), and later by Wearden and Burgess (1982). McDowell (1986) noted that the logic Herrnstein (1970) used to obtain single-alternative forms from Equation 1 also could be used to obtain single-alternative forms from the power function version of Equation 1. In other words, matching theory could be rebuilt on a new foundational equation that was known to accurately describe a large body of data from many vertebrate species, including humans (Baum, 1974, 1979; Wearden & Burgess, 1982).

Like the classic version of matching theory, the rebuilt, or modern, version also consists of three equations, which are

4

5

and

6

where the Bs, rs, and subscripts, including the e subscript, which refers to the background alternative, have the same meanings as in Equations 1–3. Equation 4 is the familiar power function matching equation, also referred to as the generalized matching law. It is the foundation of the modern theory of matching, and introduces to the classic Equation 1 an exponent, a, on the reinforcement rate ratio, and a bias parameter, here represented by c_2e/c_1e, as a factor of the exponentiated reinforcement rate ratio. The single-alternative Equations 5 and 6 were obtained from Equation 4 by McDowell (1986, 2005) using the Herrnstein (1970) logic, as noted earlier. The parameter, r_e, is incorporated in the two c parameters in Equations 5 and 6 because it is not independently estimable in these equations (McDowell, 2005). Equations 5 and 6 also include a simplification recommended by McDowell (2005), namely, that the three exponents appearing in their original derivation be made equal.

Although Equations 5 and 6 are notationally complicated, they are conceptually straightforward. Just as for Equations 2 and 3, response rates in Equations 5 and 6 are functions of reinforcement rates obtained from both alternatives of the concurrent schedule, but now the exponent, a, that appears in Equation 4 is carried over by the derivation to the single-alternative forms. In addition, there are three parameters that include bias, one for each comparison of a target alternative with the background, c_1e and c_2e, and one for the comparison of the two target alternatives with each other. McDowell (2005) showed that this third bias parameter necessarily equals c_2e/c_1e when the recommended exponent simplification is used. Notice that Equations 4, 5, and 6 reduce to Equations 1, 2, and 3 when the exponent and all bias parameters in the equations equal unity. As noted for Equations 1–3, Equations 4–6 can also be expressed with time allocation as the dependent variable. Note finally that Equations 4–6 contain four independently estimable parameters, k, a, c_1e, and c_2e.

McDowell (2005) showed that the modern theory of matching predicts the violation of the constant-k assumption in the classic theory, and accurately describes at least some data that violate that theory's constant-k assumption. In addition, Dallery, Soto, and McDowell (2005) directly tested the classic and modern theories of matching on data from human subjects working on concurrent schedules of monetary reinforcement in the laboratory. They used an ensemble method (McDowell, 2005) to fit all three equations of the classic and the modern theories simultaneously to sets of data from individual subjects using shared parameters. Dallery et al. found that the modern, but not the classic, theory of matching accurately described the behavior of their subjects.

Just as for the classic theory, the strongest test of the modern theory of matching entails considering all three of its equations. In the present article, Equations 1–3 and Equations 4–6 were fitted as ensembles to the boys' verbal-behavior data. To be consistent with findings from the basic science, the latter, but not the former set of equations must describe the data well.

METHOD

All procedures described in this section, including the coding of videotapes, were conducted by researchers at the Oregon Social Learning Center (OSLC).

Subjects

The subjects were 210 13- to 14-year-old boys participating in the fifth phase of the longitudinal Oregon Youth Study (OYS; Capaldi & Patterson, 1987), plus 210 similarly-aged male friends who served as their partners. Each pair consisted of one target child from the OYS and a friend, the peer child, who participated in this portion of the study only. The target boys had been recruited for the OYS at ages 9 and 10 in two waves during 1983 and 1984 from 10 elementary schools in high-crime neighborhoods of a medium-sized city in the northwestern United States. These boys were considered to be at risk for juvenile delinquency because they came from neighborhoods with higher than average rates of juvenile delinquency. The resulting samples were 90% European American, of lower socioeconomic status, and with a relatively high percentage of unemployed parents. The peer boys were selected by asking each target boy and his parents to name the male friend with whom the target child spent the most time. Boys from the first of two waves of the OYS comprised sample e5 (n  =  129); boys from the second wave comprised sample n4 (n  =  81).

Procedure

During the first four phases of the OYS, the target boys and their parents completed various surveys and experimental tasks on multiple occasions at the OSLC. During both waves of the fifth phase, each pair of boys participated in a videotaped 25-min session. At the start of each 25-min session, a researcher seated the 2 boys in front of a video camera set up in a room at the OSLC. In accordance with the directions of the Peer Interaction Task (Forgatch, Fetrow, & Lathrop, 1985; Panella & Henggeler, 1986), the researcher told the boys that they were to engage in conversation for 25 minutes about a variety of topics to be announced by the researcher. Each session started with a 5-min warm-up discussion about planning an activity together, followed by four 5-min segments with four randomly-ordered, assigned problem-solving discussions related to self-selected problems with the target child's and peer child's parents and peers. The researcher was present in the room only to introduce each topic; during the discussions the boys were alone.

Videotapes of the boys' conversations were transcribed and coded by trained observers. The boys' verbal behavior was coded into two mutually exclusive categories: rule-break talk and normative talk. As defined for this study, rule-break talk contained some element that indicated a violation of legal and/or conventional norms of conduct. Examples of rule-break talk included climbing out of bedroom windows, lying to parents, cheating at school, engaging in criminal behavior, and behaving defiantly. Examples of normative talk included gossiping about friends, and talking about school, family, or what to do for fun. These categories constituted two mutually exclusive, concurrently available response alternatives. The frequencies and durations of verbal bouts were recorded for each boy. Each bout began when a boy started speaking and ended when the boy stopped speaking. This permitted the calculation of both response rates and time allocations.

In addition to coding for content, social consequences from the “other” boy (namely, the peer child when the target child's behavior was under consideration, and the target child when the peer child's behavior was under consideration) for bouts of both rule-break and normative talk were also coded into two mutually exclusive categories: positive social responses and nonpositive social responses. A positive social response was assumed to reinforce a bout of talk if it immediately followed that bout in the behavior stream. Examples of positive social responses included making approving statements, smiling, nodding, laughing, and giving a thumbs-up. Nonpositive social responses included anything other than positive social responses, including remaining silent. Frequencies of positive social responses for each category of verbal behavior were recorded for each boy. This permitted the calculation of reinforcement rates for each category of verbal behavior.

Samples e5 and n4, which corresponded to the two waves of the OYS, were coded separately by two sets of coders following the instructions from the Topic Code (Poe, Dishion, Griesler, & Andrews, 1990). Coders were blind to all other data related to the participants, and they were involved in only the coding of the data. Reliability scores were calculated for a randomly-selected 12% of pairs in sample e5 and 15% of pairs in sample n4. Mean percent agreements of 90.0 and 94.2, and kappa coefficients of 0.735 and 0.674 were obtained for samples e5 and n4, respectively (Dishion, Spracklen, Andrews, & Patterson, 1996).

RESULTS

All analyses were conducted using data supplied by the OSLC in the form of SPSS files. Data were missing from 15 target boys in the e5 sample and from 1 peer boy in the n4 sample. The entire 20 minutes of conversation for each boy was used to generate a single data record for that boy, consisting of two reinforcement rates, r₁ and r₂, two response rates, B₁ and B₂, and two time allocations, T₁ and T₂. Equations 1–3 and Equations 4–6 were fitted as ensembles to the response rates and time allocations of the e5 target boys (n  =  114), the e5 peer boys (n  =  129), the n4 target boys (n  =  81), and the n4 peer boys (n  =  80). Hence, the data were separated into four subsets, a target-boy and a peer-boy subset from each sample. During their conversations, the target boys' verbal behavior was presumed to be reinforced by the peer boys' positive social responses, and the peer boys' verbal behavior was presumed to be reinforced by the target boys' positive social responses, as described in the Methods section. In all analyses, rule-break talk was taken as response alternative 1 and normative talk was taken as response alternative 2.

Ensemble fits of the classic theory to each subset of the data entailed finding a single shared k and r_e for Equations 1–3 that minimized a quantity that might be referred to as the normalized total residual sum of squares, RSS_NT, given by

7

where the RSSs represent residual sums of squares, the SSs represent total sums of squares, and the numerical subscripts refer to Equations 1 through 3. For example, RSS₂ is the sum of the squared residuals for the fit of Equation 2 to a dependent variable (B₂ or T₂), and SS₂ is the sum of the squared deviations of the dependent variable from its own mean. The logarithmic transformation of Equation 1 was used in all fits, as is customary in the basic science. This method of obtaining a single set of shared parameter estimates by simultaneously fitting a set of equations to multiple sources of variance was developed and discussed in detail by McDowell (2005). Percentages of variance accounted for (%VAF) by each equation were calculated from the individual RSSs left by the ensemble fit. In addition, an overall %VAF for the ensemble was calculated from

8

This %VAF evaluates the sum of the individual residual sums of squares against the sum of the individual total sums of squares, and thus provides an overall assessment of the quality of the ensemble fit (McDowell, 2005). The same ensemble method was used to simultaneously fit the three equations of the modern theory, yielding a single shared estimate of k, a, c_1e, and c_2e, for each subset of the data. The logarithmic transformation of Equation 4,

9

was used in all fits, as is customary in the basic science. Notice that the slope of the best-fitting log transform is the exponent, a, of Equation 4, and that the antilog of its y-intercept is the bias parameter, in this case, c_2e/c_1e. A detailed example of using this ensemble method of curve fitting is given in the Appendix.

Goodness of Fit

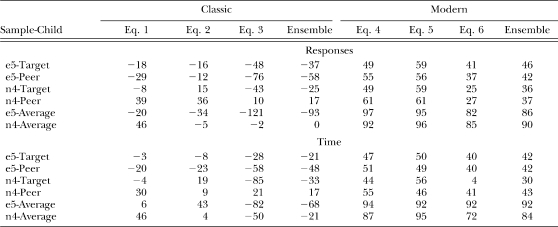
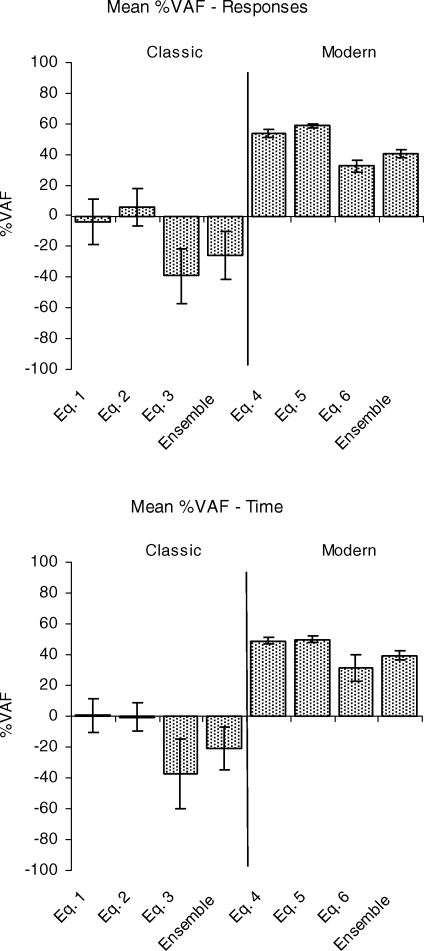
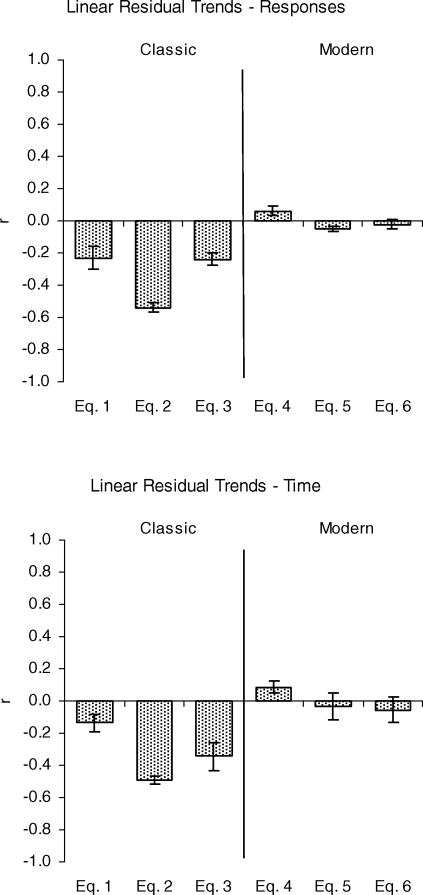
Listed in Table 1 are the percentages of variance accounted for by each set of equations, and its ensemble, for the response rates and time allocations from each of the four data subsets, e5-Target, e5-Peer, n4-Target, and n4-Peer. The %VAFs in the e5-Average and n4-Average rows of the table will be discussed later. The majority of %VAFs for the equations of classic matching theory and their ensembles were negative for the four data subsets (11 of 16 for both response rates and time allocations). A negative %VAF means the data deviate more from the fitted function than from their own mean, in which case of course the mean is a better predictor of the data than the fitted function. The average %VAFs across the four subsets of data for each equation and for the ensemble are plotted on the left sides of the top and bottom panels in Figure 1. These are not the quantities that appear in the e5-Average and n-4 Average rows of Table 1, which refer to a different kind of averaging that will be described later. As shown in the figure, on average, the equations of classic matching theory either accounted for essentially no variance in the response rates and time allocations (Equations 1 and 2), or accounted for a negative amount of variance. Hence, in none of these cases did the fitted function on average predict the data better than the mean.

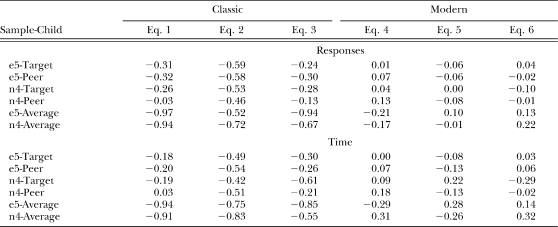
Table 1.

Percentages of variance accounted for by Equations 1, 2, 3, and their ensemble, (the classic theory), and by Equations 4, 5, 6, and their ensemble (the modern theory) for response and time allocation data.

Fig 1.

Percentages of variance accounted for (%VAF) by classic (left portions) and modern (right portions) matching theory equations and their ensembles, averaged over the four subsets of data for response rates (top panel) and time allocations (bottom panel). Error bars represent ± 1 standard error.

The %VAFs for the equations of modern matching theory and their ensembles are also listed in Table 1. Over the four data subsets they ranged from 25% to 61% with a median of 48% for the response rates, and from 4% to 56% with a median of 43% for the time allocations. The average %VAFs across the four data subsets for each equation and their ensemble are plotted on the right sides of the panels in Figure 1. Again, these are not the quantities that appear in the e5-Average and n4-Average rows of Table 1. As shown in the figure, the equations of modern matching theory and their ensemble on average accounted for about half the variance in the boys' verbal response rates and time allocations.

Properties of the Boys' Verbal Behavior

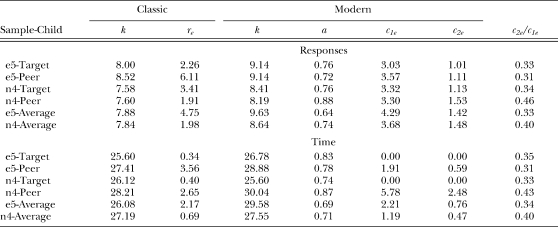
Parameter estimates from the ensemble fits of the classic and modern matching theory equations are listed in Table 2 for fits to response rates and time allocations. Again, the parameter estimates in the e5-Average and n4-Average rows of the table will be discussed later. Notice that estimates of the shared exponent, a, in Equations 4–6 for the four data subsets consistently fell between about 0.7 and about 0.9, and averaged about 0.8 for both response rates and time allocations. This means that the boys' verbal behavior was not perfectly controlled by the reinforcement rate ratios (in which case the exponent would equal unity), a finding that is referred to as undermatching, and is almost always obtained in laboratory experiments with human and animal subjects (Baum, 1974, 1979; Davison & McCarthy, 1988; Wearden & Burgess, 1982). Also noteworthy is the ratio of the two c parameters, c_2e/c_1e, which consistently fell between about 0.3 and about 0.5, indicating a strong bias in favor of normative talk (recall that rule-break talk is in the numerator of Equation 4) for all boys in both samples and for both response rates and time allocations. This means that all boys had a constant proportional preference for normative talk over rule-break talk.

Table 2.

Shared parameter estimates from ensemble fits of Equations 1, 2, and 3 (first two columns) and from ensemble fits of Equations 4, 5, and 6 (columns 3 through 6). The ratios of the two c parameters are listed in the last column.

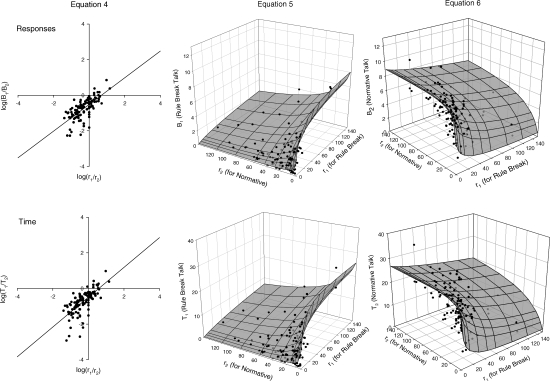
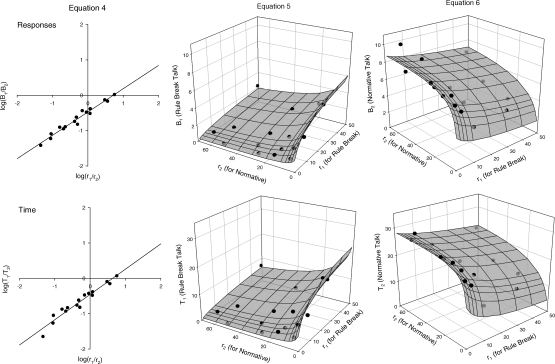
Figure 2 is a plot of the response rate (top panels) and time allocation (bottom panels) data for the e5 target boys, along with plots of Equations 4, 5 and 6 from the ensemble fit. Because the latter two equations are functions of two variables they describe surfaces, as shown in the center and right panels of the figure. The %VAFs and parameters for all fits in Figure 2 are given in Tables 1 and 2.

Fig 2.

Response rates (top panels) and time allocations (bottom panels) for the e5 target boys, along with plots of the best fitting Equations 4, 5, and 6. The percentages of variance accounted for, parameter values, and residual analyses for these fits are given in Tables 1, 2, and 3. Bias in favor of normative talk is indicated by the negative y-intercept of the best fitting log transform of Equation 4 in the left panels, and by the generally higher levels of normative than rule-break talk (right panels vs. center panels).

The straight lines in the left panels of Figure 2 are plots of the log transforms of Equation 4 from the ensemble fit. Notice that for both response rates and time allocations the line intersects the y-axis at a negative value, reflecting the strong bias in favor of normative talk (which appears in the denominator of the ratios). The slopes of these lines are also slightly less than one, reflecting exponents of about 0.8. The scatter around the fitted lines reflects the %VAFs of about 50%.

The coordinate origins of the surface plots in the center and right panels of Figure 2 are the bottom front corners where the two zero tick labels are adjacent. This is the front corner of the reinforcement rate floor. Reinforcement rate for rule-break talk, r₁, increases along the right edges of the floor, and reinforcement rate for normative talk, r₂, increases along the left edges. The vertical z-axes represent response rates (top panels) or time allocations (bottom panels). Notice that the response rates and time allocations of these boys' rule-break talk (center panels) increased with the rate of reinforcement for rule-break talk provided by their peers, r₁, and decreased with the rate of reinforcement for normative talk, r₂. This decrease in responding on one alternative of a concurrent schedule as the reinforcement rate increases on the other alternative is the well known contrast effect that is routinely observed on concurrent schedules in laboratory experiments.

The plots in the right panels of Figure 2 show that the rate and time allocation of the boys' normative talk increased with the rate of reinforcement for normative talk (r₂) provided by their peers, and decreased with the rate of reinforcement their peers provided for rule-break talk (r₁), again showing the expected contrast effect. Notice the generally higher levels of normative talk, shown in the right panels, than rule-break talk, again reflecting the strong bias in favor of normative talk. Plots of the other three data subsets showed similar features, including the contrast effect that is commonly observed in laboratory experiments, and a strong bias for normative talk.

Residuals

While the equations of modern matching theory appeared to provide a reasonable description of these boys' verbal behavior, it is important to examine the residuals for systematic trends that would indicate incorrect function forms. Standardized residuals were calculated for each fit and were plotted against the dependent variable predicted by the fitted equation. These plots were then examined for linear trends by calculating the correlation between the standardized residual and the dependent variable predicted by the equation, which is a common method of testing for linear trends. Correlation coefficients for the classic and modern fits are listed in Table 3. For the classic theory, 23 of the 24 correlations for the four data subsets were negative. The mean correlations across the four data subsets are plotted in the left portions of Figure 3 for response rates (top panel) and time allocations (bottom panel). The mean correlation over all four data subsets and fits was −0.34 for the response rates and −0.32 for the time allocations. Given that the fits of the classic theory equations failed to describe these data well, it is not surprising that they also showed strong trends in their residuals. The correlations for the modern theory fits varied around zero, as is evident from the entries in Table 3. The mean correlations across the four data subsets are plotted in the right portions of Figure 3 for each equation. The mean correlation over all data subsets and fits was zero to two decimal places for both response rates and time allocations. Hence, there was no evidence for systematic trends in the residuals left by fits of the modern theory equations.

Table 3.

Correlations of standardized residuals with values predicted by ensemble fits of Equations 1–3 (the classic theory) and ensemble fits of Equations 4–6 (the modern theory).

Fig 3.

Correlations of standardized residuals with response rates (top panel) and time allocations (bottom panel) predicted by the equations of classic (left portions) and modern (right portions) matching theory. Correlations not equal to zero indicate linear trends in the residuals. Error bars represent ± 1 standard error.

Averages Over a Quartile Grid

The modern theory of matching provided a reasonable description of these boys' verbal behavior. In addition, fits of the equations evidently left random residuals, which indicated that the boys' verbal behavior conformed to the equations' specific function forms. A disappointing feature of these analyses, however, was that the equations of modern matching theory accounted for only about half the variance in the response rate and time allocation data. In laboratory experiments, including experiments with human subjects, at least 80% of the variance is typically accounted for by matching theory equations, and it is common to find 90% or more of the variance accounted for (Baum, 1974, 1979; Davison & McCarthy, 1988; Wearden & Burgess, 1982). An important difference between these verbal behavior data and typical laboratory data is that the former are between-subjects data whereas the latter are almost always within-subject data. It may be that the unaccounted-for variance in the boys' data was due to individual differences in the between-subjects data sets. Indeed, fits to within-subject data from laboratory experiments typically produce at least slightly different parameter estimates for different individuals, which would add error variance to a between-subjects data set that might be constructed from within-subject data from multiple subjects.

One way to remove presumably random individual differences from a data set is to average across subjects. This is problematic in the case of the present data because it entails dependent variables that are functions of two independent variables. This means that it is not possible to average over simple independent–dependent variable pairs. One approach to averaging across subjects in this type of data set is to divide the range of each of the two independent variables into quartiles. This produces a grid of 16 rectangles of varying sizes on the reinforcement rate floors (of, e.g., plots of Equations 2, 3, 5, and 6). Each point falling in a rectangle has associated with it values of r₁, r₂, B₁, B₂, T₁, and T₂ for one participant. Averaging each of these values over all points that fall in a given rectangle produces a single data record that is an average over participants whose independent variable values fall in that rectangle of the grid. This method is preferable to using a grid with equal-sized square cells because, for the present data at least, the equal-grid method produces cells with very different ns and leaves many cells empty.

The quartile-grid method of averaging the data was used on the total e5 sample and the total n4 sample. In other words, for each sample, data from the target boys and the peer boys were pooled. The equations of classic and modern matching theory were then fitted to the averaged data using the ensemble method described earlier. The %VAFs for these fits are listed in Table 1 in the rows labeled e5-Average and n4-Average. Evidently, averaging the data did not rescue the classic theory. It did, however, considerably improve the goodness of fit of the modern theory. For Equations 4–6, over both samples and both independent variables, the %VAFs ranged from 72% to 97%, averaging 90%. These %VAFs are well within the range typically obtained in laboratory experiments with animal and human subjects (Baum, 1974, 1979; Davison & McCarthy, 1988; Wearden & Burgess, 1982). Parameter estimates from these fits are listed in Table 2 in the rows labeled e5-Average and n4-Average. The exponents, a, are slightly lower than those obtained for the four subsets of the data, but are nevertheless well within the range typically found in laboratory experiments. The bias parameters, c_2e/c_1e, for the averaged data fell within the range of bias parameters obtained for the four data subsets, indicating, as for the data subsets, a strong bias in favor of normative talk.

Figure 4 is a plot of the response rate and time allocation data for the pooled, averaged e5 data, along with the best ensemble fits of Equations 4, 5, and 6. The improved %VAFs are reflected in the greatly reduced scatter in all plots in the figure. Notice, however, that the same properties that characterized the plots and fits for the separate data subsets also can be seen in the plots of the averaged data. These include y-intercepts <0 in the left panels, reflecting the strong bias in favor of normative talk, generally higher levels of normative talk than rule-break talk, shown in the center and right panels of the figure, and a contrast effect for both rule-break talk and normative talk. Plots of the data and the ensemble fits for the pooled, averaged n4 sample are similar to those shown in Figure 4, and reflect all the response and time allocation properties described for the averaged e5 sample. Evidently, quartile-grid averaging across subjects produces results that are representative of the pooled individual-subject data subsets, and that are as good as those typically obtained from within-subject data generated in the basic science laboratory.

Fig 4.

Response rates (top panels) and time allocations (bottom panels) for the e5 target and peer boys, pooled and then averaged over a quartile grid. The percentages of variance accounted for, parameter values, and residual analyses for these fits are given in Tables 1, 2, and 3. Averaging considerably reduced the scatter about the fitted functions. Bias in favor of and higher levels of normative talk are still evident in the averaged data, as are the lips on the rule-break surfaces in the center panels.

Residuals from fits to the averaged data were calculated and examined as described for the data subsets. Correlations of the standardized residuals with values predicted from the fitted equations are listed in Table 3 in the rows labeled e5-Average and n4-Average. Not surprisingly, fits of the classic theory showed strong linear trends in the residuals. All of the large negative correlation coefficients for these fits were statistically different from zero (α  =  0.05, two tails). For fits of the modern theory, the correlation coefficients across samples, response rates, and time allocations ranged from −0.29 to 0.32, averaging 0.05. None of these correlation coefficients was statistically different from zero (α  =  0.05, two tails). These results indicate that the averaged response rates and time allocations conformed to the specific function forms required by the equations of modern matching theory.

DISCUSSION

Dishion et al. (1996) analyzed these data in a different way. They considered each pair of boys to be a dyad that responded as a unit and that reinforced its own behavior. Hence, for example, a conversational rule-break exchange that shifted back and forth between boys constituted one instance of rule-break talk. Similarly, a positive social response that might shift back and forth between boys counted as one reinforcer. Dishion et al. plotted the proportion of dyadic rule-break responses against the proportion of positive dyadic social responses for rule-break talk, and found what they described as a linear relationship between the two proportions. The relationship, shown in their Figure 1, was actually more interesting—it was a sigmoidal relationship immediately recognizable as indicating a degree of undermatching in the dyad's responding. The authors did not attempt to fit Equations 1 or 4 to their data. Dishion et al.'s analyses are interesting, but they differ from the typical behavior-analytic focus on the behavior of individual organisms.

One issue with the analyses reported here is that the positive social responses from the target and peer boys for their partners' verbal behavior were only presumed to be reinforcers. Although there is overwhelming evidence that these kinds of social responses in fact act as reinforcers (e.g., O'Leary & O'Leary, 1977), it would nevertheless be ideal to demonstrate that this was the case for each study of naturally occurring behavior in an undisturbed environment. This could be accomplished after the naturalistic data were collected, by making the putative reinforcers contingent on behavior in experiments with a subset of subjects using, perhaps, a reversal design to show control of behavior by the putative reinforcer (Snyder & Patterson, 1995; St. Peter et al., 2005).

A second concern that may be raised about these data and analyses bears on the ratio of responses to reinforcers. Considering the reciprocal nature of conversation, it seems possible that the ratio of responses to reinforcers could be close to 1∶1 for these data, in which case there would be too few “extra” behaviors to be affected by reinforcement allocation, and hence behavior could not stray far from the matching relation. For example, if every response was reinforced, a reinforcement allocation of, say, 2∶1 would be associated with a response allocation of exactly 2∶1. But response allocation is a true dependent variable only when it can vary from the reinforcer allocation, and of course this is possible only when there are more responses than reinforcers. The additional responses might or might not be allocated in a way that is consistent with matching. To examine this issue in the present data, the normative and rule-break talk of the target and peer boys in the e5 and n4 samples were combined. On average, the boys in the combined sample, across response categories, emitted 20 responses for each reinforcer. This response/reinforcer ratio is comparable to ratios found in laboratory experiments. For example, Dallery, McDowell, and Lancaster (2000) studied the lever pressing of 7 rats working on variable-interval schedules of sweetened water. The rats in their 0.32M condition, to take a relatively high response-rate example, emitted an average of 12 responses for each sweet-water reinforcer. Evidently, the verbal behavior of the boys in the present study had ample leeway to deviate from matching.

A third issue that might be raised about these analyses is that the equations of classic matching theory entail two free parameters whereas the equations of modern matching theory entail four free parameters. It might seem that this gives the latter theory an advantage and that the tradeoff between the modern theory's additional %VAF and the additional parameters in its equations should be assessed using an F-test or the Akaike Information Criterion (Motulsky & Christopolous, 2004). But as McDowell (2005) pointed out, this sort of comparison is necessary only when the competing theories both provide reasonable descriptions of the data, that is, when both account for a respectable amount of data variance and leave random residuals. When this is the case, the only issue that remains is whether the additional variance accounted for by one of the theories is worth the additional parameters it entails. But the classic theory of matching accounted for no variance and left systematic residuals. Hence its account of these data cannot be correct under any circumstance.

A fourth issue with these data is the considerable amount of scatter around the functions fitted to the four data subsets. This produced %VAFs that were not as large as those typically observed in laboratory experiments. Averaging over subjects produced much larger %VAFs, which suggested that the scatter in the data subsets was likely due to variance caused by individual differences in the between-subjects data. But there is still a chance that each boy's verbal behavior was only loosely governed by the equations of modern matching theory, in which case within-subject data would also exhibit considerable scatter. The 20-minute conversations from which the present data were obtained were too short to permit calculating reliable within-subject response rates and time allocations for these boys, although obviously it would be desirable to conduct naturalistic studies that permitted the collection of within-subject data. A different way to investigate whether the scatter is due to individual differences is to ask if within-subject data that showed minimal scatter would show greater scatter when pooled with other individual-subject data in a constructed between-subjects data set.

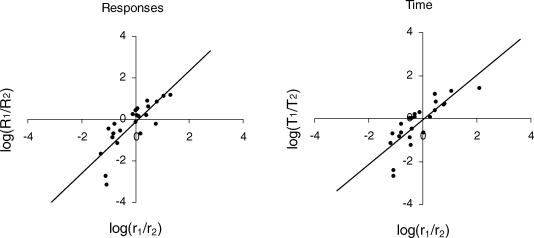
Such an investigation was conducted by compiling data from all laboratory studies of concurrent schedules using human subjects published through 1990 that reported at least five response and time allocations for each subject. This yielded 24 individual-subject data sets from five experiments (Bradshaw, Szabadi, & Bevan, 1979; Bradshaw, Szabadi, Bevan, & Ruddle, 1979; Cliffe & Parry, 1980; Ruddle, Bradshaw, & Szabadi, 1981; Ruddle, Bradshaw, Szabadi, & Foster, 1982). The behavior of the individual subjects in these experiments was well governed by Equation 4, which accounted for between 72% and 100% of the individual subjects' data variance, with a median of 98% of the variance accounted for by the equation. In other words, the data from these subjects showed very little scatter around the best fit of Equation 4. One data point was drawn at random from each of the individual-subject data sets, and these 24 data points were then pooled to form a between-subjects data set to which Equation 4 was fitted. This random sampling from the individual within-subject data sets was repeated a total of 20,000 times. The resulting %VAFs for the 20,000 fits of Equation 4 ranged from 15% to 89%, with a median of 66%. By comparison, the %VAFs shown in Table 1 for fits of Equation 4 to the boys' response rate and time allocation data ranged from 44% to 61%, with a median of 50%, which are roughly comparable figures. Plots of the constructed between-subjects data sets that yielded the median %VAFs are shown in Figure 5 for response and time allocation data, along with the best fits of the log transform of Equation 4. Clearly, these plots are similar in appearance to the plots in the left panels of Figure 2. It is not unreasonable to suppose, then, that individual boys' verbal behavior in the present study was governed closely by the equations of modern matching theory.

Fig 5.

Human between-subjects data sets constructed by random sampling from 24 within-subject data sets that showed little scatter around the best fits of Equation 4. The response rate and time allocation data shown are for the two constructed between-subjects data sets out of 20,000 that yielded the median %VAFs for fits of the log transform of Equation 4 (straight lines drawn through the plots). Evidently, the scatter in these plots is similar to that for plots of the boys' verbal response rates and time allocations (as shown, for example, in the left panels of Figure 2).

A fifth issue that may be raised about these analyses is that they apparently ignore the interlocking nature of conversation between individuals. The verbal behavior of one boy is affected by the verbal behavior of the other boy, which in turn affects the verbal behavior of the first boy, and so on. Basic behavior analysis deals with the interlocking nature of behavior and environment by means of feedback functions (Baum, 1992; McDowell & Wixted, 1986, 1988; Soto, McDowell, & Dallery, 2006). In the laboratory, the organism's environment is arranged and presented by machinery. In the case of naturally-occurring conversation, however, each boy's environment is “arranged” and presented by the other boy's social behavior. But these two situations are not so different, for even in the laboratory behavior and environment change and are changed by each other, and hence are engaged in an interlocking conversation of sorts. Behavior–environment feedback in laboratory experiments is far from completely understood (e.g., Baum, 1992), and often it is simply ignored. For example, feedback is completely ignored in all the equations of both classic and modern matching theory. The independent variables in these equations are rates of obtained reinforcement, which are not known in advance, and which can be, and often are, very different from their scheduled rates. The reinforcement rates that are obtained depend on the organism's behavior, and yet that behavior is considered to depend on the very reinforcement rates the behavior itself generates. The ultimate solution to this problem is to incorporate feedback functions into the equations of matching theory that specify how behavior produces obtained reinforcement rates from scheduled reinforcement rates, thus restoring true independent variables to the equations. The same must be true in applications of the equations to social behavior. There is no doubt that additional research on how feedback works in both basic and applied environments is needed.

The findings reported here add to the literature showing that human behavior in natural, unengineered environments is governed by matching theory, and hence lends further support to the assertion that the principles and processes that govern behavior in laboratory environments also govern behavior in undisturbed natural human environments. These findings are especially interesting because they entail verbal behavior and social reinforcement in reciprocal social interactions where each person's behavior is regulated by consequences naturally provided by the other person. This type of social exchange is the hallmark of human social interaction.

These analyses also make use of contemporary theoretical and analytic developments in the basic science that may be of interest to applied workers. If modern matching theory supplants its classic version, as McDowell (2005) contends it must, then the classic Herrnstein (1970) hyperbola, the quantitative law of effect, must be replaced by the more complicated form derived from Equation 4:

This is modern matching theory's version of the quantitative law of effect. McDowell (1986, 2005) explained how this single-alternative form is derived from the power-function matching equation (Equation 4), and how it is related to Equations 5 and 6. McDowell and Caron (2007) discussed some of the difficulties that may be encountered when attempting to fit this equation to data.

Another feature of the present analyses that is novel in translational research is the simultaneous fitting of all three equations of matching theory. As noted earlier, this is a much stronger test of the theory than is usually undertaken when only the relative response rate equation (viz., Equation 1 or 4) is fitted to data. The simultaneous fitting entails a new, ensemble, method that minimizes a normalized total residual sum of squares by adjusting parameters that are shared by all the equations.

And finally, these analyses are interesting from a basic science perspective because they add support to the assertion that the classic theory of matching is false (McDowell, 2005). It is safe to say that no basic scientist will be surprised to learn that Equation 1 did not describe the boys' verbal behavior well. The restricted applicability of this equation has been known for at least 35 years (Baum, 1974, 1979; Davison & McCarthy, 1988; Wearden & Burgess, 1982). But, upon reflection, it should be surprising to basic scientists that Equations 2 and 3 did not describe the boys' behavior well or, in fact, at all. This is because, as noted earlier, Equations 2 and 3 are forms of the single-alternative hyperbola that has been studied extensively in many experiments, and that appears to describe the behavior of many vertebrate species, including humans, quite well. But McDowell (2005) showed that this appearance can be deceiving; that is, the hyperbola can appear to accurately describe behavior when in fact it does not.

Further research on behavior in natural, undisturbed environments may improve our understanding of how important classes of naturally-occurring human behavior are regulated, and this in turn may lead to a wider and fuller acceptance of the idea that basic principles and processes discovered in the laboratory also govern human behavior in everyday life.

APPENDIX

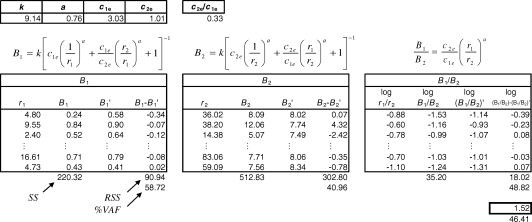
The ensemble method of simultaneously fitting Equations 4–6 to a set of data using shared parameters is illustrated in Figure A1. Estimated values of the shared parameters, k, a, c_1e, and c_2e are given in the top left of the figure. The parameters are shared across the three equations, also shown in the figure, which means that each parameter is required to have the same value in every equation in which it appears. The ratio of the c parameters, shown to the right of the four estimated parameters, is not itself estimated by the fitting procedure; instead, it is calculated from the estimated values of the two c parameters.

Fig A1.

Example of fitting Equations 5, 6, and 4 simultaneously as an ensemble with parameters, k, a, c_1e and c_2e, shared across all equations. The total sum of squares (SS), residual sum of squares (RSS), and percentage of variance accounted for (%VAF) are identified for the first data block. The value in the bold box in the lower right is the sum of the three RSS/SS ratios and is the quantity that is minimized by adjusting the four parameters. The quantity underneath the bold box is the ensemble %VAF.

The block beneath each equation contains information pertaining to the least-squares fit of that equation. The vertical ellipses indicate data that were omitted to save space in the figure. The total sum of squares, SS, is calculated for the three dependent variables, B₁, B₂, and B₁/B₂. The SS for B₁ is indicated in the figure by a label and an arrow. The third column in each block contains the value of the dependent variable predicted by the applicable equation, using the parameter values listed in the top left of the figure. In an actual spreadsheet, this column contains the formula for the applicable equation, where the independent variables and parameter values of the equation are represented by appropriate cell references. The fourth column in each block contains the residuals, which are the differences between observed and predicted values of the dependent variable. The residuals are squared and then summed to obtain the residual sum of squares, RSS, which is identified in the figure for B₁ by a label and an arrow. The percentage of variance accounted for (%VAF) by each equation, also identified in the figure for B₁, is given by

The %VAF values shown in the figure can be verified using the RSS and SS values given in each block.

The quantity in the bold box in the lower right of Figure A1 is the normalized total residual sum of squares, calculated from Equation 7. Its value in the figure can be verified by substituting the RSS and SS given for each block into Equation 7. The normalized total residual sum of squares is the quantity that a fitting algorithm must minimize by iteratively adjusting the four parameters entailed by Equations 4–6. Every iteration (i.e., change) of the parameter values causes the predicted values of the dependent variables in the three blocks to change, and hence also causes the residuals and RSSs in the three blocks to change. As a consequence, all three equations are fitted simultaneously by minimizing the single quantity in the bold box. A variety of optimization algorithms can be used to carry out this ensemble fit. The most convenient is the generalized reduced gradient algorithm developed by Lasdon and Waren (1978) and implemented by Microsoft Excel's Solver tool, for which extensive help is available. The quantity beneath the bold box in Figure A1 is the %VAF for the entire ensemble, and is calculated from Equation 8. Again, this quantity can be verified using the RSS and SS values given in the figure.

The three equations of classic matching theory are fitted as an ensemble in the same way, using the shared parameters, k and r_e.