Concurrent Reinforcement Schedules for Problem Behavior and Appropriate Behavior: Experimental Applications of the Matching Law

Abstract

This study evaluated how children who exhibited functionally equivalent problem and appropriate behavior allocate responding to experimentally arranged reinforcer rates. Relative reinforcer rates were arranged on concurrent variable-interval schedules and effects on relative response rates were interpreted using the generalized matching equation. Results showed that relative rates of responding approximated relative rates of reinforcement. Finally, interventions for problem behavior were evaluated and differential reinforcement of alternative behavior and extinction procedures were implemented to increase appropriate behavior and decrease problem behavior. Practical considerations for the application of the generalized matching equation specific to severe problem behavior are discussed, including difficulties associated with defining a reinforced response, and obtaining steady state responding in clinical settings.

The generalized matching equation (GME) has provided robust and precise accounts of response allocation, or choice (Catania, 2007), between two or more concurrently available schedules of reinforcement (Baum, 1974; 1979; Dallery, Soto, & McDowell, 2005; McDowell, 2005). The logarithmic version of the GME is:

where B₁ and B₂ refer to the frequency of responding on the alternatives, and R₁ and R₂ represent the relative rates of obtained reinforcement from each alternative. The y intercept (b), represents a bias for one alternative independent of relative rates of reinforcement. The slope (a) of the function reflects sensitivity to relative reinforcement rates. The GME has been evaluated in numerous studies using nonhumans (e.g., Baum, 1974; Belke & Belliveau, 2001; Crowley & Donahoe, 2004; Herrnstein & Loveland, 1975). For example, Baum (1974) analyzed a number of data sets using the GME to describe pigeons' responding on concurrent VI VI schedules. Response allocation was explained by the equation, but Baum noted that the potential for bias and undermatching must be considered (see Baum, 1974, for a detailed description). In addition to explaining responding with pigeons, the GME has been used to evaluate the response allocation of other non-humans. Baum (1979) reviewed 103 data sets from studies designed to evaluate choice and reanalyzed the data using the GME. He reported that for nearly all, response allocation could be described by the GME. Data sets from Baum (1975), in which humans were asked to engage in an arbitrary response (i.e., key press) to access reinforcers, were also reviewed. In this review of data sets, the response allocation of rats and humans was evaluated in addition to the response allocation of pigeons on concurrent schedules, further demonstrating the generality of the GME.

The GME has also been evaluated in a number of studies to assess human behavior (e.g., J. C. Borrero et al., 2007; Conger & Killeen, 1974; Horne & Lowe, 1993; Rasmussen & Newland, 2008) involving both experimental and descriptive analyses of responding for both arbitrary and socially significant responses. Conger and Killeen (1974) extended the generality of the GME by applying the equation to human behavior in a more natural context where the conversation of individuals in a discussion group was evaluated. In order to do this, they formed a discussion group with a number of confederates, who provided verbal approval following participant statements according to concurrent VI VI schedules. Results showed that the amount of time the participant allocated towards talking to an experimenter was proportionally related to the amount of approval provided by that experimenter. This investigation provided the first demonstration that the GME could be applied to assess response allocation with humans and socially significant behavior.

Applications of the GME were then extended to academic human behavior (Mace, Neef, Shade, & Mauro, 1994; Neef & Lutz, 2001; Neef, Mace & Shade, 1993; Neef, Shade & Miller, 1994). Neef, Mace, Shea, and Shade (1992) assessed human performance of students with emotional and learning disorders under concurrent reinforcement schedules when reinforcer quality was or was not held constant, by having participants select arithmetic problems from identical stacks of problems. Correct responses resulted in nickels or tokens, delivered according to the VI schedule of reinforcement in place for that alternative. Neef et al. (1992) then evaluated two additional conditions: (a) equal-quality reinforcers, during which identical reinforcers (i.e., either nickels or tokens) were delivered according to concurrent VI schedules, and (b) unequal-quality reinforcers, during which high-quality reinforcers were delivered on the leaner schedule of reinforcement while low-quality reinforcers were delivered on the richer schedule of reinforcement. Matching was obtained during the equal-quality reinforcers condition; however, matching was not obtained during the unequal-quality reinforcers condition, and the time allocated to one alternative was greater than the obtained reinforcement from that alternative. Using the same general procedures just described, Neef and colleagues (Mace et al., 1994; Neef et al., 1993; Neef et al., 1994) extended their previous work and evaluated additional reinforcement parameters including reinforcer delay. These studies highlight some potentially important considerations, including the use of additional procedural manipulations (e.g., timer to signal reinforcement intervals) to improve discrimination between concurrent VI VI schedules, and biased responding, which may occur if choice involves asymmetrical alternatives.

Descriptive studies that have assessed the matching law generally have focused on severe problem behavior such as self-injurious behavior (SIB), aggression, and property destruction (Borrero & Vollmer, 2002; Hoch & Symons, 2007; Martens & Houk, 1989; McDowell, 1982; Oliver, Hall, & Nixon, 1999; St. Peter et al., 2005; Symons, Hoch, Dahl, & McComas, 2003). For example, Borrero and Vollmer conducted descriptive analyses for 4 individuals diagnosed with developmental disabilities who engaged in severe problem behavior as well as appropriate behavior (e.g., vocal requests). After identifying reinforcers for problem behavior via functional analyses (Iwata, Dorsey, Slifer, Bauman, & Richman, 1982/1994), Borrero and Vollmer evaluated the descriptive data using the simple matching equation (Herrnstein, 1961) and the GME, and demonstrated that the relative rate of problem behavior approximately matched the relative rate of reinforcement for problem behavior, when aggregated data were subjected to matching analyses.

Although applications of the GME have demonstrated its generality across species and responses, response allocation between problem and appropriate human behavior has not been assessed under experimentally arranged contingencies. While it is often assumed that individuals with developmental disabilities allocate their responding in direct proportion to relative rates of reinforcement, we are unaware of any studies that have involved experimental evaluations of the matching law when problem behavior and functionally equivalent appropriate behavior are conceptualized as concurrent response alternatives. Specifically, the generality of the matching law has not been extended to the application of differential reinforcement procedures to reduce severe problem behavior. The GME may be ideal for this purpose. The effectiveness of differential reinforcement procedures to effectively reduce severe problem behavior has been demonstrated in a multitude of settings and arrangements (see Petscher, Rey & Bailey, in press; Vollmer & Iwata, 1992, for a review).

The inclusion of differential reinforcement components may be conceptualized as a concurrent schedule with one set of contingencies for one response and another set of contingencies for a second response. Although typical treatment arrangements place problem behavior on extinction it is possible that (a) it may not be feasible to incorporate extinction into a treatment package, such as with severe self-injurious behavior (SIB) (e.g., Hoch, McComas, Thompson, & Paone, 2002), or automatically reinforced behavior (e.g. Worsdell, Iwata, Hanley, Thompson, & Kahng, 2000) or (b) implementation of the procedures may not be conducted with high integrity by caregivers (i.e., problem behavior is sometimes reinforced and appropriate behavior is sometimes not reinforced). In these cases, reinforcement is provided following both problem behavior and appropriate behavior on competing schedules (i.e., a concurrent schedule arrangement), preferably with the denser schedule in place for appropriate behavior. Failure to implement treatment contingencies correctly in the natural environment will likely result in a concurrent schedule arrangement similar to choice arrangements evaluated in laboratory settings (e.g., Johnson, McComas, Thompson, & Symons, 2004; St. Peter Pipkin, Vollmer, & Sloman, 2009; Wilder, Atwell & Wine, 2006). Given that many interventions for severe problem behavior involving extinction are implemented without perfect integrity, concurrent schedules may serve as an effective method to study the response suppressive effects of interventions that do not involve extinction.

Although previous experimental applications of the matching law have included the use of additional procedures [e.g., schedule-correlated stimuli, change-over delay (COD)] to make discrimination between schedules more likely, such procedures are not often incorporated into typical differential reinforcement procedures and may make conclusions regarding response allocation more difficult. It is unclear if stimulus control (i.e., related to signals) or schedule control is responsible for responding. When evaluating socially significant human behavior, conditions are often designed to be as similar as possible to those in the natural environment, and additional procedural variations may deviate further from naturally occurring concurrent schedules.

Therefore, the purpose of this investigation was to experimentally evaluate problem behavior and appropriate behavior exposed to concurrent schedules of reinforcement in order to further assess the generality of the GME (Baum, 1974), in the absence of additional schedule-correlated stimuli, and to implement interventions to decrease problem behavior, further demonstrating behavioral sensitivity to concurrent reinforcement schedules.

METHOD

Participants and Settings

Three individuals diagnosed with developmental disabilities who engaged in severe problem behavior participated. Greg was an 8-year-old boy diagnosed with mild mental retardation and autism who engaged in screaming and disruption. Alice was a 13-year-old girl who was diagnosed with childhood disintegrative disorder who engaged in disruption and aggression. Amy was a 14-year-old female diagnosed with mental retardation who engaged in SIB.

For Greg and Alice, all sessions were conducted on an inpatient hospital unit for the assessment and treatment of problem behavior located at a university hospital, in a room with a table and chairs. Amy's sessions were conducted at a local school, and sessions were conducted in an available classroom, furnished with desks and chairs.

Target Behavior, Data Collection, and Interobserver Agreement (IOA)

All sessions were conducted by trained graduate students serving as experimenters. Observers were graduate and undergraduate students who received in-vivo training in behavioral observation and had previously demonstrated high interobserver agreement (IOA) scores (> 90%) with trained observers. Observers were seated behind a one-way mirror or sat unobtrusively at a table in the room or classroom and collected data on handheld computers that provided real-time data and scored events as either frequency or duration. Sessions were conducted two to three times each day, 4 days per week, and were 10 min in duration.

We collected data on child behavior, including screaming, disruptive behavior, aggression, and SIB. Screaming was defined as vocalizations at a volume louder than conversation level, disruptive behavior was defined as throwing, hitting, or kicking objects inconsistent with engagement with items, and aggression was defined as hitting or kicking others. Self-injury (Amy only) was defined as hitting the chin, nose, and face with a closed fist, as well as self-choking (i.e., pushing her fingertips into her throat). Appropriate behavior was selected on an individual basis. For Greg, appropriate behavior included vocal requests for preferred tangible items (e.g., “Toys”), and compliance with instructional demands without physical guidance (e.g., hygiene tasks). For Alice, appropriate behavior was defined as requests for a break from instructional demands through the use of a microswitch which played “break, please” when pressed. Finally, for Amy, appropriate behavior was defined as gestural requests for preferred tangible items; specifically reaching for the preferred item. Amy was required to reach her hand past a line marked on a table to access the item, to a distance of approximately 43 cm.

Data were also collected on therapist behavior including the delivery of tangible items, which was defined as the therapist providing access to the preferred tangible item for at least 1 s within close physical proximity (within 3 cm) of the child. Escape from instructional demands was defined as the therapist removing all task materials away from the participant and termination of any verbal instructions for at least 1 s. No additional measures of therapist integrity were included in these analyses, however, daily anecdotal reports indicated that therapists delivered reinforcement according to the schedule in place.

Functional analyses using procedures similar to those described by Iwata et al. (1982/1994) were conducted for each participant to identify reinforcers for problem behavior. Results showed that Greg engaged in screaming reinforced by access to tangibles, and disruption reinforced by escape from demands. Alice engaged in problem behavior reinforced by adult attention, and escape from demands, and Amy engaged in problem behavior reinforced by access to tangibles and escape from demands. Functional analysis results have been published previously for Greg and Alice (Samaha et al., 2009), and Amy (Samaha et al.; St. Peter et al., 2005). Additional details about functional analysis procedures are available from the corresponding author.

Two independent observers collected data on each participant's problem and appropriate behavior to assess IOA. Observations were divided into 10-s bins, and the number of observed responses was scored for each bin. The smaller number of observed responses (or s for duration measures) within each bin was divided by the larger number of observed responses (or s) and converted to agreement percentages (Iwata, Pace, Kalsher, Cowdery & Cataldo, 1990). Agreement on the nonoccurrence of behavior within any given bin was scored as 100% agreement. The bins were then averaged across the session. Although interobserver agreement on occurrence of behavior would have been more conservative and therefore preferred, computer software errors prevented that calculation (data summaries were maintained but interval-by- interval comparisons became unavailable following a time period after the initial calculations were made). For Greg, IOA was scored for 47% of assessment sessions during the tangible condition, and averaged 100% for disruption, 95% for screaming (range, 80% to 100%), 94.4% for appropriate requests (range, 80.8% to 100%), and 91.7% for access to tangible items (range, 84.1% to 100%). IOA was scored for 44% of assessment sessions during the escape condition, and averaged 89.6% for disruption (range, 87.5% to 100%), 94.3% for compliance with instructional demands (range, 85.8% to 100%), and 88.7% for escape from instructions (range, 84.7% to 100%).

For Alice, IOA was scored for 32% of assessment sessions, and averaged 98.5% for aggression (range, 94% to 100%), 93.2% for disruption (range, 82% to 100%), and 100% for a request for a break from instructional demands. IOA averaged 88% for escape from instructions (range, 64% to 96%). For Amy, IOA was scored for 36% of assessment sessions, and averaged 95.2% for SIB (range, 80% to 100%), and 95% for reaching for tangible items (range, 80% to 100%), and 83% for access to tangible items (range, 15% to 97%).

Procedure

All participants were exposed to an initial baseline condition and four conditions using a reversal design in order to assess response allocation for both problem behavior and appropriate behavior on concurrent schedules of reinforcement. The order of the conditions varied slightly for each participant, and was assigned randomly. Reinforcers were delivered for problem behavior and appropriate behavior according to the condition. For Greg and Amy no additional training was necessary to teach the appropriate response. For Alice, training sessions were conducted prior to the analysis consisting of prompting Alice to press the microswitch using a three-prompt instructional sequence (Iwata et al. 1982/1994). Prior to the first session of each day, the therapist provided a trial for both problem behavior and appropriate behavior, which resulted in access to the reinforcer for 30 s. All participants could engage in both problem and appropriate behavior at any time during the sessions.

Baseline

The baseline condition was identical to the condition(s) associated with problem behavior during the functional analysis and included the tangible and escape conditions for Greg, the escape condition for Alice, and the tangible condition for Amy. During baseline, the first instance of problem behavior following the removal of reinforcement resulted in delivery of the reinforcer (i.e., access to tangible items for Greg and Amy, or escape from instructions for Greg and Alice). No programmed consequences were in place for appropriate behavior. Given that we began Greg's analyses with the tangible condition, we did not conduct an additional baseline in the escape condition, and began the analysis of his escape function with the matching analysis, as described below.

Matching analysis

Unsignaled concurrent VI VI schedules of reinforcement were in place for both problem and appropriate behavior. The intervals were timed using a computer program that signaled to observers when each schedule had elapsed. The interval values were chosen from a triangular distribution with a range of +5 to −5 (i.e., 5 s above and below the average for the VI schedule). When a reinforcer was available for a response an observer signaled the therapist by holding up a blue or yellow card to signal available reinforcement for a given response. The card display was kept outside of the participants' line of vision. The first instance of behavior following availability of a reinforcer resulted in delivery of the reinforcer for 30 s. The timer was stopped during the reinforcement period. After 30 s of reinforcer access, the reinforcer was removed and the timer was reset for that response. Participants were exposed to a subset of conditions, including the problem behavior (rich), equal concurrent schedules, and appropriate behavior (rich). A COD was implemented (Greg only) after it was observed that problem and appropriate behavior occurred closely together (within 1 s) and seemed to be forming a chained response. The COD was initially implemented at 2 s, and was increased to 5 s, when the responses continued to occur as a chain with the 2-s COD. This concern was not observed with Alice or Amy and therefore no COD was necessary to separate their responses.

The problem behavior (rich) condition involved concurrent VI VI schedules, in which the higher rate of reinforcement was associated with problem behavior while the lower rate of reinforcement was associated with appropriate behavior. The equal concurrent schedules condition included concurrent VI VI schedules during which the schedules were equal for problem and appropriate behavior. The appropriate behavior (rich) condition included concurrent VI VI schedules in which the higher reinforcer rate was associated with appropriate behavior while the lower reinforcer rate was associated with problem behavior. Finally, the full treatment condition was designed to eliminate problem behavior, and during this condition, DRA was implemented. During DRA, problem behavior was placed on extinction and, initially, each instance of appropriate behavior resulted in reinforcer delivery (i.e., continuous reinforcement [CRF]).

Experimental design

A reversal design was used for all participants, and the sequence of conditions for each participant is described in Table 1. All participants were exposed to the baseline, appropriate behavior (rich), and full treatment conditions. For Greg, the assessment included the problem behavior (rich) condition for the tangible and escape functions for problem behavior; and for Alice and Amy, the assessments included the equal concurrent schedules condition.

Table 1.

Summary of Conditions and Sequence of Conditions.

Data Analysis

Results were evaluated using the GME (Baum, 1974) using least squares regression for the problem behavior (rich), equal concurrent schedules, and appropriate behavior (rich) conditions only (i.e., values from the baseline and full treatment conditions were not included in these analyses). In order to do so, rates of reinforcement for both problem (R₁) and appropriate behavior (R₂) were calculated for the last five sessions of each condition and applied to the GME to determine if the relative rates of responding for problem (B₁) and appropriate behavior (B₂) “matched” the relative rates of reinforcement.

Reinforced responses were defined as those responses for which a reinforcer was delivered according to the programmed reinforcement schedule. In other words, if problem behavior was followed by an instance of appropriate behavior in 2 s, and the VI schedule for problem behavior timed out first, problem behavior was considered the reinforced response.

The rate of responding and reinforcement were calculated for both problem and appropriate behavior. The rate of responding was calculated by taking the number of responses during a session and dividing by the duration (min) of the session. The rate of reinforcement was calculated by taking the number of reinforced responses and dividing by the duration (min) of the session. The values obtained were then incorporated into the GME.

RESULTS

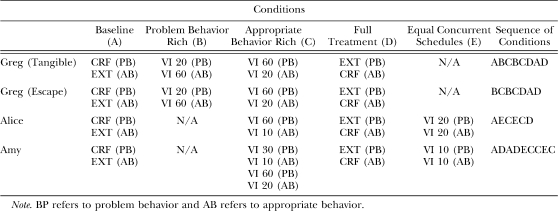
Figures 1 and 2 show the response rates of problem and appropriate behavior expressed as responses per min for all phases. A summary of means for all participants by condition is shown in Table 2. The top panel of Figure 1 shows the results of the analysis for Greg, for behavior maintained by tangible reinforcement (screaming). Greg engaged in higher rates of problem behavior than appropriate behavior during the problem-behavior (rich) conditions. During the initial appropriate-behavior (rich) condition Greg engaged in nearly identical rates of problem behavior and appropriate behavior. However, during the replication of this phase, Greg engaged in lower rates of problem behavior than appropriate behavior. During the second behavior (rich) condition, it was observed that Greg's screaming occurred contiguous with appropriate requests for tangible items, and a 2-s COD was introduced. Greg engaged in both problem behavior and appropriate behavior in the full treatment condition although by the end of both treatment conditions, he engaged in less problem behavior than appropriate behavior. In addition, because problem and appropriate behavior continued to occur contiguously, the COD was increased to 5 s.

Fig 1.

Response rates by session for problem and appropriate behavior for Greg. Response rates of problem and appropriate behavior during tangible sessions (top panel) and of problem and appropriate behavior during escape sessions (bottom panel).

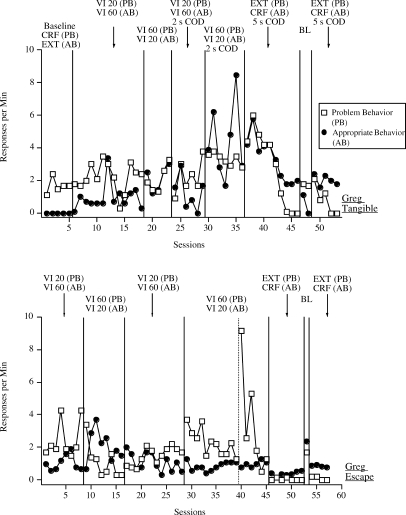
Fig 2.

Response rates by session for problem and appropriate behavior for Alice and Amy. Response rates of problem and appropriate behavior for Alice (top panel) and response rates of problem and appropriate behavior for Amy (bottom panel).

Table 2.

Mean responding per minute for problem behavior (PB) and appropriate behavior (AB) during each initial condition and replication.

The lower panel of Figure 1 displays the results of the analysis for Greg for problem behavior that was negatively reinforced by escape (disruptive behavior). Generally, Greg engaged in higher levels of problem behavior than appropriate behavior during the problem-behavior (rich) condition, and less problem behavior than appropriate behavior during the initial appropriate- behavior (rich) condition. During the replication of the appropriate-behavior (rich) condition, problem behavior appeared to be decreasing in rate, and at that time, Greg left the hospital for approximately 2 weeks (depicted on Figure 1 by the dashed vertical line). Following his return to the inpatient unit, levels of problem behavior decreased over time while levels of appropriate behavior remained stable. Disruptive behavior decreased to near zero levels and appropriate behavior occurred at stable levels during the treatment conditions as compared to the baseline conditions.

The top panel of Figure 2 shows the results of the analysis for Alice. Alice engaged in high rates of problem behavior and no appropriate behavior during the initial baseline. During the initial equal concurrent-schedules condition, problem behavior occurred at a lower rate relative to appropriate behavior. For all subsequent conditions of the matching analysis [i.e., appropriate behavior (rich) and equal concurrent schedules], Alice engaged in higher levels of problem behavior relative to appropriate behavior. A treatment phase was conducted during which problem behavior occurred at relatively low rates and appropriate behavior occurred at relatively high rates. Alice's assessment was brief and additional replications were not conducted, due to her short stay in the hospital.

The bottom panel of Figure 2 shows the results of the analysis for Amy. Amy engaged in relatively high rates of SIB and low levels of appropriate behavior during both the initial baseline phase and the replication, although when the full treatment was introduced and replicated, problem behavior decreased and appropriate behavior increased. When the equal concurrent-schedules condition was implemented and replicated, Amy engaged in similar levels of problem behavior and appropriate behavior. In addition, when the appropriate behavior (rich) condition was implemented and replicated, she engaged in lower levels of problem behavior relative to appropriate behavior, although this effect was observed only towards the end of the final phase. As noted previously, due to the severity of Amy's SIB, full treatment was implemented immediately following baseline. Full treatment procedures for Amy continued to be implemented outside the context of this research.

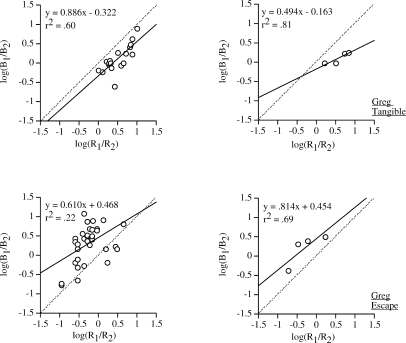
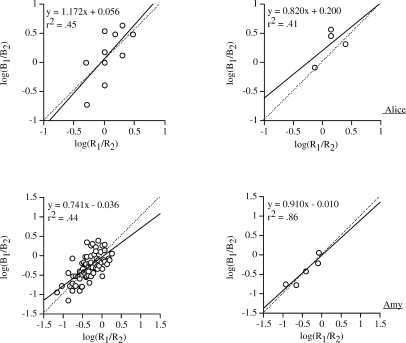
Figures 3 and 4 depict scatter plots with log response ratios plotted as a function of log reinforcer ratios. The linear equation depicts a (i.e., the slope of the function) and b (i.e., the y intercept). The coefficients of determination (r²) are presented for all scatter plots. The dashed diagonal line represents perfect matching. The solid line is the best fit line. The left panels show the results for the last five sessions of each condition (i.e., each data point represents one session) and the right panels show the means for each condition (i.e., each data point represents the last five sessions of each condition, or if less than five sessions were conducted in a condition, all sessions were included).

Fig 3.

Log response ratios plotted against log reinforcer ratios for Greg's tangible (top panels) and escape assessments (bottom panels) for problem behavior (B₁) and appropriate behavior (B₂). The linear equation depicts intercept and slope during all conditions of the escape assessment. Fits of Equation 1 and the coefficient of determination (r²) are shown in each panel. The panels in the left column show individual sessions, and panels in the right column show means across sessions.

Fig 4.

Log response ratios plotted against log reinforcer ratios for Alice (top panels) and Amy (bottom panels) for problem behavior (B₁) and appropriate behavior (B₂). The linear equation depicts intercept and slope during all conditions of the escape assessment. Fits of Equation 1 and the coefficient of determination (r²) are shown in each panel. The panels in the left column show individual sessions, and panels in the right column show means across sessions.

Figure 3 (top panels) shows the results for Greg during the tangible sessions. Due to a computer virus that erased data on reinforcer presentations for a small number of sessions, calculations could not be conducted for the last five sessions of each condition of Greg's analyses (i.e., tangible and escape). However, the majority of sessions were available. Generally, for this analysis, the proportional rates of problem behavior were correlated with the proportional reinforcement rates for problem behavior and the best fit line indicated close adherence to the matching equation. The results also indicated a bias towards appropriate behavior.

Figure 3 (bottom panels) shows the results for Greg during the escape sessions. The proportional rates of problem behavior were correlated with the proportional reinforcement rates for problem behavior; however, the best fit lines did not indicate matching. Bias for problem behavior was also observed.

Figure 4 (top panel) shows the results for Alice during the escape sessions. The proportional rates of problem behavior were correlated with the proportional reinforcement rates for problem behavior; however, the best fit lines did not approximate perfect matching. Bias for problem behavior was also observed.

Figure 4 (bottom panel) shows the results for Amy during the tangible sessions. The proportional rates of problem behavior were positively correlated with the proportional reinforcement rates for problem behavior; however, the best fit line indicated matching for the means of each condition only. Minimal bias was also observed towards appropriate behavior.

In summary, analysis of the data using the GME indicated that for all participants, relative rates of problem behavior were positively correlated with the relative rate of reinforcement for problem behavior. Bias was observed for all participants, and was observed for problem behavior in two cases (Greg and Alice) and for appropriate behavior in two cases (Greg and Amy). In addition, interventions were implemented and successfully decreased levels of problem behavior to clinically acceptable levels. Results suggest that the matching law can provide an accurate description of response allocation between appropriate and problem behavior exhibited by individuals with developmental disabilities. Although matching is a steady state phenomenon and all participants were exposed to the various conditions only briefly, in most cases the matching analysis accounted for a substantial proportion of variance in response rates.

DISCUSSION

We reinforced problem behavior and appropriate behavior on concurrent schedules of reinforcement and analyzed the results using the GME. For all evaluations, the relative rate of responding was influenced by the relative rate of reinforcement. Bias was observed for all participants, with two analyses indicating a bias towards problem behavior (Greg [escape] and Alice) and two indicating a bias towards appropriate behavior (Greg [tangible] and Amy). Finally, DRA and extinction were successful in reducing problem behavior and increasing appropriate behavior to clinically significant levels.

One notable difficulty in such analyses involves defining a “reinforced response.” It is not always clear how responses are reinforced, even with a schedule of reinforcement in place. In concurrent schedule arrangements, the response for which a reinforcer is delivered is controlled by the experimenters. However, it is not clear whether, or to what extent, that reinforcer influences other responses. While not presented here, different results would have been obtained by changing the definition of a reinforced response. Future researchers should evaluate sequential relations between a response and a known reinforcer (i.e., the last response prior to reinforcer delivery counts as “reinforced”) or temporal relations between a response and a known reinforcer (i.e., all responses occurring within a set period of time prior to reinforcer delivery count as “reinforced”).

In addition to reducing problem behavior, one of the goals of this investigation was to further demonstrate the generality of the GME (Baum, 1974). Although a lengthy analysis of concurrent schedules of reinforcement would not likely be necessary from a purely clinical standpoint, useful information can be gathered from such matching analyses. In addition to providing further support for the generality of the GME, in an experimental application with severe problem behavior, there are important applied considerations to this investigation. It is important to note that merely reinforcing appropriate behavior more than problem behavior did not decrease problem behavior to a clinically significant level. It is likely that during naturally occurring interactions between caregivers and children, concurrent schedules of reinforcement are in place. That is, sometimes a caregiver reinforces problem behavior (more than likely on a variable schedule), and sometimes reinforces appropriate behavior. As previous research on treatment integrity has suggested, this could affect the long term success of interventions to reduce problem behavior (Vollmer, Roane et al., 1999; Wilder et al., 2006; Worsdell et al., 2000).

The present experiment suggests several areas for future research in which similar analyses may be conducted using concurrent-schedule arrangements based on naturalistic observations. For example, descriptive analyses (Bijou, Peterson, & Ault, 1968) could be conducted with careproviders and the results could be analyzed using reinforcers identified in a functional analysis (Iwata et al. 1982/1994) with procedures similar to those described by Borrero and Vollmer (2002). For example, if descriptive analysis data showed that problem behavior was reinforced approximately every 20 s, and appropriate behavior was reinforced every 40 s, experimental analyses could be designed to represent naturally occurring reinforcement rates in an experimental context. Concurrent schedules of reinforcement could be based on the derived schedules of reinforcement observed during naturally occurring situations, and a subsequent matching analysis could be conducted. The extent to which relative response allocation is similar under both descriptive and experimental arrangements may provide greater support for the generality of the matching relation. It is often difficult and perhaps unrealistic to train parents to refrain from providing reinforcement following problem behavior. Matching analyses may suggest the lower limit of caregiver reinforcement that may be provided while maintaining clinically acceptable levels of appropriate behavior (Vollmer, Roane, Ringdahl, & Marcus, 1999).

An additional area of future research may include analyses of various parameters of reinforcement. Previous research (e.g., Borrero, Vollmer, Borrero, & Bourret, 2005; Mace et al., 1994; see Stromer, McComas, & Rehfeldt, 2000 for a comprehensive review) has suggested that duration of reinforcement (e.g., Fisher, Piazza, & Chiang, 1996) delay to reinforcement (e.g., Neef et al., 1994; Vollmer, Borrero, Lalli, & Daniel, 1999), quality of reinforcement (e.g., Francisco, Borrero, & Sy, 2008; Mace, Neef, Shade, & Mauro, 1996), response effort (e.g., Cuvo, Lerch, Leurquin, Gaffaney, & Poppen, 1998; Zhou, Goff, & Iwata, 2000) and magnitude of reinforcement (e.g., Lerman, Kelley, Vorndran, Kuhn, & LaRue, 2002; Volkert, Lerman, & Vorndran, 2005) are important variables for evaluating response allocation, in addition to relative rate of reinforcement. Similar investigations could be conducted with different parameters of reinforcement by holding constant rate of reinforcement. In addition, the implications for the treatment of severe problem behavior may be significant. Often, problem behavior is so severe (e.g., head-banging on hard surfaces) that it is not possible to withhold reinforcement (i.e., extinction). That is, especially in the case of behavior reinforced by attention, it is not possible to ignore the behavior and some attention (e.g., blocking the response) will likely be necessary to ensure the safety of the individuals in the situation. However, it may be possible to manipulate other reinforcement parameters such as duration or quality of reinforcement (Athens & Vollmer, in press).

One limitation of these experiments may be the small number of concurrent-schedule values. For Greg and Alice, we only manipulated two values for the concurrent schedules. For Amy, we manipulated three values; however, we did not conduct a thorough analysis of the third value (i.e., VI 60-s VI 20-s), nor did we conduct a reversal to that phase. Future research may also include parametric schedule-value evaluations. For example, the schedules could initially start with VI 20-s for problem behavior and VI 60-s for appropriate behavior, and then values in between (e.g., VI 25-s VI 55-s) until the schedules are reversed (i.e., VI 60-s VI 20-s). Such evaluations may be useful in quantifying reinforcer value by identifying indifference points (i.e., schedule values that produce comparable response allocation). Using the above example, it is possible that when the schedules are VI 35-s for problem behavior and VI 40-s for appropriate behavior, responding would be allocated similarly.

A second limitation of these experiments may be the brevity of the conditions. In a basic preparation, it is usually possible to conduct conditions until meeting a stability criterion. However, in applied settings it was not always possible to bring each condition to stability before exposing behavior to another condition. Therefore, the matching analyses conducted in these experiments may not be based on stable responding, and this could account for some of the variability observed. It is likely that the early sessions in each condition represent a transition state, during which the participant begins to discriminate between the concurrent schedules of reinforcement, and that stable responding occurs towards the end of each condition. While only the last five sessions of each condition were included in the matching analyses, comparisons of the session-by-session scatter plots and the mean scatter plots were also analyzed and suggested that closer approximations to matching were observed by calculating the mean of the last five sessions of each condition rather than calculating all sessions in each condition. This effect was observed for all participants. It is also possible that the history of reinforcement for problem behavior and appropriate behavior could have affected these results, or made problem behavior more likely. It is unknown whether the participants' histories of reinforcement favored problem or appropriate behavior.

A third potential limitation may be that the results were somewhat variable, and the rates of responding did not always correspond to the rates of reinforcement. Prior matching studies have programmed schedule-correlated stimuli (e.g., Neef et al., 1992) to make the conditions more discriminable. It is possible that better correspondence would have been obtained had we included schedule-correlated stimuli. While this was not an investigation of responding during naturally occurring situations, it is not likely that schedule-correlated stimuli are programmed in natural environments. Our goal was simply to assess behavior under these conditions without additional schedule-correlated stimuli and to observe how responding was allocated. Similar procedural limitations may be noted in the absence of a COD for Alice and Amy. Although the COD is a common manipulation in matching research (e.g., Herrnstein, 1961), a COD was implemented for Greg only to eliminate a chained response that was observed. It may be the case that a COD would not be programmed, or at least not implemented with high integrity, in natural environments. Again, given that the participants engaged in severe problem behavior, conditions were designed to be more similar to naturally occurring concurrent schedules. However, even though the conditions were designed in this manner, it is important to note that we observed undermatching in three of four data sets. As Baum (1974) pointed out, undermatching could be related to poor discrimination between the schedules. It is possible that by incorporating a COD or schedule-correlated stimuli the GME could have better described responding. Davison and Jenkins (1985) and Davison and Nevin (1999) offered an alternative to the GME that would take into account the discriminability of available reinforcers in concurrent schedule arrangements. This “detection-theory model” may provide an alternative explanation of these data and should be considered in future studies.

The present experiment focused on evaluating the rate of reinforcement and the effects on problem and appropriate behavior to determine if the GME provided descriptions of response allocation on concurrent schedules of reinforcement. This preliminary experimental investigation is the first such demonstration with 3 individuals with developmental disabilities who engaged in severe problem behavior. While the results were variable, generally they indicated that the GME described response allocation. The limitations associated with this investigation suggest numerous areas of future research related to problem behavior and the matching law that could provide further support for this relation, and address some of the difficulties noted above. From a research standpoint, this investigation contributes to the empirical work supporting the generality of the matching law, although from a clinical standpoint, the contributions may not be as clear. However, there are clinical benefits in assessing response allocation by determining how responses may be reinforced on concurrent reinforcement schedules, particularly because concurrent schedules are likely to be in place in natural environments. It may be particularly difficult to determine how responses are reinforced (temporally, sequentially, or scheduled) in the natural environment, which is an important consideration when training caregivers or generalizing treatments to other settings (e.g., home protocols, schools). It is possible that there may be some discrepancy between what we as researchers define as a reinforced response, and what actually functions as a reinforcer.