Multivariate approach for the enantioselective analysis in micellar electrokinetic chromatography-mass spectrometry

Abstract

A mixture of two molecular micelles polysodium N-undecenoxy carbonyl-l-leucinate, (poly-l-SUCL) and polysodium N-undecanoyl leucylvalinate, (poly-l-SULV) was utilized in micellar electrokinetic chromatography-electrospray ionization-mass spectrometry (MEKC-ESI-MS) to simultaneously separate and detect enantiomers of binaphthyl derivatives. Separation parameters such as background buffer composition, voltage, temperature, and nebulizer pressure were optimized using a multivariate central composite design (CCD).Baseline enantioseparation for both analytes was achieved. The CCD was also used in the optimization of sheath liquid and spray chamber parameters to achieve optimum ESI-MS response. The results demonstrate that CCD is a powerful tool for the optimization of MEKC-MS parameters and the response surface model analysis can provide in-depth statistical understandings of the significant factors required to achieve maximum enantioresolution and ESI-MS sensitivity.

1. Introduction

The binaphthyl derivatives such as 1,1′-bi-2-naphthol (BOH) and 1,1′-binaphthyl-2,2′-diyl hydrogen phosphate (BNP) are very important chiral ligands for asymmetric catalysis [1,2]. They are also used to evaluate the enantioselectivity of chiral stationary phase (CSP) and chiral selectors in chromatography and capillary electrophoresis (CE), respectively [3–5]. In the last several years, surfactants bearing amino acid or small peptide head groups have been developed for the micellar electrokinetic chromatography (MEKC) separation of binaphthyl derivatives. The chiral pseudo-stationary phases (PSPs) include sodium N-[4-n-dodecyloxy-benzoyl]-l-leucinate (SDLL), sodium N-[4-n-dodecyloxybenzoyl]-l-isoleucinate (SDLIL), polysodium N-undeccanoly-l-leucylvalinate (poly-l-SULV), polysodium N-undecanoyl-l-isoleucylvalinate (poly-l-SUILV), polysodium N-undecenoxy carbonyl-l-leucinate (poly-l-SUCL), and polysodium N-undecenoxy carbonyl-l-isoleucinate (poly-l-SUCIL) [6–8]. However, all of the aforementioned chiral PSPs have been used in MEKC with UV detection, which has comparably less sensitivity and specificity. In several recent publications [9–16], it is shown that the problems encountered with the electrospray stability and the poor signal-to-noise (S/N) ratio associated with the conventional unpolymerized micelle in MEKC-MS can be overcome with the hyphenation of microemulsion electrokinetic chromatography to atmospheric pressure photoionization mass spectrometry (MEEKC-APPI-MS) [9.10] or by using molecular micelles (also known as polymeric surfactants) as pseudo-stationary phase [11–16]. Molecular micelles, when used in MEKC-MS, are difficult to ionize, providing a much improved S/N in electrospray ionization-mass spectrometry (ESI-MS). Other important features of using molecular micelles in MEKC-MS include zero critical micelle concentration (CMC) [17] as well as compatibility with the use of higher concentration of organic solvents [18] and volatile buffers [9]. Thus, the molecular micelles have a great potential to be used as a MS compatible PSP in routine hyphenation of CE to MS.

Our previous work on univariate approach, which focuses on only one factor at a time is mainly used to optimize the separation and detection parameters in MEKC-MS [11,12,15]. However, univariate approach does not guarantee a global optimum and often results in poor predictions. On the other hand, the multivariate optimization using design of experiments (DOE) provides simultaneous and much more efficient way of identifying experimental factors in MEKC-MS. Several papers have reported the use of experimental design for CZE-MS [19,20] and MEKC-MS [11] optimization of achiral compounds. However, to our knowledge, not much work involving multivariate optimization of chiral MEKC-MSmethod has been published [11]. Thus, with the aim of providing additional data on the potential of MEKC-MS, simultaneous enantioseparation and ESI-MS detection of two binaphthyl derivatives using a multivariate approach is developed.

We present herein, the application of central composite design (CCD) to evaluate the importance of selected MEKC-MS parameters in a simultaneous analysis of two chiral compounds [(e.g.) (±) BOH and (±) BNP] in the negative ion mode. The use of CCD allowed us to determine the optimal conditions for resolution, analysis time and S/N in MEKC-MS using a mixture of two molecular micelles containing one single amino acid based polymeric surfactant, i.e., polysodiumN-undecenoxy carbonyl-l-leucinate (poly-l-SUCL) and one dipeptide polymeric surfactant (polysodium N-undecanoyl-l-leucylvalinate (poly-l-SULV).

2. Materials and methods

2.1. Chemicals and reagents

Both (±) BOH and (±) BNP as racemic mixtures were obtained from Aldrich (Milwaukee, WI). Standard solution of 7.5M ammonium acetate (NH₄OAc) was purchased from Sigma–Aldrich (St. Louis, MO). Methanol (MeOH, HPLC grade), acetonitrile (ACN, HPLC grade), and acetic acid (glacial) were obtained from Caledon Laboratories Ltd. (Georgetown, ON, Canada). Ammonium hydroxide (NH₄OH, 28–30% ammonia solution) was purchased from EM Science (Gibbstown, NJ). Deionized water (18MΩcm) was purified by a Barnstead Nanopure II Water System (Dubuque, IA). Chemicals used to synthesize l-SUCL, such as ω-undecylenyl alcohol, pyridine, triphosgene, l-leucine, dichloromethane, sodium bicarbonate, sodium hydroxide, hydrochloric acid, and ethyl acetate were purchased from Sigma–Aldrich (St. Louis, MO). Chemicals used to synthesize l-SULV such as undecylenic acid, N-hydroxysuccinimide, and N,N′-dicyclohexylcarbodiimide were also obtained from Sigma–Aldrich (St. Louis, MO). Tetrahydrofuran was obtained from Caledon Laboratories Ltd. (Georgetown, ON, Canada). Isopropanol was purchased from Fisher Scientific (Fair Lawn, NJ). Leucine-valine and leucine was obtained from Bachem California Inc. (Torrance, CA). All the chemicals have the purity of 98% or higher if not stated otherwise and were used as received.

2.2. Synthesis of poly-l-SUCL and poly-l-SULV

The surfactant monomers of l-SUCL and l-SULV were synthesized using the procedure developed by Rizvi and Shamsi [21] and Wang and Warner [17], respectively. The monomers were polymerized using a total dose of 20 Mrad of ⁶⁰Co radiation by Phoenix Memorial Laboratory (University of Michigan, Ann Arbor, MI).

2.3. Preparation of running buffer and analyte solutions

The background electrolyte (BGE) used in the running buffer was NH₄OAc at different concentrations. The pH of the buffer was adjusted as needed by NH₄OH or acetic acid. The buffer was then filtered by 0.45 µm PTFE syringe filter (Fisher Scientific, Pittsburgh, PA) and ultrasonicated for 15min. Next, different amount of poly-l-SUCL and poly-l-SULV surfactant were added into the buffer. The molar concentration of the polymeric surfactants was calculated using the molecularweight of their respective monomers (referred to as equivalent monomer concentration, EMC). The final polymer surfactant containing running buffer was vortxed and ultrasonicated for another 15–20 min before use. Standard stock solutions of (±) BOH (1 mg/mL) and (±) BNP (1 mg/mL) were prepared in MeOH. Working solution containing a mixture of (±) BOH and (±) BNP were prepared by diluting the mixed standard stock solution with equal volume of H₂O to obtain the desired final concentration of 0.25 mg/mL of each binaphthyl compound.

2.4. MEKC-ESI-MS instrumentation

The MEKC-ESI-MS experiments were performed on an Agilent capillary electrophoresis system (Palo Alto, CA) interfaced to an Agilent 1100 series quadrupole mass spectrometer (Palo Alto, CA). Sheath liquid was delivered by an Agilent 1100 series HPLC pump with a 1:100 splitter. The Agilent 3D-CE/MSD ChemStation software (Rev. A.08.04) was used to control the instrument and analyze the raw data. The fused silica capillaries (50 µm i.d., 360 µm o.d.) with a total length of 60cm (Polymicro Technologies, Phoenix, AZ) was used for the MEKC-MS experiments. New capillary was flushed with 1M NH₄OH for 40min followed by deionized water for 15min before usage. Before each run, the capillary was rinsed with actual running buffer for 5min as pre-conditioning. After each run, the capillary was flushed with water (1min), NH₄OH (2min) and water (2 min) as post-conditioning protocol. Positive voltage (varied according to experimental design) was applied for all the CE runs. Analytes were kept at 15 °C temperature in the auto sampler and injected hydrodynamically at the pressure of 5 mbar for 3 s. Sheath liquid containing various proportions (20–50, v/v) of MeOH/H₂O and 5–40 mM NH₄OAcwas delivered by an Agilent isocratic pump at 5 µL/min for all the experiments. MS detection was carried out in selected ion monitoring (SIM) mode for deprotonated molecular ion [M–H]⁻. The following m/z was monitored as group SIM: 285 for (±) BOH and 347 for (±) BNP. Other MSD parameters were set as follows: fragmentor voltage, 90 V; capillary voltage, 3000 V; gain setting, 3.

2.5. Experimental design and data analysis

Experimental design and response surface methodology (RSM) data analysis were performed on Design-Expert (version 7.0.3, Stat-Ease, Inc. Minneapolis, MN) software. Six factors were chosen for the MEKC optimization: F₁: buffer pH, F₂: total concentration of polymeric surfactants ([poly-l-SUCL] + [poly-l-SULV]), F₃: concentration of NH₄OAc, F₄: voltage, F₅: temperature, F₆: nebulizer pressure. Three levels were set for each of the factors. The detailed values for each level are shown in Table 1, rows 1–6. Enantiomeric resolution and analysis time (measured as the migration time (t_m) of the last peak) were used as response (Table 2 ) for MEKC optimization. CCD was used to design the experiment, which covers all the combinations of factors and provides most information about factorial interactions. Though this type of design requires more runs, we considered the 86 runs generated by the software to be necessary to obtain true and practical global optima. All the data obtained from the actual experiments were input into the Design-Expert software. After which the data was fit into quadratic model for the analysis of resolution and 2 factor interaction (2FI) model for the analysis time. Models were chosen based on F-test and lack of fit test. Critical factors were then screened out by analysis of variance (ANOVA). The 3-D surface plots were created by the software to show the interactions between significant factors. Finally, the optimum combination of all variables was generated by the software. To achieve a good trade-off between resolution and analysis time, maximum resolution for both analytes and minimum analysis time were set as experimental goals. The optimization of MS detection was performed by varying the sheath liquid composition and spray chamber parameters, respectively using the same methodology. Detailed designs of sheath liquid and spray chamber parameters are shown in Table 1, rows 7–12. Average peak area and signal to noise ratio (S/N) of the two enantiomers for both (±) BOH and (±) BNP are used as response (Table 4).

Table 1.

Level of factors in the CCD used for the optimization of separation parameters, sheath liquid parameters, and spray chamber parameters in MEKC-MS.

MEKC parameters
Level	F1: pH	F2: [Surfactant] (mM)	F3: [NH4OAc] (mM)	F4: Voltage (kV)	F5: Temperature (°C)	F6: Neb. Pres. (psi)
−1	10.00	15.0	15.0	10	16.0	3
0	10.75	22.5	25.0	15	20.5	4
+1	11.50	30.0	35.0	20	25.0	5

Sheath liquid parameters					Spray chamber parameters
Level	F1: %MeOH (v/v)	F2: pH	F3: [NH4OAc] (mM)		Level	F1: DGFa (L/min)	F2: DGTb (°C)
−1	20	6.00	5.0		−1	4.0	150
0	50	7.25	22.5		0	5.0	200
+1	80	8.50	40.0		+1	6.0	250

^aDGF: drying gas flow rate.

^bDGT: drying gas temperature.

Table 2.

Resolution and migration time data gathered from the CCD experiment for the optimization of MEKC parameters.

Exp. #	Experimental parameters						Experimental/model predicted responses
	pH	[Surfactant] (mM)	[NH4OAc] (mM)	Voltage (kV)	Temperature (°C)	Neb. Pres. (psi)	Resolution				Migration timec
							BNP		BOH		(min)
1	11.50	15.0	15.0	20	16.0	3	0.45	0.64	0.70	1.06	6.5	6.8
2	11.50	30.0	15.0	20	16.0	5	0.46	0.52	0.99	0.90	6.9	6.8
3	10.00	30.0	35.0	10	16.0	3	1.24	1.11	0.49	0.54	19.3	18.5
4	11.50	15.0	15.0	10	16.0	3	0.66	0.46	1.11	0.78	12.7	11.8
5	11.50	30.0	35.0	10	25.0	5	0.02	0.11	0.22	0.50	13.9	13.6
6	10.75	22.5	25.0	15	20.5	4	0.82	0.73	1.26	1.11	11.5	10.4
7	11.50	15.0	35.0	20	25.0	3	0.63	0.50	1.61	1.27	8.7	8.3
8	10.75	22.5	25.0	15	20.5	4	0.90	0.73	1.25	1.11	12.1	10.4
9	10.75	22.5	25.0	15	20.5	4	0.89	0.73	1.44	1.11	11.0	10.4
10	11.50	30.0	15.0	20	25.0	3	0.76	0.78	1.22	1.24	7.5	6.9
11	11.50	30.0	15.0	20	25.0	5	0.75	0.45	1.58	0.93	6.9	6.4
12	10.00	30.0	15.0	10	25.0	5	0.75	0.46	0.52	0.40	13.9	11.3
13	11.50	15.0	35.0	20	25.0	5	0.28	0.12	0.65	0.43	7.8	7.0
14	10.00	30.0	35.0	10	25.0	3	1.22	1.15	0.66	0.62	20.3	17.8
15	10.00	30.0	35.0	10	16.0	5	0.69	0.55	0.31	0.39	16.1	15.4
16	11.50	30.0	35.0	10	16.0	5	0.08	0.03	0.62	0.48	14.6	14.2
17	10.00	30.0	35.0	20	16.0	5	0.76	0.51	0.57	0.37	8.6	8.1
18	10.75	22.5	25.0	15	20.5	4	0.80	0.73	1.26	1.11	10.3	10.4
19	10.00	30.0	35.0	20	16.0	3	1.12	1.08	0.78	0.67	9.8	9.8
20	10.00	15.0	15.0	20	25.0	3	0.32	0.19	1.02	0.79	7.1	6.8
21	10.75	22.5	40.7	15	20.5	4	0.77	0.78	1.23	1.24	11.5	12.1
22	10.75	22.5	9.4	15	20.5	4	0.67	0.73	1.22	1.21	8.7	8.7
23	10.00	30.0	35.0	10	25.0	5	0.67	0.61	1.16	0.38	12.1	14.5
24	10.00	15.0	15.0	20	25.0	5	0.20	−0.02	0.25	0.28	5.7	5.9
25	11.50	30.0	15.0	10	25.0	3	0.68	0.62	1.15	0.89	12.1	12.5
26	10.75	10.8	25.0	15	20.5	4	0.32	0.41	1.22	0.96	8.4	9.4
27	10.00	15.0	15.0	10	25.0	5	0.01	0.18	0.36	0.26	9.6	9.6
28	10.00	30.0	15.0	20	16.0	5	0.36	0.48	0.39	0.41	6.8	7.2
29	10.00	15.0	35.0	10	16.0	3	0.68	0.80	0.65	0.87	15.1	16.2
30	10.00	30.0	15.0	20	25.0	3	0.74	0.68	0.73	0.59	7.7	7.4
31	11.50	15.0	35.0	10	25.0	5	0.07	−0.02	0.06	0.13	12.3	11.9
32	11.50	30.0	15.0	10	16.0	3	0.93	0.65	0.89	0.85	13.1	13.3
33	10.75	22.5	25.0	23	20.5	4	0.67	0.53	1.42	1.12	6.8	5.7
34	10.00	15.0	15.0	10	25.0	3	0.55	0.38	0.71	0.63	12.1	11.9
35	10.75	22.5	25.0	15	20.5	2	1.21	1.08	1.89	1.54	11.5	12.1
36	11.50	30.0	15.0	20	16.0	3	0.87	0.88	1.00	1.12	7.1	7.0
37	11.92	22.5	25.0	15	20.5	4	0.29	0.33	0.58	0.56	10.9	9.8
38	10.00	15.0	35.0	10	25.0	3	0.66	0.73	0.69	0.90	15.3	15.6
39	10.00	15.0	35.0	10	25.0	5	0.36	0.34	0.34	0.32	12.3	12.3
40	11.50	15.0	35.0	10	25.0	3	0.36	0.34	0.84	0.84	14.4	14.6
41	10.00	15.0	35.0	10	16.0	5	0.42	0.39	0.37	0.38	13.8	13.2
42	10.75	22.5	25.0	15	20.5	4	0.75	0.73	1.21	1.11	10.4	10.4
43	10.75	22.5	25.0	15	20.5	4	0.81	0.73	0.91	1.11	10.6	10.4
44	10.00	15.0	35.0	20	25.0	5	0.10	0.18	0.27	0.41	7.5	6.9
45	10.00	15.0	15.0	20	16.0	5	0.11	0.25	0.11	0.33	6.7	6.5
46	11.50	15.0	15.0	10	16.0	5	0.26	0.26	0.52	0.37	10.4	10.3
47	10.75	22.5	25.0	15	20.5	4	0.71	0.73	0.70	1.11	10.9	10.4
48	11.50	30.0	15.0	10	16.0	5	0.34	0.30	0.70	0.77	12.2	11.7
49	11.50	15.0	35.0	10	16.0	3	0.36	0.33	0.84	0.78	15.5	14.8
50	11.50	15.0	15.0	20	25.0	5	0.11	0.25	0.41	0.49	5.5	6.3
51	11.50	15.0	15.0	10	25.0	5	0.22	0.15	0.33	0.26	9.3	9.4
52	11.50	30.0	35.0	20	25.0	5	0.30	0.30	0.64	0.79	7.5	7.5
53	10.75	22.5	25.0	15	27.5	4	0.65	0.68	0.88	0.83	10.0	10.0
54	11.50	15.0	15.0	10	25.0	3	0.22	0.32	0.61	0.77	11.0	11.2
55	11.50	15.0	15.0	20	25.0	3	0.17	0.44	0.61	1.13	6.1	6.7
56	10.00	15.0	35.0	20	16.0	5	0.26	0.30	0.43	0.38	7.4	7.1
57	10.00	30.0	15.0	10	25.0	3	0.66	0.81	0.16	0.44	12.3	13.7
58	11.50	15.0	35.0	10	16.0	5	0.00	−0.05	0.05	0.16	11.0	12.4
59	11.50	15.0	35.0	20	16.0	5	0.00	0.15	0.38	0.37	6.7	6.9
60	11.50	30.0	15.0	10	25.0	5	0.02	0.30	0.38	0.72	9.9	10.7
61	10.00	30.0	15.0	10	16.0	5	0.47	0.56	0.52	0.49	11.3	12.6
62	10.00	15.0	15.0	10	16.0	3	0.53	0.60	0.56	0.68	12.7	12.9
63	11.50	30.0	35.0	10	16.0	3	0.02	0.50	0.90	0.76	16.1	16.7
64	10.00	30.0	15.0	20	16.0	3	0.81	0.86	0.56	0.50	8.2	7.9
65	10.00	30.0	15.0	10	16.0	3	0.83	0.93	0.36	0.44	14.2	14.8
66	10.00	15.0	15.0	10	16.0	5	0.51	0.38	0.51	0.40	11.1	10.8
67	11.50	15.0	15.0	20	16.0	5	0.70	0.43	0.56	0.51	5.8	6.6
68	10.75	22.5	25.0	15	20.5	4	0.68	0.73	0.99	1.11	9.6	10.4
69	11.50	30.0	35.0	20	16.0	3	0.94	0.77	0.89	1.10	8.0	8.6
70	10.00	30.0	15.0	20	25.0	5	0.28	0.31	0.13	0.41	6.1	6.5
71	10.00	30.0	35.0	20	25.0	5	0.33	0.50	0.15	0.46	7.2	7.8
72	10.75	34.2	25.0	15	20.5	4	0.82	0.80	0.78	1.05	10.1	11.3
73	11.50	30.0	35.0	20	16.0	5	0.10	0.22	0.70	0.67	7.5	7.5
74	10.75	22.5	25.0	15	20.5	6	0.16	0.33	0.40	0.75	8.4	8.7
75	10.00	15.0	15.0	20	16.0	3	0.56	0.48	0.92	0.75	7.8	7.2
76	10.00	15.0	35.0	20	25.0	3	0.54	0.58	1.01	1.12	8.0	8.7
77	10.75	22.5	25.0	15	16.0	4	0.65	0.77	0.84	0.97	10.4	10.6
78	10.75	22.5	25.0	15	20.5	4	0.64	0.73	1.00	1.11	9.4	10.4
79	9.58	22.5	25.0	15	20.5	4	0.57	0.60	0.20	0.22	10.1	10.9
80	11.50	30.0	35.0	20	25.0	3	0.76	0.82	1.25	1.30	8.3	8.9
81	11.50	15.0	35.0	20	16.0	3	0.54	0.55	0.96	1.13	8.1	8.0
82	10.00	30.0	35.0	20	25.0	3	0.85	1.05	0.64	0.84	9.8	9.7
83	10.75	22.5	25.0	15	20.5	4	0.73	0.73	1.10	1.11	10.3	10.4
84	10.75	22.5	25.0	7	20.5	4	0.27	0.47	0.54	0.84	16.1	15.1
85	11.50	30.0	35.0	10	25.0	3	0.86	0.62	0.92	0.88	16.0	16.3
86	10.00	15.0	35.0	20	16.0	3	0.83	0.72	1.10	1.00	8.6	8.7

^cMigration time of the last peak.

Table 4.

Peak areas and S/N ratios from the CCD experiment for the optimization of sheath liquid parameters and spray chamber parameters.

Sheath liquid parameters
Exp. #	Experimental parameters			Experimental response
	MeOH%	pH	[NH4OAc]	Average peak area		(S/N)avg
	(v/v)		(mM)	BNP	BOH	BNP	BOH
1	20	8.50	40.0	14427	99432	21	113
2	50	5.15	22.5	49152	290824	206	960
3	50	7.25	22.5	40602	241814	115	559
4	50	7.25	51.9	29718	223362	115	706
5	50	7.25	22.5	39097	232124	99	492
6	20	6.00	40.0	9252	67256	16	93
7	50	7.25	22.5	45068	298748	106	562
8	100	7.25	22.5	15281	222053	23	273
9	0	7.25	22.5	3478	10883	7	18
10	20	6.00	5.0	63326	177618	90	196
11	50	7.25	22.5	42950	275642	100	506
12	50	7.25	22.5	48909	272059	133	594
13	50	9.35	22.5	49445	296241	132	623
14	50	7.25	0.0	208453	242844	125	127
15	80	8.50	40.0	37082	307778	165	1092
16	20	8.50	5.0	59459	159065	93	211
17	80	6.00	5.0	11830	492208	178	596
18	50	7.25	22.5	52173	302398	156	678
19	80	6.00	40.0	38757	327795	139	913
20	80	8.50	5.0	139984	540163	247	749

Spray chamber parameters
Exp. #	Experimental parameters		Experimental response
	DGF (L/min)	DGT (°C)	Average peak area		(S/N)avg
			BNP	BOH	BNP	BOH
1	6.4	200	111512	400420	30	95
2	5.0	200	133235	427354	30	83
3	3.6	200	87505	293752	27	84
4	5.0	200	109555	366425	25	71
5	5.0	200	71654	269713	25	83
6	5.0	200	76124	276415	22	70
7	5.0	129	71120	226286	27	74
8	6.0	150	73594	246687	27	72
9	4.0	150	76428	325822	26	96
10	5.0	200	83234	276337	24	70
11	5.0	271	105381	377627	23	70
12	6.0	250	78936	283556	29	83
13	4.0	250	103499	388948	23	71

3. Results and discussion

Simultaneous separation and MS detection of binaphthyl derivatives (± BOH and ± BNP) were optimized by selecting the most important parameters of MEKC-ESI-MS in terms of resolution, analysis time, peak area, and S/N ratio. The first set of multivariate experiments was related to optimization of MEKC parameters (buffer pH, NH₄OAc concentration, EMC of polymeric surfactant, voltage, temperature, and nebulizer pressure). The second set of multivariate experiments was conducted by varying the sheath liquid parameters (MeOH/H₂O ratio, NH₄OAc concentration, pH). Finally, the spray chamber conditions (drying gas flowrate and drying gas temperature) were studied to achieve the highest possible sensitivity under optimum resolution.

3.1. Preliminary experiments

A sequential preliminary study was carried out before the multivariate DOE experiment. In this study, all the factors that could influence enantiomeric resolution and migration time of the two binaphthyl derivatives were optimized individually. There are two purposes for this study. First, to determine which factors are the most important ones for the enantioseparation. Second, to decide the range of all the factors to be further explored in CCD experiment. The buffer pH, NH₄OAc concentration, surfactant concentration, ratio of the two types of polymeric surfactant in the mixed micelle, voltage, temperature, organic modifier, and nebulizer pressure were chosen in this study. A fairly wide range for each factor was explored. The best enantioseparation condition was determined as follows: pH, 11.5; voltage, 15 kV; total surfactant (poly-l-SUCL and poly-l-SULV) concentration, 25mM EMC; NH₄OAc concentration, 25mM; temperature, 20 °C; nebulizer pressure, 4 psi. Organic solvents (MeOH and ACN) was found to be ineffective to enantioselectivity. Thus, it was excluded from the multivariate experiments. The preliminary study suggested that poly-l-SUCL gives better separation for (±) BOH, but poly-L-SULV is better for (±) BNP. As a result, a mixture of both polymeric surfactants was utilized and set at 1:1 molar ratio for the multivariate experiments.

3.2. Multivariate approach

The six factor, three level full-factorial CCD to optimize MEKC parameters is summarized in Table 1(rows 1–6). To determine the three levels for each factor, we placed some of the aforementioned sequentially optimized values in the middle level i.e., level 0, and then a reasonable value was created both at the high and low levels (level +1 and −1). The effect of buffer pH, from 10.5 to 11.5 was investigated. The pH higher than 11.5 was not studied because it is difficult to adjust the pH of NH₄OAc buffer over pH 11.5. Buffer pH lower than 10.0 was not investigated because this pH range was found not good for the resolution of both analytes in preliminary studies. The concentration range of polymeric surfactant was also determined by the preliminary studies. Concentration lower than 15mM EMC usually does not provide enough enantioresolution; while higher concentration (i.e., higher than 30mM EMC) causes suppression of MS signal. The concentration of NH₄OAc used as BGE in the running buffer ranged from 15 to 35mM. When the concentration of NH₄OAc was too low, the buffer strength and pH was not well maintained and the current was also unstable. On the other hand, too high of NH₄OAc concentration suppressed the MS signal. A voltage range of 10–20 kV was chosen to compromise between analysis time and Joule heating. For temperature, the lowest stable temperature our CE instrument could reach is 16 °C, so we set the range from 16 to 25 °C. As for the nebulizer pressure, it is found that the nebulizer pressure higher than 5 psi gives significant suction on the capillary, which deteriorated enantiomeric resolution. On the other hand, nebulizer pressure lower than 3 psi causes current breakdown during MEKC run. Therefore, we chose nebulizer pressure over the 3–5 psi range.

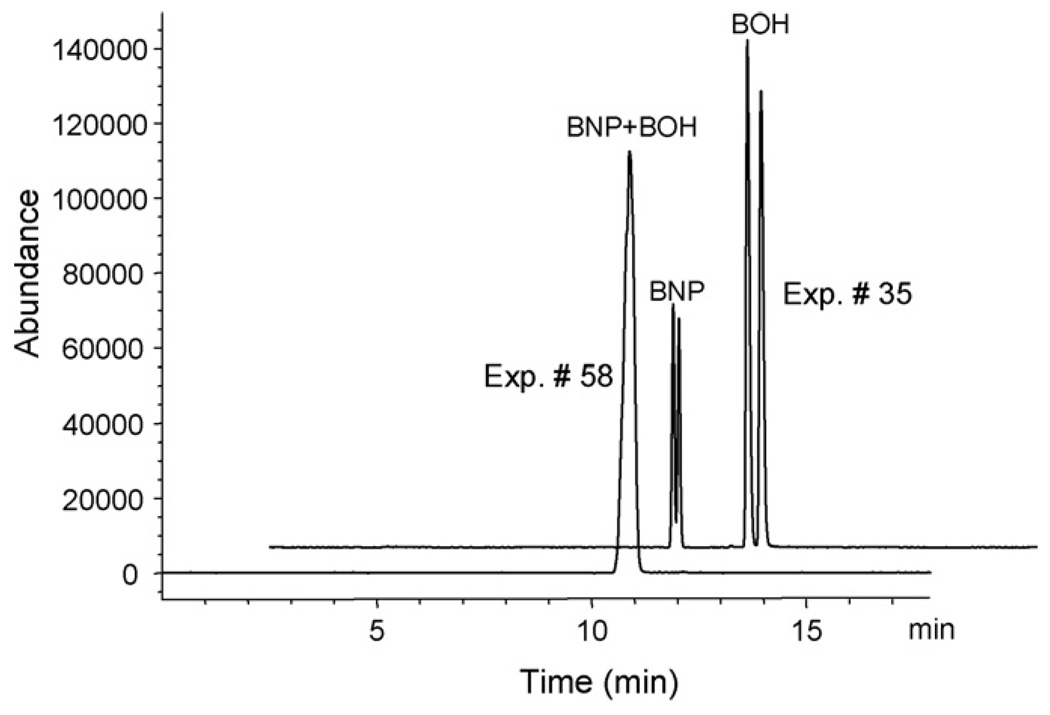
The CCD design layout, which includes the combinations of all the factors at different levels in randomized order as well as the experimental and predicted responses are listed in Table 2. Chiral resolution for both enantiomers and the analysis time (i.e., t_m of the last eluting peak) were considered as quality responses. Among all 86 runs, 10 of them (experiment 6, 8, 9, 18, 42, 43, 47, 68, 78, 83) are repetitive runs of center points (meaning that all factors are at the mean values). The pure error from these replicates are compared with the excess design points (α = 1.565) in the F-test and lack of fit test in the ANOVA to screen out the most critical factors and evaluate the model [22]. As shown in Table 2, the experimental resolution varies from 0 to 1.24 for (±) BNP, 0.05 to 1.89 for (±) BOH, and t_m from 5.52 to 20.31min. Fig. 1 shows two of the representative electropherograms obtained from the CCD experiments (i.e., experiments 58 and 35). The experiment 58 represents one of the worst results among all the experiments because it showed almost no chiral and achiral separation at all. However, experiment 35 demonstrates one of the best separations for both enantiomers.

Fig. 1.

Comparison of the electropherograms of two selected runs obtained in experiment 35 and 58 of the MEKC condition optimization. Experimental conditions: 60 cm × 50 µm id fused silica capillary; poly-l-SUCL/poly-l-SULV (1:1); injection: 5 mbar,3 s; sheath liquid: MeOH/H₂O (50:50, v/v), 5 mM NH₄OAc, delivered at a flow rate of 5 µL/min; spray chamber parameters: drying gas flow rate 5 L/min; drying gas temperature 200 °C; capillary voltage 3000 V; fragmentor90, gain 3; monitored as group SIM at m/z= 285 and 347. CE separation conditions are shown in Table 2 (rows 35 and 58).

The regression coefficients shown in Table 3 represent all of the terms in the predictive multifactor models calculated by the Design-Expert software. For quadratic regression model, the fitted equation is in the form of:

$$\begin{array}{cc}\stackrel{⌢}{y}=\hfill & b_0+b_1{F}_1+b_2{F}_2+b_3{F}_3+\cdots +b_{12}{F}_1{F}_2+b_{13}{F}_1{F}_3+b_{23}{F}_2{F}_3\hfill \\ \hfill & +\cdots b_{11}{F_1}^2+b_{22}{F_2}^2+b_{33}{F_3}^2+\cdots \hfill \end{array}$$ (1)

For 2FI model, the equation is:

$$\begin{array}{cc}\stackrel{⌢}{y}=\hfill & b_0+b_1{F}_1+b_2{F}_2+b_3{F}_3\hfill \\ \hfill & +\cdots +b_{12}{F}_1{F}_2+b_{13}{F}_1{F}_3+b_{23}{F}_2{F}_3+\cdots \hfill \end{array}$$ (2)

Table 3.

Regression coefficient of the coded factors and analysis of variance for the response surface models of chiral resolution (quadratic model) and migration time (2FI model) for the optimization of MEKC factors.

Term	Resolution-BNP		Resolution -BOH		Migration time timec
	Coefficient	Prob>Fd	Coefficient	Prob>F	Coefficient	Prob>F
Intercept (b0)	0.74		1.1		10.38
F1: pH	−0.085	<0.0010	0.11	0.0010	−0.34	0.0022
F2: [surfactant]	0.13	<0.0010	0.028	0.38	0.60	<0.0010
F3: [NH4OAc]	0.013	0.53	0.0087	0.78	1.10	<0.0010
F4: Voltage	0.019	0.37	0.088	0.0066	−2.9	<0.0010
F5: temperature	−0.036	0.090	0.016	0.61	−0.24	0.029
F6: Neb. Pres.	−0.19	<0.0010	−0.20	<0.0010	−0.86	<0.0010
F1 F2	−0.035	0.10	0.078	0.020	−0.11	0.33
F1 F3	−0.083	<0.0010	−0.048	0.15	−0.074	0.51
F1 F4	0.075	<0.0010	0.052	0.12	0.14	0.20
F1 F5	0.022	0.30	0.0079	0.81	0.088	0.43
F1 F6	0.0061	0.78	−0.033	0.32	0.14	0.22
F2 F3	−0.0041	0.85	−0.021	0.51	0.10	0.37
F2 F4	0.012	0.57	−0.0032	0.92	−0.30	0.0098
F2 F5	0.027	0.22	0.013	0.69	−0.017	0.88
F2 F6	−0.038	0.080	0.083	0.013	−0.020	0.86
F3 F4	0.0094	0.66	0.017	0.60	−0.45	<0.0010
F3 F5	0.037	0.089	0.020	0.55	0.093	0.41
F3 F6	−0.047	0.032	−0.051	0.12	−0.23	0.039
F4 F5	−0.017	0.43	0.022	0.50	0.14	0.20
F4 F6	−0.0032	0.88	−0.035	0.29	0.35	0.0027
F5 F6	0.0055	0.80	−0.021	0.51	−0.054	0.63
F12	−0.11	0.020	−0.29	<0.0010
F22	−0.053	0.26	−0.044	0.53
F32	0.0085	0.85	0.047	0.51
F42	−0.091	0.045	−0.050	0.46
F52	−0.00065	0.99	−0.12	0.15
F62	−0.0068	0.82	0.0094	0.84
R2		0.79		0.70		0.94
Adjusted R2e		0.69		0.56		0.92
Predicted R2f		0.51		0.95		0.89
P-lack of fit		0.011		0.25		0.36

^cMigration time of the last peak.

^dProbability of the null hypothesis being true (the factor has no significant effect on the response) based on the F-test for comparing model variance with residual variance. Any term with P < 0.05 is considered significant, and call for rejection of null hypothesis.

^eCoefficient of determination adjusted for the number of terms in the model.

^fA measure of the amount of variation around the mean explained by the model, coefficient of determination is based on the predicted residuals from the model.

Where ŷ is the predicted experimental response; F₁, F₂, F₃…are the factors of interest; b₀ is the intercept coefficient; b₁, b₂, b₃, b₁₂, b₁₃, b₂₃, b₁₁, b₂₂, b₃₃…are the coefficients of all the terms in the model [23]. All the coefficients of the equations as well as their probability of having no effect on the response (i.e., Prob > F) are summarized in Table 3. Positive coefficient value means the corresponding factor is directly proportional to the response, i.e., the bigger the factor, the bigger the response. Negative value means the factor is inversely proportional to the response, i.e., the bigger the factor, the smaller the response. Enantiomeric resolution for both (±) BNP and (±) BOH as well as t_m of the last eluting peak of the MEKC runs are considered as response in this table. If the Prob > F value for each single term is higher than 0.05, it indicates that the coefficient is not significantly different from zero. As a result, the corresponding factor is regarded as a non-critical factor. The absolute value of the coefficient exhibits the relative contribution of each term to the response, the bigger the value is, the higher impact it will have to the response. The coefficients of the second-order terms will not be discussed in the following sections because of their lack of chemical denotations.

The results of the ANOVA for all three response models used in MEKC optimization are tabulated in Table 3 (the last four rows of the table). R², adjusted R², predicted R², and P-lack of fit are all tests of the goodness of fit for the models. R² close to 1, the difference between adjusted R² and predicted R² being within 0.2, or P-lack of fit value bigger than 0.05 indicates a well fitted model. For the quadratic model of (±) BNP resolution, the P-lack of fit value is smaller than 0.05, but the R², adjusted R², and predicted R² are all in acceptable range. Therefore, the model is still considered valid. For the quadratic model of (±) BOH resolution, the difference between adjusted R² and predicted R² is bigger than 0.2, but the R² value is still in acceptable range and more importantly, the P-lack of fit value is much bigger than 0.05. This suggests the model still fits well. For the 2FI model of migration time, all the R² values are perfectly within the acceptable range and P-lack of fit value is also much bigger than 0.05, which indicates the model fit the experimental data very well. Thus, all three models in the optimization of MEKC parameters are tested, fitted to the experimental data and are good enough to be used to identify the significant factors and predict optimum experimental conditions.

3.2.1. Evaluation of MEKC parameters on enantioseparation

The enantiomeric resolution for both analytes was evaluated. At least eight terms (F₁, F₂, F₆, F₁F₃, F₁F₄, F₃F₆, F₁², and F₄²) are critical to (±) BNP; and six terms (F₁, F₄, F₆, F₁F₂, F₂F₆, and F₁²) are significant to (±) BOH (Table 3). The buffer pH (F₁) and the nebulizer pressure (F₆) are both significant at the level of 0.05 for both (±) BNP and (±) BOH. Judging from the absolute values of each coefficient, it appears that nebulizer pressure has the most significant effect on the enantiomeric resolution, and as expected, the lower the nebulizer pressure, the high the resolution value. This is because that lower nebulizer pressure provides smaller suction force at the outlet end of the capillary, thus reduces the laminar flow, which in turn decrease the efficiency [24,25]. Polymeric surfactant concentration (F₂) is significant to (±) BNP, and higher concentration of polymeric surfactant gives higher resolution. However, the resolution of (±) BOH is less sensitive to F₂ factor. This may be due to the fact that the range of surfactant concentration studied in this CCD experiment is outside the range where the enantiomeric resolution of (±) BOH is occurring. It is well documented that the chiral resolution is highly dependent on the concentration of polymeric surfactant [26]. Similar phenomenon was also observed in our preliminary studies, which showed that even very low concentration of poly-l-SUCL can provide baseline enantioseparation for (±) BOH and the enantiomeric resolution does not change much at higher surfactant concentrations. The running MEKC voltage (F₄) is significant to (±) BOH and higher voltage produces higher resolution. This might be due to the fact that high voltage generally results in higher efficiency. However, voltage influence on resolution is less noticeable on (±) BNP, probably because the shorter elution time of (±) BNP offsets the effect that the voltage has on efficiency.

The NH₄OAc concentration (F₃) and capillary temperature (F₅) are not significant to the enantioseparation of either analytes in Table 3. The insignificance of NH₄OAc concentration may be attributed to the fact that (±) BNP and (±) BOH are completely ionized as negatively charged species in the studied pH range. The electrostatic attractive interactions between the analytes and molecular micelles are relatively weak. Thus, the total ionic strength of the NH₄OAc buffer in the studied range has essentially no role in the MEKC process. Finally, with regard to temperature, usually lower temperature gives better separation due to less peak broadening caused by Joule heating. Nevertheless, this parameter was poorly controlled during the whole experiment, because almost half the capillary length is actually outside the CE-MS instrument. This explains why temperature does not significantly affect enantiomeric separation.

A close examination of Prob > F from Table 3 revealed that besides the first order terms, three cross terms (F₁F₃, F₁F₄, F₃F₆) are significant to the resolution of (±) BNP, and two cross terms (F₁F₂, F₂F₆) are significant to the resolution of (±) BOH. The significance of these cross terms indicates that the interactions between the corresponding factors are not negligible. This means that NH₄OAc concentration (F₃), as a single term, is not significant to the resolution of (±) BNP. However, it is significant as a cooperative factor when combined with buffer pH (F₁) and nebulizer pressure (F₆). Similarly, voltage (F₄) is not significant as a single term, but the combination of this factor with buffer pH (F₁) is significant. For the resolution of (±) BOH, polymeric surfactant concentration (F₂) is not significant as discussed above, while the product of this factor with buffer pH (F₁) and nebulizer pressure (F₆) are significant. Besides the cross terms, some of the squared terms are also significant to the responses ($F_1^2,$ and $F_4^2$ is significant to the resolution of (±) BNP, $F_1^2$ is significant to (±) BOH). The significance of the squared terms suggests the curvature of the corresponding terms in the response surface plot.

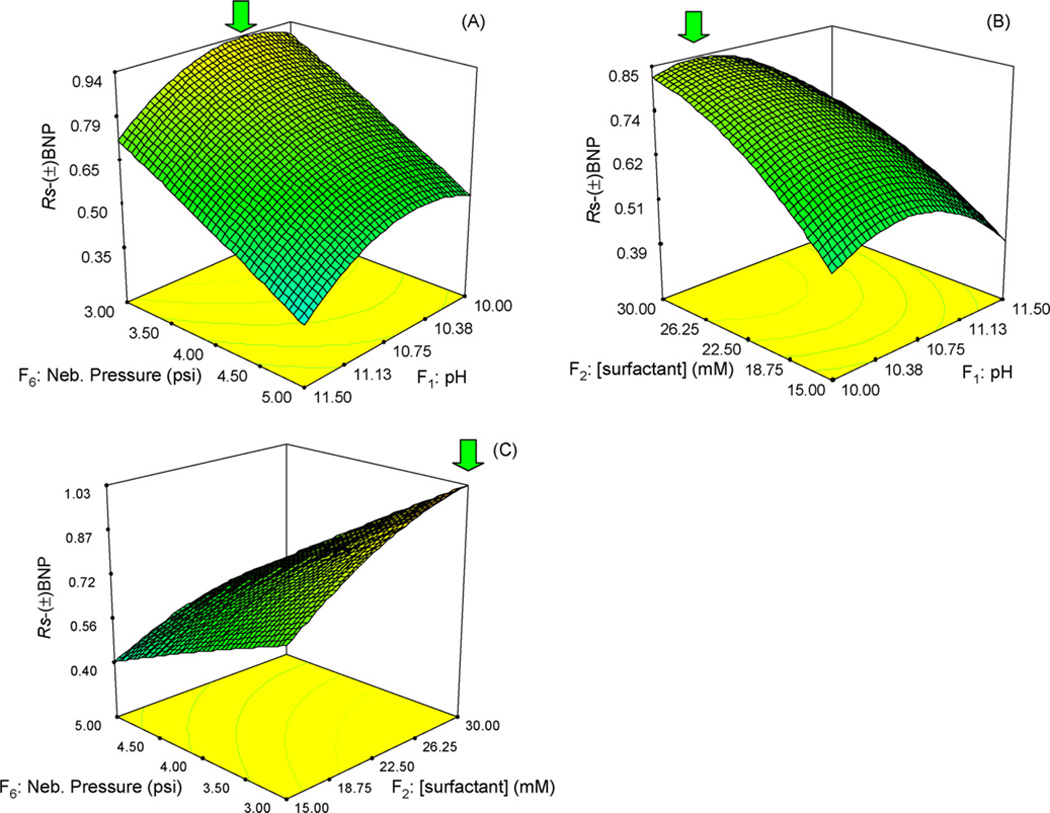
Fig. 2 and Fig. 3 show the response surface plots of enantiomeric resolution vs. any two of the three critical factors for (±) BNP and (±) BOH, respectively. When the enantioresolution of (±) BNP is plotted vs. nebulizer pressure and pH, while all the other parameters are maintained at their mean levels. The surface plot shows a steady downtrend slope along the nebulizer pressure axis (from 3 to 5 psi, Fig. 2A). This indicates an inversely proportional relationship between the resolution and nebulizer pressure as discussed earlier. Across the pH axis, the plot shows a moderate curvature, with the top of the curvature at around pH 10.5. Thus, the highest point of this plot is a combination of nebulizer pressure 3 psi and pH 10.4. Fig. 2B shows the three dimensional graph representing the relationship of surfactant concentration and pH in the running buffer. A downtrend of the response surface can be seen when the EMC of surfactant decrease from 30 to 15mM. Again, pH shows a stronger degree of curvature with the maximum resolution of (±) BNP at around 10.5 indicating pH is a crucial factor to the robustness of the method. The curvature of the whole plotturns to become flatter at the top region ([surfactant] at 30mM EMC and pH around 10.5). This region appears to be the response optimal and the most robust zone. Fig. 2C represents the interaction between nebulizer pressure and polymeric surfactant concentration. The shape of the plot is planar. A strong incline in resolution of (±) BNP can be observed from highest nebulizer pressure and lowest polymeric surfactant concentration to lowest nebulizer pressure and highest polymeric surfactant concentration. Thus, the influence of EMC of polymeric surfactant on the resolution was only significant at a low nebulizer pressure. This trend once again proves the inverse and direct correlations of nebulizer pressure and polymeric surfactant concentration, respectively to the resolution of (±) BNP. To summarize, the use of 30mM EMC of polymeric surfactant, pH 10.5 and nebulizer pressure of 3 psi is enough for achieving the maximum resolution of (±) BNP.

Fig. 2.

Response surface graphs for the enantiomeric resolution of (±) BNP involving the three most significant factors in separation optimization using CCD. Factor which is not analyzed in each plot is held at its mean value (i.e., level 0 in Table 1). Sheath liquid and spray chamber parameters are the same as those in Fig. 1.

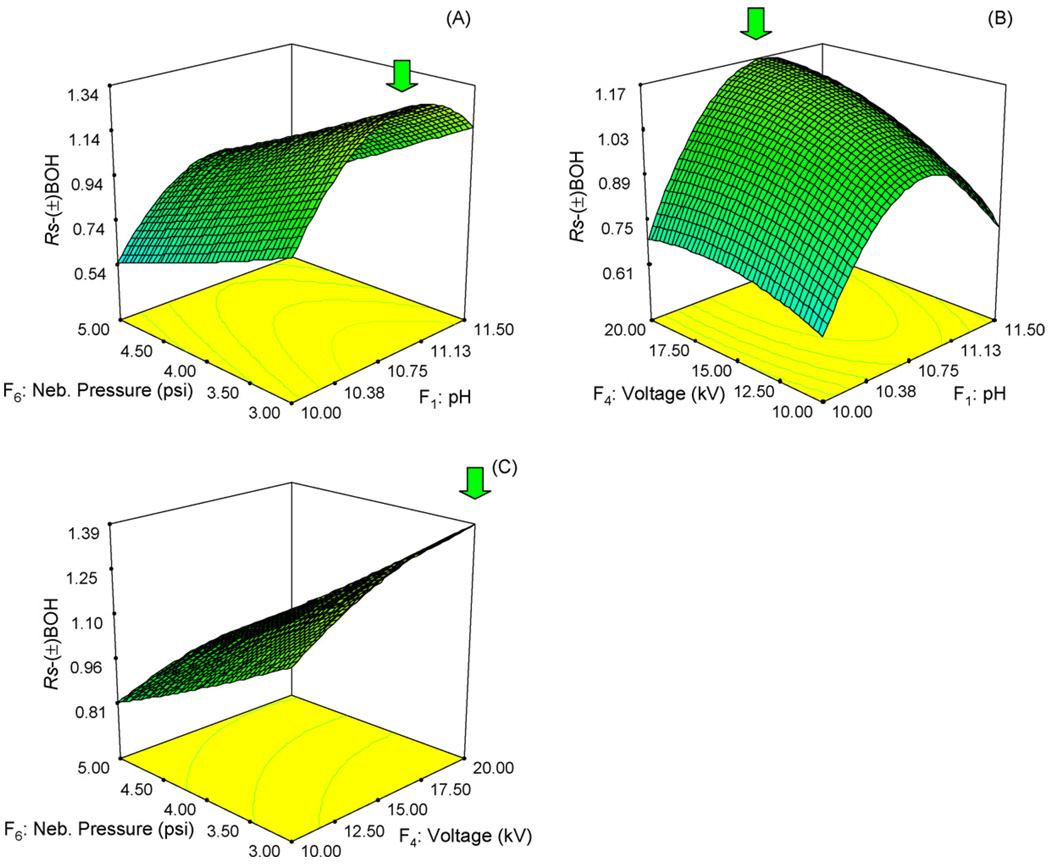
Fig. 3.

Response surface graphs for the enantiomeric resolution of (±) BOH involving the three most significant factors in separation optimization using CCD. Factor which is not analyzed in each plot is held at its mean value (i.e., level 0 in Table 1). Sheath liquid and spray chamber parameters are the same as those in Fig. 1.

Fig. 3 shows another three surface plots with the enantioresolution of (±) BOH as response. Fig. 3A exhibits a very similar plot shape as shown in Fig. 2A (except that the pH axes are reversed between the two figures). In contrast to Fig. 2A, the resolution of (±) BOH shown in Fig. 3A increases only very slightly with the decreasing nebulizer pressure, but shows an upward sloping curvature along the pH axis. However, only this time the highest point of the curvature is around pH 10.9 Fig. 3B shows the relationship between voltage and pH. The surface plot again illustrates a curvature along pH axis and a moderate uptrend along voltage axis. The highest and flattest zone for the resolution of (±) BOH is when voltage is between 15 and 20 kV while pH is around 10.9. Note that the degree of the curvature along the pH axis is very significant in this plot. This suggests a very critical role the pH plays in the enantioseparation process. Fig. 3C shows the resolution response surface of (±) BOH vs. nebulizer pressure and voltage obtained when the other factors are held constant at their mean values. As can be observed, Rs of (±) BOH increased as the main factors (nebulizer pressure decreased and voltage) increased. As a result, the optimum Rs of (±) BOH in this plot can be obtained at a voltage 20 kV and a nebulizer pressure of 3 psi.

3.2.2. Evaluation of MEKC parameters on migration time

In addition to chiral Rs, analysis time (i.e., migration time of the last eluting enantiomer) was also studied as a possible response. As shown in Table 3, nine terms (F₁–F₆, F₂F₄, F₃F₄, and F₄F₆) are significant to the response. Among them, column temperature has the minimum effect as compared to other factors (i.e., Prob > F value is 0.029, which is the largest among all the significant terms). This is probably because capillary temperature is not very well controlled in CE-MS as mentioned earlier. The buffer pH has an inverse effect on migration time. This is not surprising because higher pH of running buffer leads to faster electroosmotic flow (EOF), and thus shortens the run time. On the other hand, higher polymeric surfactant concentration will retain the analytes more in the micellar phase. This trend is observed because both type of polymeric surfactants are negatively charged over the entire pH range studied and have the tendency to migrate opposite to the direction of the EOF, increasing the run time. With regard to the BGE concentration, running time was elongated by higher NH₄OAc concentration. This trend can be attributed to the fact that the high ionic strength introduced by high BGE concentration decreases electric double layer thickness and consequently the ζ potential declines, which decreases the EOF [11,27]. Not surprisingly, the voltage is inversely proportional to the run time and has the biggest effect among all of the six factors. Finally, the nebulizer pressure also has a substantial effect on the migration time. As mentioned earlier, this could be due to the fact that higher nebulizer pressure produces higher negative pressure at the outlet end of the capillary and shortens the run time [28]. In addition to the first order terms, three cross terms are found significant to the migration time (F₂F₄, F₃F₄, and F₄F₆), which indicates the importance of the interactive effects between the corresponding factors. Voltage (F₄), as the most significant single factor, also has the most interactions with other factors. The products of this factor with polymeric surfactant concentration (F₂), NH₄OAc concentration (F₃), and nebulizer pressure (F₆) are critical to the total migration time.

3.2.3. Evaluation of sheath liquid parameters

The composition of methanol (MeOH), pH, and NH₄OAc concentration were chosen as the three important factors for the sheath liquid optimization. The settings of the factors for sheath liquid optimization were determined from our earlier MEKC-MS studies [11]. A total of three factors were studied at three levels (Table 1, rows 7–12, columns 2–4), which resulted in experimental matrix consisting of 20 experiments (Table 4) with six replicate runs (labeled as experiment 3, 5, 7, 11, 12, and 18 in Table 4). The average peak area and S/N were chosen as experimental responses. Good repeatability is shown from the experimental responses for most of the replicate runs. The %RSD for the average peak area is 11.2% for (±) BNP and 10.6 for (±) BOH. When using S/N as response, the %RSD is 18.9% for (±) BNP and 11.9% for (±) BOH. This indicates that the errors of the experiment are acceptable.

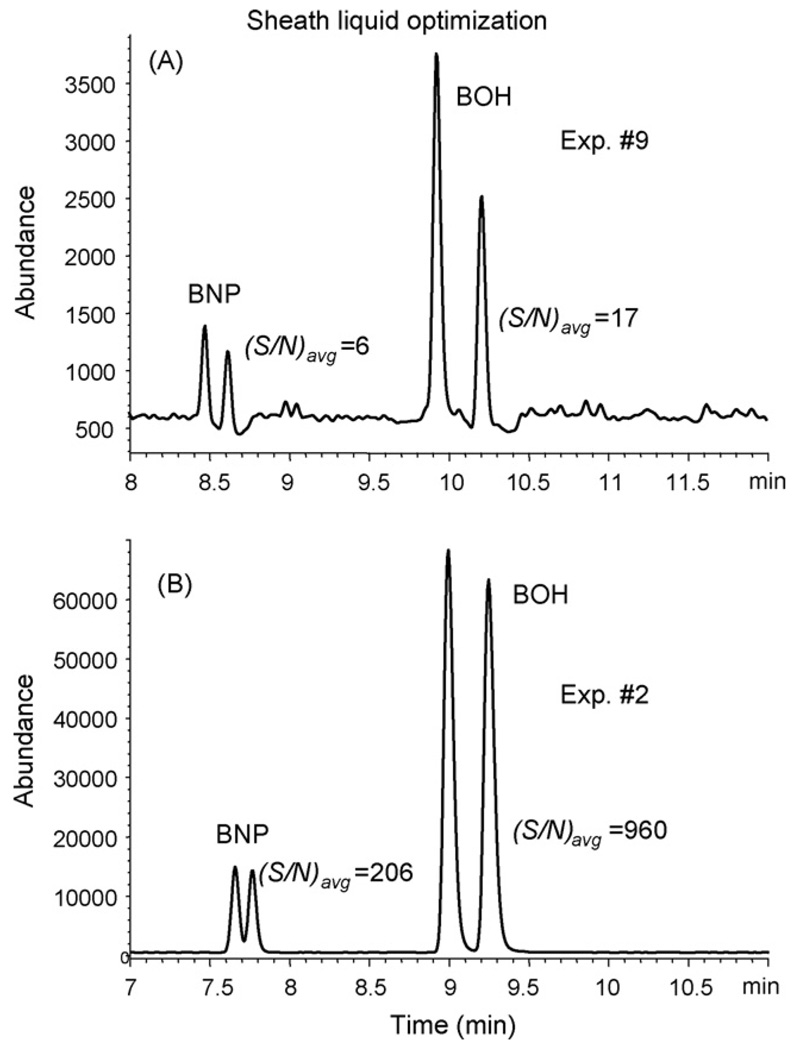
Table 5, rows 1–13 shows the coefficients of the quadratic models using both peak area and S/N of the two analytes as the responses. The NH₄OAc concentration was observed to be significant for both analytes when using peak area as response. This factor is inversely proportional to the response because NH₄OAc suppresses the ESI-MS signal at high concentration. The percentage of MeOH has a significant effect on peak area of (±) BOH only. However, both (±) BOH and (±) BNP provided higher S/N using higher percentage of MeOH in sheath liquid. Fig. 4(A) and (B) shows the electropherograms of experiment 9 and 2 giving the worst and best S/N, respectively. Note that the ammonium acetate concentration remains constant in both experiments. However, a high level of noise is observed in experiment 9 while an almost noise free baseline remains in experiment 2. The peak heights and S/N ratios of racemic mixtures of (±) BNP and (±) BOH are also clearly different. Sheath liquid flowrate was not included in our optimization study. However, a recent publication [28] showed that this factor could also be important to the MS response.

Table 5.

Regression coefficient of the coded factors and analysis of variance for the response surface models of average peak area and S/N for the optimization of sheath liquid and spray chamber parameters.

Term	Peak area-BNP		Peak area-BOH		S/N-BNP		S/N-BOH
	Coefficient	Prob > F	Coefficient	Prob > F	Coefficient	Prob > F	Coefficient	Prob > F
Sheath liquid parameters
Intercept (b0	50157		261600		115.08		548.27
F1: %MeOH	7398	0.45	111300	0.00020	39.36	0.0097	231.88	0.0018
F2: pH	9393	0.34	3710	0.85	−1.51	0.91	−14.65	0.80
F3: [NH4OAc]	−38087	0.0034	−51430	0.029	−24.65	0.092	108.84	0.094
F1 F2	15646	0.23	1789	0.94	10.81	0.52	37.14	0.62
F1 F3	2891	0.82	−28350	0.28	2.94	0.86	107.51	0.17
F2 F3	−15098	0.24	−2155	0.93	−5.14	0.76	3.74	0.96
F12	−17514	0.082	−42167	0.045	−33.17	0.020	−132.74	0.032
F22	−3401	0.71	20435	0.29	21.29	0.11	95.67	0.10
F32	23716	0.050	13276	0.55	10.81	0.46	−35.48	0.58
R2		0.72		0.83		0.72		0.77
Adjusted R2		0.47		0.68		0.48		0.57
Predicted R2		−0.90		−0.13		−0.96		−0.66
P-lack of fit		<0.0010		0.010		0.024		0.0035
Spray chamber parameters
Intercept (b0)	90906		3.1990 × 105		25.12		75.2
F1: DGF	819.32	0.91	−4209.4	0.85	1.41	0.14	0.310	0.89
F2: DGT	10108	0.17	39253	0.10	−0.810	0.38	−2.60	0.29
F1 F2					1.33	0.31	8.88	0.028
F12					1.61	0.12	7.14	0.022
F22					−0.240	0.80	−1.64	0.52
R2		0.18		0.25		0.54		0.73
Adjusted R2		0.013		0.095		0.21		0.53
Predicted R2		−0.19		−0.26		0.076		0.017
P-lack of fit		0.92		0.72		0.95		0.56

Fig. 4.

Comparison of S/N of MEKC-MS runs from the CCD experiments for the optimization of sheath liquid composition. Detailed sheath liquid and spray chamber conditions can be found in Table 4 (rows 9 and 2).

3.2.4. Spray chamber parameter optimization

Two factors, drying gas flow rate (DGF) and drying gas temperature (DGT), are included in the evaluation of spray chamber parameter at these levels using a CCD with 2³ runs and five central points. The lower half of Table 4 shows the experimental matrix with 13 runs generated by the software. Again, the repeatability of replicate runs (labeled as experiment 2, 4, 5, 6, and 10) is acceptable. The %RSD for the average S/N is 11.7% for (±) BNP and 9.2% for (±) BOH. The RSM model generated by the software indicates that neither factor has any significant influence on peak area or S/N of binaphthyl derivatives at the level of 0.05 (see Table 5, rows 14–20) under the selected experimental range. Therefore, further optimization of drying gas temperature and drying gas flow rate was not performed and they were fixed at 250 °C and 4 L/min, respectively.

3.2.5. ANOVA

The original ANOVA data (sum of squares, degree of freedom, mean square, F-ratio, and Prob > F value) for all the models used in MEKC, sheath liquid, and spray chamber experiment are listed in Table 6. In this ANOVA table, model sum of square and residual (error) sum of square for all the models were calculated first. The sum of square values was then divided by degree of freedom to get corresponding mean square values. In the end, F-ratio is calculated by model mean square divided by residual mean square. If these two mean squares are close to each other, i.e. F-ratio is close to 1, it suggests that the null hypothesis (none of the factors has significant effect on the response) is true. In addition, the Prob > F value (probability of the null hypothesis being true) should be bigger than 0.05. On the other hand, if Prob > F is equal or smaller than 0.05, at least one of the terms in the model is considered significant to the response. A close examination of Table 6 reveals that all three models used for the optimization of MEKC factors are significant (have at least one significant factor). All four models used in the sheath liquid study are either significant or very closed to significant (with the Prob > F value slightly bigger than 0.05). However, none of the models used for the spray chamber study is significant (except for the S/N of (±) BOH which is close to significant).

Table 6.

ANOVA table for models used in the optimization of MEKC, sheath liquid, and spray chamber parameters.

Responses	Source	Sum of squares	Degrees of freedom	Mean square	F-ratio	Prob > F
MEKC parameters
Resolution-BNP	Model	6.40	27	0.24	8.12	<0.0001
	Residual (error)	1.69	58	0.029
	Corrected total	8.09	85
Resolution-BOH	Model	9.07	27	0.34	4.97	<0.0001
	Residual (error)	3.92	58	0.068
	Corrected total	12.98	85
Migration time	Model	804.96	21	38.33	48.31	<0.0001
	Residual (error)	50.78	64	0.79
	Corrected total	855.73	85
Sheath liquid parameters
Peak area-BNP	Model	3.03 × 1010	9	3.38 × 109	2.84	0.0597
	Residual (error)	1.19 × 1010	10	1.19 × 109
	Corrected total	4.22 × 1010	19
Peak area-BOH	Model	2.42 × 1011	9	2.69 × 1010	5.48	0.0069
	Residual (error)	4.90 × 1010	10	4.90 × 109
	Corrected total	2.91 × 1011	19
S/N-BNP	Model	5.46 × 104	9	6.07 × 103	2.91	0.0557
	Residual (error)	2.09 × 104	10	2.09 × 103
	Corrected total	7.55 × 104	19
S/N-BOH	Model	1.41 × 106	9	1.57 × 105	3.80	0.0245
	Residual (error)	4.13 × 105	10	4.13 × 104
	Corrected total	1.82 × 106	19
Spray chamber parameters
Peak area-BNP	Model	9.41 × 108	3	3.14 × 108	0.76	0.5423
	Residual (error)	3.70 × 109	9	4.11 × 108
	Corrected total	4.64 × 1012	12
Peak area-BOH	Model	1.25 × 1010	2	6.23 × 109	1.63	0.2443
	Residual (error)	3.83 × 1010	10	3.83 × 109
	Corrected total	5.08 × 1010	12
S/N-BNP	Model	47.69	5	9.54	1.62	0.2709
	Residual (error)	41.22	7	5.89
	Corrected total	88.91	12
S/N-BOH	Model	7.71 × 102	5	1.54 × 102	3.74	0.0575
	Residual (error)	2.89 × 102	7	41.25
	Corrected total	1.06 × 103	12

3.3. Final optimum conditions

In the MEKC optimization study, three models were generated to represent the Rs of (±) BNP, the Rs of (±) BOH, and migration time, respectively (see Table 3). Highest resolution for the two analytes and a shortest possible total analysis run time were set as criteria in the optimization. A desirability function calculated as the geometric mean of all transformed responses was generated in the form of:

$$D={(d_1\times d_2\times \dots \times d_n)}^{\frac{1}{n}}={\left({\displaystyle \prod _{i=1}^n{d}_i}\right)}^{\frac{1}{n}}$$ (3)

where d_i is the response (i.e., two resolutions and migration time in MEKC) to be optimized, n is the number (in our case, three) of responses in the design. D is the desirability that ranges from 0 (the least desirable) to 1 (the most desirable). The goal of the optimization is to find the maximum of the desirability function based on the given criteria. The whole process was conducted by the DOE software and the best conditions (a combination of factors with the highest possible D value) for MEKC separation was obtained as the optimum. Similar strategy was also used to predict the best conditions for sheath liquid and spray chamber, each has two models (the S/Ns for the two analytes). Therefore, the final overall optimum conditions are acombination of the three optimums from the three parts of the study (MEKC, sheath liquid, and spray chamber optimizations).

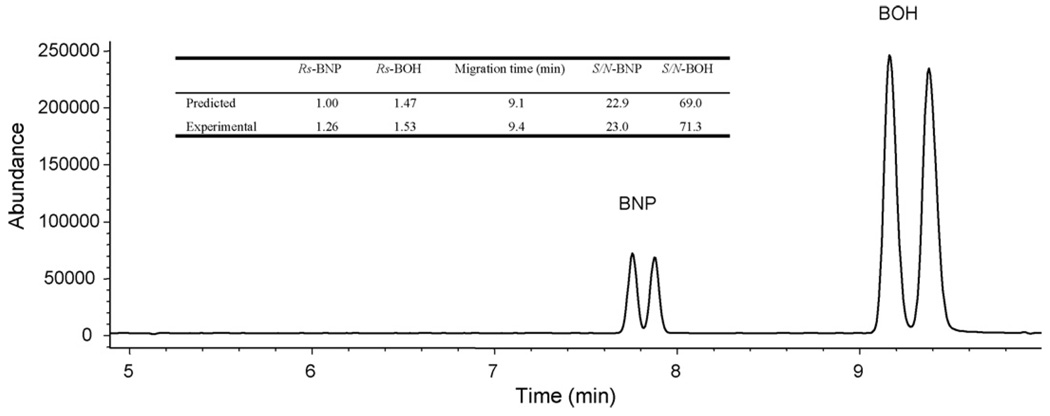
Finally, the aforementioned optimized prediction was validated experimentally by 20 replicate runs at the following optimum conditions (one of the representative electropherograms is shown in Fig. 5). The best MEKC parameters are determined as following: F₁ (buffer pH): 10.8, F₂ (total concentration of polymeric surfactants): 27mM EMC, F₃ (concentration of NH₄OAc): 35mM, F₄ (voltage): +20 kV, F₅ (temperature): 22 °C, F₆ (nebulizer pressure): 3 psi. Sheath liquid conditions are: MeOH/H₂O (80:20, v/v), 5mM NH₄OAc, pH 8.5. Spray chamber: drying gas flow rate: 4 L/min; drying gas temperature: 250 °C. The average enantiomeric resolutions are 1.26 and 1.53 for (±) BNP and (±) BOH, respectively which are 26% and 4% different from the predicted values. The average migration time is 9.4 min which is 3% higher than the predicted value. The S/N ratios are also very close to the predicted values for both analytes as shown in the inset table of Fig. 5. These results obtained from the response surface models are better than what we got from the sequential optimization experiment (data not shown).

Fig. 5.

Experimental electropherogram of (±) BNP and (±) BOH under the final optimized MEKC-MS conditions: 35 mM NH₄OAc buffer, pH 10.8, 27 mM poly-l-SUCL/ploy-l-SULV (1:1); sheath liquid: MeOH/H₂O (80:20, v/v), 5 mM NH₄OAc, pH 8.5, sheath liquid flow rate 5 µL/min; spray chamber: nebulizer pressure 3 psi, DGF 4 L/min, DGT 250 °C. Other MEKC-MS conditions are the same as those in Fig. 1.

4. Concluding remarks

This paper demonstrates the successful simultaneous optimization of two binaphthyl derivatives [(±) BOH and (±) BNP] by MEKC-ESI-MS methodology using a mixture of poly-l-SUCL and poly-l-SULV. Six factor three level CCD experiments were carried out to optimize the MEKC conditions. Data of resolution and analysis time were fitted into models and coefficients of the each term were evaluated. Results showed that nebulizer pressure and pH are the two most significant factors to the enantioresolution of both (±) BNP and (±) BOH. Besides these two factors, polymeric surfactant concentration is significant to the enantioresolution of (±) BNP and voltage is significant to that of (±) BOH. As to analysis time, all six factors were determined to be significant. After the screening of the significant factors, the separation condition with best enantioseparation and shortest analysis time was determined from the model.

Similar strategies were applied to optimize the sheath liquid composition to get the highest S/N for both analytes. Three factors were examined and MeOH/H₂O ratio is found significant to the S/N of both analytes. Two factors (DGF and DGT) of the ESI spray chamber were optimized as well. None of them were found significant within the range studied. The final optimized condition (including the optimum MEKC, sheath liquid, and spray chamber parameters) predicted from the desirability function was tested. The experimental data were in agreement to the predicted results. In this study, CCD experimental design was found to be an effective tool to analyze and optimize the parameters for MEKC-ESI-MS experiment. In our forthcoming studies, we will perform similar multivariate approach to optimize enantioseparation of other binaphthyl compounds in the positive ion mode.