The spatial frequency tuning of optic-flow-dependent behaviors in the bumblebee Bombus impatiens

Abstract

Insects use visual estimates of flight speed for a variety of behaviors, including visual navigation, odometry, grazing landings and flight speed control, but the neuronal mechanisms underlying speed detection remain unknown. Although many models and theories have been proposed for how the brain extracts the angular speed of the retinal image, termed optic flow, we lack the detailed electrophysiological and behavioral data necessary to conclusively support any one model. One key property by which different models of motion detection can be differentiated is their spatiotemporal frequency tuning. Numerous studies have suggested that optic-flow-dependent behaviors are largely insensitive to the spatial frequency of a visual stimulus, but they have sampled only a narrow range of spatial frequencies, have not always used narrowband stimuli, and have yielded slightly different results between studies based on the behaviors being investigated. In this study, we present a detailed analysis of the spatial frequency dependence of the centering response in the bumblebee Bombus impatiens using sinusoidal and square wave patterns.

INTRODUCTION

The ability to visually estimate the angular speed of an image on the eye (termed optic flow) plays a critical role in many important insect behaviors. In honeybees (Apis mellifera L.), these behaviors include: flight speed control, in which the bee will vary its flight speed so as to maintain a constant rate of optic flow (Srinivasan et al., 1996; Baird et al., 2005); the centering response, in which a bee will fly through the center of a narrow tunnel by matching the apparent speed of the walls (Kirchner and Srinivasan, 1989); depth perception, in which honeybees will use the relative speed of objects in the environment to judge their distance (Srinivasan et al., 1989); and visual odometry, in which a honeybee will integrate the apparent image speed experienced during flight to estimate the distance traveled (Esch and Burns, 1995; Srinivasan et al., 1996). Given the importance of visual speed estimation to insect behavior, it is surprising that we know little of the underlying neuronal mechanisms. Although many different models have been proposed, both correlation type (Higgins, 2004; Riabinina and Philippides, 2009) and gradient based (Srinivasan et al., 1991), none has strong electrophysiological and anatomical support while still being sufficiently robust to match the results from behavioral experiments.

David (David, 1982) provided early evidence of a speed-tuned motion detection system in insects. In his studies, Drosophila virilis (Sturtevant, 1916) flew through a horizontally oriented cylindrical wind tunnel. The walls of the tunnel held a ‘barber’s pole' pattern that, when rotated, created the illusion of moving bars. He found that flies would ‘hover’ against a headwind when the surrounding pattern was moved at a specific speed, regardless of whether the striped pattern had a wavelength of 40 deg. or 72 deg. Studies of honeybees provided conclusive evidence for the existence of a small field optic flow detection system that is relatively insensitive to direction (Srinivasan et al., 1993; Dacke and Srinivasan, 2007) and spatial frequency (Srinivasan et al., 1991; Srinivasan et al., 1997; Si et al., 2003; Baird et al., 2005). These properties clearly differentiated the visual speed estimation system from the wide-field, directionally selective mechanism underlying the optomotor response described by the Hassenstein-Reichardt (HR) model (Hassenstein and Reichardt, 1956).

The sensitivity of these behaviors to speed has created difficulty in identifying the mechanisms underlying visual speed estimation because overwhelming biological evidence supports the use of correlation-type detectors that are not generally speed-tuned (Buchner, 1984; Borst, 2007). This has led to many competing theories as to how the insect brain computes optic flow, including gradient-based detectors (Srinivasan et al., 1991), modified correlation detectors (Zanker et al., 1999; Higgins, 2004; Riabinina and Philippides, 2009), combinations of multiple correlators with different spatiotemporal optima (Srinivasan et al., 1999), the adaptation of correlation model time constants in response to motion (O'Carroll et al., 1996), ‘token-matching’ algorithms measuring the time delay between two subsequent photoreceptor activations (Blanes, 1986; Aubépart and Franceschini, 2007) and arguments for the sufficiency of the HR model in real world scenarios (Dror et al., 2001).

One key response property that can be used to distinguish between many of these models is their spatiotemporal frequency tuning. Gradient models, token-matching schemes and population codes all encode the angular speed of the image independently of the spatial frequency, whereas the modified correlation detectors retain some spatial frequency dependence. Behavioral studies generally suggest that optic-flow-dependent behaviors are not dependent on the spatial frequency of a stimulus, but there has been some evidence from honeybees and Drosophila that this may not be entirely correct (Srinivasan et al., 1991; Fry et al., 2009).

Further compounding the problem is the lack of electrophysiological data from the early visual pathways. While velocity-sensitive descending neurons have been reported in the ventral nerve cord of honeybees (Ibbotson, 2001), the spatial frequency dependence of potentially speed-tuned neurons in the optic lobes has not been comprehensively investigated. Most of our understanding of motion detection in insects has come from studies of lobula plate tangential cells (LPTCs) (Hausen, 1981; Hausen, 1982) that are believed to underlie optomotor behaviors (Borst and Bahde, 1987; Egelhaaf and Borst, 1993).

The goal of the present work was to acquire a detailed spatial frequency tuning of the optic flow system using the centering response of the bumblebee, Bombus impatiens (Cresson 1863). We chose the centering response because it depends on the difference between the optic flow estimates of each eye, enabling the direct comparison of speed estimates from two different patterns. Furthermore, it is not dependent on cues from the dorsal or ventral visual fields and is an easily measured behavior that requires little subjective interpretation from the observer.

Although the bulk of behavioral experiments have been performed using honeybees, bumblebees are closely related and exhibit a rich visual ecology and complicated foraging behaviors (Osborne et al., 1999). In addition, bumblebees have larger eyes and better visual acuity than honeybees (Spaethe and Chittka, 2003), allowing us to acquire a broader spatial frequency tuning curve of the underlying speed estimation mechanism. They are also well suited for the electrophysiological investigations that will be necessary in order to uncover the neuronal circuitry responsible for the visual estimation of speed (Riveros and Gronenberg, 2009; Paulk and Gronenberg, 2008; Paulk et al., 2008). Finally, the large size variations in bumblebees provide opportunities to explore the effects of optical variation on motion-related behaviors (Spaethe and Chittka, 2003) and their larger size makes them more amenable to remote tracking (Riley et al., 1999; Osborne et al., 1999).

MATERIALS AND METHODS

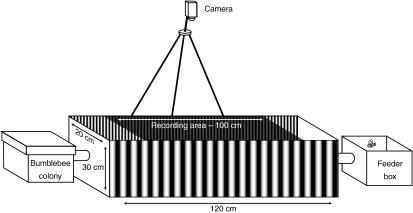
Experiments were performed in a 120 cm long, 20 cm wide and 30 cm high tunnel constructed of transparent acrylic sheets (Fig. 1). Holes were cut in the acrylic walls at both ends of the tunnel so that a box containing a bumblebee colony (Bombus impatiens; Biobest, Leamington, Ontario, Canada) and a feeder box could be connected at opposite ends. The feeder and colony were connected to the tunnel by gated, clear plastic tubes. These entrances were marked by cork perches from which the bees could take off and land. The bottom of the tunnel was lined with white paper in order to maximize the contrast between the bees and the floor of the tunnel for an overhead camera. The only available food was in the feeder box and consisted of two containers full of BIOGLUC® sugar solution (Biobest). The entire experimental setup was housed inside a climate-controlled room with an average temperature of 24°C. The lighting in the room was provided by multiple incandescent lights, which were on for 8 h each day. Two different colonies were used over the course of the experiments.

Fig. 1.

Experimental setup. A box containing a bumblebee colony was connected directly to a clear acrylic tunnel through which the bees navigated to reach the sugar solution housed inside of the feeder box. Bees traveling through the shaded region of the tunnel were recorded using a tripod-mounted video camera situated above the tunnel. The inside walls of the tunnel were lined with different patterns; in the case illustrated, two sinusoidal gratings of different spatial frequencies.

The inside walls of the tunnel were lined with sinusoidal or square wave gratings of different spatial frequencies and contrasts, or with a uniform gray pattern. Each pattern was printed onto a single length of photo paper using a high quality inkjet poster printer (Hewlett Packard Designjet) and cut to a length of 120 cm and width of 30 cm. We tested sinusoidal patterns of spatial frequency 0.05, 0.1, 0.15, 0.17, 0.2, 0.3, 0.4, 0.6, 0.8, 1.2 and 1.6 cycles cm⁻¹ with apparent spatial frequencies of 0.016, 0.023, 0.03, 0.032, 0.037, 0.053, 0.08, 0.11, 0.14, 0.21 and 0.28 cycles deg.⁻¹ when viewed from the center of the tunnel. We convert spatial frequency into angular units as measured from the center of the tunnel when comparing our results to those of previous studies. In data plots, the uniform gray pattern is labeled as having a spatial frequency of zero. We also printed square wave gratings at two sample frequencies of 0.15 and 0.6 cycles cm⁻¹ (0.03 and 0.11 cycles deg.⁻¹, respectively) and low contrast sinusoidal patterns with a spatial frequency of 0.15 cycles cm⁻¹ (0.03 cycles deg.⁻¹). These sample frequencies were chosen because they were well within the resolvable range, but still different enough to potentially yield response differences. All gratings were printed at the maximum achievable Michelson contrast of 0.6 (limited by the printer) unless otherwise noted, where the Michelson contrast C is defined as follows:

$$C=\frac{I_{\max }-I_{\min }}{I_{\max }+I_{\min }},$$ (1)

where I_max and I_min are the maximum and minimum luminance of the pattern, respectively. The average luminance in the tunnel was approximately 380 lux. Patterns were taped to the inside walls of the tunnel and the bees were allowed to forage through the tunnel when experiments were not being run.

Patterns were introduced into the tunnel immediately before recording began with each successive trial following the previous experiment, such that the patterns were varied continuously across trials. After entering an arena with new wall patterns the bees would orient themselves within the tunnel and scan their immediate surroundings before flying through the tunnel. Changes in the flight trajectories across the length of the tunnel were observed immediately at the beginning of each trial and remained consistent over the length of the experiment.

In some cases the bees would perform what we term scanning flights, in which they would face one wall of the tunnel and fly slowly across the tunnel, maintaining an approximately constant body angle and distance from the fixated wall over the length of the tunnel. These flights would sometimes be repeated many times in both directions across the tunnel. Because bees did not appear to be comparing the optic flow between the two walls during these flights they were not included in our data analysis.

A high-definition digital video camera (Canon Vixia HG20) was situated 140.5 cm above the tunnel and captured a 1 m section of the tunnel (Fig. 1). Video sequences were recorded at 30 frames per second with a resolution of 1440×1080 pixels. For each experimental trial, video was recorded continuously for 30–120 min. Video sequences were first edited to include only sections in which bees were flying through the tunnel. The edited video clips were then analyzed frame-by-frame in Matlab (The Mathworks, Natick, MA, USA) using the image processing toolbox. Owing to their exceedingly large size, the images were converted to grayscale and downsampled in size by a factor of two, yielding a resolution of approximately 1.3 mm per pixel at the middle heights of the tunnel. Because the floor was covered in white paper, the bee created a high contrast black object against a white background. To pick out the bumblebees as bright features against a black background, the contrast in each frame was first inverted, and then the image was spatially band-pass filtered to eliminate any noise. The image was then passed through a simple threshold operation, leaving only the clear, high contrast objects (bumblebees). The centroid, major axis, orientation angle and size of each bee for each frame were calculated and time-stamped.

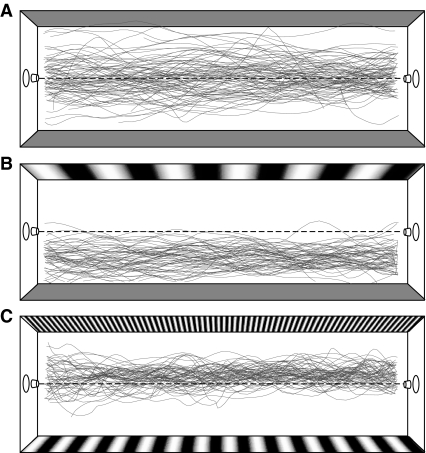
Once we had the positions of the bees at each time point, we reconstructed the paths of individual bees using freely available tracking software by Crocker and Grier (Crocker and Grier, 1996) and Blair and Dufresne (http://physics.georgetown.edu/matlab/). For each flight path we calculated the mean lateral position, speed and size of the bee. Flight speed was calculated by dividing the total displacement of the bee in each frame (including the forward and lateral components) by the frame duration, and this was averaged over the entire flight to obtain average flight speed. Because we were only interested in paths in which the bees flew directly and continuously across the length of the tunnel, we selected only the paths from bees moving at a minimum speed of 26 cm s⁻¹ whose body angle relative to the center of the tunnel never exceeded 60 deg. Both of these values were determined empirically and were partially chosen in order to remove the scanning flights (discussed above) from our analysis. Example flight path data for three different trials are shown in Fig. 2.

Fig. 2.

Representative flight paths. All the recorded flight paths are shown for experimental trials comparing (A) two gray walls (zero spatial frequency), (B) a 0.05 cycles cm⁻¹ sinusoidal grating and a gray wall, and (C) 0.6 and 0.15 cycles cm⁻¹ sinusoidal gratings. The dashed line denotes the center of the tunnel.

The automated tracking of the bees did not allow us to identify the number of individual bees recorded during experiments. In order to ensure that we were not simply recording the paths from only one or two individual bees, we tagged bees for a small subset of experiments and counted the number of individual bees recorded during single trials. These tests indicated that the minimum number of individuals recorded over a single trial was no less than six, but generally ranged between 10 and 14 individuals. In order to justify our treatment of each path as an independent data point, we compared the variation in the flight paths of eight individual bees from two control trials, for each of which we had a minimum of six different flights. The results from a one-way ANOVA comparison indicated that the intra-individual and inter-individual path variation were approximately equivalent (F=1.34, P=0.25).

Statistical analyses of the mean lateral flight paths and speeds of the bees for each experimental condition were performed in Matlab. One-way ANOVA comparisons were used to determine the significance of the results and the Tukey–Kramer method (Kramer, 1956) was used when performing multiple comparisons between the trials.

RESULTS

Before testing the narrowband spatial frequency tuning of the centering response, we first attempted to identify the range of perceptible and behaviorally relevant spatial frequencies. The perception of high spatial frequencies is limited by the spatial resolution of the eye (Land and Nilsson, 2002), while very low spatial frequencies change so gradually as the bees fly that they are unlikely to be perceived as periodic patterns and may be removed by high-pass temporal filtering in the visual processing pathways. In order to test the upper resolution limits, we lined one wall of the tunnel with a sinusoidal grating and the opposite wall with a uniform gray pattern. If the bees were unable to resolve the grating pattern, therefore perceiving two gray walls of equal intensity, then we would expect them to fly through the center of the tunnel on average. If, however, they were able to resolve the gratings one would expect them to fly closer to the gray wall because it would provide fewer motion cues and therefore appear to be moving slower.

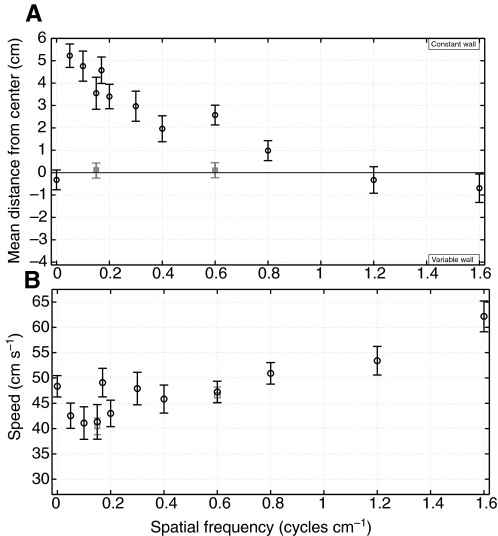
The results plotted in Fig. 3A show the mean lateral positions of the bees as a function of the spatial frequency of one wall. Two control trials in which the walls were lined with the same sinusoidal patterns are provided for comparison. At low spatial frequencies the flight paths of the bees are strongly biased towards the gray wall. This lateral path bias gradually decreases with increasing spatial frequency until it eventually disappears, presumably because the bees are no longer able to resolve the pattern.

Fig. 3.

Gray wall experiments. (A) The mean lateral distance from the center of the tunnel (black circles) is plotted for bees flying through a tunnel lined with a uniform gray pattern on one wall (constant wall) and a sinusoidal pattern of varying spatial frequency on the opposite wall (variable wall). For comparison, two control trials in which both walls carried the same sinusoidal grating (dark gray squares) are also plotted. (B) The average flight speed is plotted against spatial frequency (black circles) and compared with control trials (dark gray squares). Error bars denote the 95% confidence intervals between groups derived from a Tukey–Kramer multiple comparison test on the one-way ANOVA results. The number of paths analyzed was N=1139, with a minimum of 34 and maximum of 144 paths per trial. Zero spatial frequency represents a uniform gray pattern.

In addition to the changes in the mean lateral position, the average flight speed becomes higher as the spatial frequency of one wall is increased (Fig. 3B). However, the changes in the flight speed are much smaller and less consistent than the lateral path deviations. The average flight speeds at spatial frequencies below 0.2 cycles cm⁻¹ are significantly lower than those observed at or above 0.6 cycles cm⁻¹, with the exception of the data points at zero and 0.18 cycles cm⁻¹. This trend is also supported by the data from the control trials showing a significant increase in flight speed when both walls hold sinusoidal patterns of 0.6 cycles cm⁻¹ compared with 0.15 cycles cm⁻¹ patterns.

Although our data show an unexpected increase in speed at 0.18 cycles cm⁻¹, one would expect the highest flight speeds at zero spatial frequency (two gray walls) because of the relative dearth of motion cues. This is not what we observed; rather, the flight speeds at zero were the same as those measured at the midrange spatial frequencies (between 0.3 and 0.8 cycles cm⁻¹). Similar results have been reported previously (Srinivasan et al., 1991; Baird et al., 2005) and it has been proposed that adaptation of the visual system to low contrast patterns may enable the bees to use otherwise invisible motion cues.

Interestingly, the bees fly at much higher speeds when one wall has a high spatial frequency pattern. One possible explanation for these results is that the bees are unable to resolve the high spatial frequency patterns and instead perceive them similarly to uniform gray walls. This hypothesis, addressed further in the Discussion section, does not fully account for the fact that the average flight speeds at 1.2 and 1.6 cycles cm⁻¹ are significantly greater than for two gray walls.

An alternative explanation is that the bees perceive the higher spatial frequency walls as moving more slowly, causing the bees to fly faster in order to reach a preferred rate of optic flow. This would result in the bees centering their paths in the tunnel because of the low rate of optic flow from the two walls; one wall giving a lower estimate because of the dearth of motion cues and the other because of its high spatial frequency. Furthermore, if one considers the possibility that the optic flow from the high spatial frequency wall is lower than that of the gray wall, this could explain both the increased flight speed at high spatial frequencies (Fig. 3B) and the negative bias in the mean lateral position at 1.6 cycles cm⁻¹ (Fig. 3A).

The relatively weak effects of spatial frequency on flight speed compared with the biases in lateral position may be due to the fact that motion signals from the ventral visual field remain constant across trials. Thus, while the bees are seeing fewer motion cues from the walls, the variations in the global optic flow estimate are lower than the differences in the optic flow estimates between eyes. Honeybees are known to use cues from the ventral visual field for both flight speed control (Baird et al., 2006) and visual odometry (Si et al., 2003). Baird et al. (Baird et al., 2006) previously noted that honeybees appear to be capable of acquiring motion cues from the floor of a tunnel despite it being lined with blank white paper. When replaced with a high contrast axially striped pattern the honeybees will fly through a tunnel faster, suggesting they are detecting fewer motion cues from the axial stripes than from the blank floor.

Also of note is that bees were less likely to fly through the entire length of the tunnel when one wall had a uniform gray pattern. Instead they would repeatedly fly through a small section of the tunnel, orient themselves, and loop back. This behavior would be repeated, with the bee flying progressively farther into the tunnel each time, until it would finally fly to the opposite end of the tunnel.

There was greater variation in the mean lateral positions between flights when the walls were lined with two gray walls as opposed to one gray wall and one grating pattern or two grating patterns (Fig. 2). As can be seen, the flight corridor is constricted to a fraction of the tunnel when at least one of the walls has a grating pattern, but when the walls of the tunnel are lined with two gray patterns the bees utilize the entire width of the tunnel.

The within flight variation in the lateral position was significantly greater in experiments in which at least one of the walls of the tunnel had a gray pattern than in control experiments with the same grating pattern on both walls (one-way ANOVA: F=39.83, P<0.001) as measured by the standard deviation in the lateral position over the course of a single flight. However, specific conclusions about the within flight variability between different gray wall experiments could not be made as there were few significant differences between trials. Visual inspection of the individual flight paths suggests that the increase in variability is at least partially due to the larger flight corridors in many of the gray wall experiments. The larger corridor allowed for more direct, diagonal paths across the tunnel such that the standard deviation in the lateral positions appeared larger despite the paths being relatively straight.

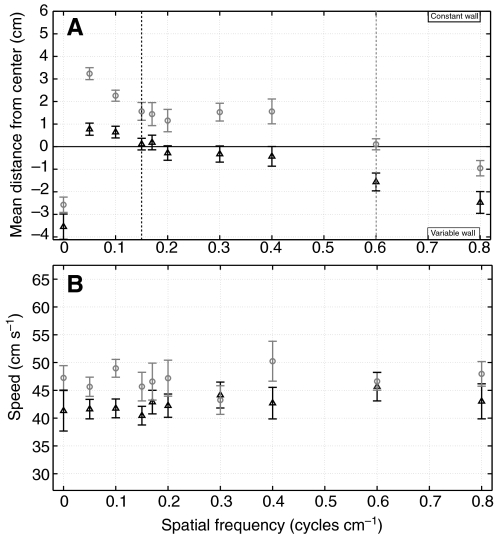
Next, we tested the spatial frequency tuning of the centering response by lining the tunnel walls with sinusoidal (narrowband) patterns of different spatial frequencies. We used only spatial frequencies that appeared to be resolvable from the gray wall experiments, such that the mean lateral position of the bee was significantly different from the control trials. Direct comparisons were made for all of the sinusoidal gratings between 0.05 and 0.8 cycles cm⁻¹. Representative results of these experiments for two sample spatial frequencies of 0.15 and 0.6 cycles cm⁻¹ are shown in Fig. 4. These two frequencies were chosen because they were comfortably within the resolvable range of the insect optics and allowed for direct comparison between the behavioral responses at high and low frequencies.

Fig. 4.

Spatial frequency tuning curves of the centering response. (A) The dependence of the mean lateral flight position on spatial frequency is compared for experiments in which one pattern was held constant (constant wall) at either 0.15 cycles cm⁻¹ (black triangles) or 0.6 cycles cm⁻¹ (gray circles) while the spatial frequency of the opposite wall was varied. The dashed lines indicate the predicted zero crossings when both walls hold the same pattern of either 0.15 cycles cm⁻¹ (black) or 0.6 cycles cm⁻¹ (gray). (B) The average speed of the bees versus the spatial frequency of the variable wall. Error bars represent the 95% confidence intervals for N=1961 unique paths (minimum of 35 and maximum of 188 paths per trial).

We observed no significant deviations in the lateral flight paths when any combination of 0.15 to 0.4 cycles cm⁻¹ gratings were compared, such that the centering response was insensitive to narrowband spatial frequency varying by a factor of 2.5. For spatial frequencies outside this range we observed consistent average path deviations towards the wall with the higher spatial frequency. This can be seen in Fig. 4A, where the two tuning curves have a similar shape but the 0.6 cycles cm⁻¹ curve is shifted in the positive direction. The fact that the bees are flying closer to the high spatial frequency wall suggests that the bees are acquiring a lower speed estimate from the higher frequency patterns. This shift is also apparent in the plot of average flight speed (Fig. 4B), although the flight speeds are much more variable and the differences are not always significant. We did not observe any differences in the variability between or within flights for any of the spatial frequency comparison experiments.

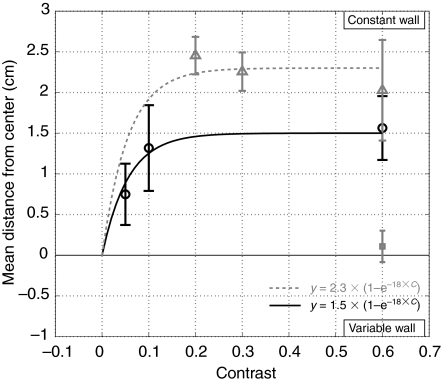
The optics of the bee's eye attenuate the contrast of high spatial frequency patterns on the bee's retina (Land and Nilsson, 2002). We wanted to determine whether the spatial frequencies used in our centering experiments were close to the high spatial frequency cutoff. To accomplish this, we lined one wall of the tunnel with a high frequency sinusoidal grating (0.6 cycles cm⁻¹) with a contrast of 0.6 and the other wall with low frequency sinusoidal gratings (0.15 cycles cm⁻¹) with contrasts of 0.6, 0.3, 0.2, 0.1 and 0.05 (Fig. 5).

Fig. 5.

Contrast sensitivity of the centering response. The mean distance from the center of the tunnel when one wall was lined with a 0.6 cycles cm⁻¹ sinusoidal, 0.06 contrast pattern (constant wall) and the other wall was lined with a 0.15 cycles cm⁻¹ gratings with varying contrast. Data from the first and second colonies are shown in black and gray, respectively. The single black square denotes the combined mean lateral positions for controls in which both walls had either 0.6 cycles cm⁻¹ or 0.15 cycles cm⁻¹ patterns. The lines denote two exponential functions fitted to the data of either the first (black solid line) or the second (dashed gray line) colony. The error bars indicate the 95% confidence intervals for N=942 paths (minimum of 38 and maximum of 201 paths per trial).

If the 0.6 cycles cm⁻¹ grating was close to the cutoff frequency we would expect the previously observed flight path bias of the bee to disappear as a result of contrast attenuation. The results demonstrate that the path bias is decreased, but not eliminated, at extremely low contrast, making it unlikely that the flight path differences seen at high spatial frequencies are due to attenuation by the optics.

The large number of experiments in the present work required that half of the contrast experiments be run with a second colony of bees that were individually much larger. The results from the two colonies are qualitatively the same, but the magnitude of the lateral path deviations were significantly larger for the second colony. The largest path deflections were seen for contrasts of 0.2 and 0.3, which used bees from the second larger colony. Because of this observation, we reanalyzed the data from the first colony by calculating the average size of all of the bees and splitting them into two groups based on whether they were larger or smaller than average. Bees from the larger group did not show contrast-dependent path variations, even when the contrast was 0.05 (data not shown). By contrast, the mean distance from the center of the tunnel was significantly reduced for the smaller bees. However, there was still a significant difference between the mean lateral positions of the bees in the second colony when compared with the larger bees from the first colony, suggesting that there is genetic variability between the bees in the magnitude of the centering response.

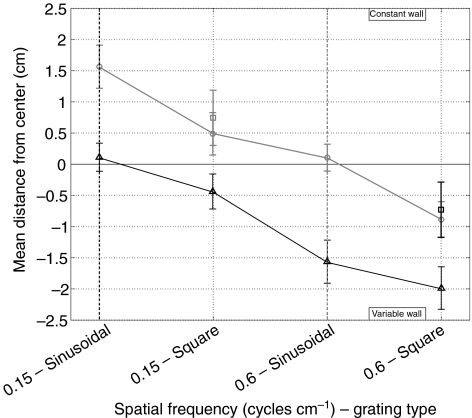
Previous experiments using square wave gratings failed to uncover the spatial frequency dependence of the centering response, although a weak dependence was observed for sinusoidal gratings (Srinivasan et al., 1991). In order to determine if bees respond differently to square wave and sinusoidal stimuli, we lined the walls of the tunnel with different combinations of sinusoidal and square wave patterns with spatial frequencies of 0.15 and 0.6 cycles cm⁻¹. As can be seen in Fig. 6, the previously observed spatial frequency dependence is still present when the walls are lined with square wave gratings, but it is significantly reduced. The bees uniformly perceive the square wave patterns as moving slower as evidenced by the path biases towards the wall carrying the square wave grating. We did not observe any significant differences in the flight speeds between the sinusoidal and square wave pattern experiments, consistent with our earlier observation that flight speed provides a less sensitive measure of the difference between two patterns.

Fig. 6.

Response differences between square wave and sinusoidal stimuli. The mean distance from the center of the tunnel is plotted when the constant wall holds a sinusoidal pattern with a spatial frequency of 0.15 cycles cm⁻¹ (black triangles, solid line) or 0.6 cycles deg.⁻¹ (dark gray circles, solid line) while the variable wall is lined with square wave and sine wave gratings of different spatial frequencies. The squares represent the mean distance from the center when the constant wall has either a 0.15 cycles cm⁻¹ (black) or a 0.6 cycles cm⁻¹ (gray) square grating. Vertical dashed lines indicate the predicted zero crossing when the constant wall has a 0.15 cycles cm⁻¹ (black) or 0.6 cycles cm⁻¹ (gray) sinusoidal pattern. Error bars indicate the 95% confidence intervals for N=1091 paths (minimum of 41 and maximum of 188 paths per trial).

Based on our previous results, this suggests that the bees perceive the square wave patterns as having higher spatial frequency content than a sinusoidal grating of the same spatial frequency. However, the path bias between two square wave patterns is lower than that between two sinusoidal gratings. This is different from what would have been predicted based on the narrowband spatial frequency comparisons where the magnitudes of the path deviations were larger at higher spatial frequencies. These results suggest that, despite the high-pass filtering inherent in the insect compound eye, square wave patterns are not perceived as narrowband stimuli by insects. Similar results have been observed in more controlled studies of the optomotor response (McCann and MacGinitie, 1965).

DISCUSSION

Our experiments indicate that the centering response, and by extension the underlying optic flow system, is dependent on the spatial frequency of a stimulus. Although these results appear to contradict the conclusions of previous studies, the apparent discrepancies can be explained by differences in the behavioral measures and visual stimuli between studies.

Previously, the most comprehensive studies of the narrowband spatial frequency sensitivity of the optic flow system were those of Baird et al. (Baird et al., 2005). They trained honeybees to forage within a narrow tunnel and measured their flight speeds through the tunnel. They did not observe any significant variation in flight speed when both walls were lined with sinusoidal gratings of frequencies of either 0.03, 0.06 or 0.11 cycles deg.⁻¹.

Our results indicate that changes in flight speed provide a much weaker measure of the perceived optic flow than the centering response. It has been previously observed that bees use optic flow information from both the lateral and ventral visual fields (Srinivasan et al., 1997; Si et al., 2003), even when the floor is lined with a blank white pattern (Baird et al., 2006). Hence, the bee's flight speed probably depends on the optic flow information from the entire visual field, making it difficult to make definitive conclusions about the spatial frequency sensitivity based only on flight speed. By contrast, the centering response relies on a direct comparison of the optic flow from each eye providing a more accurate measure of the perceived differences. Furthermore, Baird et al. (Baird et al., 2005) noted that honeybees do not adjust their flight speed until the optic flow deviates by 10–15 deg. s⁻¹ from a preferred rate, raising the possibility that spatial-frequency-dependent changes in the optic flow estimate may be too subtle to significantly impact flight speed.

Past studies of the centering response by Srinivasan et al. (Srinivasan et al., 1991) suggested that the optic flow estimate depended weakly on spatial frequency. They tested square wave and sinusoidal gratings with angular spatial frequencies of 0.01, 0.02 or 0.04 cycles deg.⁻¹ and 0.02, 0.04 or 0.07 cycles deg.⁻¹, respectively. They found a significant change in the lateral flight path only for mismatched sinusoidal gratings of 0.02 and 0.07 cycles deg.⁻¹, but they did not compare square wave gratings to sinusoidal patterns. This is in general agreement with our results in that we found the spatial frequency dependence of the centering response only becomes apparent for frequencies outside the 0.03–0.08 cycles deg.⁻¹ range.

Two studies have tested the spatial frequency sensitivity of the visual odometer. Srinivasan et al. (Srinivasan et al., 1997) trained honeybees to collect a sugar reward from a tunnel holding a square wave grating with a spatial frequency of 0.05 cycles deg.⁻¹. In test trials in a tunnel with no feeder, they found that the bees searched at the former location of the feeder regardless of whether the spatial period was halved or doubled, resulting in spatial frequencies of 0.1 and 0.03 cycles deg.⁻¹, respectively. We did not observe a significant difference in the centering response when a sinusoidal grating of 0.053 cycles deg.⁻¹ was compared with gratings of either 0.03 or 0.08 cycles deg.⁻¹. Because we observed smaller path deviations when using square wave gratings, we believe our observations are consistent with these results.

Si et al. (Si et al., 2003) measured the distance estimates of bees, as measured by the duration of the waggle dance, foraging in narrow tunnels. They lined both walls of the tunnel with sinusoidal gratings of either 0.02, 0.03 or 0.06 cycles deg.⁻¹ and noted a significant decrease in the mean waggle duration for the 0.02 cycles deg.⁻¹ pattern compared with the other higher frequency sinusoids. However, none of these estimates were significantly different from those of the checkerboard control, leading them to conclude that the visual odometer was insensitive to spatial frequency. The relative decrease in the distance estimate for the low spatial frequency grating is the opposite of what would be predicted by both our results and those of Srinivasan et al. (Srinivasan et al., 1991), in which the apparent speed of the stimulus appeared to increase with decreasing spatial frequency. We are unable to reconcile these results with ours aside from the statement by Si et al. (Si et al., 2003) that the distances interpreted from the waggle dance appeared to be less accurate than the actual odometer. It is therefore possible that the human interpretation of the waggle dance was not precise enough to measure differences in the speed estimates.

Fry et al. (Fry et al., 2009) have used ‘one parameter open-loop’ experiments to probe the spatiotemporal tuning of the speed estimation system in Drosophila. In their experimental setup, they induced a fly to hover against a headwind by modulating the speed of a visual stimulus projected onto the walls of a wind tunnel. Once the fly was stationary, they would move the pattern at fixed spatial and temporal frequencies and measure the fly's acceleration response. They observed a plateau in the spatiotemporal frequency tuning such that, for stimuli moving at a set speed, the acceleration responses were relatively constant for the midrange spatial frequencies, but dropped off at both higher and lower ends. Our results are qualitatively similar, but cannot be directly compared because of the lower resolution of the Drosophila compound eye.

We also attempted to identify the resolution limit of the optic flow system by comparing different sinusoidal gratings to a uniform gray pattern. Our results suggest that spatial frequencies greater than 0.14 cycles deg.⁻¹ are not resolved by the optic flow system, corresponding to a minimum spatial wavelength of 7 deg. Other studies have reported that the minimum angular separation at which bumblebees (Bombus terrestris L.) can still resolve two points is 3.5 deg. for large bees and 7 deg. for small bees (Spaethe and Chittka, 2003). Studies in honeybees have reported a minimum angular separation of 5 deg. (Giurfa et al., 1996), while the minimum resolvable spatial wavelength of a moving grating is 2.6 deg. (Hecht and Wolf, 1929).

Our estimate of the minimum resolvable spatial wavelength for the centering response is much higher than would be predicted from these previous studies. In free flight experiments, the apparent spatial frequency of a grating changes with the distance of the bee from the wall. From our data, the bees fly closer to a high spatial frequency pattern, thus lowering the apparent spatial frequency because the optic flow estimate varies inversely with spatial frequency. This would result in an overestimate of the minimum resolvable wavelength, supporting our conclusion that the bees were resolving the gratings in our spatial frequency comparison experiments.

The sensitivity and spatial resolution of the eye has previously been shown to vary with size in bumblebees (Spaethe and Chittka, 2003). We observed a similar result in our contrast experiments, in which there was a size-dependent change in behavior when the pattern contrast of one wall was decreased to 0.05. We concluded that the contrast of the high spatial frequency pattern was being attenuated because it was close to the high spatial frequency cutoff of the optics for the smaller honeybees. However, we did not observe any size-related differences in any of our other spatial frequency comparison experiments, some of which used higher spatial frequencies (data not shown). This raises the possibility that the decreased sensitivity to light of the smaller honeybees may be partially responsible for these behavioral differences.

Another interesting result was that the bumblebees perceived square wave gratings as moving slower than sinusoidal gratings of the same wavelength. Our results suggest that there is a subtle but significant difference between the bees' perception of square and sine wave gratings, indicating that the higher harmonics present in square-wave patterns are not entirely filtered out by the optics of the visual system.

Although many of the experiments with which we compared data were conducted on honeybees, we performed our experiments on bumblebees. Although some differences between our results and previous studies may be due to species-specific variation, we believe that these differences are minimal. Both organisms rely on visual estimates of distance traveled while foraging, fly at similar heights and speeds when foraging (Osborne et al., 1999; Capaldi et al., 2000), and have similar optic capabilities (Spaethe and Chittka, 2003). Optic-flow-related behaviors have been observed in a wide range of insects, including flies (David, 1982; Fry et al., 2009), wasps (Ugolini, 1987) and stingless bees (Hrncir et al., 2003), such that the estimation of optic flow appears to be an elementary operation of the visual system.

Finally, our in-depth analysis of the spatial frequency dependence of the visual speed estimation system provides ample evidence with which to improve future modeling studies. Our results show that whereas the optic flow system is speed-tuned for certain ranges of spatial frequencies, the estimate varies inversely with spatial frequency outside of this range. These results are consistent with the non-directional speed estimation models of Higgins (Higgins, 2004), Rivera-Alvidrez (Rivera-Alvidrez, 2005), Pant (Pant, 2007) and ours (J.P.D. and C.M.H., unpublished), all of which have speed estimates that drop off at high spatial frequencies. These models also match other properties of the visual speed estimation system, such as being small-field and sensitive to motion regardless of direction.