Dynamics of acoustic droplet vaporization in gas embolotherapy

Abstract

Acoustic droplet vaporization is investigated in a theoretical model. This work is motivated by gas embolotherapy, a developmental cancer treatment involving tumor infarction with gas microbubbles that are selectively formed from liquid droplets. The results indicate that there exists a threshold value for initial droplet size below which the bubble evolution is oscillatory and above which it is smooth and asymptotic, and show that the vaporization process affects the subsequent microbubble expansion. Dampening of the bubble expansion is observed for higher viscosity and surface tension, with effects more pronounced for droplet size less than 6 μm in radius.

Gas embolotherapy (GE) refers to intended occlusion of the blood flow in the vasculature by means of gas bubbles.^{1, 2} The envisioned therapeutic application for GE is the treatment of cancer by occluding blood flow to tumors and for localized drug delivery. The process of GE involves the injection of superheated dodecafluoropentane (DDFP, C₅F₁₂) droplets, each encapsulated in an albumin or lipid shell, into the blood stream. The blood flow carries these droplets into the tumor microcirculation where high-intensity ultrasound is used to initiate acoustic droplet vaporization (ADV) to form bubbles near the desired occlusion sites.

Some important issues regarding the implementation of GE to the clinical setting were pointed out by Bull.² One of these issues is to understand the dynamics of ADV and the stresses ADV induces on the vessel wall. High wall stresses can lead to a range of bioeffects, including vessel rupture and changes in vessel permeability, which could deleterious or advantageous depending on the treatment strategy and the severity of the bioeffects. Thus, a thorough understanding of the ADV process is needed in translating this treatment modality to the clinic.

Recent invitro experiments^{3, 4, 5} that were focused from a radiological perspective indicate that when the ultrasound beam hits the superheated DDFP microdroplets, a nucleation site is formed. This nucleation site located inside the droplet triggers the vaporization event. Similar experimental observations were reported by Shepherd and Sturtevant⁶ for large superheated butane droplets with the difference that the phase change initiation was achieved by direct heating. Related work by Farhat et al.⁷ investigated a cavitation bubble inside a water droplet in microgravity. The cavitation was achieved using a spark discharge, a toroidal collapse via a jet formation was observed. A modified Rayleigh–Plesset theory was utilized to explain the bubble collapse mechanism. The only models of bubble expansion in ADV were presented by Ye and Bull,^{8, 9} where direct numerical simulations were carried out for the expanding bubble inside rigid and flexible tubes. Important trends of pressure, velocity, and stress distribution in rigid and flexible tubes were revealed by this study.

In the present work, we propose an ADV model for bubble evolution from microdroplets in the rigid tube. The results obtained from the proposed model where compared with the experimental studies.¹⁰ In the experiments, ultra-high speed images of the bubble evolution were taken for initial droplet size ranging from 10–20 μm in radius inside a microdialysis tube of 200 μm diameter. These images were processed and the bubble expansion ratios as a function of time were obtained for all set of experiments.

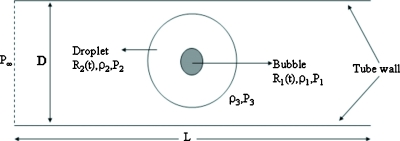
The schematic of the ADV model is shown in Fig. 1. It is assumed that at time zero the nucleation site is already formed and the vapor inside the nucleation site follows the ideal gas law. The evaporation rate (J) is assumed to be constant and equal to its maximal possible value, which is obtained by kinetic theory limit to the mass flux that can be attained in a phase change process.¹¹ Also, it is assumed that the bubble growth remains spherical throughout the evolution process. This assumption is justified for droplets that are small compared to the tube diameter, and is consistent with experimental observations for small droplets. Thus, for spherically symmetric bubble evolution, the radial component of the velocity is defined by conservation of mass as,

$$\text{V}=\frac{{\text{R}}_1^2}{{\text{r}}^2}{\text{V}}_{{\text{R}}_{1+}},$$ (1)

where the subscript “+” and “−” indicates the region just outside and inside the interface and “r” is the radial coordinate. Applying conservation of mass at the bubble surface we get

$${\rho }_1\left({\text{V}}_{{\text{R}}_{1-}}-{\dot{\text{R}}}_1\right)=\text{J}{\rho }_2\left({\text{V}}_{{\text{R}}_{1+}}-{\dot{\text{R}}}_1\right)=\text{J}.$$ (2)

Applying momentum conservation at the bubble surface and dynamic boundary condition at the liquid interface (R₂) and combine then using Eq. 2 yields

$${\text{P}}_{{\text{R}}_{2-}}-{\text{P}}_{{\text{R}}_{1+}}={\text{P}}_{{\text{R}}_{2+}}-{\text{P}}_{{\text{R}}_{1-}}+\frac{2{\sigma }_1}{{\text{R}}_1}+\frac{2{\sigma }_2}{{\text{R}}_2}+\frac{4{\mu }_2}{{\text{R}}_1}{\dot{\text{R}}}_1+\frac{4{\mu }_3}{{\text{R}}_2}{\dot{\text{R}}}_2+{\text{J}}^2\left(\frac{1}{{\rho }_2}-\frac{1}{{\rho }_1}\right).$$ (3)

In order to determine the rate of change of R₁ with respect to time inside the droplet the r-direction momentum equation is integrated with limits from R₁→R₂ to yield

$${\ddot{\text{R}}}_1{\text{R}}_1{\rho }_2\left(1-\frac{{\text{R}}_1}{{\text{R}}_2}\right)+{\dot{\text{R}}}_1^2\left[2{\rho }_2\left(1-\frac{{\text{R}}_1}{{\text{R}}_2}\right)+\frac{1}{2}{\rho }_2\left(\frac{{\text{R}}_1^4}{{\text{R}}_2^4}-1\right)\right]+{\dot{\text{R}}}_1\left[2\text{J}\left(\frac{{\text{R}}_1}{{\text{R}}_2}-1\right)+\text{J}\left(1-\frac{{\text{R}}_1^4}{{\text{R}}_2^4}\right)\right]+\frac{1}{2}\frac{{\text{J}}^2}{{\rho }_2}\left(\frac{{\text{R}}_1^4}{{\text{R}}_2^4}-1\right)={\text{P}}_{{\text{R}}_{1+}}-{\text{P}}_{{\text{R}}_{2-}}.$$ (4)

Further, to obtain the velocity of the droplet surface (liquid interface, R₂), the unsteady Bernoulli equation with head loss term (H_L) is utilized which is given by,

$${\text{P}}_{{\text{R}}_{2+}}-{\text{P}}_{\infty }={\rho }_3{\int }_{{\text{R}}_2}^{\text{L}∕2}\frac{\partial \overline{\text{U}}}{\partial \text{t}}\text{ds}+\frac{1}{2}{\rho }_3\left({\text{U}}_{\text{L}∕2}^2-{\dot{\text{R}}}_2^2\right)+{\text{H}}_{\text{L}}.$$ (5)

Conservation of mass is applied to determine the cross-sectional average velocity $\left(\overline{\mathrm{U}}\right)$, and Poiseuille flow is assumed to obtain

$$\frac{16{\rho }_3}{\beta {\text{D}}^2}\left(\frac{\text{L}}{2}-{\text{R}}_2\right)\left[{\ddot{\text{R}}}_2{\text{R}}_2^2+2{\text{R}}_2{\dot{\text{R}}}_2^2\right]+\frac{512{\mu }_3}{\beta {\text{D}}^4}\left(\frac{\text{L}}{2}-{\text{R}}_2\right){\text{R}}_2^2{\dot{\text{R}}}_2+\frac{1}{2}{\rho }_3\left[{\left(\frac{{\text{D}}^2}{32{\mu }_3}\frac{\text{dp}}{\text{dx}}\right)}^2-{\dot{\text{R}}}_2^2\right]={\text{P}}_{{\text{R}}_{2+}}-{\text{P}}_{\infty },$$ (6)

where β represents the number of tube outlets (1 or 2).

Figure 1.

Schematic of ADV Model.

Thus the final expression for the ADV model which is obtained by adding Eqs. 4, 6 and by using Eqs. 1, 2, 3, is given as,

$${\ddot{\text{R}}}_1{\text{R}}_1{\rho }_2\left[\left(1-\frac{{\text{R}}_1}{{\text{R}}_2}\right)+\frac{{\text{AR}}_1}{{\rho }_2}\right]+{\dot{\text{R}}}_1^2\left[2{\rho }_2\left(1-\frac{{\text{R}}_1}{{\text{R}}_2}\right)+\frac{1}{2}{\rho }_2\left(\frac{{\text{R}}_1^4}{{\text{R}}_2^4}-1\right)+2{\text{AR}}_2\left({\text{R}}_1-{\text{R}}_1^4\left(1-\frac{1}{{\text{R}}_2^4}\right)\right)\right]+{\dot{\text{R}}}_1\left[2\text{J}\left(\frac{{\text{R}}_1}{{\text{R}}_2}-1\right)+\text{J}\left(1-\frac{{\text{R}}_1^4}{{\text{R}}_2^4}\right)+\frac{2{\text{R}}_2\text{JA}}{{\rho }_2}\left(2{\text{R}}_1^4\left(1-\frac{1}{{\text{R}}_2^4}\right)-{\text{R}}_1\right)+{\text{BR}}_1^2\right]+\frac{{\text{J}}^2}{{\rho }_2}\left[\frac{1}{2}\left(\frac{{\text{R}}_1^4}{{\text{R}}_2^4}-1\right)+\frac{2{\text{R}}_2{\text{AR}}_1^4}{{\rho }_2}\left(\frac{1}{{\text{R}}_2^4}-1\right)-\frac{{\text{BR}}_1^2}{\text{J}}\right]+\frac{1}{2}{\rho }_3\left[{\left(\frac{{\text{D}}^2}{32{\mu }_3}\frac{\text{dp}}{\text{dx}}\right)}^2-\frac{{\text{R}}_1^4}{{\text{R}}_2^4}{\left({\dot{\text{R}}}_1-\frac{\text{J}}{{\rho }_2}\right)}^2\right]={\text{P}}_{{\text{R}}_{1-}}-{\text{P}}_{\infty }-\frac{2{\sigma }_1}{{\text{R}}_1}-\frac{2{\sigma }_2}{{\text{R}}_2}-\frac{4{\mu }_2}{{\text{R}}_1}{\dot{\text{R}}}_1-\frac{4{\mu }_3}{{\text{R}}_2}{\dot{\text{R}}}_2-{\text{J}}^2\left(\frac{1}{{\rho }_2}-\frac{1}{{\rho }_1}\right),$$ (7)

where,

$$\text{A}=\frac{16{\rho }_3}{\beta {\text{D}}^2}\left(\frac{\text{L}}{2}-{\text{R}}_2\right),\text{B}=\frac{513{\mu }_3}{\beta {\text{D}}^4}\left(\frac{\text{L}}{2}-{\text{R}}_2\right),\text{and}{\dot{\text{R}}}_2=\left({\dot{\text{R}}}_2-\frac{\text{J}}{\rho }\right)\frac{{\text{R}}_1^2}{{\text{R}}_2^2}.$$ (8)

The term P_R1− in Eq. 7 represents the pressure inside the nucleation bubble and is assumed to follow the ideal gas law under isothermal conditions. This initial bubble pressure is a combination of acoustic pressure (P_us) and the pressure achieved due to the instantaneous phase change phenomena. This instantaneous phase change pressure was obtained by using the ideal gas law with the assumption that the mass of DDFP was conserved in the gas bubble after an instantaneous phase change but with no change in the diameter. The acoustic pulse was modeled as

$${\text{P}}_{\text{us}}={\text{P}}_{\text{a}}\text{\hspace{0.17em}exp}\left[-{\left(\frac{\omega \text{t}}{\text{N}\pi }\right)}^2\right]\text{sin}\left(\omega \text{t}\right),$$ (9)

where, P_a, ω, and N represent peak acoustic pressure, frequency, and number of cycles in the pulse, respectively.

For all the calculations the initial conditions at t=0 are

$${\text{R}}_1={\text{R}}_{10},{\dot{\text{R}}}_1=0,{\text{R}}_2={\text{R}}_0,{\dot{\text{R}}}_2=0.$$

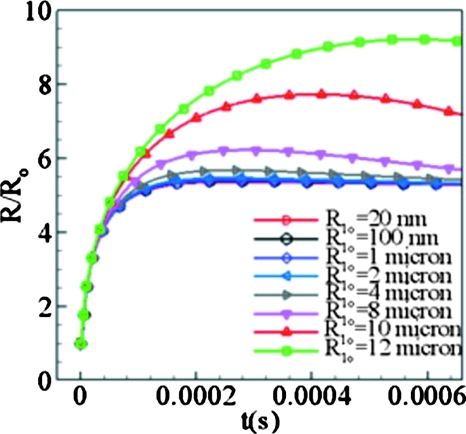
We note that the ADV model is sensitive to initial nucleation size (R₁₀) when a large nucleation radius is assumed, compared to the initial droplet radius (R₀) as depicted in Fig. 2. However, for small R₁₀∕R₀ the solution is not particularly sensitive to the initial nucleation size, and the experiments suggest that R₁₀∕R₀ is small for the size droplets examined here. Therefore, we considered small R₁₀, whose limiting value can be evaluated by solving Eq. 3 for R₁ at t=0.

Figure 2.

Bubble evolution for different initial nucleation size for droplet size of R_o=12 μm.

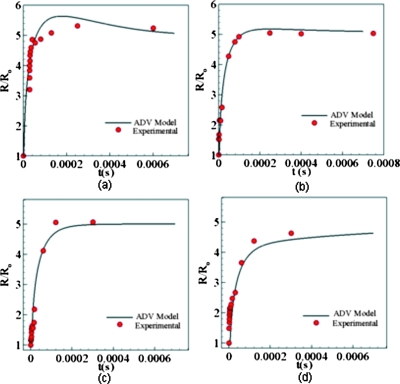
The above ADV model is numerically solved for the parameters corresponding to the experimental cases. Figure 3 shows a comparison of the results obtained by the ADV model with the experimental results. The results are for initial droplet radius of 9.72, 11.61, 13.84, and 18.90 μm while matching the experimental acoustic parameters. The results obtained from the ADV model are in good agreement with the experimental results. The results indicate that the expansion of the bubble is almost linear until around 100 μs and then it approaches its maximum value asymptotically between 100 to 150 μs. The theoretical calculations in,¹⁰ suggest that the maximum final expansion ratio should be less than 5.27, which is also predicted by the ADV model.

Figure 3.

Time evolution of bubble for (a) R_o=9.72 μm, P_a=10.8, and N=4, (b) R_o=11.61 μm, P_a=7.7, and N=13, (c) R_o=13.84 μm, P_a=9.9, and N=4, and (d) R_o=18.9 μm, P_a=7.7, and N=4.

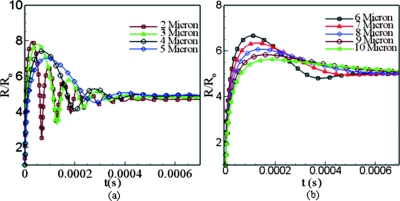
As pointed out in Ref. 8, the initial droplet size, viscosity, and surface tension play an important role in bubble evolution. The current model was utilized to investigate the effects of these parameters. Figure 4 shows the results obtained from the ADV model for different initial droplets size ranging from 2–10 μm in steps of 1 μm with P_a=7.7 MPa, N=4, and f=3.5 MHz. The results signal an interesting pattern. The ADV model suggests that for droplet size, less than 6 μm, the bubble evolution is oscillatory in nature (this oscillatory nature was also observed by some experimental studies^{3, 4} for small droplets) and for the droplet size greater than 6 μm a smooth evolution of the bubble is observed. Thus, it was inferred that there exists a critical initial droplet size (depending upon the geometric, fluid, and acoustic properties) below which the evolution is oscillatory in nature and above that it is smooth and asymptotic.

Figure 4.

Bubble evolution for varying initial droplet size.

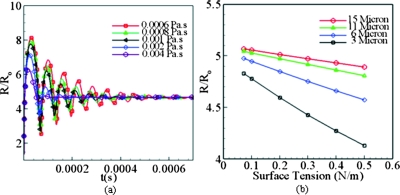
To further elucidate the role of fluid properties in the ADV process, the model was solved by varying viscosity of the dispersed fluid. Figure 5a shows the bubble evolution under varying viscosity for R_o=2 μm. The model indicated that the final bubble size is not significantly affected. However, a dampening effect is visible in the bubble evolution. This dampening behavior is attributed to an increase in the viscous losses in the tube and also to an increase of normal stresses at the bubble interface. Since the same bubble pressure drives the evolution against the higher normal stresses in the dispersed fluid it tends to decelerate the rate of bubble evolution.

Figure 5.

Bubble evolution for (a) varying viscosity and (b) varying surface tension.

To investigate the effect of surface tension on the bubble evolution dynamics, the ADV model was solved by varying the surface tension for different droplet sizes. Figure 5b shows the final bubble expansion ratio as a function of surface tension for droplet sizes of 3, 6, 11, and 15 μm. A linear dependency is observed for all the droplet sizes investigated. Also, for smaller droplet sizes (less than 6 μm) the surface tension influence is more prominently observed which is attributed to the inverse relation of droplet radius with the surface tension force (2σ∕R₂).

In conclusion, the proposed model predicts the ADV process and following bubble evolution reasonably well under varying acoustic impulse. The role of initial droplet size and fluid properties on the bubble evolution were highlighted and found to be significant. In the future, this model can be coupled as a boundary condition to the Navier–Stokes solver to estimate the stress distribution on the vessels.