Four-dimensional intensity-modulated radiation therapy planning for dynamic tracking using a direct aperture deformation (DAD) method

Abstract

Purpose: Planning for the delivery of intensity-modulated radiation therapy (IMRT) to a moving target, referred to as four-dimensional (4D) IMRT planning, is a crucial step for achieving the treatment objectives for sites that move during treatment delivery. The authors proposed a simplistic method that accounts for both rigid and nonrigid respiration-induced target motion based on 4D computed tomography (4DCT) data sets.

Methods: A set of MLC apertures and weights was first optimized on a reference phase of a 4DCT data set. At each beam angle, the apertures were morphed from the reference phase to each of the remaining phases according to the relative shape changes in the beam’s eye view of the target. Three different planning schemes were evaluated for two lung cases and one pancreas patient: (1) Individually optimizing each breathing phase; (2) optimizing the reference phase and shifting the optimized apertures to other breathing phases based on a rigid-body image registration; and (3) optimizing the reference phase and deforming the optimized apertures to the other phases based on the deformation and translation of target contours. Planning results using scheme 1 serves as the “gold standard” for plan quality assessment; scheme 2 is the method previously proposed in the literature; and scheme 3 is the method the authors proposed in this article. The optimization results were compared between the three schemes for all three cases.

Results: The proposed scheme 3 is comparable to scheme 1 in plan quality, and provides improved target coverage and conformity with similar normal tissue dose compared with scheme 2.

Conclusions: Direct aperture deformation method for 4D IMRT planning improves upon methods that only consider rigid-body motion and achieves a plan quality close to that optimized for each of the phases.

INTRODUCTION

Intensity-modulated radiation therapy (IMRT) allows for better tumor coverage and normal tissue sparing than conventional three-dimensional (3D) conformal radiation therapy. However, the high dose gradient created with IMRT makes the treatment plans more susceptible to breathing-induced target movements,¹ which leads to dosimetric uncertainty and discrepancies between planned and delivered doses. This problem is a major concern for all the tumor sites in the thorax and abdomen, especially in the lung,^{2, 3} liver,⁴ and pancreas.^{5, 6}

Several methods have been proposed to manage the effects of respiratory motion, including margin expansion,⁷ respiratory gating,⁸ active breath holding,⁹ and active breathing control.¹⁰ However, these methods either increase the doses to the surrounding normal tissues causing undesirable side effects, or increase the treatment time and patient discomfort. Tumor tracking is a technique that dynamically repositions and reshapes the radiation beam to track the tumor movement. Under ideal situations when tracking can be performed with 100% accuracy, tumor motion related margin can be reduced or eliminated without compromising target coverage or prolong treatment delivery. With these motivations, several dynamic tracking methods have been proposed to manage target motion. Keall et al.¹¹ initially proposed the use of dynamic mutileaf collimator (MLC) to track the movement of the target where the leaf position is dynamically controlled to follow the target under real-time monitoring. Alternatively, D’Souza et al.¹² described a technique that uses the movement of the patient support system (couch) rather than the MLC to cancel out the target motion holding the target stationary in space. Recently, Yi et al.¹³ introduced a less technically challenging technique called dose rate regulated tumor tracking (DRRT) to achieve dynamic tumor tracking, where the treatment delivery is speeded up or slowed down by dynamically changing the dose rate. In dynamic tracking methods using preprogrammed MLC sequences, such as in DRRT, the aperture shape and location are functions of breathing phases, which, in turn, is a function of time. Radiotherapy planning method that incorporates the time component as the fourth dimension,¹⁴ denoted as four-dimensional (4D) planning,¹⁵ becomes necessary to realize this 4D delivery.

With the advent of 4D computed tomography (4DCT),¹⁶ information of the anatomical changes over time can be obtained from multiple^{12, 13, 14} 3DCT data sets corresponding to different phases of the breathing cycle. Based on 4DCT information, Keall et al.¹⁵ proposed a 4D planning that matches the MLC-defined beam aperture to the beam’s eye view (BEV) of the planning target volume (PTV) at each respiratory phase. Because the beam aperture shapes generally differ from the BEV of the PTV in IMRT, this method is not readily applicable to IMRT of moving targets.

A key advantage of dynamic tracking over gating is in the delivery efficiency. However, dynamic tracking places additional physical requirements on the treatment plan. Because the MLC apertures must move with the target, a fundamental requirement for 4D delivery is that the aperture shapes between successive phases must be geometrically linked, such that all the MLC leaves can make the transition within the time frame of the two breathing phases. How this connectivity requirement can be satisfied also depends on the mode of delivery.

3D IMRT treatments can either be delivered dynamically with the so called sliding window technique or in an aperture by aperture fashion with the so called step-n-shoot technique. Both of these delivery modes have their counterparts in 4D treatment. If the sliding window technique is used, the aperture shape variation must serve both the purpose of intensity modulation and tumor tracking. The 4D plan can either be created by modifying a 3D IMRT plan developed on one phase¹⁷ or by considering all phases using the complete 4DCT data set in the optimization process.¹⁸ The counterpart of the step-n-shoot method in 4D is that each static aperture is converted into a dynamic sequence that tracks the target motion. Here, the aperture shape variation serves the sole purpose of tracking the movement of the target. It is therefore more straightforward to create such step-n-shoot 4D plan by starting from a 3D step-n-shoot IMRT plan optimized for one phase, and then adding motion consideration as separate steps. Each of these dynamic sequences is delivered separately by starting each sequence at a predetermined breathing phase. The beam is turned off after the delivery of each sequence. The 4D step-n-shoot planning and delivery method described above is the framework of this study.

An example of planning 4D step-n-shoot delivery was proposed by McQuaid et al.¹⁹ using a direct aperture optimization algorithm. They incorporated both target motion and MLC mechanical constraints into the optimization process, requiring massive computational power and specially designed software. A simpler 4D planning method was proposed by Suh et al.^{20, 32} in which rigid translation of the target was considered based on 4DCT; however, in their work, no nonlinear motion or deformation of the target was accounted for.

In this study, we develop a 4D IMRT planning technique using a direct aperture deformation (DAD) method²¹ that morphs the aperture shape and position from a reference phase to the other phases. This method is simple and feasible for current clinical setup and considers both the rigid and nonrigid organ motions; meanwhile MLC connectivity between adjacent phases is also ensured.

METHODS AND MATERIALS

4D planning method

4D IMRT planning aims at optimizing the dose distributions according to the time-dependent anatomical changes observed from 4DCT data sets. As categorized in Sec. 1, the strategy we are taking is to generate a deliverable 4D plan by starting with a step-n-shoot IMRT plan on one breathing phase. Each static segment of the 3D step-n-shoot IMRT plan is converted into a sequence of dynamically deliverable apertures, each corresponding to a different breathing phase. Therefore, the design of the new apertures for the respiratory phases other than the planned phase is the focus of this work.

The proposed 4D IMRT planning scheme consists of the following steps. First, an IMRT plan is optimized on a reference phase of 4DCT to produce MLC aperture∕segment shapes and weights for each beam angle. Then, based on the shape and position changes in the target from the reference phase to the successive phases, the MLC aperture is modified while keeping the same segment weights. These newly modified apertures, aimed at creating optimal dose distribution at every phase of the breathing cycle, forms a sequence of geometrically connected apertures that can be delivered dynamically. The length of, or the number of aperture shapes in, a sequence depends on the weight of the segment in the 3D plan for the reference phase. For apertures with large weights, the corresponding dynamic sequence can last several breathing cycles and the aperture variations cyclically repeats. For the original apertures with small weights, the dynamic sequence may last only part of a breathing cycle. As with delivering a 3D step-n-shoot plan, once the MUs assigned for a sequence are delivered, the beam will be turned off to allow the MLC to shape the first shape of the next sequence. However, unlike the delivery of 3D step-n-shoot plan, the beam will not be ready to turn back on until the patient’s breathing also reaches the phase corresponding to the first shape of the next dynamic sequence.

In creating new apertures from an aperture optimized on the reference phase, we consider both the target movements and deformations. Therefore, both the position and the shape of the apertures change from one phase to the next. In addition, to ensure that the sequence of apertures can be delivered dynamically, they must also be geometrically connected such that during the transition from one breathing phase to the next, the field aperture can physically change from one to the next. Using the 3D to 4D conversion scheme as described above, aperture connectivity is inherently guaranteed. This is because respiration-induced target motion is continuous with the peak-to-peak movement ranging from 1 to 3 cm in lung,²² and with the maximum target motion speed of about 1.5 cm∕s. To track target movement along leaf motion direction, these motion characteristics require the MLC leaf motion speed to be faster than 1.5 cm∕s, which is well within typical MLC speed limits of 2–2.5 cm∕s. For tracking target movements perpendicular to the direction of leaf motion, the movement of the backup jaws would be required. By using dynamic jaws in conjunction with MLC, it is possible to track target motion in any direction with carefully designed leaf sequences.

Different methods can be used for generating a sequence of apertures from an optimized aperture at the reference phase. One way is to only consider the rigid translation of the target by shifting the aperture position according to the translation of the centroid of the target.³² However, this scheme ignores the significant complexities^{23, 24, 25} of respiratory-induced target movement and may lead to suboptimal plan quality. In this study, we adopted a DAD method^{21, 26} that directly modifies the aperture positions and shapes according to the geometric variation in the target. This method considers both the translation and the deformation of the target while avoiding a lengthy optimization process.

To understand the DAD method, let us first consider the simplest case where the 3D plan for the reference phase is a conformal plan using one aperture per beam shaped as the BEV of the target. For a given beam angle, the aperture shape for another breathing phase would simply be the BEV of the target determined from the corresponding 3D CT images for that phase. Both translation and deformation of the target would be considered in such 4D conformal therapy plan. However, if an IMRT plan is generated for the reference phase, multiple apertures, each covering only a part of the BEV of the target, are necessary to achieve intensity modulation. To translate the aperture boundaries that fall within the boundary of target BEV, we must know the amount of motion not only on the boundary of the BEV but also on every point contained within the BEV. The segment aperture morphing (SAM) algorithm²¹ adopted in our study estimates the shifts in the points within the boundary of the target BEV by linearly interpolating between the boundary positions. Once the shifts within the boundary of the target BEV are estimated, all the apertures can be deformed to match the anatomical changes in the target projection in the BEV plane between the two successive breathing phases. This method mirrors how a 3D CRT plan is converted into a 4D CRT plan by changing the aperture shape and location according to the BEV of the target. The difference is that the movements of all points within the boundary of the BEV of the target are linearly interpolated. Such interpolated movements are used to determine the MLC positions if they fall within the boundary of the BEV of the target. Basically, by keeping the relative distance of the MLC to the BEV of the target the same for leaves within the boundary of BEV of the target and the absolute distance constant for the leaves outside the boundary of the BEV of the target, a one-to-one mapping is made. This method can account for both the rigid shift and deformation in the target without requiring any kind of registration or other complex calculation. A simple algebraic relationship is the only information needed for the implementation.

In the end, there is a complete 3D step-n-shoot plan for each phase. Doses for each phase can be separately computed on each of the 3D image set corresponding to a breathing phase using a conventional IMRT planning system and the dose-volume histograms (DVHs) can be analyzed.

Data acquisition and processing

The 4DCT data sets for one lung cancer patient and one pancreas cancer patient are acquired on a CT scanner in helical mode (Philips Medical Systems, Cleveland, OH) with a respiration monitoring device (RPM, Varian Medical Systems, Inc., Palo Alto, CA). The respiratory cycle is divided into ten discrete respiratory phases, where phase 0 is defined as the end of exhale and used as the reference data set. The gross tumor volumes (GTVs) are contoured by an experienced physician manually on the ten phases for each of the two clinical cases.

As noted by others,^{20, 31} it is uncommon to find tumors undergo both large translational movements and large deformation. The two clinical cases show both translation and deformation but neither is large. To better demonstrate the feasibility of our proposed scheme, a new case is simulated using a 4DCT data set of a lung patient whose tumor is located near the diaphragm. The tumor contoured by the physician is digitally replaced by a spherical “tumor” of 3 cm in diameter. A translational motion is applied to the tumor with a peak-to-peak distance of 1.5 cm in superior-inferior direction and 0.5 cm in anterior-posterior direction. In addition, the spherical tumor at the reference phase is considered as a stack of disks. These disks are moved horizontally relative to their reference phase locations according to cosine functions of amplitudes equal to 2∕5 of the disk’s distance from the edge and a period identical to that of patient breathing. As a result, the tumor experiences cyclic deformation with the disks at the top and bottom edge stationary and the central disk moving the largest distance. This digitally created tumor undergoes both large translation and deformation as shown in Fig. 1 and should serve as a stringent test of the proposed DAD scheme.

Figure 1.

The simulated tumor motion at ten phases (p0–p9) based on a 4D lung patient data.

The PTVs in each of the two clinical cases and the simulated case are obtained by adding 5 mm margin from the GTV to account for setup error, and no microextenstion or motion-induced margin are added. All treatment plans are created in PINNACLE³ treatment planning system (Philips Medical Systems, Madison, WI) using the p³IMRT module with the direct machine parameters optimization algorithms.²⁷

Three planning schemes used for comparison

For each data set, three planning schemes are evaluated. In the first scheme, plans are optimized for each phase independently. Theoretically, it should generate the best dose distribution because the plan for every phase is optimal. Note that such a scheme is computationally costly due to the need for multiple plan optimizations and the resultant 4D plan cannot be delivered because the apertures for successive phases are not connected geometrically. This “individual phase optimization” (IPO) scheme is used to create the “gold standard” for comparison purpose. In the second scheme, a plan is first optimized for the reference phase. The optimized apertures are then shifted from the reference phase to each of the successive phases based on the target centroids movement. This method only accounts for rigid translation and is denoted as the “SHIFT scheme.” In the third scheme, denoted as “DAD scheme,” the optimized apertures for the reference phase are deformed to the successive phases based on the deformation and translation of target contours using the SAM algorithm. Regardless of which scheme is used, each of the 4D plans consists of ten 3D IMRT plans, one for each phase.

All three schemes start with the same 3D IMRT plan optimized on the geometry of the reference phase. Therefore, for each scheme only the nine 3D IMRT plans corresponding to the remaining nine breathing phases are used for comparing the three schemes. The V_95% of the target (the target volume receiving at least 95% of prescription dose) and conformity index are estimated. The conformity index measures the extent of the overlap between the PTV and the volume contained within 100% isodose line. It is defined as the ratio of twice the intersection volume to the sum of the two volumes. It ranges from 0 to 1 with higher ratio indicating better conformity. For each patient, paired student t-test is used for the nine plans to evaluate the statistical difference between the three schemes. The dose to surrounding organs-at-risk (OARs) is measured and compared as well. DVHs for individual plans of the nine phases created with different schemes are also compared. Since the exact deformation is known in the simulated case, the dose distributions for the nine phases were deformed back to the reference phase and summed to generate the accumulated dose. DVHs of the accumulated dose distributions were compared for the three schemes.

It is important to note that the DAD scheme and the SHIFT scheme produce the same results when there is no deformation component in target motion. In other words, the SAM method used in our 4D planning is able to compensate for both complex and simple target motion. The difference between the results of these two schemes should increase with the amount of deformation. To quantify the amount of deformation, we performed rigid-body registration of the target volume at the reference phase to that of other phases by matching their centroids. The percentage volume overlap between the translated target volume from the reference phase and the contoured target volume for the subsequent phases were calculated. A lower overlapping percentage indicates a larger deformation component.

RESULTS

The lung case

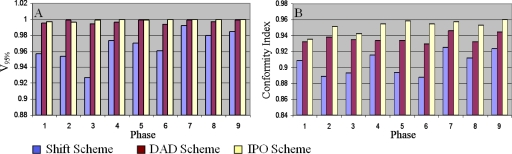
Figure 2a shows the comparison of the fraction of the PTV receiving at least 95% of the prescription dose (V_95%) using the three different planning schemes for the lung case. A larger V_95% indicates a better dose coverage of the PTV. Because all three schemes result in a treatment plan for every phase, the comparisons are made for all phases except the reference phase. Therefore, for each of the two clinical cases, nine sets of plans are compared to each set consisting three plans generated using the three planning schemes.

Figure 2.

Comparison of the V_95% (a) and conformity index (b) values for target between the three schemes for the lung case.

Figure 2b shows the comparison of the conformity indices calculated from the nine sets of plans. The conformity index measures how tight the high dose volume conforms to the PTV. A higher conformity index indicates a more conformal plan.

The phase-by-phase dosimetric comparison for each of the two clinical cases also allows us to perform a simple statistical analysis. Table 1 tabulates the mean and standard deviation of the V_95% and the conformity indices for the three planning schemes, as well as the p values of their intercomparisons.

Table 1.

The target dosimetric comparison and the p values between the three schemes for the lung case.

		V95%	Conformity index
Mean±STD	SHIFT scheme	0.967±0.020	0.905±0.015
	DAD scheme	0.997±0.002	0.936±0.006
	IPO scheme	0.999±0.001	0.952±0.080
p value	SHIFT vs IPO	p=0.0015	p<0.000 05
	DAD vs IPO	p=0.059	p=0.0002
	SHIFT vs DAD	p=0.0012	p=0.0001

From Fig. 2, we can see DAD target dose coverage and conformity are consistently improved over SHIFT throughout all nine phases. Table 1 shows statistical significance in the comparisons of V_95% and conformity index: DAD improves by ∼3% in both indices compared to SHIFT. When comparing the target coverage with IPO scheme, SHIFT shows lower V_95% and conformity index by around 3% (statistically significant); DAD shows similar V_95% and only ∼1% lower conformity index.

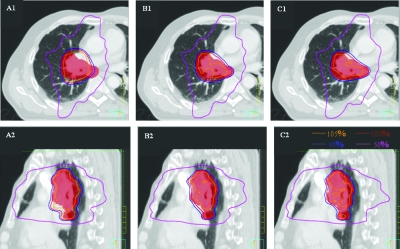
As an example, Fig. 3 shows the isodose distribution of the plan for phase 3 in the lung case. It clearly illustrates the difference in the dose coverage and conformity of target among the three schemes.

Figure 3.

Dose distributions of individual phase (phase 3 for lung case) plan showed the target (red colorwash) dose coverage and conformity between the SHIFT (A1, A2), DAD (B1, B2), and IPO (C1, C2) schemes for the lung case.

Table 2 tabulates the mean and standard deviation of the OARs for the lung case and the p value for the intercomparison. In comparison of DAD with SHIFT, two out of the four OARs receive higher doses in DAD; two receive lower doses in DAD. When comparing with IPO, neither SHIFT nor DAD has shown obvious tendency that one is superior to the other.

Table 2.

The OARs dosimetric∕volumetric comparison and the p values between the three schemes for the lung case.

Measurements		OARs
		Lung V20 (cc)	Cord D0.1 cc (Gy)	Esophagus V55 (cc)	Heart V40 (cc)
Mean±STD	SHIFT scheme	781.9±21.5	34.7±1.8	0.35±0.1	1.01±0.04
	DAD scheme	773.5±10.1	34.4±2.7	0.57±0.4	0.97±0.05
	IPO scheme	739.0±13.0	35.3±2.8	0.43±0.3	0.97±0.04
p value	SHIFT vs IPO	p<0.000 05	p=0.5574	p=0.3286	p=0.0189
	DAD vs IPO	p=0.0008	p=0.1168	p=0.0016	p=0.9264
	SHIFT vs DAD	p=0.362	p=0.7198	p=0.0642	p=0.0103

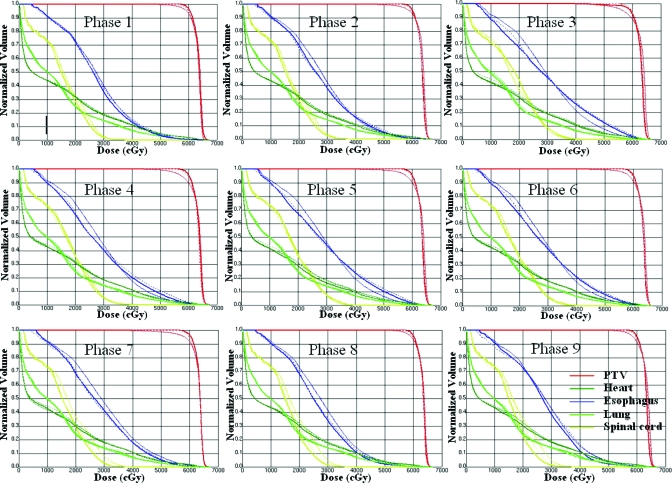
Figure 4 compares the DVHs resulting from the three schemes for all nine phases. For the PTV, DVHs of the DAD scheme are always close to IPO, while the DVHs of the SHIFT scheme tend to separate from the other two. Relatively higher doses in esophagus were observed in IPO and DAD compared to the SHIFT scheme.

Figure 4.

The DVHs of the nine individual plans for the SHIFT (thin solid), DAD (dashed), and IPO schemes (medium solid) for the lung case.

The pancreas case

Figure 5 compares the V_95% and conformity indices resulting from the three different planning schemes for the pancreas case for the nine breathing phases other than the reference phase. The mean and standard deviation of the V_95% and the conformity indices for the three planning schemes, and the p values of their intercomparisons are shown in Table 3.

Figure 5.

Comparison of the V_95% (a) and conformity index (b) values for target between the three schemes for the pancreas case.

Table 3.

The target dosimetric comparison and the p values between the three schemes for the pancreas case.

		V95%	Conformity index
Mean±STD	SHIFT scheme	0.967±0.013	0.895±0.015
	DAD scheme	0.995±0.018	0.938±0.006
	IPO scheme	0.996±0.006	0.954±0.007
p value	SHIFT vs IPO	p<0.000 05	p<0.000 05
	DAD vs IPO	p=0.72	p<0.000 05
	SHIFT vs DAD	p=0.0001	p<0.000 05

Similar to the lung case, DAD improves target dose coverage and conformity over SHIFT throughout the nine phases in the pancreas case. Statistical significance is reached in the comparisons of V_95% and conformity indices: DAD improves by ∼3% in both indices compared to SHIFT. When comparing the target coverage with IPO scheme, SHIFT shows lower V_95% and conformity index by around 3% (statistically significant); DAD shows similar V_95% and only ∼1% lower conformity index.

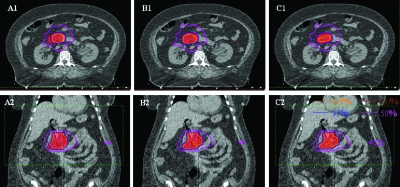
Figure 6 shows the isodose distributions resulting from the three schemes for phase 3. The differences in target coverage among the three schemes can be clearly observed.

Figure 6.

Dose distributions of individual phase (phase 3 for pancreas case) plan showed the target (red colorwash) dose coverage and conformity between the SHIFT (A1, A2), DAD (B1, B2), and IPO (C1, C2) schemes for the pancreas case.

Table 4 tabulates the mean and standard deviation for the OARs, as well as the p values for the intercomparisons among the three schemes. When comparing DAD with SHIFT, three out of the five OARs receive higher doses in DAD; two receive lower doses in DAD. IPO shows higher dose or volume measurements than the other two schemes.

Table 4.

The OARs dosimetric∕volumetric comparison and the p values between the three schemes for the pancreas case.

Measurements		OARs
		Left kidney D50% (Gy)	Right kidney D50% (Gy)	Liver D50% (Gy)	Bowel V35 (cc)	Cord D0.1 cc (Gy)
Mean±STD	SHIFT scheme	3.48±0.19	6.93±0.11	0.39±0.02	15.3±1.3	19.02±0.89
	DAD scheme	3.62±0.38	6.79±0.41	0.40±0.03	20.1±5.7	18.28±0.29
	IPO scheme	4.43±0.59	7.11±0.45	0.41±0.02	20.6±4.8	19.21±1.01
p value	SHIFT vs IPO	p=0.0015	p=0.2631	p=0.0087	p=0.0077	p=0.3953
	DAD vs IPO	p=0.008	p=0.1885	p=0.091	p=0.3561	p=0.0086
	SHIFT vs DAD	p=0.286	p=0.2594	p=0.5929	p=0.0318	p=0.0118

DVH comparisons among the three schemes for all the nine phases are shown in Fig. 7. DAD scheme resulted in very similar DVHs to IPO scheme in terms of both target coverage and OAR sparing. In contrast, obviously inferior target coverage is observed for the SHIFT scheme.

Figure 7.

The DVHs of the nine individual plans for the SHIFT (thin solid), DAD (dashed), and IPO schemes (medium solid) for the pancreas case.

The simulated case

Because the transformation vectors from phase to phase is known for the simulated case, it is possible to compute the cumulative dose distributions on the reference phase. Therefore, besides the individual phase comparison, cumulative doses are also compared.

V_95% and conformity indices for the simulated case resulting from the three different planning schemes are compared in Table 5. DAD target dose coverage and conformity indices are improved over SHIFT when comparing all nine individual phases. DAD scheme improves by ∼3% in V_95% (statistically significant) and ∼2% in conformity index over SHIFT scheme. When comparing the target coverage with IPO scheme, SHIFT shows lower V_95% and conformity index by ∼3% (statistically significant), while DAD shows similar V_95% and only ∼1% lower conformity index.

Table 5.

The target and OAR dosimetric comparison and the p values between the three schemes for simulated lung case.

		V95%	Conformity index	Lung V20 (cc)	Liver D50% (Gy)	Cord D0.1 cc (Gy)
Mean±STD	SHIFT scheme	0.967±0.020	0.878±0.018	539.4±34.4	1.91±0.46	8.48±0.20
	DAD scheme	0.995±0.002	0.898±0.012	519.3±27.6	1.44±0.36	8.21±0.22
	IPO scheme	0.996±0.006	0.907±0.008	557.2±39.2	1.89±41.6	8.70±0.56
p value	SHIFT vs IPO	p=0.0011	p=0.0055	p=0.3197	p=0.9387	p=0.2760
	DAD vs IPO	p=0.5488	p=0.0801	p=0.0306	p=0.0241	p=0.0274
	SHIFT vs DAD	p=0.0010	p=0.007	p=0.1913	p=0.0269	p=0.0167

Comparisons for OARs are also tabulated in Table 5. All three OARs receive lower radiation in DAD compared to SHIFT and IPO. Two out of the three OARs receive a higher dose in IPO, and the other one receives a lower dose compared to SHIFT.

Figure 8 shows the comparison of the cumulative DVH calculated on the CT images of the reference phase. Similar results to the phase-by-phase comparison are observed as expected for the three schemes. Specifically, DAD shows similar target dose coverage compared to IPO, while the SHIFT scheme resulted in 3% lower V_95% as compared to the other two schemes. Differences are negligible among the three schemes for OAR sparing.

Figure 8.

The DVHs of the 4D accumulated plans for the SHIFT (thin solid), DAD (dashed), and IPO schemes (medium solid) for the simulated lung case.

DISCUSSION

4D IMRT planning aims to optimize dose coverage of the target while sparing healthy tissues in the presence of respiratory-induced internal organ motion. Suh et al.^{20, 32} proposed to shift the aperture position based on the translation of the target centroids, without considering the complexity of respiration related target motion, such as deformation. In our study, we employed a direct aperture deformation algorithm called SAM that can account for both rigid translational motion and nonrigid motion, resulting in better 4D plans.

The plans created with DAD scheme demonstrated statistically significant improvement in both target coverage and dose conformity as compared to the SHIFT scheme for the two clinical cases tested. The same conclusion also applies to the simulated case, in which a large translational motion and a large deformation are present. This difference can be explained by Table 6, where the percentage overlap between the target volumes obtained by shifting the target from the reference phase to the other phases in the SHIFT scheme and that contoured by the physician for the respective phases are compared. The volume overlap ranges from 87% to 93%, indicating the presence of target shape differences. As shown in several previous studies, significant intrafractional tumor deformation exists in lung,^{2, 3} liver,⁴ and pancreatic tumors,^{5, 6} indicating that deformation needs to be accounted for in 4D planning.

Table 6.

The percentage overlap between the target volumes obtained by shifting the target from the reference phase to the other phases in the SHIFT scheme and that contoured by the physician for the respective phases.

	Percentage volume overlap (%)
Phase	Lung	Pancreas	Simulated lung
1	92.2	89.5	91.9
2	90.0	87.6	83.7
3	88.0	87.6	73.2
4	88.3	90.3	68.9
5	88.1	86.9	62.4
6	90.2	87.7	68.9
7	89.7	93.0	73.2
8	91.0	89.5	83.7
9	91.2	92.1	91.9

For all three cases, the DAD scheme produces very similar target coverage to that of the IPO scheme. This seems to indicate that a plan optimized for the reference phase and geometrically “transformed” to another phase is almost as good as a plan optimized for that phase. The difference between the DAD scheme and the SHIFT scheme in their ability to match the quality of the IPO scheme lies in their ability to compensate for the deformation of the tumor.

Due to the limited number of cases tested, this conclusion should not be generalized for all cases subject to respiratory-induced motion. Nevertheless, the present work illustrates the feasibility that the simple aperture deformation scheme can produce 4D treatment plans that approaches the optimal 4D plan, such as those generated by the IPO scheme, in plan quality.

As for the OAR sparing, these three schemes did not show obvious tendency that one is superior to the other for the three cases. This is because OAR is not considered in either the DAD or the SHIFT scheme, and the aperture shape and position changes are solely dependent on that of the target. This is also a potential limit for both the DAD and the SHIFT schemes. In addition, although some dose differences are observed for some OARs, both the absolute doses and the volume differences are very minor and all the values are within the clinical tolerances.

In this study, contouring accuracy for the two clinical cases is limited by the soft-tissue contrast of the CT imaging technique, and inevitably by human errors. Therefore, there is likely an overestimation or underestimation of the deformation in the 4D contours in both cases. However, the accuracy of contour definition should not affect the validity of the main conclusions of this study due to the fact that the same set of contours were used for all three schemes. Even if the contours are completely artificial, the results of the comparisons among the three schemes would still be valid. The fact that the same conclusion is reached using the simulated case, in which there is no contouring error, is another indication that the contouring errors play a negligible role in the analyses.

Ideally, one should use the deformation field to sum the doses from individual phases to a reference phase for evaluation. In the study, the deformation field is only available for the simulated case. For the two clinical cases, the DAD method did not need the deformation fields and they were not generated. The final doses are evaluated only on individual phases and not on the 4D accumulative dose. Another reason for not generating the deformation field is the lack of tissue contrast in the region. We have tested a few deformable image registration routines and none of them can generate a reasonable deformation field for matching different hand-drawn 4D contours, which also contain uncertainties as we mentioned.

Since all the planning is based on 4DCT data sets, the quality of the 4DCT images directly determines the 4D plan quality.²⁰ Artifacts, as a main issue of 4DCT imaging, can cause systematic errors in target delineation and dose calculation. Various studies are ongoing to improve the 4DCT image quality for achieving more accurate plan results.^{29, 30}

Generally, the 4D plans can be optimized either by independently optimizing each of the phases or by considering all the phases simultaneously.²⁸ Theoretically, optimizing each phase independently prohibits mutual compensation among the phases and thus limits the freedom of the optimizer. As a result, this approach theoretically may not produce the optimal solutions. In reality, however, the planning geometry among the phases are largely identical; if the plans for all individual phases are optimal, the end result should not be much different from the optimization scheme that considers all phases simultaneously. Many practical factors, such as the ease of planning, the requirement of computational capacity, and the ease of delivery, should also be considered. Optimizing 4D plans by simultaneously considering all phases aims to solve an optimization problem with at least ten times more (ten phases of 4DCT) variables as input, including aperture weights and MLC leaf positions for all the beam angles. The amount of computation time as a function of the number of variables drastically increases with the number of the variables. Meanwhile, deformable dose summation during the optimization process will also place large demand on computational resources. Significant simplifications are often required to reduce the complexity and computational burden.¹⁴ Moreover, MLC speed limit would be another major concern during the optimization process. With these limitations, the final 4D plan quality may be compromised, and with greater variations in plan quality among phases. These effects, in turn, make the delivery more complex and could cause unexpected errors. In contrast, individually considering each phase is much simpler and no significant change is required in existing planning systems for 4D planning. Attributed to the continuity of the tumor motion-induced by breathing, the MLC speed is normally guaranteed to be within the mechanical limit if 4D plans are created based on the optimal 3D plan for the reference phase. Furthermore, the same dose rate can be achieved by keeping the weights of the corresponding aperture the same throughout all the phases, further simplifying delivery. Due to the relative independent planning of each phase, this method can also be considered in real-time planning by modifying the individual plan accordingly when a real-time imaging modality is available.

CONCLUSIONS

The proposed DAD scheme for 4D IMRT planning of dynamic tumor tracking is a practical and simple approach to accounts for both rigid and nonrigid target motion. Improved target coverage and conformity are observed using this scheme compared to the one that only compensates for rigid motion. It provides similar plan quality as compared to the individual phase optimization scheme, which creates an optimal solution specific for the geometry of each phase. According to the fact that the target motion is continuous, this DAD method also guarantees the continuity of MLC sequence between apertures of successive phases. The DAD scheme is easy to implement and no image registration or other complex computation is required. It could be performed with minor additions under current clinical planning environment.