Health Status and Health Dynamics in an Empirical Model of Expected Longevity

Abstract

Expected longevity is an important factor influencing older individuals’ decisions such as consumption, savings, purchase of life insurance and annuities, claiming of Social Security benefits, and labor supply. It has also been shown to be a good predictor of actual longevity, which in turn is highly correlated with health status. A relatively new literature on health investments under uncertainty, which builds upon the seminal work by Grossman (1972), has directly linked longevity with characteristics, behaviors, and decisions by utility maximizing agents. Our empirical model can be understood within that theoretical framework as estimating a production function of longevity. Using longitudinal data from the Health and Retirement Study, we directly incorporate health dynamics in explaining the variation in expected longevities, and compare two alternative measures of health dynamics: the self-reported health change, and the computed health change based on self-reports of health status. In 38% of the reports in our sample, computed health changes are inconsistent with the direct report on health changes over time. And another 15% of the sample can suffer from information losses if computed changes are used to assess changes in actual health. These potentially serious problems raise doubts regarding the use and interpretation of the computed health changes and even the lagged measures of self-reported health as controls for health dynamics in a variety of empirical settings. Our empirical results, controlling for both subjective and objective measures of health status and unobserved heterogeneity in reporting, suggest that self-reported health changes are a preferred measure of health dynamics.

1 Introduction and Motivation

Expected longevity is an important factor influencing older individuals’ decisions such as consumption, savings, purchase of life insurance and annuities, claiming of Social Security benefits, and labor supply. It has also been shown to be a good predictor of actual longevity, which in turn is highly correlated with health.¹ Since the seminal work of Grossman (1972), longevity has usually been introduced in human capital models of health as endogenously determined through the characterization of death as the event that occurs when the stock of health falls below a certain threshold. Grossman’s original presentation of longevity as an endogenous choice, within his celebrated health production model, was problematic, as he acknowledges (and amends) in Grossman (1998) and Grossman (2000). The role of longevity as an endogenously determined process in models under certainty has been more properly characterized and discussed in Ehrlich and Chuma (1990) and Ried (1998). In particular, Ehrlich and Chuma (1990) show that in order to correctly solve the original model it is necessary to characterize a demand function for longevity (along with the demand for health and the demand for consumption goods), which clarifies the mechanisms that link health investment with the optimal choice of life span.

A particularly important, but much less discussed set of extensions to that original research on health investments, has introduced uncertainty in multiperiod models that allow for the dual role of health as an input to the production of future health, and as a source of current utility. Most of that research, however, does not provide new insights into the endogenously determined longevity process.² Ehrlich (2000) and Ehrlich and Yin (2005), in contrast, directly tackle the role of longevity within a model of health investments under uncertainty. In their model, mortality probabilities depend not only on natural and biological factors as well as other initial conditions, but also on health investments as self-protection (using the insights from Ehrlich and Becker (1972)). Self-protection is described as a function of time allocated to these investments, health expenditures, and efficiency indicators like education.³

The estimation of the determinants of longevity expectations we present in this paper could therefore be understood within the general framework of health investments under uncertainty, where our main estimated equation is in fact a reduced form characterization of the survival probability equation presented in Ehrlich (2000). It is therefore akin to a production function of longevity. The Health and Retirement Study (HRS) asks individuals to assess the chances of surviving to a certain age. Since the latter is of course conditional on being alive, we will consider this probability to be what Ehrlich (2000) presents as the expected probability of survival.

Given that expected longevity is therefore naturally a function of health, it is key to decide how health is to be measured. Empirical researchers have used a variety of self-reported indicators, both subjective and objective, as proxies for health status, such as self-rated health, incidence of chronic diseases, Activities of Daily Living (ADLs), Instrumental Activities of Daily Living (IADLs), and measures of health limitation. Self-rated health has been found to play a significant role in explaining individuals’ mortality by many researchers.⁴ Idler and Benyamini (1997) present a review on 27 studies, and conclude that self-rated health is an independent predictor of mortality, even controlling for objective measures of health. They propose a variety of interpretations to this result, one of which states that “self-rated health is a dynamic evaluation, judging trajectory and not only current level of health.”

But does self-rated health—while controlling for other objective health measures—capture all the important information regarding health that could help understand longevity expectations? We argue that a measure of health dynamics should be of value in understanding how individuals are assessing future states of the world.⁵ This is especially true given that the dynamic component of health can come from a variety of sources which are likely linked with any assessment of how long a person is likely to live. First, individuals invest in their health through, for example, visits to health professionals for preventive care, changes in their diets, exercise, and changes in habits such as smoking or drinking. It is natural to believe that the outcomes of these investments on a person’s health status are uncertain, and in many cases these health investment decisions are the result of previous diagnoses of particular conditions. Second, health depreciates in a fairly continuous fashion through the natural aging process and through the worsening of chronic conditions. Third, health can deteriorate (or improve) significantly in rather discontinuous (and non-monotonic) ways as health shocks occur. The effects on a person’s health of the last two types of events are also uncertain and can depend on their interaction with the first type of investments, as well as on attitudes towards treatment and recovery, and towards life in general.

No single measure is likely to capture all these components. Therefore, the absence of a “gold standard” to assess the validity (longitudinal criterion validity, in the sense of ability to capture meaningful health changes) of measures of health changes, justifies a discussion of the advantages and disadvantages of different measures, and their assessment in the empirical arena. We argue below that using differences in self-reported health status can be problematic since they can fail to capture meaningful health changes among respondents. We also emphasize that its use in panel studies can exacerbate the biases intrinsic to measuring any continuous latent variable, due to cut-point shifts (the cut-points between health categories might not be fixed over time for a given individual, or they might even be areas dividing health categories) and reference groups effects (individuals might report their health as compared with people their age). Notice that the same criticisms would apply to the use of lagged health measures. Therefore, we advocate for the use of a direct health change measure which is less exposed to biases, and avoids loss of information connected with the discretization of a continuous latent variable.

In this paper, we find that self-reported health changes are a cleaner measure of health dynamics than computed measures using differences in health status, or lagged measures of health status. Furthermore, we find that the effect of our preferred measure of health changes on longevity expectations has the same order of magnitude as that of the self-reported health level. These results suggest that self-reported health changes should be used, when available, in empirical and behavioral models as an important complement to standard measures of health, in order to capture the dynamics of health, and to consistently estimate the effects of self-reported health status. The insights from this study are likely to influence the empirical characterizations in a large number of studies regarding, for example, health care expenditures, consumption over the life cycle, and retirement behavior, in which the variables of interest are likely to be affected by the dynamic evolution of health.

The rest of the paper is organized as follows: Section 2 describes and critically analyzes measures of health status and health changes from both a conceptual as well as an empirical perspective. Section 3 presents the data used in our econometric estimations. In Section 4, we discuss the empirical methods used in this study. Section 5 presents the results of our panel analysis of longevity expectations formation, and Section 6 concludes.

2 Measuring Health and Health Dynamics

Self-reported measures of health are pervasively used in empirical work to capture the role of health on individual behavior and expectations formation. However, in recent years a large number of researchers have questioned the validity of these measures. In general, the concept of validity of a health measure is taken to mean whether the measure accurately reflects health status, and therefore can be considered as a useful indicator in empirical and behavioral economic models. The discussion in the economic literature regarding validity of self-reported health measures is mainly focused on its cross-sectional validity, even if authors were using panel and time-series data of the variables of interest. Researchers have been concerned with the use of these variables because of the possible econometric problems that using these measures could introduce.⁶

The economic literature has paid relatively little attention to the issue of how to measure health changes, or how to analyze whether this type of variables belong in our models. Even if it is widely recognized that health is a dynamic concept, in most cases researchers have focused on measuring the stock of health. In the cases where researchers have tried to measure health dynamics, they have either limited themselves to including lagged values of the self-reports in their specifications, or did not discuss the consequences of using different measures to capture health dynamics.

In other disciplines, however, measuring health changes is at least as important as measuring the level of health. This is mainly because in those fields they are concerned with measuring the consequences of some type of intervention that can affect a person’s health. For example, a literature in the medical and medical care fields, which has especially focused on studies of quality of life indicators, argues that the ability to detect changes (which is a characteristic defined as responsiveness or sensitivity to change) is an intrinsic part of the general validity of any self-reported measure of health. Therefore, researchers should not evaluate the validity of a measure without paying attention to its ability to detect changes.⁷ Terwee et al. (2003) emphasize a very important distinction regarding the link between validity and responsiveness. They argue that many researchers have failed to distinguish between cross-sectional validity and longitudinal validity of the measures they use, with only the latter concept being linked to responsiveness.

The absence of a widely accepted measure of health dynamics motivates a discussion of the weaknesses and strengths of some of the measures available to the empirical researchers. We present this discussion below, and section 3 provides the empirical background for the discussion. The ultimate assessment of the measures is presented in the empirical results section, where we estimate a production function of longevity through the analysis of longevity expectations.

2.1 Dynamic Health Status: heterogeneous reporting and information loss

To understand how changes in self-reported health can be linked to changes in other measures of health is an essential part of an analysis on the validity of self-reported health. Furthermore, we need to understand whether reported changes in health are measures of health trajectories, and whether these trajectories can influence how individuals report their longevity expectations and other useful and important variables. Notice that using the diagnose of diseases seems like a reasonable strategy too, however, the onset of the disease is usually not observed. Therefore, if we do not observe a particular diagnose, it does not necessarily mean an individual is free from that ailment. Moreover, in a given period, individuals who have experienced the diagnosis of a disease could be in an even better health status than those who have not been diagnosed, because the latter could actually have already experienced the onset of the disease but do not know it and therefore are not treating it.

Although true health status is in principle a continuous (latent) variable, it is discretized in a particular way when asked to individuals. Hence, we give below two general arguments against the idea that health status (and its lags) alone should be used in empirical models that try to control for the dynamics of health. First, self-reports of health status may be affected by unobserved heterogeneity. Second, using its changes over time to proxy for health dynamics could lead to information loss.

Heterogeneity in reporting health status across individuals and over-time: cut-point shifts, gray areas, and peer-effects

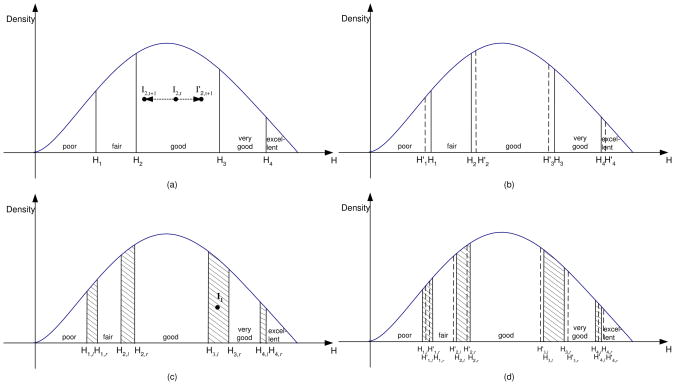
Forcing individuals to discretize their reported health status can result in different self-reported health levels for individuals with the same latent health status, due to the lack of clear cut differences between the ad-hoc health categories proposed to the respondents. This can also result in a situation where even if an individual’s real health does not change over time, her(his) self-rated health might change. Figure 1, panels (a) to (d), illustrates these situations. Panel (a) in the upper left-hand corner, represents individuals who are able to make clear distinctions between those five health categories (bins) when reporting their health status. There is no reason to believe that the cut-points would be the same for everyone and overtime, but for the moment, and for this type of individual, we assume that they would be the same for a given individual over time. Most empirical studies implicitly assume that individuals are of this type.⁸

Figure 1.

Heterogeneous Health Reports

Panel (b), exemplifies the case in which even though individuals can clearly distinguish different health categories, the cut-points might be shifting over time for a given individual. This might be caused by changing perceptions of what particular health levels mean, due to changes in a reference group, or even changes in their own understanding of their health.

In summary, individuals in panel (a) and panel (b) would have little difficulty to differentiate their health between two consecutive categories, but in panel (b) the reports might change even if actual health does not change. In contrast, individuals in panel (c) and (d) would find it rather difficult to decide what their health is if their health falls within one of the shaded regions. Moreover, the difficulties increase with the thickness of those areas.

Panel (c), represents individuals who do not have clear cut distinctions between each two consecutive health categories. Instead, these respondents have what we call gray areas, like the one represented by the distance between H_3,l to H_3,r. The idea is that if their health status falls within these areas, individuals cannot clearly categorize it, and their actual reports could be a function of the context, and hence seem arbitrary to the econometrician.⁹ Furthermore, there is no reason to believe that these gray areas would be the same for everyone. In fact, individuals could be heterogeneous in terms of the width of these areas.

Finally, panel (d) depicts the case in which the gray areas might be changing over time for a given individual, partly due to the same reasons as in the shifts in panel (b): changes in the reference groups or informational changes with respect to their own health. This case can be understood as combining both time-invariant and time-variant unobserved heterogeneity in reporting. As long as the shifts are partially correlated with observables, and not too large, an estimator that captures time-invariant unobserved heterogeneity might be subject to relatively small biases.

A number of researchers have suggested the existence of cut-points shifts in assessing self-reported health. However, these authors have only discussed it in the context of differences across individuals in a given population, or differences in individuals’ responses across countries, but not in the context of responses by the same individual over time, and they have not discussed the gray areas that we describe above. The possible existence of these gray areas is key, since it allows us to reformulate the econometric problem as arising from unobserved heterogeneity.¹⁰

If we assume the gray areas are stable over-time, an estimation strategy that can account for time-invariant unobserved heterogeneity, can be successful in consistently estimating the effects of health changes. We acknowledge that there could still be cut-point shifts of different magnitudes, or gray area changes over time for a given person. The latter would be difficult to account for within any estimation strategy.

Besides heterogeneity, peer effects can be another explanation for these apparently inconsistent reports, and for the thickness of these gray areas. Self-reported health status is likely to be the result of an introspection that requires individuals to compare themselves either with a reference group or with themselves at previous points in time. In the former case it is plausible that when reporting health status individuals are making a comparison with people of a similar age who they interact with or know about. This means that someone might report that they are in good health, while what they really mean is that they are in good health in comparison with their particular reference group. In the following period, depending on the evolution of their health with respect to the reference group, they might report their health as being in a better or worse category than before, even if there has been no change in their actual health, or even if their true health has evolved in the opposite direction. If these peer effects are present, it will be especially problematic to use changes in self-reported health status as measures of change.

In contrast, self-reported health changes were asked to individuals by giving them a clear reference point.¹¹ Respondents were asked: “Compared with your health when we talked with you in the previous wave (interview month-year), would you say that your health is better now, about the same, or worse?” In this case, measurement errors and possible biases due to inconsistent replies of self-reported health status over time, are likely to be lower. The wording of the question forces individuals to provide a comparison with their own health at a different point in time, which mitigates the peer effects described above. It also avoids the issue of cut-point shifts, since the assessment of the health change is not category-specific. Intuitively, however, we acknowledge that this variable might be exposed to measurement error problems of its own, given the likelihood of respondents having recall problems. These recall problems are essentially equivalent to a situation in which people use different points in time as reference when faced with this question. This is not a big problem as long as the measure actually captures the direction of health changes and its effects on contemporaneous reports of other variables and decisions.¹²

It will be critical in our estimations to account for this unobserved heterogeneity, and possibly also for the likely event that the unobserved components are correlated with the very reports of health and health changes.

Information loss

Even if individuals do not change the standards they use to evaluate their health, we may still lose information if we restrict attention to differences of health status to measure health dynamics. This could also be explained by the example shown in panel (a) in Figure 1. Assume individual I₂ has real health I_2,t in period t, his health in period t+1 could be either I_2,t+1 or $I_{2,t+1}^{\prime }$. Although his self-rated health is good in both periods, unless we use a different measure of health changes from the computed one, we would have thrown away information regarding his health change. It is difficult to assess how large this information loss could be, given that the range of each of the self-reported health bins can vary widely in the population. But it is easy to argue that it is something empirical researchers should worry about. In fact, researchers in the medical field have described this type of information loss when analyzing how to assess change in health among severely ill patients, which they call floor phenomenon.¹³ Baker et al. (1997), elaborating on this phenomenon, show that this loss of information can vary in size depending on the level of baseline health, with larger losses of information among people reporting worse health status. The self-reported measures in the HRS will naturally suffer from similar problems. Furthermore, since it can also happen in every possible health category, we can be facing a very important source of information loss, which might depend on how wide these categories are for given individuals, and the persistence of these health states among HRS respondents.

3 The Data: Descriptive Analysis

The Health and Retirement Study is a nationally representative longitudinal survey of 7,700 households as of the first wave of interviews, headed by an individual aged 51 to 61 as of 1992–93. It is a survey conducted by the Survey Research Center (SRC) at the University of Michigan and funded by the National Institute on Aging.¹⁴ In the empirical work we use the first six waves of the HRS, and construct a set of consistent variables on different sources of income, financial and non-financial wealth, health, and socio-demographic characteristics which will be assigned to each decision maker appropriately. The HRS collects information on both subjective and objective health measures on health status, such as self-rated health, chronic diseases, Activities of Daily Living (ADLs), and Instrumental Activities of Daily Living (IADLs).

3.1 Variables of Interest

The two main dependent variables in our empirical models are questions about individuals’ subjective survival probability of living up to a certain age. First, “(What is the percent chance) that you will live to be 75 or more?” was asked to those who are not older than 65. Second, “(What is the percent chance) that you will live to be 85 or more?” was asked to whoever is not older than age 75.¹⁵ Responses to these two questions are taken as measures of individuals’ expected longevity.¹⁶ \

Regarding health variables, self-rated health is a categorical variable, which in our empirical work we divide into five binary indicators, representing poor health, fair health, good health, very good health, and excellent health.¹⁷ We also use chronic disease indicators with information on seven conditions; namely, high blood pressure, diabetes, cancer, lung disease, heart disease, stroke, and arthritis. We have further generated four ADL-IADL indexes following the suggestions in Wallace and Herzog (1995) and only including questions asked consistently across waves: mobility, use of large muscles, other ADLs, and IADLs. Each of these indexes takes the value 1 if the individual has difficulties in doing all that type of activities, and 0 if he has no difficulty performing any of them. For example, the ADL-Mobility includes six different activities, such as running a mile, walking one block, walking multiple blocks, walk across the room, climb multiple flights of stairs, and climb one flight of stairs. Each of these activities contributes 1/6 to the index.¹⁸

Functional limitation is measured as a binary indicator for whether the individual has any health problems which limit his ability to work. We also construct an indicator for psychological problems, an indicator of self-reported memory ability, and an indicator of self-reported changes in memory ability.

The two main health change variables we have generated are, first, the direct health change measure, which is individuals’ self-reports of their health changes compared to last interview. It is 2 if the individual reported his health is much better, 1 if the individual reported his health is a little better, 0 if his health stays the same, and −2 and −1 if his health has worsened considerably or just a little, respectively. Second, the computed health flow measure is an indicator of whether individuals’ health gets much better (a value of 2), a little better (1) same (0), much worse (−2), or little worse (−1), based on the computed difference between the reports on his contemporaneous health and lagged health. In the empirical work we construct binary indicators for belonging to each of these categories.¹⁹

In order to include them in our model of changes in the probabilities of living to certain ages, additional measures of health changes between each two consecutive waves have also been incorporated in the study. We include indicators for newly diagnosed chronic conditions, and variables measuring the changes in the ADL-IADL indexes. Binary indicators of new occurrence of working limitation in between waves, as well as changes in health insurance coverage have been constructed. Living habits such as smoking and drinking, and their changes between two consecutive waves have been measured as binary indicators.²⁰

We have also included in our analysis information on individuals’ demographic characteristics, such as measures of age, gender, marital status, race and education. Education is measured by the number of years the individual received formal education. Marital status takes the value one if the individual is married, and 0 otherwise. Additionally, parents’, siblings’ and kids’ information has been collected in the HRS, which allows us to generate a series of variables that are likely to capture a number of possibly unobserved features correlated with expected longevity. Binary indicators for whether the individuals’ mothers (fathers) lived up to age 75 and age 85 are constructed. Parents’ education have been measured by the years of formal education they received. These six measures are mainly used to capture genetic effects on expected longevities, as suggested by the theoretical framework in Ehrlich (2000). We also use a measure on number of living siblings from the supplement data provided by RAND which is constructed based on the HRS. Moreover, we construct an indicator for whether respondents have children living within 10 miles. The number of grandchildren is used in our analysis as well.

Finally, variables on economic status and labor supply are constructed. Household net wealth has been adjusted to dollars of 1992, includes savings and checking accounts, bonds, stocks, real estates, business owned, IRAs, trust, housing, and other assets net of debts. Individual income is taken from the RAND data.

3.2 Health Dynamics

In the Health and Retirement Study, we are able to measure health changes in three different ways: self-reported health changes, computed health changes of self-rated health status, and new diagnose of diseases. There are reasons, as discussed in Section 2, to believe that self-reported health changes could be the best measure among the three.

Table 1 presents the relationship between the computed health changes and the direct reports on health changes. Individuals in the diagonal (in the oblique ellipse) are respondents with consistent reports, since their computed health changes are in line with their self-reported health changes. Given that both measures of health changes are categorical, in order to assess their level of correlation we use the suggestions in Cohen (1960) and Fleiss (1981), and estimate the kappa-statistic, which accounts for the fact that when comparing categorical variables a sizable proportion of the agreement can be observed just by chance. Our estimate of kappa is very low, around 0.08, suggesting only a slight agreement between the measures beyond what could be expected by chance. This clearly provides another motivation for the further analysis of these measures.

Table 1.

Computed health changes and self-reported health changes

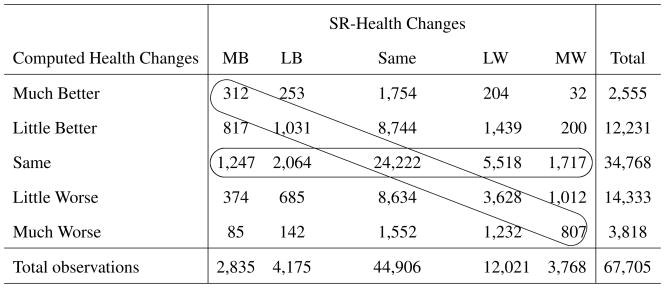Those individuals whose computed health changes are zeros (in the horizontal ellipse), that is, their self-rated health status falls into the same category as in the previous period, but are off the diagonal, represent cases where the computed health changes could lead to a loss of information, due to the fact that the health change might not be large enough to warrant a category jump. Notice that these observations comprise a bit more than 15% of our sample, which should raise a flag of caution for researchers who rely solely on self-reported health status and its lags without exploiting the self-reported changes.

Those with inconsistent reports, but not due to loss of information, are the individuals in the left bottom cells and right top cells, who are not in the two ellipses. These respondents account for 38.63% of the sample. As discussed in the last section, possible explanations of these inconsistencies include the presence of gray areas, cut-point shifts, and also the peer effects. However, it is not possible for us to assess the relative weight of these mechanisms in explaining the inconsistencies. But notice, that in line with Eriksson et al. (2001), the group reporting to be in better health is considerably larger if we use the computed health changes than if we use the self-reported health changes. This suggests the possible overestimation of health changes when using a measure more open to inter-personal comparisons. In any case, given that it is debatable which measure is better without controlling for additional characteristics, we should be very careful in interpreting the effects of computed health changes in any empirical model that tries to properly control for health status and health dynamics, in the presence of these inconsistencies.

Table 2, using our full sample from all six waves of the data, shows that self-reported health changes seem to have more information than the computed changes, since the average values of a longevity expectations, and a variety of subjective and objective measures of health status vary considerably more when the self-reported measure changes. Notice that for all the measures, the difference between reporting better (or much better) and worse (or much worse) health is much larger for the self-reported measure, meaning that the effect a particular health trajectory is more explicit for this measure than for the computed measure. These tabulations give us some initial evidence on the likely effects of these two variables in the conditional moments estimations we present in Section 5.²¹

Table 2.

Informational Content of Computed and Self-Reported Health Changes

	Pliv75		Pliv85		ADL Mobility		ADL Muscles		Doctor Visits
Health Changes	Mean	Sd.	Mean	Sd.	Mean	Sd.	Mean	Sd.	Mean	Sd.
MB Comp. Health	0.666	0.296	0.484	0.340	0.221	0.283	0.060	0.184	9.07	28.26
LB Comp. Health	0.659	0.285	0.478	0.319	0.210	0.266	0.044	0.149	8.29	13.65
LW Comp. Health	0.644	0.289	0.451	0.318	0.240	0.286	0.058	0.174	9.48	15.85
MW Comp. Health	0.616	0.315	0.429	0.335	0.303	0.321	0.097	0.235	13.19	26.42
MB Rept. Health	0.720	0.270	0.560	0.318	0.155	0.224	0.028	0.117	9.58	14.67
LB Rept. Health	0.676	0.277	0.487	0.313	0.203	0.256	0.042	0.146	10.31	21.79
LW Rept. Health	0.557	0.317	0.375	0.318	0.383	0.317	0.108	0.227	13.76	19.06
MW Rept. Health	0.408	0.352	0.270	0.321	0.621	0.327	0.306	0.354	24.04	37.47

3.3 Sample and sample restrictions

Given the skip pattern of the longevity expectations variables we only include in our sample age eligible respondents who were asked the questions about their survival probabilities, and were 65 years old or younger in order to have a consistent set of responses to the longevity expectations questions. Furthermore, those with missing information on their parents’ mortality have been excluded from our sample, since these variables play an important role in our empirical analysis. We believe it is important to account for these genetically related health measures in our empirical work. Additionally, individuals who died between our sample period (from 1992 to 2003) have automatically dropped from our sample after they died.

As a result, the sample used in the estimations includes more than 24,000 observations from more than 9,000 individuals. Summary statistics for the full sample are presented in Table 3. 37% of the sample are male, and 86% are whites. The sample is 58 years old on average, with 12.75 years of education. 82% are married.

Table 3.

Summary Statistics

Variable	Full Sample Mean (Sd.)	Reported Pliv Mean (Sd.)	Did not report Pliv Mean (Sd.)
Observations	24,555	23,717	842
Probability of Living to 75	0.663(0.279)	0.663 (0.279)	—
Probability of Living to 85	0.464 (0.310)	0.464 (0.310)	—
Excellent Health	0.186 (0.389)	0.189 (0.392)	0.099 (0.298)
Very good Health	0.339 (0.473)	0.343 (0.475)	0.207 (0.405)
Fair Health	0.135 (0.341)	0.131 (0.337)	0.238 (0.426)
Poor Health	0.054 (0.225)	0.051 (0.219)	0.137 (0.344)
SR. Health Much Better	0.046 (0.210)	0.046 (0.211)	0.046 (0.210)
SR. Health Little Better	0.071 (0.258)	0.072 (0.258)	0.059 (0.236)
SR. Health Little Worse	0.144 (0.351)	0.142 (0.349)	0.181 (0.385)
SR. Health Much Worse	0.031 (0.174)	0.030 (0.171)	0.068 (0.251)
Comp. Health Much Better	0.030 (0.171)	0.030 (0.170)	0.034 (0.182)
Comp. Health Little Better	0.174 (0.379)	0.174 (0.379)	0.163 (0.369)
Comp. Health Little Worse	0.208 (0.406)	0.209 (0.407)	0.182 (0.386)
Comp. Health Much Worse	0.047 (0.212)	0.046 (0.209)	0.087 (0.282)
High Blood Pressure	0.413 (0.492)	0.410 (0.492)	0.494 (0.500)
Diabetes	0.121 (0.327)	0.119 (0.324)	0.195 (0.396)
Cancer	0.076 (0.265)	0.076 (0.265)	0.082 (0.274)
Lung Disease	0.081 (0.273)	0.081 (0.272)	0.089 (0.285)
Heart Disease	0.139 (0.346)	0.138 (0.345)	0.157 (0.364)
Stroke	0.033 (0.179)	0.032 (0.177)	0.052 (0.223)
Arthritis	0.485 (0.500)	0.483 (0.500)	0.561 (0.497)
ADL-Mobility	0.172 (0.233)	0.170 (0.231)	0.216 (0.275)
ADL-Muscles	0.176 (0.265)	0.173 (0.263)	0.256 (0.313)
ADL-Other	0.022 (0.101)	0.021 (0.099)	0.049 (0.146)
IADL	0.031 (0.089)	0.030 (0.087)	0.066 (0.136)
Smoking	0.200 (0.400)	0.201 (0.401)	0.181 (0.385)
Drinking	0.546 (0.498)	0.554 (0.497)	0.335 (0.472)
No Health Insurance	0.181 (0.385)	0.179 (0.383)	0.233 (0.423)
Health Limitation	0.223 (0.416)	0.220 (0.414)	0.298 (0.458)
Doctor Visits	8.025 (14.357)	7.981 (14.327	9.260 (15.132
Hospital Stays	0.405 (2.304)	0.397 (2.225)	0.624 (3.920)
SR. Memory Ability	3.221 (0.944)	3.234 (0.940)	2.863 (0.988)
Age	58.014 (5.020)	57.981 (5.035)	58.935 (4.478)
Male	0.365 (0.482)	0.367 (0.482)	0.306 (0.461)
White	0.860 (0.347)	0.867 (0.339)	0.654 (0.476)
Married	0.822 (0.383)	0.825 (0.380)	0.733 (0.443)
Years of Education	12.749 (2.833)	12.826 (2.760)	10.595 (3.842)
Net Wealth ($100,000)	3.500 (12.739)	3.454 (11.628)	4.797 (30.400)
Total Income ($10,000)	2.106 (2.804)	2.130 (2.784)	1.427 (3.235)
Indicator of Father Living to 75	0.456 (0.498)	0.455 (0.498)	0.482 (0.500)
Indicator of Mother Living to 75	0.599 (0.490)	0.601 (0.490)	0.565 (0.496)
Mother’s years Education	9.761 (3.472)	9.837 (3.421)	7.620 (4.133)
Father’s years Education	9.422 (3.826)	9.491 (3.790)	7.481 (4.297)
Indicator of Kids Living Close	0.522 (0.500)	0.521 (0.500)	0.545 (0.498)
Number of Grandkids	3.512 (4.493)	3.464 (4.437)	4.876 (5.698)

There are reasons to suspect that sample selectivity might be an issue in this study, given that we are only able to observe individuals’ subjective survival probabilities for those who answered the questions. In the sample, we do observe people who are age eligible to answer these two probability questions did not give any answer. More than 90% reported these two subjective survival probabilities as of the first wave of interviews, but depending on the wave the reporting rate has gone down between 5 and 8 percentages points since then, although is less of an issue in our sub-sample of individuals 65 or younger. Table 3 also presents summary statistics after dividing the sample between individuals who reported expected longevity and those who did not, for comparison. We observe that respondents with better health status (both better self-rated health, and less chronic diseases, or less functional limitations), with more education, and those who are white, are more likely to report. Also parents’ education have a positive correlation with the likelihood of reporting. Males and those with health insurance coverage are more likely to report too; Finally, richer respondents are less likely to report their expected longevities.

4 Econometric Specifications

Our objective is to obtain consistent estimates of the effects of a variety of regressors on individual longevity expectations that are measured by the self-reported probabilities of living to age 75. As discussed in the introduction, our empirical model can be understood as estimating a production function of longevity, since it is better characterized as a reduced form (in the sense, for example, of Malinvaud (1966)) of the survival probabilities of a model of health investments under uncertainty with endogenous longevity, following the formulation in Ehrlich (2000) and Ehrlich and Yin (2005). Those authors provide us with the economic justification for the host of variables we include in our econometric specifications, where all of them should be understood as belonging to one of the following three groups: variables proxying for natural and biological initial conditions; variables linked to the decisions made up to the period in which the longevity expectation is observed or the depreciation of health over time, that modify the original initial conditions; and variables related to the self-protection activities expected to have an effect on future longevity.

To reach this goal, a couple of econometric issues need to be tackled. First, we want to take into account the unobserved heterogeneity potentially present in our characterization of the econometric model, which we suspect might have a lot to do with the way individuals report their health. Without controlling for the unobserved components, we will be confounding partial and total effects of our variables of interest. The panel data set we use allows us to model explicitly how those unobserved components enter the econometric specification. Second, we need to consider the possible presence of sample selection biases, since a non-trivial proportion of eligible individuals did not answer the longevity questions. It is reasonable to believe that respondents who answered the questions might not be a random sample from the population of interest, since those who are more likely to expect to live longer would also be more likely to respond. We can perform this correction with the techniques suggested by Heckman (1979) and Hsiao (1986). As we discuss in the next section, we find no evidence of selection bias in the models we estimate in this paper.

The HRS provides us with repeated observations of the same individuals, and this allows us to control for potential unobserved components that could enter our econometric model. Our main equation of interest can be written as

$$\mathit{Pliv}{75}_{it}={\alpha }_1+X_{it}^{\prime }\beta +Z_{it}^{\prime }\gamma +H_{it}^{\prime }\lambda +{\mu }_i+{\nu }_{it},$$ (1)

where Pliv75_i represents the measure of expected longevity reported by individuals in the sample, and on the right hand side we include, first, the set of individual characteristics X_i consists of various socio-demographic, and family related variables which could be linked with the initial conditions that determine the biological and natural longevity of individuals. Second, the set of variables included in Z_i capture the effects of the previous decisions and stochastic events occurred up to the time of the report of the longevity probability (including depreciation of health) that modify the original initial conditions. These include the chronic conditions indicators, the indexes of ADLs, the health limitation indicator, the insurance indicators, net wealth, income, and education, as well as the current health status. Third, H_i is a vector of variables linked to the self-protection activities that modify the natural factors, and the effects of the previous decisions on longevity. These include measures of health changes, health care utilization, and health habits. Notice that μ_I represents the unobserved heterogeneity component, and the ν_it are the idiosyncratic disturbances. In this longevity estimation the econometrician cannot observe either the idiosyncratic component or the individual component, while the individual does know his individual specific term. In the results we also present OLS estimates with the pooled sample of observations controlling for clustering (see Deaton (1997)), assuming there is no individual component.

The panel data model can be estimated either assuming no correlation between observed explanatory variables and the unobserved individual effect (random effects), or allowing for arbitrary correlation between the unobserved individual effect and the observed explanatory variables (fixed effects). We can then test whether the random effects specification or the fixed effect specification is more appropriate, and whether the former is more appropriate than the pooled OLS regression. In our case, even though we are also interested in estimating the effects of a number of time invariant regressors, the possibility of allowing for correlation between the unobserved component and the regressors makes the fixed effect the most appropriate estimator. This decision will be supported by the specification tests.²²

The econometric specifications we have described so far only exploit the fact that individuals responded repeatedly to the same longevity expectations questions, but have not directly focused on why these reports might change from period to period. We further perform an additional econometric analysis to directly explain how these reports have changed over time. Given the interpretation of the previous model as an estimation of survival probabilities within a model of health investment under uncertainty, the underlying hypothesis is that the relationship should be fairly stable and therefore the observed changes should not be easily explained by variables which could be predicted with some accuracy by individuals. We then estimate a model of changes in longevity expectations as a function of changes in a variety of exogenous regressors, including changes in the health variables of interest. We can think of this alternative model as trying to capture the source of the innovations to the self-reported longevity expectations. We follow Benítez-Silva and Dwyer (2005) to set up the appropriate econometric model in order to capture the role of new information. One conclusion from that work is that individuals integrate new and old information with weights attached to each of these sources when updating their expectations.

Assuming the linearity of the function that individuals use to process information regarding the variables of interest, and further assuming that the elements of the information set (Ω) used to formulate the expectations are jointly normally distributed, we can then write

$$\mathit{Pliv}{75}_{t+1,i}=\mathit{Pliv}{75}_{t,i}+\gamma ({\omega }_{t+1}-E[{\omega }_{t+1}\mid {\mathrm{\Omega }}_t]),$$ (2)

where the term in parenthesis is the difference between the observed new information (ω_t+1 will be represented in our empirical estimation by the changes in the exogenous characteristics) and the expectation of this information individuals had in the previous period. If we had all these elements, it would be possible to estimate (2) by a conditional moments estimator like OLS, and would expect a coefficient of one in front of the longevity expectations as of time t under the rational expectations hypothesis. The coefficients in γ (which we will assume are time invariant) could be interpreted as the effect of the unanticipated components of new information on changes in expectations. However, we do not observe the second element in the brackets. Although it could be estimated by making further assumptions about the relationship between new and current information, it is likely to be a very noisy procedure. Instead, we estimate the following equation

$$\mathit{Pliv}{75}_{t+1,i}=\alpha +\beta \mathit{Pliv}{75}_{t,i}+\gamma {\omega }_{t+1,i}+{\epsilon }_{t+1,i},$$ (3)

where there is no reason to believe that β should be equal to 1: since the unobserved expectation term from (2) would enter into the error term, leading to possible biases in the coefficients of interest. We will treat these possible biases as a problem of measurement error, which can be ameliorated by using IV techniques. The estimates of the vector γ, are interpreted as the effects of changes in specific factors of Ω on longevity expectations formation. A nonzero coefficient of a given change in a member of the information set can be interpreted as information not perfectly anticipated, and therefore not embedded in the individuals’ longevity expectations as of period the previous period.

It is also very common in a variety of literatures to use a formulation that implicitly assumes rational expectations, and proceeds by subtracting the self-reports of a given year from the self-reports of the following year. We will see that our own results from estimating (3) cannot reject the utilization of the specification shown below, at least on statistical grounds. The changes in expected survival probabilities between periods can be formulated as:

$$\mathrm{\Delta }\mathit{Pliv}75=\alpha +\mathrm{\Delta }{H}_i{\beta }_1+\mathrm{\Delta }{X}_i{\beta }_2+\mathrm{\Delta }{Z}_i{\beta }_3+{\epsilon }_i,$$ (4)

where ΔH_i represents health changes between two particular periods, and ΔX_i and ΔZ_i are controls for time varying individual characteristics.

5 Empirical Results

5.1 Estimations of Expected Longevity

In Table 4 and Table 5 we provide the results of estimating expected longevity probability models, using both cross-sectional and panel data. In all cases all the key health status and health changes variables, and most of the other regressors in the estimation are significant and have the intuitive signs. The results across specifications vary quantitatively, but they all tell essentially the same story in qualitative terms.²³ Our main result is that both health status and health changes significantly affect self-reported expected longevity, and most strikingly, which measure of health changes is used matters a great deal.

Table 4.

Estimation of Pliv75²⁹

Variable30	Pooled OLS Coef. (S.E.)	Random Eff. Coef. (S.E.)	Fixed Eff. Coef (S.E.)
Excellent Health	0.206 (0.008)	0.155 (0.008)	0.044 (0.012)
Very Good Health	0.145 (0.007)	0.110 (0.007)	0.036 (0.009)
Good Health	0.087 (0.006)	0.063 (0.006)	0.020 (0.007)
SR. Health Change-Same	−0.029 (0.005)	−0.021 (0.005)	−0.016 (0.005)
SR. Health Change-Little Worse	−0.046 (0.007)	−0.034 (0.006)	−0.025 (0.007)
SR. Health Change-Much Worse	−0.104 (0.012)	−0.084 (0.011)	−0.063 (0.012)
Comp. Health Change-Same	0.023 (0.004)	0.017 (0.004)	0.0001 (0.005)
Comp. Health Change-Little Worse	0.054 (0.006)	0.037 (0.005)	−0.002 (0.006)
Comp. Health Change-Much Worse	0.102 (0.009)	0.072 (0.008)	0.008 (0.010)
High Blood Pressure	−0.002 (0.004)	−0.004 (0.004)	0.004 (0.007)
Diabetes	−0.029 (0.005)	−0.026 (0.006)	−0.008 (0.011)
Cancer	−0.034 (0.006)	−0.036 (0.007)	−0.036 (0.012)
Lung Disease	−0.033 (0.006)	−0.034 (0.007)	−0.012 (0.012)
Heart Disease	−0.031 (0.005)	−0.032 (0.006)	−0.024 (0.009)
Stroke	−0.016 (0.010)	−0.026 (0.011)	−0.040 (0.018)
Arthritis	0.009 (0.004)	0.003 (0.004)	0.001 (0.007)
ADL-Mobility	−0.054 (0.010)	−0.057 (0.010)	−0.050 (0.012)
ADL-Muscles	0.012 (0.010)	−0.006 (0.009)	−0.010 (0.011)
ADL-Other	−0.091 (0.020)	−0.069 (0.018)	−0.054 (0.022)
IADL	−0.060 (0.021)	−0.043 (0.020)	0.004 (0.024)
Smoking	−0.039 (0.004)	−0.033 (0.005)	0.001 (0.009)
Drinking	0.014 (0.003)	0.010 (0.004)	0.001 (0.006)
No Health Insurance	−0.007 (0.004)	−0.011 (0.004)	−0.012 (0.005)
Health Limitation	−0.003 (0.005)	−0.010 (0.005)	−0.010 (0.006)
Doctor Visits	0.0001 (0.0001)	−0.0001 (0.0001)	−0.0003 (0.0001)
Hospital Stays	−0.002 (0.001)	−0.002 (0.001)	−0.002 (0.001)
SR. Memory Ability	0.022 (0.002)	0.014 (0.002)	0.004 (0.002)
Years of Education	0.003 (0.001)	0.005 (0.001)	—
Net Wealth ($100,000)	0.0002 (0.0001)	−0.0001 (0.0001)	−0.0002 (0.0002)
Total Income ($10,000)	−0.001 (0.001)	−0.0004 (0.001)	−0.0003 (0.001)
Indicator of Dad Living to 75	0.045 (0.003)	0.040 (0.004)	−0.002 (0.019)
Indicator of Mom Living to 75	0.046 (0.003)	0.039 (0.005)	0.007 (0.013)
Years of Mother’s Education	0.004 (0.001)	0.004 (0.001)	—
Years of Father’s Education	0.000 (0.001)	0.001 (0.001)	—
Kids Living Close	−0.010 (0.003)	−0.003 (0.004)	0.007 (0.005)
Number of Grandkids	0.002 (0.000)	0.001 (0.000)	0.001 (0.001)
Observations	24,052	24,052	24,052
R2	0.182	0.181	0.054
Predicted Pliv75	0.661	0.661	0.662

²⁹Breusch-Pagan Test: χ² = 4267.2, p-value: 0.000; Hausman Test: χ² = 328.89, p-value: 0.000.

³⁰We also include a constant, age, age-squared, number of siblings, and indicators of gender, race, marital status, psychological problems, and interview wave.

Table 5.

Sensitivity Analysis of Pliv75 estimation using Fixed-Effect Model

Variable31	Coef. (S.E.)	Coef (S.E.)	Coef (S.E.)	Coef. (S.E.)	Coef (S.E.)
Excellent Health	0.051 (0.009)	0.049 (0.012)	0.042 (0.009)	0.054 (0.009)	0.044 (0.009)
Very Good Health	0.042 (0.007)	0.041 (0.009)	0.034 (0.008)	0.044 (0.007)	0.035 (0.008)
Good Health	0.026 (0.006)	0.025 (0.007)	0.020 (0.007)	0.027 (0.007)	0.020 (0.007)
Excellent Lagged Health	—	—	—	0.014 (0.008)	0.017 (0.008)
Very Good Lagged Health	—	—	—	0.009 (0.007)	0.012 (0.007)
Good Lagged Health	—	—	—	0.007 (0.007)	0.009 (0.007)
Comp. Health Change-Same	—	−0.001 (0.005)	—	—	—
Comp. Health Change-Little Worse	—	−0.004 (0.006)	—	—	—
Comp. Health Change-Much Worse	—	0.002 (0.010)	—	—	—
SR. Health Change-Same	—	—	−0.016 (0.005)	—	−0.017 (0.005)
SR. Health Change-Little Worse	—	—	−0.025 (0.007)	—	−0.026 (0.007)
SR. Health Change-Much Worse	—	—	−0.058 (0.012)	—	−0.063 (0.012)
Cancer	−0.040 (0.012)	−0.038 (0.012)	−0.038 (0.012)	−0.037 (0.012)	−0.034 (0.012)
Heart Disease	−0.024 (0.009)	−0.023 (0.009)	−0.024 (0.009)	−0.022 (0.009)	−0.023 (0.009)
Stroke	−0.039 (0.018)	−0.038 (0.018)	−0.041 (0.018)	−0.037 (0.018)	−0.039 (0.018)
ADL-Mobility	−0.052 (0.012)	−0.055 (0.012)	−0.048 (0.012)	−0.054 (0.012)	−0.049 (0.012)
ADL-Muscles	−0.012 (0.011)	−0.013 (0.011)	−0.010 (0.011)	−0.012 (0.011)	−0.010 (0.011)
ADL-Other	−0.062 (0.022)	−0.063 (0.022)	−0.054 (0.022)	−0.063 (0.022)	−0.054 (0.022)
No Health Insurance	−0.012 (0.005)	−0.012 (0.005)	−0.012 (0.005)	−0.012 (0.005)	−0.012 (0.005)
Hospital Stays	−0.002 (0.001)	−0.002 (0.001)	−0.002 (0.001)	−0.002 (0.001)	−0.002 (0.001)
SR. Memory Ability	0.005 (0.002)	0.005 (0.002)	0.005 (0.002)	0.004 (0.002)	0.004 (0.002)
Indicator of Dad Living to 75	0.000 (0.019)	−0.001 (0.019)	0.000 (0.019)	−0.001 (0.019)	−0.001 (0.019)
Indicator of Mom Living to 75	0.007 (0.013)	0.007 (0.013)	0.007 (0.013)	0.007 (0.013)	0.007 (0.013)
Indicator of Kids Living Close	0.007 (0.005)	0.007 (0.005)	0.007 (0.005)	0.007 (0.005)	0.007 (0.005)
Number of Grandkids	0.001 (0.001)	0.001 (0.001)	0.001 (0.001)	0.001 (0.001)	0.001 (0.001)
Observations	24,169	24,059	24,156	24,059	24,052
R2	0.050	0.052	0.049	0.063	0.064
Predicted Pliv75	0.662	0.662	0.662	0.662	0.662

³¹We also include a constant, age, age-squared, number of siblings, wealth, income, index of IADL, doctor visits, and indicators of marital status, psychological problems, health limitation, smoking, drinking, high blood pressure, diabetes, arthritis, lung disease, and interview wave.

Table 4 presents the results of three different econometric specifications of the longevity expectation in equation (1). The preferred econometric model is the Fixed Effect specification.²⁴ The presence of an individual specific unobserved heterogeneity component is supported by the standard econometric tests, and further tests show that it is not appropriate to assume that this unobserved heterogeneity is uncorrelated with the variables of interest.²⁵

The Fixed Effect estimator captures the type of heterogeneity we have been describing in relation to reporting. Fixed Effect estimates are unbiased under the assumption that each individual has a particular pattern regarding the areas in which they distinguish the health categories, even if the reporting of health might be varying over time due to the gray areas problem, The Fixed Effect estimator is able to account for time-invariant unobserved heterogeneity, but it cannot remove any remaining time-variant biases created by omitted variables.

From Table 4, it is clear that self-reported health changes are cleaner measures of health dynamics, compared with the computed health change which uses the differences in self-reported health status. Self-reported health change indicators for being in little worse or much worse health than in the previous period have a negative sign in the estimations, indicating their intuitive correlation with a decrease in the probabilities of living to age 75. This is true even after controlling for indicators of excellent, very good, and good self-reported health status. Where the latter are positively correlated with the probabilities of living to those ages. Interestingly, the magnitude, in absolute value, of the effects of the self-reported health change indicators is very similar to that of the effects of the self-reported health level indicators, while that of the effects of the computed health change indicators on the probability of living to age 75 is much smaller.

Rather surprisingly for us at first, the computed health change indicator for being in much worse health has a very small positive (and in our preferred specification, insignificant) effect on the self-reported longevity measures. There could be a number of possible interpretations for this result. But all of them suggest caution to researchers in the use of self-reported health measures in longitudinal studies, and especially the use of computed self-reported health changes as proxies for health changes. In line with our discussion in section 2, we believe that the computed health changes are very likely to be exposed to considerably more problems of unobserved heterogeneity in reporting. This is because of the fact that many individuals might have a difficult time in distinguishing between the imposed cut-points for the health levels in a consistent way over the period of analysis, leading to wide gray areas (in the terminology we have introduced). This version of the cut-point shifts problem that is described in some detail in the literature on cross-country comparisons of health, comes from the fact that there is nothing in the questionnaire suggesting to individuals that they should use the same assessment as they did in the previous interviews, or even use the same cut-points between health levels. The more pervasive this problem is, the more likely that computed health changes could capture the importance of the gray-areas problem (or the problem of shifting cut-points) that we presented in Figure 1. If that is the case, once we control for health levels, computed changes in health are more likely to be an expression of the difficulty to pinpoint their own health level. This is true even after controlling for education and other socio-demographic measures. In most cases its effects disappear once we account for unobserved heterogeneity that allows for correlation between the individual effect and the regressors of interest. These cut-points shifts or movements of the gray areas seem to be correlated with events we are not quite able to control for, and therefore could proxy for unobserved factors correlated with higher life expectancy.

A companion interpretation is linked to the peer effects discussed in section 2. If many individuals report their health using a reference group as a comparison basis, then changes in health status might be more of an expression of the evolution of health compared with that reference group and less of an expression of their own health. And the latter is the one that we believe is more likely to be correlated with expected longevity. If computed deterioration in self-reported health is more likely to capture a worse than your peers measure of health, there is no reason to expect them to have a significant negative correlation with expected longevity, which is more likely to be mainly driven by actual health, regardless of interpersonal comparisons. In fact, it is easy to believe that in general, the information flow from your peers, among people this age, is more likely to be related to bad news about health events of people you know or your peers know. If individuals mostly receive bad news about other people’s health, and still think they are doing worse on a health measure open to interpersonal comparisons, it might be they are overestimating their health problems.

The insignificant and sometimes positive effects of the computed health deterioration indicators, contrast with the more intuitive, negative and significant effect of the self-reported health deterioration variables. Remember that the latter is the result of a question that gives individuals a reference point by asking them to compare their current health to their own health two years prior. Even though we might expect recall errors on these responses, the formulation of the question is likely to result in individuals performing an intra-personal comparison when reporting their health change. Whether they take the exact health level two years ago (a level not given to them by the interviewer) as a reference point, or if they respond with respect to some other point in a more recent past, is not essential to our arguments. The fact is that this report is consistent with their answers regarding expected longevity in a completely different section of the survey.

Overall, the results do indicate that self-reported health levels have the intuitive positive correlation with the self-reported expected longevity in a cross-sectional sense. However, the problems arise when using differences in health status over time as measures of health changes. Although we believe the differences in health reports over time do provide some information to researchers, they are more likely a proxy for unobserved heterogeneity in reporting than in assessments of health changes. Therefore, it is less problematic to use the self-reported health changes as measures of health dynamics to avoid the problems with the computed measure.

Notice that the use of the Fixed Effect estimator in Table 4, and also Table 5, has two main effects on our results. First, it decreases considerably the effect of self-reported health status indicators. For example in Table 4, the magnitude of the coefficients indicating excellent, very good, and good health, is reduced to about a third in the fixed effect specification compared with the random effects model. Namely, being in excellent health instead of increasing the average expected probability by about 30%, as estimated in the OLS specification, or almost 23% as in the Random Effect specification, it increases the longevity probability by only 6.6% in the Fixed Effect model. This means that not accounting for unobserved heterogeneity, which correlates with the exogenous variables of interest, can lead to serious biases and misleading inference. Second, the coefficients on the computed health change indicators are sharply reduced as we move from the OLS specification to the Fixed Effect estimator. Even if the coefficients are not very precisely estimated, they are very close to zero, and become almost the smallest coefficients in the table. In contrast, the Fixed Effect estimator does not affect as much the coefficients of the self-reported health change indicators. The latter coefficients are slightly reduced, in absolute value, and very precisely estimated. The results predict that the much worse self-reported health change indicator decreases the average expected probability of living to age 75 by almost 10%, while reporting being in little worse health than in the previous wave decreases the average expected probability of living to age 75 by around 4%.

Notice that the estimates of the other variables have the expected signs, and are in line with the previous literature estimating both expected and actual longevity. For example, having most chronic diseases or higher index of ADLs decreases the expected longevity probabilities, and the same is true for those who were hospitalized more often. Furthermore, those in better cognitive health (measured here by memory ability) expect to live longer, and the same is true for those with kids living close to them, or those with more grandkids.

We have also estimated all these specifications accounting for possible sample selection biases, due to lack of response to the longevity questions. The presence of sample selection bias is not supported, and none of the coefficients vary in any significant way. Therefore we have chosen to omit those results here but they are available from the authors upon request.²⁶

Table 5 provides some sensitivity analysis of different specifications, using subsets of the health indicators.²⁷ We only provide the results of our preferred Fixed Effect specification. We can see that the effects of self-reported health status indicators are very stable, and significantly increase the average expected probability of living to age 75 more or less by the same magnitude as reported in Table 4. The effects of the self-reported health changes are also stable and of similar magnitude. The last two columns are especially interesting since they estimate a model with lagged health status, which follows a fairly standard literature that uses this kind of specification to account for the dynamics of health. Notice that especially when we include the little worse or much worse self-reported health change indicators, the lagged health indicator of being in excellent health is estimated to have a significant but very small effect on expected longevity. The effects are about three times smaller than the effects of the current health status indicators. More importantly, they are much smaller in absolute value than the effects of the self-reported health change indicators. The conclusion from this is twofold. Although lagged health indicators can have a significant but small effect on expected longevity, they fail to capture the dynamic effect of health picked up by the self-reported health change indicators. The coefficients on the latter indicators are basically unaffected by the inclusion of the lagged health indicators.²⁸

5.2 Changes in Expected Longevity

Table 6 presents the estimates of the model from equation (3) trying to capture the effect of new information on the changes in expected longevities. Following some of the recommendations of Benítez-Silva and Dwyer (2005) we use an Instrumental Variables procedure, without assuming rational expectations, in which variables with a significant effect would capture what has not been anticipated by individuals.²⁹ Therefore, it is not surprising to see in the table that some of the computed health change indicators are significant in this context, since they can capture innovations either regarding the comparisons between the evolution of the person’s health with that of their peers, or regarding cut-point shifts, which are more likely to come as a “surprise” than the information on their own health. The computed health changes do play a significant role in this specification, which confirms the argument that although it is clearly a problematic measure to use to proxy for health dynamics, it indicates that the self-reported health status is longitudinally valid, since it captures unanticipated changes, even in a conditional moments estimation.

Table 6.

Estimation of Changes in Pliv75

Variable32	IV Coef. (S.E.)	IV Coef. (S.E.)	IV Coef. (S.E.)	RE Coef. (S.E.)
Pliv75 in Previous Wave	0.972(0.093)	0.970(0.099)	0.964(0.097)	—
Comp. Health-Same	−0.021(0.006)	—	−0.007(0.007)	−0.003(0.007)
Comp. Health-Little Worse	−0.036(0.008)	—	−0.020(0.012)	−0.014(0.009)
Comp. Health-Much Worse	−0.055(0.016)	—	−0.055(0.025)	−0.066(0.016)
SR. Health-Same	—	−0.009(0.007)	−0.020(0.006)	−0.018(0.006)
SR. Health-Little Worse	—	−0.027(0.012)	−0.033(0.009)	−0.033(0.007)
SR. Health-Much Worse	—	−0.063(0.025)	−0.047(0.017)	−0.056(0.012)
Newly Diagnosed High Blood Pressure	0.020(0.010)	0.019(0.011)	0.021(0.010)	0.017(0.011)
Newly Diagnosed Diabetes	0.020(0.020)	0.026(0.019)	0.025(0.019)	0.032(0.016)
Newly Diagnosed Cancer	−0.024(0.021)	−0.028(0.020)	−0.024(0.020)	−0.014(0.020)
Newly Diagnosed Lung Disease	−0.008(0.024)	−0.007(0.024)	−0.004(0.024)	−0.015(0.020)
Newly Diagnosed Heart Disease	−0.018(0.017)	−0.015(0.017)	−0.015(0.017)	0.002(0.015)
Newly Diagnosed Stroke	−0.062(0.040)	−0.054(0.039)	−0.054(0.039)	−0.027(0.029)
Newly Diagnosed Arthritis	−0.002(0.010)	−0.002(0.010)	−0.001(0.010)	0.003(0.009)
Change in ADL-Mobility	−0.038(0.015)	−0.038(0.016)	−0.033(0.016)	−0.022(0.013)
Change in ADL-Muscles	−0.013(0.014)	−0.015(0.014)	−0.012(0.014)	−0.006(0.012)
Change in ADL-Other	−0.113(0.036)	−0.111(0.037)	−0.107(0.036)	−0.071(0.025)
Started to Smoke	0.0001(0.021)	−0.0001(0.021)	0.0004(0.021)	0.006(0.018)
Started to Drink	0.002(0.010)	0.002(0.011)	0.002(0.010)	−0.0004(0.010)
Change in Doctor Visits	−0.0003(0.0002)	−0.0003(0.0002)	−0.0003(0.0002)	−0.0003(0.0002)
Change in Days Hospitalized	−0.002(0.001)	−0.002(0.001)	−0.002(0.001)	−0.001(0.001)
New Widowhood	0.020(0.021)	0.021(0.021)	0.019(0.021)	0.005(0.017)
Newly Father’s Death	0.011(0.013)	0.010(0.013)	0.011(0.013)	0.007(0.014)
Newly Mother’s Death	0.001(0.011)	0.001(0.011)	0.002(0.011)	−0.003(0.011)
Changes in Num of Grandkids	0.002(0.001)	0.002(0.001)	0.002(0.001)	0.002(0.001)
Observations	12,245	12,242	12,232	13,822
Test of Weak Instruments	Reject, p=0.000	Reject, p=0.000	Reject, p=0.000	—
Test of Over-Id. Restrictions	Cannot Rej. p=0.286	Cannot Rej. p=0.276	Cannot Rej. p=0.262	—

³²We also include a constant, years of education, changes in wealth, income, siblings alive, and memory ability, and indicators of race, gender, loss of health insurance, kids moving close, onset of psychological problems, and onset of a health limitation.

Notice that not too many variables are significant in this specification, in fact in the preferred specifications in columns 3 and 4, the only consistently significant variables are the self-reported health change indicators, the change in the index of ADL-Mobility, the new diagnosed of high blood pressure and diabetes (which actually have a positive effect on the changes of Pliv75, probably indicating illnesses finally being treated and therefore more likely under control than before), and the change in the number of grandchildren. In line with the findings by Benítez-Silva and Dwyer (2005) on a very different context, the results seem to be consistent with the Rational Expectations Hypothesis.³⁰

However, as those authors emphasize, this specification is not strictly speaking a rational expectations test, due to the informational requirements it imposes, assuming that individuals are forming expectations over the changes in the variables affecting the dependent variable. Column four actually uses the fact that the coefficient on the lagged expected longevity is not significantly different from 1, to estimate the more common specification that has the difference in expected longevity probabilities as dependent variable, as presented in equation (4). The results are very similar. The main difference is that the effects of the self-reported and computed health change to much worse are now considerably larger, which we interpret as indicating that although not statistically incorrect, assuming that the coefficient on lagged Pliv75 is 1 can create some biases in the coefficients of variables that are correlated with the lagged expectation.³¹

6 Conclusions

This is one of the first papers to directly study the use of subjective measures of health changes in order to capture the dynamic effect of health on both individuals’ expected survival probabilities and how they evolve over time. The former empirical model should be understood as an object akin to a production function of longevity within a model of health investments under uncertainty à la Grossman (1972), following the formulation in Ehrlich (2000). Our findings are important for a wide range of behavioral or empirical studies in which health dynamics are likely to play an important role along with the standard health status measures.

In our sample, we observe that for a large proportion of the individuals, the difference between the self-reported health in two consecutive waves is not consistent with the self-reported health changes between the same two waves. This fosters our discussion that allows us to provide possible explanations for these differences, and at the same time illuminates the estimation results that suggest caution to researchers using self-reported health status and computed self-reported health changes in many empirical applications. Our findings provide support for the use of self-reported health changes, whenever possible, to capture the dynamic component of health, as a key complement to self-reported health status. We find that the effect of our preferred measure of health changes on longevity expectations is of the same order of magnitude as the effect of the self-reported health level, while using computed measures of health changes would lead to a downward bias of the effects of health changes on longevity expectations.

Moreover, we compare the effect of the two measures of health changes on the changes in the expected survival probabilities. Our results show that after controlling for the change of self-reported health and the change of other objective health measures, there is evidence that computed health changes are not perfectly anticipated and therefore have some explanatory power in this kind of econometric specification. This suggests that self-reported health measures are longitudinally valid. However, the explanation for the reason behind their significance in these types of econometric models could also be linked with possible time-variant unobserved heterogeneity regarding reporting behavior of health status.

Most of the efforts in the profession have been concentrated in the cross-sectional properties of health indicators. However, with the growing number of panel data sets that provide self-reported measures of a variety of variables, there is a growing need to understand the pros and cons of using these measures in longitudinal econometric models. We believe our findings will foster further research on the longitudinal properties of self-reported measures in household surveys, the dynamics of health, and the measures of health changes in general. Although we have paid particular attention to self-reported health given the wide use of these measures in just about any empirical application using household level data, our findings could be of use in many other contexts where self-reports are used, and the dynamics of self-reported measures are considered to be important.