Measurement of the Copy Number of the Master Quorum-Sensing Regulator of a Bacterial Cell

Abstract

Quorum-sensing is the mechanism by which bacteria communicate and synchronize group behaviors. Quantitative information on parameters such as the copy number of particular quorum-sensing proteins should contribute strongly to understanding how the quorum-sensing network functions. Here, we show that the copy number of the master regulator protein LuxR in Vibrio harveyi can be determined in vivo by exploiting small-number fluctuations of the protein distribution when cells undergo division. When a cell divides, both its volume and LuxR protein copy number, N, are partitioned with slight asymmetries. We measured the distribution functions describing the partitioning of the protein fluorescence and the cell volume. The fluorescence distribution is found to narrow systematically as the LuxR population increases, whereas the volume partitioning is unchanged. Analyzing these changes statistically, we determined that N = 80–135 dimers at low cell density and 575 dimers at high cell density. In addition, we measured the static distribution of LuxR over a large (3000) clonal population. Combining the static and time-lapse experiments, we determine the magnitude of the Fano factor of the distribution. This technique has broad applicability as a general in vivo technique for measuring protein copy number and burst size.

Introduction

Quantitative analyses are playing an increasingly vital role in efforts to define the design principles underlying gene regulatory networks (1). Indeed, many design features—e.g., those relating to robust regulation of signaling fidelity (2), control of noise levels enabling population heterogeneity (3), and precise regulation of circadian oscillations (4)—are inherently quantitative. We report measurements on the protein LuxR, which is a master regulator in the quorum-sensing network of the model bacterium Vibrio harveyi. At low cell densities, LuxR is repressed, whereas at high cell densities, it is highly expressed. We describe two sets of experiments that together determine the values of the copy number of LuxR within a cell, as well as the burst size (the average number of proteins produced from a luxR mRNA molecule) in the high-cell-density limit. The technique described is broadly applicable for quantitative studies of stochasticity and fluctuations in gene expression in other systems.

Considerable progress in understanding stochasticity in gene regulation has come from applying in vivo imaging techniques based on fluorescent reporter genes and fusion proteins to large clonal populations of cells. Elowitz et al. (5) introduced a two-reporter technique in Escherichia coli that was capable of distinguishing intrinsic from extrinsic noise. A study of protein fluctuations measured in Bacillus subtilis has shown that increased translational efficiency is the predominant source of increased phenotypic noise (6). The relation between efficient transcription and large cell-cell variation was inferred from the two-reporter technique applied to yeast (7). Noise propagation has also been studied in synthetic networks (8). The experiments above may be characterized as providing static snapshots of stochasticity. A recent advance is the application of time-lapse microscopy by Rosenfeld et al. (9,10) to measure the temporal evolution of the reporter fluorescence in E. coli at the single-cell level. By applying binomial distribution analysis to the partitioning errors of the proteins measured at cell divisions (under the implicit assumption of equal daughter-cell volumes), crucial information was obtained on transcriptional regulation of the protein production from target genes. These studies underscore the importance of stochasticity in gene regulation and the role that small-number fluctuations play (11). However, experimental determination of the protein copy number in vivo is a difficult challenge.

V. harveyi communicates by synthesizing, releasing, and detecting the population-dependent accumulation of extracellular signal molecules called autoinducers (AIs) (12,13) (Fig. 1 A). When extracellular AI concentrations exceed a threshold level, bacteria transition from a program of gene expression appropriate for individual behavior to a program of gene expression that underpins collective behavior (14). Quorum-sensing uses master regulators like LuxR to control a range of group activities including secretion of virulence factors, biofilm formation, exchange of DNA, sporulation, and bioluminescence. In V. harveyi, LuxR directly or indirectly activates and represses >70 genes in a precise temporal order (15).

Figure 1.

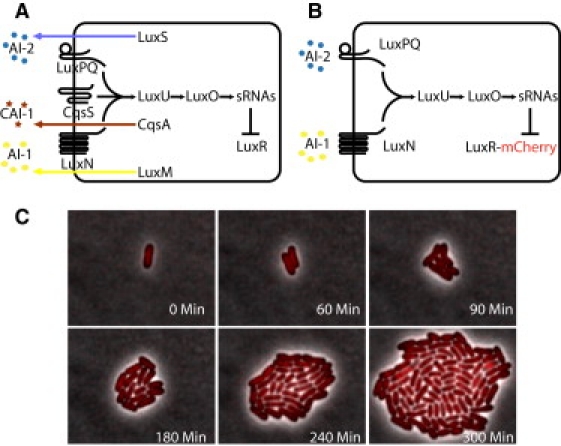
The quorum-sensing circuit and growth of a colony of V. harveyi. (A) Wild-type V. harveyi uses three autoinducers (AIs) to gauge the population density as well as the species composition of the vicinal community. The AIs are AI-1, an intraspecies signal; CAI-1, an intragenera signal; and AI-2, an interspecies signal. In V. harveyi, detection of AI-1, CAI-1, and AI-2 involves the transmembrane receptors LuxN, CqsS, and LuxPQ, respectively. Black arrows denote the direction of phosphate flow when the concentration of AIs is low. In the absence of AIs (low cell density), the receptors are kinases that funnel phosphate through a shared pathway that ultimately represses translation of the mRNA encoding the master quorum-sensing regulator, LuxR. In response to AIs (i.e., at high cell density), the receptors convert from being kinases to being phosphatases. Phosphate is drained from the signaling pathway, which relieves repression of luxR mRNA translation. (B) In the V. harveyi strain used here, only exogenously added AI-1 and AI-2 are detected (by the sensors LuxN and LuxPQ, respectively), which ultimately controls production of the master regulator LuxR (here labeled with mCherry). (C) Sequence of fluorescent images (red) overlaid with simultaneous phase images (gray) showing the growth of V. harveyi cells containing LuxR-mCherry.

We report a sequence of experiments that combine the time-lapse and static snapshot approaches in V. harveyi to measure the copy number, N, of the master regulator protein LuxR, as well as its burst size, b, when LuxR is highly expressed. As in Rosenfeld and colleagues (9,10), we determined the relative partitioning error of LuxR (fused to mCherry protein) at cell division by single-cell fluorescence time-lapse microscopy. When a cell divides, both N and the cell volume, V, are partitioned between the daughter cells in nearly even proportions. In individual cells, however, slight asymmetries in the partitioning of both N and V occur stochastically. As a result, the bell-shaped distribution curves describing the partitioning of the fluorescence signal and the volume acquire widths that we have measured in detail. We show that it is essential to measure the distribution function governing volume partitioning (in addition to the fluorescence partitioning function). Relative fluctuations in the two quantities are comparable in magnitude. Applying binomial distribution analysis to the two measured distributions, we obtain N or, equivalently, the calibration between the observed fluorescence signal and the LuxR copy number. Turning to the snapshot approach, we next captured the distribution of LuxR-mCherry fluorescence density over a population of ∼3000 cells. Past studies have shown that the width of the distribution is much larger (overdispersed) compared to a Poisson distribution. In models analyzing the distribution (16–18), the burst size, b, is identified with the Fano factor (the ratio of the variance to the mean). However, if the copy number, N, is not known, b can be determined only up to an unknown constant (this also precludes quantitative comparisons of distributions taken on different samples). By fixing the copy number, we provide the final link that allows the numerical value of b to be obtained from these broad distributions. We find that the burst size is ∼50 dimers in the high-cell-density limit when LuxR is highly expressed. This implies that, on average, ∼11 messenger RNAs are transcribed during a cell cycle. These are the first measurements of burst values of a key protein in a quorum-sensing network (b has been measured recently in E. coli using other techniques (19,20)).

Materials and Methods

V. harveyi strain construction

The mCherry plasmid pRSET-B was a generous gift from Roger Tsien (University of California at San Diego) (21). V. harveyi strains used in the experiment were derived from wild-type V. harveyi BB120 (22). The N-terminal mCherry-LuxR construct was engineered using overlapping polymerase chain reaction to generate a (Gly⁴Ser)³ amino acid linker between the two proteins in the fusion. The gene encoding the fusion protein was linked to a Cm^R marker and used to replace the native luxR gene in a genomic library cosmid containing the luxR locus (pBB1805) to generate pKT1550 (23). A Kan^R marker was recombined into pKT1550, to replace the Cm^R marker and generate pKT1630. This construct was subsequently conjugated into the V. harveyi reporter strain TL27 (ΔluxM, ΔluxS, ΔcqsA, ΔcqsS) (24) to generate strain KT792. The luxR-mCherry construction was introduced onto the V. harveyi chromosome by allelic replacement (25). A plasmid pTL93 carrying gfp driven from the constitutive Ptac promoter was constructed to make an internal indicator Ptac-GFP. The cosmid, pTL65, was constructed by recombining the Ptac-GFP-Kan^R fragment into the intergenic region downstream of the entire lux operon (23). Final insertion of Ptac-GFP-Kan^R onto the V. harveyi chromosome was accomplished by allelic recombination to generate strain TL112.

Time-lapse microscopy and distribution measurement

Time-lapse fluorescence images of V. harveyi KT792 cells were obtained with an epifluorescence microscope TE-2000U (Nikon, Melville, NY). Custom Basic code was used to control the microscope and related equipment. To monitor gene expression in real time, fluorescent images were taken every 2 min via a 100× oil-immersion objective (NA 1.4; Nikon). In our optical system, the pixel size corresponds to a width of 160 nm. To track dividing cells, phase-contrast images were also taken and used for autofocusing the cells. The fluorescent signal was collected with a cooled (−60°C) CCD camera (Andor iXon, South Windsor, CT). The total power from the objective is 67 μW at λ = 570 nm, and the variance between experiments was <8%. Time-lapse movies were recorded every 2 min over a period of 6 h with the exposure time fixed at 0.3 s. To minimize bleaching, the appropriate shutter was opened only during the exposure time. The sample was heated by a temperature-regulated heating stage (Warner, Hamden, CT) and maintained at 30°C during the experiment (Fig. S2 in the Supporting Material). An electronic feedback system stabilized the temperature within ±0.3°C. The drift of the focus was automatically corrected throughout the experiment via a contrast-based autofocus algorithm. Data analysis was performed using MATLAB (The MathWorks, Natick, MA). V. harveyi TL112 was grown in AB medium (0.3 M NaCl, 0.05M MgSO₄, 0.2% vitamin-free casamino acids, 0.01M potassium phosphate, 0.01 M L-arginine, and 1% glycerol, pH 7.5) overnight for static distribution measurement, rediluted, and grown to an OD₆₀₀ ≈ 0.05 at 30°C. After concentrating by centrifugation, cells were observed on microscope slides at room temperature. Cells were observed with an automated stage (Prior, Rockland, MA), and ∼3000 cells were measured per sample.

Results

Time-lapse fluorescence microscopy results

In the V. harveyi circuit, at low cell density, small antisense RNAs (sRNAs) are made that bind to and repress translation of the luxR mRNA. At high cell density, the sRNAs are not synthesized; luxR mRNA is translated and LuxR protein is produced. Current evidence suggests that the functional unit of LuxR is a dimer (26). (Note that the V. harveyi LuxR protein, unlike the LuxR in Vibrio fischeri, is not an acyl-homoserine lactone binding protein.) To understand quantitatively how LuxR directs this cascade, it is important to know the copy number in individual cells, and to understand how it changes in response to changing AI inputs. To image the protein, we engineered a functional LuxR-mCherry fluorescent protein fusion and introduced it onto the V. harveyi chromosome at the native luxR locus. We verified that our LuxR fusion retains its functionality (see Supporting Material). Fig. S1 shows that both wild-type LuxR and LuxR-mCherry activate and repress candidate genes to the same extent, implying that the wild-type (wt) and fusion proteins are produced at nominally the same level.

The V. harveyi quorum-sensing circuit is shown in Fig. 1 A. The strain of V. harveyi used for this work lacks the genes encoding the three AI synthases (luxM, luxS, and cqsA), and is therefore incapable of producing endogenous AI. The background strain is also deleted for the cqsS gene encoding the CAI-1 receptor CqsS, so the strain is impervious to CAI-1. Thus, the CAI-1-CqsS system neither contributes nor removes phosphate from the quorum-sensing circuit (24). The LuxR-mCherry construct was introduced into this strain (Fig. 1 B).

We recorded the red fluorescence signal, F(t), versus time, t, from LuxR-mCherry in time-lapse movies during the growth of the above V. harveyi strain, in both the absence and presence of AIs. In each experiment, we monitored the fluorescence signal from three well-separated colonies growing under nearly identical conditions. We define the total number, M ∼ 250, of cell-division events (indexed by i) in the three colonies as one sample. Altogether, six samples (labeled 1–6) were investigated (see Table 1). The mCherry fluorescence, F(t), and the phase-contrast image, from which the cell areas, A(t), were computed, were recorded every 2 min for 5 h (Fig. 1 C). Because the cells grow densely packed in the confined space, V is proportional to the imaged area, A (see Supporting Material). An automated program computes the boundaries of each cell, and also traces the lineage trees of all cells in the colony (Fig. 2). To eliminate uncertainties caused by temperature fluctuations, we regulated the temperature of the sample chamber to within ±0.3°C of 30°C over the entire 5 h. Several tests were performed to verify that our results are not affected by errors in cell area estimation or by nonlinear response in F to the incident light intensity (see Supporting Material).

Table 1.

Experimental parameters for cell-division events in the absence and presence of AIs

Sample	[AI] (nM)	M	F0 (count)	σA	σN	N0 (copy)
1	0	230	12559 ± 2794	3.39% ± 0.13%	5.64% ± 0.20%	79 ± 5
2	0	256	19133 ± 3693	3.49% ± 0.10%	4.80% ± 0.12%	108 ± 5
3	0	178	23916 ± 5682	3.19% ± 0.15%	4.30% ± 0.20%	135 ± 12
4	10	292	27485 ± 4371	3.94% ± 0.25%	3.84% ± 0.20%	169 ± 18
5	18	156	33726 ± 7123	3.15% ± 0.20%	3.75% ± 0.22%	178 ± 21
6	22.5	264	16902∗ ± 2589	3.97% ± 0.18%		360∗ ± 55

AI is the exogenous concentration of AI-1 and AI-2 during growth of the colony. M is the total number of division events in each sample. F⁰ is the ensemble-averaged peak fluorescence immediately before cell division. σ_A and σ_N are the standard deviations of P_A(x) and P(y/x), respectively, inferred by MLE (see text). N₀ is the LuxR dimer number immediately before cell division inferred by MLE (in Samples 1–5). In Sample 6, the incident power was reduced significantly to avoid phototoxicity arising from the enhanced photon absorption by the much higher concentration of LuxR-mCherry (incident powers are identical for Samples 1–5). In Sample 6, the value of σ_N was too small to be reliably obtained by MLE. In this case, values of N₀ are inferred from F⁰ using the scaling constant ν established in Fig. 4C.

Figure 2.

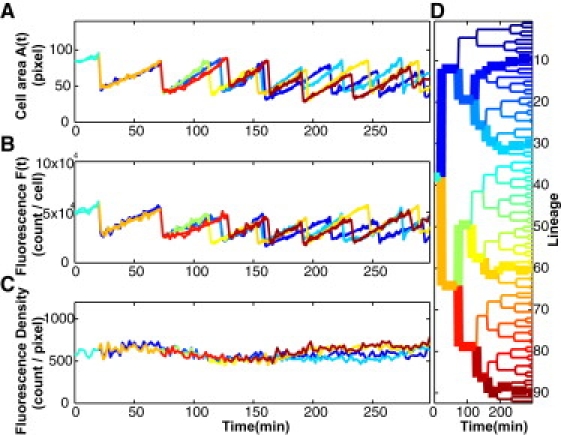
Time traces of the cell area, A(t), and LuxR-mCherry fluorescence signal, F(t), at fixed concentrations of AI. (A) Time trace of cell area, A(t) (expressed as pixel count), derived from the time-lapse fluorescence-phase movie shown in Fig. 1C. (B) The observed LuxR-mCherry fluorescence I(t) measured in photon counts. A second-order, linear-regression fit to A(t) and F(t) during each cell cycle was used to obtain the quantities A⁰_i, and F⁰_i at the ith cell division (the peak values in the traces in A and B). The ensemble-averaged peak fluorescence, F⁰, is defined as 〈F⁰_i〉. (C) The time trace of the fluorescence density, F(t)/A(t) ∼ [LuxR](t). (D) Lineage tree diagram of a colony growing from a single mother cell. Each branch point i represents a cell-division event. The four highlighted lineages correspond to the plots in A–C. The average cell cycle (45 ± 10 min) at 30°C is roughly equal to that observed in agitated liquid medium (∼40 min).

We find that in each of the six samples, the trace of A(t) displays a regular saw-tooth pattern (Fig. 2 A). At the time of cell division (event i), the trace splits into two branches as the mother cell area, A⁰_i, divides into two approximately even halves, A_i and A′_i = A⁰_i − A_i. We define the subscripted quantities A_i and A′_i as the areas measured immediately after the ith cell division (superscript or subscript 0 refers to the mother cell). Subsequently, the daughter cell areas increase to values close to A⁰_i, whereupon cell division repeats. A similar branching pattern is observed in the trace of the mCherry fluorescence signal (Fig. 2 B). Analogous to the area measurements, we have F⁰_i = F_i + F′_i, where F⁰_i is the peak mCherry signal in the mother cell immediately before cell division. In each sample, the values of F⁰_i cluster tightly around the ensemble-averaged value, F⁰ = 〈F⁰_i〉 (the standard deviation in each sample is reported in Table 1). The ensemble-averaged peak fluorescence, F⁰, is a convenient parameter that distinguishes the six samples. It is clear that F⁰ is proportional to the ensemble-averaged copy number in the mother cell, N⁰, viz. F⁰ = νN⁰, with the scaling constant ν yet to be fixed. At time t, the normalized signal F(t)/A(t) defines the fluorescence density, which is proportional to the LuxR concentration, [LuxR](t). The trace of the fluorescence density (Fig. 2 C) shows that if the AI concentration is unchanged during the 5-h experiment, [LuxR](t) remains nominally constant.

For each of the Samples 1–6, we collected two sets of area and fluorescence data {A⁰_i, A_i} and {F⁰_i, F_i}, where i indexes the cell-division events. As we are interested in the relative fluctuations of these quantities about their mean, we computed the fractional areas, x_i = A_i/A⁰_i, and fractional fluorescence, y_i = F_i/F⁰_i. Each cell-division event (x_i,y_i) can be represented as a point in the xy plane. The scatter plot of the events {(x_i,y_i)} (shown in Fig. 3 A for Sample 1) suggests an ellipse centered at (x₀,y₀) = (1/2,1/2). The value of the tilt angle, θ (∼70°), of the semimajor axis to the x axis demonstrates that a correlation exists between fluctuations in x and fluctuations in y. The histogram obtained by projecting the distribution onto the x axis represents the area-partition distribution P_A(x), which defines the probability distribution for partitioning of cell area without regard to fluorescence distribution. The error in the area partitioning is small (∼3.5%), in close agreement with previous experiments (27,28). Empirically, we find that P_A(x) in all six samples is well described by a Gaussian function centered at x = 1/2, viz. $P_A\left(x\right)=1/\sqrt{2\pi {\sigma }_A^2}{e}^{-{\left(x-x_0\right)}^2/2{\sigma }_A^2}$. For each sample, we have fixed the standard deviation σ_A using the method of maximum likelihood estimation (MLE) discussed below. The bold curve in Fig. 3 B represents P_A(x) in Sample 1. The corresponding projection onto the y axis yields the fluorescence-partition distribution, P_F(y), which also fits a Gaussian form (Fig. 3 C). It is significant that the standard deviation σ_F of P_F(y) (also found by MLE) is larger than that of P_A(x) (5.64% vs. 3.4%). This implies that in addition to area fluctuation, the total standard deviation, σ_F, derives an additional contribution, which we identify with small-number fluctuations of the protein population. (As discussed in the Supporting Material, pixelation and defocusing contribute a negligible uncertainty of 0.8% to A⁰_i and A_i. The uncertainties in our final determination of σ_A are further reduced by the large sample size, M, involved in MLE.)

Figure 3.

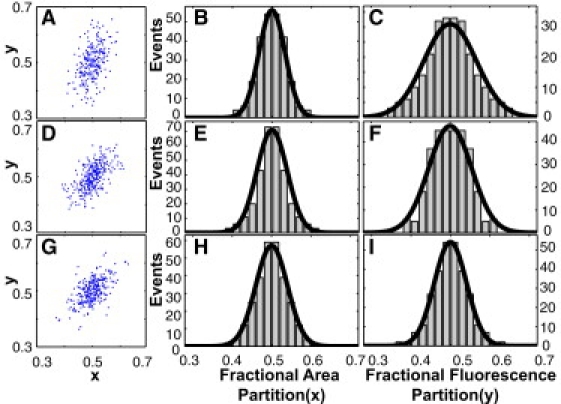
Scatter plot and the area and fluorescence signal distributions in Samples 1, 4, and 6 (in successive rows), with AI-1 and AI-2 each at = 0, 10, and 22.5 nM, respectively. (A) Distribution of the events {x_i,y_i} in Sample 1 in the xy plane, where x_i = A_i/A⁰_i and y_i = F_i /F⁰_i. (B) Histograms created by projection of the data onto the x axis are approximations of the area-partitioning distribution, P_A(x). (C) Projections onto the y axis approximate the fluorescence-partitioning distribution, P_F(y). Bold curves in B and C are Gaussian functions with values of σ_A and σ_F derived from MLE (see text). The corresponding quantities are displayed for Sample 4 (D–F) and Sample 6 (G–I). Note that in the right column, P_F(y) decreases in width from C to I. In the scatter plots, a correlation exists between the fluctuations in x and y. The correlation coefficient is 0.45, 0.60, and 0.58 in A, D, and G, respectively.

We next examine how the standard deviations σ_F and σ_A change with N₀. In Table 1, we have ranked Samples 1–6 in the order of increasing average peak fluorescence F⁰ ∼ N₀. (As noted, the variance of F⁰_i measured within each sample is small, so we may regard N₀ as a nominal constant in our analysis. The small cell-cell fluctuation in N₀ within each sample colony is the main source of uncertainty in N₀.) The peak fluorescence, F⁰, increases rapidly with AI concentration, [AI], but even when [AI] = 0, F⁰ is sample-dependent, as in Samples 1–3. In this experiment, the crucial observation is the systematic narrowing of the widths of the fluorescence distribution functions, P_F(y), as F⁰ increases. By contrast, P_A(x) remains unchanged within our resolution. Results for Sample 4 are shown on the second row of Fig. 3, D–F, whereas those for Sample 6 are shown in the third row (Fig. 3, G–I). Compared with Sample 1 (Fig. 3, A–C), the, F⁰ values in Samples 4 and 6 are larger by a factor of 2.2 and 3.3, respectively. Inspection of Fig. 3, C, F and I, reveals that the fluorescence distribution, P_F(y), narrows systematically with increasing F⁰.

Determining the copy number, N₀

We show that narrowing of the distributions reflects the suppression of the small-number fluctuation contribution to σ_F with increasing N₀. As discussed, the area of the mother cell is partitioned in the ratio x: (1 − x), according to the probability P_A(x). We assume that at cell division, the N₀ dimers of LuxR move freely in the cytoplasm. Hence, they distribute between the daughter cells stochastically. For a given area partitioning x, we model the stochastic process as N₀ tosses of a coin of bias x (Supporting Material). The conditional probability that, given x, N copies are found in the daughter of area A_i is the binomial distribution $P\left(N\right|x)=\left(\begin{array}{c}{N}_0\\ N\end{array}\right)x^N{\left(1-x\right)}^{N_0-N}$. In the limit N, N₀ » 1, we have $P\left(y\right|x)=1/\sqrt{2\pi {\sigma }_N^2}{e}^{-{(y-x)}^2/2{\sigma }_N^2}$, where y = N/N₀ and ${\sigma }_N^2=x\left(1-x\right)/N_0$ is the variance of the binomial distribution P(y|x). If σ_N could be found, we would know N₀.

We proceed to find σ_N from the scatter plots in Fig. 3, A, D, and G. The probability density for observing an event (x,y) is the joint probability P(x,y) = P(y|x)P_A(x), viz.

$$P(x,y)=\frac{1}{2\pi {\sigma }_A{\sigma }_N}{e}^{-{(y-x)}^2/2{\sigma }_N^2}{e}^{-{(x-x_0)}^2/2{\sigma }_A^2},(x_0=1/2)\text{.}$$ (1)

Within our assumptions, Eq. 1 describes the distribution of events in the scatter plots. We note that the contours of P(x,y) are ellipses with axes tilted in agreement with the observed θ. To find the two unknowns (σ_A,σ_N) in Eq. 1, we apply the MLE method to the set of M pairs {(x_i,y_i)} (29,30). In this method (Supporting Material), we maximize the likelihood function L(σ_A,σ_N), defined as the joint probability density that all M pairs are described by Eq. 1 with the same (σ_A,σ_N). L(σ_A,σ_N) displays a sharp peak at the optimal values (σ^∗_A,σ^∗_N) when displayed as a contour plot in the (σ_A,σ_N) plane. Finally, from σ^∗_N, we obtain the desired number N₀ ≈ 1/(4σ^∗_N²) at cell division. The inferred N₀ values are listed in Table 1.

Returning to Fig. 3, we may now understand the trends observed in the widths of the distributions. The fluorescence distributions P_F(y) (Fig. 3, C, F, and I) are obtained by integrating out x in P(x,y) in Eq. 1. We find

$$P_F\left(y\right)=\frac{1}{\sqrt{2\pi {\sigma }_F^2}}{e}^{-{(y-x_0)}^2/2{\sigma }_F^2},({\sigma }_F^2={\sigma }_A^2+{\sigma }_N^2)\text{.}$$ (2)

The resulting standard deviation, σ_F, of the fluorescence distribution is the Pythagorean sum of σ_A and ${\sigma }_N\sim 1/\sqrt{N_0}$. For sufficiently small N₀, we have σ_N » σ_A, so that σ_F is significantly larger than σ_A. This is the case in Fig. 3 C. However, as N₀ increases, σ_F decreases until σ_N < σ_A, when σ_F saturates to σ_A (as in Fig. 3 I). The analysis shows that small-number fluctuations contribute the term σ_N to the observed width σ_F of P_F. The narrowing of the distribution with increasing N₀ results from the suppression of σ_N.

Further support of this conclusion is obtained by plotting the observed variance σ_F² (calculated from σ_A and σ_N) versus 1/F⁰ for Samples 1–5. As is apparent in Fig. 4 B, σ_F² varies linearly with 1/F⁰ with a positive intercept as 1/F⁰ → 0. Since the x axis scales as N₀⁻¹, the straight line verifies that σ_N² is proportional to 1/N₀. The plot directly confirms that the variation in the width of P_F(y) (Fig. 3, C, F, and I) comes from small-number fluctuations. This supports our starting assumption that the LuxR dimers move freely in the cytoplasm. Moreover, the intercept of σ_F² agrees with σ_A². The relatively large intercept underscores the importance of including the area fluctuation in any analysis of small-number fluctuations. As discussed above, the area fluctuation distribution is independent of the LuxR copy number, so the width, σ_A, of P_A(x) is insensitive to F⁰. This is confirmed in Fig. 4 A. Fig. 4 C summarizes the linear relationship between N₀ inferred from the MLE and the F⁰ measured in Samples 1–5. As the peak fluorescence, F⁰, increases from 1.2 × 10⁴ to 3.4 × 10⁴ counts in Samples 1–5, N₀ rises in proportion from 80 to 180. The slope of this linear relationship fixes the scaling constant ν = F/N.

Figure 4.

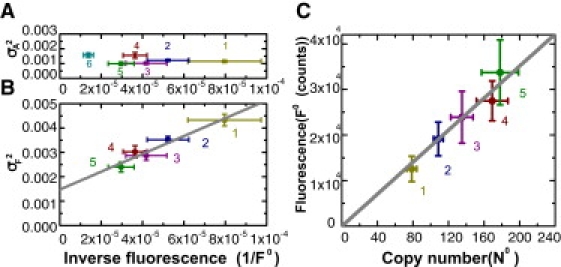
Test of the model (Eqs. 1 and 2) and of linear scaling between N₀ and the observed peak fluorescence, F⁰, in Samples 1–5. (A) Plot of σ_A² (obtained from MLE) versus 1/F⁰ ∼ 1/N₀ in Samples 1–5. (B) Plot of σ_F² (calculated from σ_A and σ_N) versus 1/F⁰ ∼ 1/N₀ in Samples 1–5. The straight-line fit to σ_F² verifies that σ_N² is proportional to 1/N₀. (C) Plot of F⁰ versus N₀ obtained from MLE in the five samples. The straight-line fit confirms that N₀ scales linearly with the ensemble-averaged peak fluorescence, F⁰. In all panels, error bars along the axes F⁰ and 1/F⁰ reflect the standard deviations of F⁰_i reported in Table 1. Error bars for N₀ (C) reflect the variation in σ_N caused by decreasing log_eL by one unit from its peak value in the contour plot (see Supporting Material).

Protein burst and the Fano factor

After transcription, protein molecules are produced stochastically at the translation stage. There is now strong evidence for the hypothesis that protein production occurs in bursts, with a burst of proteins translated from a single mRNA molecule (the luxR mRNA half-life τ_m ∼ 3 min (31)). Bursts associated with mRNA transcription in E. coli were recently imaged (32), but in vivo cytoplasm protein bursts from a single mRNA have not been imaged to date. Stochastic fluctuations at the transcription and translation stages lead to a broad, skewed distribution, G(p), of the protein concentration p measured on a large population (the static snapshot). Numerical simulations suggest that the Fano factor—the ratio of variance to mean—greatly exceeds 1, the value predicted for a Poisson distribution. The relation between the Fano factor and the mean burst magnitude b, has drawn considerable theoretical attention (16–18).However, experimental progress has been slower. As noted, although the snapshot distribution is readily captured, the Fano factor cannot be pinned down unless the scaling constant ν = F/N is known.

Using the calibration for ν, we have obtained the Fano factor for LuxR in V. harveyi in the two extreme quorum-sensing modes of low and high cell densities. As in the time-lapse experiment, LuxR proteins are imaged by mCherry fluorescence. In addition, we introduced a constitutively expressed GFP, which is under the control of the P_tac promoter, into the chromosome. Because the gfp gene is not part of the quorum-sensing circuit, this reporter serves to evaluate the effect of global fluctuations. We assayed the response of single cells to two different levels of external autoinducers by using automated snapshot fluorescence microscopy. In each experimental run, we measured the cell area, A, and the fluorescence signals of both mCherry and GFP reporters in each of the ∼3000 cells in the sample. We are interested in the distribution, G(p), of protein concentration p rather than copy number over the whole sample (this factors out the twofold cell-to-cell fluctuation in volume or area). Fig. 5 A shows the scatter plot of the fluorescence levels for the entire population in the low density limit ([AI] = 0 nM). (The vertical axis plots the concentration of LuxR dimers, p. To facilitate computation of the Fano factor, however, we express p in the dimensionless form, N_p = p〈A〉, where 〈A〉 is the mean value of the observed cell area in the sample. N_p would be the number of dimers/cell if all cells had an area equal to 〈A〉. The Fano factor is then 〈δN_p²〉/〈N_p〉. See Supporting Material for details.)

Figure 5.

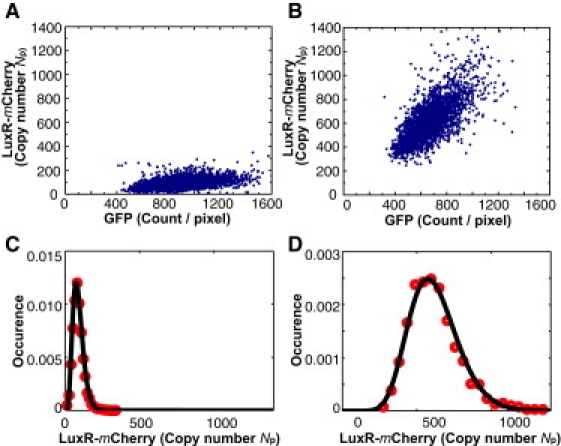
Scatter plot and fluorescence density distributions in two samples with the concentration [AI] set at 0 and 1000 nM, respectively. (A and B) Scatter plots of LuxR concentration, p, versus the GFP reporter count for ∼3000 cells in the samples with [AI] = 0 and 1000 nM, respectively. With ν = F/N known, we can calibrate concentration p (on the vertical axis). We express p as N_p = p〈A〉, where 〈A〉 is the mean of the cell area. On the horizontal axis, the GFP signal is expressed in counts/pixel. (C and D) Distribution function G(N_p) of the LuxR concentration is plotted versus N_p for the zero-AI and large-AI samples, respectively. Solid circles are histogram values obtained by projecting the scatter plot onto the y axis. The Fano factor, 〈δN_p²〉/〈N_p〉 equals 12 and 50 in C and D, respectively. This implies that the burst size, b, is ∼50 dimers/mRNA in D. The bold curves are fits to the gamma distribution using MLE.

At low cell density, the average LuxR concentration, 〈N_p〉, is ∼80 dimers/cell. At high cell density, ([AI-1] + [AI-2] = 1000 nM), 〈N_p〉 is observed to increase to ∼575 dimers/cell (Fig. 5 B), implying a sevenfold increase of LuxR concentration between the two limits.

Projecting the data in the scatter plots onto the y axis, we obtain the distribution function, G(p) (Fig. 5, C and D) in the low- and high-cell-density limits, respectively. We note that the Fano factor in the high-cell-density limit is significantly larger than that in the low-cell-density limit. At low cell densities, the expression of LuxR is regulated posttranslationally by sRNAs that bind to luxR mRNAs and target them for degradation. This leads to a decrease in the average luxR mRNA lifetime, and a corresponding reduction in the average bust size, b. In contrast, at high cell densities, sRNAs are not produced, and mRNAs are no longer degraded by the sRNAs, resulting in a larger average burst size, b. Due to the complexity of posttranscriptional regulation by sRNAs, the Fano factor corresponds to the burst size only at high cell densities. At low cell densities, the Fano factor becomes a more complicated function of the burst size and other sources of noise associated with mRNA-sRNA binding (33). Nonetheless, the increase in width of G(p) between Fig. 5, C and D, is consistent with this scenario. It is of significance that the Fano factor 〈δN_p²〉/〈N_p〉 also increases by a factor of 4 (from ∼12 in Fig. 5 C to ∼50 in Fig. 5 D).

In the simplest situation, when the mRNA concentration exceeds that of the sRNAs (high cell density), the Fano factor reduces to the burst size, viz. 〈δN_p²〉/〈N_p〉 ≈ 1 + b (17,18). Applying this relation to Fig. 5 D, we find that b ≈ 50 dimers—on average, each mRNA produces 50 LuxR dimers in the high-cell-density limit.

Discussion

We have developed an in vivo method to measure the copy number of LuxR-mCherry in V. harveyi. By capturing the time trace of the cell volume and LuxR-mCherry fluorescence over six cell cycles, we measured both the distribution functions that govern the volume partitioning and the fluorescence partitioning during cell division. Applying binomial analysis to the distribution functions, we can then infer the copy number in each cell. By varying the concentration of autoinducers outside the cell, we verified that the inferred LuxR copy number scales linearly with the observed fluorescence signal. With the scaling factor, ν, between the two quantities so determined, we next investigated the distribution of fluorescence over a large population of cells (in a snapshot measurement). In the high-cell-density limit, the Fano factor of this distribution allows the burst size of LuxR proteins to be found.

Our finding of the absolute number of LuxR dimers under no AI, low-cell-density conditions (80 dimers/cell), and saturating AI, high-cell-density conditions (575 dimers/cell), is intriguing given what we know about Vibrio quorum-sensing regulons. Numerous studies in different Vibrio species suggest that typically ∼70 genes are under LuxR control. If we make the simple assumption that one or two LuxR dimers is required to bind DNA per regulated promoter (we note that this is probably an underestimate, given that DNA binding regulatory proteins often oligomerize on DNA), then in low-cell-density conditions, according to our measurements, there is insufficient LuxR in the cell to occupy all of its cognate sites and control the set of target genes. Thus, under the low-cell-density condition, LuxR-repressed target genes are expressed, whereas LuxR-activated target genes are not. By contrast, at high cell density, with 575 LuxR dimers present, sufficient LuxR is present to bind to and control all of the target genes. Even under this latter condition, however, there is not a large excess of LuxR in the cell. We suspect that possessing only a fewfold more LuxR proteins than are absolutely required to control the regulon enables cells to rapidly transition back to the low cell density, LuxR-limited mode when AIs disappear (i.e., upon dilution). Thus, we conclude that evolution has driven the quorum-sensing network to maintain LuxR numbers within a narrow concentration window even under dramatically changing AI conditions. This strategy restricts LuxR levels to within the sweet spot that ensures maximal sensitivity to changing cell population density. Consistent with the idea that strict control over LuxR must be maintained, two negative feedback loops repress LuxR production (31). Specifically, LuxR autorepresses its own transcription, and LuxR activates the expression of a set of small RNA genes, the products of which bind to LuxR mRNA and prevent its translation. Furthermore, upstream of LuxR, two topologically analogous negative feedback loops repress LuxO. Because LuxO indirectly controls LuxR levels (see Fig. 1), these latter two loops thus also play roles in keeping LuxR levels low (34).

The experiments described provide a first quantitative picture of LuxR transcription and translation in the quorum-sensing network of V. harveyi in the high-cell-density mode. Using the mean value 〈N_p〉 = 575 and the burst size b = 50 observed in this limit, we find that the number of luxR-mRNAs produced per cell cycle, a = 〈N_p〉/b, is ∼11. Hence, when the sRNA population is strongly repressed, each cell transcribes ∼11 luxR mRNA on average during its cell cycle. In turn, each mRNA produces ∼50 LuxR dimers before it is degraded. This is a rather high translation rate. However, it is comparable with the large burst size (∼100 monomers) measured in E. coli when the repressors completely dissociate from the Lac operon (35).

By contrast, in the low-density quorum-sensing mode ([AI-1] and [AI-2] = 0), the mean value 〈N_p〉 is sharply reduced to 80, whereas the Fano factor decreases to 12 (Fig. 5 C). The smaller Fano factor is qualitatively consistent with the sharp reduction of b expected when the sRNA concentration is high. The repressive case, which extends from [sRNA] ∼ [mRNA] to the limit [sRNA] » [mRNA], is harder to treat. Other microscopic parameters enter in the expression for the Fano factor (33). In principle, these measurements can be readily extended to cover intermediate values of [AI-1] and [AI-2] to uncover empirically the full functional variation of the mean, variance, and Fano factor. Such experiments can provide detailed, quantitative data to guide the modeling of the quorum-sensing network, and to clarify how the master regulator LuxR controls downstream target genes.

Supporting Material

Seven figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00175-X.