Scale-Free Topology of the CA3 Hippocampal Network: A Novel Method to Analyze Functional Neuronal Assemblies

Abstract

Cognitive mapping functions of the hippocampus critically depend on the recurrent network of the CA3 pyramidal cells. However, it is still not known in detail how network activity patterns emerge, or how they encode information. By using functional multineuron calcium imaging, we simultaneously recorded the activity of >100 neurons in the CA3 region of hippocampal slice cultures. We utilized a novel computational method to analyze the multichannel spike trains and to depict functional neuronal assemblies. By means of event synchronization and the correlation matrix analysis method, we found that: 1), the average functional neuronal cluster consists of 23 neurons, and neurons could be part of multiple assemblies; 2), the clustering strength, size, and mean distance among cells in neuronal assemblies follow a power-law-like distribution; 3), the clustering strength and size of neuronal assemblies are not correlated with the total number of neurons and their physical distance; and 4), the clustering distance of neuronal assemblies is weakly correlated with the total number of neurons and their physical distance. These findings suggest that the functional organization of the spontaneously firing CA3 hippocampal network is a scale-free structure in slice culture.

Introduction

Recent computational and experimental evidence show that the organization of neuronal networks is nonrandom. The role of some of these features in network dynamics and information processing has been well investigated (1–6). Some studies imply a small-world structure in cortical networks (7–9), whereas others have suggested that cortical neuronal networks are scale-free (5,10). Computational models use a small-world topology to describe hippocampal networks, in which the majority of connections between cells are local, except for a few cells that have long-distance connections (8). Such architecture of the neuronal network promotes faster signal propagation and synchronization with a relatively small number of connections. Small-world principles are found in complex social and biological systems such as in the nervous system of the nematode Caenorhabditis elegans (11,12). However, scale-free networks are also defined such that connection properties of the network adhere to a power-law distribution (8,13). Such networks are known to allow for efficient information transfer and prevent signal jamming (13). Scale-free topology signifies the existence of superconnected neurons (i.e., hubs). Nodes with particularly large numbers of connections have been described in nonneuronal networks (13,14). The existence of such hubs has only been implicated most recently in normal cerebral cortex (5) and in epileptic hippocampus (4).

Neuronal ensembles in the hippocampus play a critical role in map-based spatial navigation (15,16), dead reckoning navigation (17,18), and memory processes (19,20). In pathological conditions, neuronal activity of a large number of neurons is hypersynchronized, which leads to seizure activity. Despite the importance of the hippocampal CA3 network in representation of the spatial field and in the emergence of epileptiform activity, crucial experimental details regarding the architecture of the neuronal assemblies are still lacking. Nonrandom features of synaptic connectivity in the rat visual cortex have recently been investigated by quadruple whole-cell recording technique in vitro (5), but the effort required to obtain sufficient amounts of data for analysis (i.e., several hundred simultaneous recordings) to reveal differences in connections strength between neurons is likely to discourage further similar research. Alternatively, in vitro Ca²⁺ imaging with a fast sampling rate can provide information for neuronal network topology and connectivity pattern analysis.

Action potentials produce unitary Ca²⁺ transients with a fast rise and an exponential decay (21). Thus, the activity of neurons can be reconstructed from the somatic Ca²⁺ transients and the identification of neuronal types can be obtained by spectral separation of Ca²⁺ signals (22). Based on this principle, the functional multineuron calcium imaging (fMCI) was developed to record the activity of neuron populations with single-cell resolution (23,24). The advantage of this novel method is the ability to investigate the spatial and temporal features of large number of neurons in the network.

In this study, we introduce a novel method to analyze the simultaneous spike trains reconstructed from fMCI measurement which enables us to depict functional neuronal assemblies located in a large neuronal network. Measuring the spontaneous activity of the hippocampal CA3 network, we quantitatively analyzed the formation, characteristics, and structure of neuronal assemblies.

Materials and Methods

Preparation of the organotypic slice culture

Wistar/ST rats (SLC, Schizuka, Japan) at postnatal day 6–7 were anesthetized, and brains were rapidly removed and cut into 300 μm-thick slices by using a DTK-1500 microslicer (Dosaka, Kyoto, Japan) in aerated, ice-cold Gey's balanced salt solution (Invitrogen, Gaithersburg, MD) supplemented with 25 mM glucose. Entorhino-hippocampal stumps were placed on an OMNIPORE membrane filter (JHWP02500; Millipore, Bedford, MA) that were laid on O-ring plastic disks (Hazai-Ya, Tokyo, Japan) (25). Culture medium consisted of 50% minimal essential medium, 25% Hank's balanced salt solution (Invitrogen), and 25% horse serum (Cell Culture Laboratory, Cleveland, OH), supplemented with 33 mM glucose. Slices were maintained at 37°C in a humidified and CO₂-enriched atmosphere. The details on the slice culture preparations can be found in Koyama et al. (25). Experiments were conducted in accordance with the National Institutes of Health guidelines for laboratory animal care and safety.

Recording of neuronal activity

Experiments were performed at 7–11 days in vitro, and the recording of the neuronal activity was conducted by fMCI. Slices were incubated with dye solution for 1 h in a humidified incubator at 37°C in 5% CO₂ (26). The dye solution was ACSF (127 mM NaCl, 26 NaHCO₃, 3.3 mM KCl, 1.24 mM KH₂PO₄, 1.0 mM MgSO₄, 1.0 mM CaCl₂, and 10 mM glucose) containing 0.0005% OGB-1AM, 0.8% DMSO, 0.01% Pluronic F-127, 0.005% Cremophor EL, and 100 μM sulfinpyrazone. The slice was then transferred to a recording chamber at the temperature of 30–32°C. Spontaneously emerging Ca²⁺ signals of the hippocampal CA3 network were imaged in slices loaded with Oregon Green 488 BAPTA-1AM at a sampling rate of 100 frames/s. Images were acquired with a Nipkow disk confocal microscope (CSU-X1; Yokogawa Electric, Tokyo, Japan), iXon DV897 charge-coupled device cameras (Andor, Belfast, Northern Ireland, UK), a Nikon FN1 microscope (Tokyo, Japan), a Nikon water-immersion objective (16×, 0.80 NA), and Solis software (Andor). Fluorophores were excited at 488-nm with an argon laser (10 mW, 532-BS-AO4; Omnichrome, Chino, CA) and visualized with a 507-nm long-pass emission filter. For each neuron, the fluorescence change ΔF/F was calculated as (F_i-F₀)/F₀, where F_i is the fluorescence intensity at time_i and F₀ is baseline. Then, a custom-made software (26) was applied to reconstruct the event onset times from the onsets of individual Ca²⁺ transients. Fig. 1 showed that the action potentials could result in the onsets of Ca²⁺ transients; in contrast the timing of spike-triggered events could be reconstructed from the Ca²⁺ transient signals. Because there is a decay constant for each Ca²⁺ transient (see the zoomed spike at the right of Fig. 1), the timing of reconstructed spike trains from the Ca²⁺ transients is not absolutely identical to one of actual spike trains obtained by intracellular recording.

Figure 1.

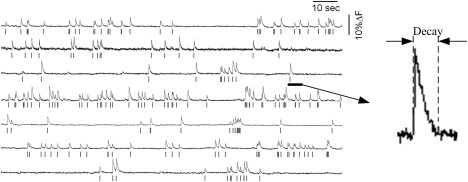
Comparison of spike trains obtained by intercellular recordings and Ca²⁺ transient signals recorded by fMCI. The timing of the Ca²⁺ transients are correlated with the actual neural spike trains indicated below the Ca²⁺ signals. The decay of a Ca²⁺ transient is illustrated.

The details of the experiments and the analysis can be found elsewhere (26). The fMCI data are available online at www.hippocampus.jp/data/.

Data analysis

The event synchronization

A variety of different measures, such as cost-based metric (27), Euclidean distance-based metric (28), cross correlation-based metric (29,30), weighted distance-based metric (31), and interspike interval-distance (32) have been proposed to calculate the overall degree of synchrony between different spike trains. The performance of these approaches has been evaluated from both simulated and real spike trains (32), and showed that all measures had high correlation (>0.91). After considering the computational cost and the robustness of the analysis against noise, and the fact that event synchronization is well suited for spike trains due to the transient dynamics of spikes, in this study the event synchronization was used.

To calculate the correlation between spike trains, event synchronization analysis was performed (33), followed by the generation of a correlation matrix from multiple spike trains. To extract the synchronicity of events, the maximum time lag ι was defined that represented the time interval in which two events were still considered synchronous. Considering two spike trains x and y, event times $t_{\mathrm{i}}^{\mathrm{x}}$ and $t_{\mathrm{j}}^{\mathrm{y}}$ (i = 1, …, m_x; j = 1, …, m_y), the number of times that an event appears in x shortly after it appears in y (within a delay τ) was denoted by c^τ (x|y), it is

$$c^{\tau }\left(x|y\right)=\sum _{i=1}^{m_{\mathrm{x}}}\sum _{\mathrm{j}=1}^{m_{\mathrm{y}}}{J}_{\text{ij}}^{\tau }\{\begin{array}{ll}{J}_{\text{ij}}^{\tau }=1& if0<t_{\mathrm{i}}^{\mathrm{x}}-t_{\mathrm{j}}^{\mathrm{y}}\le \tau \\ J_{\text{ij}}^{\tau }=1/2& if{t}_{\mathrm{i}}^{\mathrm{x}}=t_{\mathrm{j}}^{\mathrm{y}}\\ J_{\text{ij}}^{\tau }=0& \mathit{otherwise}\end{array}\text{.}$$ (1)

The event synchronization measure was defined as

$$Q_{\tau }=\left[c^{\tau }\left(y|x\right)+c^{\tau }\left(x|y\right)\right]/\sqrt{m_{\mathrm{x}}{m}_{\mathrm{y}}},$$ (2)

thus,

$$0\le Q_{\tau }\le 1,$$

called the synchronization index in this study.

Spike trains were reconstructed from the Ca²⁺ transients. A previous study has indicated that individual spikes that follow each other at >5 Hz are inseparable in the Ca²⁺ traces (33) and the decay constant of hippocampal CA3 pyramidal cells is 484 ± 123 ms. Because of the inevitable optical noise caused by the charge-coupled device camera, the precise determination of the timing of spikes is difficult. At 100-Hz sampling rate, the detection jitter could be up to 50 ms. Thus, in this study, 50-ms lag τ was selected. In addition, we ranged the τ-value from 10 to 100 ms, which resulted in similar results (not shown), suggesting that this analysis is robust against varying τ-value.

Surrogate

To test the significance of the synchronization index and other estimations, a surrogate data method (34) was applied in this study. An inhomogeneous Poisson spike train was generated with a rate equal to the instantaneous firing rate of the original spike trains; the temporal cross structure between the surrogate spike trains is random, thereby the correlation of these surrogate spike trains (as estimated using event synchronization) approaches zero. The null hypothesis was then tested by the surrogate method. This operation is to calculate a surrogate eigenvalue ($\overline{\lambda }{\prime }_{\mathrm{k}}$) for Eq. 5.

Correlation matrix analysis

The above calculation resulted in a correlation matrix C for multiple spike trains. The eigenvalue decomposition of C is given by

$$\mathbf{C}{\mathbf{v}}_{\mathrm{i}}={\lambda }_{\mathrm{i}}{\mathbf{v}}_{\mathrm{i}},$$ (3)

where λ_i is the eigenvalue and λ₁ ≤ λ₂ ≤ ⋯ ≤ λ_M, and v_i is the eigenvector corresponding to λ_i. The eigenvector describes the internal structure of synchronized clusters and satisfies

$${\sum }_{\mathrm{i}}{v}_{\text{ik}}^2=1\text{.}$$

In fact, the index $v_{\text{ik}}^2$ is the weight with which a channel, i, contributes to neuronal assembly k. Thus, information about the structure of synchronized clusters can be described by combining the eigenvalues and eigenvectors to give a participation index (PI) (35),

$$P{I}_{\text{ik}}={\lambda }_{\mathrm{k}}{v}_{\text{ik}}^2,$$ (4)

where v_ik is the i element of eigenvector v_k and λ_k is a corresponding eigenvalue. PI_ik indicates the contribution of channel i to the neuronal assembly k. To decrease noise level, neurons with very small PI_ik (<0.1, P < 0.01, giving 99% confidence levels) were ignored, whereas the others were regarded as elements of the neuronal assembly.

Quantification of neuronal assembly

When all spike trains are completely correlated, the elements of C are equal to 1 and the maximum eigenvalue is equal to the number of neurons M and the other eigenvalues are zero. Thus, the highest eigenvalue can provide information about global synchronization. To obtain a normalized value of global synchrony, we derived a global synchronization index. First, a surrogate spike train is generated, using the surrogate correlation matrix R calculated, from which the highest eigenvalue λ′ is determined. This procedure is repeated 100 times. The mean of the highest eigenvalue calculated across 100 surrogates is denoted as $\overline{\lambda }\prime$. Once we obtain the $\overline{\lambda }\prime$, the global normalized synchronization can be computed by

$$Syn\text{\_}Indx=\{\begin{array}{ll}\left({\lambda }_{\mathrm{M}}-\overline{\lambda }\prime \right)/\left(M-\overline{\lambda }\prime \right),& \text{if}{\lambda }_{\mathrm{M}}>\overline{\lambda }\prime \\ 0,& \text{otherwise}\end{array},$$ (5)

where Syn_Index ranges from 0 (no synchrony) to 1 (perfect synchrony).

If the original eigenvalue (λ_k) is greater than the mean of the averaged surrogate eigenvalues ($\overline{\lambda }{\prime }_{\mathrm{k}}$) and standard deviation (SD_k) of K (i.e., $\overline{\lambda }{\prime }_{\mathrm{k}}+K\times S{D}_{\mathrm{k}}$), it suggests the presence of clusters of synchronization. The equation to compute the number of clusters is expressed as

$$\mathit{NumCluster}=\sum _{\mathrm{k}}\mathrm{sgn}\left({\lambda }_{\mathrm{k}}>\left(\overline{\lambda }{\prime }_{\mathrm{k}}+K\times S{D}_{\mathrm{k}}\right)\right),$$ (6)

where sgn is a sign function (i.e., if ${\lambda }_{\mathrm{k}}>\left(\overline{\lambda }{\prime }_{\mathrm{k}}+K\times S{D}_{\mathrm{k}}\right)$ is true, sgn is 1, otherwise it is 0) and K is a constant (here K = 2, giving 95% confidence levels). When the participation indices of neurons (PI) in a neuronal assembly was >0.05, the neuron was defined as the node of a graph network and the edge of the network was determined by the event synchronization. Then, the shortest distance of this graph network was calculated and defined as the distance of neural assembly. Based on the distribution of the PI_ik, the contribution of each neuron to neuronal assemblies and the size of the neuronal cluster were estimated. To reveal the relationship between the PI and the characteristics of neuronal assemblies, the coefficients of variation (CVs) and Shannon entropy of PI were calculated,

$$-\sum f\left(P{I}_{\text{ik}}\right){\log }_{2}f\left(P{I}_{\text{ik}}\right),$$

where f is the probability distribution of PI_ik. As for each neuronal assembly, the mean physical distance among neurons is defined as the distance of neuronal assembly.

Statistics

In this study, the data were provided as the means ± SD. The coefficient of variation (CV) was defined as the ratio of the standard deviation to the mean, which is the normalized measure of dispersion of the probability distribution. The least-square linear regression method was used to calculate the correlation relationship between two variables. Significance for all analyses was set at p < 0.05.

Results

Using fMCI approach we simultaneously recorded in each preparation the activity of >100 neurons located in the CA3 area of the hippocampus (Fig. 2, A and B). By analyzing the full extent of the recording (>180 s), we calculated the event synchronization of multiple spike trains using Eqs. 1 and 2. Correlation matrices were obtained (Fig. 2 C) in which synchronization value of strongly pair-wised neurons was close to 1 and the uncorrelated neurons approached 0. The time delay, when two events were considered synchronous, was 50 ms. Neurons with similar activity over the full extent of recording (corresponding to a value in the correlation matrix close to 1) were considered as part of a given functional neuronal assembly (Fig. 2 D). To reduce the bias of event synchronization caused by the data length, noise, and artifacts that might have been introduced during the recording process or parameter selection, a surrogate technique was applied to estimate the threshold for Eq. 6 and to measure the number of neuronal clusters. Using this analysis, we calculated that an average 6 ± 4 (mean ± SD) neuronal assemblies were present in the CA3 region in each hippocampal organotypic slice preparation (n = 25 slices).

Figure 2.

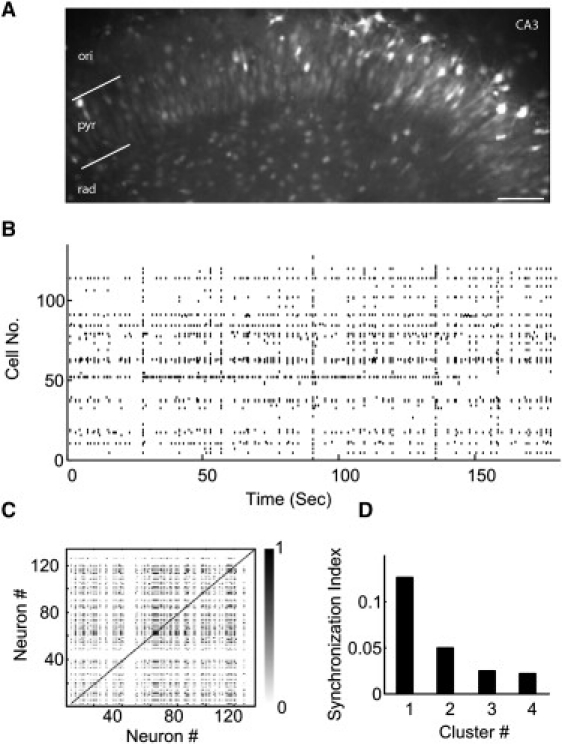
Illustration of spike train, correlation matrix, and synchronization index of the hippocampal neuronal network. (A) Confocal image of a slice loaded with Oregon Green 488 BAPTA-1. Bright signal indicates active neurons in the CA3 pyramidal cell layer. Scale: 50 μm. (B) The raster plot of the spike trains of 127 neurons is reconstructed from the Ca²⁺ imaging. (C) Correlation matrix of spontaneous activities using event synchronization at the maximal time delay of 50 ms. (D) Synchronization index of four neuronal assemblies based on the random matrix theory and surrogate techniques.

To determine the spatial distribution of neurons forming functional cell assemblies, we plotted all cells which possessed measurable Ca²⁺ transient and calculated their contribution strength (participation index). A representative example is shown in Fig. 3, depicting this particular network to contain four neuronal assemblies with a variable synchronization index. By analyzing the figure it is obvious that neuronal assemblies are sparse and complex, but importantly, not locally clustered. Interestingly, only approximately one-half of the neurons participated in formation of functional neuronal clusters (41.4 ± 29.2%). An average functional neuronal cluster consists of 23 neurons but a lower number of neurons is also able to form a neuronal assembly (e.g., Fig. 3 D; n < 6). We also found that members of a given neuronal assembly can be part of another functional cell cluster at the same time (Fig. 3). These superconnected neurons are likely the hub cells that form the skeleton of the neuronal network (5). The statistical analysis of 25 slices showed that an average 21.4 cells can be part of two, 15.2 of three, and 6.8 of four clusters. On rare occasions, hub cells were found connecting five or six different neuronal assemblies (3 and 1.5 hub cells per slice culture, respectively).

Figure 3.

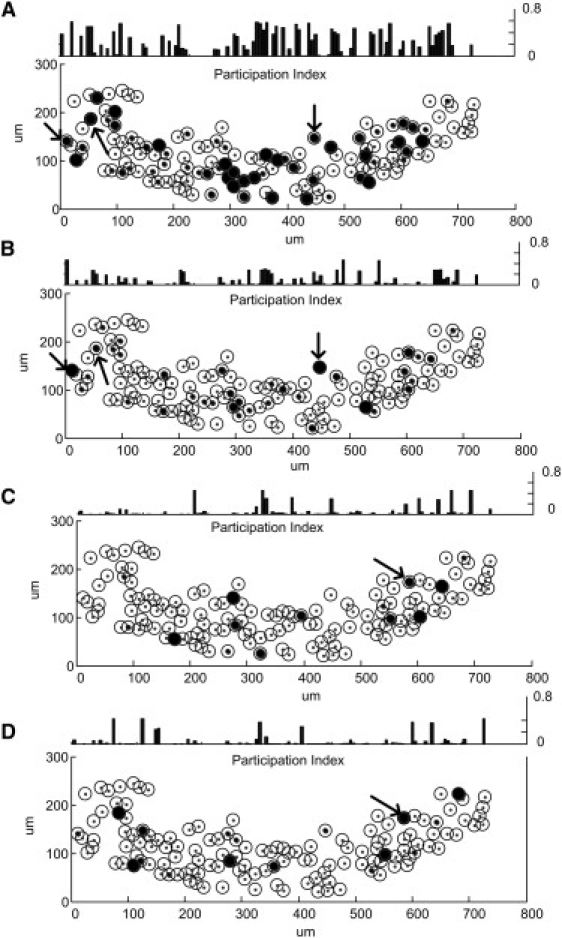
Details of the functional organization of neuronal assemblies depicted in Fig. 1. The bottom plot in each figure shows the elements of neuronal assembly. (Open circles) Neurons with Ca²⁺ signal and their physical positions in the CA3 region of the hippocampus. (Solid circles) Degree of participation of a given neuron in the neuronal assembly. The diameter of circles is proportional to the contributions to the neuronal assembly. The top plot in each figure is the contribution of neurons to neuronal assemblies (participation index). The participation index is equal to the diameter of solid circles at the bottom plot. Superconnected hub neurons belonging to more than one cluster are indicated by arrows (the different direction of arrows indicates different hub). (A) The participation index and neuronal assembly of the first cluster. (B) The participation index and neuronal assembly of the second cluster. (C) The participation index and neuronal assembly of the third cluster. (D) The participation index and neuronal assembly of the forth cluster.

Organization of neuronal assemblies

In this study, spike trains from 25 slice cultures were recorded and synchronization analysis of all slices was separately performed. All slices were from the same region of the brain and can therefore be reasonably assumed to possess the same connectivity statistics. Indeed, each slice contained 4–6 functional assemblies (total 154 neuronal assemblies were analyzed). Then, we analyzed the organization of the neuronal assemblies pooled from all the slices in detail to enable us to understand the collective dynamics of cell clusters. The number of neurons in a neuronal assembly was termed as cluster size, the shortest mean distance as cluster distance, and the synchronization index as cluster strength. By taking the logarithm of both sides (log₁₀–log₁₀) (Fig. 4), the distribution of clustering strength, size, and distance of neuronal assemblies demonstrated power-law (P(k) ∼ k^−a) distribution characteristics in all analyzed cases. The clustering strength increased with the increase of cluster size and decreased with the increase of the distance of participating neurons (Fig. 4, A and B). The calculated Pearson's correlation coefficients (r) were 0.813 (P < 10⁻⁴, 154 pairs) and –0.610 (P < 10⁻⁴, 154 pairs). The distance between the neurons of the assemblies decreased with the increase of the cluster size in the same manner (Fig. 4 C; r = 0.813, P < 10⁻⁴, 154 pairs). The Pearson's correlation coefficient was of high value (r = 0.813), indicating that the clustering strength of neuronal assemblies was strongly dependent on the cluster size. The correlation coefficient calculation also demonstrated that the cluster size was inversely dependent on the distance of clustered neurons (Fig. 4 C, r = −0.654).

Figure 4.

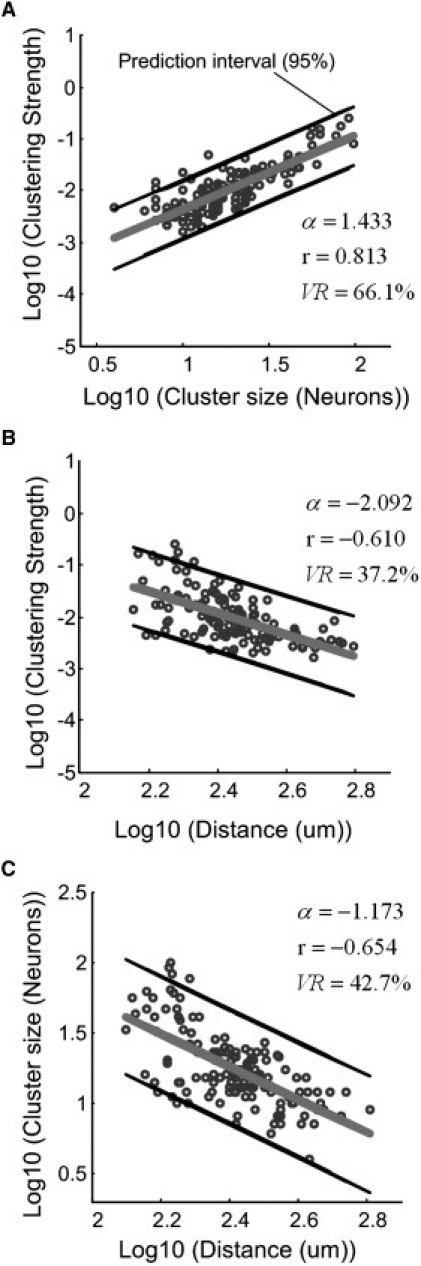
Power-law relationship among the clustering strength, size, and distance of neuronal assemblies. (A) Log₁₀–log₁₀ graph of the clustering strength and the size of neuronal assemblies. Slope: α = 1.433; Pearson's correlation coefficient (r): r = 0.813 (confidence interval (CI) 0.746–0.864, P < 10⁻⁴). The variability by regression: VR = 66.1%. (B) Log₁₀–log₁₀ graph of the clustering strength and the distance of neuronal assemblies. Slope: α = −2.092; r = −0.610 (CI −0.707–0.491, P < 10⁻⁴); VR = 37.2%. (C) Log₁₀–log₁₀ graph of the distance and the size of neuronal assemblies. Slope: α = −1.173; r = −0.654 (CI −0.742–0.544, P < 10⁻⁴); VR = 42.7%.

A similar nonlinear power-law relationship was found among the participation indices of neurons (PIs) and the clustering strength, cluster size, and cluster distance (Fig. 5). The clustering strength, cluster size, and distance were decreased with the increase of the coefficients of variation of PI (Fig. 5, A–C; r = −0.647, −0.896, and −0.695, P < 10⁻⁴, respectively). To assess the degree of randomness that a neuron contributes to a given cluster, we calculated the probability distribution of PI values (entropy). The analysis showed a potential power-law relationship between the various characteristics of neuronal assembles and the entropy of PI. The uncertainty of PI led to the increase of clustering strength, size and distance of neuronal assemblies (Fig. 5, D–F; r = 0.519, 0.860, and 0.619, P < 10⁻⁴, respectively). A closer observation indicated the presence of a knee at the point 0.35 (log₁₀ CV of PI, Fig. 5, A and B), and 0.55 (log₁₀ entropy of PI, Fig. 5, D and E) of the curves. The clustering strength and size of the cell assemblies were concentrated around these knee points. This finding indicates that two types of scale-free networks might exist in the analyzed 154 networks. Detailed analysis of these two types of networks is the subject of a separate study.

Figure 5.

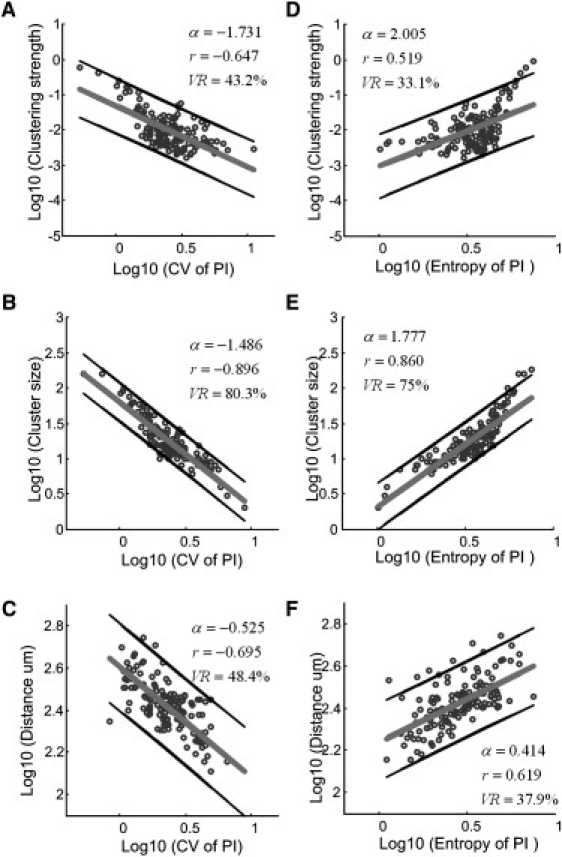
Power-law relationship between various neuronal assembly properties and the participation indices (PIs) of neurons. The clustering strength, size, and distance of neuronal assemblies decrease with the coefficients of variation (CV) of the PI and increase with the entropy of the PI. (A–C) Log₁₀–log₁₀ graph among the clustering strength, cluster size, and cluster distances with the CV of PI. (D–F) Log₁₀–log₁₀ graph of clustering strength, size, and distances with the entropy of PI.

To analyze pathologic network activity, epileptiform activity was induced by bath-application of 50 μM picrotoxin, a GABA_A receptor blocker. Almost all cells fired in synchrony at ∼30-s intervals, and thus, the cell assemblies featured by a power-law relationship were no longer found (n = 3, data not shown). This validates our analysis, and also suggests that the power-law regime in spontaneous activity could serve as a diagnostic marker for pathologic network operation.

Anatomical structure of neuronal assemblies

Using the fMCI method, we monitored the activity of >100 neurons in each CA3 area (n = 25) and determined their location in the network. We investigated the relationship between various clustering parameters and the physical distribution of the neurons that fired together. The relationship between the number of neurons or distance among neurons and clustering strength, cluster size, and distance of neuronal assemblies were analyzed, and the corresponding Pearson's correlation coefficients were plotted (Fig. 6). The results showed that the clustering strength and the size of neuronal assemblies were not correlated with the total number of neurons (Fig. 6, A and B; r = −0.107, −0.006). No correlation between the mean distance of neurons located in the slice preparation and the clustering strength and cluster size was found (r = 0.07 and 0.134; Fig. 6, D and E). However, the clustering distance had a weak linear relation to the number of neurons (r = 0.314, P = 0.105; Fig. 6 C) and to the mean distance of neurons located in the slice preparation (r = 0.280, P = 0.94; Fig. 6 F). These relations indicate that the clustering strength and size of neuronal assemblies are not correlated with the total number of neurons and their physical distance. However, the clustering distance of neuronal assemblies is weakly correlated with the total number of neurons and the physical distribution of neurons in the CA3 network.

Figure 6.

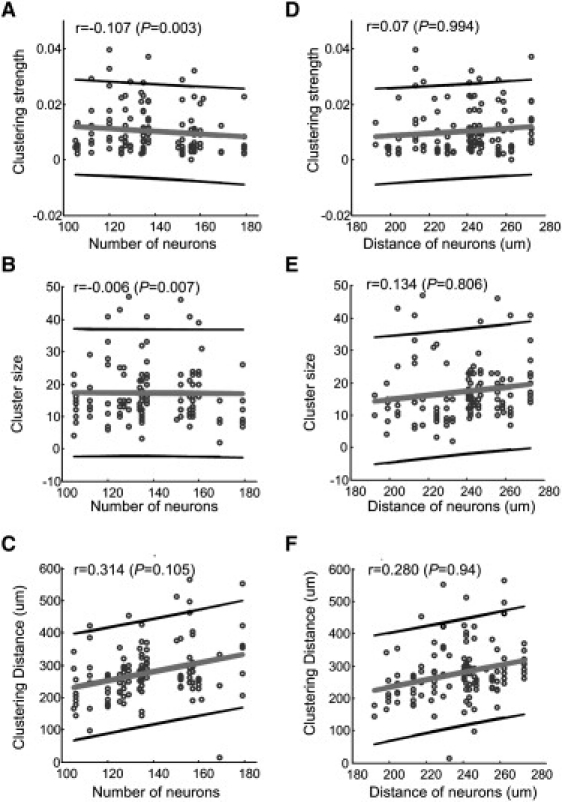
Relationships between various connectivity features of neuronal assemblies and the spatial distribution of active neurons. (A and B) The clustering strength and size of neuronal assemblies show no correlation with the number of active neurons located in the slices (|r| < 0.02). (C) The clustering distance is weakly dependent on the number of active neurons located in the organotypic slice cultures (r = 0.314). (D and E) The clustering strength and size of neuronal assemblies have no correlation with the distance of active neurons located in the slice (|r| < 0.15). (F) The distance of neuronal assemblies shows a weak relation to the distance of individual neurons (r = 0.280).

Discussion

Several methods, including cluster (44), graph theoretical (45), and mixture-of-Gaussians analysis (46), have been successfully applied to analyze the synchronization between multiple neural signals. The cluster analysis method provides information about the connection architectures (the tree), but does not describe the strength of clusters. The graph theoretical analysis method transfers the synchronization matrix into binary graphs by a threshold that is hard to determine. The mixture-of-Gaussians analysis method reveals the number of clusters and the elements of each cluster but fails to describe the strength of clustering. The correlation matrix analysis method with event synchronization that we used in this study can combine all the relevant information needed to quantify synchronization of multiple spike trains.

Most current experimental studies rely on random sampling of neurons appropriate for studying the properties of synaptic connections. Recent work has demonstrated that strong connections are embedded into the sea of weakly connected networks (5). The superconnected cells (hubs) are proposed to have large influence on network dynamics (4,5,24,36), thus it is important to selectively study particularly strong connections. Analysis of the number and distribution of hubs is important in the hippocampal network because the introduction of such superconnected cells transforms the normal functioning of the network to the epileptic state (4). Because the highly influential and strong synaptic connections in the network are few in number (5), it is challenging to find and characterize them. Because extracellular recording methods provide characterization of a limited number of simultaneously recorded neurons, they are unable to provide the spatial distribution of the cells (37). Quadruple in vitro whole-cell recoding technique is a powerful technique, but it is very labor-intensive. Although understanding normal and pathological brain function is one of the ultimate goals of neuroscience, many questions cannot be addressed in the intact brain because available technology does not allow simultaneous recording from many neurons. To overcome these limitations, we chose the fMCI technique performed on organotypic slice cultures that enabled us the simultaneous visualization of large number of neurons' activity. The slicing procedure significantly alters the connectivity pattern (38): the estimated divergence of a CA3 pyramidal cell is 5000 in vitro (39) and 15,000 in vivo (40,41). Because very small divergence is necessary to ensure strong connectivity of the CA3 recurrent network (42), the basic functional connectivity that characterizes the in vivo condition is likely to be preserved in organotypic slices. In addition, during the culturing process, axons regrow and form synaptic connections with their targets. Our observation that neurons at close proximity do not preferentially form functional cell clusters suggests that the recurrent axonal connections targeting distal elements are efficiently regenerated (43).

Traditionally, networks of complex topology have been modeled with the random-graph theory (47). It was, however, recognized that this model is unable to describe real neuronal networks because of the unrealistically large level of connectivity required. Efficient wiring of large neuronal networks can be achieved by small-world architecture, which is characterized by mainly locally connected neighboring cells with a few number of long-range connections (8), and by scale-free architecture, with power-law distributions of connectivity (13).

The random-graph and small-world models assume that the number of elements (i.e.: neurons) is unchanged. However, necrosis and apoptosis decrease the number of neuron whereas neurogenesis increases the hippocampal neuron number during development and adulthood, and only scale-invariant, or scale-free, networks are robust against changes in cell number with time. Another characteristic of a scale-free network is the existence of a superconnected hubs (13). To our knowledge, our data is the first to show the existence of such hubs, which further suggests the scale-free structure of the CA3 hippocampal network. Such organization provides functional benefit for memory formation because information can reverberate for the longest time among any other type of network (4). Consistently, oscillatory patterns, fundamental for various hippocampal functions, is achieved if the neurons contact using a power-law distribution (37). Interestingly, another hippocampal network, the dentate gyrus, has a fundamentally different organization. Computer simulation has demonstrated that, although under normal conditions the dentate gyrus neuronal network is stable, changing the structure to a scale-free topology greatly enhances the excitability of the dentate gyrus. Importantly, the presence of hubs significantly increases the excitability of the network leading to an epileptic discharge pattern (4). One could conclude that neuronal hub structure is detrimental to network operation. It is likely the case only if a large number of hubs present rendering the network is hyperexcitable. Our experiment and analysis, however, show that hub cells, especially with four or more intercluster participation, are sparse. Such an arrangement would give the hub neurons a larger role in the network and represent a hierarchal organizational scheme of the network structure (14). The scale-free topology of the hippocampal CA3 network with the existing hub cells is likely the reason why this subfield is critical for seizure generation and propagation (48–50).

In our experiment the hippocampal CA3 area was only partially monitored, therefore it is reasonable to assume that the cluster size, strength, and the clustering distance might be larger in vivo. However, the total number of neurons did not influence the cluster size and clustering strength, thus these parameters are likely to be similar in the intact brain. Previous in vivo neuroanatomical observations in the cortex (51,52) and hippocampus (40,41) are indeed in parallel with this prediction. These and numerous other studies showed that pyramidal cells are interconnected by one or very few contacts independent on the distance between the connected neurons.

Currently hippocampal networks are modeled with small-world topology (53). Although in vivo experimental work is necessary to characterize the connectivity of hippocampal cells in intact brain, our analysis combined with the described experimental work strongly support that the hippocampal CA3 network has the power-law connectivity of the scale-free network. With the advance of in vivo multineuronal recording method and the analysis, we foresee that similar scale-free topology will be discovered in other cortical regions (10,54,55), while interregional functional connectivity has small-world topology (i.e., (9,56,57)).

Conclusion

Our findings suggest that the functional organization of the CA3 network in hippocampal slice culture has a scale-free structure. The analytical method described here can also be employed to reveal fundamental properties of functional cell assemblies in other parts of the intact nervous system.