Damage, Self-Healing, and Hysteresis in Spider Silks

Abstract

In this article, we propose a microstructure-based continuum model to describe the material behavior of spider silks. We suppose that the material is composed of a soft fraction with entropic elasticity and a hard, damageable fraction. The hard fraction models the presence of stiffer, crystal-rich, oriented regions and accounts for the effect of softening induced by the breaking of hydrogen bonds. To describe the observed presence of crystals with different size, composition, and orientation, this hard fraction is modeled as a distribution of materials with variable properties. The soft fraction describes the remaining regions of amorphous material and is here modeled as a wormlike chain. During stretching, we consider the effect of bond-breaking as a transition from the hard- to the soft-material phase. As we demonstrate, a crucial effect of bond-breaking that accompanies the softening of the material is an increase in contour length associated with chains unraveling. The model describes also the self-healing properties of the material by assuming partial bond reconnection upon unloading. Despite its simplicity, the proposed mechanical system reproduces the main experimental effects observed in cyclic loading of spider silks. Moreover, our approach is amenable to two- or three-dimensional extensions and may prove to be a useful tool in the field of microstructure optimization for bioinspired materials.

Introduction

Spider silk has attracted the attention of many scientists due to its extraordinary mechanical properties, combining a very high initial stiffness, comparable in some cases to steel and even Kevlar (e.g., dragline silks), with a high ductility accompanied by a surprising capacity for undergoing large recoverable strains and for dissipating energy. A less studied, very interesting property of spider silk that will be considered in this article is the self-healing capacity of spider silk due to bond reconnection upon unloading (1–3).

The analysis and modeling of these properties, although interesting from a biological point of view in describing the web's capacity to capture different insect species, is now, from an engineering perspective, considered crucial to the design of new, bioinspired materials. In particular, the deduction of predictive models that connect the mesoscale properties of the material with the macroscopic material response can deliver crucial information for the design of materials produced by genetic engineering (4,5).

From a theoretical point of view, several compelling tasks are accomplished by this material, ranging from the description of the roles of hysteresis and recovery in the material efficiency (1,3), to the influence of humidity and spinning force (3,6) as a possible control mechanism to obtain the different silks each spider can produce (7), to the main role of supercontraction (i.e., the moisture-induced shrinkage of spider web threads (8)).

Schematically, spider silk can be viewed as a semicrystalline material constituted by amorphous flexible chains reinforced by strong and stiff crystals, thus having interesting analogies to polymer nanocomposites and semicrystalline polymers. Although the mechanics of molecular assembly and the detailed microstructure of spider silk remain unclear, important insights into the structure of the silk filaments have been recorded. First, it is now clear that the reinforcing crystals are made by hydrophobic polyalanine sequences arranged in β-sheets. Moreover, microscale studies have clarified the mechanical role of the different material components (see, e.g., (9–11)).

An important molecular model of spider dragline elasticity was proposed by Termonia (12). In that work, the author described a regular lattice of nodes connected by end-to-end vectors of chain strands that could be either crystalline or amorphous. The former case involved a linear stress-strain relationship, whereas the latter involved a nonlinear relationship based on the inverse Langevin function (see, e.g., Treloar (13)). The resulting numerical simulations give important insights into the percentage, shape, and dimensions of the crystalline fraction, which creates inside the amorphous regions stiffer layers that are crucial for the high initial macroscopic stiffness and the energy dissipation properties due to strain-induced link breaks and unbinding processes of the protein assemblies.

Beyond the Termonia model, several other approaches have been proposed in the literature to explain the mechanical properties of spider silk. For example, hierarchical chain models were proposed by Becker et al. (2) and Zhou and Zhang (14). These approaches consider spider silk as composed of many bricks organized in a hierarchy that at its deepest level has β-crystallites. In these models, the origin of the elasticity of the polymer is entropic and the overall macroscopic response is the result of the energy exchanges of the different involved scales. Moreover, Porter et al. (15) propose a mean-field theory model for polymers in terms of chemical composition and degree of order in the polymer structure using group interaction modeling procedures (www.gimprops.com).

All these computational models have become important instruments for describing the material behavior at the different scales underlying the exceptional properties of spider silks. However, the main mechanisms correlating the micro- and mesostructural properties with the macroscale response are still not understood. Such an understanding requires the deduction of analytical models—crucial also for the optimization of bioinspired dissipative materials (4)—that deliver simple stress-strain relationships, for a general loading history, as a function of the material composition.

The importance of such analytical models is particularly evident in the high variability of the material response (16). Indeed, experiments on spider silks show that the mechanism of energetic competition between the hard crystal fraction and the amorphous entropic fraction of the material is the basis of the capacity of spiders to produce silks with very different macroscopic material properties. Actually, the experiments suggest that these arthropods have the ability to control the properties of both the amorphous and the crystalline fractions through the spinning process and the chemical composition (see (1,6,7,16) and references therein). We describe in this article, for example, the significantly different behaviors of the stiffer silks, produced in the major ampullate gland and constituting radii and frame threads characterized by a higher degree of crystallization, and the more compliant silks, produced in the flagelliform glands, which are characterized by a lower degree of crystallization.

Finally, it is important to remark that an effective model must include such a description for loading, unloading, and reloading. In particular, it has to describe the energy dissipation effect associated with hydrogen bonds breaking, the energy returned upon unloading, which is important in deterring the escape of an insect, and the behavior upon reloading by accounting for the recovery properties induced by the re-cross-linking effect (1).

In this article, we deduce a simple analytical model to describe the mechanical behavior of silk threads. More specifically, starting from the basic idea of the Termonia model, we propose a miscrostructure-based continuum model of spider silk relying on two basic building blocks: an amorphous network and an ordered network rich in β-sheets. Our model is a natural extension of the model proposed by De Tommasi et al. (17,18) to analyze the damage-induced softening behavior of rubberlike materials. The key feature of this approach is the assumption of a material configuration evolving at the microstructure scale. The role of this point of view in modeling polymeric materials is discussed by De Tommasi et al. (17,18). A second crucial assumption of our model is the introduction at each material point of a distribution of materials with variable properties, reproducing the amorphous character of the hard fraction that is constituted by different-sized and differently oriented crystal sheets (19).

Our simple model allows us to include all the main experimental effects previously described. Specifically, we obtain the two different behaviors observed in major ampullate and capture silk by varying the crystal fraction. We describe the ability to control chain alignment in the amorphous phase by a corresponding modification of the constitutive assumption in this phase only, and we show that in this way the model can reproduce the observed mechanical variations. In particular, we show that one of the main differences observed in the stress-strain behavior of spider silk, i.e., the presence of a stress plateau or continuous hardening (i.e., S-shaped versus J-shaped stress-strain curves) can be addressed by a competition between the (entropic) hardening effect of the amorphous fraction and the (damage-induced) softening of the hard fraction. The experimental comparison is significant not only for loading, but also for unloading and reloading.

We note that our model is amenable to three-dimensional extension (17,20), which is essential for application to the analysis of other biomaterials and bio-inspired materials. Moreover, it is important to underline that in our model, as in the model proposed by De Tommasi et al. (17), one can deduce the constitutive properties and the probability distribution functions by simple extension cyclic tests. Several generalizations of the model can be considered to describe important effects that are neglected here, such as viscoelastic behavior and permanent strains, or explicit deduction of the evolution laws for breaking and re-cross-linking of hydrogen bonds—here introduced phenomenologically—from the energy landscape at the microstructure scale.

To understand the relevance of this kind of model for spider silk, we describe here the schematic behavior of silk and numerous other biomacromolecules (21–23) (Fig. 1). The chain is represented as an alternating sequence of unraveled (soft-phase) and folded (hard-phase) segments that under chemical or mechanical loading can undergo microstructural modification. At a given microstructure configuration (fixed folded fraction), the behavior of the protein can be considered elastic and its mechanics can be well described by the theory of entropic elasticity. In this framework, the force-extension behavior is determined by the molecular chain extension and the related configurational entropy. As the force is increased, some of the weak links, e.g., H-bonds, in the hard phase may eventually break and a percentage of the linked fraction switches to the unfolded state, with two main effects: part of the material undergoes a transition from the hard phase to the soft phase, and the contour length changes (Fig. 1 B) as a consequence of the chain unraveling associated with bonds breaking. A corresponding increase in configurational entropy and a drop in force, f, is then observed.

Figure 1.

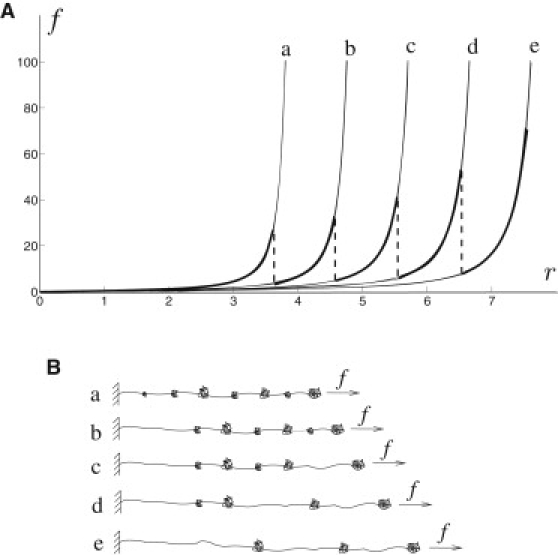
Schematic behavior of a single protein macromolecule. (A) Scheme of a typical force-displacement diagram (bold lines) under a WLC assumption, using different equilibrium branches with different contour lengths (a–e). (B) Schematic of the microstructure configuration of the equilibrium branches in A.

As an explicit example, we show the transition of the chain between different equilibrium force-displacement branches—corresponding to different folded fractions—under the hypothesis of a wormlike chain (WLC) law (24) (Fig. 1 A, bold lines). Our approach takes into account the microstructural changes by considering the variations of two internal variables: phase percentage and contour length.

If we then consider unloading, single-molecule experiments show that some of the previously broken links can reform (1,21,23). This effect is reflected in the observation of force discontinuities also upon reloading similar to those observed during the primary loading. In the framework of our model, this corresponds to the reverse transition, upon unloading, of part of the soft phase to the hard phase and a corresponding decrease in the contour length. This important effect leads to a definition of spider silk, as well as other protein-constituted materials (1,2,21), as self-healing materials.

Note that the mesoscopic structure we wish to model is complex, because spider silks are constituted by a full distribution of β-sheet crystals with variable strength and orientation (19) inside a matrix of amorphous material. Therefore, in our model, we assume that at each point there exists a mixture of hard and soft phases. As the strain is increased, the hard fraction can undergo a transition to the soft phase, and it is assigned a probability distribution of materials with variable activation and transition thresholds. Based on previous considerations (see also Oroudjev et al. (23)), we describe the corresponding microstructure modification through a simple phenomenological assumption of the dependence of a macroscopic contour length on the percentage of soft (unraveled) fraction.

Finally, because our focus is on a description of rate-independent dissipative effects, we assume that the activation and transition thresholds and the variation of the contour length depend only on the deformation of the thread, and we thus neglect inertia and rate effects (see Puglisi and Truskinovsky (25) for a related theoretical discussion in a different context).

The Model

Consider a homogeneous one-dimensional body with reference length L, constituted at each point x ∈ (0, L) by a distribution of different materials. A fraction α (soft fraction) of such mixture describes the amorphous percentage of macromolecules. This fraction is here modeled as a WLC, with a stress-strain law that, according to the approximate form proposed in Marko and Siggia (24), can be written as

$${\sigma }_{\text{s}}={\widehat{\sigma }}_{\text{s}}\left(\varepsilon ,{\varepsilon }_{\text{c}}\right)=E_{\text{s}}\left(\frac{1}{4}{\left(1-\frac{\varepsilon }{{\varepsilon }_{\text{c}}}\right)}^{-2}-\frac{1}{4}+\frac{\varepsilon }{{\varepsilon }_{\text{c}}}\right).$$ (1)

Here, σ_s is the stress in the soft fraction, ɛ is the strain, ɛ_c plays the role of a contour length and assigns a limit strain, as in Termonia (12), whereas E_s is the elastic modulus of the soft fraction (dependent on the persistent length and temperature in the original model; see, e.g., Marko et al. (24,26) and references therein). It is important to note that the architecture of our model does not depend on the explicit choice of ${\widehat{\sigma }}_{\text{s}}$: it is possible to consider other stress-strain constitutive equations that describe the high-strain entropic hardening effect, such as equations based on the inverse Langevin function or other phenomenological relations (27).

The remaining fraction of the mixture (hard fraction) describes the stiffer percentage of material in the crystalline state, covering the possibility of strain-induced damage. For simplicity, similar to De Tommasi et al. (17,18), we consider here a linear elastic behavior in the hard phase, i.e.,

$${\sigma }_{\text{h}}\left(\varepsilon \right)=\{\begin{array}{lll}0,\hfill & \text{if}\hfill & \varepsilon \le {\varepsilon }_{\text{a}},\hfill \\ E_{\text{h}}\left(\varepsilon -{\varepsilon }_{\text{a}}\right),\hfill & \text{if}\hfill & {\varepsilon }_{\text{a}}<\varepsilon <{\varepsilon }_{\text{t}},\hfill \\ {\sigma }_{\text{s}}\left(\varepsilon ,{\varepsilon }_{\text{c}}\right),\hfill & \text{if}\hfill & \varepsilon \ge {\varepsilon }_{\text{t}},\hfill \end{array}$$ (2)

where E_h is the elastic modulus of the hard fraction, ɛ_a represents the activation threshold, and ɛ_t represents the transition threshold (see Fig. 2 A). Thus, the material is activated at ɛ = ɛ_a and at ɛ = ɛ_t it undergoes a transition to the soft phase due to the process of strain-induced hydrogen debonding.

Figure 2.

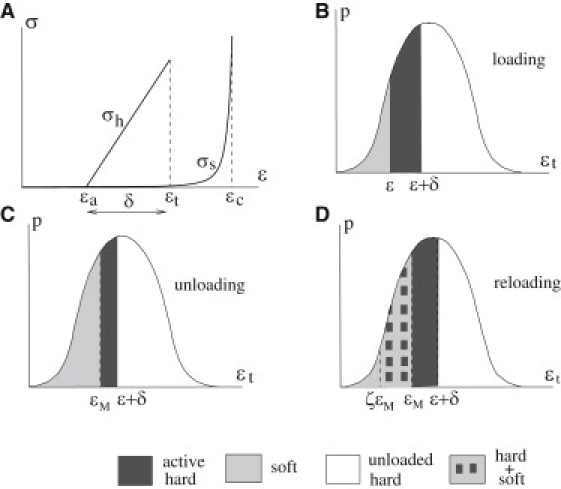
Constitutive assumptions. (A) Stress-strain relation of the hard phase. (B–D) Distribution of the hard and soft phases in the probability space during loading (B), unloading (C), and reloading (D).

To take care of the irregular and strongly variable structure of the crystallites, depending on the processing characteristics (19), we assign this fraction as a distribution of materials with variable activation and transition thresholds. More specifically, we assume for simplicity that although both ɛ_a and ɛ_t may change, the strain domain of each hard material,

$${\varepsilon }_{\text{t}}-{\varepsilon }_{\text{a}}=\delta ,$$ (3)

is fixed, so that each protein chain undergoes a transition to the soft phase after a fixed strain increment from activation. As a consequence, the distribution of the hard material can be represented by a single-parameter probability function, p = p(ɛ_t). For the sake of definiteness, we consider a Gaussian type distribution:

$$p\left({\varepsilon }_{\text{t}}\right)=\xi e^{-\beta {\left({\varepsilon }_{\text{t}}-\gamma \right)}^2}.$$ (4)

The parameter ξ accounts for the normalization condition ${\int }_0^{\mathrm{\infty }}p\left({\varepsilon }_{\text{t}}\right)d{\varepsilon }_{\text{t}}=1$.

We point out that to ensure that all activation thresholds are nonnegative (i.e., ɛ_a ≥ 0), we restrict Eq. 3 to the links with ɛ_t > δ, whereas for all other links, with ɛ_t ≤ δ, we assume that ɛ_a = 0. This assumption ensures also that at ɛ = 0, the finite fraction of links ${\int }_0^{\delta }p\left({\varepsilon }_{\text{t}}\right)d{\varepsilon }_{\text{t}}$ is contemporarily activated, with a nonzero initial stiffness of the system. We remark also that although important information on the various constitutive functions may be deduced from single-molecule force spectroscopy (23) and solid-state NMR measurements (11), in the spirit of De Tommasi et al. (17), it is possible to deduce such information by simple cyclic force-displacement experiments on the spider silk threads.

Finally, in accordance with the previous discussion, to show that the contour length of the protein chains grows with the percentage of unfolded material, we assume that

$${\varepsilon }_{\text{c}}={\widehat{\varepsilon }}_{\text{c}}\left(\alpha \right),$$ (5)

where ${\widehat{\varepsilon }}_{\text{c}}$ is an increasing function.

To describe the behavior of the introduced damageable amorphous material, we consider separately the responses of the system upon loading, unloading, and reloading. In all three cases, we show that it is possible to quantitatively reproduce the experimental curves. We remark, however, that due to the small reproducibility of the experimental behavior of spider silks (see, e.g., Guinea et al. (6)), the main aim of comparison with the experiments relies on the ability of our model to relate different classes of experimental curves to different microstructural distributions.

Primary loading

Consider first a primary loading path, starting from an initial configuration characterized by a fraction α₀ of material in the soft phase. At the given ɛ, according to Eq. 2, all the hard material for which ɛ_a = ɛ_t – δ < ɛ is activated. Within this fraction, the material for which ɛ_t > ɛ is still in the hard phase, whereas the material for which ɛ_t < ɛ has changed state to the soft phase (see Fig. 2, A and B). Thus, during the primary loading path, the fraction of soft material is given by

$$\alpha ={\alpha }^{\text{l}}\left(\varepsilon \right)={\alpha }_0+{\int }_0^{\varepsilon }p\left({\varepsilon }_{\text{t}}\right)d{\varepsilon }_{\text{t}}.$$ (6)

As shown in Fig. 2 B, the fraction of hard material, ${\int }_{\varepsilon +\delta }^{\mathrm{\infty }}p\left({\varepsilon }_{\text{t}}\right)d{\varepsilon }_{\text{t}}$, is still unstressed, i.e., nonactive, whereas the fraction of active hard material is ${\int }_{\varepsilon }^{\varepsilon +\delta }p\left({\varepsilon }_t\right)d{\varepsilon }_t$. As a result, under an additive assumption of the stress of the hard and the soft phase, and under the hypothesis in Eq. 5, we can deduce the overall stress-strain relation during loading:

$$\sigma ={\sigma }^{\text{l}}\left(\varepsilon \right)={\alpha }^{\text{l}}\left(\varepsilon \right){\widehat{\sigma }}_{\text{s}}\left(\varepsilon ,{\widehat{\varepsilon }}_{\text{c}}\left({\alpha }^{\text{l}}\left(\varepsilon \right)\right)\right)+E_{\text{h}}({\int }_{\varepsilon }^{\delta }\varepsilon p\left({\varepsilon }_{\text{t}}\right)d{\varepsilon }_{\text{t}}+{\int }_{\max \left(\varepsilon ,\delta \right)}^{\varepsilon +\delta }\left(\varepsilon -\left({\varepsilon }_{\text{t}}-\delta \right)\right)p\left({\varepsilon }_{\text{t}}\right)d{\varepsilon }_{\text{t}})\text{.}$$ (7)

(Note that here and in the text below, for the sake of simplicity, we assume that the integrals are null if the upper integration limit is lower than the lower limit). In Eq. 7, in accordance with the previous discussion, the first integral represents the hard material with ɛ_t < δ for which we assumed ɛ_a = 0, and the second integral represents the hard material with ɛ_t > δ and ɛ_a = ɛ_t – δ.

The stress-strain behavior obtained when the soft fraction varies is shown in Fig. 3 A. As noted above, the markedly different experimental response of the silks of different spider species or of different glands of the same spider should be considered a result of an ability to control (through spinning speed, water content, and chemical composition) the properties of both the amorphous and the crystalline fraction (1,7,8,28). A first example of this ability is the dependence of the stress-strain response on the constitutive properties of the amorphous phase (Fig. 3 A). In particular, curves a–c are characterized by an increasingly stiffer amorphous fraction, whereas the hard phase remains the same. Observe that for curve c the system shows a hardening behavior up to breaking, whereas for a and b the system is characterized by a significant softening in anticipation of the hardening of the amorphous phase. This is qualitatively in accordance with experimental effects described by others (6,8,28) in studies of the effect of increased stiffness controlled by spinning forces or spinning speed (Fig. 3 B). The same experiments also show that when the stiffness of the soft phase is increased, the ultimate stress grows, whereas the ultimate strain decreases, and this was reproduced by our model (Fig. 3 A). The theoretical curves well describe the experimental curves in Fig. 3 B corresponding to different prestrains performed on the threads before the loading experiments. Prestrain induces chain alignment in the amorphous fraction, with corresponding increasing stiffness from a to c.

Figure 3.

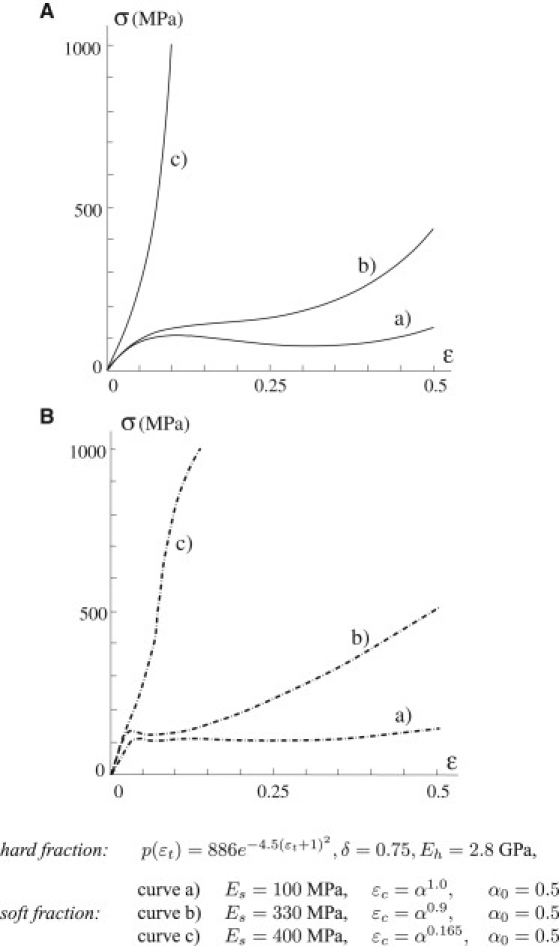
Mechanical behavior under a variable soft fraction. (A) Primary loading path for three systems (a–c) characterized by different assumptions of the soft fraction. (B) Depiction of the experimental behavior when the soft fraction is varied, as described by Guinea et al. (6) and reproduced by our model (A). The constitutive parameters are listed beneath the figure. Prestrain induces an alignment in the soft fraction, with increasing stiffness.

The effect of variation of the percentage of crystal fraction is described in Fig. 4. The ability of spiders to vary the degree of crystallization, thus delivering different stiffness and toughness to differently aimed silks, is well documented (1,7). In particular, the experiments show (see also Fig. 4 B) that the frame silk, with higher crystallization, is characterized by an S-shaped force displacement curve. On the contrary, the viscid silk, with lower crystallization, is characterized by an always increasing hardening, i.e., a J-shaped curve. This behavior is shown in Fig. 4 A, where two materials with different crystal fractions are considered. Similar considerations can be extended to the important influence of humidity on the mechanical response of spider silk. Indeed, as the humidity increases, the degree of crystallization decreases (12).

Figure 4.

Mechanical behavior when the hard and soft fraction are both varied. (A) Primary loading path for two systems characterized by two different assumptions of the crystalline fraction. The constitutive parameters are listed below the figure. (B) Depiction of the experimental behavior reported by Denny (1) and reproduced by our model (A), where the different curves correspond to frame (a) and viscid (b) silk, characterized by a large and small crystalline fraction, respectively.

Unloading

Consider now the case of unloading. For the given strain, the stress upon unloading is lower than during loading, because of the evolution of the reference configuration and because of the lower hard fraction due to previous hard-soft transition. Specifically, if we consider an unloading path, $\varepsilon :{\varepsilon }_M\to 0$, we find that all the material with ɛ_t < ɛ_M changed state to the soft phase (Fig. 2 C):

$$\alpha ={\alpha }^{\text{u}}\left({\varepsilon }_M\right)={\alpha }_0+{\int }_0^{{\varepsilon }_M}p\left({\varepsilon }_{\text{t}}\right)d{\varepsilon }_{\text{t}}.$$ (8)

Thus, the contribution of the hard fraction is the result of the mechanical response of the amount of hard material that did not undergo a phase transition (i.e., ɛ_t < ɛ_M) that has ɛ_a = ɛ_t – δ < ɛ. As a result, the stress-strain relation upon unloading is given by the following law:

$$\sigma ={\sigma }^u\left(\varepsilon ,{\varepsilon }_M\right)={\alpha }^{\text{u}}\left({\varepsilon }_M\right){\widehat{\sigma }}_{\text{s}}\left(\varepsilon ,{\widehat{\varepsilon }}_{\text{c}}\left({\alpha }^u\left({\varepsilon }_M\right)\right)\right)+E_{\text{h}}{\int }_{{\varepsilon }_M}^{\varepsilon +\delta }\left(\varepsilon -\left({\varepsilon }_{\text{t}}-\delta \right)\right)p\left({\varepsilon }_{\text{t}}\right)d{\varepsilon }_{\text{t}}$$ (9)

To describe the behavior of our system upon unloading, in Fig. 5 we show the cyclic force-displacement curves for the same materials described in Fig. 4. The results well reproduce the experimental behavior observed by, e.g., Gosline et al. (7). Observe in particular the transition from an S shape for loading to a J-shaped curve upon unloading. Also, these results show the possibility of regulating both the dissipated and the returned energy upon unloading by varying the fraction of crystallized material. This ability is crucial to the production of differently used silks. We remark that, although we ignore this in the interests of compactness, our model can deliver, in the spirit of De Tommasi et al. (17), a complete energetic analysis with an analytic decomposition of the external work into stored and dissipated energy.

Figure 5.

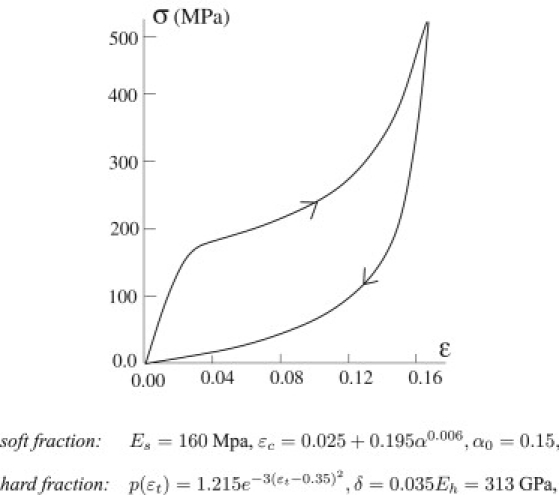
Unloading behavior. The system is unloaded at ɛ_M = 0.18. The constitutive parameters are listed below the figure.

Reloading

One of the most interesting properties of spider silks is the possibility of recovering upon simple rest after unloading (1,3). This crucial effect is due to the possibility of healing some or all of the previously broken hydrogen bonds.

To introduce this effect in the model here considered, in the spirit of D'Ambrosio et al. (29), one should describe the evolution law regulating the process of reforming links. Here again, we consider a simple phenomenological approach and assume that part of the material that changed phase during loading—i.e., the material with ɛ_t < ɛ_M, where again ɛ_M is the maximum value of the previously attained strain—can undergo the reverse transition, soft → hard (Fig. 2 D), in the unloading, $\varepsilon :{\varepsilon }_{\text{M}}\to 0$. Specifically, we assume that a fraction χ of the material with ɛ_t ∈ (ζɛ_M, ɛ_M) undergoes this transition. Both the parameter χ ∈ (0, 1) and ζ ∈ (0, 1) should be considered as temperature-dependent and are macroscopic counterparts of the complex reconnecting processes at the microscale.

Under these assumptions, if we consider a reloading path $\varepsilon :0\to {\varepsilon }_{\text{M}}$, the fraction of soft material during reloading is given by

$$\alpha ={\alpha }^r\left(\varepsilon ,{\varepsilon }_M\right)={\alpha }_0+{\int }_0^{\max \left(\varepsilon ,\zeta {\varepsilon }_M\right)}p\left({\varepsilon }_{\text{t}}\right)d{\varepsilon }_{\text{t}}+\left(1-\chi \right){\int }_{\max \left(\varepsilon ,\zeta {\varepsilon }_M\right)}^{{\varepsilon }^m}p\left({\varepsilon }_{\text{t}}\right)d{\varepsilon }_{\text{t}}.$$ (10)

The stress due to the hard fraction is related to the contributions of the healed fraction χ and the hard fraction that never changed phase (Fig. 2 D). Thus, we find that upon reloading, the stress-strain law is given by

$$\sigma ={\sigma }^r\left(\varepsilon ,{\varepsilon }_M\right)={\alpha }^r\left(\varepsilon ,{\varepsilon }_M\right){\widehat{\sigma }}_{\text{s}}\left(\varepsilon ,{\widehat{\varepsilon }}_{\text{c}}\left({\alpha }^r\left(\varepsilon ,{\varepsilon }_M\right)\right)\right)+\chi E_{\text{h}}{\int }_{\max \left(\varepsilon ,\zeta {\varepsilon }_M\right)}^{\min \left(\varepsilon +\delta ,{\varepsilon }_M\right)}\left(\varepsilon -\left({\varepsilon }_{\text{t}}-\delta \right)\right)p\left({\varepsilon }_{\text{t}}\right)d{\varepsilon }_{\text{t}}+E_{\text{h}}{\int }_{{\varepsilon }_M}^{\varepsilon +\delta }\left(\varepsilon -\left({\varepsilon }_{\text{t}}-\delta \right)\right)p\left({\varepsilon }_{\text{t}}\right)d{\varepsilon }_{\text{t}}.$$ (11)

Fig. 6 shows the behavior under reloading of the same system considered in Fig. 5. In this case also, our simple model reproduces the main experimental effects (see, e.g., (1,3)). In particular, we observe that the system describes an hysteretic behavior and an S-shaped force-displacement behavior for both loading and reloading. Moreover, when reloaded, the system reconnects at ɛ = ɛ_M to the primary loading path, and if the strain is increased even more, it follows the same path as primary loading. For a fixed maximum strain, in successive cycles, ${\varepsilon }_{\text{M}}\to 0\to {\varepsilon }_{\text{M}}$, the system follows the same hysteresis loops. These effects are described explicitly in the experiments by Vehoff et al. (3).

Figure 6.

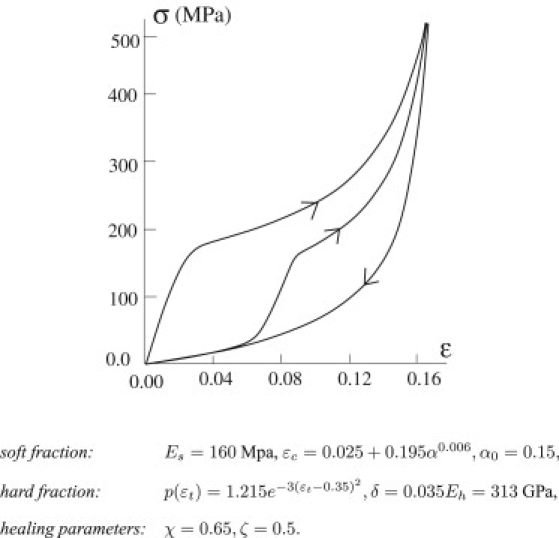
Cyclic loading. The system is unloaded at ɛ_M = 0.18. The constitutive parameters are listed below the figure.

We also remark that the experiments of Denny (1) show that by increasing the temperature, T, the material can undergo a complete recovery. This effect can be described in our model by simply considering temperature-dependent recovery parameters: $\zeta =\widehat{\zeta }\left(T\right)$ and $\chi =\widehat{\chi }\left(T\right)$.

Conclusions

As a concluding comparison with experiments, we show in Fig. 7 that our model can describe quantitatively the behavior experimentally observed by Denny (1) in cyclic loading of frame and viscid silks. The possibility of reproducing accurately the main experimental effects observed in spider silks relies on the ability of the model to reproduce the principal mechanisms underlying the amazing properties of these materials, i.e., the mechanisms of entropy release associated with chain unraveling during bond breaking and the amorphous character at the microstructure scale, with distributed processes of breaking and reforming of H-bonds.

Figure 7.

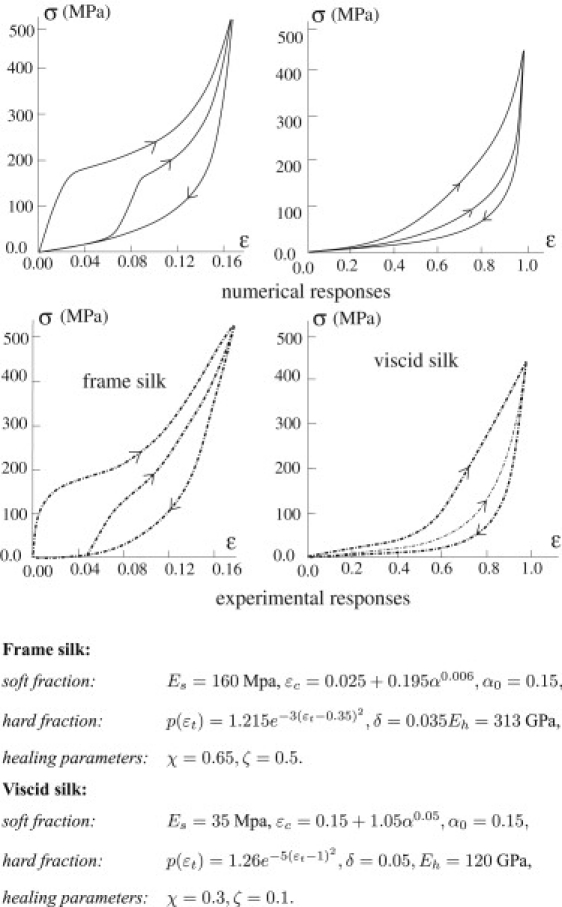
Cyclic loading for frame and viscid silks. (Upper) Model behavior. For the frame silk, we unloaded at ɛ_M = 0.18, whereas for the viscid silk we unloaded at ɛ_M = 1. The constitutive parameters are listed below the figure. (Lower) Experimental behavior of frame and viscid silk, reproduced from Denny (1).

It is important to remark that our model is amenable to three-dimensional extension (17,20,30), and this is essential for the analysis and design of bioinspired materials. Moreover, we underline that although in all comparisons with experiments we chose the constitutive functions to reproduce the macroscale experiments, important information on these functions may be deduced from single-molecule force spectroscopy (23) and solid-state NMR measurements (11). Finally, we remark that using the approach in De Tommasi et al. (17), it is possible to experimentally deduce the constitutive parameters and the distribution function p by simple cyclic extension tests on the material.

Thus, our microstructure-based continuum model may provide an instrument that can describe how the macroscale material properties vary with the microstructure and it thus constitutes, in our opinion, an important tool in the field of design of new dissipative materials. Moreover, the approach here proposed can be extended to other biomaterials characterized by similar mechanisms of dissipation at the microscale (22,31).