Abstract
An increasing number of functional studies of proteins have shown that sequence and structural similarities alone may not be sufficient for reliable prediction of their interaction properties. This is particularly true for proteins recognizing specific antibodies, where the prediction of antibody-binding sites, called epitopes, has proven challenging. The antibody-binding properties of an antigen depend on its structure and related dynamics. Aiming to predict the antibody-binding regions of a protein, we investigate a new approach based on the integrated analysis of the dynamical and energetic properties of antigens, to identify nonoptimized, low-intensity energetic interaction networks in the protein structure isolated in solution. The method is based on the idea that recognition sites may correspond to localized regions with low-intensity energetic couplings with the rest of the protein, which allows them to undergo conformational changes, to be recognized by a binding partner, and to tolerate mutations with minimal energetic expense. Upon analyzing the results on isolated proteins and benchmarking against antibody complexes, it is found that the method successfully identifies binding sites located on the protein surface that are accessible to putative binding partners. The combination of dynamics and energetics can thus discriminate between epitopes and other substructures based only on physical properties. We discuss implications for vaccine design.
Introduction
Understanding protein-protein interactions is a crucial step in the development of a molecular view of biological processes and in learning how to manipulate them. The progress of genomics and proteomics provided a great deal of information on the sequences, thermodynamics, kinetics, biological functions, and structures of an ever-growing number of protein complexes. However, these techniques can be expensive and time-consuming. Consequently, computational methods have gained increasing importance in the field: the ability to predict interaction interfaces is in fact a fundamental prerequisite to understand complex formation, particularly for novel folds with little or no similarity with known molecules.
Protein interaction sites have been analyzed in terms of sequences, physico-chemical profiles, B-factors, solvent accessibility, structures, homologies, and similarities, etc. (1–10). These properties have been combined in different ways in algorithms for the prediction of protein interfaces in biomolecular complexes (for a review on methods and their performances, see (1)).
A particular role in protein-protein interactions is played by antigen-antibody recognition. The limited number of available protein-antibody structures has somehow hampered the development of methods for the prediction of antibody binding sites, known as epitopes (11,12). However, the renewed interest in vaccine development gave new impulse to this field. Vaccination represents one of the most reliable strategies to fight infections and overcome the onset of drug-resistance by an ever-growing number of pathogens (13–17). One of the main challenges in the discovery of new vaccines is the discrimination of the components capable of eliciting a protective immune response from the thousands of different (macro)molecules of the pathogen. In this context, the reverse vaccinology approach (RV) (18–22) has introduced a new paradigm of candidate selection and vaccine development. RV involves the analysis of multiple genomes of related pathogens, followed by in silico identification and experimental expression of potential surface-exposed proteins. Vaccine candidates are then produced and tested for their capacity to induce protective immunity (20,23). This strategy led to the identification of protective vaccines against Neisseria meningitidis or Group B Streptococcus.
Complementing RV strategies with structural information on the antigens may open up a new era of vaccinology based on the possibility of rationally designing new protein-vaccines with optimized properties. High-resolution structural information on relevant antigens in complex with their respective antibodies or in isolation has indeed begun to appear (24,25).
A fundamental step toward structural-vaccinology relies on our ability to predict epitopes for a given protein and elucidate their physico-chemical properties. The structure, dynamics, and energetics of a specific site on a protein domain, or of the protein domain as a whole (24), play a main role in determining the antigenic properties of specific (fragments of) protein constructs, the interaction of epitopes with antibodies, and their relevance for a protective response (26).
An epitope may be either a short linear stretch from the protein sequence, defined as a continuous or linear epitope, or a three-dimensional, organized substructure consisting of different segments that come together in the three-dimensional structure, but are distant in the primary sequence, known as discontinuous or conformational epitope. Most neutralizing epitopes in antibody-mediated responses are discontinuous. The fundamental mechanism of action of most vaccines in clinical use is to present these complex structures to antibodies that specifically bind them and start neutralization processes (24,27).
Prediction of linear epitopes can now be reliably achieved using sequence-dependent methods (12,28). In contrast, the prediction of conformational epitopes is more challenging and the knowledge of the three-dimensional structure of the protein-antigen is a prerequisite. Several correlations among flexibility, solvent accessibility, geometrical properties, approximations of protein shape together with clustering of neighboring residues, and antigenicity, have been proposed (12,29–33).
Most epitope prediction methods are based on the use of single structures from x-ray crystallographic studies. Proteins are, however, highly dynamical entities, and their functions are intimately correlated to motions (34–38). All-atom molecular dynamics (MD) simulations allow the investigation of these motions on a range of timescales, revealing interactions, correlations, and conformations that may be relevant in determining recognition processes. The utility of MD simulations in functional elucidation, analysis, and drug design has already been proved (29,35,39–42).
Herein, we report on the application of a novel method for epitope prediction based on the integrated analysis of the energetic and structural-dynamical properties of antigens (43–47). Our approach aims at identifying ab initio antigen substructures poised to interact with binding partners in general, and antibodies in particular. The method is based on the physico-chemical properties of the antigen protein in isolation (Table 1, and Table S1 in Supporting Material), without requiring any previous knowledge on antibody binding of related homologs, or training with a data set of known sequences, geometric descriptors, antibody-protein interactions, etc. Reliable physics-based prediction of a discontinuous epitope may have implication for vaccine design, allowing the development of mutants or mimics that favor the specific conformation required for antibody binding or the optimization of antigen stability without affecting the epitope site.
Table 1.
Performance of the MLCE method in epitope prediction
| Antigen | Antibody complexes | MD AUC | MM AUC | Sensitivity | Specificity | Accuracy | PPV∗ | No. of epitopes | Interface residues |
|---|---|---|---|---|---|---|---|---|---|
| 1AO3 | 1FE8, 2ADF | 0.5 | 0.37 | 0.12 | 0.77 | 0.65 | 0.1 | 2 | 33 |
| 1AUQ | 1OAK | 0.89 | 0.95 | 0.78 | 0.79 | 0.79 | 0.15 | 1 | 9 |
| 1BV1 | 1FSK | 0.64 | 0.41 | 0.35 | 0.78 | 0.74 | 0.16 | 1 | 17 |
| 1CK4 | 1MHP | 0.88 | 0.71 | 0.92 | 0.78 | 0.79 | 0.22 | 1 | 12 |
| 1CMW | 1BGX | 0.64 | 0.62 | 0.3 | 0.77 | 0.76 | 0.05 | 1 | 30 |
| 1D7P | 1IQD | 0.82 | 0.85 | 0.67 | 0.80 | 0.79 | 0.3 | 1 | 18 |
| 1GWP | 1AFV | 0.58 | 0.55 | 0.3 | 0.90 | 0.72 | 0.58 | 3 | 47 |
| 1HCN | 1QFW | 0.81 | 0.73 | 0.54 | 0.86 | 0.81 | 0.38 | 2 | 28 |
| 1K59 | 1H0D | 0.87 | 0.87 | 0.73 | 0.85 | 0.84 | 0.41 | 1 | 15 |
| 1KDC | 1NSN, 2GSI | 0.67 | 0.66 | 0.41 | 0.85 | 0.74 | 0.45 | 2 | 32 |
| 1KZQ | 1YNT | 0.56 | 0.61 | 0.36 | 0.74 | 0.70 | 0.12 | 1 | 22 |
| 1P4P | 1RJL | 0.98 | 0.98 | 1 | 0.89 | 0.9 | 0.48 | 1 | 13 |
| 1PKO | 1PKQ | 0.84 | 0.7 | 0.56 | 0.92 | 0.86 | 0.53 | 1 | 18 |
| 1POH | 2JEL | 0.25 | 0.24 | 0 | 0.83 | 0.62 | 0 | 1 | 21 |
| 1TFH | 1AHW | 0.69 | 0.66 | 0.3 | 0.82 | 0.75 | 0.21 | 1 | 27 |
| 1UW3 | 1TPX | 0.94 | 0.91 | 0.67 | 0.95 | 0.92 | 0.62 | 1 | 12 |
| 2VPF | 1BJ1, 2FJG, 2FJH, 1TZH, 1CZ8 | 0.49 | 0.56 | 0.21 | 0.89 | 0.61 | 0.57 | 2 | 40 |
| 3LZT | 1FDL, 1YQV, 1MLC, 1IC4, 1NDG, 1DQJ, 1NDM, 1P2C, 2ZNW | 0.67 | 0.66 | 0.2 | 0.92 | 0.56 | 0.72 | 3 | 65 |
| 7NN9 | 1NCA, 1NMC | 0.72 | 0.57 | 0.36 | 0.79 | 0.76 | 0.11 | 1 | 25 |
| Mean | 0.71 | 0.66 | 0.46 | 0.84 | 0.75 | 0.32 | 1.42 | 18.6 |
Columns 1 and 2: List of the Protein DataBank (PDB) codes of the isolated proteins studied and used for prediction in this article and of the complexes with their respective antibodies, which were used for benchmarking. Columns 3–9: Area under the curve (AUC) values calculated with the matrix of local coupling energies (MLCE) approach on the structures obtained from extensive molecular dynamics (MD) simulations; from molecular mechanics (MM) minimization on the PDB structure; sensitivity; specificity; accuracy; positive predicted value (PPV); number of epitopes in the protein; number of residues in the epitopes, calculated from MD simulations.
Calculated according to Ponomarenko and Bourne (11).
Material and Methods
Theoretical justification
Epitopes are parts of the protein that can be recognized by a binding partner. Their sequences are typically mutation-tolerant (32), suggesting that they are not involved in the stabilization of the antigen fold. These sites have evolved, and must continuously evolve, to escape recognition by the host immune system, without impairing the native structure of the protein necessary for function in the pathogen (see (24) and references therein). Moreover, epitopes can be flexible and easily undergo conformational fluctuations (11,29,48–50). In other words, they are not involved in major intramolecular stabilizing interactions with other residues of the protein important to preserve the fold.
From the conformational and topological standpoints, epitopes are exposed regions on the protein surface, accessible for antibody binding (30). Moreover, specifically in the case of discontinuous epitopes, high-resolution x-ray structures of antigen-antibody complexes showed they consist of residues whose spatial proximity relationships define a (large) patch on the surface of the antigen (25,51).
Based on these considerations, we have set out to combine an analysis of protein energetics obtainable from MD simulations with the topological information obtainable from the contact matrix of the representative structure of the trajectory (47). We wish to identify contiguous regions in the three-dimensional conformation of the antigen that are minimally coupled to the rest of the protein, and are thus likely sites for the dynamic modulation that would play a role in recognition events.
The analysis of energetics is based on our energy decomposition method, which allows the detection of residue-residue couplings that are important in the stabilization of a fold (see details in the next paragraph). The method provides a simplified view of residue-residue pair interactions, extracting the major contributions to energetic stability of the native structure from the results of all-atom MD simulations. For a protein of N residues, the N×N matrix (Mij) of average nonbonded interactions between pairs of residues can be built by averaging over the structures visited during an MD trajectory (43–47). The rather noisy energy matrix is then simplified through eigenvalue decomposition. Analysis of the N components of the eigenvector associated with the lowest eigenvalue was shown to identify residues that behave as strong interaction centers. These interaction centers are themselves characterized by components that have an intensity higher than the threshold value, and which correspond to a flat normalized vector with residues that would all provide the same contribution. We verified that applying this analysis to the representative conformation of the most populated structural cluster from the simulation yields the same results as the averaging over the equilibrated part of the trajectory (52). As a caveat, it is worth noting that the latter approximation is valid when the most frequented cluster is significantly more populated than the others, so as not to neglect significant structural deviations captured by other clusters. In all the cases studied here this holds true, as we did not observe any major domain rearrangements, domain motions, or folding-unfolding events during simulations. The method was validated against experimental data and a relationship was found between the topological and energetic properties of a protein and its stability (43–47).
The map of pair energy-couplings filtered with topological information can be used to identify local couplings characterized by energetic interactions of minimal intensities. Because low-intensity couplings between distant residues in the structure are a trivial consequence of the distance-dependence of energy functions, local low-energy couplings identify those sites in which interaction-networks are not energetically optimized. These regions may be regarded, therefore, as prone to interact with binding partners or to otherwise tolerate mutations that would preserve the antigen three-dimensional structure. Moreover, thanks to the lower intensity constraints to the rest of the structure, these substructures would be characterized by dynamic properties that allow them to visit multiple conformations (as shown in the flexibility graphs in Supporting Material)—a subset of which can be recognized by the antibody to form a complex. The sites identified are typically clustered at the protein surface and are easily accessible. These concepts are somewhat reminiscent of local frustration, in which highly frustrated regions are often localized near interaction sites on protein surfaces (53).
Analysis of energetics and topological properties
The energy decomposition method is based on the calculation of the interaction matrix Mij, which is determined by evaluating average, interresidue, nonbonded (van der Waals and electrostatics) interaction energies between residue pairs, calculated over the structures visited during an MD trajectory. For a protein of N residues, this calculation yields an N×N matrix. As stated above, the same results can be obtained by calculating the interaction matrix Mij from the representative conformation of the most populated cluster, in the absence of major conformational changes.
The aim of our method is to obtain a simplified picture of the most relevant residue-residue interactions in a certain fold. The matrix Mij is thus diagonalized and reexpressed in terms of eigenvalues and eigenvectors, in the form
| (1) |
where N is the number of protein amino acids, λk is the kth eigenvalue with k ranging from 1 to N, and wki and wkj are the ith and jth components of the associated normalized eigenvector. Eigenvalues are labeled following an increasing order, so that λ1 is the most negative. In the following, we refer to the first eigenvector as the eigenvector corresponding to eigenvalue λ1. The total nonbonded energy Enb is defined as
| (2) |
We showed in Tiana et al. (43) and Morra and Colombo (47) that each Mij can be effectively approximated by
| (3) |
such that the total nonbonded energy becomes
| (4) |
(A distribution of the eigenvalues and the percentage of total stabilization energy accounted for by λ1w1iw1j can be found for each protein in Table S2.)
From the physical point of view, this approximation indicates that any two residues i and j interact with energy λ1w1iw1j. The value λ1 represents a coupling parameter: a modulation of its intensity, as a result of mutations, can be interpreted as a rescaling in the intensity of protein interactions. A variation in the eigenvector components is related to a reorganization of native interactions that would modulate the contribution of a certain pair to the overall stability.
The principal eigenvector (defined as the sequence eigenvector) constitutes a simple vectorial representation of the sequence: it reports on the contribution of each residue in the stabilization of the fold, which ultimately depends on the chemical properties of the residue itself. From this we can recover an approximation to the global stabilization energy, , which was shown to correlate with the relative different stabilities of mutants of several proteins, proving thereby to be a sufficient energetic descriptor to discriminate among them (47). This method provides information on the mean coupling energy between two residues in the native state, revealing the network of most interacting residues through the structure.
The contact map of the representative structure from MD recapitulates which residue pairs are in contact in the conformation. If the distance between any two Cβ atoms is below a cutoff value, the corresponding matrix entry is set to 1, otherwise it is set to 0. The distance cutoff is set to 6.5 Å. For the sake of homogeneity with the energy matrix, contacts between nearest neighbors i, i+1 are included as well. Therefore,
| (5) |
To calculate the contact matrices we consider the representative structure of the main cluster obtained with the GROMOS method from the MD trajectory of each antigen (cutoff value of 2 Å) (54). Energy decomposition was carried out both by averaging on structures saved every nanosecond during the simulations and on the representative protein conformation of the most populated structural cluster obtained from the trajectory. The resulting structures were minimized, and solvation effects were taken into account using the molecular-mechanics (MM)-Poisson-Boltzmann surface area (PBSA) method, with the nonbonded energy term for residues i and j resulting (55) in
The results of averaging over the trajectory and of considering the most populated cluster are basically identical. A schematic of the method is reported in Fig. 1.
Figure 1.
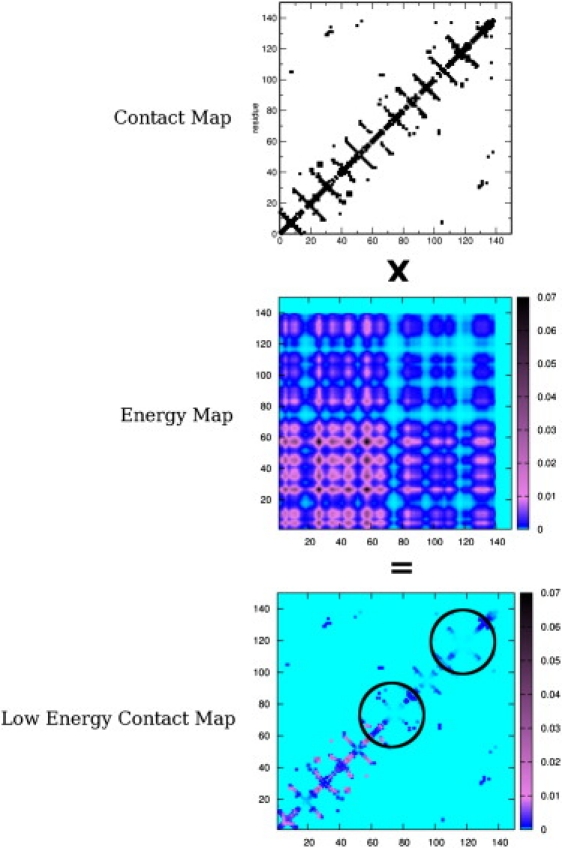
Pictorial representation of the MLCE method. The contact map is multiplied by the simplified energy-coupling matrix. The resulting matrix reports the energetic coupling intensity of two residues in contact in space, represented as a color scale assigned to each point of the matrix. The weakest local interactions vanish in the background color: predicted epitopes are identified with circles.
Epitope identification
The simplified interaction matrix defined by λ1w1iw1j is multiplied by the residue-contact matrix. This procedure allows us to filter the information contained in the simplified energy matrix λ1w1iw1j in terms of residues that are close in space, highlighting pairs within the contact cutoff that are also coupled through nonbonded interactions. This provides a compact way to highlight which local pair-contacts in the three-dimensional organization of the protein are coupled through energetic interactions.
The resulting matrix can be viewed as the matrix of local coupling energies (MLCE). The contact-filtered coupling interactions are ranked in increasing order according to their respective intensities (from weaker to stronger). Starting from the minimum value (weakest local coupling interactions, defined as “soft spots”, in contrast with the “hot spots” characterized by high coupling intensities), the set of putative interaction sites was defined by including increasing residue-residue coupling values until the number of couplings that correspond to the lowest 15% of all contact-filtered pairs was reached. This then corresponds, in our approximation, to the set of local interactions, possessing minimal intensities, which may identify antigen-antibody or protein interaction sites. The corresponding residues define putative epitope sequences.
Simulation setup
All the starting structures were downloaded from the Protein DataBank (codes in Table 1) and each was subjected to five explicit water MD simulations of 30 ns as described in the Supporting Material.
Results
Epitope prediction based on energy decomposition
To evaluate the ability of our method to predict epitopes, we studied 19 protein antigens for which crystal structures were available both in isolation and in complex with at least one specific antibody in the Protein DataBank (PDB). The dataset was constructed by searching the PDB and initially discarding all complexes involving antibodies bound with only short peptide stretches, and focusing only on real protein-protein complexes. Moreover, we selected antigen proteins whose structures had been solved in isolation via x-ray crystallography with a resolution <2.6 Å or via nuclear magnetic resonance (Table S1). The set of isolated antigens was chosen to be nonredundant and diverse in terms of structures and sequences (alignments shown in Supporting Material). Structural similarities were also minimal, because the antigens and epitopes were comprised from a diverse group of possible conformations that ranged from random loops to ordered secondary structures (Fig. 2).
Figure 2.
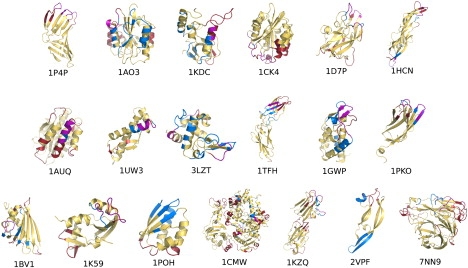
Projection of the low-energy couplings from MLCE on their respective locations on the three-dimensional structure of all proteins analyzed. Predicted epitopes are in red, actual epitopes are in blue, and their intersection is in purple. Color code: see online version for clarity.
The predictive analysis was performed based only on MD simulations starting from the x-ray structure of the antigenic proteins in isolation. The validity of the epitope prediction was benchmarked against the corresponding structure of the antibody-complexed antigen (see Table 1). Our method does not require the use of any training set of antibody-antigen complexes, as the determination of the epitope regions is based solely on structural-dynamical and energetic properties of uncomplexed antigens in isolation. The sequences for the predicted epitopes are reported in Table S3. In Fig. 2, we have reported the projection of the low energy couplings on the surfaces of the proteins of the test set.
Evaluation of epitope predictions
To assess the predictivity performance of the MLCE technique, we used the ROC analysis on all antigens analyzed. This analysis has been exploited previously in the immuno-informatics field in epitope prediction efforts (11,12,56) and is based on the calculation of four main parameters: true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN) (57).
The parameters are determined by comparing the predictions with experimental data. For benchmarking, we relied on published articles on antigen-antibody complexes and we considered as an epitope the region beginning and ending with amino acids directly forming interactions with the antibody (defined by the crystal data). Our epitope definition also includes residues directly proximal in sequence with the previous ones, even though they may not directly contact the antibody in the complex x-ray structure, as they may have a relevant role in defining the optimal conformation required for recognition.
The parameters described above are used to determine the false-positive rate measure (FPR), defined as
and the true-positive rate measure (TPR)
These are in turn related to the sensitivity, which equals TPR, or to the specificity, defined as 1-FPR. The dependency of TPR versus FPR can be plotted in a graph known as the ROC curve. The area under the ROC curve (also known as the area under the curve, or AUC) is a good indicator of the performance of the method, and has been widely used in the evaluation of other approaches (1,11). ROC curves are reported in Supporting Material.
We calculated the points in this graph by changing the cutoff threshold used on the low-energy contact matrix values to identify the possible epitope residues. To determine the ROC curve, we considered 19 different cutoff values on the ordered matrix elements, starting with the set of values containing the lowest 5% of the filtered contact energy values and increasing the threshold by 5% per step.
The area under the ROC curve, called AUC, is comprised between 0 and 1 (with a value of 0.5 for a random classifier) and it is useful to make comparisons among predictions obtained with different methods. We determined the AUC values to be the sum of the trapezoid areas calculated by considering the points in the graph. To assess the role of MD simulations, this analysis was carried out both on the representative structures obtained from the MD simulations and on single minimized structures obtained directly from the PDB. The results are summarized in Table 1.
The MLCE approach provided good performances, with an average AUC of 0.71. In only one case is the AUC value < 0.5 (for Histidine-containing phosphocarrier protein, i.e., HPr, 1poh.pdb). In all other cases, MLCE determined putative antibody-binding sites with high ranking. One case of particular interest is lysozyme, where multiple antibody-binding regions are known (Fig. 3 a). The MLCE approach proved able to identify these multiple binding sites (Table 1 and Table S1). The same considerations can be applied to the cases of the von Willebrand factor A3-domain protein (vWF-A3, 1ao3.pdb; Fig. 3 b) and human chorionic gonadotropin (HCG, 1hcn.pdb; Fig. 3 c). Two epitopes have been mapped on each protein and their location and sequences were correctly predicted by our approach.
Figure 3.
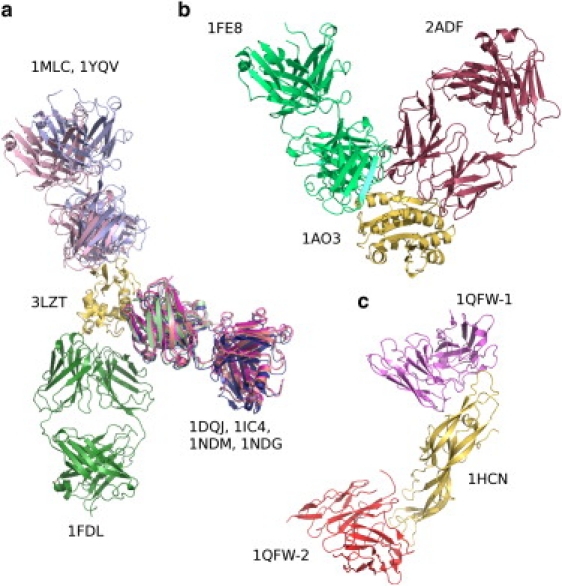
Examples of multiple antibodies binding to the same antigen (light colored), highlighting the possibility for one protein to possess multiple epitopes. The PDB code of the antigen is close to the yellow antigen, and the PDB codes of the complexes are near each respective antibody. (a) Lysozyme; (b) the von Willebrand A3 factor; and (c) human chorionic gonadotropin. Color code: see online version for clarity.
We also evaluated the sensitivity, specificity, and accuracy of our method, based on the definitions of Ponomarenko and Bourne (11). Within the chosen threshold, the sensitivity (the proportion of correctly predicted epitope residues with respect to the total number of epitope residues) gave an average value of 0.46, which is slightly better or comparable to the values reported in the literature (1,11). The results of specificity (the proportion of correctly predicted nonepitope residues with respect to the total number of nonepitope residues) and accuracy (the proportion of correctly predicted epitope and nonepitope residues with respect to all residues) provided average values of 0.84 and 0.75, respectively (Table 1). This confirms the applicability of the approach to the identification of putative binding-sites on protein surfaces.
Finally, we evaluated the positive predictive value (PPV) of MLCE. This value reports on the proportion of correctly predicted epitope residues with respect to the total number of predicted epitope residues. The results obtained with MLCE are in line with the performances of several known predictors of protein-protein interaction sites and protein-protein docking programs reported in Ponomarenko and Bourne (11) and in de Vries and Bonvin (1). Based on the comparison with other algorithms, at least one-half of our predictions may be useful to direct protein-protein docking efforts by reliably focusing on the predicted epitope region. Considering that antigens are notoriously hard to predict, this can be considered a positive result of the MLCE approach, given that it relies only on a general physical hypothesis for protein-protein interactions and on no previous assumptions regarding epitope sequences, shapes, etc.
Structural properties of predicted epitopes
The structural properties of predicted binding-sites were examined to evaluate the ability of the method to retrieve epitopes from any secondary structure motif, and to discriminate the antibody-binding properties of loops within the same structure. The case of the OspB C-terminal fragment from Borrelia burgdorferi (1p4p.pdb) is particularly interesting (Fig. 2). The antibody-binding region is defined by a discontinuous (conformational) epitope that consists of residues that belong to three different loops. The protein also presents several other loops. The MLCE method is able to discriminate the three loops making up the epitope region from the other loops. The epitope-loops are actually decoupled, in terms of stabilizing interactions, from the rest of the protein. The remaining loops provide stabilization energy to the folding core, and thus may not undergo conformational changes, interact with other proteins, or tolerate mutations without major energetic costs.
Importantly, MLCE could also detect epitopes that are part of ordered secondary structures. Epitopes with α-helical structures are predicted for 1auq, 1uw3, and 3lzt. Epitopes in β-sheet conformations are correctly detected in 1tfh, 1gwp, and 1pko.
In the case of human angiogenin (ANG, 1k59.pdb), MLCE identifies an additional region of low-energy coupling located at the opposite face of the molecule from the antibody-binding site. Indeed, crystal structure determination has shown that binding of the complementarity determining regions of the antibody induces a dramatic conformational change precisely at the region of angiogenin opposite to the epitope (58), which is used by the protein to bind to cells. Moreover, in the case of Histidine-containing phosphocarrier protein (HPr, 1poh.pdb), where the calculated AUC value from our calculation is as low as 0.25, the protein-region of lowest energy couplings coincides with the substrate-binding site (59,60).
As the epitopes identified with MLCE are minimally coupled to the rest of the protein, they are also endowed with higher flexibility, as shown by the root-mean-square fluctuation graphs reported in Supporting Material. Importantly, the analysis of flexibility profiles alone is not sufficient to discriminate between epitope and nonepitope regions. These observations corroborate our hypothesis that MLCE has the ability to detect sites poised to interact with other partners.
Impact of MD simulations on predictions
The use of MD simulations improved the results of our functional predictions. Indeed, the performance of the method appears to deteriorate slightly when applied to the structures of antigens extracted directly from the PDB, yielding an average AUC of 0.66 (Table 1).
Finally, we also tested the dependency of MLCE performance on the simulation length. To this end, each trajectory was split into 2-ns intervals and the performance was evaluated on increasing time windows. In general, the performance, in terms of the resulting AUC value, converges within the first 4–6 ns (data not shown)—showing a possibility that one might employ shorter simulation times than those proposed here. In any case, and in view of using the method in a server-based version, useful predictions can also be obtained with the use of the simple MM-PBSA approach.
Discussion
Reliable prediction of antibody-binding sites for a specific protein is a condition necessary to the discovery of new therapeutic opportunities in immunology. One fundamental aim of structural vaccinology is the selection of protein candidates with optimized properties in terms of sequence, structure, and presentation of the determinants for antibody-recognition. In this context, upon being conducted on new pathogens, high-throughput genomic investigations (such as those employing RV) may reveal target antigens that have little sequence similarity to functionally annotated ones, and which may contain novel folds.
Consequently, it is important to develop computational methods that can help identify potential epitope regions of an antigen independently of its sequence and/or shape similarity with other known proteins, and independently of the knowledge of related structures of antibody complexes.
Starting from these considerations, we set out to develop a new approach for the identification of possible antibody-binding sites based uniquely on the structure, dynamics, and energetics of the protein-antigen in isolation. The corresponding antibody-bound complexes are used for benchmarking the results.
The approach we propose is based on simple energetic and conformational concepts. Antigenic proteins must fold to a well-defined three-dimensional structure to properly carry out their functions in the pathogen. The stabilization of the folded state can be achieved through interactions of higher intensity between specific residues that define the folding nucleus. Mutations in the folding nucleus have been shown to impact on protein stability and foldability (43,45–47,61–63). In contrast, epitopes are typically mutation-prone sites (24,32): a protein from a pathogen should, in fact, be able to tolerate mutations that could help it evade the immune defense system of a host.
The energy decomposition method that we introduced and tested proved able to single out the residues of the folding nucleus and flag their contribution to stabilization energy (43,47). The ability to identify the folding nucleus complementarily determines the possibility to identify positions that are more tolerant to mutations. Typically, they coincide with the residues characterized by low energetic couplings with the remainder of the protein. Moreover, low-intensity couplings between proximal residues define sites whose interaction-networks are not energetically optimized and which are generally located on the surface. From the dynamic point of view, these substructures may easily undergo conformational transitions and fluctuations favoring the docking of potential binding partners through a conformational selection mechanism (64). Binding of a specific antibody partner would thus select specific geometries of the antigen, shifting the equilibrium toward thermodynamically stable complexes.
Based on these premises, the positioning of these sites can be identified in a compact way by multiplying the simplified energy-coupling matrix by the residue-contact matrix. This procedure allows us to filter the information contained in the simplified energy matrix in terms of residues that are close in space, highlighting pairs within the contact cutoff that are also energy-coupled through nonbonded interactions in the three-dimensional structure. By concentrating on the lowest energy-coupled pairs in contact according to the contact matrix definition, it is possible to identify surface patches that can be recognized by a putative binding partner. It is important to underline that we aim at identifying, specifically, locally organized residues with nonoptimized interaction energy-networks that are independent of possible dynamic signatures. Interestingly, analysis of normal modes or cross-correlation coefficients of residue pairs could not identify any specific, nonrandom fluctuations involving spatially localized regions with the lowest energetic-couplings. Epitopes are characterized by (anti)correlated as well as random motions with the rest of the protein or with other parts of the conformational epitope. This aspect can be interpreted in the light of the weak energy-couplings among epitope residues, which result in higher flexibility and in the absence of major conformational constraints to the rest of the protein.
The surface patches identified through our procedure define the three-dimensional, structured landscapes associated with discontinuous epitopes that are recognized by antibodies.
It is worth noting, once more, that the whole procedure for epitope identification is based on the study of the antigen in isolation, and the structures of antigen-antibody complexes are used only as a posteriori validations of the analysis. The predictivity, specificity, and accuracy of the method are in line with what has been reported recently in the literature (1,11).
Interestingly, MLCE proves able to identify multiple epitope sites encompassing different antigen regions (Fig. 3). A certain protein surface may in fact contain several possible antibody-binding sites that may not be represented in the sets of structures currently available.
Spatially localized sites with low energetic coupling to the rest of the protein may determine the dynamics required for specific function and/or recognition of partners other than just antibodies (65). In the case of angiogenin (ANG, 1k59.pdb), in addition to correctly predicting the epitope, our method detects the cell-binding region of angiogenin at the opposite part of the molecule from the combining site (58). In the case of Histidine-containing phosphocarrier protein (HPr, 1poh.pdb), the regions of low-coupling energy include the phosphate-binding site, located in the N-terminal region.
Nonoptimized interaction networks can be exploited by the protein to modulate structural plasticity and local flexibility and provide conformational and functional adaptability to possible binding partners. As is also suggested by Ferreiro et al. (53), localizing alternate conformational states or sequence mutations on specific substructures, while minimizing the influence on the three-dimensional stability required for function, could provide a mechanism of specific control of motions by concentrating only on a subregion of the protein.
The MD-based method we propose is clearly not as efficient, in terms of computational expenses, as are dedicated bioinformatics tools and servers that build on different ideas (12,56,66,67). In most cases, the use of MD structures (either the most representative conformation from cluster analysis or averaging over the trajectories) gives only slight improvements over direct minimization of the PDB structure of the antigen. MD-related performance improvements in our data set are noticed mainly for cases in which an epitope is shared between a secondary structure element and a loop. The release of strain determined by the initial crystal packing and consequent conformational relaxation determined by MD favor the geometric and energetic organization optimized for the recognition of the binding partner. In this framework, the role of MD can be most relevant in cases where major structural rearrangements are involved, e.g., in domain motions, large conformational changes, and local folding-unfolding. These cases were not present in our initial dataset, but correct epitope predictions have already been obtained for multidomain amino-acid transporting proteins from the pathogen Chlamydia (M. Soriani, P. Petit, R. Grifantini, R. Petracca, G. Gancitano, E. Frigimelica, C. Garcia, S. Spinelli, G. Scarabelli, S. Fiorucci, R. Affentranger, M. Ferrer-Navarro, M. Zacharias, G. Colombo, L. Vuillard, X. Daura, and G. Grandi, unpublished).
Given all these caveats, it is, however, important to underline that the aim of the study was to introduce a conceptually different approach. We notice that dramatic improvements in algorithms and hardware solutions (68–70) might make it possible to obtain large-scale MD-based predictions more quickly and on longer timescales.
Despite its limitations, we think that the MLCE method may be a valid tool to direct epitope-mapping experiments and possibly identify binding patches to restrict the search of binding poses in protein-protein docking algorithms. With regard to epitope mapping, our approach is already being applied to targets of industrial interest (M. Soriani, P. Petit, R. Grifantini, R. Petracca, G. Gancitano, E. Frigimelica, C. Garcia, S. Spinelli, G. Scarabelli, S. Fiorucci, R. Affentranger, M. Ferrer-Navarro, M. Zacharias, G. Colombo, L. Vuillard, X. Daura, and G. Grandi, unpublished). Further improvement of the predictions may be obtained by integrating MLCE with other predictors that are based on bioinformatics analysis.
From the point of view of possible applications, our method may be relevant for structure-based vaccine design. One could, in fact, focus antigen mutagenesis on those regions that are not part of the folding core and, by so doing, preserve the fold and leave the three-dimensional structure of the protein and epitope presentation unchanged. Random or site-directed mutagenesis could thus be concentrated upon the putative epitope sites, eventually selecting new sequences with maximum affinity for neutralizing antibodies. An alternative strategy would imply the stabilization of the structure of the antigen by engineering Cys cross-linking mutations, or by further optimization of the folding core, to obtain a dominant conformation that would stably present the antibody recognition determinants rather than transiently populate binding conformations.
Finally, by knowing which parts of the antigens can be modified and which should be left unchanged to retain efficient neutralizing antibody recognition, protein antigens could be modified and selected to optimize production and storage, with an impact on costs and distributions of potential vaccines.
Supporting Material
Three tables, 93 graphs, and 38 matrices are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00143-8.
Supporting Material
Acknowledgments
The authors gratefully acknowledge Dr. Giacomo Carrea for critical evaluation and support. Dr. Marco Soriani from Novartis V&D is kindly acknowledged for critical evaluation of the manuscript and advice.
This work was supported by grant FP6 STREP “BacAbs” LSHB-CT-2006-037325 from the European community and by the Associazione Italiana Ricerca sul Cancro. Computational facilities were provided by the Distributed European Infrastructure for Supercomputing Applications and by the CILEA.
References
- 1.de Vries S.J., Bonvin A.M.J.J. How proteins get in touch: interface prediction in the study of biomolecular complexes. Curr. Protein Pept. Sci. 2008;9:394–406. doi: 10.2174/138920308785132712. [DOI] [PubMed] [Google Scholar]
- 2.Bahadur R.P., Zacharias M. The interface of protein-protein complexes: analysis of contacts and prediction of interactions. Cell. Mol. Life Sci. 2008;65:1059–1072. doi: 10.1007/s00018-007-7451-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Rodier F., Bahadur R.P., Janin J. Hydration of protein-protein interfaces. Proteins: Struct. Funct. Bioinf. 2005;60:36–45. doi: 10.1002/prot.20478. [DOI] [PubMed] [Google Scholar]
- 4.Chakrabarti P., Janin J. Dissecting protein-protein recognition sites. Proteins: Struct. Funct. Genet. 2002;47:334–343. doi: 10.1002/prot.10085. [DOI] [PubMed] [Google Scholar]
- 5.Keskin O., Gursoy A., Nussinov R. Principles of protein-protein interactions: what are the preferred ways for proteins to interact? Chem. Rev. 2008;108:1225–1244. doi: 10.1021/cr040409x. [DOI] [PubMed] [Google Scholar]
- 6.Reichmann D., Rahat O., Schreiber G. The molecular architecture of protein-protein binding sites. Curr. Opin. Struct. Biol. 2007;17:67–76. doi: 10.1016/j.sbi.2007.01.004. [DOI] [PubMed] [Google Scholar]
- 7.Sheinerman F.B., Norel R., Honig B. Electrostatic aspects of protein-protein interactions. Curr. Opin. Struct. Biol. 2000;10:153–159. doi: 10.1016/s0959-440x(00)00065-8. [DOI] [PubMed] [Google Scholar]
- 8.Friedberg I. Automated protein function prediction—the genomic challenge. Brief. Bioinf. 2006;7:225–242. doi: 10.1093/bib/bbl004. [DOI] [PubMed] [Google Scholar]
- 9.Chen S.W.W., Van Regenmortel M.H.V., Pellequer J.L. Structure-activity relationships in peptide-antibody complexes: implications for epitope prediction and development of synthetic peptide vaccines. Curr. Med. Chem. 2009;16:953–964. doi: 10.2174/092986709787581914. [DOI] [PubMed] [Google Scholar]
- 10.Keskin O. Binding induced conformational changes of proteins correlate with their intrinsic fluctuations: a case study of antibodies. BMC Struct. Biol. 2007;17:31. doi: 10.1186/1472-6807-7-31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ponomarenko J.V., Bourne P.E. Antibody-protein interactions: benchmark datasets and prediction tools evaluation. BMC Struct. Biol. 2007;7:64. doi: 10.1186/1472-6807-7-64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ponomarenko J., Bui H.H., Peters B. ElliPro: a new structure-based tool for the prediction of antibody epitopes. BMC Bioinformatics. 2008;9:514. doi: 10.1186/1471-2105-9-514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zagursky R.J., Anderson A.S. Application of genomics in bacterial vaccine discovery: a decade in review. Curr. Opin. Pharmacol. 2008;8:632–638. doi: 10.1016/j.coph.2008.06.009. [DOI] [PubMed] [Google Scholar]
- 14.Ndifon W., Wingreen N.S., Levin S.A. Differential neutralization efficiency of hemagglutinin epitopes, antibody interference, and the design of influenza vaccines. Proc. Natl. Acad. Sci. USA. 2009;106:8701–8706. doi: 10.1073/pnas.0903427106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Garulli B., Castrucci M.R. Protective immunity to influenza: lessons from the virus for successful vaccine design. Expert Rev. Vaccines. 2009;8:689–693. doi: 10.1586/erv.09.35. [DOI] [PubMed] [Google Scholar]
- 16.Medaglini D., Olesen O.F., Rappuoli R. The European effort towards the development of mucosal vaccines for poverty-related diseases. Vaccine. 2009;27:2641–2648. doi: 10.1016/j.vaccine.2009.02.070. [DOI] [PubMed] [Google Scholar]
- 17.Yang L.L., Lv Z.Y., Wu Z.D. Schistosoma japonicum: proteomics analysis of differentially expressed proteins from ultraviolet-attenuated cercariae compared to normal cercariae. Parasitol. Res. 2009;105:237–248. doi: 10.1007/s00436-009-1387-z. [DOI] [PubMed] [Google Scholar]
- 18.Rappuoli R., Covacci A. Reverse vaccinology and genomics. Science. 2003;302:602. doi: 10.1126/science.1092329. [DOI] [PubMed] [Google Scholar]
- 19.Bambini S., Rappuoli R. The use of genomics in microbial vaccine development. Drug Discov. Today. 2009;14:252–260. doi: 10.1016/j.drudis.2008.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Medini D., Serruto D., Rappuoli R. Microbiology in the post-genomic era. Nat. Rev. Microbiol. 2008;6:419–430. doi: 10.1038/nrmicro1901. [DOI] [PubMed] [Google Scholar]
- 21.Moriel D.G., Scarselli M., Masignani V. Genome-based vaccine development—a short cut for the future. Hum. Vaccin. 2008;4:184–188. doi: 10.4161/hv.4.3.6313. [DOI] [PubMed] [Google Scholar]
- 22.Serruto D., Rappuoli R. Post-genomic vaccine development. FEBS Lett. 2006;580:2985–2992. doi: 10.1016/j.febslet.2006.04.084. [DOI] [PubMed] [Google Scholar]
- 23.Pizza M., Scarlato V., Rappuoli R. Identification of vaccine candidates against serogroup B meningococcus by whole-genome sequencing. Science. 2000;287:1816–1820. doi: 10.1126/science.287.5459.1816. [DOI] [PubMed] [Google Scholar]
- 24.Dormitzer P.R., Ulmer J.B., Rappuoli R. Structure-based antigen design: a strategy for next generation vaccines. Trends Biotechnol. 2008;26:659–667. doi: 10.1016/j.tibtech.2008.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhou T.Q., Xu L., Kwong P.D. Structural definition of a conserved neutralization epitope on HIV-1 gp120. Nature. 2007;445:732–737. doi: 10.1038/nature05580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.van den Elsen J., Vandeputte-Rutten L., Gros P. Bactericidal antibody recognition of meningococcal PorA by induced fit—comparison of liganded and unliganded Fab structures. J. Biol. Chem. 1999;274:1295–1501. doi: 10.1074/jbc.274.3.1495. [DOI] [PubMed] [Google Scholar]
- 27.Purcell A.W., McCluskey J., Rossjohn J. More than one reason to rethink the use of peptides in vaccine design. Nat. Rev. Drug Discov. 2007;6:404–414. doi: 10.1038/nrd2224. [DOI] [PubMed] [Google Scholar]
- 28.Greenbaum J.A., Andersen P.H., Peters B. Towards a consensus on datasets and evaluation metrics for developing B-cell epitope prediction tools. J. Mol. Recognit. 2007;20:75–82. doi: 10.1002/jmr.815. [DOI] [PubMed] [Google Scholar]
- 29.Ma B.Y., Wolfson H.J., Nussinov R. Protein functional epitopes: hot spots, dynamics and combinatorial libraries. Curr. Opin. Struct. Biol. 2001;11:364–369. doi: 10.1016/s0959-440x(00)00216-5. [DOI] [PubMed] [Google Scholar]
- 30.Novotný J., Handschumacher M., Rose G.D. Antigenic determinants in proteins coincide with surface regions accessible to large probes (antibody domains) Proc. Natl. Acad. Sci. USA. 1986;83:226–230. doi: 10.1073/pnas.83.2.226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Thornton J.M., Edwards M.S., Barlow D.J. Location of ‘continuous’ antigenic determinants in the protruding regions of proteins. EMBO J. 1986;5:409–413. doi: 10.1002/j.1460-2075.1986.tb04226.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Rubinstein N.D., Mayrose I., Pupko T. Computational characterization of B-cell epitopes. Mol. Immunol. 2008;45:3477–3489. doi: 10.1016/j.molimm.2007.10.016. [DOI] [PubMed] [Google Scholar]
- 33.Denisova G.F., Denisov D.A., Bramson J.L. A novel computer algorithm improves antibody epitope prediction using affinity-selected mimotopes: a case study using monoclonal antibodies against the West Nile virus E protein. Mol. Immunol. 2008;46:125–134. doi: 10.1016/j.molimm.2008.07.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kamberaj H., van der Vaart A. Extracting the causality of correlated motions from molecular dynamics simulations. Biophys. J. 2009;97:1747–1755. doi: 10.1016/j.bpj.2009.07.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Glazer D.S., Radmer R.J., Altman R.B. Improving structure-based function prediction using molecular dynamics. Structure. 2009;17:919–929. doi: 10.1016/j.str.2009.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Henzler-Wildman K.A., Lei M., Kern D. A hierarchy of timescales in protein dynamics is linked to enzyme catalysis. Nature. 2007;450:913–916. doi: 10.1038/nature06407. [DOI] [PubMed] [Google Scholar]
- 37.Kern D., Zuiderweg E.R.P. The role of dynamics in allosteric regulation. Curr. Opin. Struct. Biol. 2003;13:748–757. doi: 10.1016/j.sbi.2003.10.008. [DOI] [PubMed] [Google Scholar]
- 38.Morra G., Verkhivker G.M., Colombo G. Modeling signal propagation mechanisms and ligand-based conformational dynamics of the Hsp90 molecular chaperone full-length dimer. PLOS Comput. Biol. 2009;5:e1000323. doi: 10.1371/journal.pcbi.1000323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lerner M.G., Bowman A.L., Carlson H.A. Incorporating dynamics in E. coli dihydrofolate reductase enhances structure-based drug discovery. J. Chem. Inf. Model. 2007;47:2358–2365. doi: 10.1021/ci700167n. [DOI] [PubMed] [Google Scholar]
- 40.Meli M., Pennati M., Colombo G. Small-molecule targeting of heat shock protein 90 chaperone function: rational identification of a new anticancer lead. J. Med. Chem. 2006;49:7721–7730. doi: 10.1021/jm060836y. [DOI] [PubMed] [Google Scholar]
- 41.Colombo G., Morra G., Verkhivker G.M. Understanding ligand-based modulation of the Hsp90 molecular chaperone dynamics at atomic resolution. Proc. Natl. Acad. Sci. USA. 2008;105:7676–7681. doi: 10.1073/pnas.0802879105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wong C.F., Kua J., McCammon J.A. Molecular docking of balanol to dynamics snapshots of protein kinase A. Proteins. 2005;61:850–858. doi: 10.1002/prot.20688. [DOI] [PubMed] [Google Scholar]
- 43.Tiana G., Simona F., Colombo G. Understanding the determinants of stability and folding of small globular proteins from their energetics. Protein Sci. 2004;13:113–124. doi: 10.1110/ps.03223804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ragona L., Colombo G., Molinari H. Determinants of protein stability and folding: comparative analysis of β-lactoglobulins and liver basic fatty acid binding protein. Proteins: Struct. Funct. and Bioinf. 2005;61:366–376. doi: 10.1002/prot.20493. [DOI] [PubMed] [Google Scholar]
- 45.Colacino S., Tiana G., Colombo G. The determinants of stability in the human prion protein: insights into the folding and misfolding from the analysis of the change in the stabilization energy distribution in different condition. Proteins: Struct. Funct. and Bioinf. 2006;62:698–707. doi: 10.1002/prot.20804. [DOI] [PubMed] [Google Scholar]
- 46.Colacino S., Tiana G., Colombo G. Similar folds with different stabilization mechanisms: the cases of Prion and Doppel proteins. BMC Struct. Biol. 2006;6:17. doi: 10.1186/1472-6807-6-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Morra G., Colombo G. Relationship between energy distribution and fold stability: insights from molecular dynamics simulations of native and mutant proteins. Proteins: Struct. Funct. and Bioinf. 2008;72:660–672. doi: 10.1002/prot.21963. [DOI] [PubMed] [Google Scholar]
- 48.Zhang Q., Wang P., Peters B. Immune epitope database analysis resource (IEDB-AR) Nucleic Acids Res. 2008;36(Web Server issue):W513–W518. doi: 10.1093/nar/gkn254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Lichtarge O., Bourne H.R., Cohen F.E. An evolutionary trace method defines binding surfaces common to protein families. J. Mol. Biol. 1996;257:342–358. doi: 10.1006/jmbi.1996.0167. [DOI] [PubMed] [Google Scholar]
- 50.Westhof E., Altschuh D., Van Regenmortel M.H. Correlation between segmental mobility and the location of antigenic determinants in proteins. Nature. 1984;311:123–126. doi: 10.1038/311123a0. [DOI] [PubMed] [Google Scholar]
- 51.Bizebard T., Gigant B., Knossow M. Structure of influenza virus hemagglutinin complexed with a neutralizing antibody. Nature. 1995;376:92–94. doi: 10.1038/376092a0. [DOI] [PubMed] [Google Scholar]
- 52.Morra G., Baragli C., Colombo G. Selecting sequences that fold into a defined 3D structure: a new approach for protein design based on molecular dynamics and energetics. Biophys. Chem. 2010;146:76–84. doi: 10.1016/j.bpc.2009.10.007. [DOI] [PubMed] [Google Scholar]
- 53.Ferreiro D.U., Hegler J.A., Wolynes P.G. Localizing frustration in native proteins and protein assemblies. Proc. Natl. Acad. Sci. USA. 2007;104:19819–19824. doi: 10.1073/pnas.0709915104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Daura X., Gademann K., Mark A.E. Peptide folding: when simulation meets experiment. Angew. Chemie Intl. Ed. 1999;38:236–240. [Google Scholar]
- 55.Wang W., Lim W.A., Kollman P.A. An analysis of the interactions between the Sem-5 SH3 domain and its ligands using molecular dynamics, free energy calculations, and sequence analysis. J. Am. Chem. Soc. 2001;123:3986–3994. doi: 10.1021/ja003164o. [DOI] [PubMed] [Google Scholar]
- 56.Haste Andersen P., Nielsen M., Lund O. Prediction of residues in discontinuous B-cell epitopes using protein 3D structures. Protein Sci. 2006;15:2558–2567. doi: 10.1110/ps.062405906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Fawcett T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006;27:861–974. [Google Scholar]
- 58.Chavali G.B., Papageorgiou A.C., Acharya K.R. The crystal structure of human angiogenin in complex with an antitumor neutralizing antibody. Structure. 2003;11:875–885. doi: 10.1016/s0969-2126(03)00131-x. [DOI] [PubMed] [Google Scholar]
- 59.Jia Z., Quail J.W., Delbaere L.T.J. The 2.0 Å resolution structure of E. coli histidine-containing phosphocarrier protein HPr. J. Biol. Chem. 1993;268:22490–22501. doi: 10.2210/pdb1poh/pdb. [DOI] [PubMed] [Google Scholar]
- 60.Prasad L., Waygood E.B., Delbaere L.T. The 2.5 Å resolution structure of the jel42 Fab fragment/HPr complex. J. Mol. Biol. 1998;280:829–845. doi: 10.1006/jmbi.1998.1888. [DOI] [PubMed] [Google Scholar]
- 61.Bloom J.D., Labthavikul S.T., Arnold F.H. Protein stability promotes evolvability. Proc. Natl. Acad. Sci. USA. 2006;103:5869–5874. doi: 10.1073/pnas.0510098103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Baker D. A surprising simplicity to protein folding. Nature. 2000;405:39–42. doi: 10.1038/35011000. [DOI] [PubMed] [Google Scholar]
- 63.Grantcharova V.P., Riddle D.S., Baker D. Important role of hydrogen bonds in the structurally polarized transition state for folding of the src SH3 domain. Nat. Struct. Biol. 1998;5:714–720. doi: 10.1038/1412. [DOI] [PubMed] [Google Scholar]
- 64.Lange O.F., Lakomek N.A., de Groot B.L. Recognition dynamics up to microseconds revealed from an RDC-derived ubiquitin ensemble in solution. Science. 2008;320:1471–1475. doi: 10.1126/science.1157092. [DOI] [PubMed] [Google Scholar]
- 65.Ho B.K., Agard D.A. Probing the flexibility of large conformational changes in protein structures through local perturbations. PLOS Comput. Biol. 2009;5:e1000343. doi: 10.1371/journal.pcbi.1000343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Sweredoski M.J., Baldi P. COBEpro: a novel system for predicting continuous B-cell epitopes. Protein Eng. Des. Sel. 2009;22:113–120. doi: 10.1093/protein/gzn075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Sweredoski M.J., Baldi P. PEPITO: improved discontinuous B-cell epitope prediction using multiple distance thresholds and half sphere exposure. Bioinformatics. 2008;24:1459–1460. doi: 10.1093/bioinformatics/btn199. [DOI] [PubMed] [Google Scholar]
- 68.Friedrichs M.S., Eastman P., Pande V.S. Accelerating molecular dynamic simulation on graphics processing units. J. Comput. Chem. 2009;30:864–872. doi: 10.1002/jcc.21209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Klepeis J.L., Lindorff-Larsen K., Shaw D.E. Long-timescale molecular dynamics simulations of protein structure and function. Curr. Opin. Struct. Biol. 2009;19:120–127. doi: 10.1016/j.sbi.2009.03.004. [DOI] [PubMed] [Google Scholar]
- 70.Halling-Brown M.D., Moss D.S., Shepherd A.J. A computational grid framework for immunological applications. Philos. Trans. A Math Phys. Eng. Sci. 2009;367:2705–2716. doi: 10.1098/rsta.2009.0046. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


