AFM Imaging and Analysis of Electrostatic Double Layer Forces on Single DNA Molecules

Abstract

Electrical double layer (EDL) forces develop between charged surfaces immersed in an electrolyte solution. Biological material surrounded by its physiological medium constitutes a case where these forces play a major role. Specifically, this work is focused on the study of the EDL force exerted by DNA molecules, a standard reference for the study of single biomolecules of nanometer size. The molecules deposited on plane substrates have been characterized by means of the atomic force microscope operated in the force spectroscopy imaging mode. Force spectroscopy imaging provides images of the topography of the DNA molecules, and of the EDL force spectrum. Due to the size of the molecule being much smaller than that of the tip, both the tip-substrate and tip-molecule interactions need to be considered in the analysis of the experimental results. We solve this problem by linearly superposing the two contributions. EDL force images are presented where DNA molecules are clearly resolved. The lateral resolution of the EDL force is discussed and compared with that of the topography. The method also allows the estimation of the DNA surface charge density, thereby obtaining reasonable values.

Introduction

Most surfaces immersed in an electrolyte solution develop a surface charge, due to various mechanisms. Charged surfaces lead to a concentration gradient in the electrolyte called the electric double layer (EDL). When the surfaces approach each other, an interaction comes out due to the overlapping of their corresponding EDLs (1). The EDL interaction plays an important role in many processes of colloid science, such as coagulation (2). However, we focus our interest in biological systems. In fact, it is well established that EDL interaction plays a crucial role in many biological processes due to its long-range character, to the physiological medium containing a small concentration of ions, and to the substantial charge of molecules like amino and nucleic acids. Examples of these processes are cell adhesion (3), stability of protein structure (4), and DNA condensation (5), as well as protein-membrane (6), protein-protein (7), and protein-DNA (8) interactions.

The atomic force microscope (AFM) has demonstrated its capability to provide images of biomolecules with high resolution (9). To correctly interpret these images it is important to know which forces are acting between tip and sample. A powerful methodology to study these forces is force spectroscopy, where tip-sample forces are measured as a function of their separation. A further step is single molecule force spectroscopy (10) where forces are measured at the level of a single molecule.

In this work, we are interested in the measurement and imaging of EDL forces arising between the AFM tip and the sample surface (11). For this, we have employed an interesting improvement, which is to simultaneously combine AFM imaging with spatially resolved force spectroscopy. This involves acquiring a force-distance curve at each pixel of a simultaneously acquired AFM topography image. The method has been named in different ways: imaging spectroscopy (12), force mapping (13), and force volume (14). We are going to use force spectroscopy imaging (FSI) to emphasize not only the high-resolution AFM imaging of surface topography, but also the spectroscopy and imaging of EDL forces. Some problems of these techniques, usually associated with long acquisition times, have commonly resulted in a low lateral resolution (15). In this work, however, a substantial increase of resolution has been achieved. An important effort has been devoted to data processing, because of the large amount of force values (>10⁶) produced by a single FSI measurement.

In a recent work (16), we applied the FSI operation mode to study the EDL force exerted by a biomolecule of nanometer size—more precisely, dsDNA deposited on poly-lysine-coated mica, obtaining a complete set of experimental data. Furthermore, this is a special case of a charged heterogeneous surface, the most common situation in practice. Modeling of these complex systems (which would include macromolecular charged colloids and biological material) is not an easy task, although a considerable theoretical effort has already been undertaken (17).

An important characteristic of force spectroscopy imaging is the possibility to extract interesting physical properties of the sample. The property that can be inferred from EDL force measurements is the surface charge density. We show that, by operating in the FSI mode, this property can be measured and imaged down to the single DNA molecule level. However, relating EDL force measurements to surface charge density presents some difficulties. One is the poor knowledge of tip size and shape. This could be overcome by gluing a spherical micrometer-sized particle to the end of an AFM cantilever, a technique known as colloid probe microscopy (18). However, this is not an option if nanometer lateral resolution is required. An additional difficulty comes from the small size of both tip and sample, being DNA smaller than the tip. To address this problem, we present a simple model for the EDL force where tip-molecule and tip-substrate contributions are included. It is based on the Derjaguin approximation, which provides us with simple analytical expressions that are easy for an experimentalist to handle. We are aware that this is a crude approximation for distances and sizes smaller than the Debye length. Also for simplicity, we approximate the cylindrical geometry of DNA to a sphere having the same radius. Despite that, we find that the fitting of experimental force measurements with this model provides us with reasonable values for the surface charge density of DNA molecules. We also examine lateral resolution in EDL force imaging.

Materials and Methods

Sample preparation

EcoRI-digested bacteria phage-λ DNA (cat. No. D5282; Sigma-Aldrich, St. Quentin Fallavier, France) was purchased and used without further purification. Freshly cleaved mica sheets (Electron Microscopy Sciences, Hatfield, PA) were used as a substrate. For DNA sample preparation, mica sheets were coated with poly-lysine (PL) (Sigma-Aldrich). This was done by pipetting a 10 μL PL drop onto a mica sheet. After incubation for 30 s, the surface was gently rinsed with Milli-Q water (Millipore, Billerica, MA) and dried in a nitrogen stream, to ensure that only strongly adsorbed PL molecules remained on the surface. Afterwards, the surface was incubated in a DNA water solution for 1 min at a concentration of 1 μg/mL. After incubation, samples were rinsed with Milli-Q water. Immediately after rinsing, samples were placed in a homemade liquid cell filled with the imaging buffer, not allowing it to dry at any moment.

Ultrapure (Milli-Q) water was produced by an ultrapure water system (Millipore, Tokyo, Japan). Potassium chloride and sodium phosphate salts were purchased from Electron Microscopy Sciences. Potassium chloride was dissolved down to the desired concentration in Milli-Q water and its pH adjusted to 7.0 with NaOH. Sodium phosphate was prepared as a 10 mM, pH 7 solution, consisting of a 0.056% monosodium phosphate and 0.155% disodium phosphate in weight solution in Milli-Q water.

Atomic force microscopy

Atomic force microscopy (AFM) measurements have been performed using a commercial setup (Nanotec, Tres Cantos, Spain) controlled with the WSxM software (19). Rectangular silicon nitride cantilevers with a nominal spring constant of 50 pN/nm have been employed (OMLC-RC800PSA-W; Olympus, Melville, NY).

The FSI operation mode is implemented as a software method running in the digital signal processor memory. It works by performing a force curve at each point of the scanned surface. At maximum tip-sample separation, the signal on the photodiode is stored as the value corresponding to zero applied force. Then the sample is moved toward the tip for a defined distance while registering and storing the signal on the photodiode at given distance intervals. At minimum tip-sample distance, a feedback loop is closed, usually for a few milliseconds. Within this time interval, the vertical position of the sample is adjusted so that the signal on the photodiode reaches a defined set value. The precise control of a small applied force allows our maintaining the low value needed for a gentle imaging of soft surfaces. The average vertical position of the sample during this interval is stored as the height value of the probed surface point. Then the feedback loop is opened and the sample retracted from the tip for the same distance as in approaching, and the photodiode signal is again sampled and stored. Finally, the lateral movement from one pixel to another is done at maximum tip-sample distance in order to avoid lateral forces.

Data analysis

Analysis of FSI files has been performed with self-programmed routines in MATLAB (The MathWorks, Natick, MA). For final image representation, the WSxM software has been used (19).

Different steps are followed to transform raw force curves, which consist in a set of photodiode signal values obtained at different sample vertical positions, into a more physically meaningful representation. In our case, this representation consists of forces exerted on the tip for an interval of separations between the tip and the sample. First, the photodiode signal corresponding to zero deflection is calculated by averaging its value along a window of sample vertical positions far enough from the sample, and subsequently subtracted from all the photodiode signal values of the curve. Both the size and position of the window depend on the jump distance and the range of surface forces. The photodiode calibration factor is the slope of the photodiode signal when the tip is pushed against a hard surface. If deformation of the sample is neglected, the point where the slope of the cantilever deflection reaches the value of the calibration factor is associated with that point where mechanical contact is established. The zero sample vertical position is calculated as the position where a line passing through the contact point with a slope equal to the photodiode calibration factor reaches a value for the photodiode signal of zero. Mechanical contact would be established at this position in the absence of surface forces. Photodiode signal is then transformed into cantilever deflection employing the photodiode calibration factor. Sample vertical position is converted to real tip-sample distance by adding the corresponding cantilever deflection. Finally, deflection is related to force by the cantilever spring constant.

Raw data from a FSI file consist of a topography image and a force curve associated with each pixel of the probed surface area. Raw force curves must be represented in terms of force-versus-real-tip-sample distance for further analysis. A typical FSI file consists in 128 × 128 pixels, so an automatic data processing is mandatory. Force-versus-tip-sample-distance curves are transformed into force-versus-tip-substrate-distance curves by adding to the tip-sample distance the height of the corresponding pixel from the topography image. Fitting of force curves to force laws has been performed by means of the least-square method. From the fits the amplitude and decay length of the force are obtained. In this article, these magnitudes are presented as mean values calculated by averaging those obtained by fitting several curves performed at similar positions (this is, on top of the substrate or on top of the molecule). Finally, iso-distance maps are built by representing, for each position of the sample, the force exerted on the tip at a given distance from a base plane (the supporting substrate, in our case).

Results and Discussion

Model for the electric double layer force between an AFM tip and single molecules deposited onto plane substrates

As with any other charged surfaces immersed in an electrolyte solution, those of an AFM tip and the sample under study will experience an electric double layer (EDL) force when brought into proximity. The most common approach for calculating this force is to solve the Poisson-Boltzmann equation for the electrostatic potential. This is a second-order nonlinear differential equation that cannot be solved analytically. However, different sets of approximations can be applied for obtaining easy-to-handle expressions. One of these approximations is based on the following expression for the EDL interaction energy per unit area of two plane parallel half-spaces (1),

$$W_{\text{EDL}}\left(D\right)=\frac{2{\sigma }_1{\sigma }_2{\lambda }_{\text{D}}}{\varepsilon {\varepsilon }_0}{e}^{\frac{-\text{D}}{{\lambda }_{\text{D}}}},$$ (1)

where ɛ is the dielectric constant of the medium, ɛ₀ the permittivity of vacuum, σ₁ and σ₂ are the surface charge densities of both surfaces, D is the common separation and λ_D, also known as the Debye length, is the decay length of the interaction, defined as

$${\lambda }_{\text{D}}={\left(\frac{\varepsilon {\varepsilon }_0{k}_{\text{B}}T}{e^2\sum _{\text{i}}{c}_{\text{i}}{z}_{\text{i}}^2}\right)}^{1/2},$$ (2)

where k_BT is the Boltzmann factor, c_i and z_i are the concentration and valence values of the i^th type of ion present in the solution, and e is the electron charge. The interaction energy per unit area of two plane parallel half-spaces, W, which is given by Eq. 1, can be related to the force between two curved surfaces, F, by the Derjaguin approximation (1), as

$$F\left(D\right)=\left[2\pi R_1{R}_2/\left(R_1+R_2\right)\right]\times W\left(D\right),$$ (3)

where R₁ and R₂ are the curvature radii of the respective surfaces. If one of these radii is much bigger than the other, Eq. 3 reduces to $F\left(D\right)=2\pi R\times W\left(D\right)$. In most AFM experiments, the sample is considered planar and homogeneous when compared with the tip, which is considered as a sphere of radius R_t. Therefore, the EDL force between an AFM tip and a plane surface separated by a distance D, and with surface charge densities of σ_t and σ_s, respectively, can be expressed as

$$F_{\text{EDL}}\left(D\right)=\frac{4\pi R_{\text{t}}{\sigma }_{\text{t}}{\sigma }_{\text{s}}{\lambda }_{\text{D}}}{\varepsilon {\varepsilon }_0}{e}^{\frac{-D}{{\lambda }_{\text{D}}}}\text{.}$$ (4)

This work is focused on AFM EDL force measurements on single biological molecules, which are usually smaller than the probe tip. Many of these molecules, like globular proteins or nucleic acids, have sizes similar to typical values for the characteristic length of the EDL interaction λ_D. This characteristic, combined with the need of adsorbing them onto a substrate, means that the above expressions for the EDL force cannot be applied without taking into account the contribution from the substrate to the total interaction force. To model this situation we make use of a common strategy, where the total EDL force exerted on a surface by two or more other surfaces is a linear superposition of the force between each pair of surfaces (20–23). Thus, the force acting on an AFM cantilever close to a molecule is expressed (Fig. 1) as the force between the tip and the molecule, F_tm, plus the force between the tip and the supporting substrate, F_ts. The last term can be directly expressed by Eq. 4. On the other hand, if the molecule is considered as a sphere much smaller than the AFM tip, it is reasonable to consider the surface of the tip as a plane, so that Eq. 4 can also be used to model F_tm. Thus, the total EDL force exerted on the tip close to a molecule deposited on a plane substrate is

$$\begin{array}{l}{F}_{\text{EDL}}(D_{\text{ts}},D_{\text{tm}})=F_{\text{ts}}\left(D_{\text{ts}}\right)+F_{\text{tm}}\left(D_{\text{tm}}\right)=F_{\text{ts0}}\times e^{\frac{-D_{\text{ts}}}{{\lambda }_{\text{D}}}}+F_{\text{tm0}}\times e^{\frac{-D_{\text{tm}}}{{\lambda }_{\text{D}}}}\\ F_{\text{ts0}}=\frac{4\pi R_{\text{t}}{\sigma }_{\text{t}}{\sigma }_{\text{s}}{\lambda }_{\text{D}}}{\varepsilon {\varepsilon }_0}\\ F_{\text{tm0}}=\frac{4\pi R_{\text{m}}{\sigma }_{\text{t}}{\sigma }_{\text{m}}{\lambda }_{\text{D}}}{\varepsilon {\varepsilon }_0},\end{array}$$ (5)

where D_ts and D_tm are the distances between tip and substrate, and between tip and molecule, respectively; σ_m is the surface charge density of the molecule; and R_m its effective radius.

Figure 1.

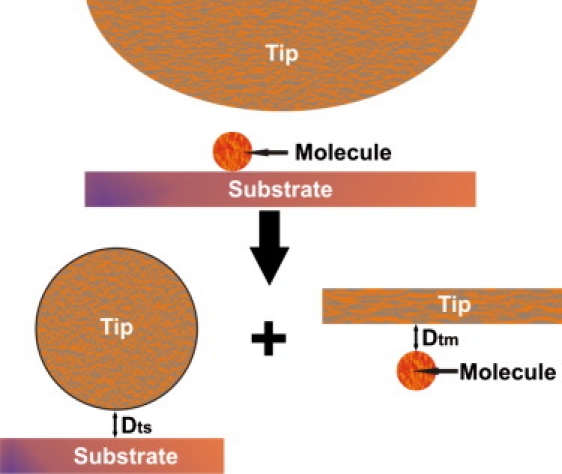
Schematic drawing of the superposition of the distinct contributions to the total EDL force on top of a molecule smaller than the tip: the force between the tip and the molecule, and the force between the tip and the supporting substrate. To model the last term, the tip is approximated as a sphere and the substrate as a plane. Likewise, to model the force between the tip and the molecule, the tip is considered as a plane and the molecule as a sphere.

At this point, the approximations employed for developing Eq. 5 will be discussed. We are aware that, as a result of being the force expressions deduced by applying the Derjaguin approximation, they will lose accuracy if the Debye length of the medium is comparable to the separation and size of the interacting surfaces. This is likely to be the case in AFM EDL force measurements. Moreover, our model also considers the molecule as a sphere smaller than the AFM tip, when this will not always be the case. Nevertheless, these approximations are commonly used to model EDL forces from AFM measurements, leading to reasonable results (11,14,15,24,25). More-accurate force expressions can be obtained applying other strategies, such as the SEI method (26). This method has been proved to fit force curves better than the Derjaguin approximation (27). We are also aware that DNA should be better modeled as a cylinder than as a sphere. However, considering DNA as a cylinder leads to integral expressions for the EDL force that have to be solved numerically (28). For this reason, we have simplified the geometry of DNA to be spherical, as this allows using the simple analytical expressions developed in the previous section.

Regardless of these considerations, we decided to employ the Derjaguin approximation because it provides us with simple force expressions that can be easily handled by experimentalists. This, together with its wide acceptance by AFM users, has been the main reason to work with Derjaguin approximation. Moreover, in the following sections it is shown that, despite its simplicity, the proposed model fits the experimental results with high accuracy.

It is also important to mention that in the following analysis we have only considered forces measured at tip-sample separations >2 nm. For smaller separations, the van der Waals (vdW) interaction would have to be taken into account.

EDL force measurements on single DNA molecules

From Eq. 5 it is expected that the EDL force exerted on the probe tip near a molecule will show a strong dependence on the separation between both (i.e., D_tm). For this reason, the operation in the FSI mode stands out as a promising strategy for studying EDL forces on single biomolecules, as in this mode the position on the sample where each force curve is performed is known with high accuracy. We have recently shown that, by operating in this mode, it is possible to achieve enough lateral resolution to resolve single nanometer-sized molecules both in the topography signal and in the EDL force (16). In this section, we prove that Eq. 5 can be successfully employed for fitting EDL forces on single biomolecules measured by operating in the FSI mode. Moreover, we show that, from these fits, it is possible to estimate the surface charge density of the probed molecules.

For validating the applicability of Eq. 5, its predictions have been compared with the EDL forces measured on single DNA molecules at neutral pH where they are negatively charged. DNA was chosen to perform this experiment due to its characteristic surface charge, which comes from the ionization of the phosphate groups in its backbone.

To perform this experiment, DNA has been electrostatically adsorbed on PL-coated mica substrates, and probed with commercial silicon nitride tips. At neutral pH, the surfaces of tip and substrate are negatively and positively charged, respectively. Fig. 2 a shows a topography map obtained by operating in the FSI mode in a sodium phosphate buffer 10 mM, pH 7, corresponding to λ_D = 2.3 nm (Eq. 2), where a DNA molecule deposited on a PL substrate is resolved. In Fig. 2 b two approach-force curves, corresponding to the same FSI file as the topography map from Fig. 2 a, are plotted. More specifically, the curves were performed at the positions pointed by arrows of the same color. The curve on top of the PL substrate (blue curve) exhibits an attractive EDL force, as expected for a negative tip approaching a positive surface. In the other hand, the EDL force on top of the DNA (red curve) exhibits a repulsive EDL force, as expected for a negative tip approaching a negative molecule. However, this is not a general behavior, as it can be seen if the liquid medium is changed to KCL 1.5 mM, pH 7 (Fig. 2, d and e), which corresponds to an increase of λ_D up to a value of 8.3 nm (Eq. 2). Fig. 2 d represents the topography map from the same FSI file as the approach force curves in Fig. 2 e. Again, the force curve corresponds to positions pointed by arrows of the same color in the topography map. In this case, the EDL force on top of the PL substrate (blue curve) remains attractive, and increases its magnitude, as expected from Eq. 4. However, in this liquid medium a counterintuitive attractive EDL force is observed on top of the DNA molecule (red curve).

Figure 2.

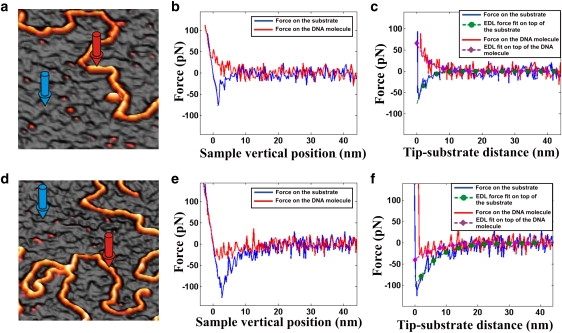
(a) Topography image of a DNA molecule adsorbed on a PL substrate in sodium phosphate buffer 10 mM, pH 7, obtained operating in the FSI mode. (b and c) Force-versus-sample-vertical position and force-versus-tip-substrate-distance curves corresponding to the same FSI file as panel a. The curves correspond to positions on top of the PL substrate (blue curve performed on the position pointed by a blue arrow in the topography map), and on top of the DNA molecule (red curve performed on the position pointed by a red arrow in the topography map). (d) Topography image of the same sample as in panel a, but in a solution of KCl 1.5 mM, pH 7. (e and f) Force-versus-sample-vertical-position and force-versus-tip-substrate-distance curves corresponding to the same FSI file as panel c. Again, the curves correspond to positions on top of the PL substrate (blue curve performed on the position pointed by a blue arrow in the topography map), and on top of the DNA molecule (red curve performed on the position pointed by a red arrow in the topography map). The fits in panels c and f were performed by using Eqs. 6 and 7, respectively.

In this section, we prove how EDL forces measured on top of DNA molecules (Fig. 2) can be explained by the force between the tip and the substrate being superposed to that between the tip and the molecule. For this purpose, we first consider within the model of Eq. 5, the two specific situations of the force curves represented in Fig. 2; that is, positions far from the molecules and just on top of them. If the tip is far from the molecule (D_tm → ∞), the EDL force reduces to that between the tip and the substrate,

$$F_{\text{EDL}}\left(D_{\text{ts}},D_{\text{tm}}\to \infty ,\right)=F_{\text{ts}0}\times e^{-\frac{D_{\text{ts}}}{{\lambda }_{\text{D}}}}\text{.}$$ (6)

On the other hand, when the tip is just on top of the molecule (D_tm = D_ts − 2R_m), the EDL force reduces to

$$F_{\text{EDL}}\left(D_{\text{ts}},D_{\text{tm}}=D_{\text{ts}}-2R_{\text{m}}\right)=F_{\text{m}0}\times e^{-\frac{D_{\text{ts}}}{{\lambda }_{\text{D}}}},$$

$$F_{\text{m}0}=F_{\text{ts}0}+F_{\text{tm}0}\times e^{\frac{2{\text{R}}_{\text{m}}}{{\lambda }_{\text{D}}}}\text{.}$$ (7)

It is noteworthy that the EDL force decays exponentially with the same distance, D_ts, and with the same characteristic length, λ_D, both on top of the molecules and far from them. Thus, force curves corresponding to these specific situations have to be transformed first into representations of the force-versus-tip-substrate distance, and subsequently fitted to exponential functions. The same force curves represented in Fig. 2, b and e, but transformed into a force-versus-tip-substrate-distance representation, are respectively plotted in Fig. 2, c and f. Moreover, in these figures the fit of each curve to a simple exponential function is also included. From these fits, it is possible to obtain the force amplitudes, F_ts0 and F_tm0, and the Debye length of the liquid medium, λ_D. For the sample represented in Fig. 2 a, values of λ_D = (2 ± 1) nm and F_ts0 = (−88 ± 39) pN, and of λ_D = (2.9 ± 1.8) nm and F_tm0 = (50 ± 20) pN are obtained by fitting force curves far from the probed molecules and on top of them, respectively. By inserting these results into Eq. 7, we obtain a value for the amplitude of the EDL force between the tip and the molecule of F_tm0 ≈ 15 pN. Moreover, the value obtained for the Debye length coincides, within experimental error, with the value of 2.3 nm expected from Eq. 2 in sodium phosphate 10 mM. We now focus on the results obtained for the same sample but now immersed in KCL 1.5 mM, pH 7 (Fig. 2, d and f). The same curves as in Fig. 2 e, but transformed into a representation of the force versus the distance between the tip and the substrate, are shown in Fig. 2 f. In this figure, the corresponding fits of the curves to Eqs. 6 and 7 are also included. These fits result in values of F_ts0 = (−110 ± 20) pN and λ_D = (6 ± 3) nm far from the molecules, and F_tm0 = (−35 ± 16) pN and λ_D = (7 ± 3) nm on top of them. Again, the λ_D values coincide with the value of 8.3 nm expected from Eq. 2 for KCL 1.5 mM, pH 7. Moreover, inserting these parameters obtained from the fits into Eq. 7, an amplitude of the EDL force between the tip and the molecule of F_tm0 ≈ 50 pN is obtained. This is a positive value that corresponds to a repulsive force, as expected for a negative tip approaching a negative molecule.

Surface charge density estimation of DNA molecules from EDL force measurements

In the previous section, the proposed model for the EDL force (Eq. 5) has been proved valid to fit EDL forces on top of single DNA molecules, and to additionally estimate these forces between the probe tip and the molecules, subtracting the contribution from the substrate. However, force measurements are not an intrinsic characterization of the sample, but of its interaction with the AFM tip. Despite this, it is possible to gain insight on some property of the sample by comparing experimental measurements of the force with expressions that, like force laws, connect both magnitudes. The property of the sample that determines its EDL interaction with a probe is its electrostatic charge, a property that appears in the EDL force expressions as the electrostatic surface charge density. In the particular case of a plane surface, it is easy to estimate this parameter. In this case, force curves can be fitted to Eq. 4, from where the parameters F_ts0 and λ_D can be obtained. Then, it is straightforward to obtain the surface charge density of the surface:

$${\sigma }_s=\frac{\varepsilon {\varepsilon }_0{F}_{\text{ts}0}}{4\pi R_{\text{t}}{\sigma }_{\text{t}}{\lambda }_{\text{D}}}\text{.}$$ (8)

In a similar way, it is also possible to estimate the surface charge density of single molecules smaller than the AFM tip. If the parameters F_ts0 and λ_D are known, the surface charge density of the molecule can be obtained from

$${\sigma }_{\text{m}}=\frac{\varepsilon \varepsilon F_{\text{tm}0}}{4\pi R_{\text{m}}{\sigma }_{\text{t}}{\lambda }_{\text{D}}}\text{.}$$ (9)

In these expressions, the most difficult parameters to determine are the tip effective radius, R_t, and the surface charge density, σ_t. When needed, we have used the value given by the manufacturer of R_t = 10 nm. For the surface charge density of the silicon nitride used in all the experiments, a value of σ_t = −0.012 Cm⁻² was employed. This value comes from assuming a density of silanol groups in the surface of oxidized silicon nitride of ρ ≈ 7.5 × 10¹⁶ m⁻² (29), and that all are negatively charged at neutral pH.

For the experiments presented in Fig. 2, the calculated values from Eq. 8 for the surface charge densities of the PL substrate are σ_s ≈ 0.02 Cm⁻² in sodium phosphate 10 mM and σ_s ≈ 0.01 Cm⁻² in KCl 1.5 mM. These values correspond to a positive charge every 10 nm² and 20 nm², respectively. This is a reasonable result if we consider that a lysine monomer occupies an area of ∼1 nm². Given that the sample and the tip were the same in both experiments, the difference in the calculated values can be probably attributed to the fact that the effective size of the tip that interacts with the sample depends on λ_D. Likewise, the calculated values for the surface charge density of the molecules in both cases is σ_m ≈ −0.04 Cm⁻². This is a reasonable value when compared with that of free DNA (−0.15 Cm⁻² for a cylinder of 1 nm radius and two negative charges every 0.34 nm). A common observation in our experiments is that similar values of σ_m were obtained for different values of λ_D, provided that the same tip and pH were employed. This observation supports the proposed model for the EDL force. However, different values were obtained for different tips, a difference that can be attributed to the diversity in shape and surface chemistry of commercially available tips. Moreover, σ_m can vary within a single experiment, probably due to a tip contamination event. This suggests the necessity to use tips with a well-defined geometry. Nevertheless, the obtained values for σ_m are situated in an interval going from −0.14 Cm⁻² to −0.02 Cm⁻².

This and the previous section show that the proposed model based on Derjaguin and cylinder-as-sphere approximations provides with a reasonable agreement with experimental results. This does not change the simplicity of these approximations. In fact, we cannot dismiss the possibility of there being a cancellation between an overestimation of the force from the Derjaguin approximation and an underestimation from the consideration of DNA as a sphere and not as a rod.

Iso-distance maps: definition

A direct application of the operation in the FSI mode is to image the distribution of different forces over the studied surfaces. To build these images, it is necessary to choose a magnitude that characterizes the force at each point of the probed surface. This magnitude, which must be inferred from an analysis of the corresponding force curves, will play the role of the intensity of the pixels of the built image. A common plan for building images of the EDL force consists in fitting all the curves of the FSI file to Eq. 4 (15), to represent the amplitude of the EDL force for each position of the probed surface. However, we have seen how the EDL force on top of single molecules is better modeled by Eq. 5. In this section, we employ a strategy for mapping EDL forces on top of single molecules that are smaller than the tip. This strategy was already introduced in Sotres and Baró (16) under the name of iso-distance maps. In this representation, the force is mapped at fixed distances from a base plane, which in our case is defined by the substrate where the molecules are deposited. This representation can be understood as a way of imaging how the molecules modify the force between the tip and the substrate.

Moreover, iso-distance maps also contain quantitative information about the charged state of the sample. Therefore, the surface charge density of the probed molecules can also be estimated from these maps. For this it is useful to take into account the axial symmetry of the problem, which allows our expressing the force in terms of the cylindrical coordinates D_ts (the vertical distance between tip and substrate) and ρ_tm (the lateral distance between the tip and the molecule) (Fig. 3). These parameters are related to the total distance between the tip and the molecule, D_tm, by the relationship

$$D_{\text{tm}}=\sqrt{{\rho }_{\text{tm}}^2+{(D_{\text{ts}}+R_{\text{t}}-R_{\text{m}})}^2}-(R_{\text{t}}+R_{\text{m}})\text{.}$$ (10)

Figure 3.

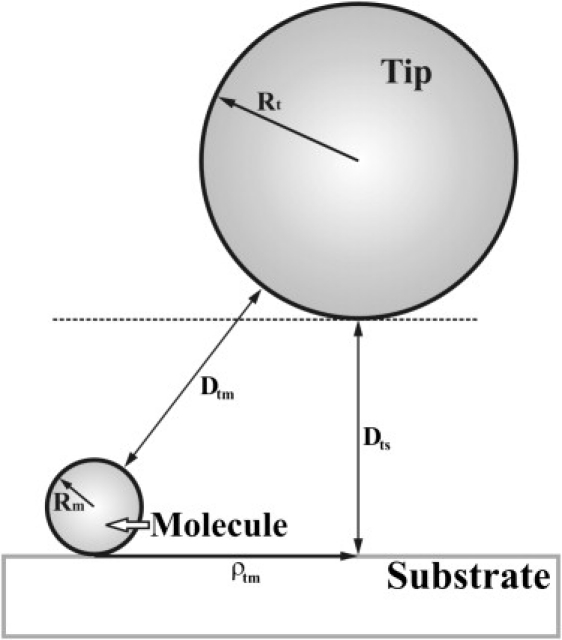
Schematic drawing of a spherical tip with radius R_t probing a spherical molecule of radius R_m deposited onto a planar substrate.

By substituting Eq. 10 into Eq. 5, the following expression for the total EDL force is obtained:

$$\begin{array}{l}{F}_{\text{EDL}}\left(D_{\text{ts}},{\rho }_{\text{tm}}\right)=F_{\text{ts}0}\exp \left[-\frac{D_{\text{ts}}}{{\lambda }_{\text{D}}}\right]\\ +F_{\text{tm}0}\exp \left[-\frac{1}{{\lambda }_D}\left(\sqrt{{\rho }_{\text{tm}}^2+{\left(D_{\text{ts}}+R_{\text{t}}-R_{\text{m}}\right)}^2}-\left(R_{\text{t}}+R_{\text{m}}\right)\right)\right]\text{.}\end{array}$$ (11)

Profiles along the iso-distance maps traced perpendicularly to the positions occupied by the molecules can be fitted with the previous equation. Indeed, these profiles are a plot of the EDL force, F_EDL, versus the lateral distance between the tip and the molecule, ρ_tm, for a constant separation between the tip and the substrate, D_ts. Of course, for carrying on these fits, profiles must be first conveniently adjusted so that the zero lateral position coincides with the position just on top of the center of the molecule. The fitting process of profiles to Eq. 11 has three adjustable parameters (λ_D can be accurately known by fitting individual force curves). These are F_ts0, R_t, and F_tm0. Then, it is straightforward to obtain the surface charge density of the probed molecules from Eq. 9.

Iso-distance maps of DNA molecules

In this section, we show why the iso-distance representation is suitable for mapping EDL forces on single DNA molecules. In Fig. 4 we show data corresponding to a FSI file obtained on a sample of DNA adsorbed onto a PL surface immersed in KCl 15 mM, pH 7. Fig. 4 a shows the corresponding topography map where a single DNA molecule is resolved, whereas Fig. 4 b shows two force-versus-tip-substrate-distance curves which are representative of the specific situations where they were performed, i.e., on top of the PL surface (blue curve) and on top of the molecule (red curve). Along with the curves, the fits to the developed expressions for the EDL force are also plotted. Moreover, the distances for which the iso-distance maps of Fig. 4, c and d, have been respectively calculated are highlighted. It is clear how in these iso-distance maps the DNA molecule is distinctly resolved as an increase of the force on top of the positions occupied by the molecule. This behavior remains for iso-distance maps calculated up to distances of ∼10 nm from the substrate, a value which is three times higher than the Debye length of the medium (∼3 nm in this case). In these maps, the lateral resolution of the molecule is similar to that of the topography, a property that will be presented and discussed in the next section.

Figure 4.

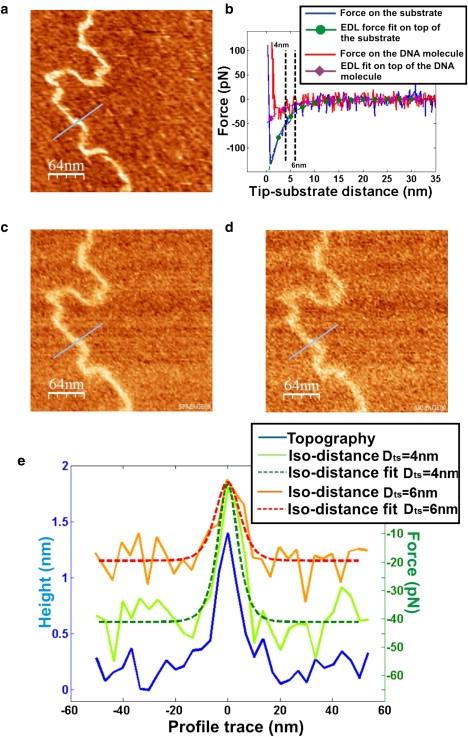
(a) Topography image from a FSI file obtained with a negatively charged silicon-nitride tip showing a DNA molecule on a PL-coated mica surface in KCl 15 mM, pH 7. (b) Representative-force-versus- tip-PL-substrate-distance curves on top of a clean area of the PL surface (blue line) and on top of the DNA molecule (red line) from the same FSI file as panel a. Fits of the curves to Eqs. 6 and 7 are also plotted. (c and d) Iso-distance maps extracted from the same FSI file as in panel a, showing the force exerted on the tip situated to 4 nm and 6 nm, respectively, from the PL surface. It can be seen that the DNA molecule is clearly resolved at both distances. This can also be seen in panel e, where three simultaneous profiles, one for each of the previous images, are plotted. Fits of the profiles to Eq. 11 are also plotted (dashed lines).

The resolution attained can also be seen in Fig. 4 e, where we simultaneously show profiles traced perpendicularly to the probed molecule on the topography and on the iso-distance maps (profile traces are highlighted in the corresponding images). Moreover, fits of the iso-distance profiles to Eq. 11 are included (dashed lines). By fitting multiple iso-distance profiles, the mean value for the EDL force amplitude between the tip and the molecule, F_tm0, can be obtained. Performance of this analysis on iso-distance profiles corresponding to D_ts = 4 nm gives a value of F_tm0 = (76 ± 15) pN, whereas for D_ts = 6 nm a similar value of F_tm0 = (80 ± 20) pN is obtained. These two values are in reasonable agreement with the one found from the fit of the force curves that compose the FSI file, which is F_tm0 = (74 ± 42) pN. This result confirms that both representations contain the same information. From Eq. 9, a similar surface charge density for the molecule of σ_m ≈ 0.11 Cm⁻² is found for the three reported values of F_tm0. This value is within the same order of magnitude as that expected, σ_m ≈ 0.15 Cm⁻². Again, the difference with the value found for the molecule shown in Fig. 2 is attributed to differences in the employed tip.

In the iso-distance maps presented, the homogeneity of the electrostatic signal on top of the PL substrate is also noticeable. This is surprising because, as reported in Surface Charge Density Estimation of DNA Molecules from EDL Force Measurements, the mean distance between charges in PL is ∼4 nm. However, the tip is too large (minimum calculated radius of ∼12 nm; see Lateral Resolution in Iso-Distance Maps) to resolve this structure. The homogeneous spatial distribution observed for the EDL force on top of the PL substrate has an important consequence. Indeed, it could be possible for the DNA to bind to areas of the sample with a local increment of the PL concentration, a behavior that would make useless the linear superposition approximation for the EDL force employed in this work. However, if regions of concentrate PL would exist, the only reason for not observing them would be that all would have been covered by DNA molecules, which is a very improbable situation. This indicates that distortion of EDL force measurements by an inhomogeneous PL distribution can be ruled out.

Lateral resolution in iso-distance maps

We now focus on the lateral resolution that can be attained in EDL force measurements with the AFM. For this, we first have to define the magnitude that will be related to lateral resolution. We have decided to use a similar parameter to that employed to characterize the lateral resolution in the topography signal: the full width at half-height (FWHH). In our case, we have employed the width of the signal originated by the molecule in the iso-distance maps, R_EDL. More specifically, R_EDL is defined as twice the distance from the center of the molecule to the point where the total EDL force reaches the half-value between those of Eqs. 6 and 7 (Fig. 5). This width is equivalent to the minimum separation distance between the same molecules, by which we are able to discriminate them in an iso-distance map. It is straightforward to find that R_EDL is given by

$$R_{\text{EDL}}=2{\lambda }_{\text{D}}\ln 2\sqrt{1+\frac{2(D_{\text{ts}}+R_{\text{t}}-R_{\text{m}})}{{\lambda }_{\text{D}}\ln 2}}\text{.}$$ (12)

Figure 5.

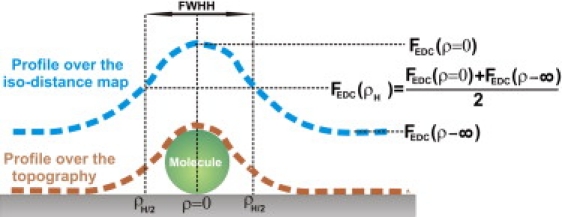
Schematic drawing of the parameter FWHH employed to characterize the lateral resolution of EDL force images on top of the molecule, including the topographic image.

From Eq. 12 it is expected that R_EDL will increase with λ_D and D_ts, although in a quite complicated way. This dependence is shown in Fig. 6 for the same experiment as the one from Fig. 4. Specifically, Fig. 6, a and b, show iso-distance maps calculated at D_ts = 6 nm for the same sample and tip but for different concentrations of KCl, pH 7: i.e., 1.5 mM and 15 mM, respectively.

Figure 6.

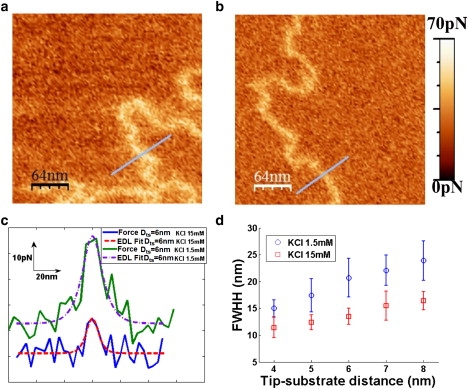
(a and b) Iso-distance maps of DNA molecules deposited on a PL substrate, obtained on the same sample, but in KCl 1.5 mM, pH 7, and KCl 15 mM, pH 7, respectively. In both maps the force exerted on the tip is represented at 5 nm from the PL substrate, subtracting the tip-substrate force far from the molecule. (c) Profiles from both iso-distance maps across DNA molecules (solid lines) and corresponding fits to Eq. 11 (dashed lines). (d) Plot of the FWHH of the molecules in the iso-distance maps calculated for the samples of panels a and b at various separations between tip and substrate.

The dependence of R_EDL with D_ts can be observed in Fig. 6 d. Whereas R_EDL= (12 ± 2) nm is obtained for D_ts= 4 nm, for D_ts = 6 nm its value increases up to R_EDL= (15 ± 2) nm.

It is also interesting to analyze the dependence of the lateral resolution of the EDL force with respect to λ_D, as this is a parameter that can be externally changed by modifying the solution used in the experiment (Fig. 6). Two iso-distance maps corresponding to the same sample of DNA molecules, but immersed in different concentration solutions, are shown. The map of Fig. 6 a corresponds to a KCl 1.5 mM, pH 7 solution, whereas that of Fig. 6 b is done at a 15 mM concentration. It can be observed by the naked eye that the signal originated from the molecule is narrower in the solution with the higher ion concentration, as a consequence of the lower Debye length. This property is also observed in Fig. 6 c, where two profiles taken across a DNA molecule corresponding to the maps in Fig. 6, a and b, are displayed. The molecules have a resolution of (23 ± 4) nm in KCl 1.5 mM solution (Fig. 6 a) and (13 ± 2) nm in KCl 15 mM solution (Fig. 6 b). These experimental findings are in agreement with those predicted by Eq. 12.

These results suggest that the best option to obtain a good lateral resolution is to work at a small separation from the substrate in a solution with a small Debye length, two conditions that look quite evident. However, there is a lower limit for D_ts of ∼2 nm, because, for smaller distances, the vdW interaction cannot be neglected. This means that iso-distance maps are only due to EDL forces for tip-sample separations >2 nm. Concerning the Debye length, it cannot be reduced either, because at λ_D <2 nm, the EDL force becomes quite weak. As a consequence, the relative importance of the vdW force increases, becoming once more not negligible. In addition, as predicted by Eq. 5 and observed in Fig. 6 c, the signal difference in the iso-distance maps between the molecule and the substrate is much larger for high Debye length values. This can be decisive in the case of a molecule having a small charge. Thus, the most appropriate choice for λ_D will depend on the specific details of each experiment.

Other authors have measured the lateral resolution from the EDL maps, though it was not treated in detail. Rotsch and Radmacher (15) obtained a value of 50 nm. The same value is reported by Johnson et al. (24), whereas Rossell et al. (30) measure a value of 30 nm. The authors of this article have already resolved DNA molecules (16).

We have also estimated the lateral resolution that can be obtained with this technique. We consider that the optimum resolution conditions can be reached at a vertical distance of 2 nm above the molecule in a solution having a λ_D value of ∼2 nm. If we consider R_t values of 20 and 10 nm, the resolution values obtained from Eq. 12 are 15 and 11 nm, respectively, in reasonable agreement with our experimental results. For similar tips, the FWHH values for the topography of DNA molecules imaged in the contact mode, calculated by employing the expressions from Margeat et al. (31), are ∼9 nm and 6 nm, respectively.

Conclusions

This work is focused on the EDL forces that appear when biological material is immersed in a physiological medium. Specifically, we have studied the EDL force between an AFM tip and a single biological molecule of nanometer size, DNA. For this purpose, the AFM was operated in the FSI mode, a methodology proved to distinguish between the EDL interaction both on top of DNA molecules and on top of the supporting substrate. As a consequence of the molecules being smaller than the probe, the influence of the supporting substrate needs to be considered in the analysis of the measured forces. We propose a model where this is done by linearly superposing the tip-sample and tip-substrate contributions to the total EDL force. This model provides us with a simple expression for the EDL force on top of single molecules that has been applied to fit experimental results. The proposed model also allows estimating the surface charge density of DNA molecules from EDL force measurements, obtaining reasonable average values. Moreover, experiments performed at different ion concentrations showed no dependence of the measured surface charge density with the Debye length of the medium. A study of the lateral resolution in EDL force imaging is also presented. It is found that the best option to obtain a good lateral resolution is to work with a Debye length slightly higher than 2 nm. Working with this optimal value for λ_D we have achieved a DNA lateral resolution in the EDL force of ∼12 nm.