Task-Oriented Modular Decomposition of Biological Networks: Trigger Mechanism in Blood Coagulation

Abstract

Analysis of complex time-dependent biological networks is an important challenge in the current postgenomic era. We propose a middle-out approach for decomposition and analysis of complex time-dependent biological networks based on: 1), creation of a detailed mechanism-driven mathematical model of the network; 2), network response decomposition into several physiologically relevant subtasks; and 3), subsequent decomposition of the model, with the help of task-oriented necessity and sensitivity analysis into several modules that each control a single specific subtask, which is followed by further simplification employing temporal hierarchy reduction. The technique is tested and illustrated by studying blood coagulation. Five subtasks (threshold, triggering, control by blood flow velocity, spatial propagation, and localization), together with responsible modules, can be identified for the coagulation network. We show that the task of coagulation triggering is completely regulated by a two-step pathway containing a single positive feedback of factor V activation by thrombin. These theoretical predictions are experimentally confirmed by studies of fibrin generation in normal, factor V-, and factor VIII-deficient plasmas. The function of the factor V-dependent feedback is to minimize temporal and parametrical intervals of fibrin clot instability. We speculate that this pathway serves to lessen possibility of fibrin clot disruption by flow and subsequent thromboembolism.

Introduction

Complex reaction networks of signal transduction, gene regulation, metabolism, etc., are ubiquitous in cells. They govern numerous vital processes, including cell reproduction, development, homeostasis, interaction with environment and apoptosis. In multicellular organisms, they can be found in the extracellular milieu as well; examples are blood coagulation and complement.

Recent advances in high-throughput technologies provided an unprecedented amount of information about biological networks. This in turn became a stimulus for rapid progress in their modeling, now widely used in its research, being both time- and cost-saving as well as providing exceptional capabilities for system analysis, chemical engineering, and experimental planning. Two general problems in this field are system reconstruction (inference of structure or parameters of a poorly known network from experimental data (1)) and analysis (understanding functioning of a well-defined network). Although the former might intuitively appear more complex, the latter poses no less significant challenges. There are powerful techniques for analysis of steady-state systems (e.g., biochemical systems theory and metabolic control analysis (2)), but few of the existing tools can efficiently deal with complex networks that are nonlinear, time-, and/or space-dependent.

One way to decrease complexity of a network model is by reduction—i.e., by a simplification that yields a more analyzable model while retaining principal features of the original one. Two reduction approaches applicable for any system are removal of nonessential components (3) and segregation of variables with different characteristic timescales (4–6). For evolutionally formed biological systems having meaningful functions, there is an additional possibility: decomposition, i.e., identification of functional or structural modules in the network (7–9). The central problem of decomposition is how to identify the modules in the most optimal manner.

We propose here a strategy for decomposition and analysis of biological networks based on the combination of modularity concept with sensitivity analysis and temporal hierarchy reduction techniques. It assumes that physiological function of a complex network can be divided into specific subtasks (formation of bistability, oscillations, self-sustained propagation, etc.), each controlled by a specific module. To identify the modules, subtasks are characterized by specific parameters within the overall system response (e.g., concentration amplitude, oscillation frequency, propagation velocity, etc.), and the system is perturbed in order to identify components responsible for each subtask. Temporal hierarchy reduction is used to ultimately simplify the model and reveal hidden regulation mechanisms.

The approach is tested and illustrated by studying control of blood coagulation, with emphasis on the recognition of activating signal. Previous studies employing different strategies were able to suggest several modules in this network. Here, we show that the module responsible for triggering coagulation response includes reactions of extrinsic tenase assembly, factor X, prothrombin, and factor V activation. To test these conclusions, we also carry out experiments on fibrin generation in normal, factor V-, and factor VIII-deficient plasmas. Their results confirm a critical role for factor V-dependent positive feedback in coagulation triggering. We suggest that the task of this module is to minimize temporal and parametrical intervals wherein the fibrin clot is not stable, thus reducing the possibility of thromboembolism. Combining results of this study with previous reports suggests that coagulation has at least five specific subtasks within the framework of its general goal, which is to form a spatially localized fibrin clot at the site of vascular damage.

Materials and Methods

Mathematical model

A model of coagulation developed earlier by our group (10) was used with modifications. An in-depth description is available as Supporting Material. Briefly, this detailed mechanism-driven model was constructed using the bottom-up principle and extensively corroborated with experiments. The model contains 24 ordinary differential equations. Its variables are concentrations of coagulation factors and inhibitors; parameters are rate constants for reactions of coagulation factor activation and inhibition, binding to phospholipids, etc. All parameters were from experimental reports without adjustment except for choosing between values reported by different groups. It was numerically integrated using the ode45 solver implemented in MATLAB (Ver. R2008a; The MathWorks, Natick, MA).

Materials

Rabbit brain TF from Renam (Moscow, Russia) was calibrated using an Actichrome TF chromogenic activity kit from American Diagnostica (Stamford, CT). Human plasma-derived affinity-purified factor VIII (11) was a generous gift of Prof. Eugene L. Saenko (University of Maryland School of Medicine, Baltimore, MD). Specific factor XIIa inhibitor (corn trypsin inhibitor, CTI) was prepared from corn seeds as described (12).

Plasma preparation

Normal and factor VIII-deficient plasmas were prepared from whole blood collected from healthy volunteers and severe hemophilia A patients, respectively, under Center for Theoretical Problems of Physicochemical Pharmacology Ethical Committee approval. Blood was drawn into 3.8% sodium citrate (pH 5.5) at 9:1 blood/anticoagulant volume ratio, supplemented with CTI at 0.4 mg/mL final concentration to inhibit contact activation, and centrifuged at 1000 g for 25 min. The supernatant was additionally centrifuged at 10,000 g for 5 min to obtain platelet-free plasma. Plasma was lactate-treated to stabilize pH at 7.2–7.4 (13). Frozen human pooled factor V congenitally deficient plasma was from George King Bio-Medical (Overland Park, KS). It was supplemented with CTI and incubated at 37°C for 4 h after thawing to allow inhibition of enzymes generated due to cold-induced activation (14); then it was processed as normal plasma.

Fibrin generation experiments

The assay was carried out in 96-well plates as described (14) with minor modifications. Coagulation was started by addition of TF/CaCl₂ (final concentration 20 mM CaCl₂, which corresponds to 2.5 mM free calcium). The plate was read for 300 min in a Thermomax microplate reader (Molecular Devices, Sunnyvale, CA), thermoregulated at 37°C, at the wavelength of 405 nm.

Task-oriented decomposition

Basic assumption

The global task of a complex biological network can be differentiated into several subtasks, each controlled by a specific module (though modules can overlap and control more than one subtask); each subtask can be characterized by numerical parameters in the system output; system perturbation can be used to identify modules corresponding to each output parameter and, respectively, each subtask.

Step 1. Development of a detailed quantitative mathematical model of the network. A detailed mechanism-driven model of the studied network is a prerequisite.

Step 2. Identification of subtasks and outputs. A hypothesis about subtasks of the network should be formulated as a starting point. Another critical element is choice of output parameters for each subtask. Most sensitivity analysis approaches use scaled sensitivity coefficients for concentrations or fluxes in steady-state cases or more sophisticated indicators suitable for time-dependent systems (15,16) to evaluate some overall response. Importantly, we suggest an opposing strategy: that dynamics of a complex biological network is a combination of several simpler responses, and that the selected outcomes should be specific.

Step 3. Task-oriented decomposition and reduction. 1), For each subtask, the responsible module is identified using necessity and sensitivity analysis. 2), The model of each module is reduced using temporal hierarchy of processes.

Step 4. Analysis of the reduced model and experimental test of the predictions. Ideally, reduced models of the individual modules should contain few differential equations and be susceptible to analysis. With such simplification, the phenomena observed could be readily linked to specific reactions. It would then be possible to propose a more detailed decomposition of the networks if necessary, and to make predictions to be tested experimentally.

Blood coagulation

Coagulation is a network of enzymatic reactions in blood plasma and on membranes of blood, vascular, and extravascular cells (17) that turn fluid plasma into a gel upon injury, thus sealing the defect and preventing blood loss. Maintaining a balance between fluid and solid states makes this network vital: insufficient clotting can result in disabling or life-threatening hemorrhages, whereas excessive clotting in the form of thrombosis, disseminated intravascular coagulation, or other vascular disorders is even more dangerous, making up for the lion's share in human mortality and morbidity.

The cascade enzymes are serine proteases activating each other via proteolysis. Their lifetimes are limited due to protease inhibitors. Primary activator is a transmembrane protein tissue factor (TF) which is localized to extravascular tissues and comes in contact with blood upon injury. The complex of TF and factor VIIa activates factor X into Xa that activates prothrombin into thrombin; thrombin converts fibrinogen into fibrin; fibrin polymerizes to jellificate blood. In addition, thrombin activates factors VIII, V, XI, and VII in positive feedback loops, and protein C in a negative feedback; factor VII is also activated by factor Xa.

A striking observation is that only two reactions in the network have obvious functions: binding of factor VIIa to TF recognizes the damaged site, and fibrin polymerization converts plasma into gel. At a first glance, there is no reason why coagulation cannot consist just of the VIIa-TF complex activating fibrinogen: such a system would seemingly have all necessary parts, i.e., the sensor and the effector. However, it is currently understood that the task of coagulation is more complex. Several groups attempted to identify its specific subtasks and link them to individual reactions:

• 1.to clot or not to clot: to recognize the site of damage and respond depending on TF concentration (18,19), size, and shape of the damaged region (20,21);
• 2.to propagate in space, i.e., to form a solid three-dimensional clot closing the wound instead of a thin fibrin film (10,22–24);
• 3.to localize growing thrombus (10); and
• 4.to prevent spreading of active factors downstream that would threaten secondary thrombi (25).

Results

Step 1: Mathematical model

A detailed mechanism-driven model of coagulation constructed using the bottom-up principle was used (see Materials and Methods).

Step 2: Identification of subtasks and outputs

The focus of this study was on the control of activation recognition in coagulation. Therefore, we considered a homogeneous system, without spatial heterogeneity and diffusion. This is justified by the following considerations:

• 1.Homogeneous activation of clotting can occur in vivo when caused by circulating TF (26); it is also a good approximation of coagulation in a complete reaction-diffusion-convection system if applied to a thin, well-mixed layer of plasma adjacent to the activating TF-expressing cells (27).
• 2.Most clotting assays in vitro such as thrombin generation (28) are homogeneous, and our conclusions would be valid for them as well.
• 3.Use of homogeneous approximation will allow us to build useful and illustrative analytical solutions and phase diagrams.

Coagulation was initiated in uniformly mixed samples of plasma by addition of TF. Fibrin concentration (in the model) or fibrin clot optical density (in the experiments) was monitored (Fig. 1). For screening of network components, clot time defined as time required to achieve 50% conversion of fibrinogen into fibrin (14) was used. Note that it is different from time of fibrin jellification, which proceeds almost instantaneously in an explosive manner after fibrin concentration exceeds some threshold level that is <5% of plasma fibrinogen (29,30).

Figure 1.

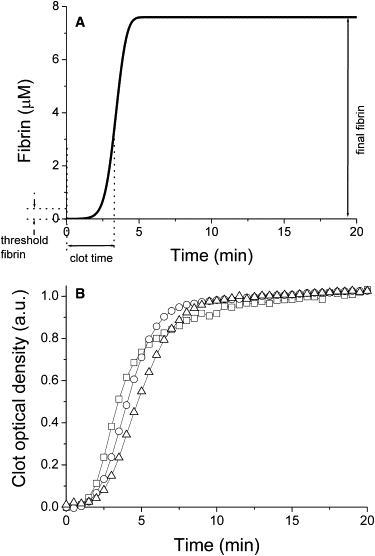
Kinetics of blood clotting in a homogeneous system. (A) Fibrin generation in plasma activated with 5 pM TF, computer simulations. using the model defined by Eqs. S1–S35 in the Supporting Material. Parameters in the panel: clot time (i.e., the time required to achieve 50% fibrinogen cleavage); approximate fibrin jellification threshold; and total fibrin concentration at the end of experiment. (B) Optical density increase in plasma upon addition of 5 pM TF, three independent experiments each performed with pools from three normal plasmas.

There are experimental indications that the coagulation network has an activation threshold (31–33), i.e., the ability to ignore small nonzero activation but respond fully once it exceeds some value. However, its nature and responsible mechanisms are unclear. One definition of threshold in clotting is sharp transition of thrombin generation from linear to explosive (31); another is existence of bifurcation (18) or bistability (34) in thrombin formation response; the third one is lack of clotting at low activation (21,32). Although such properties could be related, it is not necessarily so. As noted above, there is a threshold fibrin concentration required for gel formation, and fibrin jellification can occur before, or without, reaching explosive kinetics. This means that even if thrombin amplitude were a linear function of activation, the whole system might still have a clotting threshold. To distinguish between possible definitions, we shall henceforth introduce the following distinction: nonlinear, explosive response will be called “activation triggering”, whereas the term “fibrin jellification threshold” will be reserved for the ability to not clot plasma at low activation.

Step 3: Task-oriented module identification and reduction

Essential components

Components essential for fibrin formation were identified by task-oriented necessity and sensitivity analysis (see Supporting Material). Briefly, protein concentrations and rate constants were either set to zero to determine relative changes of clot time Δt_clot or perturbed to obtain control coefficients C_tclot (Table S2). There were noncontrolling necessary components such as fibrinogen and factor X (small |C_tclot|, infinite Δt_clot), as well as controlling unnecessary ones such as factor VII (large |C_tclot|, finite Δt_clot). Importance could depend on conditions: for example, C_tclot for AT-III was 0.25 at 5 pM of TF but infinite as TF concentration approached zero (Fig. S1). Factor V activation was the only positive feedback that affected t_clot. This was due not to the network architecture, but to different reaction rates: if other feedbacks were more rapid, their contribution could have become significant (Fig. S2). Many components were neither necessary nor controlling with regard to t_clot and could be eliminated, among them the negative feedback of the protein C pathway.

Ultimately, this step allowed us to reduce the model down to 15 differential equations (see Supporting Material) without significant changes in system kinetics at low TF (Fig. 2). Extrinsic tenase VIIa–TF, factor Xa, and thrombin concentrations rapidly reached quasi-steady-state values (Fig. 2, insets) and then changed slowly.

Figure 2.

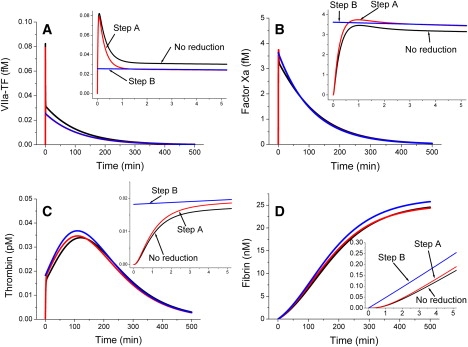
Model reduction. Kinetics of coagulation in plasma activated with TF at 0.01 pM: (A) the VIIa-TF complex; (B) factor Xa; (C) thrombin; (D) fibrin. Model reduction steps: 1), No reduction, computer simulations with the original model; 2), Step A, nonessential components are removed; and 3), Step B, temporal decomposition.

Tikhonov's theorem

Tikhonov's theorem (4,5) was used to carry out temporal reduction (see Supporting Material). This identified three crucial slow variables: the pool of TF-containing complexes (x_3p), thrombin (x₂), and factor Va (x₅). The reduced model for the coagulation initiation module was

$$\{\begin{array}{l}\frac{d{x}_{3p}}{dt}=-b_2\times x_{3p}\\ \frac{d{x}_2}{dt}=b_3\times x_{3p}\times \left(a_3+a_4\times x_5\right)-a_5\times x_2\\ \frac{d{x}_5}{dt}=a_6\times x_2\\ x_1=a_7/a_6\times x_5\end{array},$$ (1)

where a_j and b_j are constant parameters defined in Supporting Material. It is important to point out that absence of variables for the concentrations of factors VIIa, VII, Xa, X, V, AT-III, etc., in this set does not mean that these factors are absent from this model; they just do not have their individual differential equations. The principle of temporal hierarchy reduction employed during the stage B is that, during the timescale of interest, these concentrations are either constant (and are included in the parameters) or quasi-steady (and can be calculated for any given timepoint on the basis of other concentrations). This is fundamentally different from the cases of protein C or factor VIII that do not affect clot time at all and were removed during the stage A of the reduction.

At low TF, concentrations could be obtained as explicit functions of time:

$$\{\begin{array}{l}{x}_{7-3}={x_3|}_{t=0}\times b_1\times e^{-b_2\times t}\\ x_{10}={x_3|}_{t=0}\times b_3\times e^{-b_2\times t}\\ x_2={x_3|}_{t=0}\times b_4\times e^{b_5\times {x_3|}_{t=0}\times \left(1-e^{-b_2\times t}\right)}\times e^{-b_2\times t}\\ x_1={y_1|}_{t=0}\times \left(1-e^{-\frac{b_6}{{y_1|}_{t=0}}\times \left(e^{b_5\times {x_3|}_{t=0}\times \left(1-e^{-b_2\times t}\right)}-1\right)}\right)\end{array}\text{.}$$ (2)

Fig. 2 confirms that time courses of the variables are accurately described by the expressions in Eq. 2, except for the rapid processes of quasi-steady-state achievement.

Step 4: System analysis and experimental confirmation

Steady states and dynamics

These are convenient to investigate in the phase space, where coordinates are model variables, dynamics is represented as trajectories, and steady states as attractors for them. Both original (Eqs. S1–S35 in the Supporting Material) and reduced (expressions in Eq. 1) models have a single stable steady state wherein concentrations of active enzymes are zero (Supporting Material). Projection of the original model phase space on the x_3p-x₂ plane is shown in Fig. 3, A and B. Addition of activator x_3p causes a pulse of thrombin concentration x₂ followed by return to the point of origin. Response amplitude is a strongly nonlinear function of x_3p (Fig. 3 B): with initial x_3p increase from 0.03 to 0.04 pM, maximal x₂ is increased by more than three orders of magnitude. This phase portrait can be deciphered and illustrated using a modified version of the reduced model, wherein all positive feedbacks are retained and factor Va inhibition is added for “robusterization” (see Supporting Material):

$$\{\begin{array}{l}\frac{d{x}_{3p}}{dt}=-b_2\times x_{3p}\\ \frac{d{x}_2}{dt}=\left(x_{3p}+\left({\alpha }_3+{\alpha }_4\times x_2\right)\times \left(x_{3p}+{\alpha }_5\times x_2\right)\right)\times \left({\alpha }_1+{\alpha }_2\times x_2\right)-h\times x_2\end{array}\text{.}$$ (3)

Its portrait (Fig. 3 C) qualitatively retains principal features of the complete system. There is a stable node at the point of origin, and a strongly curved dx₂/dt = null-cline. A difference is a saddle at x₂ ≠ 0 that was hard to observe in the complete system (Fig. 3, A and B) because of the limited supply of pro-cofactors. But for this, thrombin generation would become self-sustained and unstoppable if the threshold is exceeded. Curiously, this threshold is in no way related to fibrin formation: the saddle point and threshold are formed by the positive feedback of XI activation by thrombin (compare Fig. 3 C with Fig. S3) that does not affect clot time (Table S2).

Figure 3.

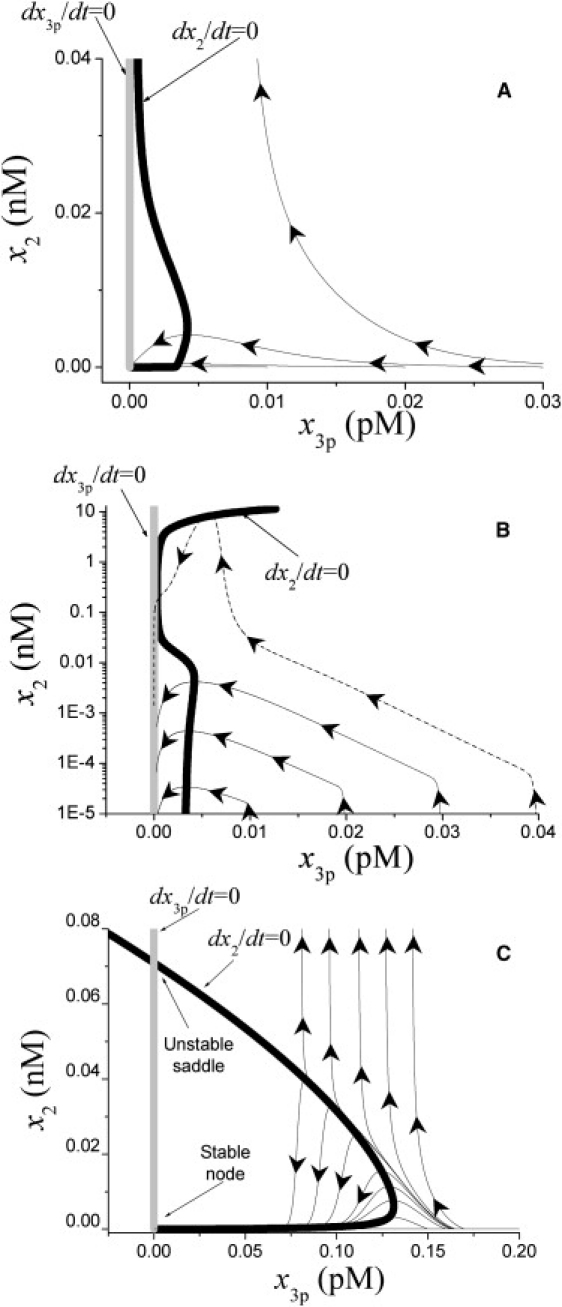
Dynamics of the system. (A and B) Projections of phase space of the complete model (see Eqs. S1–S35 in the Supporting Material) on the x_3p-x₂ plane in linear (A) or semilogarithmic (B) scale. Null-cline projections dx₂/dt = 0 and dx_3p/dt = 0 are thick solid and shaded lines, respectively. Arrows show directions of phase trajectories. Phase trajectories are thin solid lines; thin dotted line in panel B shows trajectories at high TF concentrations, when limitation on the amount of inactive precursors becomes important. (C) Phase portrait for the reduced robusterized model (see expressions in Eq. 3).

Explosive clotting kinetics is determined by positive feedback of factor V activation. Kinetics of fibrin formation in normal plasma was simulated using the original model (Fig. 4 A). Fibrin production over time was nonlinear, with almost zero initial slope followed by exponential rise, as retained in the reduced model (Fig. 4 B):

$$\text{Fibrin:}{x}_1={y_1|}_{t=0}\times \left(1-e^{-\frac{b_6}{{y_1|}_{t=0}}\times \left(e^{b_5\times {x_3|}_{t=0}\times \left(1-e^{-b_2\times t}\right)}-1\right)}\right)\approx b_6\times \left(e^{b_5\times b_2\times {x_3|}_{t=0}\times t}-1\right),\text{if}t<<\frac{1}{b_2}=110\min \text{.}$$ (4)

The complete and the reduced models predict exactly identical results for initial stages of clotting or for low TF concentrations.

Figure 4.

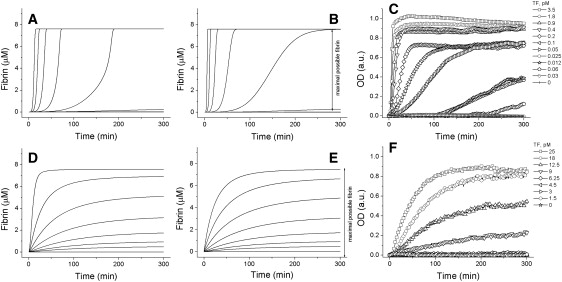
The effect of factor V on the time course of clotting. Theoretical (A, B, D, and E) and typical experimental (C and F) kinetics of clotting in normal (A–C) and factor V-deficient (D–F) plasma. (A and D) Computer simulations using the original model; (B and E) reduced model (Eqs. 2); (C and F) experiments. TF concentrations are: (A and B) 0.64, 0.32, 0.16, 0.08, 0.04, 0.02, 0.01, and 0 pM, top to bottom; (D and E) 64, 32, 16, 8, 4, 2, 1, and 0 pM, top to bottom; and (C and F) shown in the figure.

To test this prediction, experimental studies in citrate-anticoagulated plasma, where coagulation was initiated by addition of TF and calcium, were performed. In agreement with predictions and current concepts (35), the fibrin generation had a nonlinear profile with a lag time followed by a rapidly escalating increase (Fig. 4 C). Consideration of the reduced system having a single factor V-dependent feedback suggests that this nonlinearity is due to factor V activation by thrombin. Additional analysis (Supporting Material) confirms that, without this feedback, thrombin would follow a decaying exponent, and fibrin would be linear during the initial periods:

$$\text{IIa:}{x}_2=\frac{a_3\times b_3}{a_5}\times {x_3|}_{t=0}\times e^{-b_2\times t}\text{.}$$ (5)

$$\text{Fibrin:}{x}_1={y_1|}_{t=0}\times \left(1-e^{-\frac{1}{{y_1|}_{t=0}}\times \frac{a_7\times a_3\times b_3\times {x_3|}_{t=0}}{a_5\times b_2}\times (1-e^{-b_2\times t})}\right)\approx \frac{a_7\times a_3\times b_3\times {x_3|}_{t=0}}{a_5}\times t,\text{if}t<<\frac{1}{b_2}=110\min \text{.}$$ (6)

Accordingly, computer simulations using the original (Fig. 4 D) and the reduced (Fig. 4 E) mathematical models predicted a linear dependence for fibrin formation.

To test this, experimental studies were performed in factor V-deficient plasma (Fig. 4 F). In good agreement with the prediction, kinetics of fibrin generation without factor V was linear, and not sigmoidal as in normal plasma (Fig. 4 C), thus confirming the role of the factor V-dependent positive feedback in the explosive coagulation response.

To estimate the sigmoidal nature of the curves in Fig. 4 more quantitatively, the data were fitted using the Hill function. The theoretical Hill parameters (means ± SEs) for normal and factor V-deficient plasma were 4.2 ± 0.6 (n = 7) and 1.3 ± 0.1 (n = 7), respectively; the corresponding values for experimental curves were 3.7 ± 0.2 (n = 18) and 1.4 ± 0.2 (n = 5). This confirms the effect of factor V on the explosive response of coagulation.

Final fibrin as a function of activation: triggering

At large times and small TF concentrations, the final fibrin concentration achieved is an exponentially growing function of initial TF both in the complete (Fig. 5 A) and in the reduced model:

$$\text{Fibrin:}{x}_1\approx b_6\times \left(e^{b_5\times {x_3|}_{t=0}\times \left(1-e^{-b_2\times t}\right)}-1\right)\approx b_6\times \left(e^{b_5\times {x_3|}_{t=0}}-1\right),\text{if}t>>\frac{1}{b_2}=110\min \text{.}$$ (7)

Considering that fibrin concentration is limited by initial fibrinogen, that there is a threshold fibrin concentration required for jellification, and that clot strength is increased with a fibrin concentration increase, this exponent becomes a triggerlike step function (Fig. 5 A). There is no clotting at TF < 0.03 pM (fibrin is below jellification threshold), and clotting is maximal at TF > 0.04 pM. The reduced model shows that this trigger behavior is also defined by factor V. Without it, the dependence would be linear, with plateau if we account for fibrinogen consumption (Fig. 5 B).

Figure 5.

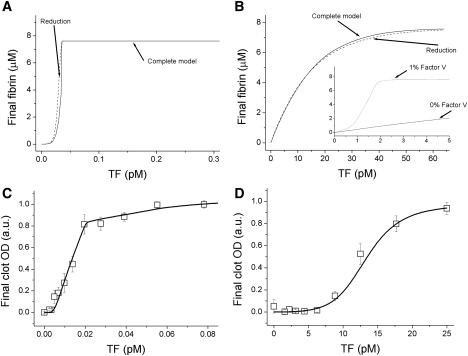
The effect of factor V on the stimulus-response relationship. Theoretical (A and B) and experimental (C and D) dependences of final fibrin clot density (after 5 h) on TF concentration in either normal (A and C) or factor V-deficient (B and D) plasmas. (A and B, solid curves) Computer simulations with the original model. (Dotted curves) Calculations with reduced models. (B, inset) Compares the curves for complete factor V deficiency (0% of protein activity) and 1% deficiency. (C) Results presented are means ± SE of n = 2 separate experiments each performed in quadruplicate using pools from three normal plasmas. (D) Results are means ± SE for n = 3 experiments.

Experimental data qualitatively confirm the predictions for normal plasma (Fig. 5 C). There is no clotting for >5 h at TF < 0.005 pM, and clot density rapidly increases over a narrow range of TF concentration until it is maximal. Interestingly, final clot density as a function of activation in factor V-deficient plasma (Fig. 5 D) is not linear as predicted in Fig. 5 B, but sigmoid like normal plasma (although clotting occurs at dramatically higher TF concentration confirming a controlling role of factor V). A likely reason is that congenitally factor V-deficient plasma does not completely lack factor V activity; an estimated 1% of residual activity is sufficient to turn the curve into a sigmoid (Fig. 5 B, inset). Another possible explanation can be some minor contribution from another positive feedback loop.

Triggering versus threshold

When t_clot in simulations (Fig. S5 A) or experiments (Fig. S5 B) is plotted versus TF concentration, there is no qualitative difference between normal plasma and factor V deficiency. If threshold is defined as nonclotting at a nonzero TF concentration, then it exists independently of feedbacks (Fig. S5). This illustrates the difference between definitions of threshold discussed above. These experiments show that coagulation has two distinct threshold-related properties: the activation triggering that ensures rapid, complete, and irreversible transition of plasma from fluid to the stable gel state; and the jellification point threshold that causes nonclotting at low TF.

Clotting in factor VIII-deficient plasma

To test the prediction that factor VIII-dependent feedback regulates neither triggering nor threshold, clot formation experiments were performed in factor VIII-deficient plasma (Fig. S6). The effect of factor VIII was small and observable only at times larger than clot time (panels A and B), and in a narrow range of TF concentrations (panels C–F).

Discussion

Here we proposed and tested an approach for modular decomposition and analysis of biological networks. The principal results are:

• 1.The approach was proposed and tested with blood coagulation.
• 2.The controlling role of factor V activation by thrombin in coagulation triggering was identified and confirmed experimentally.
• 3.The data, together with previous reports, allow segregation of coagulation into a number of modules each responsible for a specific subtask.

That factor V-dependent feedback is the principal part of the module responsible for triggering, is in line with previous theoretical studies predicting that positive feedbacks play crucial roles in creating an explosive response (18,19) and with their established role in formation of triggers (36). Our study adds:

• 1.Elucidation of the specific form of triggering in coagulation, i.e., exponential nonlinearity instead of bistability.
• 2.Identification of the specific responsible feedback.
• 3.Experimental confirmation.

An essential difference between previous studies and ours is that factor V-dependent feedback in our case generates a sigmoid response, but not bistability. The principal reason is that early models assumed that activating signal does not decay, but factor Va is instead rapidly inhibited (18). In contrast, we take into account experimental evidence that extrinsic tenase is inhibited by TFPI, and factor Va accumulates; because of this and of pro-cofactor consumption, there is no true steady state in our model but zero. If one neglects consumption, it is possible to find bistability in our model of coagulation as well (Fig. 3 C). However, it results from another feedback, factor XI activation by thrombin. The bistability has no role in fibrin formation because factors VIII, IX, and XI become effective only at times larger than t_clot (Fig. S2 B and Fig. S6). We speculate that the importance of this dynamical feature can be seen only if coagulation is considered as a two- or three-dimensional reaction-diffusion process, where bistability becomes essential for spatial propagation (10,22). One might even hypothesize that an advantage of nonlinearity versus bistability in the triggering of this network is that bistability is usually linked to the spatial self-sustained expansion of the excited state in an active medium. From a physiological point of view, it might be desirable to uncouple triggering and spatial propagation for safety reasons, and that might explain why coagulation triggering is a nonlinearity, and not a bistability.

Our experiments on clotting in normal, factor V-, and factor VIII-deficient plasmas confirmed the following model predictions:

Prediction 1. Existence of an explosive response in normal plasma.

Prediction 2. Disappearance of this explosive response in factor V-deficient plasma.

Prediction 3. Existence of nonclotting at low TF concentrations.

Prediction 4. Sigmoid dose-response to TF addition in normal plasma.

Prediction 5. Effects 1, 3, and 4 are retained in factor VIII-deficient plasmas.

These prediction were not intuitively obvious or expected with the exception of Prediction 1 (35). The only prediction that was not confirmed experimentally was dose-response in factor V-deficient plasma. It turned out to be sigmoid, and not linear as predicted; this can be explained by trace amounts of factor V in this plasma.

An assumption and limitation of this study is that it considers homogeneous systems only. Although its results are likely to be applicable to initial stages of blood coagulation in the spatially heterogeneous systems as discussed above, additional regulation by diffusion and flow may occur. For example, our previous data indicated that clotting initiation in a reaction-diffusion system can be regulated by factor Xa diffusion (10). Furthermore, there are theoretical and experimental reports on coagulation triggering regulation by the size of the activating region (20,21), and by flow velocity (20,25,33). Additional studies are required to elucidate the molecular mechanisms that control these spatial phenomena.

In our experiments, there was no normal plasma jellification for >5 h at TF concentrations <∼0.005 pM. This agrees with a recent report that clot formation in blood or plasma activated with immobilized TF depends on TF surface density in a thresholdlike manner (32). Most curiously, we observed that this fibrin jellification threshold was retained in the absence of factor V; only explosive, nonlinear response was lost in factor V-deficient plasmas. Our decomposition of coagulation suggests that these two features, i.e., activation triggering, with its strongly nonlinear dependence of fibrin formation on TF concentration, and fibrin jellification threshold, which is nonclotting at low TF, are distinct properties regulated by different modules.

These conclusions are illustrated by Fig. 6, where temporal and terminal responses of several hypothetical enzyme cascades are shown. If the coagulation cascade consisted of a single reaction, both dependences on time and on the activator concentration would be linear near the point of origin (Fig. 6 A). Addition of a second step into the cascade would only add second-order temporal kinetics (Fig. 6 B). If the concentration of the enzyme in this step were a rapid variable (as really is the case with factor Xa and thrombin), even this advantage would be lost (Fig. 6 C). Addition of a feedback to this latter case would change the situation, dramatically transforming both dependences into exponential growth and making them triggerlike (Fig. 6 D); and this is the case of blood coagulation. All four cascades do not have a true threshold in form of a bistability. However, if product P polymerizes in a threshold manner, all four cascades would have a polymerization threshold in their ultimate response.

Figure 6.

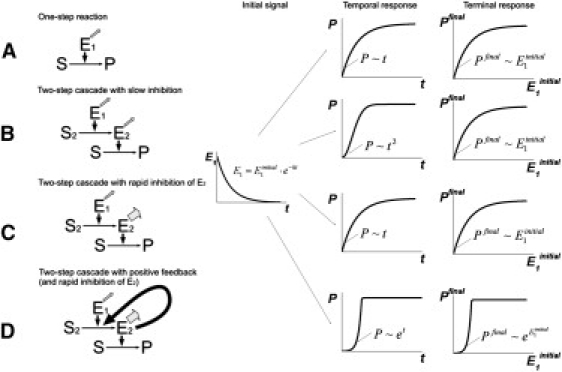
Constructing a trigger: temporal and terminal responses of different enzyme cascades. The diagram illustrates the effect of cascade structure on their response. The cascades (A–D) begin with an initial signal (enzyme E₁), which is a decaying exponent. On the right, two system responses are shown: the dependence of the product P concentration on time (temporal response), and the dependence of the final (achieved at infinite time) concentration of P on the amplitude of the initial signal (terminal response). In a simple one-step cascade (A), both dependences are linear near zero. Addition of steps in a cascade (B) can make the temporal response nonlinear, with no effect on the terminal response. If the added step is a rapid variable (C), even this advantage is lost. However, a positive feedback (D) can make both responses nonlinear and create a true trigger. This latter case corresponds to blood coagulation if E₁ is factor Xa, E₂ is thrombin, and P is fibrin.

It is tempting to link threshold properties of clotting with the problem of circulating TF in blood (26,32). The results of this study allow us to speculate that fibrin jellification threshold in coagulation might be specifically important in the prevention of clotting from low concentrations of circulating TF. In contrast, factor V-dependent triggering might be critical for prevention of weakly attached infirm thrombi with low fibrin content, because it minimizes temporal and parametrical intervals where the clot is not firm. Indeed, sufficient rate of thrombin generation is required to form solid clots with dense fibrin fibers (35), and low-density clots could, due to blood flow stress, become detached and occlude downstream vessels. One prediction that follows is that factor V deficiency could lead to thromboembolism because of the increased possibility of infirm thrombi formation. Most curiously, there are indeed paradoxical reports that factor V deficiency (which is a rare congenital bleeding disorder) can be accompanied by recurrent thromboembolism (37,38).

Two studies recently reported that jawless vertebrates have fewer positive feedback loops in coagulation (39) or even none (40). It might be speculated that lower flow velocities and pressures in lamprey make thrombus disruption and embolization less probable, and trigger in coagulation less essential, than in higher vertebrates.

Development of another method of network analysis is justified by problems currently encountered when dealing with complex and time-dependent networks. Blood coagulation provides a good example: existing bottom-up models of coagulation are large sets with up to 100 differential equations, and their analysis is complex and nonintuitive. The only available strategies were direct simulations (10,27) or various forms of time-dependent sensitivity analysis (15,16). However, these methods were not able to give a comprehensive response to the principal questions: Why is coagulation so complex? What are these reactions for? How can we control this system pharmacologically?

The principal idea of our task-oriented modular decomposition is based on the hypothesis that biological networks can be divided into modules, each being responsible for a specific subtask. This line of thinking received significant development in the analysis of bacterial stress response (7,8). In coagulation, there also were attempts to ascribe specific roles to individual reactions (10,17,22,23). A new element in our approach is use of task-oriented necessity and sensitivity analysis as a simple and nonbiased method to identify the modules in question, supplemented with temporal hierarchy reduction to enable us to understand their structure. Findings of this study and data from previous reports allow us to suggest the following decomposition of coagulation into modules (Fig. 7):

• 1.Cascade skeleton: no regulation (this study). Curiously, the cascade does not affect clot formation kinetics. Its only apparent function is to provide foundation, upon which the regulation is built. All concentrations of factors of the cascade are rapid variables; therefore, without feedbacks, thrombin kinetics (Eq. 5) would be identical to that of factor VIIa-TF (Eq. 2). The old hypothesis that the cascade functions as a signal amplifier (41) does not seem convincing either. From the evolutional point of view, it would be much simpler to achieve the same amplification with a single rapid reaction than with a cascade of numerous slow ones.
• 2.Threshold: fibrin polymerization (previous reports and this study). Final fibrin concentration is a nonlinear function of TF (Fig. 5 A) albeit a smooth one. Most likely, clotting has a threshold (Fig. 5 C) because fibrin polymerization itself has a threshold (29,30).
• 3.Triggering: positive feedback of factor V activation (this study).
• 4.Regulation by flow: positive feedback of factor VII activation (previous reports). Computer simulations of proteolytic cascades in flow (20) suggested that positive feedbacks can switch clotting on and off, depending on the wall shear rate that prevents clotting in the presence of rapid flow. That the wall shear rate does, indeed, switch clotting on and off has been recently confirmed experimentally (33). Simulations using a mechanism-driven mathematical model suggested that factor VII activation by factor Xa is responsible for this (25).
• 5.Spatial propagation: positive feedbacks of factor VIII and factor XI activation (previous reports). Roles of these feedbacks become clear only in spatially nonuniform systems, where these pathways regulate spatial propagation of coagulation from the TF-bearing cells to platelets and into the bulk of plasma (14,17,22,23).
• 6.Termination of spatial propagation: negative feedback of protein C pathway (previous reports). This feedback can function to localize spatial clot propagation (10), but has no effect on the initial stages of coagulation (this study).

Figure 7.

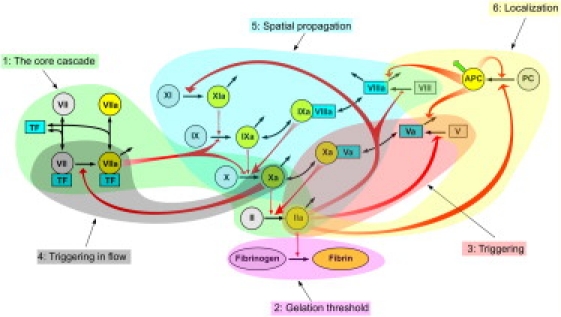
Modular decomposition of blood coagulation. Findings of this study combined with those from other reports allow us to identify six modules responsible for different subtasks. The reduced models (Eqs. 1 and 2) of this study include modules 1, 2, and 3.

Coagulation provides an interesting example of an enzyme network, which can be rather minutely decomposed into modules. Its major positive feedbacks are used for a variety of purposes, such as triggering an explosive response, for self-sustained spatial propagation, or to create a flow-dependent switch. Its negative feedback is used for better control of spatial propagation. Decomposition appears to leave no redundant components in the network, although our consideration was focused on coagulation alone and necessarily excluded many links to other systems (platelet-dependent hemostasis, immunity, and angiogenesis); their analysis can be a task for future research.

Current therapeutic strategies are usually based on the approximation that impacts of drugs are either pro- or anticoagulant, without regard for complexity of the network response; and the consequence is that treatment of thrombosis can be associated with danger of bleeding. This analysis suggests that this can be resolved by targeting specific reactions to selectively regulate its properties such as the activation threshold level or size of the thrombus.

Supporting Material

One hundred and twenty equations, three tables, and six figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00160-8.