Particle-Based Methods for Multiscale Modeling of Blood Flow in the Circulation and in Devices: Challenges and Future Directions

Abstract

A major computational challenge for a multiscale modeling is the coupling of disparate length and timescales between molecular mechanics and macroscopic transport, spanning the spatial and temporal scales characterizing the complex processes taking place in flow-induced blood clotting. Flow and pressure effects on a cell-like platelet can be well represented by a continuum mechanics model down to the order of the micrometer level. However, the molecular effects of adhesion/aggregation bonds are on the order of nanometer. A successful multiscale model of platelet response to flow stresses in devices and the ensuing clotting responses should be able to characterize the clotting reactions and their interactions with the flow. This paper attempts to describe a few of the computational methods that were developed in recent years and became available to researchers in the field. They differ from traditional approaches that dominate the field by expanding on prevailing continuum-based approaches, or by completely departing from them, yielding an expanding toolkit that may facilitate further elucidation of the underlying mechanisms of blood flow and the cellular response to it. We offer a paradigm shift by adopting a multidisciplinary approach with fluid dynamics simulations coupled to biophysical and biochemical transport.

INTRODUCTION

Computational fluid dynamics (CFD) has long been applied to biomechanical phenomena, particularly to blood flow. There are many physiological as well as pathological problems for which CFD can be a potentially powerful means to understand and elucidate the mechanism of healthy and diseased state. The CFD modeling method and numerical scheme may vary according to the flow phenomenon it is applied to. Besides physical and/or computational considerations, there are several basic problems that pose significant challenges when attempting to model the behavior of a living tissue, such as flowing blood, from a biomechanical viewpoint. Blood constituents that respond to biomechanical and chemical stimuli adapt their functions and configurations to their environment and remodel in response to it; this needs to be taken into account in the modeling process. Typical examples would be flow-induced blood clotting and thrombus formation in cardiovascular pathologies, and in cardiovascular devices. It is clear that an approach based purely on a continuum assumption such as CFD may fail to capture these special features, or may require prohibitive computational resources for tackling the multiscale nature characterizing such complex problems. Recent progress in computational methods and high-performance computing (HPC) have put within reach major challenges in whole blood simulations, including the deformable nature of red blood cells, and the cellular response of blood constituents participating in the coagulation cascade under pathological blood flow conditions, such as platelets. It is noteworthy that the 2004 report from the NSF-NIH sponsored workshop on Transport Processes in Biomedical Systems concluded that “the time is right for a national initiative to advance our understanding of biotransport processes in living systems to a new level that will have a major impact on important problems in biology and medicine”.⁶⁵

MULTISCALE MODELING OF FLOW-INDUCED BLOOD CLOTTING: FROM MACROSCOPIC THROUGH MESOSCOPIC TO MICROSCOPIC SCALES OF CLOTTING

Particle-Based Lagrangian Methods for Studying Microscopic Physiological Flows

In the case of blood flow, blood is not merely a continuum or a monophasic fluid whose physical characteristics are parametrically determined. It is composed of various cellular components and complex solution of physiologically active substances including a variety of proteins. Physical properties of those cellular components drastically change, for example during blood coagulation. Even minute change of the physical properties of the cellular component, e.g., stiffness of the cellular membrane of the RBC, will significantly affect the flow behavior. It is therefore obvious that the modeling of the blood flow must include biological responses and interactions of those cellular components. To implement this, the usual continuum mechanics-based method such as CFD is insufficient. We need alternative means to be able to compute the response of the cellular components in the blood under physiological and pathological flow conditions. In this context, the blood should be characterized as composed of objects with different phases and material properties, e.g., plasma, red RBCs, WBCs, and platelets. Plasma is essentially an aqueous solution of electrolyte and colloidal substances and therefore could be assumed to be a simple viscous fluid (Newtonian). The individual RBC can be regarded as a soft shell capsule whose content is a very viscous fluid that does not have a nucleus or significant organella in the cellular space. This may make mechanical modeling of RBC easier than of other cellular components such as WBCs that have a more complex internal structure.

Platelets are important in many physiological and pathological conditions. However, they are smaller than other components of the blood and can be modeled as small reactive bodies whose internal structure may not be important. They are therefore well suited to be modeled by the so-called discrete element method (DEM).¹⁵ Though original DEM does not include fluid–solid interactions, the analysis of fluid phase and solid phase can combine by introducing separate analysis of fluid mechanics, such as the Stokesian dynamics method (SDM).¹³

The approach is to treat all the constituents in the blood flow field by a unified method by adopting a particle-based method with Lagrangian framework. In this framework, the plasma flow as well as the motion of the cellular components is modeled by using particle-based representations. Solid components are modeled as connected particles whose connection is fixed so they can deform but not be broken. Plasma is modeled by so-called (in narrow sense) particle method, such as moving particle semi-implicit (MPS)⁴³ or smoothed particle hydrodynamics (SPH) methods.⁴⁷ Although various numerical methods have been proposed for blood flow analysis, such as a boundary element method,^59,60 an immersed boundary method,^4,5 and a lattice-Boltzmann method,²¹ there is growing interest in the particle-based Lagrangian method because of its simplicity and applicability to the blood flow-related problems. In the following, we describe recent advances in three kinds of particle-based Lagrangian methods: a SDM in conjunction with the DEM, a particle method in conjunction with the MPS method, and a discrete and dissipative particle dynamics (DPD).

Stokesian Dynamics Method in Conjunction with a Discrete Element Method

In analyzing microscopic physiological flows, there are two important forces acting between particles: hydrodynamic forces and chemical-binding forces. Although chemical bindings are complex chemical phenomena, their overall mechanical properties may be calculated by simplified empirical models. In our first study,⁴⁶ we simulated thrombogenesis and thrombolysis processes using DEM to model the mechanical interactions between blood flow, platelets, the vessel wall, and von Willebrand factor. The results demonstrate that the chemical-binding forces can be successfully calculated by using DEM.

The hydrodynamic force can be calculated by the SDM developed by Brady and Bossis.¹³ At negligible particle Reynolds number, motions of N particles in a 3D space can be given in the matrix form as:

$$\left(\begin{array}{c}\mathbf{F}\\ \mathbf{L}\\ \mathbf{S}\end{array}\right)=\mathbf{R}\left(\begin{array}{c}\hfill \mathbf{U}-\langle \mathbf{u}\rangle \hfill \\ \hfill \mathit{\omega }-\langle \mathit{\omega }\rangle \hfill \\ \hfill -\langle \mathbf{E}\rangle \hfill \end{array}\right),$$ (1)

where F, L, and S are, respectively, the force, torque, and stresslet a particle exerts on the fluid. U and Ω are the translational and rotational velocities of a particle, and 〈u〉, 〈ω〉, and 〈E〉 are the suspension average velocity, rotational velocity, and rate of strain tensor, respectively. R is called “grand resistance matrix.” In the original SDM, R is given by:

$$\mathbf{R}={\mathbf{R}}^{\mathit{\text{far}}}-{\mathbf{R}}_{2B}^{\mathit{\text{far}}}+{\mathbf{R}}_{2B}^{near}.$$ (2)

R^far is the far-field contribution of grand resistance matrix, which is invert of the far-field contribution of grand mobility matrix, i.e., R^far = {M^far }⁻¹ . M^far is derived from the Faxen laws for the force, torque and stresslet (a force dipole) for a particle, in which the disturbed flow field is expressed in terms of the multipole expansion of other particles.³² As discussed by Durlofsky et al.,²² inverting the mobility matrix sums an infinite number of reflected interactions among all particles, so it is a realistic multiple body approximation to the resistance matrix. R^far still lacks near-field interactions, because they are reproduced only when all multipoles are included. To include the near-field interactions, Durlofsky et al.²² add near-field multipoles in a pairwise additive fashion; ${\mathbf{R}}_{2B}^{\mathit{\text{far}}}$ is the far-field two-body resistance matrix, and ${\mathbf{R}}_{2B}^{near}$ is the near-field two-body resistance matrix.

By using this method, one can efficiently calculate multiple body interactions in a suspension. It can solve accurately the lubrication forces as well as long-range hydrodynamic interactions among many particles. The high efficiency comes from the small number of unknowns per particle. In the above equation (1), three components of the force (or the translational velocity), three components of the torque (or the rotational velocity), and five components of the stresslet are unknowns: in total, just 11 unknowns per particle. There are much more simplified methods than the original SDM. In a dilute suspension or very concentrated suspension, one may construct R by assuming additivity of forces; this is because, in the dilute limit, higher order reflections decay rapidly as a function of the distance between particles, and one may add forces in a pairwise fashion. In a very concentrated suspension, on the other hand, most of the forces acting on the particles are lubrication forces. Thus, they act locally between two near-contact surfaces, and one may again add forces in a pairwise fashion. In the dilute limit, one can further assume the additivity of velocities in constructing the grand mobility matrix, which is the inverse of the grand resistance matrix. If one is interested only in the translational velocity, the unknowns in the governing equation can be reduced to just three per particle, and the computational time for constructing the grand mobility matrix is usually not so large. Thus, one can deal with large system size, such as millions of particles in the system.

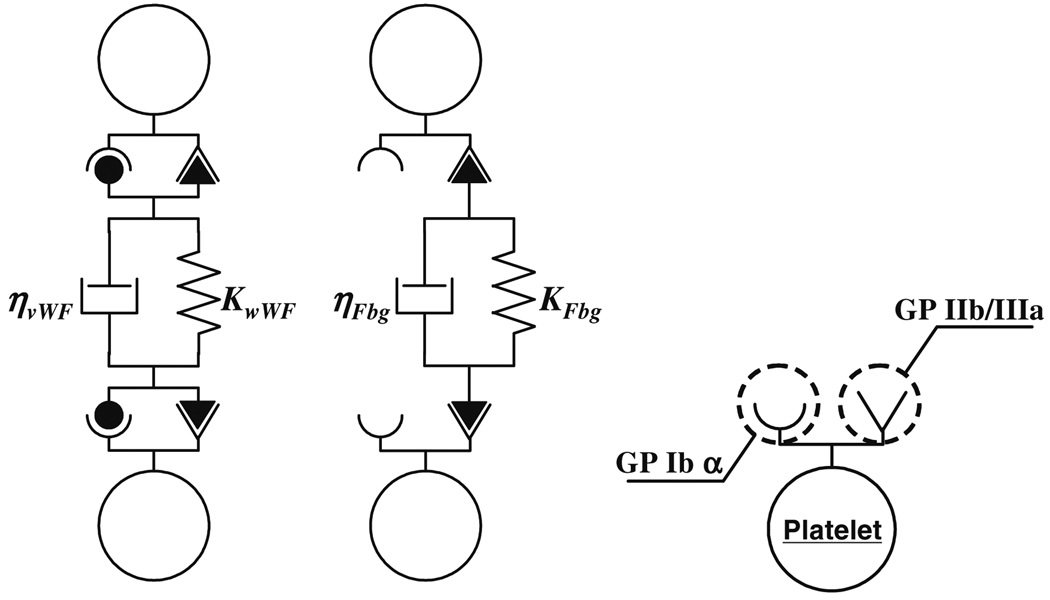
We have applied this simplified numerical method to investigate primary thrombus formation and destruction.^48,49,71 The hydrodynamic interactions can be efficiently calculated by this method. In addition, we incorporated DEM in order to include biochemical processes during the thrombus formation. We assumed that the binding force results exclusively from two plasma proteins: von Willebrand factor and fibrinogen, which are known to be main participants in the platelet adhesion and aggregation. To distinguish the properties of fibrogen and von Willebrand factor, we introduced the Voigt model with different characteristics for each protein (Figs. 1a and 11b). Their preferential configuration with GP Ibα or GP IIb/IIIa was also modeled by setting receptors on each platelet (cf., Fig. 1c). The simulations included various physiological and pathological phenomena in primary thrombus formation and destruction. Our simulations demonstrate that SDM in conjunction with DEM can be a powerful tool in modeling chemical bonding involved in multicellular biomechanical processes.

Figure 1.

Voigt models for vWF (a) and Fbg (b), and the receptor models on the platelet (c).

We have also applied full SDM to investigate a suspension of locomotive cells, such as sperm, and bacteria in the intestines.^32,33 Though we simplified the shape of locomotive cells as spherical, we could solve the fluid dynamics precisely from far-field hydrodynamic interactions to lubrication between two near-contact surfaces. Figure 2 shows instantaneous positions of 216 locomotive cells in a fluid otherwise at rest, where solid lines are trajectories during the five previous time intervals. The simulation results illustrated that coherent structures, such as aggregation, mesoscale spatiotemporal motion, and band formation, were generated by purely hydrodynamic interactions. Though we introduced here only two applications to microscopic physiological flows, we expect that SDM will be applied to a wide variety of phenomena in the future.

Figure 2.

Instantaneous positions of 216 locomotive cells in a fluid otherwise at rest. Solid lines are trajectories during the five previous time intervals, calculated by the full Stokesian dynamics method.

Particle Method in Conjunction with the Moving Particle Semi-Implicit Method

Flow-induced deformation of cells is an important process in microscale flows, but the SDM is in general limited to particulate flows of rigid particles. RBCs, for example, are highly deformable cells that consist of cytoplasm enclosed by a thin membrane. The MPS method based on the Lagrangian description of continuity and Navier–Stokes equations is suitable for modeling deformable RBCs. All the components of blood are expressed as a cluster of particles. The velocity of particles is computed at the position of each particle, and they move according to the computed advection velocity at each time step. Conventional numerical methods for solving Navier–Stokes equations require computational meshes for discretizing the equations. When an RBC approaches other RBCs, computational meshes can become too distorted for computation. In contrast, the MPS method does not require a computational mesh so simulations can be stable even for problems involving many cell–cell interactions. The membrane of RBCs is expressed by the cluster of particles, and the motion of these membrane particles can be tracked directly by solving the Navier–Stokes equations. Tsubota et al. demonstrated the efficiency of the method for RBC flows,⁶⁸ and further investigated the effect of the deformability of RBCs and hematocrit value on the flows.^69,70

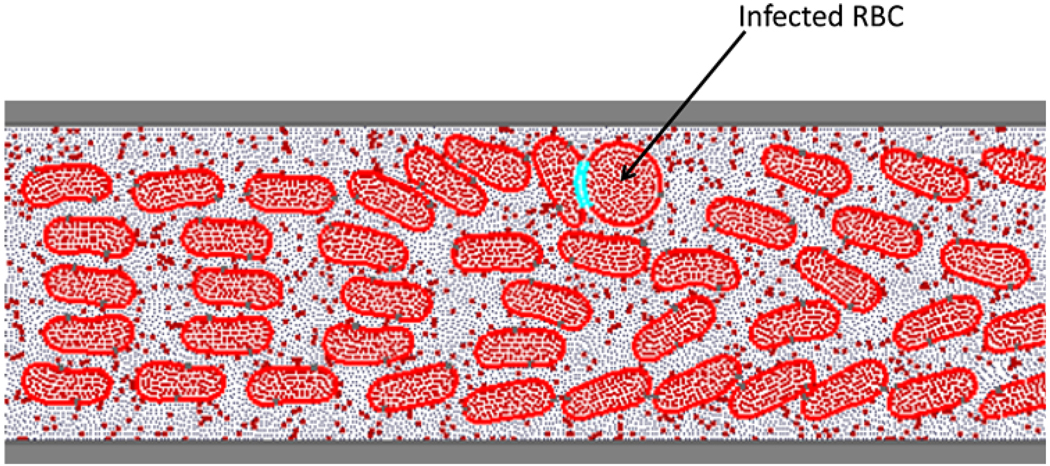
While this method is based on the continuum approach for fluid motion, it retains the advantageous features of particle modeling in the treatment of chemical-binding forces. As Kamada et al.³⁶ demonstrated, this method successfully simulated the formation and collapse of primary thrombus by introducing a platelet aggregation model. More recently, the method was applied by us to model hemodynamics arising from a serious infectious disease, malaria. When a malaria parasite invades and matures in an RBC, the infected RBC becomes stiffer and cytoadherent. These changes in the RBC property have been postulated to cause microvascular occlusion. Kondo et al.⁴⁰ proposed a numerical model to investigate the relationship between the hemodynamics and pathology of malaria. Their results indicated that the adhesive interactions between infected RBCs and endothelial cells significantly increased flow resistance in the microcirculation. As reviewed here, this method is readily applicable not only for hydrodynamic interactions but also for chemical interactions. In future studies, we plan to develop a wide range of biofluid models under various disease states based on the MPS method (Fig. 3).

Figure 3.

Malaria-infected blood flow between flat plats solved by MPS method. ⁴⁰ Infected RBC adheres to a healthy RBC. The adhered particles are shown in blue.

High-Performance Computing and Parallelized Codes

The rapid growth of computer power over the past decades has led to the development of large-scale simulation techniques capable of simulating processes on a molecular level,⁶³ among them molecular dynamics, Monte Carlo and hybrid techniques.^11,39,64 Tsubota et al.⁶⁷ used a state-of-the-art parallel computer “Earth Simulator” for solving RBC and platelets motions using particle methods such as described above. Parallel computing provides the potential to meet the continuously increasing computational complexity of molecular dynamics simulations with efficient scalable programs.^35,54 There are several molecular dynamics programs that can be used as an open source code for modeling large biomolecular systems, among them the NAMD-Scalable Molecular Dynamics,⁵⁴ the LAMMPS,^34,58 and the GROMACS.⁶ The NAMD-Scalable Molecular Dynamics is a molecular dynamics code for large biomolecular systems simulations designed for HPC.⁵⁴ It scales to hundreds of processors on high-end parallel platforms, and facilitates interactive simulation by linking to the visualization code VMD.⁵² Since its introduction over a decade ago, NAMD has matured, adding many features and scaling to thousands of processors. Another efficient molecular dynamics package—MDoC—for physical and life science modeling^1,12,17–20 was recently adapted for ultrascalable supercomputers.^14,26,53 The combination of a powerful parallel computing code with a state-of-the-art parallel computer can provide optimum scalability of the molecular problem under consideration.⁴⁴

DISCRETE AND DISSIPATIVE PARTICLE DYNAMICS

CFD simulations can be verified experimentally and used to predict quantitative results. However, they are limited to continuum systems,^23,29 representing a gap from 10 nm to 100 μm between microscopic experimental biochemistry and the macroscopic scales. Discrete and DPD paradigms do not have such a long history as CFD. However, it possesses important properties of mesoscopic systems: it can model easily heterogeneous fluids, allowing simulating processes which are very difficult to model by continuum approaches. Initial work focused on multiphase nature of these flows^8,25 due to the limitations of continuum mechanics models to represent consistently such flows. The dynamics of colloidal particle transport requires beyond passive transport additional processes such as agglomeration/dispersion, driven interfaces, adsorption, etc.^3,16,38 Several approaches, e.g., multiscale methods,^31,50 lattice-Boltzmann gas (LBG),⁴⁵ and atomistic-continuum hybrid algorithms^30,51 validate the use of fluid particle models for simulating hydrodynamic problems at mesoscopic scales.⁶⁶ Initial work has been done in molecular dynamics with the use of Lennard-Jones potential functions in simple geometries for modeling continuum hydrodynamics and applying the no-slip boundary conditions characteristic of viscous flows,^41,42 expanding the problems to higher Reynolds numbers⁶¹ and validated with a continuum hydrodynamic models. Several approaches were used for the proper application of no-slip boundary conditions,^56,62 although more systematic studies for higher Re and complex geometries are needed.

The DPD approach departs widely from the traditional continuum approach for solving fluid flow problems. It simulates flow by interactions between discrete-particles and enables bridging the gap between the macroscales of blood flow and the microscales of thrombus formations. In recent years, RBCs flowing in a capillary vessels were explored applying the DPD approach,²⁴ with plasma represented by dissipative fluid particles, and RBC and capillary walls by “solid” particles represented as a coarse-grained ensemble.^9,10 The whole system, composed of several million particles, demonstrated RBC aggregation and deformation, confirming clinical observations of clotting of deformed cells close to choking points. Modeling thrombosis using the DPD method²⁷ further incorporated interactions between the blood constituents, specifically platelets, where for platelet attachment (aggregation, wall deposition) the local attractive (bonding) force has a spring attached to the platelet’s surface.^27,28 Several factors may limit the DPD approach; they can lead to erroneous transport properties of the highly coarse-grained DPD systems, and thus to incorrect fluid dynamics.^37,55,57 The main disadvantage of implementing the DPD methodology compared to MD is the much higher memory and load requirements.¹² This can be alleviated by the use of larger parallel systems.

DPD Simulations of Blood Flow in Devices

The pioneering DPD simulations of blood flow in capillaries described earlier^9–11 were confined to very small scales (D ≈ 10 μm). While demonstrating certain blood particulate behavior (e.g., RBC folding), it was conducted in very low velocities and was not verified to behave like viscous flow. Thus, it is essential to run DPD simulations in much larger scales in order to examine whether a discrete particle approach can emulate the inertial effects of large-scale viscous flows. Accordingly, we conducted simulations in geometries orders of magnitude larger (including a full scale 3D valve) and realistic velocities, i.e., spanning the multiscales characterizing blood flow in devices, and verified those against continuum viscous flow solutions (manuscript in preparation). We have used the NMAD open source code to validate its use for simulating viscous blood flows in a 3D tube with a constriction resembling an occluded blood vessel. The results demonstrated the hallmarks of viscous flow behavior (no-slip at the wall, mass conservation, flow acceleration through the constriction and recirculation zones distal to the constriction) and compared very well with Navier–Stokes CFD solutions (Fig. 1).

Applied to the complex problem of flow through MHV, it may focus on flow regions in devices and pathologies that have a high propensity to activate platelets and form aggregates. Forces and potentials around particles representing platelets are carefully characterized, using Lennard-Jones equations and a summation of viscosity forces, to calculate the motion of particles representing the different phases in the domain (solid, fluid, and blood particulates) and their interactions. A constant force emulating the pressure gradient to overcome the viscous forces was applied to the fluid particles following the approach of Zhu et al.⁷²

The MDoC and NMAD packages were adapted by us to model platelet interactions using the DPD approach by entering new force parameters characterizing blood flow; two Lennard-Jones potential and force equations characterize forces between the platelets and other particles, the first for fluid–fluid (ff) particle-interactions and the second for wall–fluid (wf) particle-interactions:

$$\begin{array}{l}{U}_{\mathit{\text{ff}}}=4\epsilon \left[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6\right]\\ U_{\mathit{\text{wf}}}=4{\epsilon }_{\mathit{\text{wf}}}\left[{\left(\frac{{\sigma }_{\mathit{\text{wf}}}}{r}\right)}^{12}-{\delta }_{\mathit{\text{wf}}}{\left(\frac{{\sigma }_{\mathit{\text{wf}}}}{r}\right)}^6\right]\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left[\frac{r}{2^{1/6}}\right]\end{array}$$ (3)

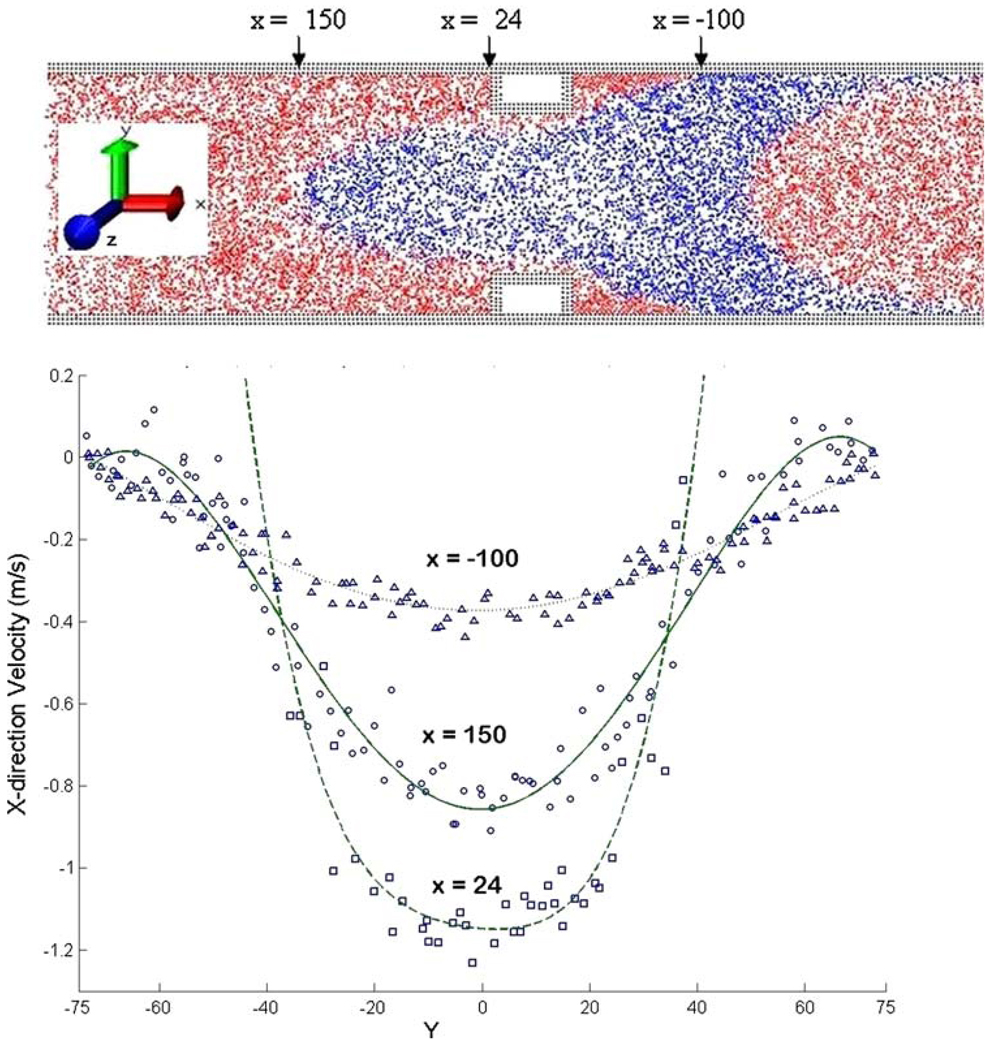
σ is equal to the particle’s diameter where the energy is set to zero, and ε represents the minimum value of the energy. The viscous forces acting on the particles are proportional to the spatial velocity gradients and the viscosity. To allow the system to maintain its momentum without an increase in the particles velocity, a driving pressure gradient was added according to the method by Zhu et al.⁷² The MDoC code is parallelized by breaking the equations above into several variables representing wall particles, fluid particles, and spatial components of the viscous forces. Those are broadcasted to the different processors using MPI Bcast, and reassigned to their appropriate values following computation. We recently validated the application of DPD to simulating viscous blood flow in 3D tube with a constriction resembling an occluded blood vessel, using approx. 1 million particles. The results demonstrated the hallmarks of viscous flow behavior (no-slip at the wall, mass conservation, flow acceleration through the constriction, and recirculation zones distal to the constriction), and compared very well with Navier–Stokes solutions (Fig. 4). The method was then applied to a complete 3D mechanical heart valve (MHV) geometry (Fig. 5). Platelet dispersion patterns are depicted during regurgitation around the tip of the leaflets (Fig. 6). Animation of the solution depicts a well-formed recirculation zone, as predicted by traditional continuum approaches.⁷

Figure 4.

DPD simulation using NMAD of blood flow through a constriction (top), and corresponding velocity profiles (bottom).

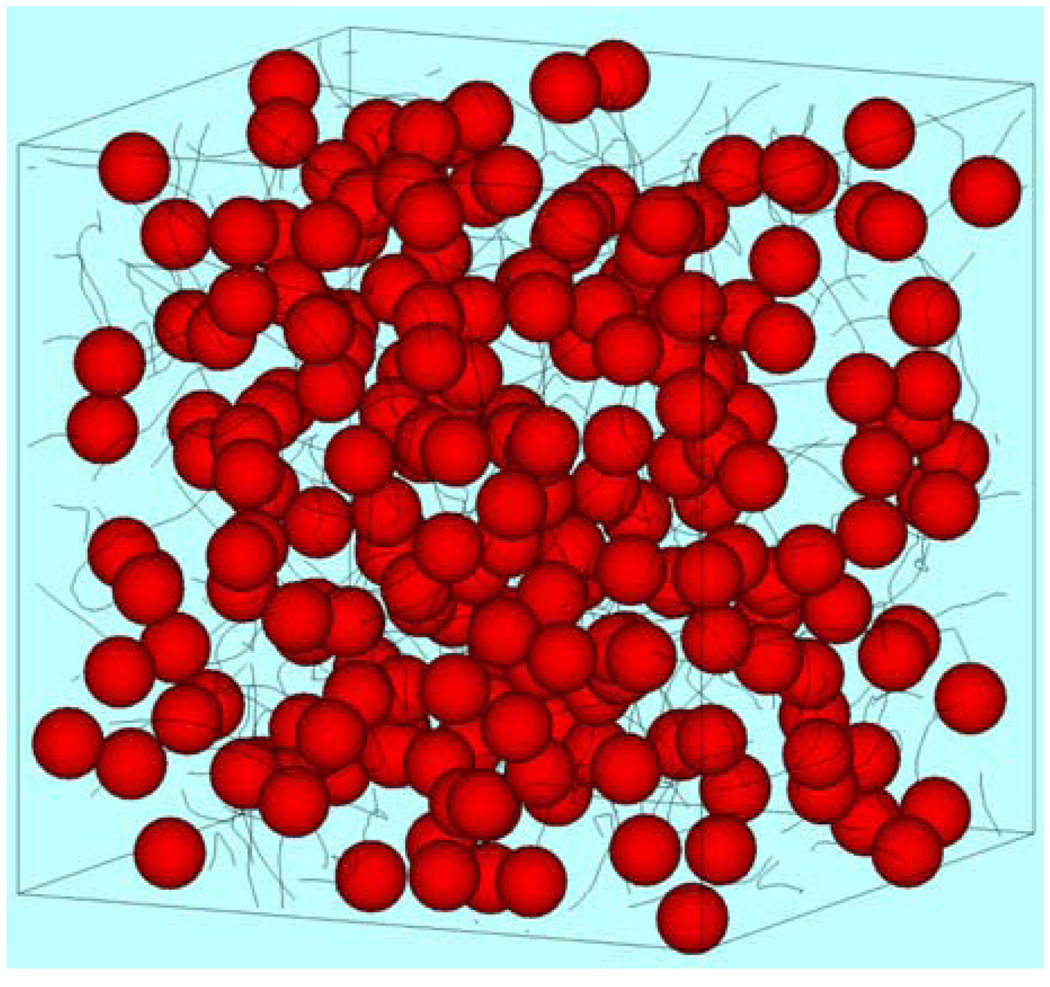
Figure 5.

DPD simulation of MHV blood flow—both fluid and solid domains consist of discrete-particles only.

Figure 6.

Flow around the valve’s leaflet tip during regurgitation (DPD).

Discrete Particle Dynamics for Modeling Platelets in the Micro/Nano Scales

In the microscopic scales, the blood can be regarded as an ensemble of interacting discrete-particles clusters of matter, conceived as a coarse graining of blood molecules.^25,66 The temporal evolution of the particle ensemble obeys Newtonian equations of motion (each particle defined by its mass, moment of inertia, translational and angular momentum), and represents a collective unit of fluid (plasma) or a fragment of a solid. The platelet interactions and force parameters characterizing blood flow can be formulated using Lennard-Jones potential, and force equations characterize forces between the platelets and other particles. The viscous forces acting on the particles are proportional to the spatial velocity gradients and the viscosity. Computer scripts stack the particles according to the radius of the fluid particles (determined by the σ parameter that describes the interaction between fluid and/or solid particles in the Lennard-Jones potential function⁶¹). The 3D macroscopic geometry is generated with a commercial grid generator. The force field functions assume that every particle interacts with the rest of the system.⁵⁴

Coarse-Grained Ensembles Representing Platelets

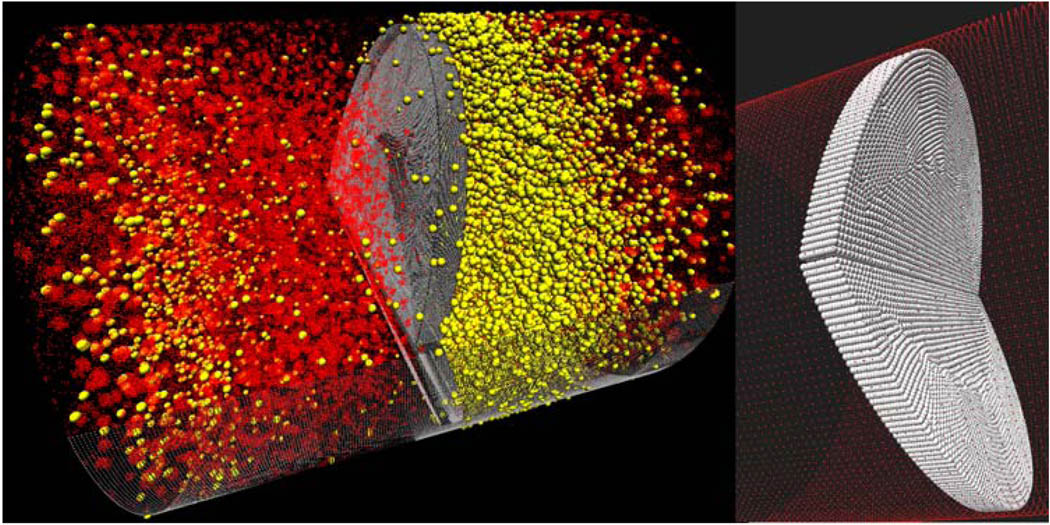
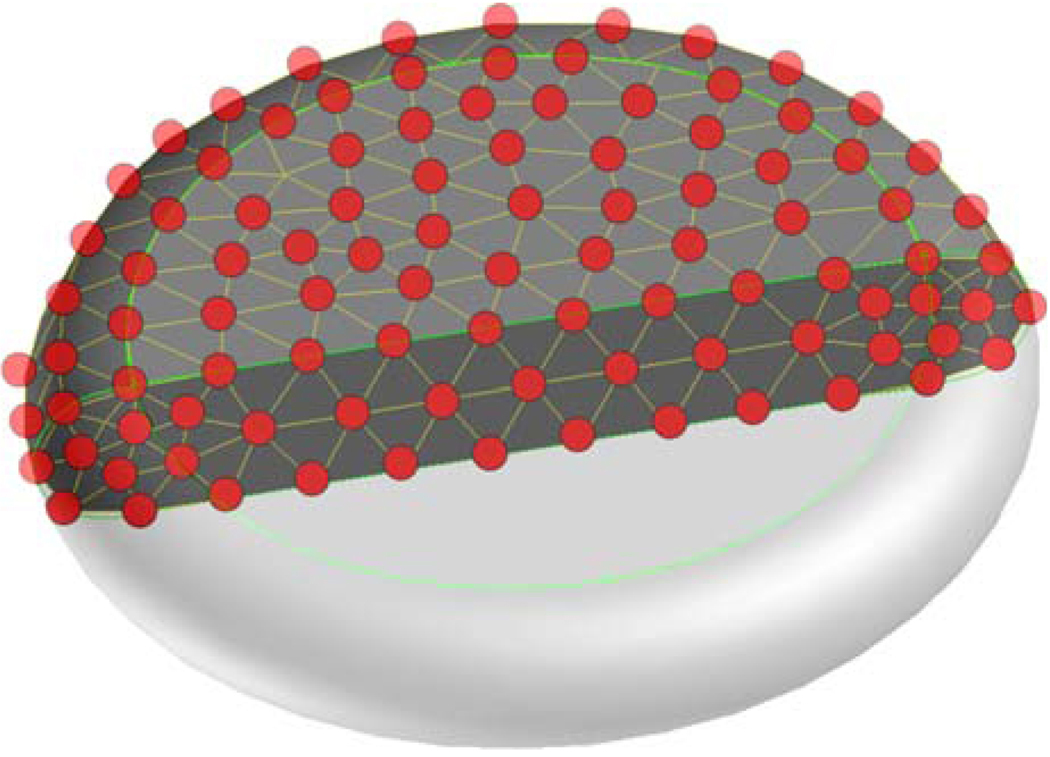
Coarse graining (upscaling) of the molecular models leading to mesoscopic scales in the micrometer scale of RBC and platelets^25,66 can be used to create their effective particle ensembles. A 3D mesh with particles connected with elastic bonds can be applied to model the cytoskeleton network of the platelets, as well as their internal contents. The ensemble has a typical discoid shape for quiescent platelets (Fig. 7). The same can be applied for simulating the typical biconcave disc shape for RBC. The particle ensemble provides structural integrity and elastic deformability, according to the forces acting upon it by the surrounding fluid flow. The temporal evolution of the particle ensemble obeys Newton’s equations of motion.

Figure 7.

Representation of a platelet composed of bonded solid particles.

CONCLUSIONS

We have reviewed recent advances in various particle-based Lagrangian methods. The SDM in conjunction with the DEM has an advantage in dealing with rigid particulate flow, such as platelet motions in plasma. The combination facilitates accurate calculation of the lubrication forces between particles as well as long-range hydrodynamic interactions among many interacting solid bodies. The computational load of this method is smaller than most particulate methods because of the small number of unknowns per particle. A particle method in conjunction with the MPS method is efficient for modeling deformable cells as well as rigid particles. The motion of a large number of RBCs can be efficiently calculated. One of the major advantages of this method is its applicability for modeling the chemical interactions between cells. The rapid growth of computing power over the past decades enables harnessing HPC for solving complex biological flows using particle-based Lagrangian methods. We expect particle-based Lagrangian methods to be applied to a wide variety of physiological and pathological problems in the future.

In discrete and DPD, the fluid phase is no longer assumed to be a continuum, setting it apart from traditional CFD approaches as well as MPS. Because of its discrete nature, DPD lends itself to molecular dynamics modeling and is therefore applicable to phenomena in the nanoscales where biochemistry plays a major role. DPD is also efficient for modeling blood flow in the capillaries, and for simulating whole blood flow in complex and confined environs of cardiovascular blood recirculating devices such as MHVs. It does pose the challenge of fine-tuning the parameters of the energy functions used to characterize the multiple particles dynamics in a way that will make a large ensemble of these particles behave like viscous blood flow. While using DPD for simulating blood flow in devices may require high performance computational resources, it offers the opportunity to study very complex multiscale phenomena such as flow-induced blood clotting in devices that truly incorporate the complex biomechanical interactions that take place when attempting to model the flow of a living tissue such as blood.

In summary, the various modeling approaches described here provide new insights into the mechanisms underlying complex flow-induced phenomena on the nano- to microscales, bridging the gap between molecular dynamics and continuum mechanics of the mesoscopic and macroscopic scales. These innovative modeling approaches may overcome some of the inherent limitations encountered by the more traditional numerical simulations approaches when modeling problems of complex biofluids.

ABBREVIATIONS

CFD

Computational fluid dynamics

DEM

Discrete element method

DPD

Dissipative particle dynamics

HPC

High-performance computing

MHV

Mechanical heart valve

MPS

Moving particle semi-implicit method

SDM

Stokesian dynamics method

SPH

Smoothed particle hydrodynamics method