Nuclear Resonance Vibrational Spectroscopy applied to [Fe(OEP)(NO)]: The Vibrational Assignments of Five-Coordinate Ferrous Heme Nitrosyls and Implications for Electronic Structure

Abstract

This study presents Nuclear Resonance Vibrational Spectroscopy (NRVS) data on the five-coordinate (5C) ferrous heme nitrosyl complex [Fe(OEP)(NO)] (1, OEP²⁻ = octaethylporphyrinato dianion) and the corresponding ¹⁵N¹⁸O labeled complex. The obtained spectra identify two isotope sensitive features at 522 and 388 cm⁻¹, which shift to 508 and 381 cm⁻¹, respectively, upon isotope labeling. These features are assigned to the Fe-NO stretch ν(Fe-NO) and the in-plane Fe-N-O bending mode δ_ip(Fe-N-O), the latter has been unambiguously assigned for the first time for 1. The obtained NRVS data were simulated using our quantum chemistry centered normal coordinate analysis (QCC-NCA). Since complex 1 can potentially exist in 12 different conformations involving the FeNO and peripheral ethyl orientations, extended DFT calculations and QCC-NCA simulations were performed to determine how these conformations affect the NRVS properties of [Fe(OEP)NO]. These results show that the properties and force constants of the FeNO unit are hardly affected by the conformational changes involving the ethyl substituents. On the other hand, the NRVS-active porphyrin-based vibrations around 340 – 360, 300 –320, and 250 – 270 cm⁻¹ are sensitive to the conformational changes. The spectroscopic changes observed in these regions are due to selective mechanical couplings of one component of E_u-type (in ideal D_4h symmetry) porphyrin-based vibrations with the in-plane Fe-N-O bending mode. This leads to the observed variations in Fe(OEP) core mode energies and NRVS intensities without affecting the properties of the FeNO unit. The QCC-NCA simulated NRVS spectra of 1 show excellent agreement with experiment, and indicate that conformer F is likely present in the samples of this complex investigated here. The observed porphyrin-based vibrations in the NRVS spectra of 1 are also assigned based on the QCC-NCA results. The obtained force constants of the Fe-NO and N-O bonds are 2.83 – 2.94 (based on the DFT functional applied) and about 12.15 mdyn/Å, respectively. The electronic structures of 5C ferrous heme nitrosyls in different model complexes are then analyzed, and variations in their properties based on different porphyrin substituents are explained. Finally, the shortcomings of different DFT functionals in describing the axial FeNO subunit in heme nitrosyls are elucidated.

Introduction

Nitric oxide (NO), a poisonous and corrosive gas, is a classic “double-edged sword” in biological systems. On the one hand side, it plays a pivotal role in many biological processes in humans, including nerve signal transduction, blood pressure control (arterial vasodilation), blood clotting, and immune response by white blood cells.¹ Correspondingly, malfunctioning of the NO generating network is now invoked in a steadily growing number of human diseases. However, as mentioned above, NO is also a toxic molecule, and malfunctioning of the NO regulating network, leading to its overproduction, is no less of a problem. Because of this, the concentration of free NO in human blood is under tight control, and the biological mechanisms for the regulation of NO are currently being heavily investigated.² Release of large quantities of NO leads to nitrosative stress, which, just like oxidative stress, has been related to many health problems³ including the initiation of cancer, cell damage and death, atherogenesis, and sporadic Parkinson’s disease.⁴

Many of the biologically important functions and transformations of NO are catalyzed by heme proteins.⁵ The generation of NO in vivo is catalyzed by the nitric oxide synthase (NOS) class of enzymes, which belong to the family of heme-thiolate enzymes that includes cytochrome P450.⁶ Here, NO is produced by the stepwise oxidation of l-arginine to citrulline, which is accompanied by the generation of one molecule of NO. The important cardiovascular regulation by NO (produced by endothelial NOS) is then mediated by soluble guanylate cyclase (sGC).⁷ This enzyme serves as the biological NO sensor/receptor. In its active form, sGC contains a five-coordinate (5C) heme with proximal histidine (His) coordination in the ferrous oxidation state. Interestingly, the heme site in this protein has a very high affinity for NO, but only a low affinity toward dioxygen.⁸ Upon binding of NO, a six-coordinate ferrous heme nitrosyl is believed to form as an intermediate. Due to the strong σ trans effect of NO on the axial His ligand,^9,10 the Fe(II)-His bond is broken, leading to the corresponding 5C ferrous heme NO complex. This is believed to be accompanied by large structural changes of the enzyme, which correlates with activation of the catalytic site of sGC for the conversion of guanosine triphosphate (GTP) to cyclic guanosine monophosphate (cGMP).⁸ The latter serves as a secondary messenger molecule involved in the relaxation of vascular smooth muscles, which induces vasodilation of the arteries, and hence, controls the blood flow.

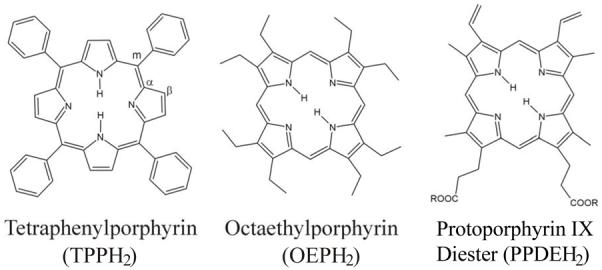
Due to the many biological functions of ferrous heme nitrosyls, in particular in sGC as described above, but also in enzymes of the denitrification process,⁵ many corresponding model complexes have been synthesized and structurally and spectroscopically characterized.¹¹ In these studies, tetraphenylporphyrin (TPPH₂), octaethylporphyrin (OEPH₂) and protoporphyrin IX diester (PPDEH₂) are the most commonly used macrocycles (cf. Scheme 1). Within the many spectroscopic methods applied to study the corresponding ferrous heme nitrosyl model complexes, vibrational spectroscopy has always been a key technique, because the vibrational properties of these complexes are very sensitive to coordination number, oxidation state, spin state, etc., of the metal. In the case of ferrous heme nitrosyls, it has been demonstrated that binding of the axial ligand (N- or S-donor ligands) weakens the Fe-NO and N-O bonds in comparison to the corresponding 5C species, and in this way, increases the amount of radical character (spin density) on the coordinated NO.9a,b^,10,12 Vibrational methods applied to proteins and model complexes include IR, resonance Raman, and Nuclear Resonance Vibrational Spectroscopy (NRVS).¹³ The interpretation of these vibrational data, but also DFT studies on reaction mechanisms of heme proteins, are frequently based on the porphine approximation, i.e. all porphyrin ring substituents are neglected. Whereas this is intuitively a good approximation for systems with approximately D_4h-symmetric macrocycles (for example TPP complexes), the biologically observed hemes all contain asymmetric substitution pattern of the porphyrin ring. In general, not much attention has been paid to the influence of the peripheral substituents on the properties of the central Fe-axial ligand(s) subunit.

Scheme 1.

In this study, the vibrational properties and electronic structure of 5C ferrous heme nitrosyl model complexes are evaluated using [Fe(OEP)(NO)] (1; cf. Scheme 2) as an example.¹⁴ The main goals of this work are to (a) clarify the vibrational assignments of 5C ferrous heme nitrosyls, (b) determine the influence of porphyrin substituents on the properties of the axial FeNO unit, and (c) explain trends in the electronic structures of these complexes. Previous work on the corresponding TPP complex [Fe(TPP)(NO)] (2) had identified the Fe-NO stretching mode ν(Fe-NO) at ~530 cm⁻¹ as an intense, isotope sensitive band in resonance Raman spectroscopy.^15,9b This assignment is also in agreement with results from NRVS,¹⁶ which show ν(Fe-NO) at 538 cm⁻¹ for powder samples of 2. On the other hand, the assignment of the corresponding bending mode δ_ip(Fe-N-O) (ip = in plane) is less clear. Based on IR spectroscopy, this mode was identified as a weak, isotope sensitive feature at 371 cm⁻¹ for compound 2.^9b This is in contrast to a NRVS study on 2, where δ_ip (Fe-N-O) was assigned to a band at 470 cm⁻¹.^16a However, this latter assignment is problematic for several reasons. First, no isotope labeling is provided in ref. 16a to positively confirm that the 470 cm⁻¹ feature is in fact related to the FeNO unit. Second, this feature is absent in [Fe(OEP)(NO)].^16c Third, NRVS data on the corresponding 6C species [Fe(TPP)(MI)(NO)] also show the 470 cm⁻¹ band, which is not ¹⁵N¹⁸O isotope sensitive in this case.^9c Finally, published NRVS data on 1 show ν(Fe-NO) at 521 cm⁻¹, but no clear assignment of δ_ip(Fe-N-O) was obtained.^16c In order to clearly identify δ_ip(Fe-N-O), and to confirm the assignment of this mode for 2, we have performed NRVS measurements on complex 1 and the corresponding ¹⁵N¹⁸O isotope labeled complex. The obtained NRVS data are further analyzed using simulated NRVS spectra based on density functional theory (DFT) calculations on complex 1 without any simplifications (i.e., with all ethyl substituents in place), followed by normal coordinate analysis (NCA) fits of the vibrations of the FeNO subunit of this complex. Previous work by Scheidt and coworkers has shown that 1 can exist in different conformations in the solid state as shown in Scheme 2.¹⁴ In addition, ferrous heme nitrosyls show in general low energy barriers for rotations of the NO ligand around the Fe-NO bond,^17,18 leading to further structural diversity. This is evident from the solid state structures on these compounds which frequently show disorder in the NO orientation (see, for example, ref. 19). Our calculations show that the conformation adopted by the NO ligand relative to the ethyl substituents has a distinct effect on the NRVS data in the region of Fe-porphyrin core vibrations, whereas the electronic structure of the FeNO subunit is hardly affected by changes in the conformation.

Scheme 2.

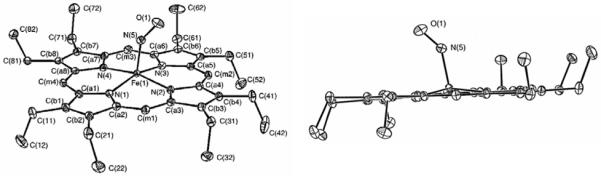
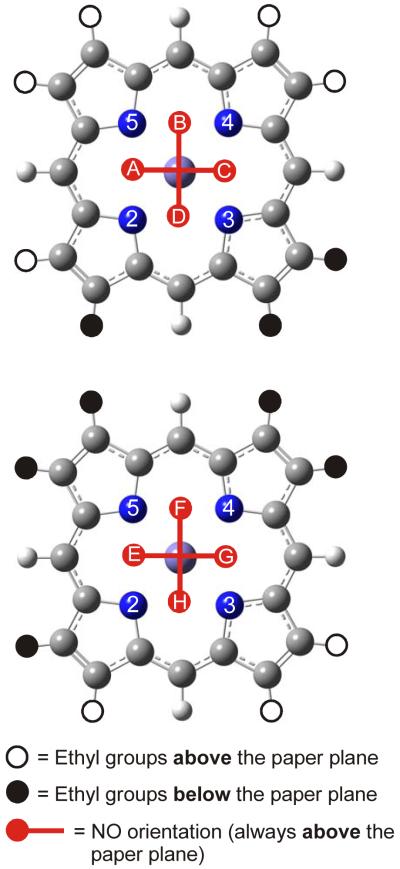
Crystal structure of [Fe(OEP)(NO)] (1) from monoclinic (left; form I) and triclinic (right, form II) crystals taken from ref. 14. In form I, 5 neighboring ethyl groups of OEP point to one face of the porphyrin, whereas the remaining 3 point in the opposite direction. In contrary, in form II, 4 neighboring ethyl groups point to each face of the porphyrin core as indicated on the right. (Reprinted with permission from Ref. 14. Copyright 1997 and 2000, American Chemical Society.) (Comment: permission request will be submitted when needed)

Experimental and Computational Procedures

Chemicals

Reactions were performed using Schlenk techniques using carefully purified solvents. NO (98%, Matheson Gas) was purified by passing the gas through KOH pellets and a cold trap (dry ice/acetone) to remove higher nitrogen oxides. ¹⁵N¹⁸O (98 atom % ¹⁵N, 95 atom % ¹⁸O) was purchased from Aldrich Chemical Company and was used as received. Octaethylporphyrin (H₂OEP) was purchased from Mid-Century Chemicals. ⁵⁷Fe₂O₃ was purchased from Cambridge Isotope Laboratories. Hydrochloric acid (36.5-38%) and DMF (99.8%) were purchased from EMD Chemical Inc.

Synthesis of [⁵⁷Fe(OEP)Cl]

To a CH₃OH suspension (10 ml) of ⁵⁷Fe₂O₃ (140 mg, 0.86 mmol) was added HCl (1.5 ml) and stirred overnight at 60 °C under N₂. The yellow solution was filtered into another Schlenk flask, and a dark brown solid was obtained after removing the solvent in vacuo at 160 °C for 6 h. A DMF (30 mL) solution of H₂OEP (350 mg, 0.66 mmol) was added and then stirred vigorously for 2 h at 150 °C. The resulting [⁵⁷Fe(OEP)Cl] (264 mg, 65% yield) was purified by a published method.²⁰ The precursor [⁵⁷Fe(OEP){S-2,6-(CF₃CONH)₂C₆H₃}] is obtained from [⁵⁷Fe(OEP)Cl] using a published procedure.²¹

Synthesis of [⁵⁷Fe(OEP)(NO)] (1)

The spectroscopically pure (in ⁵⁷Fe) five-coordinate compound [⁵⁷Fe(OEP)(NO)] was obtained from the reaction of a powdered sample of [⁵⁷Fe(OEP){S-2,6-(CF₃CONH)₂C₆H₃}] with excess NO gas at room temperature for 1 day, presumably via the six-coordinate intermediate [⁵⁷Fe(OEP)(NO){S-2,6-(CF₃CONH)₂C₆H₃}].²¹ The IR spectrum of this compound shows the NO stretching vibration ν(N-O) at 1671 cm⁻¹, indicative of the formation of 1. In addition, the NRVS spectrum obtained for this complex is similar to the one published by Scheidt and coworkers.^16c This is due to the fact that NRVS only monitors vibrations that involve motions of the ⁵⁷Fe; other components of the sample that do not contain ⁵⁷Fe remain completely undetected, which is different from IR or Raman spectroscopy.

Synthesis of [⁵⁷Fe(OEP)(¹⁵N¹⁸O)]

The synthesis of this complex was performed as described above using ¹⁵N¹⁸O labeled nitric oxide.

IR Spectroscopy

Middle Infrared spectra (MIR) were recorded on Perkin-Elmer FT-MIR spectrometer SPECTRUM Bx and Gx using KBr disks. The resolution was set to 2 cm⁻¹. IR spectra were recorded at room temperature.

Nuclear Resonance Vibrational Spectroscopy (NRVS)

NRVS data were collected as described in reference ²² at beam line 3-ID-XOR of the Advanced Photon Source (APS) at Argonne National Laboratory. This beamline provides about 2.5·10⁹ photons/sec in ~1 meV bandwidth (= 8 cm⁻¹) at 14.4125 keV in a 0.5 mm(vertical) × 0.5 mm (horizontal) spot. This is achieved using a water-cooled diamond double crystal monochromator with 1.1 eV bandpass, followed by a high resolution monochromator consisting of two asymmetrically cut Si (4 0 0) and two asymmetrically cut Si (10 6 4) crystals, respectively.²³ Delayed nuclear fluorescence and Fe K fluorescence were detected using a single avalanche photodiode.²⁴ Spectra were recorded between −40 and 90 meV in steps of 0.25 meV. Each scan took ~60 min, and all scans were added and normalized to the intensity of the incident beam. The spectra presented in Figure 3 represent averages of 4 and 5 scans for 1 and the ¹⁵N¹⁸O labeled compound, respectively. During the NRVS measurements, the samples remained at cryogenic temperatures using a liquid helium cryostat. Because the temperature sensor of the cryostat is not in direct contact with the sample, the exact temperatures for individual scans are not exactly known. The ratio of Stokes to anti-Stokes intensities could be used to calculate sample temperatures. However, since the low-frequency (<100 cm⁻¹) anti-Stokes bands are not well resolved, and the anti-Stokes intensities of higher energy modes are negligible, this was not possible in this case. Nevertheless, the latter finding indicates that the sample temperature is well below 50 K. Hence, the temperature uncertainty does not affect the NRVS intensities in the > 130 cm⁻¹ spectral region, because the intensities are not sensitive to temperature variations in the 0-50 K range. Comparison of initial and final scans confirms the absence of spectroscopic changes due to radiation damage. In addition, MIR spectra were recorded of the samples prior and after exposure to the X-ray beam (cf. Figure S1), showing no degradation. The NRVS raw intensities were converted to the Vibrational Density of States (VDOS) using the program Phoenix.^16b NRVS VDOS integral intensities were obtained by fitting the observed peaks with Gaussian functions using the program PeakFit.

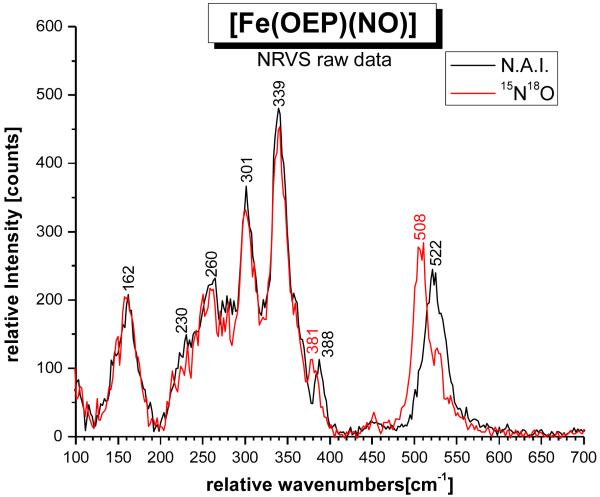
Figure 3.

NRVS spectrum of [⁵⁷Fe(OEP)(NO)] (1; black, n.a.i. = natural abundance isotopes NO), and of the corresponding ¹⁵N¹⁸O labeled complex (red).

Density Functional Theory (DFT) Calculations and Quantum Chemistry Centered Normal Coordinate Analysis (QCC-NCA)

The structure of the model complex [Fe(OEP)(NO)] (S = 1/2) was fully optimized without simplifications for a total of 12 different conformations of this complex using the B3LYP functional and the basis sets LanL2DZ. These conformers were chosen in accordance to the crystallographically observed forms I and II of this complex shown in Scheme 2, as further elucidated in the Results and Analysis, Section B. The structures of the twelve different conformers A – H and K – N (cf. Figures 1 and 2) were all fully optimized using B3LYP/LanL2DZ. Vibrational frequencies were calculated for all optimized structures obtained this way showing no imaginary frequencies. The LanL2DZ basis set applies Dunning/Huzinaga full double zeta (D95)²⁵ basis functions on first row and Los Alamos effective core potentials plus DZ functions on all other atoms.²⁶ For three selected structures (E, F, N), geometry optimization has also been performed using BP86/LanL2DZ*, which gives superior molecular geometries compared to B3LYP/LanL2DZ. The LanL2DZ* basis set consists of LanL2DZ plus polarization functions from TZVP on all non-hydrogen atoms (G98 implementation; cf. Table S18).^9a TZVP corresponds to Ahlrich’s triple-ζ valence polarization basis set.²⁷ All calculations were performed using Gaussian 03.²⁸

Figure 1.

The eight possible orientations of NO in form I (cf. Scheme 2, left) of [Fe(OEP)(NO)]. In this case, 5 neighboring ethyl groups of the OEP ligand point to one face of the porphyrin, whereas the remaining 3 point in the opposite direction. The bound NO ligand occupies positions between two adjacent nitrogen atoms of the porphyrin core, leading to the eight different structures indicated as A – H. Each structure was fully optimized using B3LYP/LanL2DZ and corresponds to an energy minimum on the potential energy surface.

Figure 2.

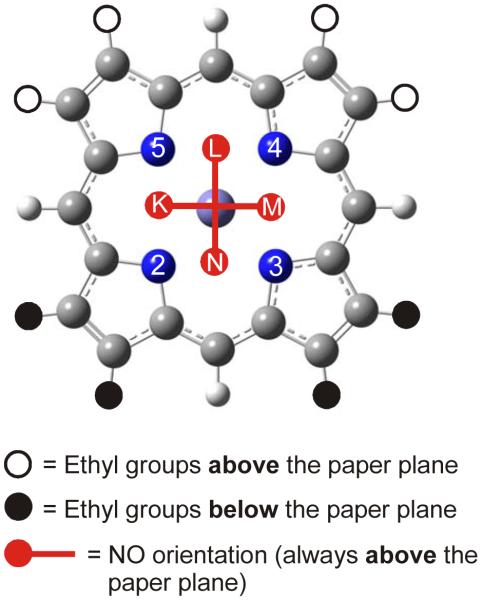
The four possible orientations of NO in form II (cf. Scheme 2, right) of [Fe(OEP)(NO)]. Here, 4 neighboring ethyl groups of the OEP ligand point to each face of the porphyrin, respectively. The bound NO ligand occupies positions between two adjacent nitrogen atoms of the porphyrin core, leading to the four different structures indicated as K – N. Each structure was fully optimized using B3LYP/LanL2DZ and corresponds to an energy minimum on the potential energy surface.

In order to calculate the NRVS spectra from the G03 frequency calculations, we used our quantum chemistry centered normal coordinate analysis (QCC-NCA) package.^9b Here, the cartesian force field from G03 was first transformed into internal coordinates using a modified version of Allouche’s program Redong (QCPE 628).²⁹ In the next step, we used our modified NCA programs, based on QCPE 576 by M.R. Peterson and D.F. McIntosh, to calculate the NRVS spectra.^9c This software was also used to subsequently fit the vibrational energies of the FeNO subunit of 1 in all twelve conformers. This was achieved by varying the force constants listed in Table 1 in the DFT-calculated force fields, according to the QCC-NCA approach.^9b,30

Table 1.

Force constants invoked in the fit of the vibrations of the FeNO subunit of [Fe(OEP)(NO)] (1) using the QCC-NCA approach. The calculated and NCA force constants are averages of the different conformations of 1 shown in Figures 1 and 2. Note that the force constants of the FeNO subunits of the individual conformers are extremely similar

Force Constant	B3LYP/LanL2DZ A – H // K – M a	QCC-NCA A – H // K – M a	BP86/LanL2DZ* E, F, N b	QCC-NCA E, F, N b	Fe(TPP)(NO) QCC-NCA c
fN-O [mdyn/Å]	10.99 // 10.97	12.17 // 12.16	12.80	12.15	12.530
fFe-NO [mdyn/Å]	2.25 // 2.24	2.83 // 2.82	3.86	2.94	2.975
fFe-N-O [mdyn·Å]	0.45 // 0.45	0.338 // 0.336	0.47	0.361	0.336
fN-O/Fe-NO [mdyn/Å]	−0.04 // −0.04	0.4472 (fixed) d	0.68	0.4472 (fixed) d	0.4472
fN-O/Fe-N-O [mdyn]	0.12 // 0.11	0.3486 (fixed) d	0.35	0.3486 (fixed) d	0.3486 (*)
fFe-NO/Fe-N-O [mdyn]	0.14 // 0.14	0.3565 (fixed) e	0.33	0.3863 (fixed) e	0.2966 (*)

^aAveraged for A – H and K – M, respectively. As can be seen in Figure S3, the vibrational properties of the FeNO unit do not depend much on the conformation of the complex. Correspondingly, the DFT-calculated and NCA force constants are very similar for the different conformations (average value ± 0.5%). The only exception is the B3LYP/LanL2DZ calculated value for f_N-O/Fe-NO, which shows larger changes. However, this force constant is predicted incorrectly by this method.

^bAveraged for the selected conformations E, F, N. As stated under footnote a, the vibrational properties of the FeNO unit do not depend much on the applied conformation.

^cTaken from ref. 9b; the fit was performed using [Fe(P)(NO)] (P = porphine²⁻) as a model.

^*original value from the BP86/TZVP calculation on [Fe(P)(NO)], which was not changed in the NCA treatment.

^dTaken from the QCC-NCA on [Fe(TPP)(NO)] from ref. 9b (see right column).

^eDetermined by optimizing the NRVS-VDOS intensity ratio of ν(Fe-NO) and δ_ip(Fe-N-O) for conformer F, and then fixed in the NCA fits of the other conformers.

Results and Analysis

A. Nuclear Resonance Vibrational Spectroscopy (NRVS) on [Fe(OEP)(NO)] (1)

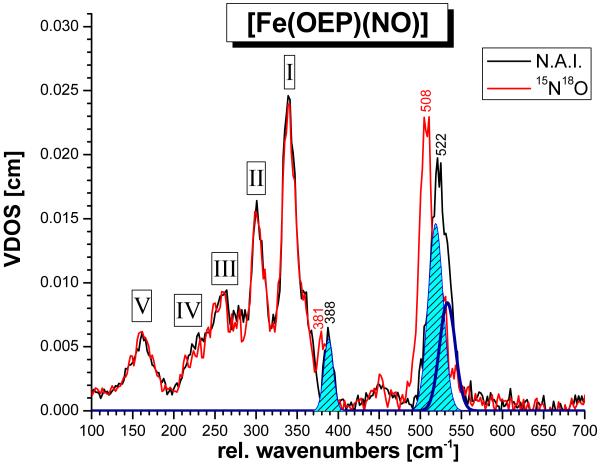
Nuclear Resonance Vibrational Spectroscopy (NRVS) is a method that is advantageous for the investigation of the vibrational properties of transition metal nitrosyl complexes, because these compounds are often times photolabile. Hence, the application of resonance Raman spectroscopy can be problematic for these compounds.^9c,31 On the other hand, NRVS measures the inelastic scattering that is observed upon excitation of the ⁵⁷Fe nucleus at the 14.4125 keV nuclear resonance (Mössbauer) line.^22,32 NRVS is ideal for the identification of metal-ligand stretching vibrations, since NRVS intensities are proportional to the amount of iron motion in a normal mode.^16b Hence, metal-ligand stretching vibrations are often very intense in NRVS, and correspondingly, this method has recently been successfully applied to ferrous heme nitrosyls and carbonyls.^33,16a,c,9c Figure 3 shows the NRVS raw data of [⁵⁷Fe(OEP)(NO)] (1) and of the corresponding ¹⁵N¹⁸O labeled analogue. Two isotope sensitive features are observed at 522 and 388 cm⁻¹, which shift to 508 and 381 cm⁻¹, respectively, in the isotope labeled complex. In comparison to [Fe(TPP)(NO)] (2, cf. Table 2),^9b the feature at 522 cm⁻¹ can be assigned to the Fe-NO stretch ν(Fe-NO), and the 388 cm⁻¹ feature must then correspond to the in-plane Fe-N-O bend δ_ip(Fe-N-O). Figure 4 shows the vibrational density of states (VDOS) obtained from these data. As shown by Sturhahn and coworkers, the integrated VDOS intensity from NRVS is proportional to the square of the amount of iron motion, e_Fe², of a given normal mode.^16b From Figure 4, the ratio e_Fe²[522 cm⁻¹]/e_Fe²[388 cm⁻¹] is determined to ~3.5 experimentally. Interestingly, the (powder) NRVS spectra of 1 previously published by Scheidt and coworkers show the 388 cm⁻¹ feature with a larger intensity, leading to an estimated intensity ratio of e_Fe²[522 cm⁻¹]/e_Fe²[388 cm⁻¹] = 1.6 – 1.8.^16c This difference could be related to the presence of different conformers of 1 in the samples applied in these different measurements (vide infra), or the different methods of sample preparation. Alternatively, the comparatively low intensity of the 388 cm⁻¹ feature compared to the other NRVS bands could be due to a (partial) preferential orientation of the sample during our measurements. The fact that this is observed for both the unlabeled and the ¹⁵N¹⁸O-labeled complex in exactly the same manner argues against this explanation. Note that although the 388 cm⁻¹ band is present as a strong feature in the NRVS spectra of 1 in ref 16c, no assignment of this mode could have been made in this work due to the lack of NO isotope labeling.

Table 2.

Geometric and vibrational properties of [Fe(P*)(NO)] complexes (P* = substituted porphyrin²⁻ or porphine²⁻ ligand; cf. Scheme 1) ^a

Molecule	Geometric Parameters [Å]					Vibrational Frequencies [cm−1]
	Fe-N	N-O	∠Fe-N-O	Fe-NP	Ref.	ν(N-O)	ν(Fe-NO)	δip(Fe-N-O) c	Ref.	Condition
[FeII(OEP)(NO)]  (1) Monoclinic (form I) Triclinic (form II)	1.722 1.731	1.167 1.168	144 143	2.004 2.010	14	1671	522 e	388 e	d	KBr (N-O), solid
[FeII(OEP)(15N18O)]						1597	508 e	381 e
[FeII(TPP)(NO)] b  (2)	1.72	1.12	149	2.00	47	1697	532	371	9b	KBr
[FeII(TPP)(15N18O)]						1625	515	365
[FeII(TPP)(NO)]						1678	524		15b	benzene
[FeII(TPP)(NO)]							538		16a	solid
[FeII(DPDME)(NO)]	1.723	1.187	143	2.005	48	1651			48	KBr
[FeII(PPDME)(NO)]						1655			49	KBr
						1673				toluene
[FeII(OEP)(NO)], struct. E f Calc: B3LYP/LanL2DZ	1.742	1.215	143	2.020	d	1615	503	403	d	-
[FeII(OEP)(NO)], struct. N f Calc: B3LYP/LanL2DZ	1.742	1.215	143	2.020	d	1616	499/504	408	d	-
[FeII(OEP)(NO)], struct. E f Calc: BP86/LanL2DZ*	1.687	1.190	144	2.023	d	1713	620	406	d	-
[FeII(OEP)(NO)], struct. N f Calc: BP86/LanL2DZ*	1.687	1.190	144	2.022	d	1712	620	416	d	-
[FeII(P)(NO)] Calc: BP86/TZVP	1.705	1.179	146	2.019	9a	1703	595	427	9a	-
[FeII(P)(NO)] Calc: BP86/6-311G*	1.695	1.181	144	2.012	d	1712	624	439	d	-
[FeII(P)(NO)] Calc: BP86/6-31G*	1.686	1.192	144	2.008	d	1725	632	439	d	-
[FeII(P)(NO)] Calc: BP86/LanL2DZ*	1.688	1.188	144	2.021	d	1726	619	428	d	-
[FeII(P)(NO)] Calc: B3LYP/TZVP	1.718	1.161	142	2.021	d	1790	585	444	d	-
[FeII(P)(NO)] Calc: B3LYP/LanL2DZ*	1.712	1.169	141	2.020	d	1825	538	435	d	-
[FeII(P)(NO)] Calc: B3LYP/LanL2DZ	1.742	1.212	143	2.019	9b	1637	507	425	9b	-
[FeII(TPP)(MI)(NO)]	1.750	1.182	138	2.008	50	1630	437 e	563 e	9b,c	KBr (N-O), solid
[FeII(TPP)(MI)(15N18O)]						1556	429 e	551 e
[FeII(To-F2PP)(MI)(NO)]	1.752	1.202	138	2.012	9b	1624			9b	KBr
[FeII(P)(MI)(NO)] Calc: BP86/TZVP	1.734	1.186	140	2.022	9a	1662	609	482	9a	-
[FeII(P)(MI)(NO)] Calc: B3LYP/LanL2DZ	1.810	1.215	142	2.030	9b	1611	505	430	9b	-

^aDPDME = deuteroporphyrin IX dimethylester²⁻; PPDME = protoporphyrin IX dimethylester²⁻; MI = 1-methylimidazole; P = Porphine²⁻ ligand used for calculations; values for Fe-N_P distances are averaged; the Fe-N-O angle (∠Fe-N-O) is given in degrees.

^bHighly disordered structure.

^cThe δ(Fe-N-O) in-plane (ip) bending vibration.

^dThis work.

^eDetermined from NRVS using ⁵⁷Fe. Compared to natural abundance isotopes (n.a.i.) Fe, the modes ν(Fe-NO) and δ_ip(Fe-N-O) appear about 1 – 2 cm⁻¹ shifted to lower energy.

^fConformer E corresponds to the monoclinic form I whereas conformer N corresponds to the triclinic form II from crystallography (cf. Scheme 2).

Figure 4.

Vibrational density of states (VDOS) for [⁵⁷Fe(OEP)(NO)] (1; black, n.a.i. = natural abundance isotopes NO) and of the corresponding, ¹⁵N¹⁸O labeled complex (red), calculated from the NRVS raw data using Phoenix.^16b The obtained fit (shaded light blue and dark blue curves) is indicated. The shaded areas of the isotope sensitive features at 522 and 388 cm⁻¹ in the spectrum of the n.a.i. complex yield iron motions, e_Fe², of ~0.3 (522 cm⁻¹) and 0.08 (388 cm⁻¹), respectively.

The intensity ratio e_Fe²[ν(Fe-NO)]/e_Fe²[δ_ip(Fe-N-O)] can be calculated from a normal coordinate analysis (NCA) or a quantum-chemical frequency calculation in a straight-forward fashion.^16c,9c Here, we use DFT to predict the NRVS spectra of 1 and, as discussed below, the DFT results are in strong support of the assignments of ν(Fe-NO) and δ_ip(Fe-N-O) presented here. In addition, as shown in Table 2, the assignment of ν(Fe-NO) to the band at 522 cm⁻¹ is in good agreement with vibrational data obtained for other 5C ferrous heme nitrosyls.

The additional features observed in the NRVS spectra of 1 below 380 cm⁻¹ must then correspond to vibrations of the Fe(OEP) core of the complex. These signals can be subdivided into five groups labeled I – V in Figure 4. Previously, NRVS spectra of a number of OEP complexes, including [Fe(OEP)] and [Fe(OEP)(MI)(CO)],^33c,d have been reported, but detailed spectral analyses of porphyrin vibrations in nitrosyl and carbonyl complexes have so far mostly focused on the analogous TPP complexes.^16a,c,33c,d The lower energy region of the NRVS spectra of complex 1 in Figures 3 and 4 shows strong similarities to the spectrum of [Fe(OEP)(MI)(CO)].^33d This, of course, is not surprising, since the axial ligands only have a moderate influence on the properties of the Fe(porphyrin) core, as long as the metal oxidation and spin states are similar, no large out-of-plane distortions of the porphyrin ring are observed, and no oxidation or reduction of the porphyrin ligand forming a corresponding radical occurs. Based on our DFT results presented in the next chapter, the broad, intense features at 162, 230, 260, 301, and 339 cm⁻¹ in the NRVS data of 1 are assigned.

B. DFT calculations of the NRVS spectra of [Fe(OEP)(NO)] (1)

In order to further investigate the assignments of the NRVS spectra of 1 systematically, we have performed DFT calculations on this complex applying the B3LYP functional together with the LanL2DZ basis set to screen the twelve different conformers that this complex most likely exists in. In contrast to previous DFT studies by us^9a-c and other groups,³⁴ the complete OEP²⁻ ligand has been applied here in order to (a) assign the complete NRVS data including vibrations of the Fe(OEP) core, and (b) to explore whether the presence of the ethyl substituents has an influence on the properties of the FeNO unit of the complex.

Previous crystallographic investigations on 1 by Scheidt and coworkers have shown that this complex exists in two different conformations of the OEP²⁻ ligand as shown in Scheme 2.¹⁴ In form I (Scheme 2, left), 5 neighboring ethyl groups of the macrocycle point to one face of the porphyrin, whereas the remaining 3 point in the opposite direction. In addition to this complication, the bound NO ligand can rotate around the Fe-NO bond, and occupy four basically isoenergetic positions on each side of the porphyrin ring where the oxygen atom of NO is placed between two adjacent nitrogen atoms of the macrocycle.¹⁹ Since the two faces of the porphyrin ring are not equivalent, form I can potentially give rise to eight different conformers (A – H) as shown in Figure 1. In form II of complex 1 (Scheme 2, right), 4 neighboring ethyl groups of the OEP²⁻ ligand point to each face of the macrocycle, and hence, the two faces of the Fe(OEP) unit are now symmetry-related. Because of this, form II gives rise to only four different conformers as shown in Figure 2, labeled K - N. In order to investigate the effect of the conformer on the geometric, electronic, and NRVS properties of complex 1, we have fully optimized the geometries of all twelve conformers A – H and K – N shown in Figures 1 and 2. Here, the experimentally observed structures of forms I and II in Scheme 2 correspond to conformers 1-E and 1-N in the labeling scheme applied in Figures 1 and 2. In order to keep the computational effort reasonable for this endeavor, the B3LYP/LanL2DZ method has been applied, which has proven to give good results for five-coordinate ferrous heme nitrosyls in a previous study.^9b Figure 5 shows the obtained structure of [Fe(OEP)(NO)] in conformation E (1-E) as an example. In general, the geometric properties of the FeNO unit are very similar in all twelve conformers investigated here as indicated by their identical structural data listed in Table S1. In agreement with this, the force constants and vibrational frequencies of the FeNO units in these conformers are virtually identical (cf. Table S1 and Figures S3 and S4). The crystallographically observed conformers 1-E and 1-N (cf. Scheme 2) are chosen as representatives for comparison with experimental data and are included in Table 2. Deviations from the values listed for 1-E and 1-N for other conformers are negligible. Consistent with this finding, all twelve conformers are de facto isoenergetic: the energy difference between the highest and lowest energy structure is only about 50 cm⁻¹, in agreement with previously reported values in the literature.^17,18 Comparison of the structural data in Table 2 shows that the B3LYP/LanL2DZ calculations on 1 overestimate the Fe-NO and N-O bond lengths by about 0.01 – 0.02 Å and 0.04 – 0.05 Å, respectively. Correspondingly, the Fe-NO and N-O stretching frequencies are underestimated in the calculations; these are predicted at ~503 and ~1615 cm⁻¹ compared to the experimental values of 522 and 1671 cm⁻¹, respectively. The Fe-N-O angle and Fe-N(pyrrole) bond distances are reproduced very well. This includes the asymmetry of the Fe-N(pyrrole) bonds observed in high-resolution crystal structures of 1: experimentally, it was found that the two Fe-N(pyrrole) distances of the N-atoms adjacent to the FeNO unit (N(2) and N(3) in Scheme 2, left) are shorter by 0.020 – 0.026 Å compared to those of the other two N-atoms on the opposite side of the macrocycle (N(1) and N(4) in Scheme 2).¹⁴ This is reproduced in the DFT calculations on all structures A – H and K – N considered here. The observed asymmetry is almost identical for all structures, about 0.013 Å, and slightly smaller compared to experiment. The slight off-axis tilt of bound NO observed in the crystal structures is also present in the calculated geometries. Finally, the Fe-N-O bending mode is predicted at ~403 cm⁻¹ and observed at 388 cm⁻¹ (vide supra). In summary, the calculations predict the geometric and vibrational properties of 1 well, with exception of the N-O bond in the case of which the deviations are larger. B3LYP/LanL2DZ is therefore overall a good method to screen the twelve potential conformers of 1 shown in Figures 1 and 2, and to evaluate NRVS changes related to these different structures.

Figure 5.

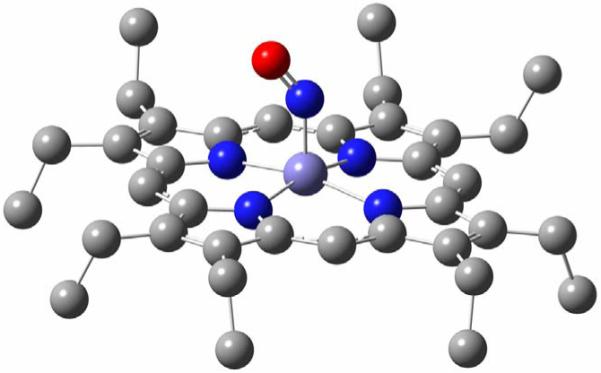
Fully optimized structure of [Fe(OEP)(NO)] in conformation E (1-E), which corresponds to the experimentally observed structure of 1 in the monoclinic form I shown in Scheme 2, left. Hydrogen atoms are omitted for clarity. Important structural parameters are given in Table 1.

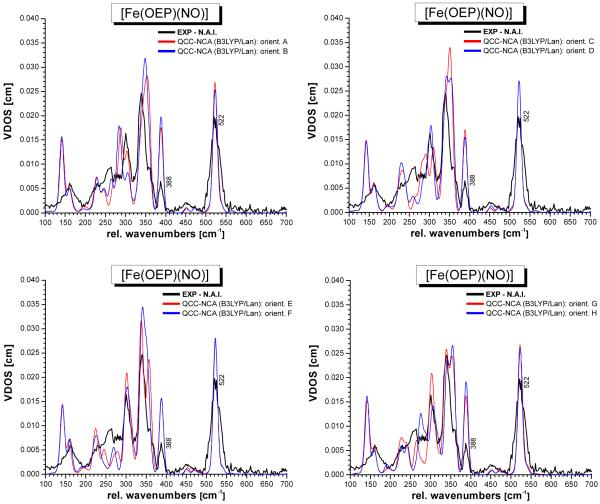
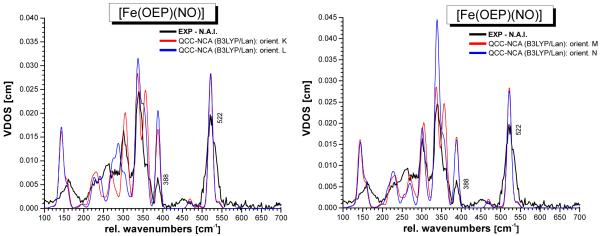
Figures S3 and S4 show the calculated NRVS spectra for conformations A – H and K – N, respectively, obtained with B3LYP/LanL2DZ. The DFT-predicted vibrational spectra for the Fe(OEP) core of complex 1 are overall in good agreement with experiment. A similar observation had been made before for the IR and Raman spectra of [M(TPP)Cl], especially with M = Fe, Mn,³⁵ and [Ni(TPP)].³⁶ In all of these cases, DFT has also been able to provide very good estimates of the vibrational spectra. Obviously, DFT calculations are able to treat the M(porphyrin) core of metalloporphyrins well.³⁰ Importantly, the Fe-NO stretch and Fe-N-O bend are not affected much by a change in conformation, and give rise to comparable signals in all cases as evident from Figures S3 and S4. However, distinct changes are observed for the lower energy vibrations (< 380 cm⁻¹) of the Fe(OEP) core as a function of the conformation of the complex. In particular, the intensity and magnitude of splitting between the two components of the 339 cm⁻¹ feature are affected, as well as the intensity and position of the 260 and 230 cm⁻¹ signals. Since the calculated force fields are quite similar³⁷ in all of these conformers, the changes observed in the calculations are to a large extent caused by differences in the mechanical couplings between the FeNO unit and the porphyrin vibrations. In order to compare the calculated spectra for the different conformers with the experimental data in more detail, it is necessary to correct the energies of the Fe-NO stretch and Fe-N-O bend first. This is achieved using our quantum chemistry centered normal coordinate analysis as described in the next section.

C. Quantum-Chemistry Centered Normal Coordinate Analysis (QCC-NCA)

In order to obtain proper simulations of the NRVS spectra of 1, a quantum chemistry centered normal coordinate analysis (QCC-NCA) was then performed to correct for the deviations in the vibrations of the FeNO subunit in the DFT-calculated NRVS spectra. From the DFT results, conformer F was chosen for the initial QCC-NCA fit, because in this case, a very good agreement of the predicted Fe(OEP) core modes with experiment is observed. Conformer N also shows good overall agreement with experiment, but the NRVS intensity of the 339 cm⁻¹ feature is clearly overestimated in this case, which makes F a better choice. The initial force field obtained for 1-F with B3LYP/LanL2DZ was therefore used, and the force constants of the FeNO subunit of [Fe(TPP)(NO)] obtained in a previous QCC-NCA fit from ref. 9b as listed in Table 1 were then applied as a starting point for the simulation. In the first step of the fitting procedure, the non-diagonal force constant between the Fe-NO stretching and Fe-N-O bending internal coordinates, f_Fe-NO/Fe-N-O, was varied in order to reproduce the observed NRVS VDOS intensity ratio e_Fe²[522 cm⁻¹]/e_Fe²[388 cm⁻¹] of 1. In a previous study, we were able to show that this force constant is very sensitive to the NRVS intensity ratio of the Fe-NO stretching and Fe-N-O bending mode.^9c Interestingly, using a reasonable value for f_Fe-NO/Fe-N-O, the e_Fe²[522 cm⁻¹]/e_Fe²[388 cm⁻¹] intensity ratio is estimated to be between 1.5 – 2.0 in agreement with NRVS data of 1 published by Scheidt and coworkers.^16c The intensity ratio observed in our data cannot be reproduced this way, but the reason for this is not clear. This might relate to the presence of additional (other) conformers in our powders of 1 that have not been observed previously using X-ray crystallography. Finally, a few selected force constants of the FeNO unit (cf. Table 1) were refined to reproduce the vibrational energies and isotope shifts of ν(N-O), ν(Fe-NO), and δ_ip(Fe-N-O).

As shown in Table 3 and Figure 6, bottom left (blue line), excellent agreement between the NRVS spectra from the NCA treatment and the experimental data is obtained. The isotope shifts of ν(Fe-NO) and δ_ip(Fe-N-O) from the QCC-NCA simulation (cf. Table 3) are somewhat smaller compared to experiment, but still in very good agreement. The force constants of the N-O and Fe-NO bonds are determined to be 12.17 and 2.84 mdyn/Å, respectively. These values are quite similar compared to complex 2, where N-O and Fe-NO force constants of 12.53 and 2.98 mdyn/Å have been obtained.^9b The similar bond strengths (force constants) in 1 and 2 reflect similar electronic structures in these compounds where NO serves as a strong σ donor and π acceptor ligand.⁹ The small differences that are observed between the Fe-NO and N-O force constants of these compounds indicate that in the OEP²⁻ complex, the Fe-NO σ interaction is somewhat weaker compared to 2, which leads to both weaker Fe-NO and N-O bonds (force constants) in the case of 1. This aspect is further evaluated in the Discussion.

Table 3.

QCC-NCA results for [Fe(OEP)(NO)] for conformer 1-F based on different computational methods

Method	Vibrational Frequency [cm−1]			Force Constant [mdyn/Å] a
	ν(N-O)	ν(Fe-NO)	δip(Fe-N-O)	fN-O	fFe-NO	fFe-N-O
B3LYP/LanL2DZ: DFT	1617	501	407	11.032	2.246	0.448
QCC-NCA b	1671 (1599)	522 (510/507)	388 (383)	12.169	2.841	0.324
BP86/LanL2DZ*: DFT	1712	620	414	12.798	3.854	0.469
QCC-NCA b	1671 (1598)	522 (508)	388 (381)	12.148	2.938	0.346

^aThe force constant f_Fe-N-O is given in [mdyn·Å]

^bValues in brackets are calculated for the corresponding ¹⁵N¹⁸O labeled complex

Figure 6.

QCC-NCA simulated NRVS spectra of conformers A – H of complex [Fe(OEP)(NO)] (1) (cf. Figure 1), based on the B3LYP/LanL2DZ calculations.

Finally, the obtained QCC-NCA force constants of 1-F (cf. Table 1 for the six force constants included in the fit) were used as a starting point to fit the NRVS data of the remaining conformers A – H and K – N. For this purpose, only the three Fe-NO and N-O stretching and Fe-N-O bending diagonal force constants were varied to reproduce the experimental NRVS data; the three non-diagonal force constants in Table 1 were left unchanged from the initial fit of 1-F. Table S2 lists the obtained force constants for all twelve conformers obtained this way, which are extremely similar. Table 1 contains averaged force constants for A – H and K – N for comparison. The NRVS spectra obtained from these QCC-NCA simulations are shown in Figures 6 and 7.

Figure 7.

QCC-NCA simulated NRVS spectra of conformers K – N of complex [Fe(OEP)(NO)] (1; cf. Figure 2), based on the B3LYP/LanL2DZ calculations.

Based on these simulations, the Fe(OEP) porphyrin core vibrations, including bands I – V in Figure 4, can also be assigned. In the experimental NRVS VDOS, ν(Fe-NO) at 522 cm⁻¹ can be fit with two bands at 519 and 533 cm⁻¹ as shown in Figure 4, indicating that the Fe-NO stretch is mixed with a porphyrin-based vibration. This is reproduced in the QCC-NCA simulation, where the Fe-NO stretching coordinate is in fact mixed with one component of the pyrrole rotation (Pyr.rot, ν₄₉; see below) of E_u symmetry (in ideal D_4h symmetry), which is observed at ~527 (conformers A – H) and ~523 cm⁻¹ (K – N), respectively, but the predicted interaction is weaker compared to experiment. The second component of ν₄₉ occurs at higher energy (~540 cm⁻¹ for all conformers).

In general, our DFT calculations show that the low-energy porphyrin core modes in the case of OEP²⁻ complexes are strongly mixed with bending modes δ(Et) and torsions τ(Et) of the ethyl substituents. In fact, all vibrations below 400 cm⁻¹ show about 30 – 40 % δ(Et)/τ(Et) character! This strongly complicates the vibrational assignments of porphyrin core modes for 1. The large signal I observed around 340 - 360 cm⁻¹ in the experimental spectrum corresponds to a superposition of four NRVS active modes, which mainly show Fe-N(pyrrol) stretching ν(Fe-N_Pyr), pyrrole translation (Pyr.trans), and symmetric C_β-C(Et) bending δ(C_β-C_Et)^sym character. In addition, out-of-plane core motions of pyrrole tilting (Pyr.tilt) and swiveling (Pyr.swiv) type are mixed into these modes. Using the established nomenclature developed by Spiro and coworkers,³⁸ these can be mostly identified with the E_u modes ν₅₀/ν₅₃/ν₅₂ for the in-plane vibrations and γ₂ (A_1u) and γ₆ (A_2u) out-of-plane motions (ignoring the presence of low-symmetry deviations from these ideal D_4h–symmetric normal modes). The four NRVS active modes in region I have on average 25 % ν(Fe-N_Pyr) character and 13 % contributions from ethyl modes. Signal group II in the 300 – 320 cm⁻¹ range again corresponds to a cluster of mostly four NRVS-active modes that show very similar contributions from in-plane ν(Fe-N_Pyr), Pyr.trans, and δ(C_β-C_Et)^sym vibrations and out-of-plane Pyr.tilt and Pyr.swiv type motions. However, in this case the contributions from ν(Fe-N_Pyr) (12% on average) and the ethyl-based motions (31 %) are inversed in magnitude compared to signals I. This can be rationalized by vibrational mixing between the ν(Fe-N_Pyr)/Pyr.trans porphyrin core modes ν₅₀/ν₅₃ and the δ(C_β-C_Et)^sym ethyl mode ν₅₂ where the higher energy features I have more ν₅₀/ν₅₃ character (and hence, more NRVS intensity), and the lower energy features II have more δ(C_β-C_Et)^sym contribution. In addition, due to the low-symmetry of 1 and the out-of-plane displacement of the ethyl substituents and the iron center, these vibrations become further mixed with out-of-plane Pyr.tilt and Pyr.swiv type modes as mentioned above. This leads to quite complex normal mode descriptions in the 300 – 360 cm⁻¹ region. The weaker signal III around 250 – 270 cm⁻¹ corresponds to δ(ON-Fe-N_Pyr) octahedral bending modes with some ν(Fe-N_Pyr) as well as out-of-plane Pyr.tilt and γ(C_α-C_meta) character. Signal IV around 220 – 230 cm⁻¹ is observed as a shoulder in the experimental data, but more defined in the calculations. There are several modes in this area with > 60 % δ(Et)/τ(Et) character. In the calculation, 1 – 2 of them gain NRVS intensity by small ν(Fe-N_Pyr) stretching or δ(N-Fe-N) octahedral bending admixtures. Finally, the experimental signal in region V around 160 cm⁻¹ is identified with the δ(C_β-C_Et)^asym ethyl-based mode ν₅₁ (see ref. 38 for nomenclature). The calculations also predict a quite intense, strongly z-polarized feature at 140 – 145 cm⁻¹, which corresponds to the doming mode γ₉. Interestingly, no corresponding signal seems to be observed experimentally, and this in fact constitutes the largest deviation between the experimental and the DFT-calculated NRVS spectra with respect to the Fe(OEP) core vibrations. One possible explanation for this finding is that the absence of a strong γ₉ signal experimentally is due to solid state effects: low energy molecular modes can show quite strong couplings to lattice vibrations, and in this way, their intensity can be spread out and dampened significantly. This would be particularly significant if the energy of γ₉ would be overestimated in the DFT calculations such that this mode would be closer to about 100 cm⁻¹ in the actual compound.

The assignments obtained for the Fe(OEP) porphyrin core modes described above are generally in good agreement with recent work by Durbin and coworkers on [Fe(OEP)].³⁹ The most significant difference between our assignments and their work is the relative energy of δ(C_β-C_Et)^sym (ν₅₂) versus δ(C_β-C_Et)^asym (ν₅₁): for [Fe(OEP)] is has been proposed that ν₅₁ is higher in energy than ν₅₂, whereas we find the opposite energy sequence as described above. This difference might relate to the out-of-plane displacement of iron or the presence of the axial NO ligand in 1 compared to the four-coordinate complex [Fe(OEP)].

D. Conformational Analysis of the NRVS Data of [Fe(OEP)(NO)] (1)

The QCC-NCA simulated NRVS spectra show good agreement with experiment with respect to the vibrations of the FeNO subunit. As shown in Table S2, the corresponding force constants are very similar, indicating that the properties of the FeNO subunit are independent of the conformation of the complex. On the other hand, distinct changes are observed for the lower energy vibrations (< 380 cm⁻¹) of the Fe(OEP) subunit in the different conformers. In particular, the intensity and magnitude of splitting between the two main components of the 339 cm⁻¹ feature are affected, as well as the intensity and position of the 301, 260, and 230 cm⁻¹ signals II – IV (cf. Figures 6 and 7). In the case of form I (conformers A – H), the structures where the NO ligand is located on the same face as the 3 ethyl substituents (Figure 1, bottom) show lower NRVS intensities for the 339 cm⁻¹ feature, and hence, are in better agreement with the NRVS data presented here. This is in agreement with the crystal structure of form I shown in Scheme 2, left, where the NO is also observed on the face of the 3 ethyl substituents. Considering both intensities and peak shapes of the Fe(OEP) core vibrations, conformer F shows the best agreement with experiment, which is different from conformer E observed crystallographically. In the case of 1-E, the calculated spectrum shows a too pronounced splitting of the 339 cm⁻¹ feature. However, it is reasonable to assume (a) that in the case of the microcrystalline material applied in our study, a different conformer of the complex might be dominant compared to the single crystals used for the structural studies, and (b) that the compound is very likely not fully ordered even at the sample temperature applied here. Combined with the standard inaccuracies of DFT calculations, this certainly restricts the accuracy to which the absolute conformation of the complex can be determined. In the case of form II shown in Scheme 2, right, the agreement of the calculated spectra with experiment is not as good as for form I. Conformers K – M exhibit too strong of a splitting of the 339 cm⁻¹ feature. Conformer N (observed experimentally for form II) is overall in good agreement with experiment, but the intensity of the 339 cm⁻¹ band is overestimated, which is due to the fact that the four NRVS-active vibrations found in this energy region (vide supra) are too close in energy. Interestingly, the observed larger NRVS intensity of the 339 cm⁻¹ band in 1-N reflects the published NRVS spectra of compound 1 by Scheidt and coworkers,^16c indicating that in this case, conformer N might have been dominant in their sample.

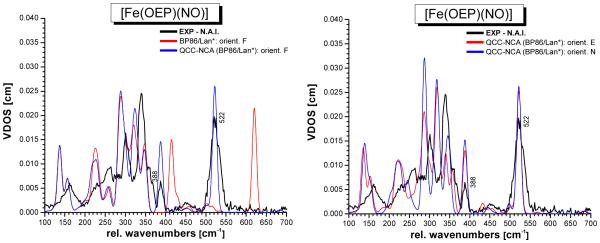
Finally, a closer inspection of Figures 6 and 7 shows that the intensity of the Fe-N-O bending mode at 388 cm⁻¹ exhibits an interesting variation in intensity in the different conformers of the complex. This is due to the fact that this mode is (mechanically) coupled to a number of Fe(OEP) modes, in particular one component of the signal I cluster around 340 - 360 cm⁻¹, and vibrations in the signal groups II at 300 - 320 cm⁻¹ and III at 250 - 270 cm⁻¹ (c.f. Figure 4). It is this coupling that is mostly affected by a change in the conformation of the complex. In this way, the change in coupling of the Fe-N-O bending mode to the porphyrin core modes is mostly responsible for the observed variations in the Fe(OEP) core mode energies and intensities in the predicted NRVS data of the different conformers in Figures 6 and 7.⁴⁰ Importantly, this will also induce anisotropy of degenerate in-plane porphyrin modes of E_(u) symmetry since the Fe-N-O bend will selectively interact with only one component of the degenerate pair. These results suggest that in particular, the magnitude of the splitting of the two main components of the 339 cm⁻¹ feature in the different conformers could be used as a marker to experimentally distinguish between different conformers. In this respect, only a small splitting is observed in our powder and corresponding powder literature spectra (cf. ref. 16c) of 1, limiting the number of possible conformations of the complex. In order to investigate whether the observed difference in Fe(OEP) core modes is reproduced at a higher level of theory, BP86/LanL2DZ* calculations were then performed on the selected conformations 1-E (crystal structure: form I), 1-F (best match of Fe(OEP) core modes), and 1-N (crystal structure: form II).

E. Effect of DFT Method

The fully optimized structure of [Fe(OEP)(NO)] in conformation E (1-E) obtained with BP86/LanL2DZ* is very similar to the corresponding B3LYP/LanL2DZ structure shown in Figure 5. Table 2 lists the calculated structural and vibrational properties of 1-E and 1-N obtained with BP86/LanL2DZ*. The structures of the different conformers again show very little variation, indicating that the conformation of the complex has little effect on the properties of the FeNO unit. The overall agreement of the structural and vibrational properties of the FeNO unit from BP86/LanL2DZ* with experiment is slightly better compared to B3LYP/LanL2DZ as one would expect. The largest deviation occurs here for the Fe-NO bond strength, which is overestimated by the BP86 calculation. This leads to too short Fe-NO bond lengths and overestimated Fe-NO stretching frequencies of ~620 cm⁻¹ as shown in Table 2. The overestimation of Fe-NO bond strengths is very typical for gradient-corrected functionals like BP86, and has been observed before for both ferrous and ferric heme nitrosyls.9a,b^,42 The predicted NRVS spectra for 1-E, 1-F, and 1-N are shown in Figure S5 in comparison to the B3LYP/LanL2DZ results. Interestingly, the porphyrin-based vibrations are reproduced much better with B3LYP/LanL2DZ, in particular in regions I and II (cf. Figure 4). With BP86/LanL2DZ*, the energy splittings of the underlying NRVS-active features observed in these regions (vide supra) are too large, leading to poor agreement of the calculated NRVS spectra with experiment. In the next step, the QCC-NCA method was applied to correct for the deviations in the vibrational energies of the FeNO subunit. For this purpose, the six QCC-NCA force constants refined for 1-F with B3LYP/LanL2DZ (cf. Table 1) were introduced into the BP86/LanL2DZ* force field of 1-F, followed by refinement of these force constants to reproduce the experimental vibrational energies and isotope shifts as well as NRVS VDOS intensities of the Fe-N-O normal modes of 1. Table 3 provides details for the fit obtained this way. Based on the result for 1-F, the spectra of 1-E and 1-N were then simulated. Table S2 lists details of the individual fits, and averaged force constants for the three conformers treated with BP86/LanL2DZ* are included in Table 1. As observed before, the QCC-NCA force constants obtained this way for 1-E, 1-F, and 1-N are very similar. The predicted NRVS VDOS data from the QCC-NCA treatment of 1-E, 1-F, and 1-N with BP86/LanL2DZ* are shown in Figure 8. The QCC-NCA is able to reproduce the energies and isotope shifts of the vibrations of the FeNO unit better compared to B3LYP/LanL2DZ as shown in Table 3. Because of this, the obtained force constants of the N-O and Fe-NO bonds, determined to be 12.15 and 2.94 mdyn/Å (cf. Table 1), from the BP86/LanL2DZ*-based QCC-NCA can be considered more reliable. On the other hand, the assignments of the porphyrin-based vibrations are better based on the B3LYP/LanL2DZ result as discussed above.

Figure 8.

QCC-NCA simulated NRVS spectra of [Fe(OEP)(NO)] (1) for the selected conformers 1-E (crystal structure form I), 1-F (best fit of NRVS data with B3LYP/LanL2DZ), and 1-N (crystal structure of form II) based on the BP86/LanL2DZ* calculations.

Discussion

In this paper, Nuclear Resonance Vibrational Spectroscopy (NRVS) data of [⁵⁷Fe(OEP)(NO)] (1; OEP²⁻ = octaethylporphyrinato dianion) and of the corresponding ¹⁵N¹⁸O-labeled complex are presented. Whereas NRVS spectra for the natural abundance isotopes (n.a.i., but with ⁵⁷Fe) complex 1 had been published before,^16a,c this is the first time that data of the NO-labeled species are presented. This allows for an unambiguous assignment of all of the vibrations of the FeNO subunit. The NRVS data show the Fe-NO stretch ν(Fe-NO) at 522 cm⁻¹ and the in-plane Fe-N-O bending mode δ_ip(Fe-N-O) at 388 cm⁻¹, which shift to 508 and 381 cm⁻¹ in the ¹⁵N¹⁸O complex (cf. Figures 3 and 4), respectively. From IR measurements, the N-O stretch is identified at 1671 cm⁻¹. Importantly, these results validate previous assignments for [Fe(TPP)(NO)] (2; TPP²⁻ = tetraphenylporphyrinato dianion) obtained from Raman- and IR spectroscopy, where ν(Fe-NO) and δ_ip(Fe-N-O) were identified as weak signals at 532 and 371 cm⁻¹, respectively, and ν(N-O) was observed at 1697 cm⁻¹.9a,b These vibrational energies are therefore typical for 5C ferrous heme nitrosyls as indicated in Table 2. An extended summary of structural and vibrational data of heme nitrosyls published before 2002 is included in refs. ^11a,c. As elaborated in the Introduction, most of the more detailed analyses and simulations of the vibrational data of heme nitrosyls available from the literature have utilized the porphine macrocycle as an approximation for the more complicated and biologically relevant heme systems. However, it is unclear on exactly how much the porphyrin substituents might effect the properties of the central FeNO unit and the Fe-porphyrin core. In this paper, this aspect is investigated in detail.

In order to completely assign the NRVS spectra of 1, our quantum chemistry centered normal coordinate analysis (QCC-NCA) was then applied. As observed by us and others, DFT calculations generally reproduce the vibrational spectra of the Fe(porphyrin) core well,^35,36,41 but the vibrations of the axial FeNO unit are only poorly described.^{9a-c,16c,31,42} As evident from Table 2, gradient corrected functionals like BP86 combined with a good basis set greatly overestimate the Fe-NO bond strength and Fe-NO stretching frequency (predicted: ~ 620 cm⁻¹), whereas B3LYP overestimates the N-O stretching frequency (>1800 cm⁻¹). Using the QCC-NCA approach, these errors can be corrected, reliable experimental force constants for the FeNO unit can be determined, and simulations of the NRVS spectra of heme-nitrosyls of excellent quality can be obtained. In the case of the OEP²⁻ ligand, however, there is one important complication: the eight ethyl substituents of the OEP²⁻ ligand can be oriented to either one of the two faces of the porphyrin ring, giving rise to a number of different conformers, which cannot interconvert in the solid state. In contrast, conformational isomers of this kind are not possible for TPP²⁻. Previous crystallographic work of Scheidt and coworkers has shown that the Fe(OEP) unit in 1 exists in two forms in the solid state as shown in Scheme 2.¹⁴ In addition to the variation in porphyrin substituent orientation, the bound NO ligand can rotate along the Fe-N(O) axis, giving rise to four different orientations where the oxygen atom of NO is located between two adjacent porphyrin-N atoms. These different orientations are almost isoenergetic in the gas phase. In the case of the TPP²⁻ complex 2, these four conformers are equivalent. Correspondingly, most vibrational analyses of the NRVS spectra of heme model complexes in the literature have focused on TPP²⁻ complexes,⁴³ where the existence of different conformations is insignificant for the vibrational spectra. On the other hand, the four conformers generated from the rotation of the bound NO ligand are not equivalent in complex 1, because they lead to different relative orientations of the NO ligand and the ethyl substituents of OEP²⁻. As shown in Figures 1 and 2, a total of 12 different conformers results for the two forms of 1 observed crystallographically (cf. Scheme 2). In this work, we have performed DFT calculations to predict the NRVS spectra of all twelve possible conformers of 1 to explore how a change in conformation would affect the NRVS spectra. Our results clearly show that the properties of the FeNO subunit and the electronic structure of the complexes are hardly affected. However, the mechanical coupling of the Fe-N-O bending mode with the porphyrin vibrations changes in the different conformers, which leads to (a) changes in the NRVS intensity of δ_ip(Fe-N-O) at 388 cm⁻¹, (b) small frequency shifts for the mixed ν₅₀/ν₅₃/ν₅₂ + γ₂/γ₆ modes at ~339 cm⁻¹ which also appear split in some conformers, (c) large frequency shifts and splittings of the ν₅₂/ν₅₀/ν₅₃ and δ(ON-Fe-N_Pyr) modes at ~301 and ~260 cm⁻¹, respectively. This coupling also introduces localization⁴⁰ and anisotropy into degenerate in-plane porphyrin modes of E symmetry since the Fe-N-O bend will selectively interact with only one component of the degenerate pair.

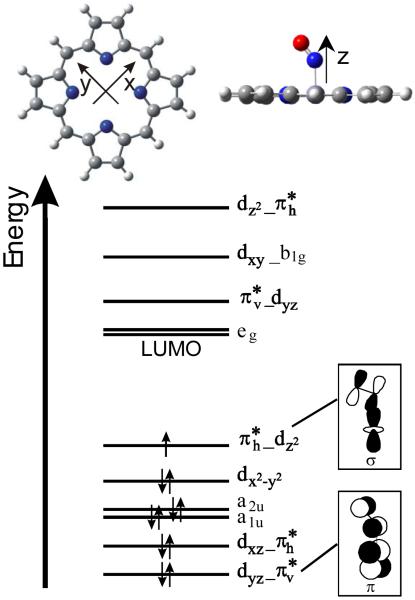
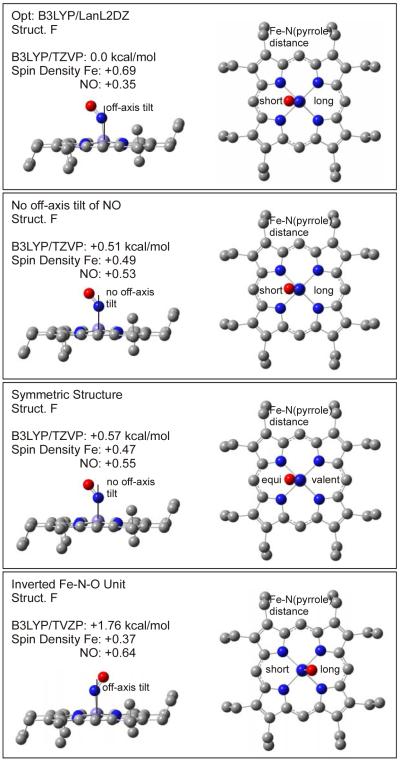
In principle, these results would allow one to identify the exact conformer of 1 from NRVS measurements. However, the exact shape of the NRVS spectrum is certainly not well enough defined from DFT calculations to really pinpoint the conformer in comparison to experiment. In addition, heme-nitrosyls could potentially exist as mixtures of conformers at typical temperatures for NRVS experiments, which would greatly complicate the conformational analysis. Nevertheless, the data and DFT calculations presented in this work indicate for the first time that there is a quite distinctive dependence of the NRVS spectra of 1 (and potentially other five- and six-coordinate OEP²⁻ compounds) on the actual conformer of the complex. This is particularly of interest for low-symmetry hemes like the ones found in proteins. On the other hand, the exact conformation of the complex has no effect on the electronic structure and vibrational properties of the axial FeNO unit itself, since the change in vibrational coupling is mostly mechanical in nature. Therefore, application of the porphine approximation is reasonable if only an understanding of the properties of the axial FeNO unit in heme-nitrosyls is sought (assuming the porphyrin ring does not carry strongly electron donating or withdrawing substituents). Correspondingly, the calculated properties of the FeNO unit for 1 are almost identical to those obtained with the porphine approximation, i.e. model system [Fe(P)(NO)] where the OEP²⁻ ligand is replaced by porphine²⁻ (P²⁻), as evident from Table 2, but at a fraction of the computational cost. Hence, the porphine approximation is also useful to screen for functional/basis set combinations that give reasonable descriptions of the FeNO unit of heme nitrosyls. This is particularly valid since DFT shows a distinct lack of accuracy in describing the properties of the Fe-NO bond (vide supra), which requires NCA simulations in any case to correct for these errors. In this way, significant savings in computational time can be achieved. Enemark and Feltham were the first to point out that ferrous heme nitrosyls show a certain degree of radical character of the coordinated NO.⁴⁴ This was later confirmed by DFT calculations by a number of groups, although the application of different functional/basis set combinations led to diverging results with respect to the actual spin-density distribution in the complex.^17,34 In recent studies, the electronic structures of five- and six-coordinate (5C and 6C) ferrous heme nitrosyl complexes have been analyzed in detail using magnetic circular dichroism (MCD), NMR, and vibrational spectroscopies coupled to density functional calculations.^9,10,12 Scheme 3 shows a simplified (restricted open shell) sketch of the electronic structure of these complexes, which helps to understand their vibrational properties.^9a-c,17 Nitric oxide is a diatomic radical with one unpaired electron occupying the π* orbitals of this molecule. The iron(II) center is in the low-spin state and is diamagnetic, which leads to a total spin of S = ½ for the iron(II)-NO adducts. The singly-occupied π* orbital of NO, labeled π*_h (h = horizontal; α-π*_h in a spin-unrestricted scheme⁴⁵), forms a strong σ bond with the d_z² orbital of the low-spin iron(II) center. In the 5C case, the mixing between these orbitals is very strong, leading to a full delocalization of the unpaired electron of NO over the FeNO subunit. Correspondingly, the calculated spin populations are about +0.5 on iron and +0.5 on NO, which indicates a significant amount of radical character on the iron center.9a,b The bonding combination of these orbitals, labeled π*_h_d_z² in Scheme 3, constitutes the SOMO of these complexes. Furthermore, the unoccupied π* orbital of NO, π*_v (vertical), forms a strong π-backbond with a fully occupied d_π orbital (d_yz in Scheme 3) of the iron(II) center. The corresponding bonding combination, d_yz_π*_v, is shown in Scheme 3. The strength of this interaction is better estimated from the corresponding antibonding combination, π*_{v_}d_yz, which has about 25% metal-d character.^9b Note that the π-backbond between π*_v and d_yz in most calculations only shows small spin polarization effects, and hence, does not contribute significantly to the observed spin densities. Finally, in a spin-unrestricted scheme, an additional π-backbond results from the interaction of the (unoccupied) β-π*_h orbital with d_xz. This interaction leads to a transfer of β electron density from Fe to the NO ligand, and hence, further increases the α (positive) spin density on Fe and decreases the α spin density on NO. Hence, both the σ-donation from α-π*_h into α-d_z² and the π-backbond from β-d_yz into β-π*_h contribute in the same way to the observed spin density distribution. Importantly, however, the DFT calculations show that the σ bond is the dominating factor. Nevertheless, a variation of the calculated spin densities is possible upon variation of the Fe-N-O core conformation as shown in Figure 9. Scheidt and coworkers discovered in high-resolution structures of [Fe(OEP)(NO)] that the Fe-N-O core shows a slight off-axis tilt of the bound NO ligand and an asymmetry in the Fe-N(pyrrole) distances as indicated in Figure 9, top.¹⁴ Our optimized structures fully reproduce these subtleties. Our calculations summarized in Figure 9 also show that the energetic stabilization due to these distortions is very small, < 1 kcal/mol, compared to the corresponding, symmetrized molecule. It is therefore surprising that these energetically small effects show quite a strong influence on the calculated spin densities, which vary between +0.69 (Fe) and +0.35 (NO) in the optimized and +0.47 (Fe) and +0.55 (NO) in the symmetrized molecule (not considering the inverted core in Figure 9, bottom). Analysis of the spin densities shows that these variations are actually due to changes in the spin polarization of the π-backbond between π*_v and d_yz. Since the underlying change in π bonding is small, and the σ bond is not affected, this variation in the spin density distribution does not significantly affect the overall Fe-NO bond strength, and hence, the total energy. In addition, this effect is likely overestimated in the B3LYP/LanL2DZ calculation: it is in fact the B3LYP/LanL2DZ optimized structure (Figure 9, top) that leads to an unusually large amount of spin polarization of the π*_v_d_yz backbond, whereas this effect is small in the other cases, which is more in line with the published results.^9b

Scheme 3.

Figure 9.

Fe-N-O core conformation and relative energies. The calculations are based on the optimized structure of conformer F with B3LYP/LanL2DZ. Single points for the different structures where the Fe-NO off-axis tilt and the Fe-N(pyrrole) asymmetry have been removed and where the core has been inverted were calculated with B3LYP/TZVP.

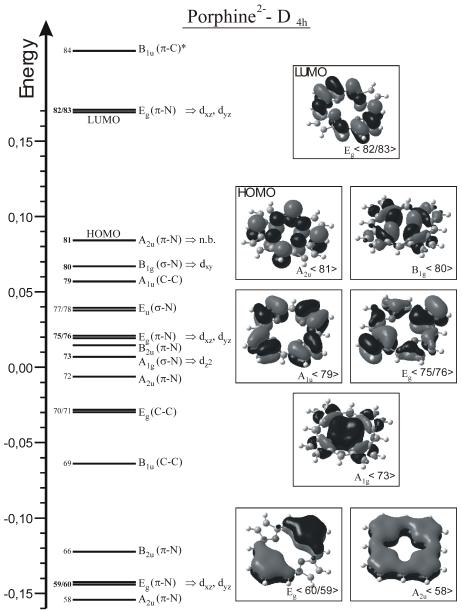
Based on this electronic structure description, trends in the properties of 5C ferrous heme nitrosyls can be understood. As shown by Spiro and coworkers, the strength of the π-backbond can be systematically varied in 5C ferrous heme nitrosyls by adding electron withdrawing or donating groups to the phenyl substituents of TPP-type ligands.^15b This leads to the typical inverse correlation of Fe-NO and N-O bond strengths and corresponding stretching frequencies, where, for example, a strengthening of the π-backbond (by introduction of an electron donating substituent) leads to a stronger Fe-NO bond and higher Fe-NO frequency. This goes along with a larger occupation of the π* orbitals of NO involved in the π-backbond, and in this way (since π* orbitals are N-O antibonding), leads to a weaker N-O bond and lower ν(N-O) frequency. In this way, Spiro and coworkers were able to modulate the N-O/Fe-NO stretching frequencies between 1663/530 cm⁻¹ for the most electron donating substituent and 1703/514 cm⁻¹ for the most electron withdrawing substituent.^15b The most likely explanation for this finding is that the electron withdrawing and donating phenyl substituents modulate the energy of the occupied porphyrin π orbitals of e_g symmetry, labeled E_g<75/76> in Scheme 4. These interact with the d_π orbitals of iron(II), responsible for the π-backbond: for example, electron donating phenyl substituents likely increase the energy of these porphyrin e_g π orbitals, which in turn “push” the d_π (d_xz and d_yz) orbitals of iron(II) to higher energy, and in this way, closer in energy to the π* acceptor orbitals of NO. In this way, the π-backbond is strengthened, which increases the Fe-NO bond strength and vibrational frequency, and weakens the N-O bond strength and decreases ν(N-O). Interestingly, a different trend is observed when comparing the vibrational properties of complexes 1 and 2 with the OEP²⁻ and TPP²⁻ ligands, respectively. Here, complex 1 shows both slightly weaker N-O and Fe-NO bonds as indicated by the vibrational frequencies, 1671/522 cm⁻¹ (~524 cm⁻¹ with n.a.i Fe) for 1 vs. 1697/532 cm⁻¹ for 2 (cf. Table 2), and as reflected by the Fe-NO and N-O force constants, ~12.15/2.83 – 2.94 mdyn/Å (based on the DFT functional applied) for 1 vs. 12.53/2.98 mdyn/Å for 2 (cf. Tables 1 and 3). This direct correlation of N-O and Fe-NO bond strengths and vibrational frequencies provides strong evidence that this is due to a change in the Fe-NO σ bond, which is mediated by d_z² of iron and the singly occupied π* orbital (π*_h in Scheme 3) of NO as elaborated above. This can be explained by a difference in porphyrin charge donation to the iron(II) center for the OEP²⁻ and TPP²⁻ ligands. In this model, TPP²⁻ would need to be a stronger donor to iron(II). This could simply increase the effective nuclear charge on iron(II), and in this way, shift the d-orbitals of the metal to higher energy, which will increase the covalent mixing of the iron(II) d-orbitals with π* of NO. This would in particular strengthen the interaction of d_z² and π*_h, and in this way, increase the donation from the singly occupied π*_h into the empty d_z² orbital of iron. This both strengthens the Fe-NO bond and at the same time, the N-O bond (since the donation comes from an N-O antibonding orbital), and hence, would give rise to the observed direct correlation of Fe-NO and N-O bond strengths in comparing 1 and 2. Alternatively, the porphyrin a_2u(π) orbital, A_2u<81> in Scheme 4, could be higher in energy in TPP²⁻ compared to OEP²⁻. Since the iron(II) center is displaced from the porphyrin ring towards NO in 5C ferrous heme nitrosyls, this orbital shows a significant interaction with d_z². If the porphyrin a_2u(π) orbital is higher in energy in the TPP²⁻ compound, then this would push d_z² to higher energy, and in this way, increase the interaction of d_z² with the singly occupied π*_h orbital of NO. As described above, this would then lead to a strengthening of both the Fe-NO and N-O bonds. This model seems more likely, because the change in effective nuclear charge would (to a certain degree) affect all metal-d orbitals, whereas a variation of the energy of the a_2u(π) porphyrin orbital would selectively affect the d_z² orbital. In principle, an interplay of both effects seems also possible for different types of porphyrin ligands. Further systematic DFT work is necessary to identify the exact mechanism by which the Fe-NO σ bond strength is mediated in 1 versus 2.

Scheme 4.

MO diagram of the free porphine(2−) ligand (cf. Scheme 3, top left) and contour plots of important MOs. Energies are given in Hartree. Metal d orbitals that could potentially interact with these MOs are indicated (labels are based on the coordinate system given in Scheme 3, top).

A much stronger change in the Fe(II)-NO σ bond can be effected by binding a sixth ligand, for example imidazole, pyridine, or other N-donor ligands, in trans position to NO.9a,b^,10,12 In this case, mixing of the singly occupied π*_h orbital of NO with d_z² of iron is distinctively reduced, due to a σ trans effect of the N-donor ligand. This weakens the Fe-NO σ bond as reflected by the lower Fe-NO stretching frequency of ~440 cm⁻¹.^9b,c,13,33a Due to the reduced donation from the π*_h orbital of NO, the N-O bond is also weakened as evident from ν(N-O) observed around 1610 – 1630 cm⁻¹ for these compounds. For example, the Fe-NO and N-O force constant of the 6C complex [Fe(TPP)(MI)(NO)] with the strong N-donor ligand 1-methylimidazole (MI) are only 2.38 and 11.55 mdyn/Å,^9c respectively, compared to 2.98 and 12.53 mdyn/Å for the Fe-NO and N-O bonds in the analogous 5C complex [Fe(TPP)(NO)] (2).^9b This change in bonding in 6C complexes is reflected by a change in spin density distribution: upon coordination of the axial N-donor ligand, the spin density is pushed back from the iron toward the NO ligand leading to spin populations of about +0.8 on NO and only +0.2 on iron in [Fe(TPP)(MI)(NO)] in agreement with EPR and MCD results.¹⁰ Based on these descriptions, the 6C complexes correspond to the prototype of an Fe(II)-NO(radical) adduct, whereas the 5C compounds have more noticeable Fe(I)-NO⁺ character relative to the 6C case due to the increased charge donation from π*_h of NO to the iron(II) center.9a,b Since this effect is mediated by metal-ligand covalency, any intermediate situation between 2 and [Fe(TPP)(MI)(NO)] is also possible, depending on the σ-donor strength of the axial N-donor ligand. In other words: the observed weakening of the Fe-NO and N-O bonds in the 6C complexes correlates with the σ-donor strength of the bound N-donor: the stronger this ligand binds to the iron(II) center, the more pronounced is the reduction of the Fe-NO and N-O bond strengths (see also ref. 46). In this respect, [Fe(TPP)(4-NMe₂Py)(NO)] with the weaker 4-dimethylaminopyridine ligand shows the N-O stretch at an intermediate position of 1653 cm⁻¹,⁵⁰ in full agreement with the above analysis.