Visualizing 3D objects from 2D cross sectional images displayed in-situ versus ex-situ

Abstract

The present research investigates how mental visualization of a 3D object from 2D cross sectional images is influenced by displacing the images from the source object, as is customary in medical imaging. Three experiments were conducted to assess people’s ability to integrate spatial information over a series of cross sectional images, in order to visualize an object posed in 3D space. Participants used a hand-held tool to reveal a virtual rod as a sequence of cross-sectional images, which were displayed either directly in the space of exploration (in-situ) or displaced to a remote screen (ex-situ). They manipulated a response stylus to match the virtual rod’s pitch (vertical slant), yaw (horizontal slant), or both. Consistent with the hypothesis that spatial co-location of image and source object facilitates mental visualization, we found that although single dimensions of slant were judged accurately with both displays, judging pitch and yaw simultaneously produced differences in systematic error between in-situ and ex-situ displays. Ex-situ imaging also exhibited errors such that the magnitude of the response was approximately correct but the direction was reversed. Regression analysis indicated that the in-situ judgments were primarily based on spatio-temporal visualization, while the ex-situ judgments relied on an ad hoc, screen-based heuristic. These findings suggest that in-situ displays may be useful in clinical practice by reducing error and facilitating the ability of radiologists to visualize 3D anatomy from cross sectional images.

Introduction

Cross Sectional Images in Medicine

Mental visualization of three-dimensional objects from two-dimensional depictions is basic to many intellectual activities in art, design, engineering, and mathematics. For example, architects and engineers interpret orthographic drawings to understand the 3D form they represent (Contero, Naya, Company, Saorín & Conesa, 2005; Cooper, 1990), and hikers and geologists use contour maps to comprehend landscapes (Eley, 1983; Lanca, 1998). Our research investigates this problem in an important medical context, namely, the interpretation of 3D data from a sequence of cross sectional images acquired through imaging technologies, such as computer tomography (CT), magnetic resonance imaging (MRI), or ultrasound.

A cross section of a 3D object is an image that results from its intersection with a 2D plane. In medicine, such images are widely used to show the internal structure of 3D anatomy. For example, using CT technology, a series of parallel cross sections of a patient’s body is scanned. When viewed one cross section at a time by the radiologist, the 3D structure is not directly visible, but rather is mentally reconstructed from the 2D images and knowledge of anatomy (Hegarty, Keehner, Cohen, Montello, & Lippa, 2007; LeClair, 2003; Provo, Lamar, & Newby, 2002). This mental reconstruction constitutes a form of visualization (McGee, 1979).

Essential to such 3D-from-2D visualization is the act of recovering the “lost” third dimension. When an observer views a cross section of a fully 3D object, he or she directly perceives a 2D image. The information about the third dimension is implied, however, if the image is known to be a cross section obtained by cutting through the object at a specific location. For this purpose, CT or MRI slices are indexed and registered to a rectangular space, and ultrasound images can be located with reference to the location and orientation of the instrument. A given cross section thus can be linked to its 3D origin, and the entire 3D structure can be reconstructed from a series of cross sections by locating their origins in space and assembling them into a coherent structure. While this seems straightforward in principle, previous research has shown, in fact, that mental reconstruction of 3D objects from 2D images is challenging (National Academies Press, 2006) and strongly depends on the observer’s spatial abilities (Hegarty et al., 2007; Lanca, 1998). In particular, the failure to understand the correspondence between 2D and 3D representations has been highlighted as an important impediment to this form of visualization (LeClair, 2003). The present research aims to investigate the factors that may impede or facilitate such spatial understanding and hence the visualization process.

We focus here on the integration of spatial information within and across a sequence of images so as to visualize an object posed in external space. An applied motivation for the present work is the widespread use of medical images to visualize the orientation of anatomical structures for identification and guidance of action. In liver biopsies, for example, it is critical to detect and avoid blood vessels lying at unpredictable angles relative to a point of penetration, and similar concerns arise with nerves. Orientation is also important in medical procedures where surgeons place a catheter in a patient requiring a central line (a PICC line). A typical PICC insertion begins with the operator scanning the patient’s arm with an ultrasound transducer to find and localize a target vein. The operator places the transducer so that its image provides a cross section of the vein, then inserts the needle so that it will penetrate the vein longitudinally. The difficulty of this procedure is such that first-attempt failure rates on the order of 35% by experienced operators have been reported (Keenan, 2002). Success requires not only that the depth of the vein be visualized correctly, but also that the local slant angle of the vein be anticipated, so that the needle will run along it rather than passing through the vessel. Ideally, the ultrasound operator performing a procedure such as PICC placement could explore the region around the needle’s point of entry with ultrasound and use the change in depth of the vessel’s cross section on the ultrasound images to reconstruct its slant. However, as was noted above, this requires a difficult visualization process.

Visualization In-situ and Ex-situ

We conceive of the process of visualizing 3D objects from cross sectional images as a 3D analogue of 2D aperture viewing, a phenomenon that was studied as early as the mid-nineteenth century (Helmholtz, 1867; Zöllner, 1862). In 2D aperture-viewing experiments, an observer is presented with a series of piecemeal views of a large figure through a narrow slit. The views may be implemented by passing the slit over a stationary figure or moving the figure behind a stationary slit. Over many variations in the paradigm, there is broad agreement that the whole figure can be perceived, albeit sometimes with distortions. Thus, people can construct a representation that transcends the limited view available at any time and location (for review, see Fendrich, Rieger, and Heinze, 2005; Morgan, Findlay, & Watt, 1982; Rieger, Grüschow, Heinze & Fendrich, 2007). The phenomenon of integration over aperture views has come to be called “anorthoscopic perception” (Zöllner, 1862).

The research described in this paper is directed at understanding whether and how 3D object representations, particularly their spatial properties such as slant, can be reconstructed from 2D aperture views, or slices. We concentrate in particular on contrasting two conditions that are expected to facilitate vs. impede the visualization of 3D structure from a set of 2D slices. Our motivation in considering these conditions is twofold: They represent two ways in which medical image data can be displayed to an interventional surgeon, and they manipulate what we assume to be a critical processing component of 3D “anorthoscopic perception,” namely, mapping a current aperture view to its spatial source. Note that in the 2D anorthoscopic paradigm, identifying an object that moves behind a stationary aperture is more difficult than when seeing the aperture itself move within the plane of the screen (Haber & Nathanson, 1968; Loomis, Klatzky, & Lederman, 1991). The latter condition facilitates mapping the features visible at different times into a common spatial framework.

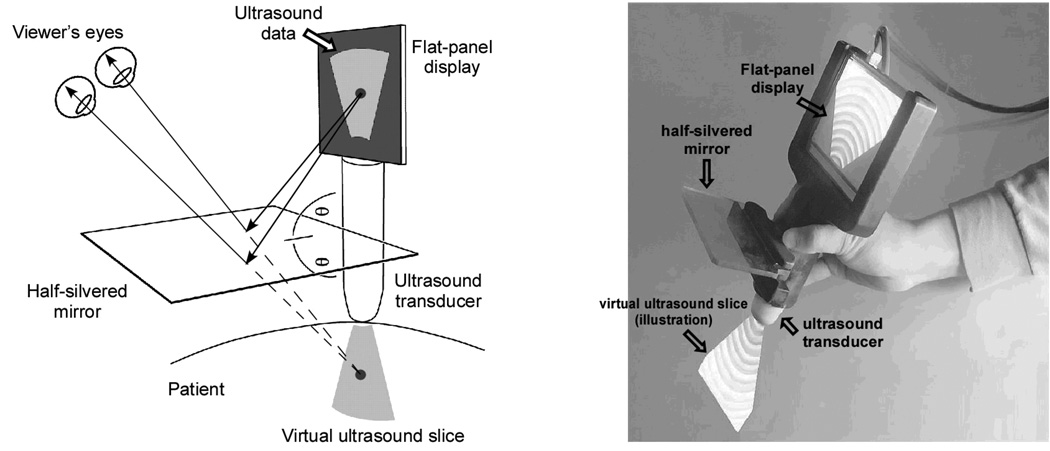
In both conditions studied here, the observer actively explores the space in which a 3D object is implicit, exposing it as a sequence of cross sectional images, and attempts to determine the object’s slant. The difference between the two conditions lies in the spatial correspondence between the visible 2D cross sections and their originating locations in the 3D world. In one case, called in-situ visualization, a 2D cross section is viewed at the same place in space where the underlying imaged object is located by using an augmented-reality (AR) display shown in Figure 3. In another case, called ex-situ visualization, the cross section is presented on a screen that is displaced from the source, resembling the displays commonly used by physicians in image-guided surgery. Briefly, in-situ visualization allows observers to directly map a 2D slice of an object to its origin in space, whereas ex-situ visualization displaces the slice away from its origin, impeding the mapping process.

Figure 3.

Schematic and photograph of the augmented-reality visualization device. Through the half-silvered mirror, the ultrasound image is projected as if it “shines out” from the transducer and illuminates the inner structures (from Wu, Klatzky, Shelton, & Stetten, 2005, with permission, © 2005 IEEE).

The specific research questions addressed here are as follows: First, what level of efficacy can be achieved in a simple spatial task involving visualization of 3D structure from 2D cross sections? The baseline task uses an object of known structure, a rod, which varies in only one spatial dimension, pitch (up/down slant) or yaw (left/right slant). Second, does performance even in such a simple task differ when the 2D slices are viewed in-situ, at the spatial origin of the rod, versus ex-situ, at a remote site? We hypothesize that ex-situ viewing will impair performance even in this simple task, because it undermines the critical process of recovering the third dimension by mapping the 2D cross sections to their spatial origin. Third, does performance worsen when multiple spatial dimensions – pitch and yaw -- must be considered simultaneously? If people are able to visualize the rod as a coherent object in 3D space, it intrinsically has an orientation in both dimensions, and performance may not differ according to whether one or both dimensions is queried. If, however, a coherent 3D representation is not achieved, and each dimension must be maintained independently, the additional load of maintaining two dimensions would be expected to impede performance, particularly with ex-situ visualization. Fourth, are there alternative systematic strategies to visualization that are used to perform this task, and if so, what are they? Here we consider in particular an alternative strategy that infers the rod’s slant from the moment-to-moment changes in the 2D display, without constructing a 3D object. This strategy is especially likely to emerge in conditions where visualization is most difficult, namely, when two dimensions of orientation must be considered simultaneously and the viewing condition is ex-situ. By pursuing these questions and predictions, these experiments have implications both for understanding fundamental visualization ability, and for the use of medical imaging devices in diagnosis and surgical guidance.

Experimental Task and Analysis

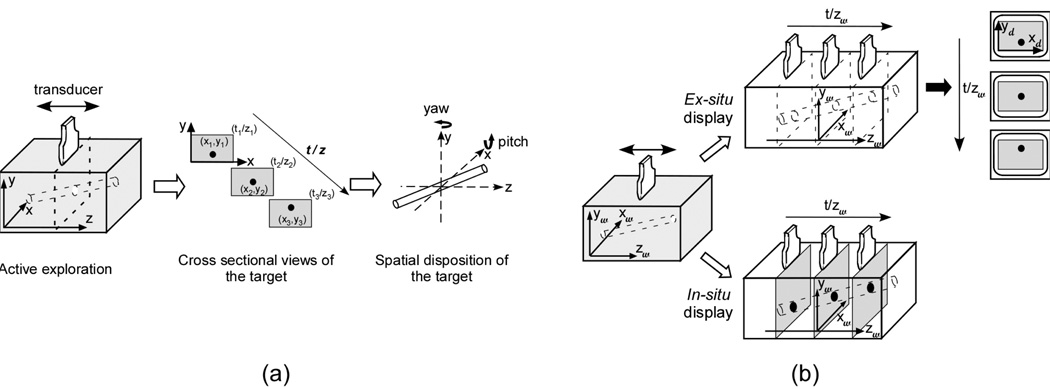
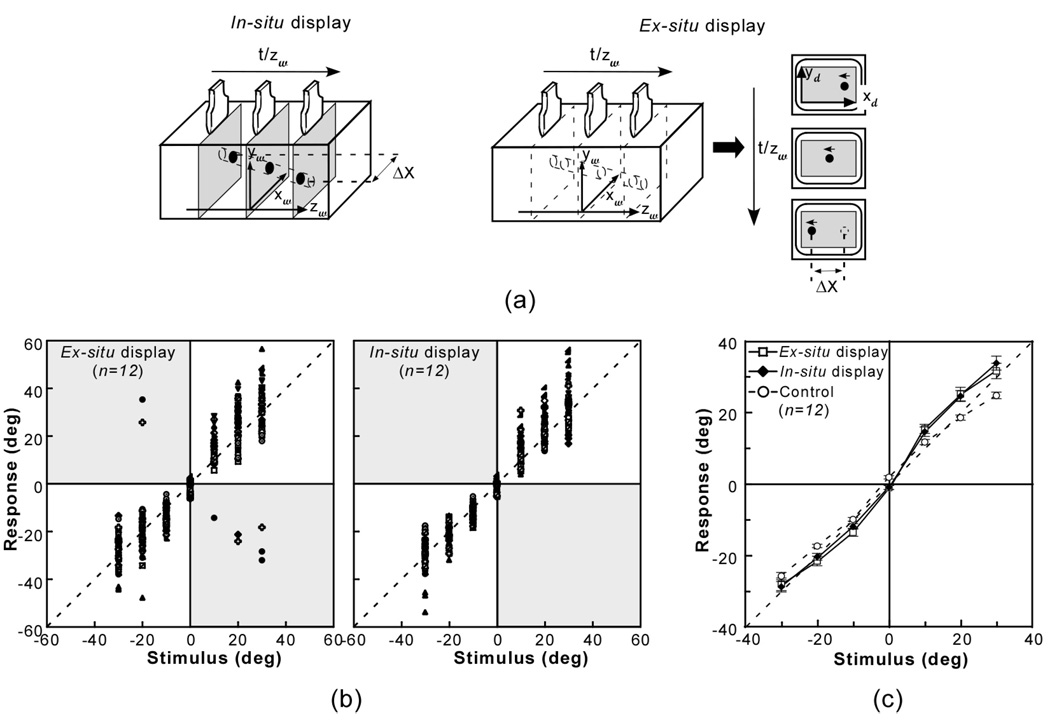
In the research presented here (Figure 1a), participants were asked to explore a hidden virtual rod with a hand-held device, exposing it as a successive sequence of cross sectional images, and then to estimate either its pitch (upward or downward rotation around a horizontal axis through its midpoint) and/or its yaw (leftward or rightward rotation around a vertical axis through its midpoint). We have pointed out that in order to visualize the rod’s slant in space, participants would have to map the position of its cross section within a 2D slice into the location where the slice was obtained. Because only one cross section is seen at a particular moment, successful visualization requires integration across time as well as space. The task also requires integration across sensory modalities, because the active exploration used to expose the rod, which gives rise to motor efference and kinesthetic feedback, provides cues to the locations of cross sections.

Figure 1.

(a) Illustration of the experimental task. Participants were asked to explore a hidden, virtual rod with a hand-held device, exposing it over time as a sequence of cross sectional images traced out along the z axis, and then to report its slant. (b) Example of the stimulus event presented to the participant when exploring a target rod in the in-situ and ex-situ viewing conditions. In the ex-situ viewing condition (top), the cross sectional image was shown on a remote monitor. With in-situ viewing (bottom), the rod’s cross section was seen at its actual location in the space of exploration. The subscripts “w” and “d” denote world and display coordinates, respectively.

As noted above, the focus of this research is to compare two conditions for displaying the sequence of 2D cross sectional slices resulting from exploration of a target object. In one condition (in-situ), the cross sectional images are shown in place where they originated. In the other (ex-situ), the images are displaced onto a remote screen. In related work, we have documented the costs of displacing the image from the framework of direct perception and action (Wu, Klatzky, Shelton & Stetten, 2005, 2008). Wu et al. (2005) found that in-situ viewing allows viewers to perceive the location of a target more accurately than using ex-situ displays. Subjects judged the location of a hidden target that was depicted by a single ultrasound image. Their performance in the in-situ viewing condition was found to be comparable to that with direct vision, while ex-situ viewing led to systematic underestimation of target depth. On the basis of these results, we next consider in detail how the two types of display might differ in promoting spatial visualization across multiple images, the topic of interest here.

With in-situ viewing (see Figure 1b, bottom, and Figure 2), because the current cross sectional slice is projected directly into the explored space using a half-silvered mirror, basic mechanisms of spatial perception should allow the viewer to map the location of the rod’s current cross section to world coordinates (designated {x_w, y_w, z_w}in Figure 1b). For convenience of exposition, we align x_w and y_w with the horizontal and vertical axes of the cross sectional image and z_w with the axis of movement (we make no further assumption about these coordinates, e.g., whether they are egocentric or allocentric). As the observer actively moves his or her arm along the length of the rod, the z_w coordinate of the current cross section is conveyed by visual cues to the position of the cross section and arm, along with kinesthetic cues from arm movement. Simultaneously, the cross section of the rod is observed translating in x_w for yaw and/or y_w for pitch. The rod can then be visualized by integrating across the collective coordinates of its cross sections.

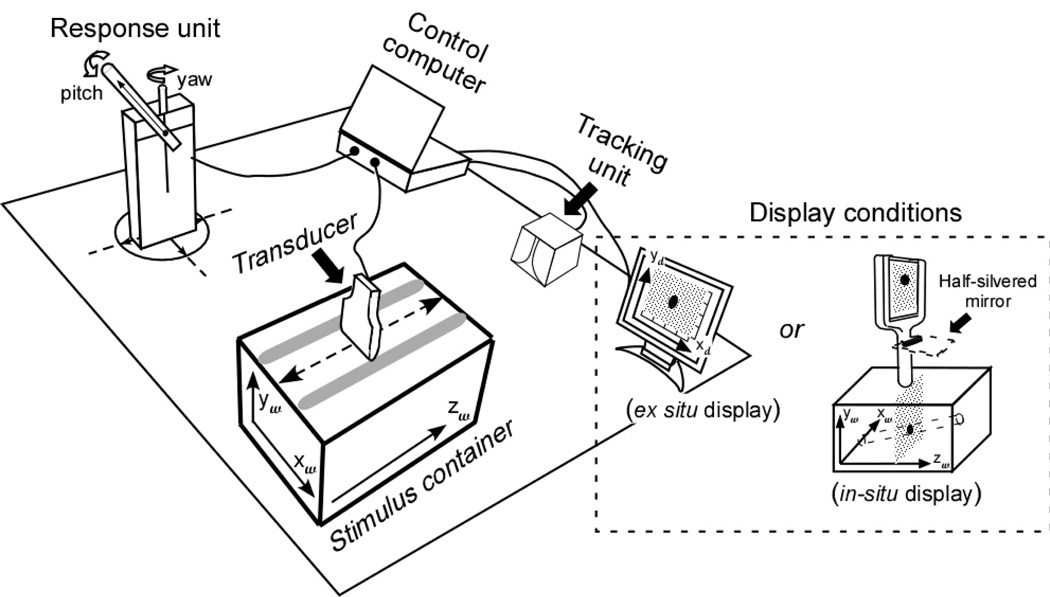
Figure 2.

Schematic of the experimental setup. Participants used a transducer to scan a target rod that was hidden inside the stimulus container, exposing it as a sequence of cross sectional images. Their judgments of the rod’s orientation were measured by making a response rod parallel to it. Two types of display (in-situ vs. ex-situ) were tested. The subscripts “w” and “d” denote world and display coordinates, respectively.

Next consider how integration might take place under the ex-situ viewing condition. Here the image from the exploring device is sent to a displaced monitor (Figure 1b, top, and Figure 2). The 3D positional information of the rod’s cross section is specified using two frames of reference: The image on the display provides spatial information in the {x_d, y_d} coordinates of its frame, while the world coordinate of the z dimension is signaled by kinesthetic (and potentially, visual) cues to arm position. Since the experimental task is to judge the orientation of a rod in 3D space, a fully world-coordinate representation of the rod needs to be formed, and hence the location information specified in display coordinates,{x_d, y_d}, must be mapped into the {x_w,y_w} space and combined with the z_w determined from exploration.

As compared to the in-situ viewing condition, additional processing is required in the ex-situ condition, in order to map information in different coordinate systems into a single framework. Mapping between the monitor and world frames of reference was facilitated here by placing the ex-situ monitor parallel to the plane of the imaged slice and maintaining 1:1 scale between the displayed and imaged data. As a result, no mental rotation was required to relate the monitor plane to the slice plane, there was also no need for mental rescaling, and the spatial-cognitive load of the transformation from monitor to world coordinates was accordingly minimized. However, the required processing of an ex-situ display may still be cognitively demanding, given the need to relate frames of reference (Klatzky & Wu, 2008), especially when separated in space (Gepshtein, Burge, Ernst, & Banks, 2005). Ex-situ processing is further complicated by the fact that the representation of the rod’s cross sectional {x_w, y_w} location results from spatial transformations at cognitive levels, whereas the z_w parameter is signaled by perceptual cues to arm location (the latter is also the case for the in-situ display). This adds the need to combine perceptual with cognitive computations to the burden of the ex-situ display (Klatzky, Wu, & Stetten, 2008; Wu, Klatzky, Shelton, & Stetten, 2008).

Alternative Strategies to 3D Visualization

We have described a process of visualization, by which 2D cross sectional images are integrated across space and time to achieve a 3D representation. However, not all 3D spatial problems must be solved by visualizing 3D objects (Gluck & Fitting, 2003; Lanca, 1998; Moè, Meneghetti, & Cadinu, 2009). For example, Lanca (1998) reported that verbal strategies could be adopted to solve a contour map cross section test without introducing a decrement in performance.

In the present task, using cues from the 2D monitor might be an alternative to fully 3D visualization. For example, knowing that the target is a straight round rod, people might judge its slant by means of the elliptical cross section. Mathematically, pictorial cues such as the aspect ratio and direction of the elliptical cross section can be used to calculate the amount of pitch and yaw. Previous work suggests, however, that these cues are likely to be ineffective for unambiguous determination of 3D orientations (Braunstein, & Payne, 1969; Cumming, Johnston, & Parker, 1993; Cutting & Vishton, 1995; Zimmerman, Legge, & Cavanagh, 1995).

An alternative strategy that also bypasses 3D visualization is suggested by the salient on-screen changes concomitant with exploration of the rod. That strategy is total reliance on the visible screen displacement in 2D. For example, when judging the rod’s pitch, a person might reduce the task to the estimation of Δy_d, the magnitude of vertical cross section displacement on the screen, relative to an estimated Δz_w, as signalled by the magnitude or duration of arm translation. The magnitude of the rod’s pitch could actually be calculated as atan (Δy_d/Δz_w), and the pitch direction (up vs. down) could be determined by the displacement on the screen for a given arm-movement direction (e.g., if distal-to-proximal movements cause the cross section to move upward on the screen, the rod is pitched upward toward the viewer). Even if people cannot accurately perform mental trigonometry to solve the problem (which seems likely to be the case), it is possible that crude heuristics based on the on-screen displacement of the cross section might suffice to give reasonably accurate performance. For example, in the context of small arm movement, a large Δy_d on the screen indicates steep pitch. If, more cleverly, the participants adopt a constant arm movement and respond proportionally to Δy_d, their responses would depend on the tangent of the stimulus angle, which is essentially linear with angle in the range tested. This screen heuristic, like true visualization, would then produce responses that vary linearly with the correct answer.

Research Plan

As was noted above, the present studies address four questions. The first asks what level of performance can be achieved with a seemingly simple task: visualizing a rod slanted in one dimension, based on 2D cross sectional views. The second asks whether in-situ visualization will be superior to ex-situ, given their differential effects on an essential process, mapping the 2D slices to their spatial source. To address these issues, Experiments 1 and 2 assessed the two viewing conditions with respect to the accuracy with which participants could determine pitch and yaw, respectively. The remaining questions are, to the extent that visualization is not achieved, i.e., particularly with ex-situ viewing, will performance be impaired when two dimensions of object orientation must be considered simultaneously, and will alternative strategies to visualization emerge in these conditions? To address these issues, Experiment 3 increased the processing load by co-varying pitch and yaw and having participants respond with both parameters, requiring a fully 3D representation. The magnitude of error and systematic error trends were used to make inferences about the underlying processes with each type of display.

Experiment 1: Judging the pitch-slant of a virtual rod

The participants explored a hidden rod and viewed its cross sections either at its physical location in 3D space (in-situ condition) or on a remote monitor (ex-situ condition). Their estimates of pitch were measured using a matching paradigm.

Method

Participants

Twelve university students participated in this experiment, seven male and five female. The average age was 22.3±7.1 years. In this and subsequent studies, all participants were naïve to the purposes of the experiment and did not participate in a similar study. All were right-handed and had normal or corrected-to-normal vision and stereo acuity better than 40” of arc as measured by the standard Snellen eye chart and the stereo fly test (Stereo Fly SO-001, Stereo Optical Co.). They all provided informed consent before the experiments.

Design

The independent variables were display mode (in-situ vs. ex-situ) and pitch of the virtual rod. The pitch values varied uniformly from −30° to +30° with a step of 10° for experimental trials; there were 4 replications for each combination. Here the +/− signs refer, respectively, to upward/downward displacements of proximal cross sections relative to the distal end of the rod. An additional four dummy trials were inserted using −40° or +40° in order to increase the stimulus variation for the participant, making a total of 64 trials. The stimulus values are plausible from a medical perspective, given the wide variation in slant of tubular structures observed with medical imaging, but were also based, to some extent, on experimental constraints: The in-situ display used here allowed the depth of the cross sectional image to vary only over 8 cm (as explained below), and therefore large slant angles would correspond to small arm movements, which would be difficult to discriminate. In addition, a relatively small range of angles encourages participants to be precise in discriminating responses, and the number of levels manipulated within the range is limited by the duration of the experiment.

Experimental trials were blocked by display mode, but otherwise randomized within each block. The testing order of display mode was balanced across participants.

Setup

The experimental setup was mounted on a table, as shown in Figure 2. It consisted of a stimulus container, a mock ultrasound transducer, a viewing display, a response unit, a tracking system and a computer for control, target simulation, and data acquisition. The stimulus container was a box with dimensions 31(L) × 17(W) × 22 (H) cm. A virtual rod of 1.0-cm diameter was generated inside it by software. Participants explored the rod by moving a mock transducer over the container and so viewing cross sectional images of the rod. Transducer movement was restricted by a pair of wood rails longitudinally mounted on the top of the container and running along its length, spaced horizontally to match the transducer width.

The mock transducer was made of wood. A sensor (miniBIRD 500) was embedded inside it to continuously trace its location and orientation. The tracker data were used to determine the relative position of the transducer with respect to the target rod, and hence controlled the view to be displayed. The view consisted of an 8.0 cm × 8.0 cm area with a background of random dots representing the cross section of the box. (The mean luminance was 4.1 cd/m² and 12.5 cd/m² in the in-situ and ex-situ conditions, respectively; as is explained below, the in-situ display uses a half-silvered mirror which results in lower luminance.) Superimposed on the viewing area was a solid circular or elliptical region (shape depending on the target rod’s orientation relative to the transducer; luminance: 94.1 cd/m² and 163.1 cd/m², respectively, for the in-situ and ex-situ conditions) representing the virtual rod’s cross section at the imaged location. A Dell laptop was used to generate and display the cross sectional video images at an updating rate of 51.7 fps.

Two types of displays were used in this study: (1) an augmented reality (AR) device (Stetten, 2003; Stetten & Chib, 2001) that creates an in-situ view of the virtual stimulus rod, and (2) a conventional CRT monitor in the ex-situ display mode. The in-situ AR display (see Figure 3) consists of a 5.2” flat panel screen and a half-silvered mirror that are rigidly mounted to the mock transducer. Note that the screen must be kept small given the hand-held nature of the device, and the viewing area of the image slice is constrained to be the same size. The half-silvered mirror is placed halfway between the tip of the transducer and the bottom of the screen. As a result of this configuration, when looking into the mirror, the reflection of the screen image is seen as if emitting from the tip of the transducer. Moreover, because of the semi-reflective characteristics of the mirror, the reflection is merged into the viewer’s sight of the container, creating an illusion of a planar slice floating inside. The AR display and the rendering of the virtual rod were calibrated so that the cross section of the rod was shown at the proper location. The viewer’s depth perception with this in-situ display has available full binocular cues, including convergence of the eyes and disparity between the left and right retinal images, and has been found to produce depth localization comparable to direct vision (Wu et al., 2005).

In the ex-situ viewing condition, the cross sectional image was scaled 1:1 with the in-situ target, so that the visual stimulus was matched in size across the two conditions (although not in visual angle due to different viewing distances). The difference was in the displayed location of the cross sectional image: In the ex-situ condition, the image was shown on the center of a 15” CRT monitor located approximately 90 cm away from the stimulus container (i.e., the target’s true location). Full depth cues were available to viewers, but by definition of the ex-situ display, these cues led to every cross sectional image being perceived at the same location -- on the CRT screen -- rather than having a unique spatial origin. The CRT was oriented so that its screen was parallel to the frontal plane of the stimulus container. In addition, along the bottom and right sides of the cross sectional image, two centimeter rulers were provided to enable accurate measurement of the x–y location of the rod’s cross section in the image.

The response-measurement unit was a wooden test rod placed next to the stimulus container. The rod had two rotational degrees of freedom: It was attached to a stand base that could be turned left or right about a vertical axis (yaw), and the rod itself could be independently rotated upward or downward around a horizontal axis (pitch). The pitch and yaw orientations were measured using a miniBIRD sensor.

In this and the following experiments, the stimulus orientations and the participants’ responses were defined in a common extrinsic frame of reference: The top surface of the stimulus container defined zero pitch, and the scanning direction as constrained by the guidance rails defined zero yaw. Lines were marked on the table surface and the stand base to indicate these reference orientations for the participant.

Procedure

The test was run in two blocks separated by a break, one for each display mode. The display testing order was counterbalanced across participants. Each block consisted of six practice trials, followed by 32 experimental trials. In addition, a control block was carried out after the experimental blocks, in which all stimulus orientations were explicitly presented in graphical form, as opposed to being inferred from cross sectional views (described in detail below).

At the beginning of each block, the participant was given an explanation of the task. Graphical animations were used to explain how cross sectional views of a slanted rod were generated and how the imaging plane and the imaged part of the rod could be located in space with reference to the transducer position and orientation. Detailed instructions were given in the ex-situ display mode about how depth measurements were made and presented in the image on the CRT screen. Participants next completed five practice trials to familiarize themselves with the display mode for the current block. The pitch values used in the practice trials were 0°, ±15°, and ±45°, presented in random order. In the practice and subsequent experimental trials, no feedback was given to participants concerning the accuracy of their response.

On each trial, the participant explored a target rod inside the container by scanning the transducer over it. He or she would see the cross section of the rod on the CRT in the ex-situ condition, or at the location being scanned in the in-situ condition. Participants were instructed to hold the transducer in the upright position and scan the whole observable length of the rod, in order to localize and track cross sections in space and thus mentally “see” how the rod was oriented. (In pilot tests, participants sometimes were observed to jump the transducer from one end of the container box to the other, indicating a strategy of imaging only two slices of the rod and from them estimating the slant. To discourage this, participants were instructed to run the transducer continuously along the box, and they were specifically told not to use the jumping strategy. The analysis of recorded trajectories showed that this instruction was obeyed by participants, and in no experimental trial was abrupt motion of the transducer observed.) Accuracy was particularly emphasized in the instruction. There was no speed constraint to the response, and participants were allowed to scan the rod as many times as they wished. To respond with the judged orientation of the virtual rod, the participant rotated the physical rod on the response unit to make it parallel to the target rod inside the container. The computer recorded the orientations of the response. During the inter-trial interval a checkerboard mask was presented on the screen for 3 sec. The typical duration of a trial was less than 1 min, and each experimental block took less than 25 min. There was a 5-min break between the two successive experimental blocks.

After all experimental trials had been completed, a control block lasting approximately 10 minutes was performed to assess the participant’s performance on a task of pure orientation matching. On a control trial, the stimulus orientation was shown explicitly as a red slanted line forming an angle with a horizontal on an LCD screen. The participant was required to make the response rod parallel to the target line. Nine orientations were tested, ranging from −40° to +40° with a step of 10°, in a random order with two measurements each.

Results

To address the first question posed by this research, namely, level of efficacy achievable in indicating one parameter of a rod’s orientation, we consider the overall level of performance by comparing reported pitch to true pitch. As shown in Figure 4(a), the rod’s pitch orientation is indicated by the displacement of its cross section in the vertical dimension (Δy) corresponding to the displacement of the transducer by arm movement (Δz).

Figure 4.

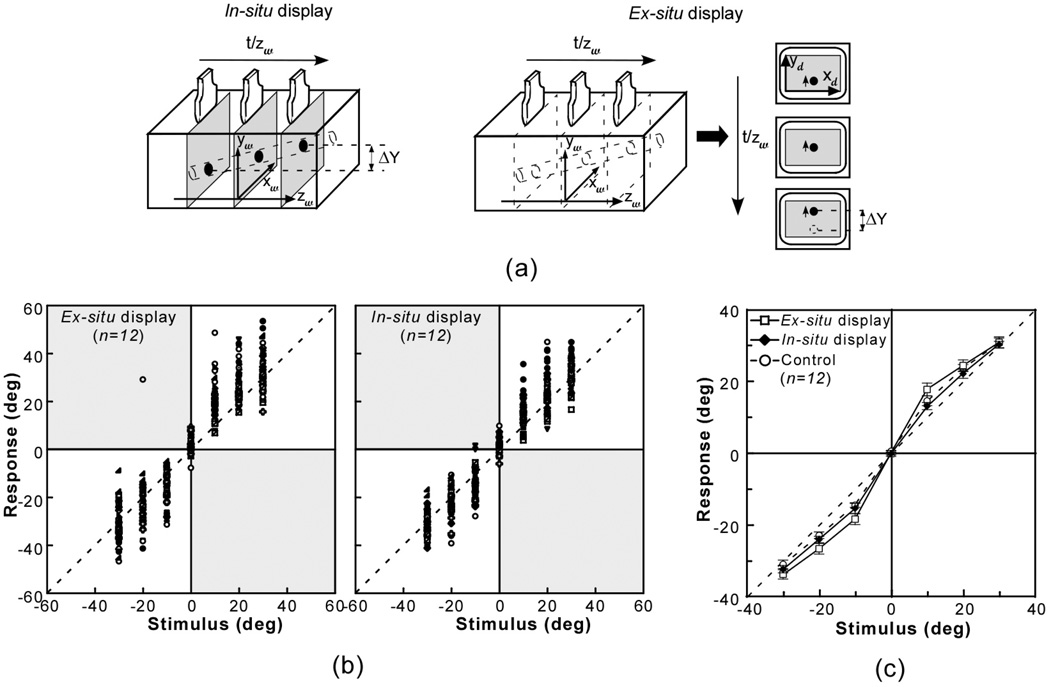
Experiment 1: Judging the pitch-slant of a virtual rod. (a) The stimulus cues. The rod’s pitch orientation could be estimated from the displacement of its cross section in the vertical dimension (Δy) with respect to the transducer movement (Δz). (b) Scatter plot of individual participant responses as a function of stimulus angle. Different symbols represent responses by individual subjects. Reversal responses, if present, appear as points in the shaded quadrants. (c) Mean judged orientation as a function of stimulus angle using the in-situ and ex-situ displays. Error bars represent the standard error of the mean.

Figure 4(b) plots participants’ individual estimates against true pitch using the two displays. The diagonal constitutes correct performance. Clearly, overall performance was close to the diagonal, indicating pitch was judged quite accurately with both displays. When the ex-situ display was used, a few responses had correct magnitude but clearly reversed the direction of slant. Because the sign of the response angle is opposite to that of the stimulus, these responses appear as points in the shaded quadrants of the plot, where they lie on the reverse diagonal from that expected. Only one of these occurred beyond the practice trials and can be observed in Figure 4(b). These reversal errors presumably resulted from confusing the direction of Δy relative to the direction of Δz. We interpret these confusions as reflecting a fragile linkage between the changing image pattern and the movements that produced it. No such error happened with the in-situ display. Reversal errors (here, <0.1% of the experimental trials) were excluded from the further statistical analyses and from calculation of mean response in this and following experiments.

Figure 4(c) shows the mean judged pitch as a function of the rod’s physical orientation. Although mean responses were close to the diagonal, they tended to exhibit a pattern typical of orientation-matching tasks (e.g. Proffitt, Bhalla, Gossweiler, & Midgett, 1995): Orientations were over-estimated at small values, particularly 10°, while larger angles were matched relatively accurately. A two-way repeated measures ANOVA was conducted to evaluate the effects of Display mode (in-situ vs. ex-situ) and Pitch (7 levels). The analysis found no significant main effect of Display (p=0.98), but a significant interaction of Display × Pitch, F(6,66)=3.43, p<0.01, partial η² = 0.24. As compared to the in-situ display, larger over-estimation at small pitch values was observed with the ex-situ display; the difference between displays was significant at ±10° (t(11)=2.71, p<0.05, partial η² = 0.40 and t(11)=2.40, p<0.05, partial η² = 0.34 for +10° and −10°, respectively), but not for other angles.

A further ANOVA for each display mode compared participants’ estimates of pitch when using 2D cross sectional images to their performance in the control condition, where they judged the pitch of visible lines; response angle was included as a second factor. Consistently with our previous findings with the in-situ display (Wu et. al, 2005), no significant Task effect (control vs. in-situ imaging) was found (p=0.13), nor was there a significant interaction with Angle (p=0.97). In contrast, a significant interaction between Task and Angle (F(6,66)=2.51, p<0.05, partial η² = 0.19) was found for the ex-situ display mode, and the difference between the experimental and control tasks was significant at −10° (t(11)=2.63, p<0.05, partial η² = 0.39).

Discussion

To briefly summarize, the data indicate that the pitch of a virtual rod can be accurately determined from exploration and visualization. There was a statistically significant advantage for the in-situ display at the smallest angle tested, where the ex-situ display produced a significant deviation from the control performance, although the effect size was not large. In addition, the ex-situ display uniquely led to a type of reversal error, such that the direction of the pitch was incorrectly reported, while its magnitude was essentially correct.

As described in the Introduction, there are multiple processing approaches that participants could adopt with both displays in order to determine the rod’s slant. Of greatest interest here is the process of visualization in 3D, by means of spatio-temporal integration across cross sectional images. Alternatively, a 2D screen-based strategy might be used; in particular, pitch might be estimated from the magnitude of change in the cross section’s height on the monitor in the context of a given arm movement. The differences between the two devices observed here argue against participants’ relying exclusively on 2D cues, which are equally available with in-situ and ex-situ displays. Before further interpreting the results observed here, we turn to a corresponding experiment on judging another direction of slant, namely, yaw.

Experiment 2: Judging the yaw-slant of a virtual rod

This experiment paralleled the first but addressed the ability to judge the yaw of a virtual rod from cross sectional images.

Method

Participants

Twelve students, nine male and three female, participated in this experiment. Their average age was 25.5±5.7. All were right-handed and had normal or corrected-to-normal vision and stereo acuity better than 40” of arc.

Design and Procedure

The experimental design and procedure were the same as the previous one, except that the rod was rotated in the yaw plane instead of the pitch plane. As shown in Figure 5(a), the yaw slant was signified by the horizontal shift of the rod (Δx) in the cross sectional images in response to a displacement of the transducer (Δz). Here the zero-yaw direction was the scanning direction defined by the guidance rails, and yaw was signed so that +/− refer to right/left displacements of proximal cross sections relative to the distal end of the rod.

Figure 5.

Experiment 2: Judging the yaw-slant of a virtual rod. (a) The rod’s yaw orientation can be estimated from the horizontal displacement of its cross section (Δx) corresponding to the transducer movement (Δz). (b) Scatter plot of individual participant responses as a function of stimulus angle. Different symbols represent responses by individual subjects. Reversal responses, if present, appear as points in the shaded quadrants. (c) Mean response as a function of stimulus angle. Error bars represent the standard error of the mean.

Results

Again, to assess overall performance and compare the displays, reported yaw was compared to the true value. Figure 5(b) plots participants’ individual estimates using two displays. No reversal error occurred with the in-situ display, but with the ex-situ display, three participants made reversal errors on the experimental trials for a total of 8 trials (1.0% of the experimental data), which were excluded from further analysis.

Figure 5(c) shows the mean judged yaw as a function of the rod’s orientation. The response pattern was similar to that of pitch: Performance was overall quite accurate, but over-estimations were observed at small angular values. However, in contrast to the Display effect found for pitch, the ANOVA on Display mode and Yaw showed no significant difference between the in-situ and e- situ display modes(p=0.47), or interaction of Display × Yaw(p=0.48). In addition, when compared to the control condition (alignment of the response rod with visually displayed angle), judgments of yaw for both displays showed small but significant deviations at large angles. In the ANOVA on Task (yaw judgment vs. control) and Angle, the interaction was significant for both display modes, F(6,66)=14.10, p<0.01, partial η² = 0.56 for the in-situ display; F(6,66)=8.97, p<0.01, partial η² = 0.45 for ex-situ. This effect size indicates that during the experimental trials, participants deviated moderately from their responses to visually displayed angles.

Discussion

The results indicate that as with pitch judgments in Experiment 1, the yaw of a virtual rod can be determined with reasonable accuracy using both displays, albeit with some over-estimation at the smaller angles. The participants’ responses with the two display modes were comparable, except that reversal errors were observed only with the ex-situ display. Both devices deviated significantly from the control responses, which exhibited underestimation at larger, positive angles. We have no explanation for this anomaly.

Experiment 3: Estimation of the rod rotation in both yaw and pitch dimensions

Experiments 1 & 2 demonstrated participants’ ability to use either display mode to visualize the rod’s slant within a single plane from cross sectional views, within a reasonable level of accuracy. However, the results do not by themselves indicate the processing mechanisms by which participants arrived at their judgments. Our interest is particularly in determining whether they achieved a representation of the rod by a process of visualization through spatio-temporal integration in 3D, or whether an alternative, 2D strategy was used.

Experiment 3, which incorporated judgments of both pitch and yaw, was devised to further test for the nature of participants’ spatial processing. We focused in particular on the screen-based strategy of using observable displacement of the cross section on the monitor, as an alternative to 3D visualization. The task complexity, i.e., the degrees of freedom of rod rotation, was increased, and participants were asked to estimate both pitch and yaw simultaneously. As will be explained in detail below, this introduces a co-dependency between the two parameters with respect to the range of visible change on the screen. For example, extreme pitch means the rod’s cross section will pass from the top to the bottom of the screen across a small region of exploration, reducing the visible range of yaw. If subjects are relying on the observable Δx_d and Δy_d from the monitor to estimate pitch and yaw, rather than 3D visualization, this strategy will be signaled by systematic errors.

Experiment 3 also pursued the observation that the participants made reversal errors only with the ex-situ display mode. This suggests that spatial displacement of the cross sectional images from the manual exploration led to error in memory for the direction of either the visual or kinesthetic component of the task. The further task load introduced here should, then, increase the tendency to make such errors.

Method

Participants

Sixteen participants with an average age of 23.8±7.5 years were tested, eleven male and five female. All were right-handed and had normal or corrected-to-normal vision and stereo acuity better than 40” of arc.

Design and Procedure

The stimulus on each trial represented a combination of yaw and pitch angles. Across trials, two sets of stimuli in the pitch-by-yaw space were constructed as follows: In each stimulus set, one variable, called the primary parameter, was manipulated over a broad range, while the other variable, the secondary parameter, was assigned to two possible levels. Specifically, across stimuli from the yaw-primary set, the rod’s yaw changed uniformly from −40° to +40° with a step size of 10° (i.e., taking 9 values) while its pitch was set to 10° or 30°. The reverse held for the stimulus distribution in the pitch-primary set. (As in the previous experiments, +/− refer to upward/downward in pitch and rightward/leftward in yaw.) This resulted in 36 pitch/yaw combinations, 18 in each stimulus set, which were presented once each in the two display modes (in-situ; ex-situ), for a total of 72 trials. Experimental trials were blocked by display mode and randomized within each block. The testing order of the two viewing conditions was balanced across participants. The test procedure and response task were identical to those in the previous experiments.

Results & Discussion

Combined pitch and yaw judgments with the two displays

The initial analysis turns to the questions of whether reports of the orientation of a virtual rod explored in cross sectional slices will be impaired when there are two dimensions of spatial variation, as compared to judgments of a single parameter, and whether the impact of multiple dimensions depends on the display mode. For this purpose we evaluate the reported pitch and yaw relative to their true values with each display. Although pitch and yaw were judged simultaneously, our analysis considers the two dimensions separately because of their mathematical independence, treating the data as in Experiments 1 and 2.

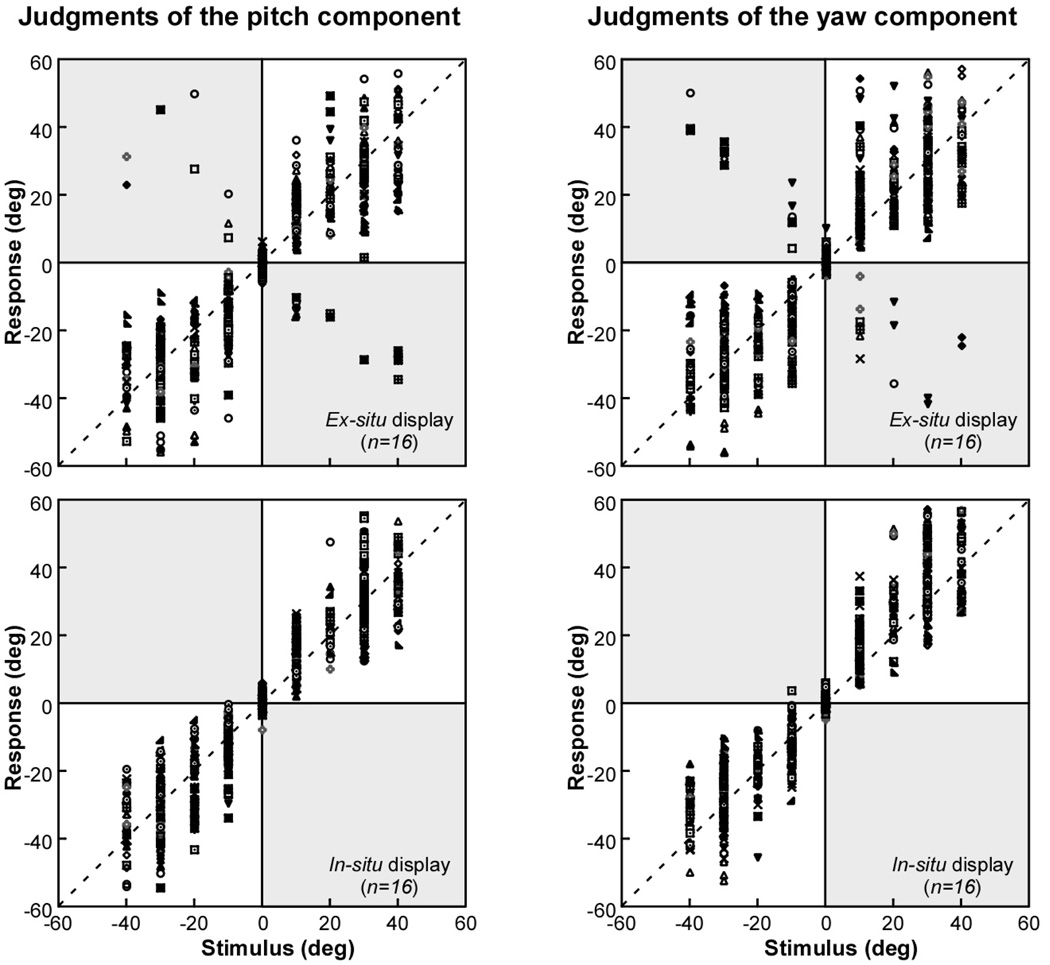
Figure 6 shows a scatter plot of the reported pitch (left panels) and yaw (right panels) against the objective value of the parameter, for each display condition, ex-situ (top panels) and in-situ (bottom panels), using data from all experimental trials. The figure shows that compared to the single-parameter judgments in the previous experiments, the increased task complexity of Experiment 3 caused a substantial increase in the number of reversal errors with the ex-situ display. Of a total of 16 participants tested, 11 made at least some reversal errors in their pitch judgments and 10 in their yaw judgments. Again, reversal errors were not evident with the in-situ display. As before, these errors (25 yaw judgments and 36 pitch judgments, or 5.3% of the experimental trials) were excluded from further consideration, including calculation of the mean response.

Figure 6.

Experiment 3: Judging yaw and pitch simultaneously. Scatter plot of the participants’ judgments of pitch and yaw with ex-situ and in-situ displays, showing response angle as a function of stimulus angle. Different symbols represent responses by individual subjects. Reversal responses, if present, appear as points in the shaded quadrants.

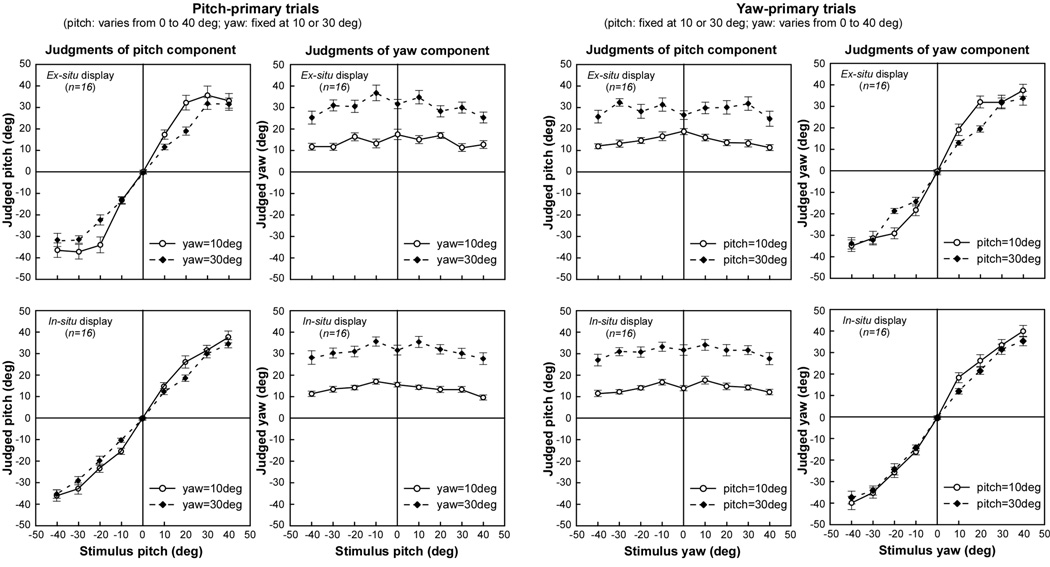
Figure 7 plots the mean judged yaw and pitch as a function of the rod’s physical slant. Recall from the design that for stimuli in the pitch-primary set, the rod’s pitch varied from −40° to +40° in 9 steps, while its yaw, the secondary parameter, was fixed at 10° or 30°, and conversely for the yaw-primary stimulus set. The figure’s left panels show pitch and yaw judgments for the pitch-primary stimuli, as a function of the objective pitch value, and the right panels show the corresponding data for the yaw-primary stimuli. The functions for the pitch-primary and yaw-primary stimulus sets appear quite similar. Different response patterns were observed, however, for the two display modes. With the in-situ display, (bottom row, Figure 7) the mean response to the primary parameter increased essentially linearly with its objective value. In contrast, obvious non-linearity was shown in the participants’ judgments of the primary parameter with the ex-situ display (top row, Figure 7), particularly when the value of the secondary parameter was small. A demonstrative example is the pitch judgments for the pitch-primary stimuli with a fixed yaw of 10° (the open-circles in the upper left panel of Figure 7): The participants’ judgments of pitch were relatively accurate when the stimulus pitch was 0° or 10°, but were reported as a constant value of about 35° for all pitch values larger than 10°.

Figure 7.

Mean judged pitch and yaw as a function of the objective primary-stimulus orientation using ex-situ (top row) and in-situ (bottom row) displays. The left and right panels show respectively the results obtained from the Pitch-primary and Yaw-primary trials. The open and filled symbols correspond to judgments of the variable orientation (pitch or yaw), when the other orientation (yaw or pitch) was fixed at 10° and 30°, respectively. Error bars represent the standard error of the mean.

When compared to Experiments 1 and 2, the systematic deviations from correct values in Experiment 3 with the ex-situ display, together with the increase in reversal errors, make it clear that the addition of a second judged parameter of the rod impaired performance with that display, as predicted. Further analyses were directed at quantifying the trends seen in Figure 7 and interpreting them in the context of task-directed strategies, both visualization and an alternative strategy based on the 2D display.

Joint effects of pitch and yaw

Figure 7 indicates a strong dependence of the judgment of the primary parameter on the level of the secondary parameter, for example, judging the pitch of pitch-primary stimuli depended also on their yaw. This is particularly evident with the ex-situ display, but there are similar but weaker trends in the in-situ condition. To statistically evaluate this dependence, ANOVAs were conducted within each stimulus set, with judgment of the primary parameter as the dependent variable, and objective values of the Primary parameter (9 levels, −40° to +40°) and Secondary parameter (10° or 30°) as the independent variables. These ANOVAs were performed separately for each display mode (in-situ, ex-situ), for a total of four analyses. In each ANOVA, a main effect of Primary parameter was expected, given that it reflects the dependence of the response judgment on the objective value of the stimulus (e.g., dependence of reported yaw on true yaw). Of greater interest were the main effects of Secondary parameter (e.g., dependence of reported yaw on level of pitch) and the interaction between Primary and Secondary parameter.

The ANOVAs confirmed an interaction between the objective primary and secondary parameters, but only for the ex-situ display (top of Figure 7). In that condition, whether pitch or yaw was judged as the primary parameter, the judgment tended to be greater when the value of the secondary parameter was 10° rather than 30° (main effect of Secondary parameter: F(1,15)=11.88, p<0.01, partial η² = 0.44 and F(1,15)=15.84, p<0.01, partial η² = 0.51 for the pitch and yaw judgments, respectively; Primary × Secondary interaction: F(8,120)=4.31, p<0.01, partial η² = 0.22 and F(8,120)=2.62, p<0.05, partial η² = 0.15 for pitch and yaw, respectively). The effect sizes were low to moderate. In comparison, in the ANOVAs with the data from the in-situ display (Figure 7, lower portion), neither the main effect of Secondary parameter nor the interaction was statistically significant (main effect: p=0.13 and p=0.19; interaction: p=0.10 and p=0.46 for pitch and yaw judgments, respectively).

The previous analyses considered the judgment of the parameter designated as primary on a given trial, but judgments of the secondary parameter, which took on only two values, are also of interest (e.g., judgments of yaw within the pitch-primary stimulus set). Similar ANOVAs to those reported above, but now with the judgments of the secondary parameter as the dependent variable, were conducted for stimulus set and display mode, to determine whether those judgments depend on the value of the primary parameter. For the ex-situ display mode, secondary-parameter judgments were significantly influenced by the value of the primary parameter (main effect of Primary parameter: F(8,120)=2.69, p<0.01, partial η² = 0.15, and F(8,120)=2.81, p<0.01, partial η² = 0.16 for pitch and yaw judgments respectively; Primary × Secondary interaction significant for pitch only: F(8,120)=2.51, p<0.02, partial η² = 0.14). In contrast, for the in-situ display mode, these effects were absent for both pitch and yaw (main effect of Primary parameter: p=0.07 and p=0.07; Primary × Secondary interaction: p=0.84 and p=0.14 for pitch and yaw judgments, respectively).

In short, the foregoing analyses confirm that, in the ex-situ display condition, judgments of one parameter of the rod’s slant depended not only on the objective value of that parameter, but on the value of the other dimension of slant as well. The systematic nature of these effects has implications for strategy, as is described next.

Implications for strategy in judgments of rod slant

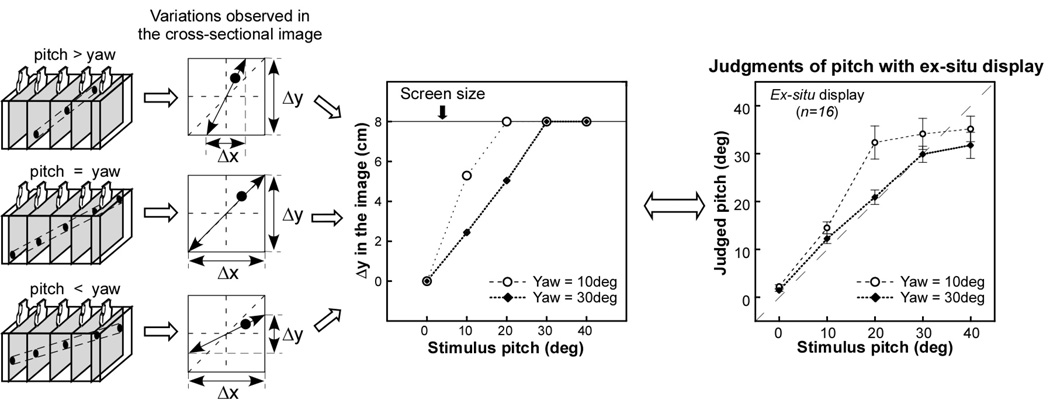
We now turn to the last question raised in the introduction, namely, whether strategies other than visualization arise when the judgment of the virtual rod’s slant becomes more difficult. The present results are consistent with the idea that performance in the ex-situ condition results from reliance on the 2D images, more than a process of visualizing in 3D. Specifically, the observed dependence of participants’ judgments of one slant dimension on the value of the other appears to derive directly from the joint effects of the parameters on the 2D cross sectional images that participants observe, as is depicted in Figure 8.

Figure 8.

(Left) Illustration of how the value of pitch relative to yaw changes the maximal screen variation in the horizontal (Δx) and vertical (Δy) position of the rod cross section; (Middle) Maximal vertical screen variation as a function of the objective value of pitch, given the two values of yaw tested in Experiment 3 (note that the analogous relation obtains when the roles of pitch and yaw are reversed); (Right) Judged value of pitch in the ex-situ condition as a function of the objective value, given fixed values of yaw (re-plotted using the same data shown in Figure 7 as a function of amplitude of pitch-slant). Note the similarity of the data (right) to the maximum screen variation (middle).

Figure 8 shows that when both pitch and yaw vary, the horizontal or vertical variation on the viewing screen corresponding to one judged angle depends on the other, such that large values of one parameter reduce the observable range of the other. If, for example, the rod’s yaw is zero, that is, it runs straight along the length of the box, then its cross section will always remain in the vertical center of the screen, and variations in pitch can be traced across the screen’s full height. If, however, yaw is large, then the cross sectional images will quickly cross the width of the screen over successive images, limiting the scanned distance (i.e., amount of the z axis) in which pitch-related changes in height are visible. At an extreme, if the rod was oriented from left to right across the box (yaw = 90°), it would be visible only for the small region when the transducer swept across its diameter, and thus no pitch-related changes could be seen. Therefore given the two fixed values (10° and 30°) of one parameter, pitch or yaw, in this experiment, the visible displacement due to the variable parameter has a profile as shown in the middle column of Figure 8.

Regression analyses were performed on the mean judged pitch and yaw, in order to assess the contributions of 3D visualization vs. a heuristic based on the on-screen displacement of the 2D cross sections over the course of exploration. Visualization, assuming it is performed accurately, makes a simple prediction: Judgments should be predicted by the objective angle. Screen-based judgments, on the other hand, should follow the dependency shown in Figure 8. To compare the relative contribution of the two strategies, a sequential regression analysis was performed on judgments of the primary parameter (excluding zero values) using two predictors: visualization (i.e., prediction = objective angle in degrees) and screen displacement (i.e., prediction = x_d or y_d displacement in cm for yaw or pitch, respectively). The visualization predictor was forced into the model first, and then the screen displacement predictor was added to assess the additional predictive power. A bivariate regression was then used to determine the relative weight of the predictors when both acted together. Given that we considered only the estimation of the magnitude of the slant angle, absolute values of pitch/yaw stimuli and responses were used in the regression (signed values would distort the linear component due to a range effect).

The results, shown in Table 1, found quite different contributions of the two predictors for the in-situ and ex-situ cases. For the in-situ judgments, the visualization predictor alone accounted for most of the variance (92%), with the addition of the screen-displacement predictor accounting for little, but significant, additional variance (4%). When the two predictors were included together, the beta weight for visualization was more than twice that of the weight for screen displacement. For the ex-situ judgments, adding the screen-displacement predictor to visualization substantially improved prediction (adding 19% to the 73% variance predicted by visualization alone). Moreover, the bivariate model showed a weight for screen displacement more than twice that for visualization. In short, some influence of the screen was apparent with the in-situ display mode, but it was small relative to the contribution attributed to visualization, whereas the balance was reversed with the ex-situ display.

Table 1.

Results of sequential and bivariate regressions on judgments in the in-situ and ex-situ conditions.

Regression analysis		In-Situ	Ex-Situ
Sequential	r2 from visualization	0.92*	0.73*
	r2 change with addition of screen displacement	0.04*	0.19*
Bivariate	r2 from both predictors	0.96*	0.92*
	Visualization beta weight	0.70	0.29
	Screen displacement beta weight	0.32	0.71

^*p<0.001

General Discussion

The present experiments assessed whether and how people can determine the spatial orientation of a rod in 3D space, that is, its pitch and yaw slants, by exposing its planar cross sections over time. We initially raised four questions about this form of visualization. One was the level of accuracy that could be achieved with a simple version of the task. The next was whether there would be a performance difference between an in-situ display mode, where the cross sectional images were projected into the same location as the virtual rod, and an ex-situ display mode, where the cross sections were displaced to a remote monitor. Third, we asked whether accuracy would suffer when multiple dimensions of the rod were judged. The final question is what processing strategies (visualization and alternatives) might be used.

We consider first questions about accuracy and the effects of multiple dimensions and displays. With in-situ viewing, people were highly accurate, albeit with some bias (also seen in ex-situ viewing) toward over-reporting of the smallest angles, even when pitch and yaw were judged together. Ex-situ viewing also led to reasonable accuracy as long as a single orientation was to be judged, although there were a number of responses in which the direction of slant was reversed (reversal errors). The demands of ex-situ visualization were clearly indicated, however, when both pitch and yaw had to be reported. The number of reversal errors then increased substantially, and the relation of the response angle to the objective value deviated significantly from linearity. We attribute these results to a difference between the two displays in how they support the process of mapping 2D slices to their spatial origins, an essential component of visualization in 3D space. The devices also differ in other ways; in particular, visual angle is larger for the in-situ display due to the shorter viewing distance, whereas illumination is reduced by the device’s mirror. However, such differences in image quality are irrelevant to the target’s 3D structure, and the simplicity of the 2D image, which is essentially a circle in a speckled field, makes it readily perceptible in both display conditions. Thus, the fundamental difference between in-situ and ex-situ displays, in terms of support for localizing the cross sectional slices in 3D space, would seem to lie at the heart of the observed difference in error patterns. We next expand on how the present task might be performed with each display; in particular, visualization versus alternative strategies.

Visualization through spatio-temporal integration

As was noted previously, the present task is a 3D extension of the 2D anorthoscopic paradigm, in which a small part of an extended figure is visible through a narrow slit. Here the counterpart was a planar intersection with a 3D object that moved along the third dimension under user control. At any instant, only a thin slice of the object was “cut” and shown to the observer. Analogously to the 2D situation, if the source locations of slices in 3D space can be determined, and multiple slices encoded across time and space can be integrated, this would constitute visualization of the object in three dimensions. The two displays used in the task differ in the information they provide about the 3D spatial location of a given slice, and hence in their support of the visualization process. In the case of the in-situ display, the slice is projected into the space of exploration, where it is directly visible. In contrast, in order for visualization to occur with the ex-situ display, directing gaze to the imaged slice means that the operator must use cues arising from arm movement to determine its source location.

Given that spatio-temporal integration is possible, once slice locations are known, a question of further interest is the level at which the integrative process might operate. This issue has been raised in the literature on 2D anorthoscopic perception, where some have suggested a “retinal painting” hypothesis, first formulated by Helmholtz (1867). This asserts that when an extended scene is viewed through a moving slit, a representation is constructed by “painting” the successive views onto adjacent positions on the retina, thus leading to an integrated percept. Given a stationary slit and moving object, eye movements are assumed to be necessary to produce different retinotopic coordinates for different pieces of the image. Undermining this hypothesis, however, is evidence that even early integration processes, operating at the level of saccades, make use of a spatiotopic frame of reference (Melcher & Moronne, 2003). Although retinal painting might account for some phenomena of 2D anorthoscopic perception, (Anstis, 2005; Anstis & Atkinson, 1967), the hypothesis has largely been ruled out (Fendrich, Rieger, & Heinze, 2005; Hochberg, 1968; Kosslyn, 1980; Palmer, Kellman, & Shipley, 2006; Parks, 1965; Rieger, Grüschow, Heinze, & Fendrich, 2007; Rock, 1981). Evidence has increasingly indicated that spatio-temporal integration occurs at levels beyond the retina, thus implicating central processes (Morgan, Findlay, & Watt, 1982; Parks, 1965; Rieger, Grüschow, Heinze, and Fendrich, 2007; Rock, 1981).

When applied to the 3D anorthoscopic problem in this study, it is very unlikely that the integrative process operates within a retinotopic frame of reference. The task here was to judge the rod as an entity in the world and to determine its orientation on two rotational axes in space. The operative reference frame should be anchored in extrinsic spatial coordinates, in which the spatial information from visual and kinesthetic inputs can be integrated. Combining kinesthetic cues to arm position together with visual cues to the cross section’s location would necessitate a spatial frame of reference accessible to both the visual and haptic modalities; that is, not exclusively retinal.

Processing strategies with different display modes

Strategies other than visualization have often been observed for solving spatial tasks (French, 1965; Gluck & Fitting, 2003; Lanca, 1998; Lohman & Kyllonen, 1983). For example, Snow (1978) reported that people could solve the Paper-Folding test by using either a mental-construction or feature-based strategy; the former strategy appeared to be more effective than the latter. In the present experimental task, the visualization strategy is to build a 3D object representation by spatio-temporal integration, as described above, and an alternative is a screen-based heuristic that relies on the displacement of the cross section within the plane of the monitor. Regression analysis of the judgments of Experiment 3 against the predictions of the two processes showed that the process of visualization made a major contribution to the in-situ judgments, while the ex-situ judgments relied largely on the perceived screen displacement.

Why should this processing shift occur? Previous research has shown that strategy use varies with task characteristics; in particular, non-visualization strategy use tends to increase with task difficulty (Barratt, 1953; Gluck & Fitting, 2003; Lohman & Kyllonen, 1983). The factors that contribute to difficulty may not always be well specified, but here it is clear that the visualization process is impaired specifically because the displayed image is spatially separated from its 3D world coordinates. As was noted in the Introduction, this condition imposes alignment across frames of reference, which is known to impose heavy spatial workload (Klatzky & Wu, 2008; Pani & Dupree, 1994). As a result, participants tended to shift to the screen-based cues when the ex-situ display mode is used.

One might ask, given the evidence for processing differences between display modes when two parameters (pitch and yaw) are judged simultaneously, whether the same differences pertain when only one is judged, requiring representation only of the horizontal (yaw) or vertical (pitch) plane. Note that in Experiments 1 & 2, when participants made judgments of the rod’s pitch or yaw in isolation, their mean judgments were comparable when using the two displays. However, there are indications that the underlying processes were not the same. As was noted in the Introduction, both screen heuristic and visualization strategies could produce responses that vary linearly with the correct answer, and partitioning a linear trend across the probable range of rod angles could produce a reasonable level of accuracy. Thus comparable accuracy does not guarantee comparable process. Note further that reversal errors occurred only in the ex-situ viewing condition. Such errors must result from a process that encoded the magnitude and direction of the rod’s slant, as signaled by the on-screen change and the arm movement, separately. Together with the fact that the in-situ display produced no comparable errors, these reversals suggest that users of the ex-situ device based their judgments of even a single parameter of orientation on the visible screen-displacement, rather than visualization of the object in the 3D world.

Conclusions and applications

We conclude that visualization of the spatial disposition of a 3D object can be accomplished by actively exploring it and viewing a continuous array of 2D sections. This process is facilitated when the cross sections are projected into the location of the object itself. Indeed, this co-location of source object and image may be necessary for 3D visualization, as spatial separation of exploration from the cross sectional view was found to have a highly negative impact on user performance. These results provide clear support for the proposition that an in-situ display can facilitate the mental visualization of 3D structures from cross sectional images and point to the difficulties of processing with conventional displays.

Our findings have implications for the use of imaging data in a variety of applied contexts, particularly medicine. Devices that deliver images in-situ have substantial potential, we believe, for expanding people’s ability to visualize the underlying 3D objects and reducing error. For example, if reversal errors were induced by ex-situ viewing in the surgical task of inserting a PICC line, the needle might be misdirected, necessitating a corrective insertion. A successor of the AR device used in this research has already demonstrated potential superiority in visualizing tissue during ultrasound-guided surgery (Chang, Amesur, Klatzky, et al., 2006) and has been proven effective in actual clinical trials (Wang, Amesur, Shukla, & Bayless, et al., 2009, and Amesur, Wang, Chang, Weiser, & Klatzky, et al., in press).

In-situ displays could be used to provide a means of exploring pre-acquired 3D data sets such as those resulting from CT or MRI in the clinical diagnosis of disease. For example, in the diagnosis of pulmonary embolism (i.e., a blockage of an artery in the lung), radiologists browse the CT scans of pulmonary vasculature and trace branches of the blood vessels back to the heart to determine whether a vessel in question is an artery or a vein. Another potential lies in medical education, for example, the teaching of anatomy. Previous studies have shown that a particular impediment to mastering anatomical knowledge is “students’ inability to understand the correspondence between 2D and 3D representations” of anatomical structures (LeClair, 2003, p. 27). One cause of such difficulty is the ex-situ display of sectional images that leads to attenuated ability to visualize. As we have shown in this study, in-situ visualization can be used to restore the spatial relationship between the image and its source.

In-situ display technology is still under development. As to the in-situ device used in this study, a limitation is that the optically reflected screen must lie within its handle, restricting its depth of view. Another approach to in-situ visualization has been to fully or partially replace the operator’s direct vision with a head-mounted display (HMD: Rosenthal, State, Lee, et al., 2002; Sauer, Khamene, Bascle, et. al., 2001; State, Livingston, Hirota, et al., 1996). These systems track the operator, patient, and tools in order to combine a medical image with a view of the patient for presentation on the HMD. These systems have limitations, however, including tracking lag, low-resolution displays, elimination of oculomotor distance cues, and reduced field of view. With the further development of display technology, we can foresee wide use of in-situ displays in medical application, particularly in image-guided surgical procedures.