Dependence of T Cell Antigen Recognition on T Cell Receptor-Peptide MHC Confinement Time

Summary

T cell receptor (TCR) binding to diverse peptide-major histocompatibility complex (pMHC) ligands results in various degrees of T cell activation. Here we analyze which binding properties of the TCR-pMHC interaction are responsible for this variation in pMHC activation potency. We have analyzed activation of the 1G4 cytotoxic T lymphocyte clone by cognate pMHC variants and performed thorough correlation analysis of T cell activation with 1G4 TCR-pMHC binding properties measured in solution. We found that both the on rate (k_on) and off rate (k_off) contribute to activation potency. Based on our results, we propose a model in which rapid TCR rebinding to the same pMHC after chemical dissociation increases the effective half-life or “confinement time” of a TCR-pMHC interaction. This confinement time model clarifies the role of k_on in T cell activation and reconciles apparently contradictory reports on the role of TCR-pMHC binding kinetics and affinity in T cell activation.

Highlights

► Potency of peptide-MHC as an agonist for TCR signaling is dependent on k_on and k_off ► A TCR-pMHC confinement time model is proposed to account for these parameters ► The model proposes that TCRs rebind the same peptide-MHC before dissociating ► The model reconciles binding kinetics and affinity in T cell activation

Introduction

Specific activation of T cells by cognate antigen is the central event in mounting adaptive immune responses. The specificity of T cell activation is achieved by tightly regulated T cell receptor (TCR) recognition of antigenic peptides in complex with major histocompatibility complex (pMHC) glycoproteins presented by antigen-presenting cells (APCs) or target cells (Burroughs and van der Merwe, 2007). Any given TCR has the ability to bind to a large number of distinct pMHCs, leading to various functional outcomes. Depending on the engaged pMHC, T cells can be activated (stronger or weaker agonist) or inactivated (antagonist), or pMHC binding can have no effect (null peptide) (Germain and Stefanová, 1999; Kersh and Allen, 1996). Although it is generally accepted that the potency of pMHC depends on the “strength” of its binding to TCR, there is controversy over which of the chemical parameters governing binding are the primary determinants of successful signaling (Kersh and Allen, 1996; van der Merwe, 2001).

The mechanism of signal transduction across the T cell membrane upon binding of pMHC to TCR, a process termed TCR triggering, is also controversial. There are several proposed models that can be divided into three groups depending on whether they invoke aggregation, conformational change, or segregation of the TCR (Choudhuri et al., 2005; Choudhuri and van der Merwe, 2007; van der Merwe, 2001). Understanding which TCR-pMHC binding properties determine the potency of pMHC will improve our understanding of the molecular processes that accompany TCR triggering and place constraints on TCR triggering models.

The ability to predict the potency of pMHC based on the TCR-pMHC bond parameters will assist in the rational design of antitumor peptide vaccines, because many tumor-specific antigens provoke only weak immune responses that are incapable of eliminating all tumor cells. One well-studied tumor-associated protein is NY-ESO-1 (Chen et al., 1997), which is presently a candidate antigen for antitumor vaccines being developed to enhance immune responses against a variety of tumors. One of the most immunogenic HLA-A2-restricted peptides derived from the NY-ESO-1 protein is NY-ESO-1_157-165 (ESO-9C peptide) (Jäger et al., 1998). However, immune responses initiated by the peptide are still not sufficient for complete tumor elimination, possibly because of its instability (see below). The design of NY-ESO-1_157-165 altered peptide ligands (APLs) that induce a better antitumor response could have important therapeutic benefits (Apostolopoulos et al., 2000; Chen et al., 2005; McMahan et al., 2006; Webb et al., 2004).

The majority of published data supports either kinetic or affinity models of pMHC potency. Kinetic models (Kalergis et al., 2001; Kersh et al., 1998; McKeithan, 1995) propose that a productive signal is transduced by the TCR provided it remains bound to pMHC for a minimum period of time. For example, the kinetic proofreading model postulates that a series of biochemical modifications accumulate at the bound TCR that are lost upon pMHC dissociation. A productive signal is transduced only if the pMHC remains bound long enough to allow the TCR to reach a critical modification. Direct and indirect support for the model has come from studies that have shown good correlation between the T cell response and the TCR-pMHC bond off rate (k_off) (Carreño et al., 2007; Kalergis et al., 2001; Kersh et al., 1998; Krogsgaard et al., 2003; Qi et al., 2006). The affinity model postulates that the total number of TCR-pMHC complexes formed at equilibrium is the primary determinant of the T cell response. In support of this model, a number of studies reported correlations between the TCR-pMHC dissociation constant (K_D), but not k_off, and the T cell response (Andersen et al., 2001; Boulter et al., 2007; Holler and Kranz, 2003; McMahan et al., 2006; Tian et al., 2007).

Many of the studies supporting the affinity and kinetic models of pMHC potency include examples of discrepancies in the correlations they report (al-Ramadi et al., 1995; Baker et al., 2001; Hudrisier et al., 1998; Krogsgaard et al., 2003). Several factors may account for these discrepancies. First, the majority of studies were performed with small numbers of pMHC agonists, limiting the reliability of observed correlations. Second, assays of T cell activation were performed by stimulating cells with various pMHC without always fully controlling for differences in peptide processing, loading, and stability. Third, solution binding parameters were mainly measured at 25°C rather than 37°C, the relevant temperature at which functional assays are performed. Fourth, TCR-pMHC solution binding or three-dimensional (3D) binding properties might be different compared to functionally relevant membrane or two-dimensional (2D) binding properties, where both pMHC and TCR are immobilized to surfaces. In such a constrained environment, the likelihood of protein rebinding after chemical dissociation is greatly enhanced, which would probably have a large impact on its 2D k_off. Finally, variations in measured TCR-pMHC bond affinity in the majority of studies result mostly from differences in k_off rather than k_on, potentially masking the importance that k_on may have in T cell activation.

In order to explore which binding properties determine pMHC potency, we have performed a detailed study of 1G4 TCR (Chen et al., 2005) binding to a large set of various NY-ESO_157-165 altered peptide ligands in complex with either wild-type or mutated HLA-A2. In separate experiments, we analyzed the activation of the 1G4 cytotoxic T lymphocyte (CTL) clone (from which the 1G4 TCR was isolated) by either immobilized pMHC or peptide-pulsed APCs, precisely controlling for equal pMHC presentation. Detailed statistical analysis reveals that models of T cell activation based solely on K_D or k_off do not robustly fit the data. However, a model based on the postulated confinement time of the TCR-pMHC interaction explains our data set. The proposed model reduces to simpler models dependent solely on K_D or k_off in certain limits, and therefore reconciles observations from previous reports.

Results

Analysis of Binding Properties of 1G4 TCR Interaction with NY-ESO_157-165 APLs and HLA-A2 Mutants

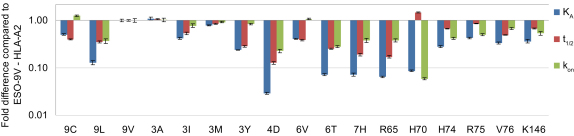
We first designed various NY-ESO_157-165 APLs and HLA-A2 mutants that bind to 1G4 TCR with a wide range of binding characteristics. It has been demonstrated that a substitution of the highly unstable cysteine amino acid to valine (ESO-9V) or leucine (ESO-9L) at the anchor position 165 of NY-ESO_157-165 improves loading efficacy of peptide onto HLA-A2 and its subsequent immunogenicity (Chen et al., 2000). We produced a set of ESO-9V APLs by substituting amino acids at the positions 3, 4, 5, 6, 7, and 8 in the peptide. In addition, we have generated a set of HLA-A2 variants with various mutations within the 1G4 TCR binding “footprint” (Chen et al., 2005) (R65, H70, H74, R75, V76, K146). The affinity, kinetics, and thermodynamics of 1G4 TCR binding to 17 pMHC variants (APLs and HLA-A2 mutants) were analyzed by SPR at 37°C (Figure 1; Figure S1 and Table S1 available online).

Figure 1.

Binding Properties of 1G4 TCR Interaction with pMHC Variants

Binding affinity and kinetics of 1G4 TCR interaction with a range of ESO-9V-HLA-A2 variants was measured at 37°C by SPR (see Figure S1). Effect of peptide or HLA-A2 amino acid substitution on 1G4 TCR binding affinity and kinetics is presented as a fold difference compared to ESO-9V-HLA-A2. Substitutions that negatively affected 1G4 TCR binding have relative affinities and kinetics lower than 1. Values shown are the mean ± SEM of at least three independently performed experiments.

Activation of 1G4 CTLs by Immobilized or Cell-Presented pMHCs

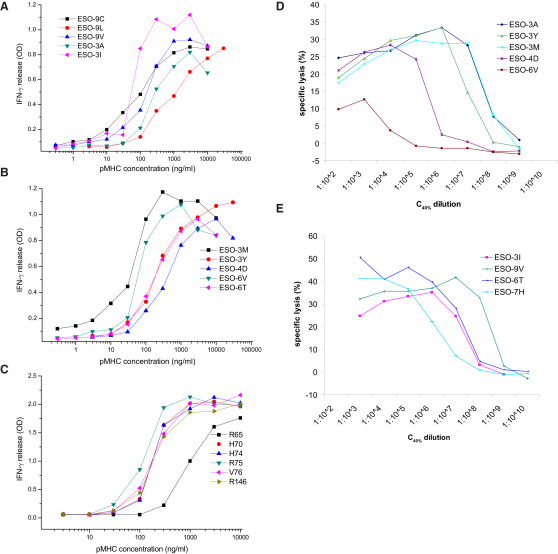
pMHC immobilized to planar surfaces is often used as an alternative to cell-based assays for T cell activation and is a potent inducer of many T cell functions (González et al., 2005; Krogsgaard et al., 2003). An important advantage of this assay is that the pMHC dose is independent of peptide affinity for MHC and can be precisely controlled. Activation of 1G4 CTLs by pMHC variants was analyzed by measuring interferon-gamma (IFN-γ) secretion by cells stimulated by graded concentrations of pMHCs (Figures 2A–2C). The activation potency (EC₅₀) of pMHCs was determined from the pMHC concentration that stimulated half-maximal IFN-γ secretion (Table S1). To control for variation in pMHC stability and concentration, the amounts of immobilized pMHC were measured with a conformation-sensitive antibody (Figures S2A–S2C).

Figure 2.

Functional Response of 1G4 T Cells to pMHC Variants

(A–C) IFN-γ release from 1G4 CTLs stimulated by plate-bound pMHC variants. 1G4 CTLs were cultured for 4 hr in 96-well plates coated with indicated concentrations of pMHC variants. Supernatants were collected and secreted IFN-γ was measured by ELISA. One of at least three independently performed experiments is shown.

(D–E) Cytotoxic response of 1G4 CTLs to NY-ESO_157-165 peptide variants. A 1:1 ratio of 1G4 CTLs and ⁵¹Cr-labeled T2 cells were pulsed with the indicated peptide dilutions starting from the concentration shown in previous experiments (Figure S2D) to give a 40% increase in surface HLA-A2 expression (C_40%) on T2 cells. After 4 hr incubation at 37°C, specific lysis of T2 cells was analyzed by measuring released ⁵¹Cr. One of at least three independent experiments is shown.

Although functional assays with plate-bound pMHC allow precise control of the amounts of ligand, they have the disadvantage of being unphysiological. We therefore also investigated the stimulatory effect of ESO-9V APLs in a more physiological, cellular context by performing a cytotoxicity assay. As target cells we used the transporter associated with antigen processing (TAP)-deficient T2 cell line (Cerundolo et al., 1990) pulsed with various ESO-9V APLs, precisely matching for surface pMHC expression (Figures 2D and 2E). The relative potency (EC₅₀) of peptides was determined from the dilution of peptide resulting in half-maximal lysis of target cells (Table S1).

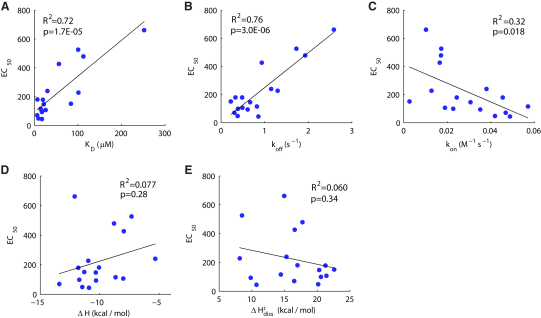
We next explored which of the measured binding parameters governing the TCR-pMHC interaction are the best predictors of the T cell response. Correlations between pMHC potency in inducing T cell responses and 17 binding parameters (not all of which are independent) are shown in Table 1, a subset of which are plotted in Figure 3. We found significant correlations (R² > 0.7, p < 0.01) only with K_D (Figure 3A), k_off (Figure 3B), and parameters derived from these measurements (e.g., ΔG, ΔG^‡_diss). There was a weak correlation with k_on (Figure 3C) but no correlation with enthalpy change (Figure 3D) or activation enthalpy change of dissociation (Figure 3E), the significance of which is discussed below. Thus we found in two different functional assays that pMHC potency correlates with both K_D and k_off.

Table 1.

Correlation between pMHC Potency and TCR-pMHC Binding Parameters

TCR/pMHC Bond Parametera	IFN-γ Release (EC50)b		Cytotoxicity (1/log(EC50))b
	R2	p Value	R2	p Value
KD	0.719	1.70E-05	0.882	1.70E-04
koff	0.776	3.04E-06	0.960	3.73E-06
t1/2	0.358	0.0111	0.652	0.0085
kon	0.320	0.0179	0.633	0.0103
1/kon	0.012	0.6735	0.709	0.0044
ΔG	0.624	0.0002	0.746	0.0027
ΔH	0.077	0.2812	0.006	0.8424
-TΔS	0.001	0.9064	0.044	0.5901
ΔC	0.221	0.0569	0.110	0.3826
ΔG‡diss	0.462	0.0027	0.603	0.0138
ΔH‡diss	0.060	0.3443	0.108	0.3884
-TΔS‡diss	0.036	0.4666	0.070	0.4921
ΔC‡diss	0.047	0.4055	0.058	0.5327
ΔG‡ass	0.202	0.0700	0.127	0.3469
ΔH‡ass	0.098	0.2219	0.030	0.6539
-TΔS‡ass	0.012	0.6793	0.082	0.4544
ΔC‡ass	0.075	0.2891	0.034	0.6360

^aMeasured EC₅₀ values are correlated to various TCR-pMHC bond parameters via data fitting in Matlab. Standard methods are used to calculate the R² statistic, which is the square of the correlation coefficient for these simple models, and p values are obtained with an F-test. Details can be found in the Supplemental Information. The quality of the fit for several bond parameters is shown in Figure 3.

^bWe use the reciprocal of EC₅₀ for the cytotoxicity assay because it is obtained from a dilution curve. We take the log to account for effects of nonlinear loading of peptide to APCs. The use of EC₅₀ in both assays is discussed in the Supplemental Information.

Figure 3.

Correlation between T Cell Response and TCR-pMHC Binding Properties

Correlations are shown between pMHC potency, represented by the concentration stimulating half-maximal IFN-γ secretion (EC₅₀), and (A) the TCR-pMHC bond dissociation constant (K_D), (B) the bond off rate (k_off), (C) the bond on rate (k_on), (D) the change in enthalpy (ΔH), and (E) activation enthalpy of dissociation (ΔH^‡_diss). Table 1 contains correlations with additional thermodynamic parameters. Significant correlations (p < 0.05) are found only for K_D, k_off, and k_on and other parameters that are directly derived from these. The R² statistic is the square of the correlation coefficient for these simple models and p values are computed with an F-test. Both quantities are calculated in Matlab with standard methods; see Supplemental Information for details.

Removing Bias by Subset Analysis

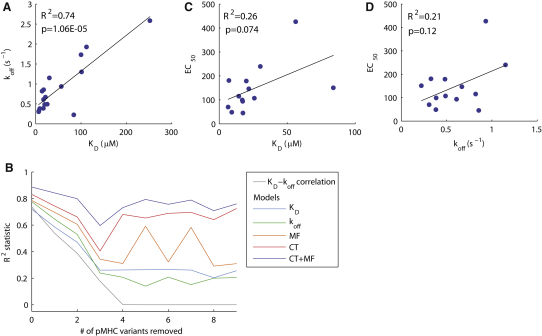
The T cell response correlated well with both K_D and k_off when examining the entire data set (Table 1, Figures 3A and 3B). However, the correlation between K_D and k_off is strong (R² = 0.73) among the pMHC variants used in the present study (Figure 4A) as the k_on varied somewhat less than the k_off (Figure 1). This made it difficult to resolve whether K_D or k_off determine potency or to identify a contribution from k_on. In order to investigate the contribution of k_on, we extracted subsets of the entire data set (17 pMHC variants for IFN-γ assay) that contain fewer pMHC variants selected to minimize the correlation between K_D and k_off and thus maximize the variation in k_on. When more than two peptides were removed, the correlation between K_D and k_off rapidly approached zero (Figure 4B). Next, we fitted both K_D and k_off models to these subsets (see Experimental Procedures). Surprisingly, we found that both exhibited a poor fit (reduced R² value) as the correlation between K_D and k_off was reduced and the variability in k_on increased (Figure 4B). This is illustrated by the poor fits of both K_D and k_off for the subset of 13 pMHC variants (Figures 4C and 4D). In Table 2 we summarize the fits (R² statistic) and their significance (p value). It is evident that once three or more pMHC variants are removed, neither K_D nor k_off correlate significantly with pMHC potency (p > 0.05).

Figure 4.

Analysis of Model Fitting to Data Subsets with Larger Variability in the On Rate

(A) The 17 pMHC variants that comprise the entire data set exhibit a large correlation between K_D and k_off (R² = 0.74). By systematically removing a fixed number of pMHC variants, we identified the subset that minimized the K_D-k_off correlation. For example, we calculated the correlation for all 17 possible subsets of 16 pMHC variants and selected the subset with the smallest K_D-k_off correlation.

(B) The square of the K_D-k_off correlation as a function of the number of pMHC variants removed for the subset with the smallest correlation. In this way, we generated data sets with lower K_D-k_off correlations and hence larger variability in the on rate. Also shown in (B) is the R² statistic for fits of the K_D, k_off, molecular flexibility (MF), confinement time (CT), and the combined model (MF+CT) to all subsets considered. Computations for subsets consisting of less than eight pMHC variants did not provide reliable results because the number of parameters approached the number of data points.

(C and D) The correlations of pMHC potency with K_D and k_off for the subset of 13 pMHC variants (i.e., when 4 pMHC variants are removed). See Figure 5 for correlations with other models. In Table 2 we report the p values associated with each fit, showing that when removing more than two pMHC variants, correlations with K_D and k_off are not significant (p > 0.05). Also shown in Table 2 are p values associated with an F-test that determines whether the additional parameter(s) in the CT, MF, and combined model is significant. The fitted parameters from each model are listed in Table S2.

Table 2.

Analysis of Model Fitting to Data Subsets

pMHCs Removeda	KD - koff Correlation	Goodness-of-Fit Statisticsb										F-Test for Model Comparisonc
		KD		koff		CT		MF		CT+MF		CT/KD	CT/koff	MF/koff	CT+MF/CM	CT+MF/MF
	R2	R2	p	R2	p	R2	p	R2	p	R2	p	p	p	p	p	p
0	0.74	0.72	1.70E-05	0.78	3.04E-06	0.83	3.94E-06	0.78	2.14E-05	0.89	2.12E-06	0.009	0.051	0.461	0.026	0.005
1	0.54	0.59	0.0005	0.65	0.0002	0.74	0.0001	0.70	0.0004	0.84	4.31E-05	0.014	0.043	0.166	0.019	0.006
2	0.39	0.47	0.0048	0.53	0.0021	0.66	0.0015	0.61	0.0038	0.80	0.0004	0.023	0.052	0.155	0.019	0.008
3	0.18	0.26	0.0621	0.24	0.0763	0.40	0.0577	0.34	0.0993	0.60	0.0235	0.131	0.108	0.213	0.054	0.031
4	1.2E-03	0.26	0.0738	0.21	0.1187	0.68	0.0034	0.31	0.1563	0.73	0.0062	0.005	0.003	0.249	0.224	0.005
5	1.0E-04	0.26	0.0876	0.14	0.2309	0.65	0.0085	0.59	0.0177	0.79	0.0041	0.011	0.005	0.012	0.048	0.024
6	4.4E-07	0.27	0.1050	0.21	0.1588	0.69	0.0095	0.32	0.2112	0.76	0.0150	0.011	0.008	0.279	0.205	0.010
7	1.2E-07	0.26	0.1313	0.15	0.2666	0.69	0.0157	0.58	0.0468	0.79	0.0191	0.016	0.010	0.031	0.156	0.053
8	1.5E-09	0.20	0.2229	0.20	0.2271	0.64	0.0463	0.29	0.3561	0.71	0.0833	0.035	0.035	0.414	0.332	0.044
9	6.3E-07	0.26	0.2004	0.20	0.2602	0.72	0.0400	0.31	0.3965	0.76	0.0994	0.033	0.028	0.424	0.486	0.052

^aThe first row corresponds to the entire data set of 17 pMHC variants and the last row, where nine pMHC are removed, corresponds to the subset of eight pMHC variants. Each subset represents the set of pMHC variants that minimize the K_D-k_off correlation. See Results and Figure 4 for details on subset analysis. The quality of the fit for K_D and k_off models are shown in Figures 3A and 3B (entire data set) and Figures 4C and 4D (subset of 13 pMHC variants).

^bR² and p values are calculated based on the quality of the fit and the number of free parameters for each model (see Experimental Procedures for details). Abbreviations: CT, confinement time model; MF, molecular flexibility model; CT+MF, combined confinement and flexibility models. The quality of the fit for the CT, MF, and CT+MF models are shown in Figure 5 for the entire data set (B, D, F) and for the subset of 13 pMHC variants (C, E, G).

^cF-test provides a p value for the null hypothesis that the simpler model (with fewer parameters) is sufficient to explain the data. Simpler models are shown after the slash. Details are provided in the Experimental Procedures.

The nine APLs used in the cytotoxicity assay also exhibited a large K_D-k_off correlation (R² = 0.89). However, it was not possible to perform the subset analysis because of the limited amount of data. Correlations for these nine APLs with IFN-γ release were similar to the cytotoxicity assay (not shown). Thus, pMHC potency cannot be described by either k_off or K_D for the present data set.

Importance of the TCR-pMHC Bond k_on in a Model of Confinement Time

The observation that the basic K_D and k_off models fit poorly when k_on varies suggested that k_on is an important determinant of the T cell response, which is consistent with the weak correlation that we observed with k_on (Figure 3C). Motivated by these observations and recent experimental work (Tolentino et al., 2008), we investigated a simple model whereby rapid rebinding of a TCR to the same pMHC molecule counters the effects of membrane diffusion (or transport), effectively confining TCR-pMHC, as schematically presented in Figure 5A. In this confinement time model, we can calculate the total time the TCR will be in complex with the same pMHC (integrated across multiple rebinding events) as T_c = (k^∗_on + k₋)/(k₋k_off) and the total time the TCR will be unbound but within the reaction radius (i.e., binding range) of the pMHC as T_f = 1/k₋. In these equations, k^∗_on (in units of s⁻¹) is the intrinsic localized on rate between a single TCR-pMHC pair and is related to the solution on rate by a multiplicative factor (see Experimental Procedures), and k₋ (in units of s⁻¹) is the rate at which TCR-pMHC move (diffuse) apart. With reasonable parameters we found that T_c > > T_f (see Experimental Procedures), indicating that the total time that TCR and pMHC are confined to one another is determined by T_c. The reciprocal of T_c determines an effective off rate (k^∗_off) that captures the rate at which TCR and pMHC move apart,

$$k_{off}^{\ast }=\frac{1}{T_c}=k\text{\_}{k}_{off}/(k_{on}^{\ast }+k_{-})\text{.}$$

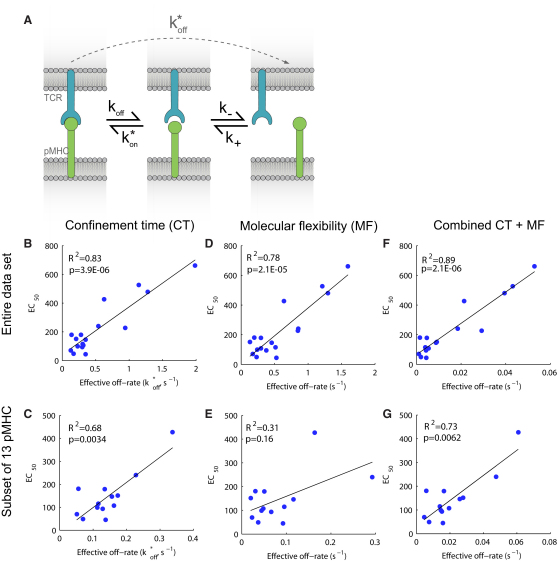
Figure 5.

Correlation of pMHC Potency with Effective Off Rates

(A) Model of TCR-pMHC confinement by rebinding. We used a mathematical model that accounted for a TCR-pMHC bound state (left), unbound but in physical proximity state (center), and a state where TCR and pMHC have moved apart (right). The rate of chemical dissociation is k_off and the rate of association is k^∗_on that is a first order rate, in units of s⁻¹, that depends on the macroscopic on rate k_on. When chemically dissociated (center), TCR-pMHC may move apart via diffusion or transport with a first order rate k₋. We propose that the potency of pMHC is governed by the amount of time it is confined to the TCR. The effective off rate to go from bound (left) to complete dissociation (right), given that potentially many rebinding events may take place, is given by k^∗_off = (k₋k_off)/(k^∗_on + k₋).

(B–G) The panels show fits of the confinement time (CT), molecular flexibility (MF), and the combined (CT+MF) models to the entire data set (B, D, F) or the subset of 13 pMHC variants (C, E, G). The abscissa represents the effective off rate from each model. In the case of the confinement time model, it is (b₂k_off)/(k_on + b₂), where b₂ is a fitted parameter. In the case of the molecular flexibility model, the abscissa is k_offexp(b₂ΔC_p), where b₂ is a fitted parameter. See Experimental Procedures for details on data fitting and representation of effective off rates.

This expression reflects the rate of unbinding and the probability of moving apart before rebinding. A full description of the model can be found in Experimental Procedures.

In certain limits, the confinement time model reduces to the basic models. When the intrinsic on rate is large compared to the diffusive rate (k^∗_on > > k₋), the confinement time is directly proportional to K_D (k^∗_off = k₊K_D). In contrast, when k^∗_on < < k₋, the effective off rate is simply k^∗_off = k_off because TCR-pMHC move apart without rebinding. Measurements of binding constants represent intrinsic rates because experiments were performed in a flow chamber (BIAcore) under conditions that minimize rebinding events. In other words, dissociation in the flow chamber leads to transport rather than localized rebinding.

In Figure 5B we showed the results of fitting the confinement time model to the entire data set. We found an improved correlation (R² = 0.83) compared to the basic models of K_D and k_off. Next, we fitted the confinement time model to the pMHC variant subsets described in the previous section and found that the R² statistic remained large for all subsets (Figures 4B and 5C for the 13 pMHC subsets). In contrast to the K_D and k_off models, we found that the confinement time model remained significant (p < 0.05) for all except one subset of the data (Table 2).

Potential Effects of Molecular Flexibility

It has been previously proposed that the heat capacity is important in relating the solution k_off to the physiological membrane k_off because heat capacity reflects molecular flexibility, and this may affect the dissociation rate of membrane-tethered molecules (Krogsgaard et al., 2003; Qi et al., 2006). This molecular flexibility model, as applied to the present data, predicts that the T cell response will be related to k_offexp(bΔC_p), where b is a constant (see Experimental Procedures for details on data fitting). Shown in Figure 5D are the results of fitting the molecular flexibility model to the entire data set. We find a small improvement in the R² statistic compared to a model of k_off alone (Figure 3B). Moreover, performing the subset analysis (Figures 4B and 5E and Table 2), we observed improved R² values for only two data subsets (five or seven pMHC variants removed).

The processes of molecular flexibility and confinement time are not mutually exclusive. We therefore formulated the combined model and performed data fitting (see Experimental Procedures). The combined model depends on k_off, k_on, and ΔC_p and has four free parameters. In Figure 5F we plot the results of data fitting to this model by using the entire data set and find, as expected, an improved fit (R² = 0.89). Results from the subset analysis can be seen in Figure 4B and Table 2 and are visualized for the 13 pMHC subsets in Figures 5E and 5G for the molecular flexibility and the combined model, respectively. Thus, the molecular flexibility model does not account for the potency of the pMHC variants in this system.

A Statistical Test for Model Comparisons Reveals the Importance of the Confinement Time Model

It is not surprising that the confinement time (three free parameters), molecular flexibility (three free parameters), and combined models (four free parameters) exhibit improved R² values compared to the simple models of K_D and k_off (two free parameters). In order to determine whether the increase in the quality of the fit, as reported by an increase in R², is not simply due to an increase in the number of free parameters, we performed an F-test for nested models. This statistical test provides a p value for the null hypothesis that the simpler model is sufficient to explain the data (Motulsky and Christopoulos, 2004) (see Experimental Procedures). In Table 2 we report p values based on this statistical test. A p value below 0.05 indicates that the model with more parameters significantly improves the fit. We found that the confinement time model provided a statistically significant (p < 0.05) improvement in the fit compared to the simple models of K_D and k_off, with the exception of three subsets. In contrast, the molecular flexibility model significantly improved the fit (compared to the basic k_off) only for the subsets with five or seven pMHC variants removed. The combined confinement time and molecular flexibility model (four free parameters) was a better descriptor of the data (p < 0.05) compared to molecular flexibility alone but only in some instances did it significantly improve the fit compared to the confinement time model.

In summary, we find that the confinement time model provides a more robust description of the data than does the molecular flexibility model. However, a combination of the two models is also able to improve the fit in some circumstances.

Discussion

In our study we have determined the functional response of 1G4 CTLs to a panel of 17 pMHC variants consisting of APLs and HLA-A2 mutants. With this large data set, we have found that pMHC potency is not well correlated to either K_D or k_off when examining data subsets with larger variability in k_on. We found that a model of TCR-pMHC confinement time provided consistently larger correlations than did alternative models. By using rigorous statistical analysis (an F-test for nested models), we have shown that these improved correlations are not simply due to the addition of extra fitting parameters.

Our study differs from previous studies in that it examines a larger number of pMHC variants with a wide variation in k_on, enabling us to clarify the role of k_on in pMHC potency. Most previous studies are nevertheless consistent with, and therefore support, our proposed confinement time model. For example, in a study in which the k_on varied little or much less than the k_off, it was found that the pMHC potency correlates with both k_off and K_D (Chervin et al., 2009). Other studies have reported a correlation between pMHC potency and either K_D (Andersen et al., 2001; Boulter et al., 2007; Holler and Kranz, 2003; McMahan et al., 2006; Tian et al., 2007) or k_off (Carreño et al., 2007; Kalergis et al., 2001; Kersh et al., 1998; Krogsgaard et al., 2003; Qi et al., 2006). This apparent conflict can be reconciled because the confinement time model reduces to the k_off or K_D models under certain conditions. When there is little rebinding (k_on is small), then k^∗_off approaches k_off, whereas if rebinding is frequent (k_on is large), then k^∗_off approaches K_D. In agreement with this, in studies where TCR-pMHC interactions had a large k_on (>10⁵ M⁻¹s⁻¹), pMHC potency correlated well with K_D (Holler and Kranz, 2003; Tian et al., 2007), whereas in studies where TCR-pMHC interactions had a small k_on (∼10³ M⁻¹s⁻¹), pMHC potency correlated well with k_off (Krogsgaard et al., 2003). In the present study, the k_on values were intermediate (∼10⁴ M⁻¹s⁻¹), providing an explanation as to why the full TCR-pMHC confinement time model, but not the reduced models, provided the best description of the data. In conclusion, the confinement time model reconciles, and is supported by, previously conflicting reports of the determinants of pMHC potency.

Two independent lines of evidence support a confinement time model. First, there is evidence that interactions at the cell-cell interface have longer half-lives than predicted from measurements in solution (Grakoui et al., 1999; Tolentino et al., 2008). Fluorescence recovery after photobleaching (FRAP) experiments have demonstrated that the effective exchange lifetime of a CD2-CD58 interaction in the membrane is 100 times longer than the lifetime measured in solution (Tolentino et al., 2008). Given that the intrinsic half life of a membrane-tethered interaction would be expected to be shorter because it is subjected to mechanical forces (Bell, 1979), this suggests that immediate rebinding after dissociation must be occurring. In agreement with this observation, we find that the calculated k^∗_off of TCR-pMHC interaction (∼0.1 s⁻¹) is 10 times slower than the k_off measured in solution (∼1 s⁻¹). We note that several factors, such as remodeling of cellular protrusions and thermal fluctuations that alter the intermembrane separation, will exert a mechanical force on the TCR-pMHC bond and therefore increase the TCR-pMHC k^∗_off. Therefore, the estimate of k^∗_off is probably a lower limit and the actual k^∗_off may be larger. Direct measurements of TCR-pMHC bond k^∗_off at cell-cell interfaces will inform on these aspects. A second line of evidence supporting the confinement time model is the finding by several groups that increasing the mobility of pMHC on the cell surface inhibits T cell antigen recognition (Luxembourg et al., 1998; Segura et al., 2008; Wettstein et al., 1991). The confinement time model can account for this hitherto unexplained finding because it predicts that an increase in pMHC mobility will decrease rebinding and therefore increase the effective k_off.

It has been pointed out that the TCR-pMHC interaction, like all interactions at a cell-cell interface, would be subjected to mechanical forces, raising the possibility that the mechanical strength of TCR-pMHC interaction might be an important determinant of pMHC potency (van der Merwe, 2001). More recently it has been proposed that a mechanical pulling force exerted by pMHC binding could induce a conformational change in TCR-CD3 complex that could contribute to TCR triggering (Choudhuri and van der Merwe, 2007; Ma et al., 2008). It has been suggested that the activation enthalpy of dissociation (ΔH^‡_diss) should correlate with mechanical strength, since, according to transition state theory, it is a measure of the number of bonds that must be broken during dissociation (Leckband, 2000), although this remains to be proven. For this reason, we have analyzed transition state thermodynamics and determined the ΔH^‡_diss for 1G4 TCR interaction with the pMHC variants. However, we failed to find a correlation of T cell activation with ΔH^‡_diss alone or in combination with any other binding characteristic (not shown). Because it remains unclear what, if any, solution binding parameter(s) correlate(s) precisely with mechanical strength, direct measurements of the mechanical properties of TCR-pMHC interactions (e.g., by atomic force microscopy) are probably required to elucidate the role of mechanical forces in TCR triggering and T cell activation.

The molecular flexibility model (Qi et al., 2006) proposes that for some, conformationally flexible TCR-pMHC interactions, immobilization in the membrane may increase the TCR-pMHC bond lifetime compared to solution measurements. The model predicts a simple relationship between the solution and membrane lifetime that depends on ΔC_p. We did not find substantial effects of molecular flexibility for the data set in the present study. We note, however, that structural studies indicate that the 1G4 TCR undergoes only minor conformational changes during binding to 9V-ESO-HLA-A2 (Chen et al., 2005). In addition, the ΔC_p values, which range from −0.37 to −0.70 kcal/mol K, are much smaller and less variable than those previously reported by Krogsgaard et al. for the 2B4 TCR (Krogsgaard et al., 2003; Qi et al., 2006). Therefore, the importance of molecular flexibility (and ΔC_p) may vary between different TCR-pMHC systems and is hence an important topic for future investigation.

The observation that pMHC potency is determined by the confinement time of TCR-pMHC has implications for models of pMHC detection and discrimination. This finding implies that the signaling state of the TCR persists during brief chemical dissociation events. The consequence of this signal persistence is that pMHC detection is based on a threshold in the confinement time and therefore, discrimination is based on both k_on and the k_off. Moreover, the ability of a T cell to discriminate between weak and strong agonist pMHC could be a result of a slower k_on rather than a faster k_off. A mathematical model that explicitly accounts for rebinding and signal persistence at the TCR confirms these observations and shows that, in certain parameter regimes, discrimination based on k_on can be just as sharp as k_off (Dushek et al., 2009). In addition, requiring pMHC with fast off rates to rebind TCR multiple times before productive signaling is initiated could act to reduce spurious signals generated by a high density of endogenous pMHC (fast off rates, small on rates) that are unlikely to rebind TCR.

As noted in the Introduction, the mechanism of TCR triggering remains controversial. Three main types of models have been proposed invoking conformation change, aggregation, or segregation of the TCR-CD3 complex upon pMHC engagement, and these mechanisms are not mutually exclusive (reviewed in Choudhuri and van der Merwe, 2007). Although our study does not directly address mechanisms of TCR triggering, our finding that T cell activation depends on the confinement time places important constraints on the details of these models. The key constraint is that the TCR signaling mechanism is not disrupted or interrupted when the TCR dissociates briefly between rebinding events. It follows that conformational change in the TCR-CD3 complex would either need to be stable between rebinding or there would need to be an early rapid modification that is stable between rebinding events but will be readily reversed after complete dissociation. In short, there is a requirement for some memory mechanism at the level of the TCR after chemical dissociation. To our knowledge no existing models of conformational change explicitly propose a memory mechanism.

The kinetic-segregation (K-S) model of TCR triggering posits that pMHC binding leads to confinement of the TCR-CD3 complex within close-contact zones deficient in tyrosine phosphatases and/or enriched in Src tyrosine kinases (Davis and van der Merwe, 1996). The confinement time model would not allow lateral TCR-CD3 diffusion out of close contact zones during the brief periods between rebinding events, so it is entirely compatible with the K-S model without any modifications. The essence of aggregation models is the induced proximity of TCR-CD3 complexes after pMHC engagement. In these models termination of signaling requires diffusion of TCR-CD3 complexes, and the confinement time model requires that there is no diffusion between rebinding, so it follows that aggregation models are also compatible with the importance of confinement time. It is noteworthy that either the aggregation or K-S mechanism could provide the “memory” necessary for conformational change models to be compatible with the confinement time model. Thus any model that combined the aggregation or segregation with conformational change would be compatible with confinement time model.

Protein interactions in the membrane environment are complex and dynamic and differ significantly from interactions in solution. Our model aims to capture the most important aspects of this complexity but it has to be mentioned that, although improved over simple models, correlation of T cell activation with confinement time calculated from the solution properties of the TCR-pMHC is not perfect. One possible explanation for this is that these solution measurements do not correlate perfectly with the actual binding properties of membrane-associated molecules. Direct measurements of 2D binding kinetics of membrane-associated TCR and pMHC are needed to address this point fully. Another possible explanation for this imperfect correlation is that conformational changes in the TCR are required for TCR triggering (Beddoe et al., 2009) and pMHC variants differ in their propensity to induce the required conformational change.

It is likely that coreceptor (CD8) binding to pMHC will increase the TCR-pMHC confinement time. If the contribution of coreceptors is similar for all pMHC variants, coreceptor binding may not affect the relationship between TCR-pMHC binding parameters and T cell activation. Our finding that confinement time correlated with pMHC potency in a system in which CD8 engagement occurs is consistent with this. Point mutations in HLA-A2 that disrupt CD8 binding strongly abrogate recognition by 1G4 T cells (Chen et al., 2005), rendering them unresponsive to low-affinity pMHC variants (K_D > 20 μM). Unfortunately this precluded an analysis of the contribution of CD8 to pMHC potency in this system because most pMHC variants have a low affinity.

In conclusion, we have demonstrated the importance of TCR-pMHC k_on in determining the outcome of T cell antigen recognition. We show that the dependence on k_on can best be accounted for by a confinement time model, in which there is repeated rebinding after TCR-pMHC chemical dissociation and the outcome of TCR engagement is dependent on the length of time until complete dissociation. Our model can account for previous, apparently contradictory, findings and provide an explanation for the hitherto unexplained dependence of TCR triggering on pMHC mobility. Although this confinement time model is compatible with existing aggregation or segregation models of TCR triggering, it requires modification of conformational change models to include a mechanism for “memory” between rebinding events.

Experimental Procedures

Surface Plasmon Resonance

Protein subunits of 1G4 TCR and HLA-A2 were expressed in E. coli, purified, and refolded in vitro, as described in Supplemental Experimental Procedures. Binding properties of 1G4 TCR interaction with ESO-9V pMHC variants were analyzed by SPR on a BIAcore 3000 (GE Healthcare Life Sciences, Little Chalfont Bucks, UK). Binding affinity was analyzed by measuring equilibrium binding of graded concentrations of 1G4 TCR to immobilized pMHC. Kinetic data were obtained by injecting 1G4 TCR over the immobilized pMHC and analysis of the dissociation phase curve fitting in BIAevaluation software. Binding thermodynamics was analyzed by measuring affinity and kinetics at the range of temperatures, calculating binding energy (ΔG and Δ^‡G_diss), and fitting data to the van't Hoff equation. Details of binding analysis by SPR can be found in Supplemental Experimental Procedures.

Assays for 1G4 CTL Activation by pMHC Variants

1G4 CTLs were stimulated by graded levels of plate-immobilized pMHC for 4 hr and levels of released IFN-γ was measured from the cell supernatant by ELISA. Cytotoxic response of 1G4 CTLs to various ESO-9V APLs was analyzed by incubating 1G4 CTLs with ⁵¹Cr loaded T2 cells pulsed with various ESO-9V APLs for 4 hr and measuring levels of released ⁵¹Cr from lysed T2 cells. Further details can be found in the Supplemental Experimental Procedures.

Model of TCR-pMHC Confinement Time

We capture the effect of TCR-pMHC confinement via the theory of diffusion-limited reactions on membranes (Lauffenburger and Linderman, 1993; Shoup and Szabo, 1982). The model can be represented as follows:

$$R+P\underset{k_{-}}{\overset{k_{+}}{\leftrightarrow }}F\underset{k_{off}}{\overset{k_{on}^{\ast }}{\leftrightarrow }}C,$$

where TCR (R) and pMHC (P) first form an encounter complex (F), where the two molecules are within physical proximity but chemically dissociated, and subsequently they may bind to form a TCR-pMHC complex (C). The diffusion-limited on rate (in units of μm²/s) is given by k₊ = 2πD/ln(b/s), where D is the diffusion coefficient, b is the mean distance between TCR, and s is the reaction radius (roughly the size of a TCR). The remaining microscopic rates (k_off, k^∗_on, k₋), on the scale of a single TCR-pMHC, are all first order (in units of s⁻¹) and are related to the experimentally measured macroscopic rates (see below). Assuming that TCR-pMHC are initially bound, we can calculate the mean time that the molecules will spend in each state before moving apart,

$$T_f=\frac{1}{k_{-}},$$

$$T_c=\frac{k_{on}^{\ast }+k_{-}}{k_{-}}\frac{1}{k_{off}},$$

where T_f and T_c are the time spent in the unbound (F) and bound (C) states, respectively, integrated across multiple rebinding events. The TCR-pMHC bond lifetime (1/k_off) is much larger than 1/k₋ (see below) and therefore T_c > > T_f, indicating that TCR-pMHC spend negligible time within physical proximity but chemically unbound. The total TCR-pMHC confinement time is then T = T_c, whose reciprocal gives an effective off rate describing the rate at which TCR-pMHC move apart, k^∗_off = 1/T (see Results). We note that a macroscopic model of pMHC confinement time to a cluster of TCR predicts that the confinement time is governed by K_D (Dushek and Coombs, 2008).

The rates in the model (k^∗_on, k_-) are first order because we are considering reactions between proteins in physical proximity and it is reasonable to assume that they are proportional to macroscopic parameters that are measured in experiments. The solution on rate (k_on) in units of M⁻¹s⁻¹ can be converted to a 2D membrane on rate (in units of μm²/s) by a confinement length (L) with a factor of 10¹⁵/(N_AL), where N_A is Avogadro's number. The 2D membrane on rate can be related to the intrinsic on rate (k^∗_on in units of s⁻¹) by the effective local TCR concentration (1 TCR in an area A = πs², where s is the previously defined reaction radius). We can therefore relate the experimentally measured solution on rate to the intrinsic on rate by a multiplicative factor, k^∗_on = σk_on where σ = 10¹⁵/(N_ALA). Assuming that diffusion is the primary determinant of the relative TCR-pMHC mobility, the rate at which TCR-pMHC move apart when unbound (k₋) is directly related to the diffusion-limited membrane on rate; k₋ = k₊/A. By using reasonable parameters (D = 0.05 μm²/s, s = 0.005 μm, b = 0.05 μm, and a TCR concentration of 100 μm⁻²), we calculated that k₊ ≈ 0.1 μm²/s and therefore 1/k₋ is several orders of magnitude smaller than 1/k_off, indicating that the TCR-pMHC confinement time is dominated by the time in the bound state (T_c > > T_f). The exact relationship between the intrinsic and macroscopic rates is not important for our conclusions.

Statistical Analysis and Model Fitting

The equations used to fit the five models we have focused on (Figure 4B) are as follows:

$${\text{y}=\text{b}}_0+{\text{b}}_1{\text{K}}_{\text{D}},$$

$${\text{y}=\text{b}}_0+{\text{b}}_1{\text{k}}_{\text{off}},$$

$${\text{y}=\text{b}}_0+{\text{b}}_1{\text{k}}_{\text{off}}/\left({\text{k}}_{\text{on}}+{\text{b}}_2\right),\text{Confinement}\text{Time}\left(\text{CT}\right)$$

$${\text{y}=\text{b}}_0+{\text{b}}_1{\text{k}}_{\text{off}}\exp \left({\text{b}}_2\Delta {\text{C}}_{\text{p}}\right),\text{Molecular}\text{Flexiblity}\left(\text{MF}\right)$$

$${\text{y}=\text{b}}_0+{\text{b}}_1{\text{k}}_{\text{off}}\exp \left({\text{b}}_3\Delta {\text{C}}_{\text{p}}\right)/\left({\text{k}}_{\text{on}}+{\text{b}}_2\right),\text{Combined}\text{CT}+\text{MF},$$

where y is the measure of pMHC potency (i.e., y = EC₅₀) and b_i are free parameters. All data fitting was performed with the Matlab function lsqcurvefit. Reported R² statistics and associated p values (calculated by an F-test) are computed with standard methods. The models we investigate contain different numbers of free parameters and therefore it is not possible to directly compare the R² statistic because additional parameters will always lead to larger R² values. To determine the significance of increased R² values in models with more parameters, we compute an F-score (Motulsky and Christopoulos, 2004):

$$F=\frac{\left(SS{R}_1-SS{R}_2\right)/\left(p_2-p_1\right)}{SS{R}_2/\left(n-p_2\right)}$$

where SSR is the sum squared residuals, p is the number of free or fitted parameters, and n is the number of data points. The subscript 1 refers to the simpler model with fewer parameters. A p value is computed based on the F-score from the F-distribution with (p₂ – p₁, n – p₂) degrees of freedom and is used to test the null hypothesis that the simpler model (with fewer parameters) is sufficient to explain the data (see Table 2).

Representation of Effective Off Rates

In order to explore the importance of TCR-pMHC confinement time, we performed data fitting with the effective off rate (y = b₀ + b′₁ k^∗_off). By using the definition of k^∗_off, we fitted the following equation: y = b₀ + b₁ k_off/(k_on + b₂). In this equation, b₁ = b′₁ k₋/σ and b₂ = k₋/σ. In order to visualize the quality of the fits, we have plotted results in terms of the effective off rate (see Figure 5), k^∗_off = b₂ k_off/(k_on + b₂), where b₂ is determined from the fit (see above). The effective off rate for the molecular flexibility model is simply k_off exp(b₂ ΔC_p), where b₂ is a fitted parameter.

Published online: February 4, 2010