Is Flanker-Based Inhibition Related to Age? Identifying specific influences of individual differences on neurocognitive variables

Abstract

Researchers frequently attempt to identify the specific neurocognitive processes that might be responsible for differences in performance associated with neurological status or other individual difference characteristics by administering two or more conditions of an experimental task to different groups of participants, and focusing on the group-by-condition interaction as the primary outcome of interest. Three limitations of this approach are discussed, and an alternative analytical method is proposed to overcome the limitations. The method is demonstrated in analyses of data from 10 cognitive tasks in two independent studies, including two flanker tasks which are often used to assess aspects of inhibition.

Neuropsychologists frequently contrast performance in two or more conditions hypothesized to differ in a single critical process in order to isolate effects of a specific theoretical process. When this strategy is applied to the study of individual or group differences, the primary interest is often on the interaction of task condition with the individual difference variable because a significant interaction is typically interpreted as evidence for the selective influence of the individual difference variable on a specific cognitive process. Variants of this general approach have frequently been applied with tasks such as the Stroop Color-Word Interference Test, the Trail Making test, the Flanker Test, and in contrasts of conditions in a variety of tasks (e.g., copy versus reproduce from memory, immediate versus delayed test). In each case, a discovery that individuals with a particular neurological disorder have a larger increase in time or errors than healthy individuals when the task includes an additional process would probably lead to an inference that the disorder selectively disrupted the added process.

Although widely used in neuropsychology and related disciplines, several issues related to measurement and analysis complicate the interpretation of results obtained with this analytical approach. One issue relevant to many individual difference comparisons is that a large number of neurocognitive variables are typically related to the individual difference variable of interest, and therefore it is important to determine whether results with new variables represent something distinct from what is already known. That is, a key question is the degree to which the individual differences on the target variable are unique, in the sense that they are statistically independent of relations that have already been established on other variables and abilities. Unless one can determine that the new results represent something different from what is already known, there is a risk that the same phenomena are being rediscovered with different labels, and that the research is not contributing to cumulative progress.

A second interpretational issue concerns the nature of the information that can be derived from contrasts between the performance measures in the two conditions. In a discussion of research on adult age differences in cognition, Salthouse and Coon (1994) distinguished between age-related effects of differential magnitude and unique age-related influences. They noted that methods such as analysis of variance (ANOVA) are primarily sensitive to effects of differential magnitude, and they suggested that different analytical methods, such as various forms of regression, should be used if the researcher was interested in determining whether the individual difference influences in one condition were statistically independent of the influences in another condition. This distinction is potentially important because a finding that group differences are larger in one condition than another does not necessarily imply that the groups differ with respect to the processes hypothesized to differ between conditions. For example, the absolute difference in performance between two conditions could be larger in a group with poorer baseline performance, and yet this could simply reflect a constant proportional relation in the two groups without any selective effects (e.g., Salthouse, 2000).

Finally, a third interpretational issue is that two or more indicators of performance are often available in each condition of the task, such as reaction time (RT) and a measure of accuracy, but the variables are typically analyzed separately, as though they were independent of one another. A problem with conducting separate analyses is that variations in performance could be manifested in different combinations of the two variables, as evident in tradeoffs between speed and accuracy. Although the speed-accuracy tradeoff phenomenon is well known, there is also a problem if the RT and error variables differ in the same direction across conditions, or across people, because quantitative comparisons become complicated, and difficult to interpret, when the effects can be manifested in two different variables but only one of the variables is analyzed, or the variables are examined in separate analyses. Solutions to this problem have been proposed, such as generating complete speed-accuracy functions (e.g., Pachella, 1974), conditional accuracy functions (e.g., Kliegl, Mayr & Krampe, 1994), or deriving parameters from a theoretical model of the relation between the two variables (e.g., Ratcliff, Thapar, & McKoon, 2001; Wagenmakers, van der Maas, & Grasman, 2007), but these procedures typically require a relatively large number of trials in each condition, and in some cases selection of a single measure from the function to represent overall performance can be somewhat arbitrary.

The current project employs several analytical procedures designed to address each of these issues. First, two methods of simultaneously considering RT and error information in the analyses were examined. The simplest method involves using one of the variables, in this case error rate, as a covariate in analyses of the other variable, RT. This method removes the linear effects of the controlled variable on the analyzed variable, with all subsequent analyses conducted on the residual variable. A second method is based on composite scores created by averaging the z-scores for the error and RT variables. Because the z-transformed RT and error variables have the same weighting in the composite scores, this method implicitly assumes that individual differences in the two variables are equally important. (If there were a sufficient number of trials in each condition, alternative methods could also be employed such as specifying a single latent construct influencing the error and RT variables for each condition, or specifying orthogonal condition and variable [i.e., RT or error] constructs. However, these methods were not feasible in the current studies because there were only 50 or 60 trials per condition in each task with relatively low error rates.)

The analytical approach can be extended to investigate individual differences on performance that are unique to one condition by first statistically controlling the variability in the measures of performance in the other condition. Within this type of model, direct relations of the individual difference variable in the second condition represent influences that are statistically independent of influences operating in the first condition. In other words, the variability in the performance measure from the first condition is regressed out of the performance measure from the second condition, such that individual difference influences are examined in the second condition residuals.

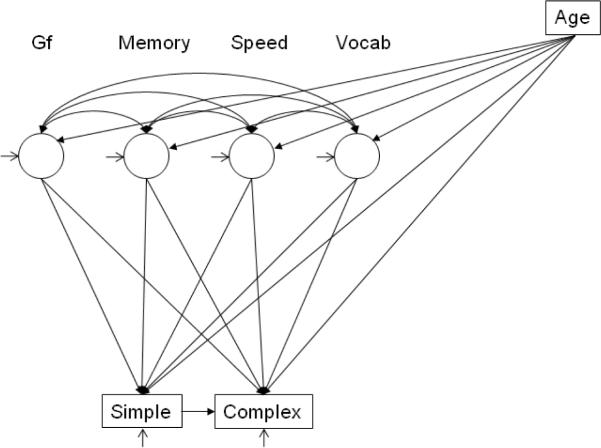
The approach can be further extended to examine individual differences on the target variables (or constructs) in the context of influences on other cognitive abilities by statistically controlling those other influences in the analyses. The resulting model is a variant of the contextual analysis model described in earlier publications (e.g., Salthouse, 2005; Salthouse, Pink & Tucker-Drob, 2008; Salthouse, Siedlecki & Krueger, 2006), and is portrayed in Figure 1. The lower portion of the figure indicates that performance in the complex condition is assumed to be partially influenced by performance in the simple condition. The top portion of the figure indicates that the individual difference influences, in this case those related to age, are examined in the target constructs while controlling any influences operating through established cognitive abilities.

Figure 1.

Illustration of the contextual analysis model. The observed variables in the target tasks, either RT or error rate, are represented by boxes. Circles represent latent constructs, with the variables listed in the appendix used to assess the reference cognitive abilities at the top of the figure. Simple and complex in the bottom of the figure refer to two different conditions (e.g., compatible and incompatible) which can be represented with methods discussed in the text.

Examination of Figure 1 reveals another advantage of the contextual analysis model, namely, that it is informative about the particular cognitive abilities that may be involved when performing the simple and complex versions of the task. That is, the relations from the reference cognitive ability constructs can be interpreted as representing the extent to which the target variable is influenced by, or dependent upon, different cognitive abilities. Note that because there are paths from age to both the reference constructs and the target variables, these relations are independent of the influences of age on any of the variables. In other words, partialling age-related influences from both the predictor reference constructs and the target variables effectively allows the predictor-target relations to be examined at the average age in the sample.

The reference constructs at the top of Figure 1 are defined by the variance shared across different cognitive variables postulated to represent the same cognitive ability. However, it is important to emphasize that the analytical method is not dependent on a specific set of reference variables or constructs because different combinations of variables could serve in this role. The particular cognitive ability constructs used in the current project were selected because they have been found to have statistically independent influences of age (e.g., Salthouse, 2005; Salthouse & Ferrer-Caja, 2003; Salthouse, et al., 2006; 2008), and each construct is based on three to six variables which all had good reliability and strong factor loadings.

Two different studies with independent samples of participants are described in the current report. The participants in Study 1 performed two versions of a flanker task (Eriksen & Eriksen, 1974), with compatible (simple) and incompatible (complex) conditions. Variants of this task are frequently used to assess the efficiency of inhibition because inhibition is assumed to be stronger when the incompatible flanking information can be inhibited, and the difference in performance (i.e., RT and error rate) between the conditions with compatible and incompatible information is smallest. In Study 2 the participants performed eight different cognitive tasks which each involved a simple condition and a more complex condition hypothesized to differ from the simple condition by a single cognitive operation. The tasks were designed to require different types of cognitive operations, but all involved relatively simple speeded decisions in two conditions, with performance in each condition assessed in terms of both RT and proportion of errors. The research participants in these studies consisted of adults across a wide age range, and therefore the individual difference variable of interest in the current project is age.

Analysis plan

Means and standard deviations for the RT and error measures in each condition of each task were initially computed, and then conventional analyses in the form of separate Age-by-Condition ANOVAs were conducted on the RT and error proportions in each task. Results of these analyses indicate whether, when the measures were considered separately, there were significant differences on the RT and error measures associated with age, task condition, or the interaction of age and condition.

The remaining analyses focused on the model portrayed in Figure 1, with four representations of performance in each condition based on error proportions, RTs, RT residuals after controlling the variance in the error proportions, and composite scores created by averaging the z-scores for the error proportion and RT variables. Model fit was evaluated with three fit statistics; the ratio of X² to degrees of freedom (df), the comparative fit index (CFI), and the root mean squared error of approximation (RMSEA). Lower X²/df ratios indicate better fit, and CFI values above .92 and RMSEA values below .08 are often considered to represent good fits (e.g., Kline, 2005).

The top portion of Figure 1 represents the structure of the reference cognitive abilities. The parameters of this portion of the model are the same across all tasks within a study involving the same sample of participants. The appendix contains the fit statistics for the cognitive reference ability measurement model in the two studies, as well as the loadings of the variables on the cognitive ability constructs. Also in the appendix is a brief description of the reference cognitive variables, with more details available in other publications (e.g., Salthouse & Ferrer-Caja, 2003; Salthouse, et al., 2006, 2008).

The middle portion of Figure 1 portrays the structural aspects of the model, which include relations of the reference cognitive abilities to the target constructs, relations of age to the reference cognitive abilities, and relations of age to the target constructs. Because all possible relations among age and the latent constructs are specified in the structural model, the primary determinants of overall model fit are the fits of the measurement models for the reference ability and target constructs.

The simple (compatible) and complex (incompatible) conditions in the target tasks in the bottom portion of Figure 1 were examined with different representations of performance in the two conditions. To provide a basis for comparison, separate analyses were initially conducted on the error and RT variables. The residual method assumes that the RT variable is of primary interest, and therefore the between-person relation between error rate and RT is used to adjust the RT variable for differences in error rate by removing the linear relation of the error variable from the RT variable. The composite method involves transforming each variable into z-scores based on the combined distribution across both conditions, and then averaging the two z-scores to create a composite score in each condition. Although seldom used with speed and error variables in speeded tasks, equal weighting to form composite scores is a common practice with scores obtained from different types of tests.

Study 1

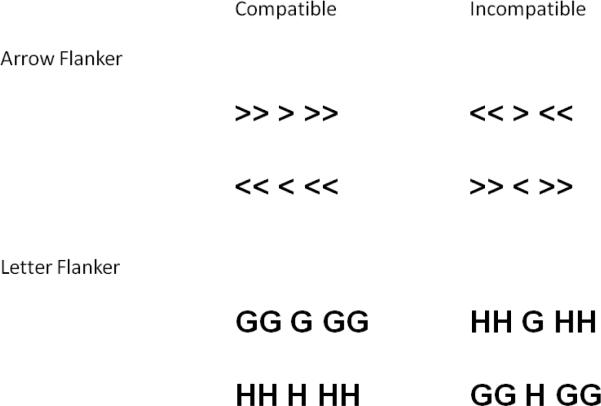
In this study two versions of the flanker task introduced by Eriksen and Eriksen (1974) were administered. Participants in these tasks are instructed to respond to the center target item and ignore adjacent (flanking) items which are either compatible or incompatible with the target. Figure 2 illustrates the types of displays for compatible (simple) and incompatible (complex) trials with the stimuli used in the two versions of the task employed in this study. The contrast of performance in the incompatible versus compatible conditions is often assumed to reflect aspects of inhibition or conflict resolution because RT is usually slower, and error rates higher, in the incompatible condition than in the compatible condition. Versions of this task have therefore frequently been used in research investigating individual differences in inhibition and aspects of executive functioning (e.g., Colcombe, Kramer, Erickson, & Scalf, 2005; Heitz & Engle, 2007; Hillman, Motl, Pontiflex, Posthuma, Stubbe, Boomsma, & de Geus, 2006; Hillman, Buck, Thamanson, Pontiflex, & Castelli, 2009; Kramer, Humphrey, Larish, Logan, & Strayer, 1994; Li & Dupois, 2008; Wild-Wall, Falkenstein, & Hohnsbein, 2008; Wylie, Ridderinkof, Eckerle, & Manning, 2006). The analytical methods described above can be used to determine whether there are unique individual differences in the more demanding, incompatible, condition, the extent to which these differences are statistically independent of individual differences on other cognitive variables, and the relations of established cognitive abilities with performance in each condition.

Figure 2.

Illustration of the stimuli used in the compatible and incompatible versions of the Arrow and Letter flanker tasks administered in Study 1.

Method

Participants

Demographic characteristics of the participants in Study 1, divided into three age groups for ease of description, are summarized in the top of Table 1. Participants were recruited from newspaper advertisements, flyers, and referrals from other participants, and they were paid for their time. All of the participants had Mini Mental Status Exam (Folstein, Folstein & McHugh, 1975) scores above 24, and the three age groups were generally similar with the exception of slightly higher levels of formal education with increased age.

Table 1.

Descriptive characteristics of the participants in the two studies

	Age Group
	18–39	40–59	60+	r(Age)
Study 1
N	62	89	114	NA
Age	27.0 (6.0)	51.2 (5.0)	72.6 (8.9)	NA
Proportion Female	.66	.74	.66	−.05
Self-Rated Health	2.1 (.8)	2.2 (.8)	2.2 (.8)	.12
Years of Education	15.2 (2.3)	15.6 (2.8)	15.6 (2.6)	.12
Scaled Scores
Vocabulary	12.1 (3.1)	11.5 (2.9)	12.0 (3.0)	.10
Digit Symbol	11.3 (3.2)	11.4 (3.3)	11.5 (3.2)	.09
Logical Memory	12.4 (2.9)	11.8 (2.9)	12.0 (3.0)	−.05
Word Recall	12.1 (3.8)	11.7 (3.5)	11.9 (3.4)	−.02
Study 2
N	56	85	83	NA
Age	25.8 (5.9)	51.6 (4.8)	70.0 (8.0)	NA
Proportion Female	.57	.73	.58	.02
Self-Rated Health	1.9 (0.9)	2.1 (0.9)	2.2 (1.0)	.13
Years of Education	14.8 (2.1)	15.6 (2.4)	16.1 (3.4)	.20*
Scaled Scores
Vocabulary	11.7 (2.6)	11.6 (2.8)	11.6 (2.7)	.01
Digit Symbol	10.4 (2.8)	10.6 (3.0)	11.5 (2.6)	.17
Logical Memory	11.8 (3.0)	11.3 (3.0)	11.5 (2.8)	.01
Word Recall	11.7 (3.1)	10.8 (3.4)	11.2 (3.0)	.00

^*p<.01

Note: Health was rated on a 5-point scale from 1 for “excellent” to 5 for “poor.” Scaled scores are age-adjusted scores from the Wechsler (1997a, 1997b) test batteries. In the nationally representative samples used to establish the norms for these tests, the age-adjusted scaled scores were designed to have means of 10 and standard deviations of 3. NA means that the statistic was not applicable.

Tasks

Two versions of the flanker task were administered in two separate sessions, with the arrow version always presented in the first session and the letter version always presented in the second session. (Different versions of the reference cognitive ability tasks were also performed on each session, but only the data from the first session were used in the contextual analyses.) The flanker tasks were identical except for the nature of the stimuli, which were either arrows (i.e., < or >) or letters (i.e., G or H). In the arrow version, the task was to press the appropriate key (“Z” for <, and “/” for >) as rapidly and accurately as possible. On 50% of the trials the flanking arrows were in the same direction as the center arrow (compatible), and on 50% of the trials the flanking arrows were in the opposite direction as the center arrow (incompatible). In the letter version, the task was to press the “Z” key for G and the “/” key for H as rapidly and accurately as possible. As in the arrow version, 50% of the trials had compatible flanker letters and 50% of the trials had incompatible flanker letters. Each task began with a short instruction phase followed by 20 practice trials and 100 experimental trials. The stimuli were displayed for 1500 msec unless a response was registered before that time had elapsed, in which case the stimuli were removed. The measures of performance in each condition were median RT for correct trials and the proportion of errors.

Results and Discussion¹

Separate ANOVAs were conducted on the RT and error rate measures in each task with age treated as a categorical variable based on the three groups described in Table 1. The top panel of Table 2 contains means and standard deviations for the RTs and error proportions, as well as results of separate Age-by-Condition ANOVAs on the RT and error proportion measures. There were significant main effects of age and condition on all measures in each task with the exception of the error measure in the Arrow task. The Age-by-Condition interaction was only significant (F[2,262] = 6.1) in the error measure in the Letter task.

Table 2.

Means for RT (in msec) and proportion of errors, and F-values for analyses of variance

	Means (SD)		ANOVA
	Simple	Complex	Age	Cond	Age-by-Cond
Study 1
Arrow Flanker
RT	560 (111)	615 (114)	51.9*	292.9*	2.0
Error	.03 (.11)	.09 (.19)	0.2	34.0*	0.4
Letter Flanker
RT	523 (89)	545 (91)	39.9*	137.2*	0.0
Error	.04 (.11)	.05 (.11)	1.0	44.3*	6.1*
Study 2
Embedded Letters
RT	1115 (256)	1775 (378)	48.1*	1528.7*	6.5*
Error	.02 (.03)	.05 (.09)	0.4	43.0*	0.3
Part Detection
RT	1010 (251)	1794 (433)	56.0*	1951.0*	26.2*
Error	.04 (.03)	.13 (.09)	6.4*	274.4*	7.8*
Symbol Integration
RT	1864 (593)	3780 (998)	48.0*	2168.4*	14.3*
Error	.04 (.05)	.21 (.08)	13.5*	1540.8*	12.8*
Pattern Integration
RT	2094 (634)	5043 (1245)	40.2*	1923.2*	6.5*
Error	.07 (.06)	.29 (.12)	4.0	1124.0*	14.6*
Plus 2
RT	1098 (297)	2844 (592)	31.8*	2302.4*	3.4
Error	.04 (.07)	.16 (.16)	7.6*	148.5*	4.8*
Pattern Rotation
RT	2030 (671)	4881 (1342)	31.4*	1405.0*	2.0
Error	.08 (.07)	.28 (.10)	5.3*	883.4*	4.7*
Letter Sequencing
RT	1301 (327)	2170 (481)	48.2*	1182.6*	4.9*
Error	.04 (.07)	.07 (.09)	9.2*	28.1*	1.9
Symbol Sequencing
RT	2120 (456)	2298 (655)	53.3*	25.7*	12.7*
Error	.07 (.09)	.16 (.16)	10.8*	74.3*	6.5*

^*p<.01

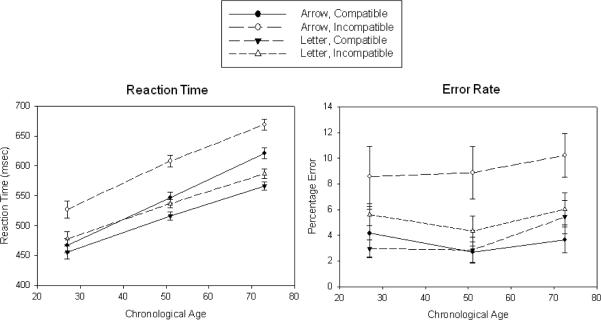
The left panel of Figure 3 portrays the mean RTs (and standard errors) in the compatible and incompatible conditions in the two tasks for three age groups, and the right panel contains the corresponding information for the error percentages. The virtually parallel RT functions for the compatible and incompatible conditions in each task are consistent with the absence of Age-by-Condition interactions. Inspection of the right panel of Figure 3 reveals that the Age-by-Condition interaction with the error rate measure in the Letter task is attributable to somewhat smaller differences between the incompatible and compatible conditions with increased age.

Figure 3.

Means and standard errors of RT (left panel) and error percentages (right panel) in the compatible and incompatible versions of the Arrow and Letter flanker tasks in three age groups.

Contextual analysis results for the flanker tasks are presented in the top of Table 3. The first column contains the total relation (i.e., simple correlation) with age, where it can be seen that with the exception of the error variables, the correlations were moderately large, and significantly different from zero. These results simply indicate that increased age was associated with slower performance in each condition of the tasks. The remaining columns contain standardized regression coefficients obtained when age and the four reference cognitive abilities were used as simultaneous predictors of the target variables in the contextual analysis.

Table 3.

Contextual analysis results for the 10 cognitive tasks

	Age			Cognitive Ability
	Total	Unique	Simple	Gf	Mem	Speed	Voc	X2/df	CFI	RMSEA
Study 1
Arrow
Errors
Simple	.06	−.22	X	−.43*	−.09	.04	.14	2.69	.94	.07
Complex	.10	−.10	.48*	−.25	−.07	.01	.02
RT
Simple	.56*	.14	X	−.36*	.30	−.56*	.03	2.66	94	.07
Complex	.50*	−.10	.90*	−.19	.02	.06	.16*
RT Resid
Simple	.55*	.14	X	−.36*	.30	−.55*	.03	2.96	.92	.09
Complex	.48*	−.09	.90*	−.17	.02	.05	.15
Composite
Simple	.46*	−.02	X	−.51*	.17	−.40*	.10	2.71	.94	.07
Complex	.36*	−.12	.65*	−.29	−.03	.02	.11
Letter
Errors
Simple	.13	−.17	X	−.26	−.09	−.10	.13	2.55	.95	.08
Complex	.06	−.05	.95*	−.02	.04	−.02	−.02
RT
Simple	.49*	−.04	X	−.32	.11	−.51*	.21	2.64	.95	.08
Complex	.48*	.03	.95*	−.01	−.00	.03	−.01
RT Resid
Simple	.47*	−.04	X	−.32	.12	−.51*	.21	5.84	.83	.14
Complex	.47*	.02	.95*	−.02	−.01	.02	−.01
Composite
Simple	.39*	−.13	X	−.37	.02	−.39*	.21	2.60	.95	.08
Complex	.36*	−.02	.95*	−.04	.03	−.02	−.01
Study 2
Embedded Letters
Errors
Simple	.17*	−.12	X	−.04	−.01	−.37	.03	2.59	.92	.08
Complex	.07	−.47*	.18*	.13	−.37	−.51*	.02
RT
Simple	.59*	.07	X	−.17	.02	−.62*	.09	2.75	.92	.09
Complex	.54*	.07	.50*	−.15	.32*	−.43*	−.05
RT Resid
Simple	.56*	.05	X	−.15	.06	−.69*	.08	2.59	.92	.08
Complex	.57*	−.11	.45*	−.08	.26	−.75*	−.06
Composite
Simple	.51*	−.02	X	−.14	.01	−.64*	.08	2.56	.93	.08
Complex	.35*	−.34*	.36*	.02	−.14	−.62*	−.01
Part Detection
Errors
Simple	.12	−.34*	X	.04	−.31	−.44*	.05	2.73	.92	.09
Complex	.29*	−.05	.42*	−.19	.04	−.33*	−.08
RT
Simple	.55*	.04	X	−.24	.16	−.65*	.17	2.71	.92	.09
Complex	.61*	.09	.54*	.08	−.03	−.32*	.17*
RT Resid
Simple	.51*	.05	X	−.21	.19	−.66*	.16	2.88	.90	.09
Complex	.58*	.05	.56*	.05	−.02	−.40*	.16
Composite
Simple	.43*	−.16	X	−.14	−.06	−.67*	.14	2.78	.92	.09
Complex	.52*	−.01	.48*	−.08	−.00	−.39*	.03
Symbol Integration
Errors
Simple	.21*	−.25	X	−.30	.08	−.50*	−.02	2.55	.93	.08
Complex	.38*	−.13	.29*	−.57*	−.02	−.19	.14
RT
Simple	.58*	.08	X	.01	−.10	−.61*	.11	2.65	.92	.08
Complex	.57*	.20*	.76*	−.05	.14	.01	.00
RT Resid
Simple	.54*	.06	X	.00	−.08	−.65*	.11	2.65	.92	.08
Complex	.54*	.18	.78*	−.15	.10	.04	.02
Composite
Simple	.49*	−.11	X	−.18	−.01	−.69*	.06	2.59	.93	.08
Complex	.60*	.07	.35*	−.37*	.06	−.26	.11
Pattern Integration
Errors
Simple	.04	−.44*	X	−.25	−.31	−.24	.03	2.60	.92	.08
Complex	.30*	−.08	.27*	−.71*	.20	−.17	.03
RT
Simple	.58*	.07	X	.03	−.00	−.72*	.13	2.66	.92	.08
Complex	.49*	.38*	.59*	.37*	−.05	.10	.05
RT Resid
Simple	.58*	−.11	X	−.10	−.02	−.86*	.15	2.74	.91	.09
Complex	.57*	.40*	.66*	.21	−.05	.21	.03
Composite
Simple	.39*	−.31*	X	−.18	−.24	−.62*	.10	2.58	.93	.08
Complex	.57*	.19	.17	−.31*	.10	−.29	.10
Plus 2
Errors
Simple	.15	−.07	X	.39	−.32	−.38	−.21	2.57	.92	.08
Complex	.25*	−.13	.31*	−.39*	.05	−.27	−.10
RT
Simple	.48*	.10	X	.06	.02	−.63*	−.08	2.59	.92	.08
Complex	.41*	.09	.19	−.24	.32	−.39	.11
RT Resid
Simple	.40*	.13	X	−.12	.18	−.46*	.02	2.51	.92	.08
Complex	.38*	.08	.19	−.26	.33	−.42	.10
Composite
Simple	.31*	−.00	X	.29	−.21	−.52*	−.18	2.55	.92	.08
Complex	.38*	−.07	.31*	−.40*	.16	−.37*	−.04
Pattern Rotation
Errors
Simple	.10	−.44*	X	−.14	−.49*	−.24	.15	2.66	.92	.08
Complex	.24*	−.29*	.10	−.68*	.24	−.45*	.06
RT
Simple	.57*	.09	X	.13	−.00	−.75*	.05	2.61	.92	.08
Complex	.40*	.27*	.63*	.20	.14	.10	.14
RT Resid
Simple	.56*	.06	X	.13	−.05	−.77*	.06	2.64	.91	08
Complex	.46*	.26*	.65*	.03	.28	.04	.11
Composite
Simple	.36*	−.27*	X	−.12	−.33	−.53*	.12	2.62	.92	.08
Complex	.48*	.01	.05	−.30	.26	−.61*	.18
Letter Sequencing
Errors
Simple	.15	−.17	X	−.14	.06	−.47*	−.11	2.63	.92	.08
Complex	.26*	−.28*	.14	−.16	−.04	−.60*	.03
RT
Simple	.50*	.02	X	−.19	.11	−.67*	−.06	2.65	.92	.08
Complex	.50*	−.01	.33*	−.22	.16	−.43*	.18
RT Resid
Simple	.43*	.08	X	−.15	.09	−.51*	−.03	2.57	.92	.08
Complex	.43*	−.01	.34*	−.22	.15	−.41*	.18
Composite
Simple	.34*	−.10	X	−.18	.09	−.63*	−.09	2.55	.93	.08
Complex	.43*	−.20	.14	−.24	.06	−.70*	.10
Symbol Sequencing
Errors
Simple	.24*	−.26	X	−.11	−.18	−.48*	.02	2.65	.92	.08
Complex	.32*	−.23*	.35*	−.58*	.09	−.28	.21*
RT
Simple	.52*	−.17	X	−.19	−.07	−.74*	.27*	2.63	.92	.08
Complex	.57*	.22*	.51*	−.47*	.15	.13	.13
RT Resid
Simple	.43*	−.20	X	−.12	−.01	−.83*	.25*	2.83	.91	.09
Complex	.48*	.27*	.61*	−.57*	.13	.32	.13
Composite
Simple	.45*	−.24*	X	−.17	−.14	−.71*	.18	2.57	.93	.08
Complex	.52*	−.04	.33	−.64*	.12	−.18	.23*

Note: X indicates that there was no path, and hence no standardized coefficient, to that variable.

^*p<.01

The second column in Table 3 contains the unique relation of age on the variable, representing the relation of age that is statistically independent of relations with the reference cognitive abilities. The relations of the different cognitive abilities on the target variables are represented by the magnitude of the coefficients from the reference constructs, contained in the remaining columns of Table 3.

Although the total relations with age were large and negative, none of the unique age relations was significant, and most of the relations shared with the reference cognitive abilities were with speed ability. There were also some significant relations with Gf, but surprisingly, they were only apparent in the simpler, compatible, version of the tasks. However, it should be noted that the effects on the incompatible measures in these analyses represent unique effects after controlling influences on the compatible measures. Particularly noteworthy is the finding that most of the standardized coefficients from the simple (compatible) to the complex (incompatible) construct were close to 1.0, which indicates almost complete overlap of the individual differences in the compatible and incompatible conditions in the tasks.

Correlations between the RT measures in each condition of the two tasks were also examined. The correlations between the compatible and incompatible conditions within the same task (i.e., .89 for Arrow and .95 for Letter), were stronger than those between the compatible or incompatible conditions across tasks (i.e., .70 and .62, respectively), which suggests that type of material is a more salient influence on the individual differences in RT performance than presence or absence of flanker conflict. Furthermore, the correlation of the incompatible-minus-compatible RT difference across the two flanker tasks was .03, and the correlation of the residual incompatible RT scores after partialling the compatible RT scores was .04.

These results are all consistent in indicating that, at least in terms of individual differences, performance in the compatible condition of the flanker tasks is not distinct from performance in the incompatible condition of the tasks. Although performance was significantly worse in the incompatible condition than in the compatible condition in both tasks, the correlations between performance in the compatible condition and in the incompatible condition were very high, which suggests that there were little or no individual differences in the magnitude of the incompatible – compatible contrast. These results suggest that, regardless of what the task is assumed to measure, the flanker task may not be useful in individual difference comparisons. Finally, it should be noted that most of the age-related relations in these tasks overlapped with relations on perceptual speed.

Study 2

The purpose of the second study was to extend the analytical method applied in Study 1 to investigate whether there were distinct individual differences in the simple and complex versions of a variety of cognitive tasks, and to identify the cognitive abilities associated with performance in each version of the task.

Participants in this study performed a variety of cognitive tasks which each consisted of a simple condition and a complex condition postulated to differ from the simple condition by an additional processing requirement. The complex conditions in the various tasks were designed to represent a variety of different types of processing requirements to investigate whether a specific kind of processing is particularly sensitive to increased age. It is obviously impossible to consider every type of cognitive process, but the goal was to examine a relatively broad range of tasks to determine whether relations associated with increasing age were limited to certain types of processing operations.

Because there has apparently been no prior age-comparative research with tasks similar to these, the past literature does not provide a basis for specific predictions regarding age effects. However, if it is assumed that age differences tend to increase whenever a complex cognitive operation needs to be performed, a unique age-related relation might be expected on the measures from the complex version of the task after controlling relations on measures from the simple version.

Method

Participants

Demographic characteristics of the participants are presented in the bottom of Table 1. Note that the sample was similar in most respects to that in Study 1, and that age was significantly related only to education, reflecting the fact that on average older participants had completed more years of education than younger participants.

Tasks

The stimuli, which were displayed until a response was registered, consisted of sets of items similar to those illustrated in Figure 4. Viewing distance was not controlled, but the stimuli ranged from about 3 to 10 cm in diameter on the display monitor. In all tasks participants were instructed to respond as rapidly and accurately as possible. Responses in all tasks involved presses of a left (Z) key for “Different” and a right (/) key for “Same”, and the decision-response assignments were visible on the bottom of the screen on all trials. Five practice trials were presented in each condition, followed by 30 trials in each of 4 blocks which were presented in the order: simple, complex, complex, and simple. One half of the trials in each block were “Same” and one half were “Different”. The measures of performance in each condition were the median RT for correct trials and the proportion of errors.

Figure 4.

Illustration of stimuli used in the simple and complex conditions of the eight tasks administered in Study 2.

All of the tasks involved “Same” or “Different” decisions with respect to visual stimuli, and examples of the stimuli in the tasks are portrayed in Figure 4. In each case the pair of stimuli on the left required a simple same-different decision with respect to whether the two stimuli were identical or not, and the set of stimuli on the right required a similar decision after carrying out an added operation. Two tasks, Embedded Letters and Part Detection, were designed to focus on a selection operation as the participant in the complex condition was asked to decide if the element in the first display was included in the second display. The Symbol Integration and Pattern Integration tasks were designed to emphasize an integration operation because the requirement in the complex condition was to decide if the contents in the third display were equal to the sum of the contents in the first two displays. Transformation was the operation of primary interest in the Plus 2 and Pattern Rotation tasks as the decision in the complex condition was whether the second display was equal to the first display after carrying out the designated transformation (i.e., either addition or rotation). The final two tasks, Letter Sequencing and Symbol Sequencing, were intended to emphasize an ordering operation because the participant in the complex condition was to decide whether the elements in the second display were in the same order as the first display after reversal of the sequence.

The tasks were administered in a single session in the following order for all participants: Embedded Letters, Symbol Integration, Pattern Rotation, Letter Sequencing, Symbol Sequencing, Plus 2, Pattern Integration, and Part Detection. The cognitive tasks used to assess the reference cognitive abilities in the contextual analysis were performed in a separate session that occurred between 1 and 14 days prior to the session with the target tasks.

Results and Discussion

Means and standard deviations of the median RTs and error proportions averaged across the two blocks in each condition are summarized in the bottom of Table 2. It should be noted that in some tasks the average RT was over 3 seconds and the average error proportion was over .20, indicating very slow and error-prone performance.

Results of ANOVAs conducted on the RT and error rate variables in each task are presented in the right columns of Table 2. It can be seen that every variable except the error proportions in the Embedded Letters and Pattern Integration tasks had significant main effects of age (F [2,221] > 5.3), and that the main effects of condition were significant (F[1,221] > 28.1) for all variables. Furthermore, the Age-by-Condition interactions were significant (F[2,221] > 4.7) for the RT measure in all tasks except Plus 2 and Pattern Rotation, and for the error measure in all tasks except Embedded Letters and Letter Sequences. The existence of significant effects on both the RT and accuracy measures when they were analyzed separately implies that conclusions based on the results of only one variable could be misleading with respect to the overall magnitude of the age or condition effects.

As in Study 1, separate contextual analyses were conducted with different representations of target task performance in the two conditions in each task, with the results reported in the bottom of Table 3. Inspection of the entries in Table 3 reveals that the error rates in either the simple or complex conditions were related to speed ability in 6 of the 8 tasks, and were related to Gf ability in one or both conditions in 5 of the 8 tasks.

The patterns of relations with age and with the reference cognitive abilities were very similar for the RT and RT residual variables. As might have been expected, the results with the composite variable were intermediate between those with the error and RT variables. The most salient relations in the analyses were those from the speed reference ability to the measure of performance in the simple condition of the tasks, which reflects the fact that the people who were faster on the speed reference tasks had shorter RTs and fewer errors in the simple condition of the target tasks. The pattern of cognitive ability relations in the complex conditions was inconsistent across tasks, and across methods of representing performance in the simple and complex conditions within the same tasks. There were a number of relations with Gf ability, but in some cases they were negative, indicating that after controlling for relations through the simple condition and the reference cognitive abilities, higher Gf was associated with fewer errors or slower RT, and in other cases the relations were positive.

Only a few unique age relations were significant, suggesting that most of the age-related influences overlap with relations shared with established cognitive abilities. It is important to note that these results contrast with the patterns from ANOVAs which indicate differential relations of age in the complex conditions of the tasks in either the RT measure, the error proportion measure, or both. The different implications of these two sets of results are consistent with the distinction discussed by Salthouse and Coon (1994; also see Salthouse, 2000), in that age relations in two variables or conditions can be of differential magnitude, and yet not be statistically independent of one other.

Another noteworthy finding from the contextual analysis results is that age-related relations in these tasks largely overlap with relations on perceptual speed. Rather than assessing age-related differences in specific cognitive processes, therefore, the results suggest that variations in performance in these tasks primarily reflect individual differences in perceptual speed.

General Discussion

There are three major results of this project. The first major result is that in most of the tasks there were significant relations of age and cognitive abilities on both RT and error rate variables when they were considered separately. Perhaps because the RT variance was much greater than the error variance, the patterns of results were very similar when only the RT variable was analyzed and when RT residuals after partialling error rate were analyzed. In most of the cases the pattern was also similar when the analyses were based on a composite variable created by weighting RT and error variables equally. The qualitatively similar patterns of relations with the different methods of representing task performance can be viewed as reassuring because they suggest that at least in these participants and these tasks, much of the variation in performance was manifested in the RT variable. Nevertheless, it is important to recognize that the quantitative relations between task performance and individual difference variables or cognitive abilities differ according to whether, and how, error information is taken into consideration.

A second major result is that although increased age was associated with slower and less accurate performance in nearly every condition of every task, very few unique relations associated with increased age were significant. These results imply that most of the cross-sectional age differences in these tasks overlapped with differences in other cognitive abilities, and therefore the tasks may not represent aspects of individual differences distinct from those already recognized on established cognitive abilities. There were also few unique relations associated with age in the flanker tasks, and the simple correlations with age were nearly the same in the compatible and incompatible conditions. The absence of unique age-related relations in the incompatible condition occurred despite the very robust interference effect, as the large condition effects in the ANOVAs in Table 2 indicate that RT was slower and error rate was higher in the incompatible conditions than in the compatible conditions in both the arrow and letter flanker tasks. The finding of nearly complete overlap of the individual differences in the compatible and incompatible conditions, with near-zero correlations of the differences and of the residuals across the two versions of the tasks with different materials, was surprising. These results suggest that the flanker task may be sensitive to conflict, but that at least in the current versions of the tasks, there are little or no systematic individual differences in the magnitude of the behavioral manifestations of this conflict. This suggestion merits additional research because it raises questions about the widespread practice of using performance in flanker tasks to assess individual differences in aspects of executive functioning (e.g., Colcombe, et al., 2005; Hillman, et al., 2009; Kramer, et al., 1994; Li & Dupois, 2008; Wylie, et al., 2006).

The third major result in the current project is that the contextual analyses revealed that performance in most of the tasks was predominantly related to speed ability in both the simple (or compatible) and complex (or incompatible) conditions. Fluid intelligence (Gf) was related to performance in the simple condition, particularly in the flanker tasks, but not in the complex condition when relations operating through the simple condition were controlled. This pattern of results suggests that relatively simple speeded tasks such as those portrayed in Figures 2 and 4, even though they might be designed to isolate individual differences in specific cognitive operations, may primarily reflect individual differences in processing speed. Moreover, it should be noted that the strong relations with perceptual speed are not attributable to common methods because the reference perceptual speed construct was assessed with paper-and-pencil tests whereas the target tasks involved reaction time procedures.

The results of these studies have at least two important implications for research in neuropsychology and neuroscience. One implication is that when two or more measures of performance are available from the same task, it can be informative to examine results with different methods of analyzing the multiple measures. For example, a discovery that a patient group differs from a group of healthy controls in RT but not in RT residuals after controlling for error rate would be consistent with the possibility that different speed-accuracy tradeoffs might be operating in the two groups. A second implication is that adoption of a broader multivariate perspective in which effects on the target variable are examined in the context of established abilities allows the researcher to determine whether the individual differences on the target variable are statistically independent of individual differences on the established abilities. A discovery of no unique effects associated with the neurological condition on the target variable might suggest that no new explanation is required to account for results with the target variable because they could simply be another manifestation of what is already known.

In summary, the proposed analytical methods have several important advantages over contemporary approaches for investigating individual differences in specific neurocognitive processes. First, even when a relatively small number of trials are available in each task, simultaneous analyses of RT and error variables can be conducted rather than treating the two variables as if they were independent. Second, statistically independent influences associated with individual difference variables can be examined, and not merely effects of differential magnitude. Third, the proposed methods allow a researcher to identify individual difference relations on the target task that are distinct from individual difference relations that are already well established. And fourth, simultaneous examination of the influences of different cognitive abilities, particularly when the abilities are represented by latent constructs determined by the systematic variance shared across multiple indicators, is informative about the relative contributions of different cognitive abilities to performance in the target task. The primary disadvantage of the analytical procedures is that they require moderately large samples, but it should be recognized that large samples are usually desirable when the focus in on individual differences.

Appendix A

Description of variables

Matrix Reasoning

Determine which pattern best completes the missing cell in a matrix.

Shipley Abstraction

Determine the words or numbers that are the best continuation of a sequence.

Letter Sets

Identify which of five groups of letters is different from the others.

Spatial Relations

Determine the correspondence between a 3-D figure and alternative 2-D figures.

Paper Folding

Determine the pattern of holes that would result from a sequence of folds and a punch through folded paper.

Form Boards

Determine which combinations of shapes are needed to fill a larger shape.

Logical Memory

Number of idea units recalled across three stories.

Word Recall

Number of words recalled across trials 1 to 4 of a word list.

Paired Associates

Number of response terms recalled when presented with a stimulus item.

Digit Symbol

Use a code table to write the correct symbol below each digit.

Letter Comparison

Same/different comparison of pairs of letter strings.

Pattern Comparison

Same/different comparison of pairs of line patterns.

WAIS Vocabulary

Provide definitions of words

WJ-R Picture Vocabulary

Name the pictured object

Antonym Vocabulary

Select the best antonym of the target word

Synonym Vocabulary

Select the best synonym of the target word

Appendix B

Standardized construct-variable loadings (Study 1 / Study 2) for reference constructs in contextual analysis

	Cognitive Ability
	Gf	Memory	Speed	Vocab
Variable
Matrix Reasoning	.88 /.84
Shipley Abstraction	.86 /.85
Letter Sets	.75 /.73
Spatial Relations	.79 /.79
Paper Folding	.79 /.75
Form Boards	.73 /.66
Word Recall		.80/.81
Paired Associates		.86 /.77
Logical Memory		.76 /.80
Digit Symbol			.79 /.79
Pattern Comparison			.86 /.80
Letter Comparison			.83 /.83
WAIS Vocabulary				.85 /.82
WJ R Picture Vocabulary				.80 /.74
Synonym Vocabulary				.91 /.86
Antonym Vocabulary				.85 /.85

	Study 1	Study 2
Construct Correlations
Gf ← → Memory	.83	.89
Gf ← → Speed	.66	.74
Gf ← → Vocabulary	.49	.47
Memory ← → Speed	.69	.75
Memory ← → Vocabulary	.38	.40
Speed ← → Vocabulary	.07	.15
Fit Statistics
X2/df	2.82	2.59
CFI	.94	.93
RMSEA	.08	.08