Inference from Multiple Imputation for Missing Data Using Mixtures of Normals

Abstract

We consider two difficulties with standard multiple imputation methods for missing data based on Rubin's t method for confidence intervals: their often excessive width, and their instability. These problems are present most often when the number of copies is small, as is often the case when a data collection organization is making multiple completed datasets available for analysis. We suggest using mixtures of normals as an alternative to Rubin's t. We also examine the performance of improper imputation methods as an alternative to generating copies from the true posterior distribution for the missing observations. We report the results of simulation studies and analyses of data on health-related quality of life in which the methods suggested here gave narrower confidence intervals and more stable inferences, especially with small numbers of copies or non-normal posterior distributions of parameter estimates. A free R software package called MImix that implements our methods is available from CRAN.

1 Introduction

In public health and social research, it is now common for researchers to collect large amounts of information on a big set of subjects. Organizations that collect and provide data often serve users that vary in their levels of statistical sophistication. As is standard in the imputation literature, we will assume here that the data-collection organization has control over the datasets provided to users, but not over the analyses they perform. The goal of the data-collection organization is to provide a set of data that users can analyze using standard complete-data techniques.

Usually, the possible recourses for people who wish to analyze such data are to ignore observations with missing data (row elimination or complete case analysis), to ignore entire variables for which there are missing values (column elimination), or to use a more sophisticated statistical technique to handle the missingness in the data.

None of these recourses is very attractive. The first two, which involve ignoring data that were collected, are inefficient and can lead to biases if the missing data are not missing completely at random. For longitudinal clinical studies, they might actually cause one to eliminate a significant fraction of the data collected. The third is the most desirable from a statistical point of view, but requires a level of technical sophistication beyond that of many users of large databases.

Multiple imputation, introduced by Rubin for survey researchers (Rubin 1978; Rubin 1987) and popularized by Schafer (1997) and the accompanying software, is intuitively appealing and relatively straightforward, and is now widely used.

The standard approach to inference about individual parameters from multiple imputation is to use a confidence interval based on the t distribution. We will show when the number of copies is small, this can lead to confidence intervals that are very wide, unstable, or both. Here we take a different approach, approximating the marginal posterior distribution of parameters or quantities of interest by a mixture of normals, as has long been a standard approach to density estimation (Ferguson 1983; West 1993; Escobar and West 1995; Roeder and Wasserman 1997; Fraley and Raftery 2002). We show that this gives narrower confidence intervals and better overall performance than the t-based intervals.

A free R software package called MImix that implements our methods is available at http://cran.r-project.org.

In Section 2 we describe our method, in Section 3 we analyze a simple simulated example, and in Section 4 we apply our method to a real data set from health-related quality of life research.

2 Methods

We denote the observed data by Y and the missing data by Z, and we assume that the analyst is interested in estimating a particular vector-valued estimand of interest (Q) (e.g. means, medians, regression coefficients, etc.).

Rubin (1996) addresses the topic from a Bayesian perspective, which we summarize here. A Bayesian approach to inference about Q centers on the posterior distribution of Q given the observed data Y. One can write the posterior distribution of Q as P(Q∣Y,X) = ∫P(Q∣Y, Z,X)P(Z∣Y,X)dZ, where P(Z∣Y,X) is the posterior distribution of the missing data Z given the observed data and X represents other information that the imputer may have. Note that the imputer is not necessarily the analyst, and may, for example, be an agency providing a small number of multiply imputed copies of the dataset for use by others. If one specifies a full probability model for the missing data, then one can in principle make posterior inference about Q. The posterior mean and variance of Q are as follows:

$$E(Q\mid Y,X)=E_Z(E_Q(Q\mid Y,Z,X)\mid Y,X)$$ (1)

$$\begin{array}{ll}\mathit{\text{Var}}(Q\mid Y,X)\hfill & =E_Z(Va{r}_Q(Q\mid Y,Z,X)\mid Y,X)+Va{r}_Z(E_Q(Q\mid Y,Z,X)\mid Y,X)\hfill \\ \hfill & =U+B.\hfill \end{array}$$ (2)

These could be estimated by simulating independent draws from the posterior distribution of the missing data Z, and replacing the expectations over Z in (1) and (2) by sample averages over the simulated values of Z.

Under the multiple imputation paradigm of Rubin (1978), the imputer generates copies of the missing data from P(Z∣Y,X), a probability model that attempts to model the missing data based on the observed responses (Y) and other information for both complete and incomplete cases (X). Conditionally on the probability model, the following are consistent estimators of Q, U and B:

$$\begin{array}{ll}\overline{Q}\hfill & =\frac{1}{M}\sum _{m=1}^M{Q}_{\ast m}\to E(Q\mid Y,X)\text{as}m\to \infty ,\hfill \\ \overline{U}\hfill & =\frac{1}{M}\sum _{m=1}^M{U}_{\ast m}\to U\text{as}m\to \infty ,\hfill \\ \overline{B}\hfill & =\frac{1}{M-1}\sum _{m=1}^M(Q_{\ast m}-\overline{Q})(Q_{\ast m}-\overline{Q})\prime \to B\text{as}m\to \infty ,\hfill \end{array}$$

where Q_*m is the complete-data estimate of the posterior mean of Q and U_*m is the complete-data estimate of the posterior variance. Rubin (1987) suggested using Q̄ as an estimate of Q and $T=\overline{U}+\left(1+\frac{1}{M}\right)\overline{B}$ as the estimate of the uncertainty about Q conditional only on the observed data.

Rubin (1987) proposed approximating the posterior distribution of P(Q∣Y) by a t-distribution with degrees of freedom that depend on the number of copies, the total number of cases, and an estimate of the amount of missing information in the problem, namely $\nu =\left(m-1\right){\left(1+r_m^{-1}\right)}^2$, where r_m is the increase in relative increase in variance due to non-response, estimated as $r_m=\left(1+\frac{1}{M}\right)\overline{B}/\overline{U}$. Barnard and Rubin (1999) gave an adjustment to the degrees of freedom for small numbers of imputations, ν* = 1/(1/ν + 1/ν₀), where ν₀ = (a + 1) *a/(a + 3) *Ū/(Ū + (1+ 1/M)B̄) and a is the number of complete data degrees of freedom. The adjustment performs better for small numbers of copies than the original degrees of freedom suggested by Rubin (1987).

Another approach is to approximate the marginal posterior distribution of interest by a mixture of estimated complete data posteriors. If one could generate M copies of the missing data from the correct probability model, {Z¹, … , Z^M}, then a Monte Carlo approximation can be used for P(Q∣Y,X), i.e. $\widehat{P}\left(Q\mid Y,X\right)=\frac{1}{M}{\sum }_{m=1}^{M}P\left(Q\mid Y,Z^m,X\right)$. If the complete-data posterior distribution of the quantity of interest is approximately normal, we could replace P(Q∣Y, Z^m, X) by normal distributions having means Q_*m and variance-covariance matrices U_*m, and thus obtain another approximation to the marginal posterior distribution (West 1993; Escobar and West 1995).

Wei and Tanner (1990) proposed two alternative approximations to the posterior distribution of the model parameters θ. The first was Poor Man's Data Augmentation (PMDA-1) where imputations are generated from an approximation to p(Z∣Y) based on the maximum likelihood estimator θ̂, namely p(Z∣Y,X,θ̂). The PMDA-1 method approximates the posterior of θ by $\frac{1}{M}{\sum }_{m=1}^{M}P\left(\theta \mid Y,Z^m,X\right)$. PMDA-1 produces asymptotically biased estimates of the posterior, but if the observed-data posterior is concentrated around θ̂ (which is the case for small amounts of missing data) then the bias will not be too large.

Wei and Tanner also suggested an importance sampling based solution, PMDA-2, which approximates the observed data posterior by

$$\sum _{m_1}^M\frac{w\left(Z^m\right)}{{\sum }_{i=1}^{M}w\left(Z^i\right)}p\left(\theta \mid Y,Z^m,X\right),$$

where

$$w\left(Z^m\right)={\left(det\sum \ast \right)}^{1/2}\frac{p\left({\widehat{\theta }}_m^{\ast }\mid Y,Z^m,X\right)}{p\left(\widehat{\theta }\mid Y,Z^m,X\right)},$$

Σ* is the inverse Hessian of log(p(θ∣Y, Z^m, X)) evaluated at ${\widehat{\theta }}_m^{\ast }$, the maximum of p(θ∣Y, Z^m, X). The weights, w(Z^m), are importance sampling weights designed to correct for the fact that one is not sampling from the correct posterior, p(Z∣Y, X), and so PMDA-2 is an unbiased estimate of the observed data posterior. If p(θ∣Y, Z, X) is not available in closed form, then one can use a different approximation for the importance weights. We can write the importance weights as

$$w\left(Z^m\right)=\frac{p\left(Z^m\mid Y,X\right)}{p\left(Z^m\mid \widehat{\theta },Y,X\right)}=\frac{p\left(Y,Z^m\mid X\right)}{p\left(Y\mid X\right)p\left(Z^m\mid \widehat{\theta },Y,X\right)}.$$ (3)

In (3), P(Y∣X) is unknown in general, but it is not needed because it cancels in the importance sampling calculation. The quantity p(Y, Z^m∣X) is needed to compute the weights, and it is often not available in closed form. This is the complete-data log-integrated likelihood, which can often be approximated by the Schwarz approximation P(Y, Z∣X, θ̂^m)n^−d/2, where d is the number of parameters and n is the total sample size for the complete data model (Schwarz 1978; Kass and Raftery 1995).

Summarizing via mixtures of normals rather than using a t distribution only slightly increases the computational burden on the user. In order to obtain point estimates (via the median of the posterior density estimate) and 95% confidence (or credible) limits, the user must simply obtain the required percentiles of the mixture distribution. Obtaining the desired mixture percentile values (say c_j) requires solving

$$\sum _{m=1}^{M}w\left(z^m\right)\phi \left(q,{\widehat{\theta }}^m,\sigma \left({\widehat{\theta }}^m\right)\right)=c_j$$

for q where ϕ represents the normal density. Numerical root-finding methods (typically available in statistical software) can be used to solve for q. If the user does not have access to such software, they could also generate samples of q from the mixture density and use the Monte Carlo samples to estimate the percentiles of interest.

3 Simulated data example

In this paper, we compare several multiple imputation methods for estimation of functional of interest, focusing on the results for small numbers of copies. It has been shown elsewhere (Rubin 1987; Meng 2000) that generating copies from the correct posterior distribution is preferable to generating copies from an approximation to the correct posterior as the number of copies used in the estimation tends to infinity. We will focus on both very small numbers of copies (3 or 5) which makes sense for imputation for “typical” users (and is commonly recommended in texts and software documentation for computational procedures), and we will also look at performance for 10 and 25 copies, which is feasible when the storage capacity allows or the research problem demands higher precision. We will compare four methods, two of which are proper, completing the missing observations via their true posterior distribution, namely Rubin's t and Monte Carlo methods. One method follows the concept of PMDA-2, which uses an improper method of imputation generation but still yields asymptotically correct inference for the parameters of interest. The last method is PMDA-1, which is both improper and inconsistent.

The simple normal example has proved enlightening in other work (Robins and Wang 2000), and we use it here as a starting example. Assume that we observe N subjects and wish to estimate a tail probability, i.e. θ = Pr(X < ξ), where we assume that X is normally distributed with an unknown mean μ and variance σ². If none of the N observations is missing, then one can obtain a model-based estimate of the tail probability, θ, namely ${\widehat{\theta }}_N=\Phi \left(\frac{\xi -{\overline{x}}_N}{s_N}\right)$, where Φ is the cumulative distribution function of the standard normal.

Using the asymptotic normality of θ̂_N to make inference about θ via the Delta method, we obtain ${\widehat{\theta }}_N\dot{\sim }\phi \left(\Phi \left(\frac{\xi -\mu }{\sigma }\right),\tau \left(\mu ,\sigma ,\xi \right)\right)$ where ϕ(a, b) indicates the normal density with mean a and variance b. Here ∼̇, denotes approximately distributed and

$$\tau \left(\mu ,\sigma ,\xi \right)=\frac{{\left\{\frac{\partial }{\partial \mu }\Phi \left(\frac{\xi -\mu }{\sigma }\right)\right\}}^2{\sigma }^2+{\left\{\frac{\partial }{\partial {\sigma }^2}\Phi \left(\frac{\xi -\mu }{\sigma }\right)\right\}}^{2}2{\sigma }^4}{N}$$

is the resulting variance from the Delta method. Given a sample x₁,…,x_N,we can estimate μ by x̄_N and σ by s_N and use the plug-in approach to obtain an approximate confidence set for the tail probability of interest.

One can also approach the problem as one of estimating the posterior distribution of θ, i.e. p(θ∣x₁, …, x_N). The posterior distribution for θ is not available in closed form, even when using the standard Normal-Inverse-χ² conjugate priors for μ and σ². However, we can easily sample from the posterior distribution of μ and σ² in closed form, so we could generate an approximate sample from p(θ∣x₁, …, x_N) by first sampling μ and σ² from their joint posterior distribution, and then calculate the resulting θ for each pair. Another possibility is to use a normal approximation to the posterior via the same delta method approximation used in the frequentist case, i.e. $p\left(\theta \mid x_1\dots ,x_N\right)\dot{\sim }\phi \left(\Phi \left(\frac{\xi -{\overline{x}}_N}{s_N}\right),\tau \left({\overline{x}}_N,s_N,\xi \right)\right)$. One can justify this approximation under the assumption that any reasonably non-informative prior distribution will have negligible effect on the normality of the likelihood asymptotically (Bernardo and Smith 1994).

In order to evaluate the imputation methods, we now assume that k of the N observations are missing, leaving N–k = n observed data points. Because the data are missing completely at random (MCAR), the obvious correct inference for the problem is based on the estimator and variance estimate using only the observed data points, i.e. θ̂_n is approximately normal with mean $\Phi \left(\frac{\xi -{\overline{x}}_n}{s_n}\right)$ and variance τ(x̄_n, s_n, ξ) where x̄_n and $s_2^n$ are the sample mean and variance of the reduced dataset. However, treating this as a missing data problem allows us to “impute” the missing data and use the “completed data” x₁, …,x_N to make inference about the parameter of interest for a situation where we know what the correct inference is.

We generate M copies of the missing data points $x_{n+1}^{(m)},\dots ,x_N^{(m)}$ according to their true posterior distribution p(· ∣x₁, …,x_n),or M copies of $x_{n+1}^{\ast (m)},\dots ,x_N^{\ast (m)}$ according to their posterior distribution conditional on the maximum likelihood estimates, p(·∣x₁, …,x_n, μ̂, σ̂). We then calculate ${\overline{x}}_N^m$ and ${\mathit{\text{s}}}_N^m\left(m=1,\dots ,M\right)\left(\text{or}{\overline{x}}_N^{\ast m}\mathit{\text{and}}{s}_N^{\ast m}\right)$ for each completed dataset. In each case, the complete data estimate of the posterior functional of interest is $\Phi \left(\frac{\xi -{\overline{x}}_N^m}{{\mathit{\text{s}}}_N^m}\right)\left(\text{or}\Phi \left(\frac{\xi -{\overline{x}}_N^{\ast m}}{s_N^{\ast m}}\right)\right)$. We consider the following approximations for p(θ∣x₁, …,x_n):

• Rubin's t: a t distribution with mean $\frac{1}{M}{\sum }_{m=1}^M\Phi \left(\frac{\xi -{\overline{x}}_N^m}{{\mathit{\text{s}}}_N^m}\right)$ and variance and degrees of freedom estimated according to Rubin (1987) and Barnard and Rubin (1999).

• Monte Carlo: a mixture of normal distributions, $\frac{1}{M}{\sum }_{m=1}^M\phi \left(\Phi \left(\frac{\xi -{\overline{x}}_N^m}{{\mathit{\text{s}}}_N^m}\right),\tau \left({\overline{x}}_N^m,{\mathit{\text{s}}}_N^m,\xi \right)\right)$

• PMDA-1: a mixture of normal distributions, $\frac{1}{M}{\sum }_{m=1}^M\phi \left(\Phi \left(\frac{\xi -{\overline{x}}_N^{\ast m}}{s_N^{\ast m}}\right),\tau \left({\overline{x}}_N^{\ast m},s_N^{\ast m},\xi \right)\right)$

• PMDA-2: an importance-weighted mixture of normal distributions, ${\sum }_{m=1}^{M}w\left(x_{n+1}^{\ast m},\dots ,x_N^{\ast m}\right)\phi \left(\Phi \left(\frac{\xi -{\overline{x}}_N^{\ast m}}{s_N^{\ast m}}\right),\tau \left({\overline{x}}_N^{\ast m},s_N^{\ast m},\xi \right)\right)$

There are at least two advantages to working with our simple example above. First, we can simulate from the true posterior distribution of the missing data (no MCMC approximation is necessary). It is in fact the posterior predictive distribution based on the n completely observed data points. Second, we can generate datasets for which we know that the distributional assumptions hold. Therefore any differences between the methods must be due to their actual properties as estimators and simple Monte Carlo variability due to the generation of datasets and the Monte Carlo sampling required of the methods, rather than to an incorrect data model or difficulties with generating samples from the posterior distribution.

We simulated 10,000 datasets with 150 observations and 20% missingness. We let ξ = −1.96. In order to reduce Monte Carlo variability as much as possible, missing observations were generated using the same uniform random variables across the four methods and the inverse-CDF transform method. Also, an imputed data set with a smaller number of copies was always taken from a subset of the corresponding imputed set with a larger m.

We can evaluate our method from two perspectives. First, we can treat the imputation procedures as Bayesian approximations to frequentist confidence sets. In that case, we are interested in the frequentist coverage properties of our estimator and interval, i.e. whether the constructed intervals contain the true value of θ over repeated datasets with the correct relative frequency. Of course, coverage is not the only concern. We also evaluate the average length of the interval and its variability. In general, we want to reach the correct coverage probability with the shortest interval possible.

The second perspective from which we can evaluate our proposed imputation methods is as an approximation to the true Bayesian posterior interval. We will focus on the Bayesian posterior coverage of our intervals, i.e. the amount of the true posterior distribution covered by our interval resulting from the imputation procedures. Again, we must take into account the length of our intervals, in that we want to have the shortest interval possible that completely covers the true Bayesian posterior interval.

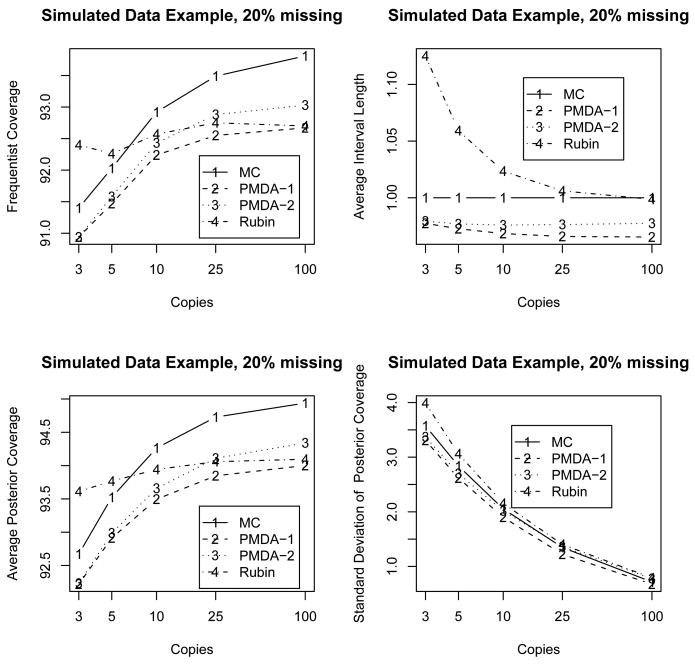
From a frequentist perspective, we focus on the performance of one application of our procedure to a number of simulated datasets. We generated 10,000 datasets from a normal distribution with mean zero and variance 1. For each dataset, we applied each of the imputation methods listed above and calculated the length and coverage of the resulting 95% confidence intervals. Figure 1 shows the estimated coverage probabilities for each of the four methods considered.

Figure 1.

Simulation results for estimation of the lower tail probability, Φ(ξ = −1.96), of a normal distribution for simulated normal datasets with 20% missing where results are the average over 10,000 random datasets. The top left figure contains the estimated frequentist coverage probabilities of the associated 95% intervals. The top right figure contains average interval lengths relative to the 95% confidence interval length for the mixture method with draws from the true posterior distribution (MC). The lower left figure contains estimated posterior coverage probabilities for 95% confidence intervals for the lower 2.5-th percentile, Φ(ξ = −1.96). The lower right figure contains the standard deviation for observed interval lengths relative to the 95% confidence interval length for the mixture method with draws from the true posterior distribution (MC).

The coverage probabilities for all 95% confidence intervals lie between 91% and 94%. For M = 3 and M = 5 copies, Rubin's t-method has the best coverage of 92.5%, which is 1 or 1.5% higher than other cases. However, the cost of that coverage is a longer interval. The top-right plot in Figure 1 shows the relative length of the credible/confidence intervals for the various methods. With 20% missing data, Rubin's method yields intervals that are over 10% longer than the standard Monte Carlo intervals when m = 3.

Frequentist coverage of the true value is not the only consideration, at least from a Bayesian viewpoint. We also consider the coverage of the true underlying posterior density of the tail probability of interest. If we view all four imputation methods as attempts to approximate the true underlying posterior density of the population tail probability, then we can examine the amount of posterior probability allocated to the true Bayesian 95% credible interval.

The bottom-left plot in Figure 1 shows the posterior coverages, which range from 92–95%, for the four imputation methods. The posterior coverage of Rubin's method levels off more quickly, which is not surprising as the mixture-based estimation methods are more directly trying to estimate the features of the underlying posterior distribution, allowing for greater posterior coverage by the approximations via a mixture of normals. The variability of the posterior coverage of Rubin's method is greater, as illustrated by the bottom-right plot of Figure 1, despite the fact that its average coverage is slightly larger. When considered closely, this is likely the case because, for small numbers of copies, the three imputation statistics of interest, (Q̄, Ū, B̄), will not be particularly robust to “extreme” copies of the missing data. The posterior density estimate is only one t distribution based on those three imputation statistics, so any large fluctuation in the summaries could cause a large fluctuation in the t approximation. The mixture approach has the advantage that such “extreme” copies will receive weight of only 1/M in the density approximation.

As pointed out by a reviewer, to refine the inference procedure, one could first construct a confidence interval for the logit transformed θ and then inversely transform the endpoints. The advantage of such an approach is that the asymptotic normality emerges faster in the transformed scenario than in the untransformed one. We did this and obtained equivalent outcomes to that of conducting direct inferences with θ̂. With the improved asymptotic normality in the transformed scenario, the coverage probabilities for all procedures improved by about 2-3%. For M = 3, 5, and 10 copies, the improved coverage probabilities for Monte Carlo and the two mixture approaches now vary between 93-94% while the coverage probabilities for Rubin's t now reach 96%. The patterns in the relative lengths of intervals are similar to those given in Figure 1: the two mixture approaches continue to give the shortest intervals, while the relative average lengths of Rubin's method to those of the standard Monte Carlo intervals increase slightly from 15%, 6% and 3% for M = 3, 5, and 10 to 17%, 8% and 6%, respectively.

4 Example: Missing data in Health-Related Quality of Life research

4.1 The model

In this section, we present a more complicated missing data example. Factor analysis models have been widely used by researchers in the social and health sciences for complex relationships between observed measurements via latent constructs. In the usual factor analysis setting, one observes a p–dimensional vector of responses, y_i = (y_i1, …,y_ip) for each of n observations (i = 1.,…n).

The factor analysis model is

$$y_i=\mu +\Lambda {\omega }_i+{\epsilon }_i$$

where μ is a (p × 1) mean vector, Λ is a (p × q) matrix of factor loadings, ω_i is a (q × 1) vector of latent construct measures, and ε_i is a vector of multivariate normal errors. The vector ω_i is typically assumed to be multivariate normal with variance-covariance matrix R; for simplicity, we will assume that R = I_q×q. The model errors, ε_i, represent variability unexplained by the latent factor structure and are assumed to be multivariate normal with diagonal variance-covariance matrix D, where diag $\left(D\right)=\left({\sigma }_1^2,\dots {\sigma }_p^2\right)$. One can assess the relative “uniqueness” of the variables through the ${\sigma }_j^2$ parameters, i.e. the larger the value of ${\sigma }_j^2$ parameter, the less that variable is explained by the factor model.

Several practical issues arise when utilizing factor analysis for either exploratory or confirmatory analyses, particularly when using Bayesian methods. First, the factor loadings, Λ, typically have to be constrained in some way in order for the loadings to be identifiable. We follow Lopes and West (2004) and use the approach of Geweke and Zhou (1996) to guarantee identifiability of the factor loadings by restricting Λ_kk > 0 and Λ_jk = 0 for j < k. Our restrictions in this context are slightly artificial, but we use them in order to ensure that the copies from a fully Bayesian analysis are compatible with the complete data factor analysis procedure.

Even with this restriction it is difficult to make inference for the factor loadings, Λ_jk. For example, although one can use asymptotic estimates via numerical differentiation to obtain standard error estimates for the model parameters, the calculation can be difficult and numerically unstable. Resampling approaches such as the jackknife and bootstrap are often used in place of difficult numerical methods. We also use the bootstrap approach here to obtain the estimated standard errors for the factor loadings. Although the loadings are asymptotically normal in theory, the convergence of its distribution to normality can be quite slow.

In the presence of missing data, there is no freely available software that can be used for factor analysis. Certain commercial software packages (e.g. M-PLUS and LEM) allow for factor analyses with missing data, but these packages can be expensive and require the user to learn a new software package. Here we assume that the user has access to readily available software that carries out complete data factor analyses, but does not implement a special purpose proper EM algorithm for the incomplete data.

4.2 The data

Systemic sclerosis (SSc) is a debilitating inflammatory tissue disease that affects over 110,000 people in the United States and Canada. The population it afflicts is similar to the populations affected by other rheumatic diseases, mostly women and patients over the age of 55, although it can appear in severe forms in males and younger patients. The most common manifestations of the disease are finger ulcers and thickening and hardening of skin tissue in the extremities. In the more severe forms, the disease can begin to inflame organ tissues. The disease can causes significant damage to organs in the gastrointestinal tract or to lung.

The data we consider here were obtained from the Canadian Scleroderma Research Group (CSRG) patient registry. One of the primary research objectives of the CSRG is to quantify the impact of the disease on patients' quality of life and general overall health. There are currently 17 rheumatologists in 11 hospitals across 9 provinces collecting data for the CSRG patient registry. The registry began collecting data in 2003 and currently over 800 patients have been added to the registry, many with three or four physician visits over a five year interval.

Missing data presents a problem for researchers using the CSRG registry, many of whom have limited limited access to statistical expertise. The CSRG registry presents a textbook example of the situation described by Rubin (1987) where many researchers who are not specialists in statistical methodology will want to conduct a wide variety of analyses with the same dataset.

The SF-36 Quality of Life questionnaire is one of the most popular instruments for measuring patient quality of life (Ware and Gandek 1998). Factor analysis has been used extensively in the analysis of quality of life data and of the SF-36 itself (Ware et al. 1998; Keller et al. 1998; Jomeen and Martin 2005; Wu et al. 2007). The SF-36 manual (Ware and Kosinski 2001) proposes a two-factor structure for the 36 items on the questionnaire. We will examine only the data from the higher order structure of 8 component subscales. These eight subscales represent eight hypothesized domains of functioning: physical functioning (PF), role physical (RP), bodily pain (BP), general health (GH), vitality (VT), social functioning (SF), role limitations due to emotional problems, and mental health (Mental Health). The 36 items from the questionnaire are used to compute a score for each of the subscales and then the subscales are normalized so that the mean population score is 50 with a standard deviation of 10.

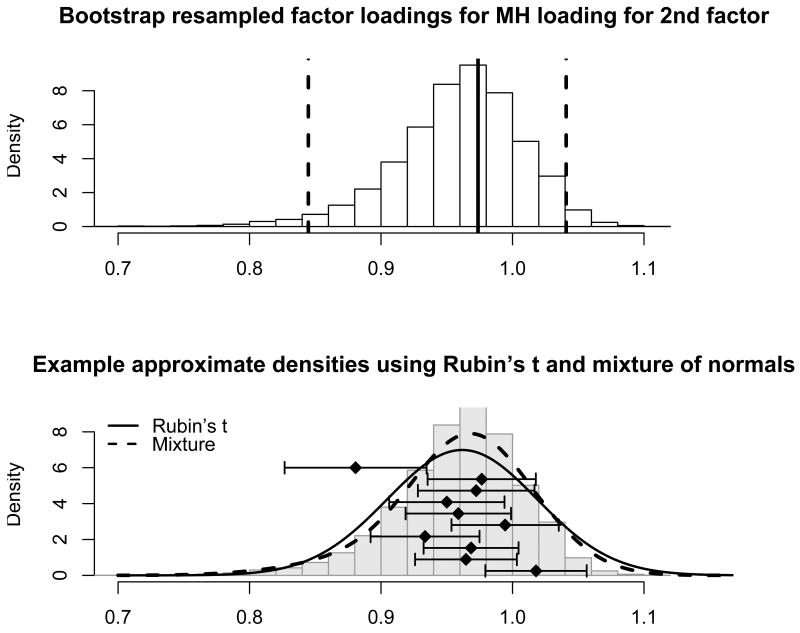
The CSRG registry contains little missing data for the SF-36. We have restricted the data set to limited and diffuse SSc patients with disease duration of 15 years or less who have complete information for the SF-36; there are 573 such subjects. We selected 230 subjects at random from the 573 and have made their subscale score for Mental Health and Role limitations due to emotional problem scores missing; the fraction of observations with missingness is approximately 40%. We focus our analyses on one of the factor loadings for the second factor in a factor analysis model that assumes two latent factors following the same structure as suggested by the original SF-36 authors. The top half of Figure 2 shows the resampled incomplete data maximum likelihood estimates of the Mental Health factor loading for the second factor. We see that the incomplete data sampling distribution is left skewed, and so the asymptotic normal approximation might not be valid due to the missing observations.

Figure 2.

Histogram of 5,000 bootstrapped maximum likelihood estimates for the Mental Health loading on the second latent factor for the SF-36 dataset with missingness. The maximum likelihood estimates were obtained via the EM algorithm. The bottom figure shows the same histogram from the top figure with density estimates using Rubin's t (solid curve) and mixture (dashed curve) summaries. The diamonds represent 10 complete data estimates from 10 selected copies with error bars for ±1 complete data standard error.

4.3 Simulation details

We examine four possible ways of generating copies of the missing data, namely:

• proper imputation via draws from the posterior distribution generated via Gibbs sampling (FB),

• proper imputation via single multivariate normal distribution and data augmentation (MVN),

• improper imputation from the maximum likelihood estimates via the EM algorithm for the factor analysis model with missing data (EM), and

• improper imputation from the maximum likelihood estimate of the population covariance matrix (EM-MVN).

The FB imputations were generated via a Gibbs sampling algorithm. We obtained 49,000 copies of the complete data, from a sample of 50,000 with the first 1,000 discarded for burn-in. From these 49,000 copies, we randomly sampled 250 copies to use for simulation purposes. The MVN imputations were drawn via a Gibbs sampler using the norm package in the R statistical language. The EM imputations were drawn from the full conditional distribution of the missing data given the observed data and the maximum likelihood estimates for the factor analysis model. The EM-MVN imputations were drawn from the full conditional distribution for the missing data given the observed data and the maximum likelihood estimates for the unrestricted multivariate normal model.

For each copy generated by each method, we used an EM algorithm to obtain complete data maximum likelihood estimates and EM with 100 bootstrap replications to estimate the complete data standard error. This resulted in 250 complete data estimates and within-copy standard errors for each imputation generation method. We then performed 100 replications of sampling 3, 5, 10 and 25 copies from the 250. The practices described in Section 3 for the purpose of minimizing pure Monte Carlo variability are carried out here. The same copies were used in every summary method for each imputation method. For the mixture summary method, we used the median of the estimated mixture density as the point estimate. One cannot calculate the exact importance weights for the PMDA-2 method for this example, because the complete data posterior distribution for the factor analysis model p(θ∣y, z) cannot be calculated in closed form. We instead used the Schwarz approximation to the complete-data integrated likelihood in the numerator of the importance weights.

Little and Rubin (2002) pointed out that the bootstrap may be inaccurate when the model is unidentifiable, which can be the case for factor analysis models. However, this does not seem to be an issue here. because the restrictions on the factor loadings ensure that they are identifiable. In all our bootstrap replications, there were no instances where the method failed to find a solution.

4.4 Results

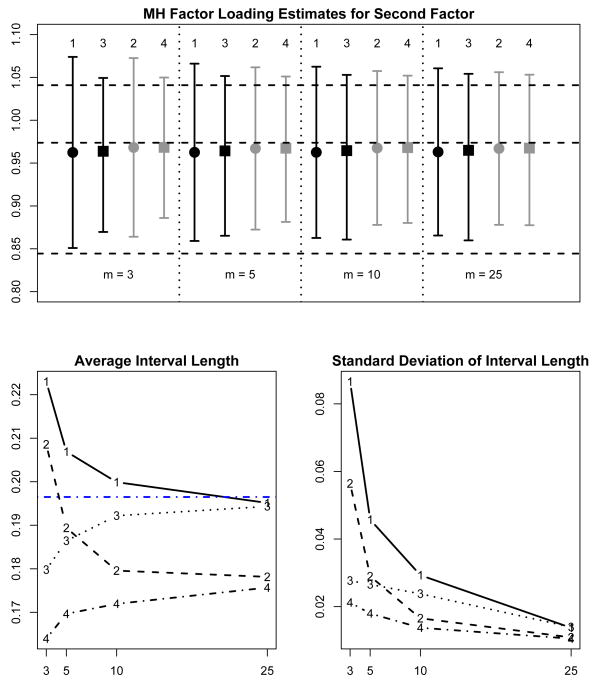
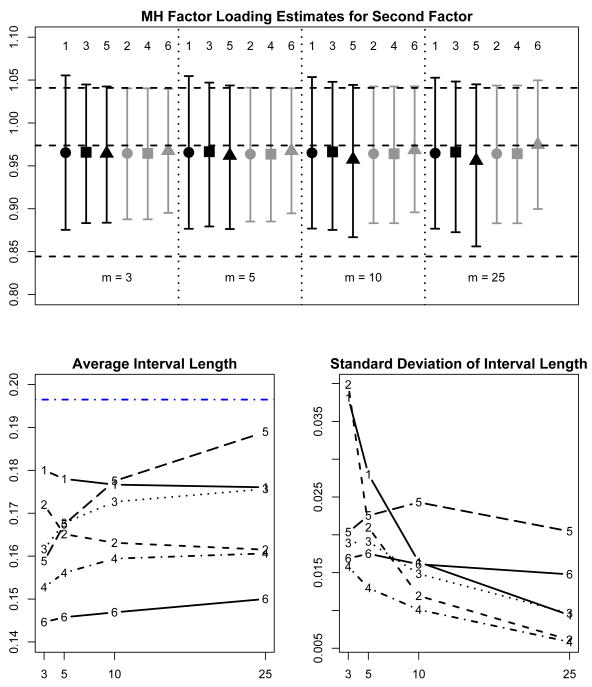
Figure 3 summarizes the results of 100 replications of imputing 3, 5, 10, and 25 copies using the two proper imputation methods (FB and MVN) and the two versions of summarizing the outcomes with imputations (Rubin's t and mixture of normals). The top figure shows the average over the 100 replications of the point estimates and 95% confidence limits for each method of summarizing for 3, 5, 10, and 25 copies.

Figure 3.

Quality of Life example: 100 replications of multiple imputation for two methods of summarizing (Rubin's t [1, 2] and mixture of normals [3,4]) using copies of missing data generated from two different models (from the target factor analysis posterior distribution [1,3] and general multivariate normal [2,4]). The top subfigure shows the average of the estimates for the Mental Health loading for the second latent factor (square or circle) and the associated 95% confidence limits (error bars) for the various methods of summarizing and generating for m = 3, 5, 10, and 25 copies. The horizontal dashed lines show the maximum likelihood estimate and 95% confidence limits obtained from the non-parametric bootstrap. The lower left subfigure shows the average interval width and the lower right subfigure shows the standard deviation of the interval widths. In the lower left subfigure, the horizontal dashed line is the interval width from the bootstrap sample.

The interval lengths and the 95% confidence limits do vary significantly across the various situations. The lower two subfigures show more clearly the difference between the t- and mixture summary methods. In general, the t-intervals are longer than the mixture summary intervals on average and the interval lengths are also more variable.

We first focus on the results for the copies drawn from the fully Bayesian factor analysis model (FB), which correspond to the results labelled 1 (t-summaries) and 2 (mixture summaries). For 3, 5, 10, and 25 copies respectively, the t-intervals are 25%, 11%, 4%, and 0.4% wider on average than the mixture summary intervals. The t-intervals are much more variable in width than the mixture summary intervals, as we also observed in the simulation study. The standard deviations of the t-intervals are 3.1, 1.7 and 1.2 times larger than the standard deviations of the mixture summary intervals for 3, 5 and 10 copies respectively. For 25 copies, the t-intervals and mixture summary intervals are roughly equal in variability and both are similar in length to the bootstrap interval from the EM implementation for the incomplete data set.

The pattern is similar for copies drawn from the posterior for the general multivariate normal model (MVN). The t-intervals are 27%, 11%, 4%, and 1% wider on average than the mixture intervals for 3, 5, 10, and 25 copies, while the t-interval widths are 2.7, 1.6, 1.2 and 1.0 times more variable. We also see that the intervals for the MVN copies are narrower than the intervals for copies generated from the fully Bayesian model.

In summary, multiple imputations from the full posterior distribution are theoretically more accurate, and correspond more closely to the bootstrap than multivariate normal imputations with larger numbers of copies. With fully Bayesian imputations, the mixture-based intervals are substantially narrower than the t-based intervals for small numbers of copies, converging when the number of copies reaches 25. The mixture-based intervals are also less variable than the t-based intervals for small numbers of copies, again converging when the number of copies reaches 25. Overall, fully Bayesian imputations with a mixture summary worked best in this example, particularly with 10 or fewer copies.

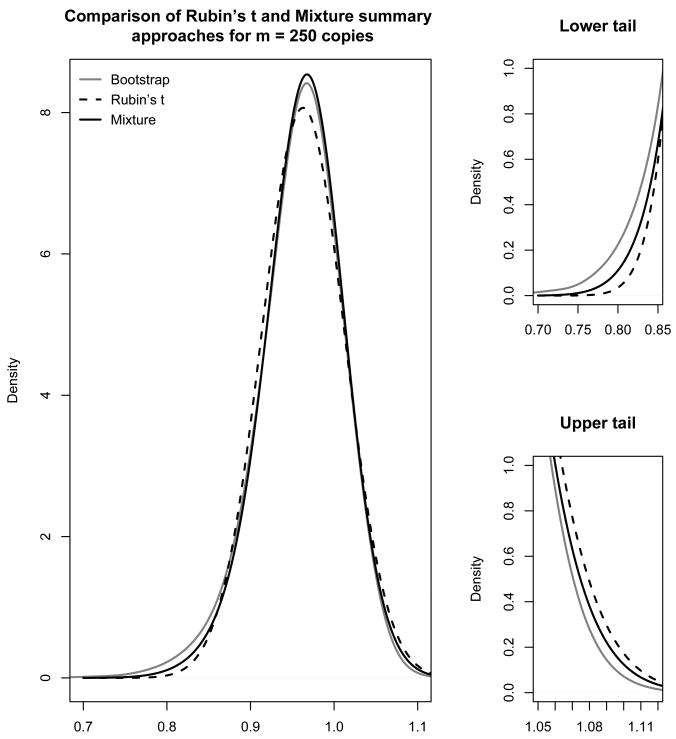
Figure 4 shows density estimates using the t- and mixture summary methods for all 250 complete data analyses generated from the posterior distribution for the factor analysis model. We compare these to the density estimate from the 5,000 nonparametric bootstrap resampled estimates using the EM algorithm for the incomplete data. With 250 copies, we can see that the mixture summaries are performing better than the t-summary because of the ability to model the slight skew in the sampling distribution of the factor loadings. The subfigures on the right side of the figure show that the t-summary underestimates the lower tail of the sampling distribution and overestimates the upper tail. In particular, in comparison to the mixture summary, the t-summary underestimates the area under the curve of the left tails to the 2.5th and 5th percentiles by 27% and 14%, while it overestimates the equivalent right tails by 19% and 34% respectively. This may be due to the restriction of the t-summary to a symmetric sampling (or posterior) distribution.

Figure 4.

Posterior density estimates for the Mental Health loading for the second factor using the Rubin's t and the PMDA-1 mixture summary approaches when imputing via 250 copies drawn from the Bayesian posterior distribution for the factor analysis model. The gray solid line is the non-parametric density estimate from 5000 bootstrap samples, the black dashed line is the summary using Rubin's t-distribution, and the black solid line is the summary using a mixture of normals.

We observe a slight bias in the estimation of the 95% confidence limits, although it is clear that the mixture summary density is less biased than the t-summary density. The bias is likely due to two reasons. First, the complete data posteriors for the factor loading, although less skewed, still exhibit some skewness. This would prevent the mixture of normals with a small number of copies from being able to capture the skewed tail behavior. Second, the posterior distribution for the copies drawn from the fully Bayesian posterior distribution would depend on the priors used and different priors had some effect on the shape and location of the posterior distribution (and thus on the copies of the missing data generated).

Figure 5 shows the results for the two improper copy generation methods (EM and EM-MVN) for three different summary methods (t-summary, mixture summary [PMDA-1], and importance weighted mixture summary [PMDA-2]). For the data generated using the EM approach, the t- and PMDA-1 summary approaches behave similarly to the proper imputation methods. The t-intervals are 11%, 6%, 2%, and 0.2% wider on average than the corresponding PMDA-1 intervals, for 3, 5, 10 and 25 copies respectively. The standard deviations of the t-interval widths are 2.0, 1.5, 1.1 and 1.0 times the standard deviations of the PMDA-1 interval widths. So once again the t-intervals are less stable than the equally weighted mixture summary intervals. Both summary methods yield intervals that are much narrower on average than either of the proper imputation methods.

Figure 5.

100 replications of multiple imputation for three methods of summarizing (Rubin's t [1, 2], PMDA-1 [3,4], and PMDA-2 [5,6]) using copies of missing data generated from two different models (from a full conditional distribution based on the incomplete data factor analysis MLE [1,3,5] and the MLE from the general multivariate normal model [2,4,6]. The top subfigure shows the average of the estimates for the Mental Health loading for the second latent factor (square or circle) and the associated 95% confidence limits (error bars) for the various methods of summarizing and generating for m = 3, 5, 10, and 25 copies. The dashed lines across the width of the plot locate the maximum likelihood estimate and 95% confidence limits obtained from the non-parametric bootstrap. The lower left subfigure shows the average interval length and the lower right subfigure shows the standard deviation of the interval length. In the lower left subfigure, the horizontal dashed line is the interval length from the bootstrap sample.

We have also included results for an importance weighted mixture summary. The purpose of the importance weights is to correct for the fact that we are sampling not from the true posterior distribution of the missing data, but instead from an approximation that uses the incomplete data maximum likelihood estimate. When the imputations were improperly generated, only PMDA-2 gave acceptable outcomes. Even for PMDA-2, a moderate to large (m = 10 or 25) number of imputation copies is needed to achieve roughly correct coverage. The average interval widths and stability of the method are comparable to those from FB-imputations and a mixture summary. A disadvantage of this approach is that more copies are needed.

For the final method of copy generation, EM-MVN, we see similar behavior to what was observed for the EM generated copies, in that the intervals have below nominal coverage on average, regardless of the summary method used.

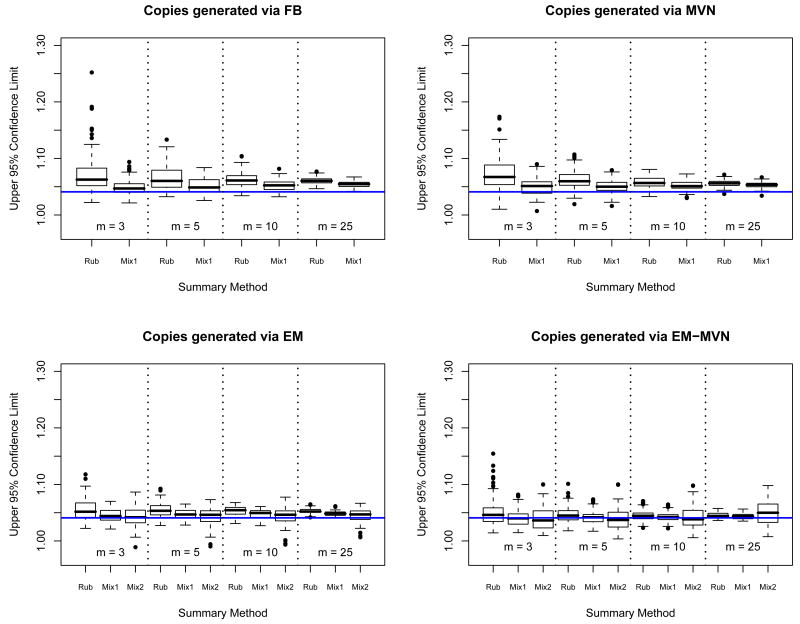
The boxplots in Figure 6 show the upper confidence limits for all 100 replications for every copy generation and summary method combination. The t- and equally weighted mixture summaries both show decreasing variability in their upper confidence limit as the number of copies increases, but the mixture summary shows less variability and less bias in estimating that upper confidence limit. The upper confidence limit for the t-intervals is quite variable for 3, 5, and 10 copies, in some cases providing misleading confidence bounds. We see that the importance weighted mixture summaries perform better than the others for the EM and EM-MVN generated copies, but at the cost of higher variability.

Figure 6.

100 replications of 95% upper confidence limits for the three methods of summarizing (Rubin's t [Rub], PMDA-1 [Mix1], and PMDA-2 [Mix2]) using copies of missing data generated from four different models (from the target factor analysis posterior distribution [FB], full conditional distribution conditional on MLE [EM], general multivariate normal [MVN], and full multivariate normal conditional distribution conditional on MVN MLE [EM-MVN]). The solid line represents the estimate of the upper confidence limit from 5000 bootstrap samples.

5 Discussion

This paper proposes a new direction for using multiple imputations for the analysis of datasets with missing data. We have shown through simulation in two examples that the usual t-distribution summary with a small number of copies, as suggested in previous multiple imputation literature, may be unstable and yield confidence intervals that are much wider than necessary. We have proposed an alternative way of summarizing the inference from multiple imputations using a mixture of normals. In our simulations and example, this gave narrower intervals and more stable inference. Our methods require no extra input from the imputer, unlike some other methods that have been proposed.

One could conclude that it is possible to improve on widely accepted methods for summarizing the inference from multiple imputation, such as Rubin's t. Because of the extra variability introduced in the sampling of the missing observations from their true posterior distribution and the restriction to using t-distributions for inference, multiple imputation with small to moderate numbers of copies can provide inefficient or even incorrect inferences. Robins and Wang (2000) looked at this problem in detail. Schafer and Schenker (2000) cited this difficulty as a potential reason for using conditional mean imputation. Carabin et al. (2001) gave an example of the failure of multiple imputation to yield useful confidence intervals in the context of censored regression models.

Arguments similar to ours were made by Fay (1996) and Rao and Shao (1996) in their discussions of Rubin (1996). Rubin's t estimators, in an effort to provide enough coverage, must inflate the variance of the complete data functionals to the point where the estimates of the observed data functional become very variable themselves. The estimated variability is often correct, but if the estimated variability is too high then the estimate could be of little use. It is important to note that the results investigated here apply only to small to moderate numbers of copies.

Our approach could be viewed as a compromise between Rubin's methods and the single imputation methods of Fay (1996) and Rao and Shao (1996). These single imputation methods use sophisticated methods to account for the uncertainty in parameter estimates while relying on the stability of a single, unbiased mean imputation to avoid the problems that multiple imputation has when drawing from the true posterior distribution. If one uses importance sampling methods like those discussed here, approximately accurate estimates of variability can be obtained.

We have approximated the complete-data posterior distribution by a normal distribution, yielding an approximation of the full posterior by a mixture of normals, and found it to work well in simulations and an example. It is possible that an even better approximation would be provided by a t distribution, leading to an approximation of the posterior distribution by a mixture of t distributions. This would also be more complicated, and an assessment of the resulting tradeoff between complexity and performance would be a worthy topic for further research. It should also be noted that doing inference on a scale where the normal approximation to the posterior is better is generally a good idea.

In our experiments we found that good results are obtained by most methods with large numbers of imputations. Thus the improvement from our methods over existing ones are likely to be greatest when the number of copies is small. This is most often the case when the copies are provided by the imputer rather than produced by the user. Increasing the number of copies produced is a good idea in any event when it is computationally feasible.

The basic idea of approximating the posterior distribution in missing data cases by a mixture of normals applies quite generally, but we have demonstrated it here only for scalar estimands. The posterior distribution of a multivariate estimand can be approximated by our method by simply simulating values of the parameters from the estimated mixture of multivariate normal distributions. Detailed assessment of the application of the method to multivariate estimands and testing problems is a topic for future research.

A free R software package called MImix that implements our methods is available at http://cran.r-project.org.